物理-有磁介质存在时的稳恒磁场(下)

第六章 磁介质一、选择题1、关于稳恒磁场的磁场强度H的下列几种说法中哪个是正确的（）A 、H 仅与传导电流有关。

B 、若闭合曲线内没有包围传导电流，则曲线上各点的H为零C 、若闭合曲线上各点的H均为零，则该曲线所包围传导电流的代数和为零D 、以闭合曲线L 为边缘的任意曲面的H通量均相等 答案：C2、磁介质有三种，用相对磁导率r μ表征它们各自的特性时（）A 、顺磁质r μ>0，抗磁质r μ<0，铁磁质r μ》1B 、顺磁质r μ>1，抗磁质r μ=1，铁磁质r μ》1C 、顺磁质r μ>1，抗磁质r μ<1，铁磁质r μ》1D 、顺磁质r μ>0，抗磁质r μ<0，铁磁质r μ>1 答案：C 3、用细导线均匀密绕成的长为l ，半径为a(l 》a)，总匝数为N 的螺线管通以稳恒电流I ，当管内充满磁导率为r μ的均匀磁介质后，管中任意一点（）A 、磁感应强度大小为B=r μμ0NIB 、磁感应强度大小为B=r μNI /lC 、磁场强度大小为H=0μNI/lD 、磁场强度大小为H=NI/l 答案：D 4、顺磁物质的磁导率（）A 、比真空的磁导率略小B 、比真空的磁导率略大C 、远小于真空的磁导率D 、远大于真空中的磁导率 答案：B 5、通电直长螺线管内的一半空间充满磁介r u ，在螺线管中，介质中与空气中相等的物理量是（） A 、B 1=B 2 B 、H 1=H 2 C 、M 1=M 2 D 、21ψψ= 答案：B6、图中所示的三条线分别表示三种不同磁介质的B-H 关系，表示顺磁质的是（）A 、第一条B 、第二条C 、第三条D 、无法判断 答案：B7、磁铁能吸引铁钉之类的小物体是由于（）A 、小物体是铁磁性的，被磁铁磁化，受到吸引力B 、小物体是顺磁性的，被磁铁磁化，受到吸引力C 、小物体是抗磁性的，被磁铁磁化，受到吸引力D 、磁铁和小物体都是顺磁性物质，相互吸引 答案：A 8、如图所示，一永磁环，环开一很窄的空隙，环内磁化强度矢量为M ，则空隙中P 点处的H的大小为（）A 、0μMB 、MC 、r μμ0MD 、0 答案：B9、如图所示，一根沿轴向均匀磁化的细长永磁棒，磁化强度为M，图中所标各点的磁感应强度是（）A 、0,3021===B M B B μ B 、M B B M B 0320121,μμ=== C 、0,,2130201===B M B M B μμ D 、0,21,30201===B M B M B μμ 答案：D10、在磁介质存在的情况下对安培环路定理=⋅⎰Ll d H()∑内L I 中，下述说法正确的是（） A 、∑I 是空间所有传导电流 B 、∑I 是穿过环路L 的传导电流和磁化电流C 、∑I 是穿过环路L 的传导电流D 、H只与传导电流有关 答案：C11、若已知铁磁质中某处的MB,，则该点处的磁场强度H必须满足的关系是（）A 、MB H-=μB 、HB0μ= C 、)(0M H B +=μ D 、HBμ= 答案：C12、在均匀各向同性的线性磁介质中（）A 、不论顺磁质或抗磁质B 总是与H 同向 B 、在顺磁质中，B 与H 同向，在抗磁质中B 与H反向C 、以闭合曲线为边界的同一曲面的B 通量与H 通量相等D 、通过任一闭合面的B 的通量与H通量不相等 答案：A13、在稳恒磁场中，有磁介质存在时的安培环路定理的积分形式是（）A 、=⋅⎰Ll d B ()∑内L I B 、=⋅⎰Ll d H()∑内L I C 、=⋅⎰Ll d H()∑内L I0μ D 、⎰⎰⎰⋅∂∂+=⋅SL S d t D I l d H答案：B 14、一均匀磁化的介质棒，、横截面半径为0.1米，长为1米，其总磁矩为3140安·米2，则棒中的磁化强度矢量M的大小为（）A 、105安/米B 、104安/米C 、98596⨯103安/米D 、103安/米 答案：A二、填空题1、一个绕有500匝导线的平均周长50cm 的细环，载有0.3A 电流时，铁芯的相对磁导率为600，（1）铁芯中的磁感应强度B 为 ；（2）铁芯中的磁场强度H 为 。

第8章 稳恒磁场 习题及答案6. 如图所示，AB 、CD 为长直导线，C B为圆心在O 点的一段圆弧形导线，其半径为R 。

若通以电流I ，求O 点的磁感应强度。

解：O 点磁场由AB 、C B、CD 三部分电流产生，应用磁场叠加原理。

AB 在O 点产生的磁感应强度为01=BC B在O 点产生的磁感应强度大小为θπμR I B 402=RIR I 123400μππμ=⨯=，方向垂直纸面向里CD 在O 点产生的磁感应强度大小为)cos (cos 421003θθπμ-=r IB)180cos 150(cos 60cos 400︒︒-=R Iπμ)231(20-=R I πμ，方向垂直纸面向里 故 )6231(203210ππμ+-=++=R I B B B B ，方向垂直纸面向里 7. 如图所示，两根导线沿半径方向引向铁环上的A ，B 两点，并在很远处与电源相连。

已知圆环的粗细均匀，求环中心O 的磁感应强度。

解：圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生，但∞A 和∞B 在O 点产生的磁场为零。

且θπθ-==21221R R I I 电阻电阻 1I 产生的磁感应强度大小为）（θππμ-=24101RI B ，方向垂直纸面向外 2I 产生的磁感应强度大小为θπμRIB 4202=，方向垂直纸面向里 所以， 1)2(2121=-=θθπI I B B 环中心O 的磁感应强度为0210=+=B B B8. 如图所示，一无限长载流平板宽度为a ，沿长度方向通过均匀电流I ，求与平板共面且距平板一边为b 的任意点P 的磁感应强度。

解：将载流平板看成许多无限长的载流直导线，应用叠加原理求解。

以P 点为坐标原点，垂直载流平板向左为x 轴正方向建立坐标系。

在载流平板上取dx aIdI =，dI 在P 点产生的磁感应强度大小为x dI dB πμ20=dx axIπμ20=，方向垂直纸面向里 P 点的磁感应强度大小为⎰⎰+==a b b x dx a I dB B πμ20bab a I +=ln 20πμ 方向垂直纸面向里。

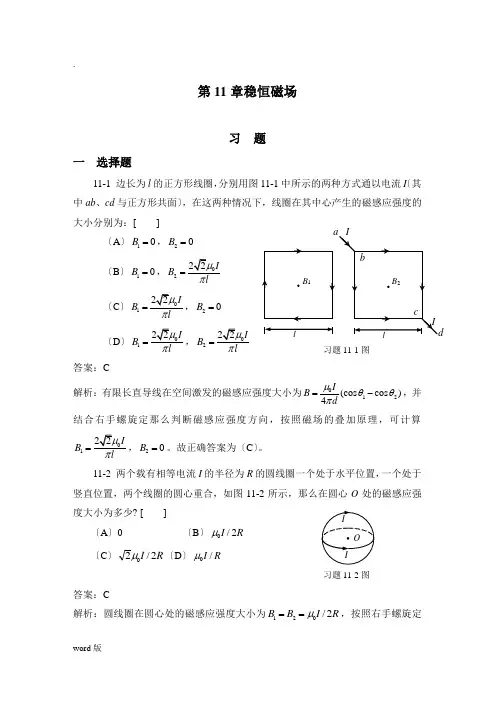
第11章稳恒磁场习 题一 选择题11-1 边长为l 的正方形线圈，分别用图11-1中所示的两种方式通以电流I 〔其中ab 、cd 与正方形共面〕，在这两种情况下，线圈在其中心产生的磁感应强度的大小分别为：[ ]〔A 〕10B =，20B = 〔B 〕10B =，02IB lπ= 〔C〕01IB lπ=，20B = 〔D〕01I B l π=，02IB lπ=答案：C解析：有限长直导线在空间激发的磁感应强度大小为012(cos cos )4IB dμθθπ=-，并结合右手螺旋定那么判断磁感应强度方向，按照磁场的叠加原理，可计算01IB lπ=，20B =。

故正确答案为〔C 〕。

11-2 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置，一个处于竖直位置，两个线圈的圆心重合，如图11-2所示，那么在圆心O 处的磁感应强度大小为多少? [ ]〔A 〕0 〔B 〕R I 2/0μ〔C 〕R I 2/20μ〔D 〕R I /0μ 答案：C解析：圆线圈在圆心处的磁感应强度大小为120/2B B I R μ==，按照右手螺旋定习题11-1图习题11-2图那么判断知1B 和2B 的方向相互垂直，依照磁场的矢量叠加原理，计算可得圆心O处的磁感应强度大小为0/2B I R =。

11-3 如图11-3所示，在均匀磁场B 中，有一个半径为R 的半球面S ，S 边线所在平面的单位法线矢量n 与磁感应强度B 的夹角为α，那么通过该半球面的磁通量的大小为[ ]〔A 〕B R 2π〔B 〕B R 22π〔C 〕2cos R B πα〔D 〕2sin R B πα 答案：C解析：通过半球面的磁感应线线必通过底面，因此2cos m B S R B παΦ=⋅=。

故正确答案为〔C 〕。

11-4 如图11-4所示，在无限长载流直导线附近作一球形闭合曲面S ，当曲面S 向长直导线靠近时，穿过曲面S 的磁通量ΦB 将如何变化？[]〔A 〕Φ增大，B 也增大〔B 〕Φ不变，B 也不变 〔C 〕Φ增大，B 不变〔D 〕Φ不变，B 增大 答案：D解析：根据磁场的高斯定理0SBdS Φ==⎰，通过闭合曲面S 的磁感应强度始终为0，保持不变。

第十二章稳恒磁场本章研究磁场的产生，磁场的基本规律，磁场与介质的相互作用。

磁感应强度是描述磁场的基本物理量。

“高斯定理”和安培环路定理是反映磁场性质的基本规律。

磁场对运动电荷的作用力——洛仑兹力——和磁场对载电流导线的作用——安培力和力矩，在许多领域均得到广泛应用。

在磁场作用下，磁介质发生磁化，磁化了的磁介质又会反过来影响磁场的分布。

我们还将讨论磁场和介质的这种相互作用规律并特别介绍有很大实用价值的铁磁质的特性。

§12－1磁场磁感应强度一、基本磁现象我国是世界上最早认识磁性和应用磁性的国家，早在战国时期（公元前300年），就已发现磁石吸铁的现象。

11世纪（北宋）时，我国科学家沈括创制了航海用的指南针，并发现了地磁偏角，地球的N极在地理南极附近百极在地理北极附近。

中国古代四大发明引为现代人的骄傲。

天然磁铁和人造磁铁都称永磁铁。

永磁铁不存在单一的磁极。

磁铁的两个磁极，不可能分割成为独立存在的N极和S极。

但我们知道，有独立存在的正电荷或负电荷，这是磁极和电荷的基本区别。

这与磁产生的机理有关。

历史上很长一段时期，人们对磁现象和电现象的研究都是彼此独立进行的。

1820年丹麦物理学家奥斯特实验发现，放在通有电流的导线周围的磁针，会受到力的作用而发生偏转，如图图4－14－1所示，其转动方向与导线中电流的方向有关。

这就是历史上著名的奥斯特实验，它第一次指出了磁现象与电现象之间的联系。

同年法国科学家安培发现，放在磁铁附近的载流导线及载流线圈，也会受到力的作用而发生运动，如图4－2，其后实验还发现，载流导线之间或载流线圈之间也有相互作用力。

（a）（b）图4－2例如把两个线圈面对面挂在一起，当两电流的流向相同时，两线圈相互吸引，如图4－3（a），当两电流的流向相反时，两线圈相互排斥，如图4－3（b）。

（a ） （b ）图4－3电子射线束在磁场中路径发生偏转的实验，进一步说明了通过磁场区域时运动电荷要受到力的作用，如图4－4所示。

磁介质一、 选择题1、 关于稳恒磁场的磁场强度H 的下列几种说法中哪个是正确的（） 答案：CA 、H 仅与传导电流有关。

B 、若闭合曲线内没有包围传导电流，则曲线上各点的H为零 C 、若闭合曲线上各点的H 均为零，则该曲线所包围传导电流的代数和为零D 、以闭合曲线L 为边缘的任意曲面的H 通量均相等2、 磁介质有三种，用相对磁导率r μ表征它们各自的特性时（） 答案：CA 、顺磁质r μ>0，抗磁质r μ<0，铁磁质r μ>>1B 、顺磁质r μ>1，抗磁质r μ=1，铁磁质r μ>>1C 、顺磁质r μ>1，抗磁质r μ<1，铁磁质r μ>>1D 、顺磁质r μ>0，抗磁质r μ<0，铁磁质r μ>13、 用细导线均匀密绕成的长为l ，半径为a(l >>a)，总匝数为N 的螺线管通以稳恒电流I ，当管内充满磁导率为r μ的均匀磁介质后，管中任意一点（） 答案：DA 、磁感应强度大小为B=r μμ0NIB 、磁感应强度大小为B=r μNI /lC 、磁场强度大小为H=0μNI/lD 、磁场强度大小为H=NI/l4、 顺磁物质的磁导率（） 答案：BA 、比真空的磁导率略小B 、比真空的磁导率略大C 、远小于真空的磁导率D 、远大于真空中的磁导率5、 通电直长螺线管内的一半空间充满磁介r u ，在螺线管中，介质中与空气中相等的物理量是（） A 、B 1=B 2 B 、H 1=H 2 C 、M 1=M 2 D 、21ψψ=答案：B6、 图中所示的三条线分别表示三种不同磁介质的B-H 关系，表示顺磁质的是（）A 、第一条B 、第二条C 、第三条D 、无法判断答案：B 7、 磁铁能吸引铁钉之类的小物体是由于（）A 、小物体是铁磁性的，被磁铁磁化，受到吸引力B 、小物体是顺磁性的，被磁铁磁化，受到吸引力C 、小物体是抗磁性的，被磁铁磁化，受到吸引力D 、磁铁和小物体都是顺磁性物质，相互吸引 答案：A8、如图所示，一永磁环，环开一很窄的空隙，环内磁化强度矢量为M ，则空隙中P 点处的H的大小为（）A 、0μMB 、MC 、r μμ0MD 、0答案：B 。

第六章稳恒磁场
1、主要的概念：电流强度，磁感应强度，电流元，磁感应线，磁通量，磁化和磁介质。

2、主要的了解定律：磁场叠加原理，毕奥—萨伐尔定律（推导一些特殊载流导线和运动电荷的B），磁场中的高斯定律，安培环路定律。

（了解定理的导出以及其重要的物理意义）
3、主要计算：利用毕奥—萨伐尔定律、安培环路定理计算一些特殊载流导线产生的磁感应强度；安培力和洛伦兹力的计算；磁介质中的磁化，以及应用介质中的安培环路定理计算磁场强度矢量（H）和磁感应强度（B）。

4、重点内容：毕奥—萨伐尔定律、安培环路定理、磁场力、力矩；磁介质的磁化、介质中的安培环路定理。

2．磁场方程： 磁场高斯定理：
（表明磁场是无源场）
（表明磁场是有旋场）
掌握推导过程
*通过霍尔电压可以求得磁场和电流大小。

6. 均匀磁化的B 、H 、M 关系及表面磁化电流密度与磁化强度的关系
）
（M H B 0 +=μ H M m χ= m r 1χμ+=
B 代表 H 代表 M 代表
—
——m r 0χμμ 4.载流线圈的磁矩 3.电磁相互作用 B
l Id f d ⨯=2)磁场对载流导线的安培力
⎰⨯=l
B
l Id f 3)磁场对载流线圈的作用力矩 B
m M
⨯=4)5.霍耳电压
1)安培定律。