大学物理稳恒磁场解读
- 格式:doc
- 大小:306.00 KB
- 文档页数:13





山东轻院第十一章稳恒磁场山东轻院基本要求1.掌握磁感应强度的概念。
理解比奥-萨伐尔定律。
并能用其计算一些简单问题中的磁感应强度。
2.理解稳恒磁场的规律:磁场高斯定理和安培环路定理。
理解用安培环路定理计算磁感应钱度的条件和方法。
3.理解安培定律和洛仑兹力公式。
了解磁矩的概念。
能计算简单几何形状载流导体和载流平面线圈在均匀磁场或在无限长之载流导线产生的非均匀磁场中所受的力和力矩。
能分析点电荷在均匀电场和均匀磁场中的受力和运动。
山东轻院 内 容 提 要(1)一、磁感应强度1.磁场是只给运动电荷一作用力的场物质。
用试探运动电荷 在某场点所受磁力的两个极值 f max 和 0 来定义 。
v q B 的定义 B 大小: max qv f B 方向:运动正电荷受力为零时其速度的方向 (即小磁针静止时N 极的指向)山东轻院 2.磁场叠加原理⎰∑==B d B B B i i 或(2)在若干电流(或电流元)产生的磁场中,某点的磁感应强度等于每个电流(或电流元)单独存在时,在该点所产生的磁感应强度的矢量和。
3.磁感应强度通量⎰⎰⋅=ϕ=ϕs s m m s d B d (3)为通过磁场中某曲面的磁感应强度线数。
φm 为标量,但有正、负。
山东轻院二、比奥-萨伐尔定律: ——— 电流元的磁场(4)203044r e l Id r r l Id B d r⨯πμ=⨯πμ=式中, 表示稳恒电流的一个电流元l Id 270104--⋅⨯π=μA N 为真空的磁导率 表示从该电流元到场点的矢径( 为单位矢量) r r re r =物理辅导 山东轻院 矢量 的大小为B d 204r sin Idl dB θπμ=r (θ为 与 的夹角) l Id 的方向垂直于 和 组成的平面,并沿矢积 的方向,即 由经小于180o 的角转向 时的右螺旋前进方向。
B d r l d rl d ⨯l Id r 原则上,只要求得电流元的磁场 ,那么任意载流导线在某场点的磁感强度 ,即可由磁场叠加原理求得 B d B ⎰⎰⨯πμ==204r e l Id B d B r (见教材P131-P132例)物理辅导 山东轻院 三、反映稳恒磁场性质的基本方程1.磁场高斯定理0=⋅⎰S s d B(5)表明 磁力线为闭合曲线,磁场为无源场。



稳恒电流的磁场解读第五章稳恒电流的磁场一稳恒电流的磁场教学内容1.磁的基本现象(1)磁铁的性质(2)磁电联系(3)磁场(4)磁性起源2.磁感应强度(1)磁感应强度矢量(2)磁感应线3•毕奥一萨伐尔定律(1)毕奥一萨伐尔定律(2)磁感应强度叠加原理(3)毕奥一萨伐尔定律的应用4.磁场的高斯定理(1)磁通量(2)磁场的高斯定理5•安培环路定理(1)安培环路定理(2)安培环路定理应用6.磁场对运动电荷的作用(1)洛仑兹力(2)带电粒子在磁场中的运动(3)回旋加速器(4)汤姆逊实验质谱仪(5)霍尔效应7.磁场对载流导线的作用(1)安培力公式(2)均匀磁场对平面载流线圈的作用(3)平行无限长直导线间的相互作用说明与要求:1.本章主要研究电流激发磁场和磁场对电流及运动电荷的作用两部分内容。
2.本章重点是2、3、5节,难点是磁感应强度的概念及安培环路定理的物理意义及应用。
3.本章研究问题的方法与第一章类似,故在教学中应加强它们的比较。
、稳恒电流的磁场教学目标1.基本磁现象1.磁铁的性质知识:2.磁电联系3.磁场4.磁性起源1.磁铁的性质2.磁现象与电现象的联系理解:节次内容目标层次1 •磁场2 •物质磁性的起源2 •磁感应强度磁感应线1.B的定义2.B线3 •毕奥一萨伐尔定律1 .毕一萨定律2. B的叠加原理3 •毕一萨定律的应用知识:1 • B线的定义2.B线的特点3.B的单位理解:1 . B的定义及意义2. B的定义与E的定义的区别及原因知识:1 •电流元2.矢量矢积的表示及方向确疋3.0的数值及单位理解:1.毕一萨定律的数学表示式 2•毕一萨定律 得到的方法 3•毕一萨定律 中各量的意义 4 . B 的叠加原 理的含义 综合应用: 根据毕一萨定 律和磁场叠加 原理,通过求积 或求和的方法, 计算电流产生 的磁场1 .磁通量 知识:2 •磁场的高斯1. B的单位定理 2. B是代数量理解: 1 . B 的定义及 意义2. 磁场的高斯 定理的内容及4.磁通量磁场 的高斯定理意义3 •磁场高斯定理与电场高斯定理的区别5.安培环路定1.安培环路定简单应用:根据B的定义和B 线的性质,证明磁场高斯定理综合应用:根据B的定义和B 的叠加原理,计算 B 知识:理理 1 .培环路定理2.稳恒磁场的中I正负号的性质确定3 •应用安培环2.安培环路定路定理求B 理求B的条件理解:1.安培环路定理的内容及意义2.安培环路定理中B和1的意义3.I与B的对称性分布分析4 .稳恒磁场与静电场的区别简单应用:根据毕萨定律和磁场叠加原理,证明安培环路定理综合应用:根据安培环路定理计算B6.磁场对运动1.洛仑兹力电荷的作用2.带电粒子在磁场中的运动3.回旋加速器4 •汤姆逊实验5.质谱仪知识:1 •汤姆逊实验内容2.质谱仪原理3.回旋加速器的作用4.霍尔效应的内6.霍尔效应容理解: 1 •洛仑兹力公式数学式2.回旋加速器的原理3.霍尔电压的正负与载流子正负的关系4.霍尔效应的主要应用5.洛仑兹力不做功简单应用:1•根据洛仑兹力公式判定运动电荷在磁场中所受洛仑兹力的方向,并计算其大小2•根据洛仑兹力解释霍尔效 应知识: 1. 磁矩的概念 2. 电流同向和 反向时,两电流 间作用力的特 占八\、理解:1. 安培力公式 的数学式及意 义2 •安培力与洛仑兹力的关系3. 电流强度的 单位一一安培 的定义 简单应用: 1.由洛仑兹力 推导安培力 2•由安培力公 式确定磁力方 向 综合应用: 1 •根据安培力 公式和磁力叠 加原理,计算B 对I 的作用7.磁场对载流 导线的作用1 •安培力 2.磁力叠加原 理3 •均匀磁场对 平面载流线圈的作用4.平行无限长载流直导线间的相互作用2.根据磁力公式和力矩的定义计算载流线圈所受到的磁力矩三稳恒电流的磁场重难点分析重点:磁感应强度的概念,以及毕奥一萨伐尔定律和安培环路定理的应用。

大学物理稳恒磁场解读 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第十一章稳恒磁场磁场由运动电荷产生。
磁场与电场性质有对称性,学习中应注意对比。
§11-1 基本磁现象磁性,磁力,磁现象;磁极,磁极指向性,N极,S极,同极相斥,异极相吸。
磁极不可分与磁单极。
一、电流的磁效应1819年,丹麦科学家奥斯特发现电流的磁效应;1820年,法国科学家安培发现磁场对电流的作用。
二、物质磁性的电本质磁性来自于运动电荷,磁场是电流的场。
注:1932年,英国物理学家狄拉克预言存在“磁单极”,至今科学家一直在努力寻找其存在的证据。
§11-2 磁场磁感强度一、磁场磁力通过磁场传递,磁场是又一个以场的形式存在的物质。
二、磁感强度磁感强度B的定义:(1)规定小磁针在磁场中N极的指向为该点磁感强度B的方向。
若正电荷沿此方向运动,其所受磁力为零。
(2)正运动电荷沿与磁感强度B垂直的方向运动时,其所受最大磁力F max与电荷电量q和运动速度大小v的乘积的比值,规定为磁场中某点磁感强度的大小。
即:磁感强度B是描写磁场性质的基本物理量。
若空间各点B的大小和方向均相等,则该磁场为均匀磁场;若空间各点B的大小和方向均不随时间改变,称该磁场为稳恒磁场。
磁感强度B的单位:特斯拉(T)。
§11-3 毕奥-萨伐尔定律一、毕-萨定律电流元:电流在空间的磁场可看成是组成电流的所有电流元在空间产生元磁感强度的矢量和。
式中μ0:真空磁导率,μ0=4π×10-7 NA 2dB的大小:d B的方向:d B总是垂直于Id l与r组成的平面,并服从右手定则。
一段有限长电流的磁场:二、应用1。
一段载流直导线的磁场说明:(1)导线“无限长”:(2)半“无限长”:2。
圆电流轴线上的磁场磁偶极矩讨论:(1)圆心处的磁场:x = 0 ;(2)半圆圆心处的磁场:(3)远场:x>>R,引进新概念磁偶极矩则:3。

大学物理稳恒磁场解读 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
第十一章稳恒磁场
磁场由运动电荷产生。
磁场与电场性质有对称性,学习中应注意对比。
§11-1 基本磁现象
磁性,磁力,磁现象;
磁极,磁极指向性,N极,S极,同极相斥,异极相吸。
磁极不可分与磁单极。
一、电流的磁效应
1819年,丹麦科学家奥斯特发现电流的磁效应;
1820年,法国科学家安培发现磁场对电流的作用。
二、物质磁性的电本质
磁性来自于运动电荷,磁场是电流的场。
注:1932年,英国物理学家狄拉克预言存在“磁单极”,至今科学家一直在努力寻找其存在的证据。
§11-2 磁场磁感强度
一、磁场
磁力通过磁场传递,磁场是又一个以场的形式存在的物质。
二、磁感强度
磁感强度B的定义:
(1)规定小磁针在磁场中N极的指向为该点磁感强度B的方向。
若正电荷沿此方向运动,其所受磁力为零。
(2)正运动电荷沿与磁感强度B垂直的方向运动时,其所受最大磁力F max与电荷电量q和运动速度大小v的乘积的比值,规定为磁场中某点磁感强度的大小。
即:
磁感强度B是描写磁场性质的基本物理量。
若空间各点B的大小和方向均相等,则该磁场为均匀磁场;若空间各点B的大小和方向均不随时间改变,称该磁场为稳恒磁场。
磁感强度B的单位:特斯拉(T)。
§11-3 毕奥-萨伐尔定律
一、毕-萨定律
电流元:
电流在空间的磁场可看成是组成电流的所有电流元在空间产生
元磁感强度的矢量和。
式中μ0:真空磁导率,μ0=4π×10-7 NA 2
dB的大小:
d B的方向:d B总是垂直于Id l与r组成的平面,并服从右手定则。
一段有限长电流的磁场:
二、应用
1。
一段载流直导线的磁场
说明:
(1)导线“无限长”:
(2)半“无限长”:
2。
圆电流轴线上的磁场磁偶极矩
讨论:
(1)圆心处的磁场:x = 0 ;
(2)半圆圆心处的磁场:
(3)远场:x>>R,引进新概念磁偶极矩
则:
3。
载流螺线管轴线上的磁场
讨论:
(1)“无限长”螺线管:
(2)半“无限长”螺线管:
例:求圆心处的B。
§11-4 磁通量磁场的高斯定理
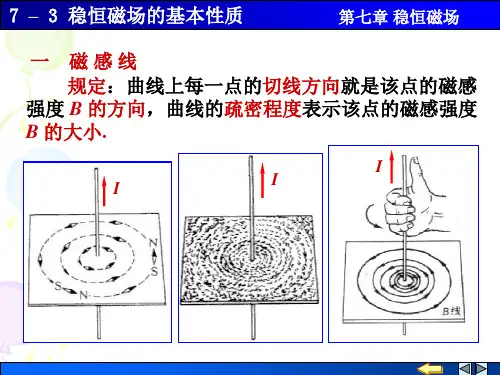
一、磁感线
作法类似电场线。
磁感线的特点:
(1)B线都是一些无头无尾的闭合曲线;
(2)B线总是与电流相套合。
二、磁场的高斯定理
1。
磁通量
定义:
磁通量的直观意义:穿过给定曲面的磁感线的根数。
磁通量是标量。
2。
磁场的高斯定理
表述:通过任意闭合曲面的磁通量必为零。
磁场的高斯定理否定了“磁荷”的存在,是电磁场基本方程之一。
§11-5 安培环路定理
一、安培环路定理
表述:真空中稳恒磁场内,磁感强度的环流等于穿过积分回路的所有传导电流代数和的μ0倍。
说明:
(1)等号右边的电流有正负。
(2)表达式中B应包括所有电流的贡献,∑I指穿过回路的电流。
(3)若电流与积分回路有N次链套,则
(4)“穿过回路的电流”指穿过一闭合回路为边界的任意曲面上的电流。
安培环路定理表明:稳恒磁场不是保守场。
二、定理的应用
1。
“无限长”均匀载流圆柱导体的磁场。
2。
环形螺线管内的磁场
对细螺线管:
小结:
(1)严格把握定理成立条件和解题条件的区别;
(2)解题步骤:①根据电流对称性分析磁场分布对称性;②选取适当安培回路,使B能以标量形式从积分号内脱出。
(3)安环与毕萨的区别:
毕-萨普适。
原则上可求任意电流的磁场:电流元的、一段电流的、整个电流的。
缺点是叉积、投影、积分都比较困难;
安环容易。
但是不能求一段或部分电流的磁场。
§11-6 洛仑兹力
洛仑兹力:运动电荷受到的磁场力。
一、洛仑兹力
说明:
(1)若q<0,则F方向为;
(2)洛仑兹公式
若空间既存在磁场,又存在电场,则运动电荷将同时受到洛仑兹力和库仑力作用。
洛仑兹力特点:
(1)静止电荷不受洛仑兹力作用;
(2)洛仑兹力对运动电荷不作功。
二、带电粒子在均匀磁场中的运动
1。
与平行:
结论:粒子保持原来匀速直线运动状态。
2。
与垂直:
结论:粒子作匀速率圆周运动。
①轨道半径;
②回旋周期;
③回旋频率
3。
与斜交(夹角为θ):
轨道半径
回旋周期
螺距
三、应用
1。
质谱仪
研究、分析同位素组成的仪器。
2。
滤速器
质谱仪的重要配件。
3。
霍尔效应
RH:霍尔系数
说明:
(1)应用广泛。
高斯计,大电流计,磁流体发电,自动控制等。
(2)根据霍尔电压极性可判断是电子型还是空穴型半导体材料。
(3)以上解释是从经典理论出发的,存在一定缺陷。
§11-7 载流导线在磁场中所受的力-安培力
一、安培力
安培力的实质就是金属导体中自由电子受到洛仑兹力的作用。
安培定律:磁场对电流元的作用力数值上等于电流元的大
小、电流元所在处磁感强度的大小及电流元与之间夹角的正弦的乘积,其方向由矢积决定。
一段有限长电流受安培力
说明:
(1)定律无法用实验直接验证;
(2)矢量积分。
只有各电流元受力方向一致时才可退化为标量积分;
(3)若非匀磁场,则B不可从积分号内提出;
(4)特例:匀强磁场,一段长为l的直电流,与B的夹角为θ
方向右手螺旋
又:θ=0或180°,则安培力为零;若θ=90°,则F=Fmax=IlB
例1:求匀强磁场中闭合电流回路受安培力。
结论:
(1)匀强磁场作用在闭合回路上的合力为零;
(2)均匀磁场作用在任意形状导线上的磁力等于连接导线始端与终端的一段直导线上受的安培力。
例2:两根无限长平行载流直导线间的相互作用力。
两根电流同向,相互吸引;反向,相互排斥。
二、匀强磁场对载流线圈的磁力矩
说明:
(1)式子适用任意形状的平面线圈;
(2)磁力矩总是力图使磁矩方向与外磁场方向一致;(3)适用条件:匀强磁场,平面线圈。
例:求圆形线圈受的磁力矩。
可见:磁力矩公式简化了磁力矩计算。