分子力场的势函数形式共45页
- 格式：ppt
- 大小：4.22 MB
- 文档页数：45
下载文档原格式
合集下载
研究生热力学第三章 分子间力与势能函数资料
3.1.1.1 离子与离子间相互作用能
两个离子 i 和 j 分别带有电荷 zie 和 z j e ，如将离子近似为
点电荷，则离子间相互作用力可以按照库仑定律计算如下：
f (r) zi z je2
4 0 Dr 2
式中 4 0 为真空介电常数， 4 0 1.112651010C2N1m2 ， r 为离子间的距离，e 为质子电荷， e 1.602177 10 19C ， D 为介质的介电常数，式中单位为 SI 制。
u(r)
0
ziei cos (4 0 )r2
1
ziei cos (4 0 )r2kT
sind
0
1
ziei cos (4 0 )r2kT
sind
ziei (4 0 )r2
0
0
c os
ቤተ መጻሕፍቲ ባይዱ
s in d
zi2e 2 i2 (4 0 )2 r4kT
cos2
0
s in d
ziei (4 0 )r2kT
• 对分子间力的认识还相差很远，为半定量与定性 的。仅对实际流体提出简单理想的模型。
Ar 的分子间势能
3.1 分子间作用力
分子间存在着势能，对简单球形对称的分子， 势能 u为分子间距离的函数。
r 时 u 0 ，势能的数值等于两质点自 r r 分离至 处时所作之功。
3.1.1 静电作用
离子、极性分子之间主要是静电作用能，可用 库仑定律描述。
为 ，可得到它们之间的相互作用能为：
u(r) qzie qzie
4 0 PL 4 0 PR
1
1
PL
r 2
rl
cos
l2 4
2
r1
分子力学与分子模拟
4
分子力学基本假设
分子模型用球表示原子，弹簧 表示化学健，弹簧的变形表示 化学键的伸缩、弯折和扭转。 非键结合的原子通过范德华相互 作用和和静电相互作用。
5
分子力学基本特点
分子力场不仅描述结构，也描述性质。 一个完整的力场包括一套函数以及相关的参数。
E
bonds
k 2
(l
l0
)2
angles
分子力学
•分子力学定义 •分子力学应用背景 •分子力学基本假设 •分子力学能量计算 •分子力学的势函数
1
分子力学定义
分子力学法(Molecular Mechanics) ，
利用牛顿力学原理,通过解力学方程,得到分子体系的运动轨迹,从而研 究分子体系的能量和各种性质.由于使用的势函数和参数都是有经验和
E
bonds
k (l 2
l0 )2
angles
k ( 2
0 )2
Vn 2 torsions
[1
cos(n
)]
i j
4 ij
ij rij
12
ij rij
6
qi q j 4 0 rij
E = 伸缩能 + 弯曲能 + 扭转能 + 非键相互作用能 + 附加能
11
分子力学的势函数形式
而分子力学的方法就不同，其忽略电子的运动，只计算 以核的位置为函数的体系能量。因此可用于计算包含大量原 子的体系。甚至在某些情况下，还能够提近乎量子力学计算 的精确解，而所需时间只是几十分之一！
注意：分子力学不能提供分子中依赖电子分布的性质。
3
分子力学基本假设
Born-oppenheimer（波恩—奥本海默）近似假设
§1.7 分子间作用力势能与真实气体物态方程
与分子作用力曲线所对应的互作用势能曲线
r
E p ( r ) F ( r )dr ~ r
在平衡位置 r = r0处，分子 力F(r) = 0，势能有极小值 , 它是负的. 在r＞r0处，F(r)＜0， 势能曲线斜率是正的—吸引 力
图中的 d 是两分子对心碰撞时相互接近最短 质心间距离，故称 d = 分子碰撞有效直径 当温度升高时，EK0 也增加，因而横轴升高， d 将减小，说明 d 与气体温度有关。 温度越高，d 越小。
• 设分子在相互分离时的吸 引力为球对称分布， 吸引力作用半径为R0， • 每一分子均有以 R0 为半径 的吸引力作用球。 • 气体内部的分子在越过界面层向器壁运动， 以及在与器壁碰撞以后返回、穿过界面层过 程中，都受到一指向气体内侧的力。
分子吸引力修正
器壁实际受到压强要比气体内部的压强小， 使气体施于器壁的压强减少了一个量值pi ， 这称为气体内压强修正量。若仪器所测出的气 体压强为p, 则 p = p内 - pi 因气体内部分子受到其它分子吸引力的合力相 消，故气体的内部压强 p内 与分子吸引力无关. 气体内部压强等于理想气体压强 p内 = p理
（三） 范德瓦尔斯方程 （Van der Waals equation of state）
将△pi = a/Vm2 代入 p +△pi = RT/ (Vm-b)
得到
a ( p 2 )(Vm b) RT Vm
m 2 a m m [p( ) ( 2 )][V ( )b] RT Mm V Mm Mm
§1.7.1分子间互作用势能曲线
（一）分子作用力曲线 设分子是球形的，分子间的互作用是对称的 中心力场。 F(r) r r0 — 斥力 r r0 — 引力 r= r0 —无相互作用 r0称为平衡距离 分子的直径 d r0 r R — 几乎无相互作用 R:称分子的有效作用距离
分子 能量 势函数 玻尔兹曼
文章标题：探寻分子在能量领域中的奥秘一、引言分子是构成物质的基本单位，其内部的能量状态由分子的结构和相互作用决定。
在能量领域中，分子所具有的势函数和玻尔兹曼分布律，是我们理解分子行为和能量转化的重要工具。
本文将以这些概念为中心，探讨分子在能量领域中的奥秘。
二、分子的能量与势函数分子的能量状态是由其内部原子和化学键的结构所决定的。
在物理学和化学领域，我们常常使用势函数来描述分子内部原子之间的相互作用，从而推导出分子的能量状态。
势函数的数学形式可以是各种各样的，但其中最为常见的包括Lennard-Jones势和Morse势。
在分子模拟和化学反应动力学研究中，我们需要借助这些势函数来计算分子的能量状态和行为。
三、玻尔兹曼分布律与分子动力学玻尔兹曼分布律是描述系统粒子在温度T下能量分布的统计物理学定律。
在分子动力学模拟中，我们常常使用玻尔兹曼分布律来描述分子集合的能量分布，从而推导出分子的动力学行为。
玻尔兹曼分布律的推导过程涉及到统计物理学中的多粒子系统和配分函数的概念，而它所揭示的分子能量分布规律对于理解分子的热力学性质和相变行为至关重要。
四、总结与展望通过以上对分子能量和势函数、玻尔兹曼分布律的探讨，我们可以更加全面和深入地理解分子在能量领域中的行为。
分子的能量状态受到其内部势能的影响，而玻尔兹曼分布律则展示了分子在不同能级上的分布规律。
在未来的研究中，我们可以进一步探讨分子在非平衡态和外场作用下的能量行为，以及寻找新的势函数形式和能量转化机制。
五、个人观点在我看来，分子在能量领域中的行为是非常丰富和有趣的。
势函数和玻尔兹曼分布律为我们解释和预测分子行为提供了重要的工具，而对于实际应用和新材料设计也具有重要意义。
我希望未来能够继续深入学习和研究这些领域，探索更多关于分子能量的新奥秘。
结语通过本文的探讨，我们不仅更深入地理解了分子的能量状态和势函数、玻尔兹曼分布律的作用，也从中汲取了丰富的知识和启发。
真实气体分子间作用力势能
真实气体分子间作用力势能真实气体分子间作用力势能1分子作用力曲线2分子相互作用势能曲线3分子势能曲线解释分子间的对心碰撞由玻意耳定律知, 当T 不变时pV =常量。
若以为纵坐标，p 为横坐标画出等温线，这些等温线都平行于横轴，然而实验结果并非如此。
/m p V R T 这是因为分子固有体积及分子之间的相互作用力不能忽略所致。
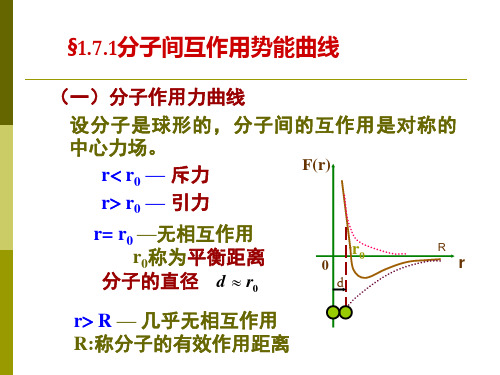
1. 分子作用力曲线（intermolecular action force curve ）r rO)(r F l 在r=r 0时分子力为零，相当于两分子刚好“接触”。
l 当r ＜r 0时,两分子在受到 “挤压”过程中产生强斥力，这时F （r ）＞0且随r 0减少而剧烈增大。
l 当r ＞r 0时两分子分离，产生吸引力，F （r ）＜0。
当r 超过某一数值时R 0，F （r ）即接近于零，R 0就是分子间引力作用半径，简称吸引力作用半径。
R 0R 0~2rd d p E F r=-()()d rp E p F r r∞=-⎰分子力是一种保守力在r ＞r 0处，F (r )＜0，势能曲线斜率是正的，这时是吸引力。
如右图所示。
在平衡位置 r=r 0处，分子力F (r )=0，势能有极小值。
在r ＜r 0处，F ＞0，势能曲线有很陡的负斜率，相当于有很强斥力。
两分子在平衡位置附近的吸引和排斥。
气体液体固体2. 分子相互作用势能曲线OrpE Orfr3. 分子势能曲线解释分子间的对心碰撞设一分子质心a1静止不动，另一分子质心a2从极远处（这时势能为零）以相对运动动能E K0向a1运动。
当 a2向 a1靠近时，受到分子引力作用的 a2具有数值越来越大的负势能，所减少势能变为动能的增量，总能量是一恒量。
O rpEkE'O'r0kErd1a2a'1a'2a"1a"2a（a）碰撞前后动能和势能变化情况（b）碰撞时两球形变示意利用势能曲线能定性地解释气体分子间对心碰撞过程。
分子模拟PPT—第二章 力场
2. 蒙特卡罗随机采样法
分子内能
分子的能量
Etot Eele Evib Erot Etrans
分子的振动自由度 = 3N-6 = 3N-6 分子的振动能 非线性 线性
Evib Ebonds Eangles Etorsions Ecross
分子间相互作用能
1. 范德华能
AMBER
• / • "Amber" refers to two things: a set of molecular mechanical force fields for the simulation of biomolecules ;and a package of molecular simulation programs which includes source code and demos. The current version of the code is Amber version 10, which is distributed by UCSF subject to a licensing agreement described below. • Amber is now distributed in two parts: AmberTools and Amber10. AmberTools 1.2 & Amber 10 is now available! • Amber was originally developed under the leadership of Peter Kollman, and Version 9 is dedicated to his memory.
第二代力场
• 第二代力场的形式远较上述的经典力场复杂，需 要大量的力常数。其设计的目的为能精确地计算 分子的各种性质、结构、光谱、热力学特性、晶 体特性等资料。其力常数的推导除引用大量的实 验数据外，还参照精确的量子计算的结果。尤其 适用于有机分子或不含过渡金属元素的分子系统。 • 第二代力场因其参数的不同，包括CFF91、 CFF95、PCFF与MMFF93等。
势函数法
势函数法
一、公式
n m r
B r A U +-=，又叫做Leonard Jones 势函数，模拟原子间的引力和斥力作用，A 、m 分别是斥力系数和阶数，B 、n 分别是吸引力的系数和阶数；
二、不同的系数和阶数可以导致完全不同的运动状态，如下图：
①、由于速度过快，导致冲过头，然后导致返回； ②、形成类似于拦截的效果；
③、形成类似于视觉追击的效果；
④、由于吸引力过小，导致运动半径极大，从而形成远离效果；
只设置斥力，形成类似于避障的效果；
设置四方墙体的势场函数，可以形成反弹的效果；
可以形成类似蜜蜂成群结队的效果；。
2 分子动力学第二章
2.2 力场函数的内容
一般而言，分子力场函数由成键项Ubonded、 交叉项Ucross和非键项Unobonded三部分构成， 所以分子总势能为：
U total = U bonded + U cross + U nobonded
成键项（Bonded Term）
• • • • 键伸缩能 键角弯曲能 二面角扭曲能 离平面振动能 Us Ua Ut Uo
1
r12
2
3
r23
二面角扭曲能(torsion
angle)
• 单键旋转引起分子骨架扭曲所产生的能量 变化.
U t = kn [1 ± cos(nϕ − ϕ 0 )] 1 2 U t = k (ϕ − ϕ 0 ) 2
1
4
2
3
离平面振动能(out of plane bending)
• 共平面的四个原子中有一个原子偏离平面 进行微小振动所引起的分子能量变化.
• 利用LJ势描述原子间vdw作用的时候,通常 有两种方式： • 1，指定反应参数 • 2，分别指定参数 举例说明:水和甲醇混合液中的vdw类型
ε i j = ε iε j
1 σ ij = (σ i + σ j ) 2
Ai j = Ai Aj Bij = Bi B j
力场函数中参数的获得
• 有两种来源： 1，实验观测的数据 2，量子力学计算的数据 • 方法： 1，提出函数形式，并估计力常数的值 2，根据一些分子（或晶体）的结构+性质数据进行拟合 3，重复进行多次，并逐渐增加拟合的结构和性质，误差小 于一定标准时即可 拟合通常采用的软件：GULP。
• 分析力学所注重的不是力和加速度，而是 具有更广泛意义的能量，同时又扩大了坐 标的概念，因而使这种方法和结论便于运 用到物理学的其它领域。 • 但是由于分析力学中数学推理较多，在历 史上曾经发生过一些不良倾向，容易使人 忘记力学的物理实质。 1. 拉格朗日力学 2. 哈密顿力学
§1[1].7分子间作用力势能与真实气体物态方程
3.说明 说明:* 说明
固体及液体中分子的振动* 二.固体及液体中分子的振动*
三.利分子势能曲线解释固体的热膨胀(阅读教材39页) 利用分子势能曲线解释固体的热膨胀(阅读教材39页 39
范德瓦斯方程* §1.7.3范德瓦斯方程 范德瓦斯方程
一.非理想气体与理想气体的本质区别
我们推导范氏方程的思路是: 我们推导范氏方程的思路是:从微观结构上找到非理 想气体与理想气体的本质区别, 想气体与理想气体的本质区别,考虑到这些区别对气体压 强造成的影响,将理想气体压强进行修正, 强造成的影响,将理想气体压强进行修正,就得到了非理 想气体的范氏方程. 想气体的范氏方程. 非理想气体与理想气体在微观结构上的区别主要是 非理想气体分子数密度大,因此: 非理想气体分子数密度大,因此: 1.分子平均距离小 分子线度与平均距离比较不能忽略. 分子平均距离小, 1.分子平均距离小,分子线度与平均距离比较不能忽略. 所以,分子不能当质点看待,即分子本身体积不能忽略(分 所以,分子不能当质点看待,即分子本身体积不能忽略( 子斥力不能忽略). 子斥力不能忽略). 2.分子间平均距离小,在引力力程之内分子引力不能忽略, 2.分子间平均距离小,在引力力程之内分子引力不能忽略, 分子间平均距离小 分子间除碰撞外还有引力作用, 分子间除碰撞外还有引力作用,这个引力的存在对分子碰 撞器壁的冲量产生一定的影响. 撞器壁的冲量产生一定的影响.
2
a p + 2 ( v − b ) = RT v
3.说明:* 说明:* 说明 4.习题: 习题: 习题
例1.根据公式 P = 2 nε t 和 ε t = 3 KT,试从分子运动论推证玻意 根据公式 3 2 马略特定律. 耳-马略特定律. 的容器内装有理想气体, 例2.在容积为V = 60l 的容器内装有理想气体,当T = 300 K 在容积为 时,气体的压强 P = 5.0 ×103 Pa .问容器中气体的分子数 是多少? 是多少? O 组成的混合气体, 例3.在容积为 5.0l的容器内贮有 2和 N 2 组成的混合气体,其 在容积为 .试求容 中O2 有3.2 ×10−5 g .已知混合气体的T =350K, P = 2.7 Pa .试求容 分子数. 器中N 2 分子数. 一容器内贮有O 试求: 例4.一容器内贮有 2,,其P = 1.0 ×10 Pa, T = 300 K ,试求: 一容器内贮有 , (1)分子数密度 分子数密度;(2)O2的密度 的密度;(3)氧分子的质量 分子间 氧分子的质量;(4)分子间 分子数密度 氧分子的质量 的平均距离;(5)分子的平均平动动能. 分子的平均平动动能. 的平均距离 分子的平均平动动能
势函数
7.2 经验性对势模型和弱赝势模型
式中，rij=| rij |。表示i和j两个原子之间的距离；ψij是对势。 不包括任何内聚力的最简单的经典对势就是硬球模型．即：
ij rij 0
r r
ij ij
r0
r0
(7.2)
式中，r0是截断半径，这里相当于硬球半径。 既包含排斥作用又包含吸引作用的较光滑的势就是所谓的 勒纳德-琼斯势，它是针对惰性气体的研究而发展起来的。
7.2 经验性对势模型和弱赝势模型
对立方系金属在取各向同性极限时 C1122-C2323=C2323/2≠0 对于六角和三角系金属，其柯西关系为 C1133=C2323和3C1212=C1111 存在于金属晶体弹性常数之间的柯西偏差，当且仅当所用 模型附加有晶格常数小于其平衡值的边界条件，才能得到 与实验值相符合的结果。第二类对势所描述的经典经验性 原子间作用力，在其中引入了赝势，并且含有较大的与平 均密度相关的贡献。然而，对模拟晶格缺陷来说，这种均 匀密度假说通常是不正确的。
7.3 各向同性多体对泛函势
各种各向同性多体或简单的对泛函势是一类改进完善的经 验或半经验势。这些模型中的大多数都具有这样一个原则： 原子内聚能主要由该原子所在格座处的局域电于密度决 定。局域电子密度来自于目标原子格座的近邻原子的负 献。 减聚能主要由反映静电排斥作用的对势贡献来解释。 各向同性多体势既可用于研究那些更严格的方法所难以处 理的复杂系统，也可用于不太依赖于能量关系细节的那些 普通性质的研究。
1 N Etot 2 i 1 j
j 1i
r U
N ij ij
(7.5)