小学数学培优之几何(二) 曲线图形

数学知识点归纳曲线与曲面的性质与刻数学知识点归纳：曲线与曲面的性质与刻在数学中，曲线与曲面是常见的几何对象，它们具有许多独特的性质与刻画方法。

本文将对曲线与曲面的性质和刻画方法进行归纳总结。

一、曲线的性质与刻画曲线是二维几何对象，它可以用参数方程或者隐函数表示。

常见的曲线有直线、圆、椭圆等。

1. 直线直线是最简单的曲线，它具有以下性质：- 无限延伸性：直线没有起点和终点，可以无限延伸。

- 线段性质：直线上的两点可以唯一确定一条直线段。

- 斜率：直线的斜率表示了其倾斜程度，可以通过两点的坐标计算得到。

2. 圆圆是一个平面上距离圆心相等的点的轨迹，它具有以下性质：- 对称性：圆具有中心对称性，任意点与圆心的距离相等。

- 弧长与扇形面积：圆的弧长与扇形面积可以通过圆心角计算得到。

- 切线：圆上的切线与半径垂直。

3. 椭圆椭圆是平面上离两个固定点距离之和为常数的点的轨迹，它具有以下性质：- 中心：椭圆有一个中心点，是两个焦点的中点。

- 长短轴：椭圆有两个重要的参数，即长轴和短轴。

- 离心率：椭圆的离心率决定了其形状，范围在0到1之间。

二、曲面的性质与刻画曲面是三维几何对象，它可以用参数方程或者隐函数表示。

常见的曲面有球面、圆柱面、圆锥面等。

1. 球面球面是空间中到定点距离相等的点的轨迹，它具有以下性质：- 中心和半径：球面由一个中心点和半径确定。

- 表面积和体积：球面的表面积和体积可以通过半径计算得到。

- 切平面：球面上的切平面与法线垂直。

2. 圆柱面圆柱面是空间中直线与一个固定曲线平行移动形成的曲面，它具有以下性质：- 直母线：圆柱面上的任意一条直线与轴线平行。

- 侧面积和体积：圆柱面的侧面积和体积可以通过圆柱的高和底面积计算得到。

3. 圆锥面圆锥面是空间中直线与一个固定点旋转形成的曲面，它具有以下性质：- 顶点和母线：圆锥面由一个顶点和沿着一个直线运动的所有点组成。

- 侧面积和体积：圆锥面的侧面积和体积可以通过圆锥的高和底面积计算得到。

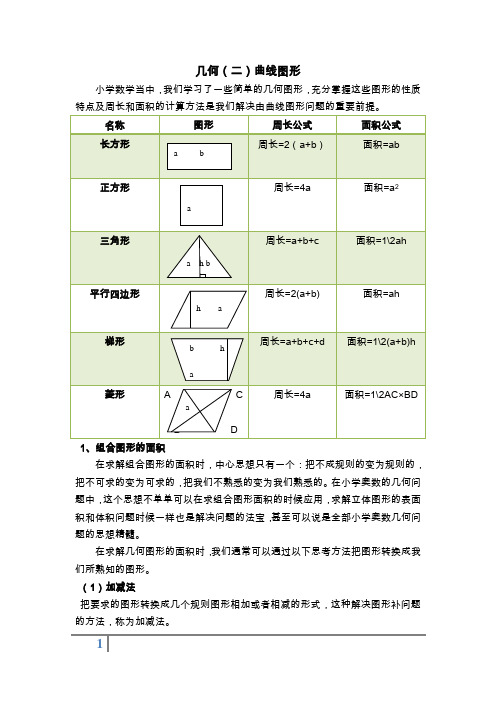
几何（二）曲线图形小学数学当中，我们学习了一些简单的几何图形，充分掌握这些图形的性质在求解组合图形的面积时，中心思想只有一个：把不成规则的变为规则的，把不可求的变为可求的，把我们不熟悉的变为我们熟悉的。

在小学奥数的几何问题中，这个思想不单单可以在求组合图形面积的时候应用，求解立体图形的表面积和体积问题时候一样也是解决问题的法宝，甚至可以说是全部小学奥数几何问题的思想精髓。

在求解几何图形的面积时，我们通常可以通过以下思考方法把图形转换成我们所熟知的图形。

（1）加减法把要求的图形转换成几个规则图形相加或者相减的形式，这种解决图形补问题的方法，称为加减法。

（2）割补法把要求的图形通过切割再拼补成规则图形，这种方法称为割补法。

（3）旋转平移法把要求的图形通过旋转或者平移，正好可以和图形的其他部分拼成规则图形，这种方法称为旋转平移法。

（4）重叠法要求的组合图形可以看作是几个规则图形的重叠部分，可以应用容斥原理求得图形的面积，这种方法称为重叠法。

（5）比例法把要求的图形分成几个部分，通过寻找各个部分之间的比例关系求解的方法称为比例方法。

2、图形旋转的问题在这里，我们主要研究的是平面图形在平面旋转所产生的问题，一般情况下，我们所能遇到的有以下两种情况：（1）求图形一边扫过的面积在遇到这类问题时，我们只要先找到要求的是哪条边扫过的面积，再看这条边是以哪个点为圆心运动。

首先你让这条边以这个点为圆心按照题目的要求旋转，旋转停止后，这条边旋转所得到的面积就是你要求的图形一边扫过的面积。

（2）求图形扫过的面积在求图形一边扫过的面积的基础上，要注意，图形中最长处旋转时所成图形，我们在旋转的图形一边停止旋转时，在相应的位置补上图形的其他部分，就很容易地找到整个图形扫过的部分。

（3）几个特殊的问题①活动范围的问题，我们先来看看下面几个问题。

●假设茫茫的草原上有一木桩，桩子上用一根30米的绳子栓着一只羊，问羊能吃到的草的面积有多大？●草场的主人因为业务发展，准备建羊圈，但是因为资金短缺，所以只先建了一道墙，于是把羊还是用30米的绳子栓在了墙角边，问羊这个时候能吃到草的面积是多大？●羊圈建成了，羊在平时被拴在羊圈的西北角，羊圈长20米，宽10米，问羊这个时候能吃到的草的面积是多大？你注意到了吗？栓着羊的绳子在碰到墙拐角的地方运动的圆心在变化，羊能吃到的草的范围活动的半径在跟着变化。

小学数学知识归纳曲线的概念在小学数学学习中，曲线是一个重要的概念。

曲线是由一系列连续的点组成的，这些点按照一定的规律连接起来，形成了一条平滑的曲线。

曲线可以用来表示各种各样的事物及其变化趋势。

下面将从曲线的定义、特点以及在数学中的应用等方面对小学数学的曲线知识进行归纳。

一、曲线的定义曲线是一种特殊的图形，由无数个连续的点沿着一定的路径相连而成。

这些点之间的连接不是直线，而是按照一定的方式连接起来，从而形成了曲线。

曲线可以是弯曲或交叉的，可以是闭合的也可以是开放的。

在数学中，常见的曲线有直线、抛物线、圆等。

二、曲线的特点1. 平滑性：曲线是由无数个点组成的，这些点之间的过渡是平滑的，不存在突变或间断点。

2. 连续性：曲线上的每一个点都与相邻的点相连，形成一条连续的线段。

3. 可变性：曲线可以根据不同的参数产生不同的形状和大小，反映不同事物及其变化趋势。

三、曲线的应用1. 图形的表示：曲线可以用来表示各种图形，比如用直线和曲线可以表示房屋的轮廓，用圆可以表示太阳、月亮等。

2. 数据的统计和分析：曲线可以根据一组数据绘制成图形，通过观察曲线的形状和趋势，可以对数据进行分析和比较。

3. 函数关系的表达：在数学中，函数关系可以通过曲线来表示。

例如，一元一次函数可以用直线表示，而二次函数可以用抛物线表示。

4. 几何变换：曲线在几何变换中有广泛的应用。

例如，通过对直线或曲线进行平移、旋转、镜像等操作，可以得到新的曲线。

综上所述，曲线是由一系列连续的点组成的，具有平滑性、连续性和可变性等特点。

它在数学中有着广泛的应用，可以用来表示图形、统计分析数据、表达函数关系以及进行几何变换等。

掌握曲线的概念和特点对小学数学学习至关重要。

通过深入理解曲线的含义和应用，可以帮助学生更好地理解数学知识，提高数学解决问题的能力。

小学数学知识归纳曲线的性质数学知识归纳：曲线的性质数学是一门抽象而又具体的学科，其中一个重要的分支就是几何学。

在几何学中，曲线是一个常见的概念。

曲线具有不同的性质，了解这些性质可以帮助我们更好地理解和运用数学知识。

本文将对小学数学中常见的曲线的性质进行归纳，从而帮助读者更好地理解这些概念。

一、直线的性质直线是最简单的一种曲线形式，它具有以下性质：1. 直线上的任意两点可以通过直线上的其他点用划线法连接起来。

2. 直线的长度是无限的，没有起点和终点。

3. 直线上的任意两点之间的距离是确定的，并且是最短距离。

二、射线的性质射线是有起点但无终点的一种曲线形式，它具有以下性质：1. 射线上的任意一点都可以通过起点和另一点用划线法连接起来。

2. 射线的长度是无限的，只有一个起点。

从起点出发的划线方向可以延伸到无穷远。

三、线段的性质线段是有起点和终点的一种曲线形式，它具有以下性质：1. 线段上的任意一点都可以通过起点和终点用划线法连接起来。

2. 线段的长度是有限的，有一个明确的起点和终点。

3. 线段上的任意两点之间的距离是确定的，并且是最短距离。

四、弧的性质弧是曲线中的一部分，它具有以下性质：1. 弧上的任意两点可以通过划线法连接起来，形成一条曲线。

2. 弧的长度是有限的，取决于弧的角度和半径大小。

3. 弧可以是圆周的一部分，也可以是椭圆、双曲线等曲线形状的一部分。

五、抛物线的性质抛物线是一种特殊类型的曲线，它具有以下性质：1. 抛物线是对称的，对称轴是垂直于抛物线的直线。

2. 抛物线上的任意一点到焦点的距离等于到对称轴的距离，这是抛物线的重要性质之一。

3. 抛物线可以打开向上或向下，取决于焦点的位置和抛物线的方程。

六、圆的性质圆是一种特殊类型的曲线，它具有以下性质：1. 圆是由一条与自己相交的曲线形成的，这个曲线称为圆的轮廓线。

2. 圆上的任意一点到圆心的距离相等，这是圆的重要性质之一。

3. 圆上的任意弧的长度是与弧所对应的角度成正比的。

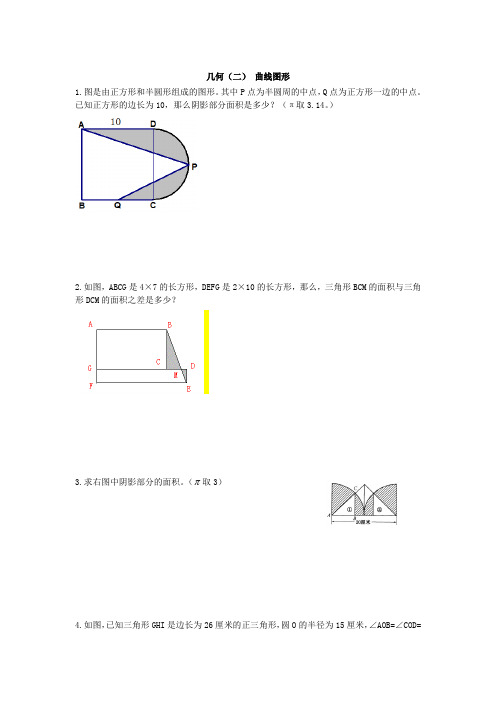
几何（二）曲线图形1.图是由正方形和半圆形组成的图形。

其中P点为半圆周的中点，Q点为正方形一边的中点。

已知正方形的边长为10，那么阴影部分面积是多少？（π取3.14。

）2.如图，ABCG是4×7的长方形，DEFG是2×10的长方形，那么，三角形BCM的面积与三角形DCM的面积之差是多少？3.求右图中阴影部分的面积。

（ 取3）4.如图，已知三角形GHI是边长为26厘米的正三角形，圆O的半径为15厘米，∠AOB=∠COD=∠EOF=90°。

求阴影部分的面积。

5.如图，ABCD 是一个长为4，宽为3。

对角线长为5的正方形，它绕C 点按顺时针方向 旋转900，分别求出四边扫过图形的面积。

（ 取3）6.求圆中阴影部分与大圆的面积之比和周长之比。

D CBA7.如图，半圆半径=40CM，BM=CN=DP=22，每个阴影部分的弧长为半圆弧长的13，求阴影部分面积？（π=3）8.如图，哨所门前的两个正三角形哨台拴了两条狼狗，拴狼狗的铁链子长为10米，每个哨台的面积为42.5平方米现在要绿化哨所所在地（哨所面积忽略不计，把其看做一点，在其周围20米范围内铺上草地）为了防止狼狗践踏，则绿化的实际面积为多大合适？（π=3）9.如图，15枚相同的硬币排成一个长方形，一个同样大小的硬币沿着外圈滚动一周，回到起始位置。

问：这枚硬币自身转动了多少圈？10、如图，四边形ABCD 是平行四边形，8AD cm =，10AB cm =，30DAB ∠=︒，高CH=4cm , BE 、DF 分别以AB 、CD 为半径，弧DM 、BN 分别以AD 、CB 为半径，阴影部分面积是多少平方厘米？11、下图中，四边形ABCD 都是边长为1的正方形，E ，F ，G ，H 分别是AB ，BC ，CD ，DA 的中点；请计算图中两个阴影图形的面积比。

12、（2004第二届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛3），如图，在平行四边形ABCD 中，已知三角形ABP 、BPC 的面积分别是73、100，求三角形BPD 的面积。

几何-曲线型几何-圆环-2星题课程目标知识提要圆环•概述圆环是由两个半径不相等的同心圆构成的，大圆面积比小圆面积多的部分就是圆环。

•面积公式S=πR2−πr2=π(R2−r2)精选例题圆环1. 如下图所示，已知圆环的面积是141.3平方厘米，那么阴影部分的面积是平方厘米．（π取3.14）【答案】45【分析】设大圆半径为R，小圆半径为r，则圆环面积为π(R2−r2)=141.3(平方厘米),所以阴影部分面积为R2−r2=141.3÷3.14=45(平方厘米).2. 如下图所示，有10个同心圆，任意两个相邻的同心圆半径之差等于里面最小圆的半径．如果射击时命中最里面的小圆得10环，命中最外面的圆环得1环．得1环圆环的面积是10环圆面积的倍．【答案】19【分析】1环、2环、10环的外圈的圆的半径值比为10:9:1，面积比为100:81:1，1环面积是10面积的(100−81)÷1=19倍．3. 如下图所示，大正方形的面积是400平方厘米，则圆环的面积是平方厘米．（π取3.14）【答案】157平方厘米【分析】将小正方形转45∘，如下图所示，可以看出大正方形的面积是小正方形面积的两倍，所以大圆面积是小圆面积的两倍．因为大正方形面积是400平方厘米，所以大圆面积为314平方厘米，小圆面积为157平方厘米，圆环面积为314−157=157(平方厘米)．4. 如图，大正方形的面积是400平方厘米，则圆环面积是平方厘米．（π取3.14）【答案】157【分析】如图所示，由大正方形的面积为400平方厘米知AB=20(厘米)．取圆心O，AB中点M，连接OM交小正方形于点E，连接OB交大圆于点F．于是MB=OM=OF=10(厘米),易知△OEF为等腰直角三角形，所以2OE2=OF2=100(平方厘米),于是OE2=50(平方厘米),所以圆环的面积为π⋅OM2−π⋅OE2=π×102−π×50=50π≈157(平方厘米).5. 两个半径不等的同心圆，内圆半径3cm，外圆直径8cm，圆环面积是多少？【答案】21.98平方厘米．【分析】注意外圆的直径是8cm，半径应是4cm，那么圆环的面积是π×4×4—π×3×3=21.98(平方厘米).6. 在直径为6米的圆形花坛的外面，围绕着一条宽1米的环形小路，这条小路的面积是多少？【答案】21.98平方米．【分析】此题相当于知道小圆直径和环宽，求圆环的面积．小圆半径3米，大圆半径4米，圆环的面积是21.98平方米．7. 大圆半径为R，小圆半径为r，两个同心圆构成一个环形．以圆心O为顶点，半径R为边长作一个正方形：再以O为顶点，以r为边长作一个小正方形．图中阴影部分的面积为50平方厘米，求环形面积．（圆周率取3.14）【答案】157平方厘米【分析】环形的面积应该用大圆的面积减去小圆的面积，但分别求出两个圆的面积显然不可能．题中已知阴影部分的面积，也就是R2−r2=50平方厘米，那么环形的面积为：πR2−πr2=π(R2−r2)=π×50=157(平方厘米)．8. 图中阴影部分的面积为50平方厘米，求环形面积．（π取3.14）【答案】157平方厘米【分析】环形的面积应该用大圆的面积减去小圆的面积，但分别求出两个圆的面积显然不可能．题中已知阴影部分的面积，也就是R2−r2=50平方厘米，那么环形的面积为：πR2−πr2=π(R2−r2)=π×50=157(平方厘米).9. 奥运会的会徽是五环图，一个五环图是由内圆直径为6厘米，外圆直径为8厘米的五个环组成，其中两两相交的小曲边四边形（阴影部分）的面积都相等，已知五个圆环盖住的面积是77.1平方厘米，求每个小曲边四边形的面积．（π=3.14）【答案】 4.1平方厘米．【分析】⑴每个圆环的面积为：π×42−π×32=7π=21.98(平方厘米)⑵五个圆环的面积和为：21.98×5=109.9(平方厘米)⑶八个阴影的面积为：109.9−77.1=32.8(平方厘米)⑷每个阴影的面积为：32.8÷8=4.1(平方厘米)10. 已知与小圆相切的线段长度是10厘米，那么图中圆环的面积是多少？【答案】 25π 平方厘米【分析】连接 OC 、OB ，则 OC ⊥AB ，在直角三角形 OBC 中，OB 2−OC 2=BC 2=(12AB)2=25, 图中圆环的面积为πR 2−πr 2=π(R 2−r 2)=π×(OB 2−OC 2)=25π(平方厘米).11. 图为一卷紧绕成的牛皮纸，纸卷直径为 20 厘米，中间有一直径为 6 厘米的卷轴．已知纸的厚度为 0.4 毫米，问：这卷纸展开后大约有多长？【答案】71.4米．【分析】将这卷纸展开后，它的侧面可以近似的看成一个长方形，它的长度就等于面积除以宽．这里的宽就是纸的厚度，而面积就是一个圆环的面积．因此，纸的长度≈纸卷侧面积纸的厚度≈3.14×102−3.14×320.04=3.14×(100−9)0.04=7143.5(厘米)所以，这卷纸展开后大约71.4米．12. 图中阴影部分的面积是25cm2，求圆环的面积．【答案】157cm2．【分析】设大圆半径为R，小圆半径为r，依题有R 22−r22=25，即R2−r2=50.则圆环面积为：πR2−πr2=π(R2−r2)=50π=157(cm2).13. 如图所示，在两个同心圆上有一条两端点都在大圆上的线段与小圆相切，其长度为10厘米．求阴影部分的面积．（π取3.14）【答案】78.5平方厘米．【分析】如图所示，从圆心连结其中一个端点，长度为大圆半径，再从圆心向线段作垂线，长度为小圆半径，图中的三角形为直角三角形，由勾股定理可得R2−r2=52=25,所以图中阴影部分面积为πR2−πr2=π×(R2−r2)=25π=78.5(平方厘米).14. 图中阴影部分的面积是25平方厘米，求圆环的面积．（π取3.14）【答案】157平方厘米．【分析】记大圆半径为R，小圆半径为r，那么圆环的面积为π(R2−r2)，只要能够求出R2−r2即可．阴影部分是两个等腰直角三角形的面积差，等于12(R2−r2)，所以R2−r2=2×25=50(厘米).由此可得圆环面积等于50×3.14=157(平方厘米).15. 如图，厚度为0.25毫米的铜版纸被卷成一个空心圆柱（纸卷得很紧，没有空隙），它的外直径是180厘米，内直径是50厘米．这卷铜版纸的总长是多少米？【答案】9388.6【分析】卷在一起时铜版纸的横截面的面积为π×(1802)2−π×(502)2=7475π(平方厘米),如果将其展开，展开后横截面的面积不变，形状为一个长方形，宽为0.25毫米（即0.025厘米），所以长为7475π÷0.025=938860(厘米)=9388.6(米).所以这卷铜版纸的总长是9388.6米．16. 如图，有一卷紧紧缠绕在一起的塑料薄膜，薄膜的直径是20厘米，中间有一直径为8厘米的卷轴，已知薄膜的厚度为0.04厘米，则薄膜展开后的面积是多少平方米？（π取3.14）【答案】 65.94【分析】 卷纸问题：依据体积不变原则求解，缠绕在一起时塑料薄膜的体积为：[π×(202)2−π×(82)2]×100=8400π(立方厘米)薄膜展开后为一个长方形，体积保持不变，而厚度为 0.04 厘米，所以薄膜展开后的面积为8400π÷0.04=659400(平方厘米)=65.94(平方米).17. 如图，有一卷紧紧缠绕在一起的塑料薄膜，薄膜的直径为 20 厘米，中间有一直径为 8 厘米的卷轴，已知薄膜的厚度为 0.04 厘米，则薄膜展开后的面积是多少平方米？【答案】 65.94 平方米．【分析】 缠绕在一起时塑料薄膜的体积为：[π×(202)2−π×(82)2]×100=8400π(立方厘米), 薄膜展开后为一个长方体，体积保持不变，而厚度为 0.04 厘米，所以薄膜展开后的面积为8400π÷0.04=659400(平方厘米)=65.94(平方米).另解：也可以先求出展开后薄膜的长度，再求其面积．由于展开前后薄膜的侧面的面积不变，展开前为π×(202)2−π×(82)2=84π(平方厘米),展开后为一个长方形，宽为0.04厘米，所以长为84π÷0.04=6594(厘米),所以展开后薄膜的面积为6594×100=659400(平方厘米)=65.94(平方米).。

六年级曲线几何知识点【正文】六年级曲线几何知识点曲线几何是数学中的重要分支，它研究的是曲线的性质、图形的变换和相关的计算方法。

六年级是学习曲线几何的关键时期，下面将介绍几个六年级曲线几何的知识点。

一、直线和曲线的基本概念1. 直线：直线是两个方向相反且不断延伸的点的集合，可以用线段无限延伸表示。

直线有始有终，没有弯曲。

2. 曲线：曲线是由连续的点组成，具有弯曲的形状。

常见的曲线有弧线、圆、椭圆等。

二、图形的对称性1. 线对称：当一个图形绕着一条直线旋转180度后，图形与原来的位置完全一致，这条直线称为图形的对称轴。

如果一个图形可以折叠后与自身完全重合，那么它是线对称的。

2. 点对称：当一个图形绕着一个点旋转180度后，图形与原来的位置完全一致，这个点称为图形的对称中心。

如果一个图形可以在对称中心处旋转180度后与自身完全重合，那么它是点对称的。

三、直角、钝角和锐角1. 直角：两条相交的线段互相垂直时，所形成的角为直角。

直角的度数为90度。

2. 钝角：大于90度小于180度的角称为钝角。

3. 锐角：小于90度的角称为锐角。

四、平行和垂直关系1. 平行线：两条直线在同一平面内没有交点，永远保持相同的距离，那么这两条直线就是平行线。

2. 垂直线：两条直线相交且互相垂直，那么这两条直线就是垂直线。

三、圆的性质1. 圆心：圆的中心点称为圆心，通常用字母O表示。

2. 半径：圆心到圆上任意一点的距离称为半径，通常用字母r表示。

3. 直径：穿过圆心的线段称为直径，直径是半径的两倍。

4. 弧长：圆上两点之间的弧长是圆上这两点之间的弧的长度。

5. 扇形：以圆心为顶点，圆上的两条半径为边的图形称为扇形。

6. 弦：圆上连接两点的线段称为弦。

五、平面和立体图形1. 平面图形：平面图形是二维图形，仅具有长度和宽度，没有高度，如矩形、三角形等。

2. 立体图形：立体图形是三维图形，具有长度、宽度和高度，如立方体、圆柱体等。

六、相似图形1. 相似三角形：具有相同形状但可能不同大小的三角形称为相似三角形。

【小升初培优专题】六年级下册数学-平面几何综合训练—曲线型（解析版）一、知识点1、圆周长：C＝πd＝2πr扩倍问题（1）：若圆的半径扩大到n倍，则直径扩大到n倍，周长扩大到n倍，面积扩大到n²倍扩倍问题（2）：若两个圆的半径比为n：m，则它们的直径比为n：m，周长比为n：m，面积比则为n²：m²构造圆在长方形中画一个最大的圆在长方形中画最大的半圆技巧：长的一半与宽比较，谁小谁是半径。

2、半圆周长：C＝πr＋d面积：πr²÷23、圆环＝大圆面积－小圆面积＝πR²－πr²圆环面积：S环4、扇形弧长：r nl π2360⨯=面积：2360r nS π=5、组合图形方中圆：正方形与圆面积之比为4：π圆中方：圆与正方形面积之比为π：2方中圆中方：大正方形面积是小正方形面积的2倍圆中方中圆：大圆面积是小圆面积的2倍割补法：重叠问题：整体减空白一、填空题。

（每道小题5分，共 40分）1. （1）一个圆的半经扩大到3倍，直径扩大到 倍；周长扩大到 倍；面积扩大到 倍。

【解答】3，3，9。

（2）大圆和小圆的半径比是3：2，它们的直径比是 ，他们的周长比是 ，它们的面积比是 。

【解答】3：2，3：2，9：4。

2. 在一个长10厘米、宽4厘米的长方形内画圆，圆的直径最大是 厘米，能画 个这样的圆且互不重叠。

【解答】如下图，4：2。

3. 如图，以B 、C 为圆心的两个半圆的直径都是3厘米，图中阴影部分的周长是 厘米。

【解答】如下图，半径为3÷2＝1.5（厘米），连接BP 与CP ，因为BC 、CP 、PB 均为半径，所以△BCP 是等边三角形，那么∠PBC ＝∠PCB ＝60（度），弧长PB ＝60＝弧长PC ＝36060×3.14×3＝1.57（厘米），阴影部分的周长为1.57＋1.57＋1.5＝4.64（厘米）。

数学学科重要知识点总结小学二年级几何形认识与绘制数学学科重要知识点总结——小学二年级几何形认识与绘制数学是一门重要的学科，对于学生的全面发展起着至关重要的作用。

在小学阶段，数学教育的重点是帮助学生建立数学基础知识和思维能力。

其中，几何形状的认识与绘制是孩子们学习数学的关键内容之一。

以下是小学二年级几何形认识与绘制的重要知识点总结。

一、直线和曲线在几何学中，直线和曲线是最基本的几何形状。

直线是由无限多个点连成的一个线段，没有弯曲或拐角；曲线则是具有弯曲和弧度的线条。

二、点、线段和射线点是几何学中最基本的元素，它没有长度、宽度和厚度，通常用小圆点表示。

线段是由两个端点确定的一段直线，具有长度，可以用线段AB表示。

射线是由一个端点和一个方向确定的一段直线，具有长度但没有终点，可以用射线AC表示。

三、平面和面平面是三维空间中的一个二维形状，它没有厚度，由无数条平行于地面的线构成。

面是平面的一部分，其边界由线段或曲线构成，可以是任意形状。

四、多边形多边形是由多条线段构成的封闭图形。

常见的多边形有三角形、正方形、长方形、菱形等。

它们的边和角都有一定的特点。

1. 三角形：三边和三角都有确定的特点，可以根据边长和角度来分类，如等边三角形、等腰三角形等。

2. 正方形：四条边长度相等，四个角都是直角。

3. 长方形：两对相对的边长度相等，四个角都是直角。

4. 菱形：四条边长度相等，相邻两边之间的角度不一定相等。

五、圆和圆形圆是平面上一组离一个点距离相等的点的集合，这个点称为圆心，距离称为半径。

圆形是由圆上的点组成的闭合曲线。

六、立体图形立体图形是在三维空间中存在的物体，它们有长度、宽度和高度。

常见的立体图形有立方体、圆柱体、圆锥体和球体。

1. 立方体：具有六个相等的正方形面，相邻面之间的边相互垂直。

2. 圆柱体：由两个平行的圆面和连接两个圆面的侧面组成。

3. 圆锥体：由一个圆面和连接圆面和顶点的侧面组成。

4. 球体：所有表面上的点距离球心相等。

曲线数学知识点总结一、曲线的类型1. 通过坐标轴的曲线平面直角坐标系中的曲线可以分为通过坐标轴和不通过坐标轴两种类型。

通过坐标轴的曲线包括直线、抛物线、双曲线、圆等，它们的方程在坐标轴上有特定的形式，可以通过这些形式来确定曲线的类型及其他性质。

2. 不通过坐标轴的曲线不通过坐标轴的曲线包括椭圆、双曲线、抛物线等，它们的方程在坐标轴上没有特定的形式，而是通过参数方程或者极坐标方程来描述曲线的形状。

二、参数方程参数方程是用参数表示的曲线方程，它表示了曲线上的点与参数之间的关系。

参数方程可以描述一些复杂的曲线，比如螺旋线、心形线、阿基米德螺线等。

参数方程的应用广泛，主要用于描述运动学问题、流体力学问题等。

三、极坐标极坐标是另一种描述平面上的点的方式，它利用极径和极角来表示点的位置。

通过极坐标可以方便地描述圆、椭圆、双曲线等曲线的形状。

极坐标在物理、工程、地理和生物等领域都有重要的应用，特别是在描述接近圆的曲线时更加简洁。

四、曲线的方程曲线的方程是用代数式表示的曲线方程，它描述了曲线上点的坐标与自变量之间的关系。

曲线的方程可以分为显式方程和隐式方程两种类型。

显式方程是指可以直接通过曲线上点的坐标表达的方程，比如圆的方程。

而隐式方程是指不能直接通过曲线上点的坐标表达的方程，比如双曲线的方程。

五、曲线的性质曲线的性质包括切线、曲率、弧长、曲线的方程等。

切线是曲线在某一点的切线与曲线在该点的倾角。

曲率是描述曲线弯曲程度的量，其绝对值越大，曲线的弯曲程度越大。

弧长是曲线一段的长度，它可以通过积分计算得到。

曲线的方程是通过解析几何和微积分分析得到曲线的方程形式，它包括直线方程、圆方程、抛物线方程等。

六、曲线的应用曲线在很多领域有重要的应用，比如工程、物理、生物等。

在工程领域，曲线可以用于描述机械构件的轨迹、电路的特性等。

在物理领域，曲线可以用于描述点、线、平面运动的轨迹、电磁场的变化等。

在生物领域，曲线可以用于描述生物体的形状、生物过程的变化等。