第三章 正弦交流电路2
- 格式:doc
- 大小:3.60 MB
- 文档页数:38









第三章 正弦交流电路本章先介绍正弦交流电的基本特征和相量表示法,然后从单一参数电路出发,并以RLC 串联电路为典型电路,讨论交流电路中电压和电流之间的关系。
同时讨论正弦交流电路中的功率和能量交换,最后介绍电路的谐振和功率因数的提高。
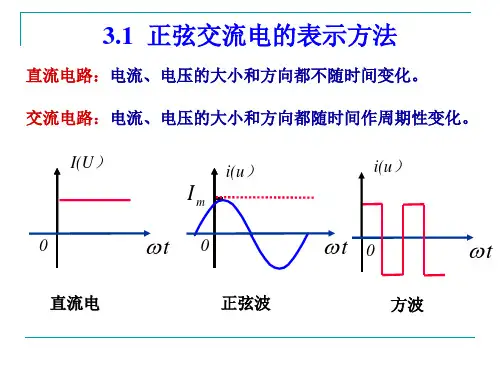
3.1 正弦交流电基本概念一、正弦电压和电流交流电是指大小和方向随时间作周期性变化的电压和电流。
所谓正弦电压和电流,就是指其大小和方向按照正弦规律周期性变化的电压和电流,其瞬时值(即在任一时刻对应的数值)分别用小写字母u 、i 来表示。
之所以采用正弦交流电,除了它易于产生、易于转换和易于传输外,还由于同频率的正弦量之和或差仍为同频率的正弦量,正弦量的导数或积分仍为频率不变的正弦量。
因此,当一个或几个同频率的正弦电压源作用于线性电路时,电路中各部分的电压和电流都是同一频率的正弦量,这将使电压和电流的测量和计算都较为方便。
此外,由于任意周期性变化的量,都可以用傅里叶级数分解为直流分量和一系列不同频率的正弦波分量,因此,只要掌握了正弦交流电的分析方法,便可运用叠加定理去分析非正弦周期电流的线性电路了。
二、正弦交流电的数学表达式和三要素正弦交流电在任一瞬时的值称为瞬时值,用小写字母来表示,如e 、u 和i 分别表示电动势、电压和电流的瞬时值。
现以电流为例说明正弦弦交流电的数学表达式和三要素。
图3-1是一个正弦电流随时间变化的曲线,这种曲线称为波形图。
图中T 为电流i 变化一周所需的时间,称为周期,其单位为秒(s ),电流每秒变化的周数称为频率,用f 表示,单位为赫(Z H )。
频率与周期的关系是图3-1 正弦交流电流1f T=(3-1) 正弦交流电波形图的横座标可用t 表示,也可用t ω表示,分别如图3-1(a )、(b)所示。
该正弦电流的数学表达式为sin()m i i I t ωϕ=+ (3-2)式中i 为正弦电流的瞬时值,m I 为正弦电流的最大值,ω称为正弦量的角频率,iϕ称为初相位,t 为时间。
由上式可知,对于一个正弦电流i ,如果m I 、ω、i ϕ为已知,则它与时间t 的关系就是唯一确定的。
因此最大值、角频率、初相位称为正弦量的三要素,现分述如下:1.最大值由于正弦函数的最大值为1,所以式3-2中m I 为电流i 的最大值,也称幅值。
正弦量的最大值用带下标m 的大写字母表示,如m I 、m U 、m E 分别表示正弦电流、、正弦电压、正弦电动势的最大值。
2.角频率式3-2中的ω在数值上等于单位时间内正弦函数辐角的增长值,称为角频率,它的单位为弧度每秒(rad/s )。
由于在一个周期T 秒内辐角增长2π弧度,故2Tπω=(3-3) 式3-1和式3-3表明,频率、周期和角频率三个物理量都是说明正弦交流电变化快慢的同一物理实质的。
三个量中只要知道一个,便可求出其它两个量。
例如我国工业和民用电的频率50f Hz =(称为工频),其周期为10.02T s ==,角频率22314/T f rad s ωππ===。
【例3-1】某正弦电压的最大值310V m U =,初相30u ϕ=;某正弦电流的最大值14.1A m I =,初相60i ϕ=-。
它们的频率均为50Hz 。
试分别写出电压和电流的瞬时值表达式。
并画出它们的波形。
【解】电压的瞬时值表达式为sin()m u u U t ωϕ=+310sin(2)u ft πϕ=+ 310sin(31430)V t =+电流的瞬时值表达式为sin()m i i I t ωϕ=+ 14.1sin(31460)A t =- 电压和电流波形如图3-2所示。
图3-2 例3-1的波形【例3-2】试求上题中电压u 和电流i 在1t s =时的瞬时值。
【解】 310sin(25030)u t π=⨯+ 310sin(250130)π=⨯⨯+ 310sin(330)π=+310sin 90310V ==14.1sin(250130060)i π=⨯⨯- 14.1sin 00==计算表明,在1300t s =瞬时,电压u 达到最大值310V m U =,而电流i 到零点。
图3-2的波形也同样说明了这一点。
二、相位差在正弦交流电路中,有时要比较两个同频率正弦量的相位。
两个同频率正弦量相位之差称为相位差,以ϕ表示。
上例中电压与电流的相位差为()()u i t t ϕωϕωϕ=+-+u i ϕϕ=- (3-4)其数值为 30(60)90ϕ=--=即两个同频率正弦量的相位差等于它们的初相差。
若0ϕ>,表明u i ϕϕ>,如图3-2所示,则u 比i 先达到最大值也先到零点,称u 超前于i 一个相位角ϕ,或者说i 滞后一个相位角ϕ。
若0ϕ=,表明u i ϕϕ=,则u 与i 同时达到最大值也同时到零点,称它们是同相位,简称同相,如图3-3(a )所示。
若180ϕ=±,则称它们的相位相反,简称反相,如图3-3(b )所示。
若0ϕ<,表明u i ϕϕ<,则滞后于i (或i 超前u 一个相位角ϕ)。
所上所述,两个不同频率的正弦量计时起点(0)t =不同时,则它们的相位和初相位图3-3 两个正弦量的同相位与反相位不同,但它们之间的相位差不变。
在交流电路中,常常需研究多个不同频率正弦量之间的关系,为了方便起见,可以选取其中某一正弦量作为参考,称为参考正弦量。
令参考正弦量的初相0ϕ=,其他各正弦量的初相,即为该正弦量与参考正弦量的相位差(或初相差)。
例如图3-2所表达的u 和i ,当选取i 为参考量,即令i 的0i ϕ=,则u 的初相为90090u ϕ=-=。
这时电流和电压的表达式分别为14.1sin A 310sin(90)Vi t u t ωω==+当选取u 为参考正弦量时,即令u 的初相0u ϕ=,则i 的初相为90090i ϕ=--=-。
这时电压和电流的表达式分别为310sin V u t ω=14.1sin(90)A i t ω=-【例3-3】已知正弦电压u 和电流1i 、2i 的瞬时值表达式为12310sin(45)V 14.1sin(30)A 28.2sin(45)Au t i t i t ωωω=-=-=+ 试以电压u 为参考量重新写出电压u 和电流1i 、2i 的瞬时表达式。
【解】若以电压u 为参考量,则电压u 的表达式为310sin V u t ω=于1i 与u 的相位差为 1130(45)15i u ϕϕϕ=-=---= 故电流1i 的瞬时值表达式为 114.1sin(15)A i t ω=+ 由于2i 与u 的相位差为 2245(45)90i u ϕϕϕ=-=--= 故电流2i 的瞬时值表达式为 228.2sin(90)A i t ω=+三、有效值交流电的瞬时值是随时间而变的,因此不便用它来表示正弦量的大小。
在电工技术中,通常所说的交流电的电压或电流表数值,都是指它们的有效值。
交流电的有效值是电流的热效应原理来规定的,即交流电流的有效值是热效应与它相等的直流电的数值。
当某一交流电流i 通过一电阻R 在一人周期内所产生的热量,与某一直流电流I 通过同一电阻在相同时间内产生的热量相等时,则这一直流电流的数值就称为该交流电流的有效值,如图3-4所示。
交流电流i 在一个周期(T 秒)内,通过某一电阻R 所产生的热量为 20Tac Q i Rdt =⎰某一直流电流I 在相同时间(T 秒)内通过同一电阻R 所产生的热量为2ac Q I RT =若两者相等,则220d TRI T Ri t =⎰由上式可得I =(3-5) 这就是交流电流的有效值。
公式(3-5)对于计算任一周期电流的有效值都是适用的,可见交流电的有效值就是它的均方根值。
电动势、电压和电流的有效值分别用大写的E 、U 、I 表示。
对于正弦交流电流,则有m 0.707I I == (3-6) 同理,交流电动势的有效值m 0.707E E == (3-7) 交流电压的有效值m 0.707U U == (3-8) 可见,正弦交流电的有效值是它的最大值的值是从能量转换角度去考虑的等效直流值。
引入有效值后,便可借鉴直流电路的分析方法去处理交流电路的问题。
通常交流电机和电器的铭牌上所标的额定电压和额定电流都是指有效值,一般的交流电压和电流表的读数也是指有效值。
【例3-4】试求例3-3中正弦电压u 和电流1i 、2i 的有效值。
图3-4 交流电有效值的定义(a) 交流电通过电阻(b) 直流电通过电阻RR【解】电压 u 的有效值 220VU === 电流1i 的有效值110V I === 电流2i 的有效值220V I === 思考题3-1-1已知15sin314A i t =,215sin(94290)A i t =+你能说2i 比1i 超前90吗?为什么?3-1-2正弦量的最大值和有效值是否随时间变化?它们的大小与频率、相位有没有关系?3-1-3 将通常在交流电路中使用的220V 、100W 白炽灯接在220V 的直流电源上,试问发光亮度是否相同?为什么?3-1-4交流电的有效值就是它的均方根值,在什么条件下它的幅值与有效值之比是 ?3-1-5有一直流耐压为220V 的交、直流电容器,能否把它接在220V 的交流电源上使用?为什么?3.2 正弦量的相量表示法前已指出,正弦量可以用三角函数式或用波形图来表示,这两种方法明确地表达了正弦量的三要素。
但是,用这两种方法进行运算十分不便。
因此,有必要寻求使正弦量运算更简便的方法。
以下介绍的正弦量相量表示法将为分析、计算正弦交流电路带来极大方便。
一、旋转矢量设有一正弦电流m sin()i I t ωϕ=+,它可以用这样一个旋转矢量来表示:过直角坐标的原点作一矢量,矢量的长度等于该正弦量的最大值m I ,矢量与横轴正向的夹角等于该正弦量的初相角ϕ,该矢量逆时针方向旋转,其旋转的角速度等于该正弦量的角频率 。
那么这个旋转矢量任一瞬时在纵轴上的投影,就是该正弦函数i 在该瞬时的数值。
如图3-5所示,当0t ω=时,矢量在纵轴上的投影为0m sin i I t ω=;当1t t ωω=时,矢量在纵轴上的投影为1m 1sin()i I t ωϕ=+, 如此等等。
这就是说正弦量可以用一个旋转矢量来表示。
求解一个正弦量必须求得它的三要素。
但在分析正弦交流电路时,由于电路中所有的电压、电流都是同频率的正弦量,且它们的频率与正弦电源的频率相同,而电源频率往往是已知的,因此通常只要分析最大值(或有效值)和初相位两个要素就够了,而旋转矢量的角速度 可以省略,只需用一个有一定长度,与横轴有一定夹角的矢量来表示正弦量。
不仅如此,正弦量还可用以复数运算为基础的相量来表示。
二、复数一个复数有多表达形式,常见的有代数形式、三角函数形式和指数形式三种。