南京大学数学物理方法课件08 分离变数(傅里叶级数)法
- 格式:pdf
- 大小:844.08 KB
- 文档页数:83



数学物理方法(II)3、二维拉普拉斯方程—热传导二维矩形区域的稳态热传导问题:y uu 0b散热片的横截面为一矩形,长和宽分别a b 。
它的一边y=b 为和它的边y 处于较高的温度,其它三边保持零度。
求横截面上的xa 0(0,0)xx yy u u x a yb +=<<<<⎧稳恒的温度分布000|0,|0|0,|x x a y y b u u u u u ====⎪==⎨⎪==⎩=?求出任意点(x,y )的温度分布u (x,y )?(,)sin u x b u A C e D e x ==+01n n n n a=⎢⎥⎜⎟⎝⎠⎣⎦∑⎧再利用三角函数的正交性,可以得到:0 C D +=小结:(1)可以采用分离变量法(,)()()u r R r ϕϕ=Φ求解平面极坐标系中的拉普拉斯方程;(2)由周期性条件确定本征值和本征函数:2 (0,1,2,3...)()cos sin m m m m m A m B m λϕϕϕ==Φ=+在径向上的边界条件可以是非齐次的。
(3)拉普拉斯方程的通解为:00(,)ln u r C D rϕ∞=+叠加系数由径向上的非齐次边界条件确定()()1 +cos sin m m m m m m m C r D r A m B m ϕϕ−=++∑叠加系数由径向上的非齐次边界条件确定。
例2可以近似地认为带电云层与大地之间的静电场是均匀分布的,且电场强度E 0的方向竖直向下。
现将一个半径为a 的无限长直导线水平架设在该电场中,求导线周围的电场分布。
++带电云分析:轴其截面在平面++•取导体线的方向沿z 轴,其截面在xy 平面;•由于导体线是无线长的,可以取其一个界面进行分析另外导体线的截面个圆故y进行分析。
另外,导体线的截面一个圆,故可以采用平面极坐标系;(,)r ϕx•均匀电场的方向沿x 轴,即00xE =E e 大地/2π/2π−。

第四章 分离变量法 §4.1 分离变法介绍1.“顾名思义,分离变量法只能求出分离变量形式的解,如果一个定解问题不是分离变量形的,用分离变量法不可能求得这个解。
”试对上述说法加以评论。
解:分离变量法解方程可得到本征解,本征值说是分离变量形式的,但定解问题的一般是本征解的某个叠加,即由本征解组成的级数,这种解已不是分离变量形式的了,事实上,一个解即使不是分离变量形式的也可展为级数,所以由分离变量法得到的解,一般并不一定是分离变量形式的。
2.演奏琵琶是把弦的某一点向旁拨开一个小距离,然后放手任其自由振动。
设弦长为l ,被拨开的点在弦长的00(1n n 为正整数)处,拨开距离为h ,试求解弦的振动。
[注意:在解答中,不存在0n 谐音以及0n 整倍数次谐音。
因此,在不同位置拨弦(0n 不同),发出的声音的音色也就不同。
]图4-1解:定解问题为:⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧≤≤=⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛≤≤--⎪⎪⎭⎫ ⎝⎛≤≤===<<=-====)4(),0(,0)3(,),(,0,|)2(,0)1( ),0(,000000002l x u l x n l x l n l l h n l x x l h n u u u l x u a u t t t l x z zx tt 第一步,分离变量:设)()(),(t T x X t x u =以此代入泛定方程和边界条件:0)()()()(2=''-''x X t T a t T x X , (5)0)()()()0(==t T l X t T X , (6)由(5)式得到)()()()(2x X x X t T a t T ''='', (7)只有上式两端均等于同一常数时才有可能成立,把这个常数记为λ-,代入(7)式成为:λ-=''='')()()()(2x X x X t T a t T , 即,0)()(2=+''t T a t T λ (8),0)()(=+''x X x X λ (9)在(6)中,若取)(t T =0,得出0)()(==t T x X u ,显然无意义,只能取0)()0(==l X X第二步,求解本征值问题: 由方程(9)来求解)(x X ,这要分0,0=<λλ和0=λ三种情况。



第八章 分离变数(傅里叶级数)法§8.1 齐次方程的分离变数法(二) 例题例1 关于第二类齐次边界条件的问题 p185()()()()()()19.1.8....0............18.1.8........ (00)17.1.8..........00002l x x u x u u u u a u t t t lx xx x xx tt <<=====-====ψϕ第一步:分离变量()()()()20.1.8...............,t T x X t x u =()()()()()()22.1.8,......0,.....0021.1.8................02='='=''-''t T l X t T X T X a T X()()()23.1.8,......0,.....00='='l X X()λ-=''=''''=''XX T a T X X T a T XT a 22221.1.8得两边同除以()()()()()25.1.8.................0;23.1.8,......0,.....0024.1.8....,.........02=+''='='=+''T a T l X X X X λλ 构成本征值问题 第二步:求解本征值问题(8.1.23)和(8.1.24)()()()()()的解是方程于是得根据无意义。
得出24.1.8,0,023.1.8,,0,0,00000>==+==≡<λλλC x X D x D C x X x X ()x C x C x X λλsin cos 21+=()确定,即由积分常数23.1.8,21C C()cos sin 0212=+-=l C l C C λλλλ(),即于是无意义。

第三章付里叶级数和付里叶变换第三章主要包括以下几点内容:1、付里叶级数教学内容要点:(1)、三角函数的正交性(2)、周期信号的付里叶展开(3)、奇、偶函数的付里叶展开(4)、付里叶级数的指数形式2、付里叶变换教学内容要点:(1)付里叶变换式(2)奇异函数的付里叶变换3、付里叶变换的性质教学内容要点:(1)、线性(2)、奇、偶性(3)、对称性(4)、尺度变换(5)、时移特性(6)、频移特性(7)、卷积定理(8)、时域微分和积分(9)、频率微分和积分4、周期信号的付里叶变换教学内容要点:(1)正、余弦函数的付里叶变换(2)一般周期函数的付里叶变换第三章内容的学时分配:湖南文理学院12课时,芙蓉学院16课时。
分为4部分:一、傅里叶级数二、傅里叶变换三、傅里叶变换的性质四、周期信号的傅里叶变换一、傅里叶变换级数教学重点:1、傅里叶变换式;2、奇异函数的傅里叶变换教学难点:1、傅里叶变换式;2、奇异函数的傅里叶变换教学目的:1、掌握傅里叶变换式;2、掌握奇异函数的傅里叶变换教学方法:讲授法,演示法教学课时:文理学院3课时;芙蓉学院4课时教学过程:1.傅里叶变换二、 傅里叶变换教学重点:1、傅里叶变换式;2、奇异函数的傅里叶变换教学难点:1、傅里叶变换式;2、奇异函数的傅里叶变换教学目的:1、掌握傅里叶变换式;2、掌握奇异函数的傅里叶变换教学方法:讲授法,演示法教学课时:文理学院3课时;芙蓉学院4课时教学过程:2. 傅里叶变换对于非周期信号,重复周期T 趋于无限大,谱线间隔趋于无穷小量d ω,而离散频率n Ω变成连续频率ω。
在这种极限情况下,n F 趋于无穷小量,但Ω=⋅n n F T F π2可望趋于有限值,且为一个连续函数,通常记为F (j ω),即dt et f F j F tjn TT T nT ωωπω--∞→∞→⎰==22)(lim2lim)(得dt et f j F tj ωω-∞∞-⎰=)()(称)(ωj F 为非周期信号)(t f 的频谱密度函数。

第八章平面坐标下的分离变量本征值问题(一)通过上一章的讨论,我们知道,在研究物理(场)量的变化时,不仅要考虑物理(场)量随时间的变化规律,有时候还需要考虑其在空间变化规律,由此便导致了反映物理规律的“偏微分方程”。
偏微分方程泛指同一类的物理规律,因此称为泛定方程。
偏微分方程若附加上边界条件、初始条件的限制,则物理过程(解)就唯一确定,此时便构成了定解问题。
对于偏微分方程用高等数学中介绍的一些方法,无法求解。
因此必须引进分离变量法。
分离变量法是把偏微分方程分解为几个常微分方程,从而达到求解之目的一个数学过程。
分离变数法的可行性问题:上一章推导出了三类偏微分方程,波动方程、输运方程和泊松方程。
第一类、第二类方程都是时间和空间的函数,我们在普通物理中曾对驻波问题进行过研究,其空间周期性和时间周期性彼此独立,由此受到启发,其解应具(,)()()的形式。
对于第三种情况——u x t X x T t泊松方程,反映的是“有源”情况下的一种作用,其效果相当于简单叠加。
由此看来,变量是可以分离的。
实际情况如何?我们可以通过实例进行验证。
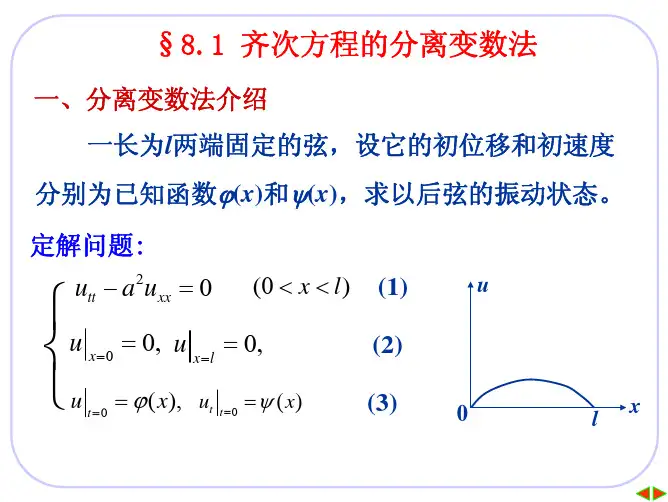
§8.1 齐次方程的分离变数法一、分离变数法简介以两端固定的均匀弦的自由振动为例。
其定解问题为2000000(0)()()tt xx x x l t t t u a u u u x l u x u x ϕψ====⎧-=⎪⎪==<<⎨⎪==⎪⎩ (8.1.1) 这里研究的弦是有限长的,它有两个端点,波就在这两端点之间往复反射。
这样,驻波解的一般表示式应当为设 (,)()()u x t X x T t = (8.1.2)在(8.1.2)中,自变数x 只能出现于X 之中,自变数t 只出现于T 之中,驻波的一般表示式具有分离变数的形式。
那么,在两端固定的弦上究竟有哪些驻波呢?把驻波的一般表示式(8.1.2)代入弦振动方程(8.1.1)和相应的边界条件,得:20(0)()0()()0XT a X T X T t X l T t ''''⎧-=⎪=⎨⎪=⎩(8.1.3) 条件(8.1.3)表示,在时刻t ,)()0(t T X 和)()(t T l X 总是零。
数学物理方法(II)3、二维拉普拉斯方程—热传导二维矩形区域的稳态热传导问题:y uu 0b散热片的横截面为一矩形,长和宽分别a b 。
它的一边y=b 为和它的边y 处于较高的温度,其它三边保持零度。
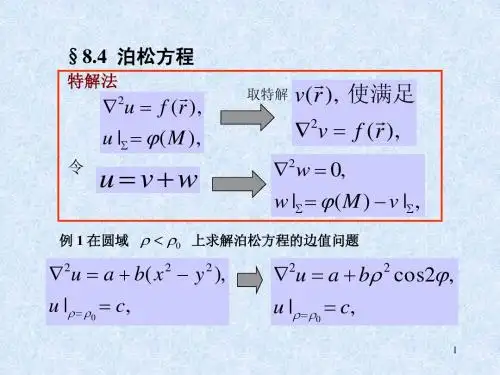
求横截面上的xa 0(0,0)xx yy u u x a yb +=<<<<⎧稳恒的温度分布000|0,|0|0,|x x a y y b u u u u u ====⎪==⎨⎪==⎩=?求出任意点(x,y )的温度分布u (x,y )?(,)sin u x b u A C e D e x ==+01n n n n a=⎢⎥⎜⎟⎝⎠⎣⎦∑⎧再利用三角函数的正交性,可以得到:0 C D +=小结:(1)可以采用分离变量法(,)()()u r R r ϕϕ=Φ求解平面极坐标系中的拉普拉斯方程;(2)由周期性条件确定本征值和本征函数:2 (0,1,2,3...)()cos sin m m m m m A m B m λϕϕϕ==Φ=+在径向上的边界条件可以是非齐次的。
(3)拉普拉斯方程的通解为:00(,)ln u r C D rϕ∞=+叠加系数由径向上的非齐次边界条件确定()()1 +cos sin m m m m m m m C r D r A m B m ϕϕ−=++∑叠加系数由径向上的非齐次边界条件确定。
例2可以近似地认为带电云层与大地之间的静电场是均匀分布的,且电场强度E 0的方向竖直向下。
现将一个半径为a 的无限长直导线水平架设在该电场中,求导线周围的电场分布。
++带电云分析:轴其截面在平面++•取导体线的方向沿z 轴,其截面在xy 平面;•由于导体线是无线长的,可以取其一个界面进行分析另外导体线的截面个圆故y进行分析。
另外,导体线的截面一个圆,故可以采用平面极坐标系;(,)r ϕx•均匀电场的方向沿x 轴,即00xE =E e 大地/2π/2π−。