导热基本定律

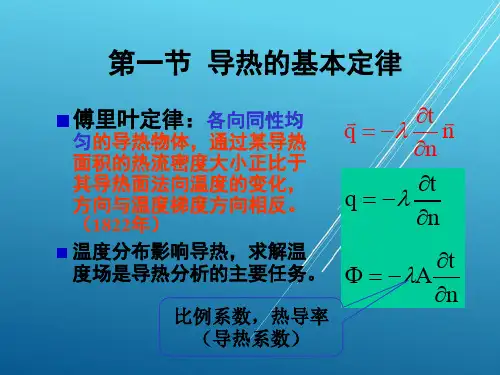
2.1 导热基本定律—傅立叶定律研究方法：从连续介质的假设出发、从宏观的角度来讨论导热热流 量与物体温度分布及其他影响因素之间的关系。

一般情况下，绝大多数固体、液体及气体都可以看作连 续介质。

但是当分子的平均自由行程与物体的宏观尺寸相比 不能忽略时，如压力降低到一定程度的稀薄气体，就不能认 为是连续介质。

主要内容：（1）导热的基本概念、导热基本定律 ；（2）导热现象的数学描述方法； （3）几种稳态导热的计算方法。

2.1 导热基本定律—傅立叶定律‹气体——导热是气体分子不规则热运动‹ 导 电 固 体——自由电子的运动‹ 非导电固体——过晶格结构的振动(弹性声波)‹液体——类似气体 or 类似非导电固体1. 温度场(温度分布)：指在各个时刻物体内各点温度分布的总称。

物体的温度分布是坐标和时间的函数 t = f (x, y, z,τ )‹ 稳态温度场(定常温度场) t = f (x, y, z)‹ 非稳态温度场(非定常温度场) t = f (x, y, z,τ )2.1 导热基本定律—傅立叶定律2. 等温面与等温线‹ 等温面：同一时刻、温度场中所有温度 相同的点连接起来所构成的面‹ 等温线：用一个平面与各等温面相交， 在这个平面上得到一个等温线簇等温面与等温线的特点：‹ 彼此不能相交 ‹ 不会中断，它们或者是物体中完全封闭的曲面（曲线），或者就终止与物体的边界上t+Δt t t-Δt2.1 导热基本定律—傅立叶定律2. 等温面与等温线 等温线图的物理意义：‹ 若每条等温线间 的温度间隔相等 时，等温线的疏 密可反映出不同 区域导热热流密 度的大小。

如图 所示是用等温线 图表示温度场的 实例。

2.1 导热基本定律—傅立叶定律3. 温度梯度在温度场中，温度沿x方向的 变化率(即偏导数)∂t = ∂xlimΔt ΔxΔx → 0明显, 等温面法线方向的温度变化率最大，温度变化最剧烈。

∂t < ∂t ∂x ∂n温度梯度：等温面法线方向的温度变化率矢量：gradt = ∂t n ∂n温度梯度是矢量，指向温 度增加的方向。

导热基本定律导热基本定律是研究物体传热过程中的一个基本原理，它描述了导热的规律和特性。

导热基本定律是热传导学中非常重要的一个定律，它对于我们理解物体的热传导行为和研究热传导过程具有重要的意义。

热传导是指热量从高温区域传递到低温区域的过程，它是由物质内部的分子热运动引起的。

导热基本定律告诉我们，热量在物体内部的传导速度与物体的温度梯度成正比，与物体的导热性能成反比。

根据导热基本定律，热量的传导速率与物体的温度梯度成正比。

温度梯度是指物体在空间上温度变化的速率。

例如，一个物体的一端温度为100℃，另一端温度为50℃，那么这个物体的温度梯度就是(100-50)/L，其中L为物体的长度。

温度梯度越大，热量的传导速率就越快。

导热基本定律还告诉我们，热量的传导速率与物体的导热性能成反比。

导热性能是指物体传导热量的能力，它与物体的导热系数有关。

导热系数越大，物体的导热性能就越好，热量的传导速率也就越快。

导热系数与物体的材料性质有关，例如金属的导热系数通常比非金属材料大。

导热基本定律的应用非常广泛。

在工程领域，我们常常需要计算物体的热传导速率，以便设计合适的散热装置。

例如，在电子设备中，为了保持设备正常工作温度，通常需要设计散热片或散热风扇来加速热量的散发。

利用导热基本定律，我们可以计算散热装置的尺寸和材料，以确保设备的热量得到有效散发。

在材料科学研究中，导热基本定律也是一个重要的工具。

通过研究不同材料的导热性能，我们可以了解材料的热传导特性，并在实际应用中选择合适的材料。

例如，在建筑材料的选用中，导热性能是一个重要的考虑因素。

对于冬季保温材料，我们希望材料导热系数较小，以减少室内热量的传导损失；而对于夏季隔热材料，我们希望材料导热系数较大，以阻止室外热量的传导入室内。

导热基本定律是研究物体传热过程中的一个基本原理，它描述了热量在物体内部的传导规律和特性。

通过了解导热基本定律，我们可以更好地理解和应用热传导学知识，为工程设计和材料选择提供科学依据。

第九章导热9-1 导热理论基础1. 导热的基本概念（1）温度场(temperature field)在τ时刻，物体内所有各点的温度分布称为该物体在该时刻的温度场。

一般温度场是空间坐标和时间的函数，在直角坐标系中，温度场可表示为t=fy),,,(τzx非稳态温度场:温度随时间变化的温度场，其中的导热称为非稳态导热。

稳态温度场:温度不随时间变化的温度场，其中的导热称为稳态导热。

(),,t f x y z=一维温度场二维温度场三维温度场(),t f xτ=()t f x=(),,t f x yτ=(),t f x y=(),,,t f x y zτ=(),,t f x y z=（2）等温面与等温线在同一时刻，温度场中温度相同的点连成的线或面称为等温线或等温面。

等温面与等温线的特征：同一时刻，物体中温度不同的等温面或等温线不能相交；在连续介质的假设条件下，等温面（或等温线）或者在物体中构成封闭的曲面（或曲线），或者终止于物体的边界，不可能在物体中中断。

（3）温度梯度(temperature gradient)在温度场中，温度沿x 方向的变化率(即偏导数)0lim x t t x x∂∂∆→∆=∆很明显,等温面法线方向的温度变化率最大，温度变化最剧烈。

温度梯度：等温面法线方向的温度变化率矢量：tt n∂=∂grad nn —等温面法线方向的单位矢量，指向温度增加的方向。

温度梯度是矢量，指向温度增加的方向。

6在直角坐标系中，温度梯度可表示为t t tt x y z∂∂∂=++∂∂∂grad i j kt t tx y z∂∂∂∂∂∂、、分别为x 、y 、z 方向的偏导数;i 、j 、k 分别为x 、y 、z 方向的单位矢量。

（4）热流密度(heat flux)d d q AΦ=热流密度的大小和方向可以用热流密度矢量q 表示d d AΦ=-q n热流密度矢量的方向指向温度降低的方向。

nt d Ad Φq在直角坐标系中，热流密度矢量可表示为x y z q q q =++q i j kq x 、q y 、q z 分别表示q 在三个坐标方向的分量的大小。

导热的基本定律导热的基本定律导热是物体内部热能传递的一种方式，它是指在物体内部由温度高处向温度低处传递热量的过程。

导热的基本定律可以通过研究物体内部温度分布和热流密度之间的关系来描述。

一、傅里叶定律傅里叶定律是描述物体内部温度分布与时间和空间变化之间关系的一个重要定律。

根据傅里叶定律，物体内部温度分布与时间和空间变化之间存在着一种数学关系，即：q=-kA(dT/dx)其中，q表示单位时间内通过面积A传递的热流量，k表示材料的导热系数，dT/dx表示单位长度上温度变化率。

二、傅里叶传导方程傅里叶传导方程是描述物体内部温度分布随时间变化的一个偏微分方程。

傅里叶传导方程可以用来求解物体内部温度随时间变化的规律。

它可以用以下形式表示：∂u/∂t=k∇²u其中，u表示物体内部温度分布函数，t表示时间，k表示材料的导热系数，∇²表示拉普拉斯算子。

三、热传导方程热传导方程是描述物体内部温度分布随时间和空间变化的一个偏微分方程。

它可以用来求解物体内部温度随时间和空间变化的规律。

热传导方程可以用以下形式表示：∂u/∂t=k∇²u+q其中，u表示物体内部温度分布函数，t表示时间，k表示材料的导热系数，∇²表示拉普拉斯算子，q表示单位时间内通过面积A传递的热流量。

四、导热系数导热系数是材料特性之一，它描述了材料对于单位面积上单位长度内温度梯度的响应能力。

在傅里叶定律中，k被称为材料的导热系数。

不同材料具有不同的导热系数，在工程设计中需要根据实际情况选择合适的材料。

五、影响导热的因素影响导热的因素主要有以下几个：1. 材料本身特性：不同材料具有不同的导热系数。

2. 温度差：温度差越大，热传导越快。

3. 材料厚度：材料厚度越大，热传导越慢。

4. 材料结构：材料结构的复杂程度会影响热传导的速率。

总之，导热是物体内部热能传递的一种重要方式，傅里叶定律、傅里叶传导方程和热传导方程等基本定律可以用来描述物体内部温度分布与时间和空间变化之间的关系。

导热的基本定律1. 介绍在我们的日常生活中，我们经常会接触到导热现象。

当我们触摸一个热的物体时，我们可以感受到热量从物体传递给我们的手。

导热是一种物质内部热能传播的过程，它是热力学的基本定律之一。

导热的基本定律可以用来描述和解释导热现象。

它提供了一种数学模型，用以计算热量在物质中的传递方式和速率。

本文将详细介绍导热的基本定律，并探讨其应用和实际意义。

2. 导热的基本定律导热的基本定律可以简述为：热量在物质中的传递速率正比于温度梯度的负值。

换句话说，当物体内部存在温度差异时，热量会从高温区域传递到低温区域。

这一定律可以用下面的方程来表示：dQ dt =−kAdTdx其中，dQdt表示单位时间内热量的传递速率，单位为瓦特(W)；k表示导热系数，是物质的一个常量，单位为瓦特/(米·开尔文)(W/(m·K))；A表示传热的面积，单位为平方米(m^2)；dTdx表示温度梯度，即单位距离内温度的变化率，单位为开尔文/米(K/m)。

这个方程可以解释为：单位面积上的热传递速率等于导热系数乘以温度梯度的负值。

这意味着热量从高温区域传递到低温区域，传递速率取决于温度差。

3. 应用和实际意义导热的基本定律在许多领域都有广泛的应用和实际意义。

下面将介绍几个常见的应用案例：3.1. 热传导热传导是导热的一种常见形式，它是指热量通过物质内部分子之间的碰撞传递。

导热的基本定律可以用来计算热量在物体中的传递速率，从而帮助我们设计和优化热传导器件，如散热器。

散热器是一种常见的设备，用于将热量从一个区域传递到另一个区域。

通过热传导，散热器能够将热量从高温的电子元件传递到环境中去，以保持元件的正常工作温度。

在设计散热器时，我们可以根据导热的基本定律来优化散热器的结构和材料，以提高散热效果。

3.2. 热传递热传递是指热量在物体间通过直接接触传递的过程，它是导热的另一种形式。

导热的基本定律同样适用于热传递过程。

例如，在建筑工程中，我们可以利用导热的基本定律来计算建筑材料的热传递速率。

导热基本定律
导热基本定律是指在恒定温度下，物质内部的热量传递速率与传热距离成反比，与传热面积成正比，与物质本身的导热性能有关。

这个定律被称为傅里叶定律。

傅里叶定律的表达式为：Q/t = -kA(dT/dx)，其中Q/t表示单位时间内通过介质传递的热量，k表示介质的导热系数，A表示传热面积，dT/dx表示温度梯度。

该式表明，在单位时间内通过介质传递的热量与介质的导热系数成正比，与传热面积和温度梯度成正比。

该定律在工程领域中具有广泛应用。

例如，在建筑领域中，设计师需要考虑墙体、屋顶和地板等建筑材料的导热性能以确保房屋能够保持舒适的室内温度；在电子设备制造领域中，设计师需要考虑材料的导电性和导热性以确保设备能够高效运行并避免过热损坏；在化学工业领域中，工程师需要考虑反应器内部的传热问题以确保化学反应能够高效进行。

总之，导热基本定律是物质内部热量传递的基础规律，对于各个领域的工程设计和生产都有着重要的意义。