成角透视原理与规律详细图文介绍

[键入文字]
成角透视原理与规律详细图文介绍
成角透视就是景物纵深与视中线成一定角度的透视，凡是与画面既不平行又不垂直的水平直线，都消失于视平线上的一点，叫余点，余点在视平线上，景物的纵深因为与视中线不平行而向主点两侧的余点消失。

凡是平行的直线都消失于同一个余点，例如楼房的每层分界线都消失于同一个余点。

所以，对于立方体景物，在成角透视中都有两个余点，这两个余点在主点两侧。

成角透视:(二点透视)就是把立方体画到画面上，立方体的四个面相对于画面倾斜成一定角度时，往纵深平行的直线产生了两个消失点。

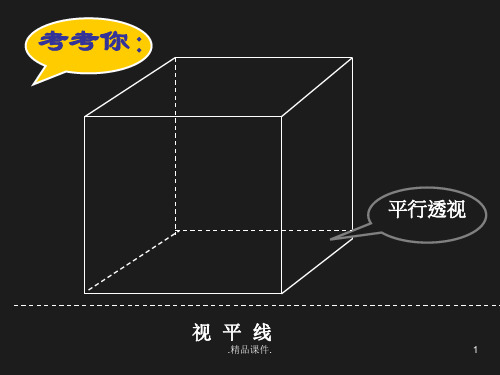
在这平行情况下，与上下两个水平面相垂直的平行线也产生了长度的缩小，但是不带有消失点.平行透视是景物纵深与视中线平行而向主点消失。

成角透视就是景物纵深与视中线成一定角度的透视，景物的纵深因为与视中线不平行而向主点两侧的余点消失。

两点透视，简单理解就是物体两面角正对着我们的眼睛。

三点透视，简单理解就是物体三面的顶点正对着我们的眼睛，多用于仰视和俯视图中。

tips:感谢大家的阅读，本文由我司收集整编。

仅供参阅！
1。

透视PERSPECTIVE绪论授课教师：乔会杰透视原理之谜“透视”一词来源于拉丁文“Perspicere”, 在英文中演变为perspicacity，意思是“透而视之”，就是透过一个假定的透明平面去观察物体。

使三维物体形状影印在这个透明的平面上，得到图形。

•透视学术语：视点、足点、心点、距点、灭点视线、视心线、视平线、地平线、原线、变线视锥、视圈、视角、视域、视高画面、基面平视、仰视、俯视透视原理之谜* 点视点、站点、心点、距点、灭点、余点视点：EP（Eye Point）：眼睛所在的位置站点：SP（Stand Point）：视点到地面的垂直投影心点：CP（Center Point）：视点到画面的垂足* 点视点、站点、心点、距点、灭点、余点灭点：VP（Vanishing Point）：过视点作直线的平行线与画面的交点（透视线的终点），也叫消失点。

距点：DP（Distant Point）：与画面呈45度角直线的灭点透视原理之谜面：基面、画面、视平面基面GP（Grand Plane）：物体放置的平面画面PP（Picture Plane）：假想的透明平面视平面HP（Horizontal Plane）：人眼高度所在平面透视原理之谜、视高线* 线：视线、视心线、视平线、基线、测线视线SL（Sight Line）：视点和物体上各点的连线视心线CVL（Central Visual Line）：视点和心点连线视平线HL（Horizontal Line）：视平面和画面交线线：视线、视心线、视平线、基线、测线、视高线视高线DL（Distant Line）：视点到站点的垂直线基线GL（Grand Line）：画面和基面的交线测线ML（Measuring Line）：为方便绘图作的辅助测量线透视原理之谜设计透视的三大元素：视高、视距、角度•视高：视高是指视平线所在的高度。

透视原理之谜设计透视的三大元素：•视距：视点到画面的距离。