11凸轮机构运动参数的测定
- 格式:doc
- 大小:608.50 KB
- 文档页数:7


实验十一机构运动参数测试一、概述本实验的实验装置,只需拆装少量零部件,即可分别构成四种典型的传动系统,即:曲柄滑块机构、导杆机构、平底直动从动件凸轮机构和滚子直动从动件凸轮机构。
而每一种机构的某一些参数,如曲柄长度、连杆长度、滚子偏心等都可在一定范围内作一些调整,学生通过拆装及调整可加深对机械结构本身特点的了解,对参数改动对整个运动状态的影响也会有更好的认识。
二、实验目的(1)通过实验、了解位移、速度、加速度的测定方法;转速及回转不匀率的测定方法;(2)通过实验,初步了解“QTD-Ⅲ型组合机构实验台”及光电脉冲编码器、同步脉冲发生器(或称角度传感器)的基本原理,并掌握它们的使用方法;(3)通过比较理论运动线图与实测运动线图的差异,并分析其原因,增加对速度特别是加速度的感性认识;(4)比较曲柄滑块机构与导杆机构的性能差别;(5)检测凸轮直动从动件的运动规律;(6)比较不同凸轮廓线或接触副对从动件运动规律的影响。
三、实验设备(1)实验机构:曲柄滑块导杆凸轮组合机构(2) QTD-Ⅲ型组合机构实验仪(单片机控制系统);(3) 打印机;(4)个人电脑一台;(5)光电脉冲编码器;(6)同步脉冲发生器(或称角度传感器)。
四、实验台结构和工作原理1.实验机构本实验配套的为曲柄滑块机构及导杆机构和凸轮机构,其原动力采用直流调速电机,电机转速可在0-3000r/min范围作无级调速。
经蜗杆蜗轮减速器减速,机构的曲柄转速为0-100r/min。
利用往复运动的滑块推动光电脉冲编码器,输出与滑块位移相当的脉冲信号,经测试仪处理后将可得到滑块的位移、速度及加速度。
图11-1(a)为曲柄滑块机构的结构形式,图11-1(b)为导杆机构的结构形式,图11-1(c)(d)是凸轮机构的结构形式。
后者是前者经过简便的改装而得到的,在本实验机构中已配有改装所必备的零件。
图11-1(a) 曲柄滑块机构 图11-1(b) 导杆机构图11-1(c)平底直动从动件凸轮机构 图11-1(d)滚子直动从动件凸轮机构在图11-1中,1.同步脉冲发生器;2.蜗轮减速器;3.曲柄;4.连杆;5.电机;6.滑块;7.齿轮;8.光电脉冲编码器;9.导块;10.导杆;11 凸轮;12 平底直动从动件;13 恢复弹簧;14 滚子直动从动件;15 光栅盘2.QTD-Ⅲ型组合机构实验仪此实验仪的外形结构如图11-2所示,图11-2(a)为正面结构,图11-2(b)为背面结构。

实验四机构运动参数测试机构运动参数测试实验以曲柄摇杆机构、曲柄滑块机构、双曲柄机构和凸轮机构等典型运动机构作为被测对象。
本着理论联系实际的作法,在实验中必须将实验检测结果与理论数据进行对比,并从中分析实验误差产生的原因及其主要影响因素。
因此,实验前大都需要按实验指导书规定的待定检测对象及其原始数据,通过在计算机上进行理论计算,求解理论数据,然后方可进行实验。
在进行实验操作之前,需要通过阅读实验装置的使用说明书,熟悉实验装置的工作原理和仪器仪表的使用操作方法。
然后才能进行独立实验操作。
一、实验目的1、通过运动参数测试实验,掌握机构运动的周期性变化规律,并学会机构运动参数如:位移、速度和加速度(包括角位移、角速度和角加速度)的实验测试方法;2、通过利用传感器、工控机等先进的实验技术手段进行实验操作,熟悉LabVIEW软件的一些常用功能和程序的编写方法,训练掌握现代化的实验测试手段和方法,增强工程实践能力;3、通过进行实验结果与理论数据的比较,分析误差产生的原因,增强工程意识,树立正确的设计理念。
二、实验装置及工具1、实验装置的组成(1)实验装置的特点该实验以培养学生的综合设计能力、创新设计能力和工程实践能力为目标。
打破了传统的演示性、验证性、单一性实验的模式,建立了新型的设计型、搭接型、综合性的实验模式。
本实验提供多种搭接设备,学生可根据功能要求,自己进行方案设计,并将自己设计的方案亲手组装成实物模型。
形象直观,安装调整简捷,并可随时改进设计方案,从而培养学生的创造性和正确的设计理念。
(2)实验装置的功用实验中,可组合出:①曲柄滑块;②双曲柄;③摆动导杆;④曲柄摇杆;⑤滑块为输出构件的简单的平面六杆机构;⑥直动从动件凸轮机构;⑦摆动从动件凸轮机构实验台等多种典型的运动机构;另外,各构件尺度参数可调,突出了测试机构的尺寸参数的多变性。
这样可增加学生的实验题目和测试目标,使同学在实验中充分理解尺寸参数、原动件运动规律等因素对机构运动学方面的影响,巩固学生在课堂中所学知识,使之产生感性认识,增加对机械学研究的兴趣,同时达到一机多用的目的。

凸轮轴凸轮表面测量方法1. 引言凸轮轴是内燃机中的一个重要零部件,它承受着凸轮的运动和转动。
凸轮轴的凸轮表面质量直接影响发动机的性能和寿命。
因此,为了确保凸轮轴的质量,需要使用合适的测量方法来检测凸轮表面的特征参数。
本文将介绍凸轮轴凸轮表面测量的常用方法,包括光学测量法、机械测量法和三维测量法等。
每种方法都有其特点和适用范围。
2. 光学测量法光学测量法是一种常用的凸轮轴凸轮表面测量方法,它利用光学原理来获取凸轮表面的形貌和特征参数。
常用的光学测量仪器有同焦面光学显微镜、投影仪和激光扫描仪等。
2.1 同焦面光学显微镜同焦面光学显微镜是一种非接触式的测量仪器,它可以在高分辨率下观察凸轮表面的特征。
通过调整焦距,可以获得不同尺寸的图像。
使用同焦面光学显微镜可以量测凸轮的直径、主凸距、凸顶高度等参数。
此外,还可以检测凸轮表面的缺陷和磨损程度。
2.2 投影仪投影仪是一种常用的凸轮轴凸轮表面测量设备,它可以投影凸轮的放大图像并测量其各项特征。
投影仪一般由光源、透镜、测量屏幕等部分组成。
通过调整透镜和光源的位置,可以得到不同分辨率和放大倍率的投影图像。
使用投影仪可以测量凸轮的轮廓曲线、圆度、平行度等参数。
2.3 激光扫描仪激光扫描仪是一种高精度的凸轮轴凸轮表面测量设备,它可以通过激光束的扫描获取凸轮表面的三维坐标信息。
激光扫描仪采用非接触式测量方式,不会对凸轮表面造成损伤。
通过后期处理,可以得到凸轮表面的三维模型,并进一步提取凸轮的特征参数,如凸轮高度、凸轮面积等。
3. 机械测量法机械测量法是一种传统的凸轮轴凸轮表面测量方法,主要依靠机械测量工具来获取凸轮表面的特征参数。
常用的机械测量工具有表面测量仪、千分尺、外径卡规等。
3.1 表面测量仪表面测量仪是一种用于测量凸轮表面粗糙度和形状的机械测量工具。
它由测量头、测量刀、测量系统等部分组成。
通过将测量头沿着凸轮表面滑动,可以得到凸轮的表面粗糙度参数,如Ra、Rz等。
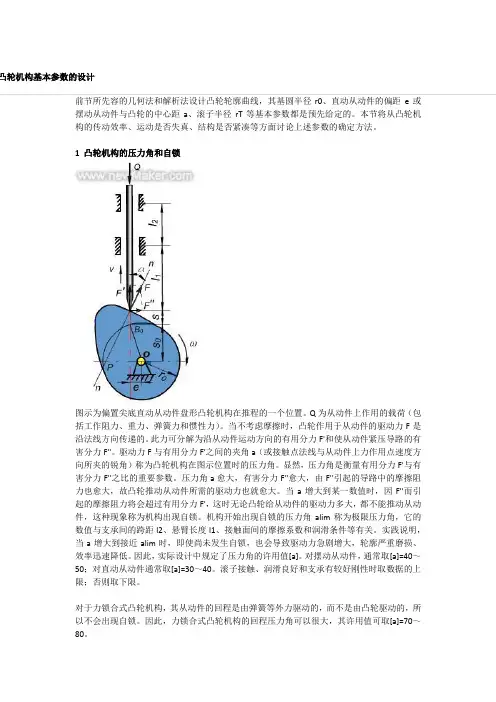
凸轮机构基本参数的设计前节所先容的几何法和解析法设计凸轮轮廓曲线,其基圆半径r0、直动从动件的偏距e或摆动从动件与凸轮的中心距a、滚子半径rT等基本参数都是预先给定的。
本节将从凸轮机构的传动效率、运动是否失真、结构是否紧凑等方面讨论上述参数的确定方法。
1 凸轮机构的压力角和自锁图示为偏置尖底直动从动件盘形凸轮机构在推程的一个位置。
Q为从动件上作用的载荷(包括工作阻力、重力、弹簧力和惯性力)。
当不考虑摩擦时,凸轮作用于从动件的驱动力F是沿法线方向传递的。
此力可分解为沿从动件运动方向的有用分力F'和使从动件紧压导路的有害分力F''。
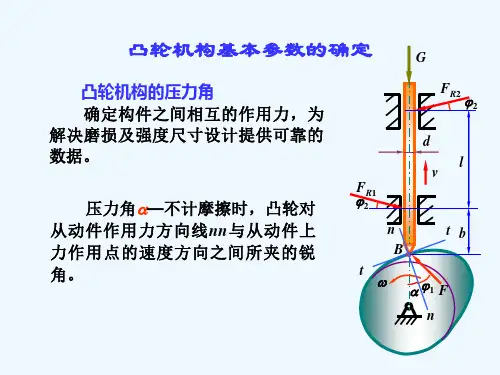
驱动力F与有用分力F'之间的夹角a(或接触点法线与从动件上力作用点速度方向所夹的锐角)称为凸轮机构在图示位置时的压力角。
显然,压力角是衡量有用分力F'与有害分力F''之比的重要参数。
压力角a愈大,有害分力F''愈大,由F''引起的导路中的摩擦阻力也愈大,故凸轮推动从动件所需的驱动力也就愈大。
当a增大到某一数值时,因F''而引起的摩擦阻力将会超过有用分力F',这时无论凸轮给从动件的驱动力多大,都不能推动从动件,这种现象称为机构出现自锁。
机构开始出现自锁的压力角alim称为极限压力角,它的数值与支承间的跨距l2、悬臂长度l1、接触面间的摩擦系数和润滑条件等有关。
实践说明,当a增大到接近alim时,即使尚未发生自锁,也会导致驱动力急剧增大,轮廓严重磨损、效率迅速降低。
因此,实际设计中规定了压力角的许用值[a]。
对摆动从动件,通常取[a]=40~50;对直动从动件通常取[a]=30~40。
滚子接触、润滑良好和支承有较好刚性时取数据的上限;否则取下限。
对于力锁合式凸轮机构,其从动件的回程是由弹簧等外力驱动的,而不是由凸轮驱动的,所以不会出现自锁。
因此,力锁合式凸轮机构的回程压力角可以很大,其许用值可取[a]=70~80。



凸轮的精度检验方法
凸轮的精度检验方法如下:
弯曲检查。
将凸轮轴装在车床两顶针间或用"V"形垫铁支住两端轴颈,放在平板上,将百分表触及中部轴颈,转动凸轮轴,表针摆动的最大值和最小值之差的一半为直线度偏差。
其数值大于0.05mm时应进行冷压校直。
轴颈检查。
用外径千分卡测量各道轴颈的圆度和圆柱度。
圆度和圆柱度偏差大于0.015mm 时,用磨削方法缩小尺寸修复,每级级差为-0.20mm,一般可加工至-1.0mm。
凸轮检查。
用样板或外径分厘米卡检查,凸轮高度比标准高度低0.4mm时,应修磨凸轮;低1.0mm时,用堆焊法修复。
凸轮起槽或有斑点要用油石修复。

% ******** 偏置移动从动件盘形凸轮设计绘图和运动分析******** disp ' ######## 已知条件########'disp ' 凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边'disp ' 从动件在推程作等加速/等减速运动,在回程作余弦加速度运动' % 基圆半径;滚子半径;从动件偏距;从动件升程rb=40;rt=10;e=15;h=50;% 推程运动角;远休止角;回程运动角;推程许用压力角;凸轮转速ft=100;fs=60;fh=90;alpha_p=35;n=200;% 角度和弧度转换系数;机构尺度hd=pi/180;du=180/pi;se=sqrt(rb^2-e^2);w=n*pi/30; omega=w*du; % 凸轮角速度(°/s)fprintf(' 基圆半径rb = %3.4f mm \n',rb)fprintf(' 滚子半径rt = %3.4f mm \n',rt)fprintf(' 推杆偏距 e = %3.4f mm \n',e)fprintf(' 推程升程h = %3.4f mm \n',h)fprintf(' 推程运动角ft = %3.4f 度\n',ft)fprintf(' 远休止角fs = %3.4f 度\n',fs)fprintf(' 回程运动角fh = %3.4f 度\n',fh)fprintf(' 推程许用压力角alpha_p = %3.4f 度\n',alpha_p) fprintf(' 凸轮转速n = %3.4f r/min \n',n) fprintf(' 凸轮角速度(弧度) w = %3.4f rad/s \n',w)fprintf(' 凸轮角速度(度) omega = %3.4f 度/s \n',omega) disp ' 'disp ' @@@@@@ 计算过程和输出结果@@@@@@' disp ' '% (1)---校核凸轮机构的压力角和轮廓曲率半径'disp ' *** 计算凸轮理论轮廓的压力角和曲率半径***'disp ' 1 推程(等加速/等减速运动)'for f=1:ftif f<=ft/2s(f)=2*h*f^2/ft^2;s=s(f); % 等加速-位移方程ds(f)=4*h*f*hd/(ft*hd)^2;ds=ds(f);d2s(f)=4*h/(ft*hd)^2;d2s=d2s(f);vt(f)=4*h*omega*f/ft^2; % 等加速-速度方程elses(f)=h-2*h*(ft-f)^2/ft^2;s=s(f); % 等减速-位移方程ds(f)=4*h*(ft-f)*hd/(ft*hd)^2;ds=ds(f);d2s(f)=-4*h/(ft*hd)^2;d2s=d2s(f);vt(f)=4*h*omega*(ft-f)/ft^2; % 等减速-速度方程endalpha_t(f)=atan(abs(ds-e)/(se+s)); % 推程压力角(弧度)alpha_td(f)=alpha_t(f)*du; % 推程压力角(度)pt1=((se+s)^2+(ds-e)^2)^1.5;pt2=abs((se+s)*(d2s-se-s)-(ds-e)*(2*ds-e));rho_t(f)=pt1/pt2; % 推程曲率半径st(f)=s;endalpha_tm=max(alpha_td);fprintf(' 推程最大压力角alpha_tm = %3.4f 度\n',alpha_tm)for f=1:ftif alpha_td(f)==alpha_tm;ftm=f;break;endendfprintf (' 对应的位置角ftm = %3.4f 度\n',ftm)if alpha_tm>alpha_pfprintf(' * 凸轮推程压力角超过许用值,需要增大基圆!\n')endrho_tn = min(rho_t);fprintf (' 最小曲率半径rho_tn = %3.4f mm\n',rho_tn)for f=1:ftif rho_t(f)==rho_tn;ftn=f;break;endendfprintf(' 对应的位置角ftn = %3.4f 度\n',ftn)if rho_tn<rt+5fprintf(' * 凸轮推程轮廓曲率半径小于许用值,需要增大基圆或减小滚子!\n') enddisp ' 2 回程(余弦加速度运动-简谐运动)'d1=ft+fs;d2=ft+fs+fh; % 回程运动角范围for f=d1:d2k=f-d1;s(f)=0.5*h*(1+cos(pi*k/fh));s=s(f); % 简谐运动-位移方程ds(f)=-0.5*pi*h*sin(pi*k/fh)/(fh*hd);ds=ds(f);d2s(f)=-0.5*pi^2*h*cos(pi*k/fh)/(fh*hd)^2;d2s=d2s(f);alpha_h(f)=atan(abs(ds+e)/(se+s)); % 回程压力角(弧度)alpha_hd(f)=alpha_h(f)*du; % 回程压力角(度)ph1=((se+s)^2+(ds-e)^2)^1.5;ph2=abs((se+s)*(d2s-se-s)-(ds-e)*(2*ds-e));rho_h(f)=ph1/ph2; % 回程曲率半径sh(f)=s;vh(f)=-0.5*pi*h*omega*sin(pi*f/fh)/fh; % 简谐运动-速度方程ah(f)=-0.5*pi^2*h*omega^2*cos(pi*f/fh)/fh^2; % 简谐运动-加速度方程endalpha_hm = max(alpha_hd(d1:d2));fprintf(' 回程最大压力角alpha_hm = %3.4f 度\n',alpha_hm)for f=d1:d2if alpha_hd(f)==alpha_hm;fhm=f;break;endendfprintf(' 对应的位置角fhm = %3.4f 度\n',fhm)rho_hn=min(rho_h(d1:d2));fprintf(' 最小曲率半径rho_hn = %3.4f mm\n',rho_hn)for f=d1:d2if rho_h(f)==rho_hn;fhn=f;break;endendfprintf(' 对应的位置角fhn = %3.4f 度\n',fhn)if rho_hn<rt+5fprintf(' * 凸轮回程轮廓曲率半径小于许用值,需要增大基圆或减小滚子!\n') enddisp ' '% (2)---计算凸轮机构的从动件运动参数'disp ' *** 计算凸轮机构从动件的运动参数***'disp ' 1 推程(等加速/等减速运动)'disp ' 凸轮转角位移s(mm) 速度v(mm/s)'for f=10:10:ftydcs_t=[f st(f) vt(f)];disp(ydcs_t)endat_1=4*h*omega^2/ft^2;at_2=-4*h*omega^2/ft^2;fprintf(' 等加速上升的加速度at_1 = %3.4f (mm/s^2) \n',at_1)fprintf(' 等减速上升的加速度at_2 = %3.4f (mm/s^2) \n',at_2)disp ' 2 回程(余弦加速度运动-简谐运动)'disp ' 凸轮转角位移s(mm) 速度v(mm/s) 加速度a(mm/s^2)'for f=d1:10:d2ydcs_h=[f sh(f) vh(f) ah(f)];disp(ydcs_h)end% (3)---绘制凸轮机构的从动件运动线图figure(1);subplot(3,2,1) % 推程位移线图f=1:ft;plot(f,st);xlabel ('凸轮转角\it \phi / \rm( °)')ylabel ('\it s / \rm(mm)')title('从动件推程位移线图');subplot(3,2,2) % 回程位移线图f=d1:d2;plot(f,sh(d1:d2));xlabel ('凸轮转角\it \phi / \rm( °)')ylabel ('\it s / \rm(mm)')title('从动件回程位移线图');subplot(3,2,3) % 推程速度线图f=1:ft;plot(f,vt);xlabel ('凸轮转角\it \phi / \rm( °)')ylabel ('\it v / \rm(mm/s)')title('从动件推程速度线图');subplot(3,2,4) % 回程速度线图f=d1:d2;plot(f,-vh(d1:d2));xlabel ('凸轮转角\it \phi / \rm( °)')ylabel ('\it v / \rm(mm/s)')title('从动件回程速度线图');subplot(3,2,5) % 推程加速度线图line([0,ft/2],[at_1,at_1]);line([ft/2,ft/2],[at_1,at_2]); % 等加速等减速之间的突变垂线line([ft/2,ft],[at_2,at_2]);xlabel ('凸轮转角\it \phi / \rm( °)')ylabel ('\it a / \rm(mm/s^2)')title('从动件推程加速度线图');subplot(3,2,6) % 回程加速度线图f=d1:d2;plot(f,-ah(d1:d2));xlabel ('凸轮转角\it \phi / \rm( °)')ylabel ('\it a / \rm(mm/s^2)')title('从动件回程加速度线图');disp ' '% (4)---计算凸轮理论廓线与实际廓线的直角坐标和向径'disp ' ****** 凸轮理论轮廓与实际轮廓的直角坐标******'nd=360;for f=1:ndif f<=ft/2 % 等加速运动s(f)=2*h*f^2/ft^2;s=s(f);ds(f)=4*h*f*hd/(ft*hd)^2;ds=ds(f);elseif f>ft/2 & f<=ft % 等减速运动s(f)=h-2*h*(ft-f)^2/ft^2;s=s(f);ds(f)=4*h*(ft-f)*hd/(ft*hd)^2;ds=ds(f);elseif f>ft & f<=d1 % 远休止角s=h;ds=0;elseif f>d1 & f<=d2 % 简谐运动k=f-d1;s(f)=0.5*h*(1+cos(pi*k/fh));s=s(f);ds(f)=-0.5*pi*h*sin(pi*k/fh)/(fh*hd);ds=ds(f);elseif f>d2 & f<=nds=0;ds=0;endxx(f)=(se+s)*sin(f*hd)+e*cos(f*hd);x=xx(f); % 理论轮廓横坐标yy(f)=(se+s)*cos(f*hd)-e*sin(f*hd);y=yy(f); % 理论轮廓纵坐标dx(f)=(ds-e)*sin(f*hd)+(se+s)*cos(f*hd);dx=dx(f);dy(f)=(ds-e)*cos(f*hd)-(se+s)*sin(f*hd);dy=dy(f);xp(f)=x+rt*dy/sqrt(dx^2+dy^2);xxp=xp(f); % 实际轮廓横坐标yp(f)=y-rt*dx/sqrt(dx^2+dy^2);yyp=yp(f); % 实际轮廓纵坐标r(f)=sqrt(x^2+y^2); % 理论轮廓向径rp(f)=sqrt(xxp^2+yyp^2); % 实际轮廓向径enddisp ' 1 推程(等加速/等减速运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y'for f=10:10:ftnu=[f xx(f) yy(f) xp(f) yp(f)];disp(nu)enddisp ' 2 回程(余弦加速度运动)'disp ' 凸轮转角理论x 理论y 实际x 实际y'for f=d1:10:d2nu=[f xx(f) yy(f) xp(f) yp(f)];disp(nu)enddisp '*** 凸轮理论轮廓与实际轮廓的向径***'disp ' 1 推程(等加速/等减速运动)'disp ' 凸轮转角理论r 实际r'for f=10:10:ftnu=[f r(f) rp(f)];disp(nu)enddisp ' 'disp ' 2 回程(余弦加速度运动)'for f=d1:10:d2nu=[f r(f) rp(f)];disp(nu)end% (5)---绘制凸轮的理论轮廓和实际轮廓figure(2);plot(xx,yy,'r-.') % 理论轮廓(红色,点划线)axis ([-(rb+h-10) (rb+h+10) -(rb+h+10) (rb+rt+10)]) % 横轴和纵轴的下限和上限axis equal % 横轴和纵轴的尺度比例相同text(rb+h+3,0,'X') % 标注横轴text(0,rb+rt+3,'Y') % 标注纵轴text(-5,5,'O') % 标注直角坐标系原点title('偏置移动从动件盘形凸轮轮廓') % 标注图形标题hold on; % 保持图形plot([-(rb+h) (rb+h)],[0 0],'k') % 横轴(黑色)plot([0 0],[-(rb+h) (rb+rt)],'k') % 纵轴(黑色)plot([e e],[0 (rb+rt)],'k--') % 初始偏置位置(黑色,虚线)ct=linspace(0,2*pi); % 画圆的极角变化范围plot(rb*cos(ct),rb*sin(ct),'g') % 基圆(绿色)plot(e*cos(ct),e*sin(ct),'c--') % 偏距圆(青色,虚线)plot(e + rt*cos(ct),se + rt*sin(ct),'m') % 滚子圆(品红色)plot(xp,yp,'b') % 实际轮廓(蓝色)******** 偏置移动从动件盘形凸轮设计绘图和运动分析********######## 已知条件########凸轮作逆时针方向转动,从动件偏置在凸轮轴心的右边从动件在推程作等加速/等减速运动,在回程作余弦加速度运动基圆半径rb = 40.0000 mm滚子半径rt = 10.0000 mm推杆偏距 e = 15.0000 mm推程升程h = 50.0000 mm推程运动角ft = 100.0000 度远休止角fs = 60.0000 度回程运动角fh = 90.0000 度推程许用压力角alpha_p = 35.0000 度凸轮转速n = 200.0000 r/min凸轮角速度(弧度) w = 20.9440 rad/s凸轮角速度(度) omega = 1200.0000 度/s@@@@@@ 计算过程和输出结果@@@@@@*** 计算凸轮理论轮廓的压力角和曲率半径***1 推程(等加速/等减速运动)推程最大压力角alpha_tm = 34.2666 度对应的位置角ftm = 50.0000 度最小曲率半径rho_tn = 35.2303 mm对应的位置角ftn = 51.0000 度2 回程(余弦加速度运动-简谐运动)回程最大压力角alpha_hm = 30.9248 度对应的位置角fhm = 213.0000 度最小曲率半径rho_hn = 30.3591 mm对应的位置角fhn = 250.0000 度*** 计算凸轮机构从动件的运动参数***1 推程(等加速/等减速运动)凸轮转角位移s(mm) 速度v(mm/s)10 1 24020 4 48030 9 72040 16 96050 25 120060 34 96070 41 72080 46 48090 49 240100 50 0等加速上升的加速度at_1 = 28800.0000 (mm/s^2)等减速上升的加速度at_2 = -28800.0000 (mm/s^2)2 回程(余弦加速度运动-简谐运动)凸轮转角位移s(mm) 速度v(mm/s) 加速度a(mm/s^2) 160 50 673 -33602170 48 358 -41220180 44 0 -43865190 37 -358 -41220200 29 -673 -33602210 21 -907 -21932220 12.5 -1031.3 -7617.1230 5.8 -1031.3 7617.1240 2 -907 21932250 0 -673 33602****** 凸轮理论轮廓与实际轮廓的直角坐标******1 推程(等加速/等减速运动)凸轮转角理论x 理论y 实际x 实际y 10.0000 21.3848 34.8977 18.7440 25.2527 20.0000 28.1459 33.4732 26.5660 23.5988 30.0000 36.0309 32.4073 34.7788 22.4860 40.0000 45.6105 31.0206 43.9004 21.1679 50.0000 57.1986 28.4142 54.4870 18.7889 60.0000 69.0579 22.5501 63.1030 14.5165 70.0000 78.5024 12.6099 70.2060 7.0270 80.0000 84.4235 -0.3453 74.7846 -3.008390.0000 86.0810 -15.0000 76.0894 -14.5890 100.0000 83.1533 -29.8936 73.7429 -26.51052 回程(余弦加速度运动)凸轮转角理论x 理论y 实际x 实际y 160.0000 15.6881 -86.9597 13.9127 -77.1185 170.0000 0.0875 -86.8780 1.9206 -77.0474 180.0000 -15.0000 -81.2321 -9.9808 -72.5829 190.0000 -27.7230 -70.8432 -20.2897 -64.1539 200.0000 -36.8131 -57.2861 -27.8219 -52.9092 210.0000 -41.8603 -42.5041 -32.0770 -40.4336 220.0000 -43.3607 -28.3394 -33.3609 -28.2733 230.0000 -42.5280 -16.1041 -32.6176 -17.4398 240.0000 -40.9188 -6.3040 -31.0634 -7.9985 250.0000 -39.9750 1.4129 -29.9813 1.0597*** 凸轮理论轮廓与实际轮廓的向径***1 推程(等加速/等减速运动)凸轮转角理论r 实际r10.0000 40.9287 31.449020.0000 43.7338 35.533930.0000 48.4609 41.414840.0000 55.1597 48.737350.0000 63.8674 57.635560.0000 72.6465 64.751270.0000 79.5088 70.556880.0000 84.4242 74.845190.0000 87.3781 77.4754100.0000 88.3634 78.36342 回程(余弦加速度运动)160.0000 88.3634 78.3634170.0000 86.8780 77.0714180.0000 82.6054 73.2660190.0000 76.0745 67.2859200.0000 68.0948 59.7783210.0000 59.6564 51.6121220.0000 51.8003 43.7302230.0000 45.4750 36.9872240.0000 41.4015 32.0766250.0000 40.0000 30.0000。
凸轮机构的实验方法(5篇)以下是网友分享的关于凸轮机构的实验方法的资料5篇,希望对您有所帮助,就爱阅读感谢您的支持。
篇一实验5.1 凸轮机构实验【实验目的】1. 了解凸轮机构的运动过程。
2. 掌握凸轮轮廓和从动件的常用运动规律。
3. 掌握机构运动参数测试的原理和方法。
【实验内容】1.实验仪器TL-I凸轮机构实验台,由盘形凸轮、圆柱凸轮和滚子推杆组件构成,提供了等速运动规律、等加速等减速运动规律、多项式运动规律、余弦运动规律、正弦运动规律、改进等速运动规律、改进正弦运动规律、改进梯形运动规律等八种盘形凸轮和一种等加速等减速运动规律的圆柱凸轮供检测使用。
该实验台可拼装平面凸轮和圆柱凸轮两种凸轮机构有关构件尺寸参数如下:盘形凸轮:基圆半径为R0=40㎜最大升程为hmax=15㎜圆柱凸轮:升程角为α=150升程为H=38.5㎜2.工作原理凸轮机构主要是由凸轮,从动件和机架三个基本构件组成的高副机构。
其中凸轮是一个具有曲线轮廓或凹槽的构件,一般为主动件,作等速回转运动或往复直线运动。
从动件与凸轮轮廓接触,传递动力和实现预定的运动规律故从动件的运动规律取决于凸轮轮廓曲线。
由于组成凸轮机构的构件数较少,结构比较简单,只要合理地设计凸轮的轮廓曲线就可以使从动件获得各种预期的运动规律。
凸轮相关参数:推程回程行程h 凸轮转角ϕ、推程运动角φ回程运动角φ’近休止角φs ‘远休止角φs 从动件的位移sTL-I凸轮机构试验台采用单片机与A/D转换集成相结合进行数据采集,处理分析及实现与PC 机的通信,达到适时显示运动曲线的目的。
该测试系统先进、测试稳定、抗干扰性强。
同时该系统采用光电传感器、位移传感器作为信号采集手段,具有较高的检测精度。
数据通过传感器与数据采集分析箱将机构的运动数据通过计算机串口送到PC 机内进行处理,形成运动构件运动参数变化的实测曲线,为机构运动分析提供手段和检测方法。
本实验台电机转速控制系统有两种方式:手动控制:通过调节控制面板上的液晶调速菜单调节电机转速。
发动机实习项目凸轮轴的测量引言在现代汽车发动机中,凸轮轴是一个至关重要的组成部分。
凸轮轴的设计和制造质量直接影响发动机的性能、可靠性和效率。
因此,对凸轮轴进行精确的测量和评估是非常重要的。
本文将介绍发动机实习项目中凸轮轴的测量方法和步骤。
一、测量步骤1. 准备工作:在进行凸轮轴的测量之前,首先需要准备好测量工具和设备,包括测量卡尺、显微镜、测量夹具等。
确保这些工具的准确性和可靠性。
2. 测量凸轮轴的长度:使用测量卡尺或显微镜测量凸轮轴的长度。
首先,将凸轮轴放置在水平的工作台上,确保凸轮轴没有变形或弯曲。
然后,使用测量工具沿着凸轮轴的轴线测量其长度。
记录下凸轮轴的长度。
3. 测量凸轮轴上各个凸轮的高度:使用显微镜或测量卡尺测量凸轮轴上各个凸轮的高度。
将凸轮轴放置在显微镜的支架上或者使用测量夹具固定凸轮轴。
然后,仔细观察每个凸轮的顶部和底部,并使用测量工具测量其高度差。
重复这个步骤,直到测量完所有凸轮的高度。
4. 测量凸轮轴上各个凸轮的直径:使用测量卡尺或显微镜测量凸轮轴上各个凸轮的直径。
将测量工具放置在凸轮的顶部和底部,并读取测量结果。
重复这个步骤,直到测量完所有凸轮的直径。
5. 检查凸轮轴的磨损和磨损程度:使用显微镜仔细检查凸轮轴的表面。
观察表面是否有划痕、磨损或其它异常。
如果凸轮轴的表面不平整或有磨损,则需要进行更详细的检查和评估。
6. 评估凸轮轴的质量和性能:根据以上测量结果和检查过程,评估凸轮轴的质量和性能。
如果凸轮轴的尺寸、形状和表面质量符合设计要求,则可以认为该凸轮轴是合格的。
如果不符合要求,则需要进行修复或更换。
二、注意事项1. 在进行凸轮轴的测量之前,确保测量工具和设备的准确性和可靠性。
每次测量之前,应该校准和检查这些工具。
2. 在测量凸轮轴的过程中,要小心操作,避免对凸轮轴造成损坏或变形。
确保凸轮轴处于稳定的位置,并避免不必要的振动或碰撞。
3. 在检查凸轮轴的表面时,使用适当的照明和放大工具,确保能够清晰地观察到表面的细节。
凸轮轴的检测方法的综述 3 凸轮轴的升程公差,常用的有两种标注方法:①标注的是带正负号的公差值,公差带的位置由凸轮轴升程的理论正确尺寸确定,且公差带位置是固定的,升程公差控制的仅是实际凸轮的轮廓尺寸。
这时,凸轮轴的升程误差应按尺寸公差来处理:凸轮轴的升程公差要求,设定了两个极限尺寸——最大实体尺寸(MMS)和最小实体尺寸(LMS)来限制升程的实际尺寸,要求凸轮轴升程的任一局部尺寸不得超出两个极限尺寸;②标注的是不带正负号的公差值,公差带的方向随凸轮的实际形状而定(变动),公差带的位置是浮动的,升程公差控制要素是实际凸轮轴的轮廓形状。
这时,凸轮的升程误差应按形位公差来处理(升程误差的测量数据,应按“最小条件”要求进行评定):凸轮的升程公差要求,设定了两个平行(或等距)的界面或界线,构成形状公差带来限制实际被测要素。
凸轮测量数据按尺寸公差要求处理时,应把升程误差与升程公差联系起来,最大限度的保证凸轮升程的合格(图2);凸轮测量数据按形位公差要求处理时,应把升程误差与“最小条件”联系起来,保证凸轮升程误差(包容区域的宽度)的最大值为最小(图3)。
处理时可根据设计要求,选择相应的处理方法。
在此应强调指出:当凸轮异侧(左、右侧)升程公差相等时,“等距”误差点也是“等值”误差点。
尺寸误差和形位误差数据的处理方法相一致。
所不同的只是,形位公差带位置浮动,尺寸公差带位置固定。
5 凸轮轴测量仪的工作原理凸轮轴的测量是二维测量系统。
目前凸轮轴测量仪的分度装置大都采用圆光栅编码器测量系统,线值装置采用直线光栅测量系统。
凸轮轴测量仪的原理框图[3] 如图4所示:由计算机发出的控制信号启动直流同步电机旋转,由驱动机构带动被测凸轮轴转动,通过Y轴圆光栅传感器,X轴直线光栅传感器分别将凸轮轴的角位移、径向、轴向位移转换成明暗条纹的光强变化信号,经光电转换电路转换成电压信号,再经前置放大和整形滤波,形成角度脉冲和径向位移脉冲经T/C计数板送入计算机。
课题十一凸轮机构运动参数的测定凸轮机构主要是由凸轮,从动件和机架三个基本构件组成的高副机构。
其中凸轮是一个具有曲线轮廓或凹槽的构件,一般为主动件,作等速回转运动或往复直线运动。
从动件与凸轮轮廓接触,传递动力和实现预定的运动规律故从动件的运动规律取决于凸轮轮廓曲线。
由于组成凸轮机构的构件数较少,结构比较简单,只要合理地设计凸轮的轮廓曲线就可以使从动件获得各种预期的运动规律。
凸轮机构能将主动件的连续运动转变为从动件的移动或转动,因而广泛用于各种机械中,特别是自动机械、自动线中的机械控制装置中。
1.凸轮机构运动参数的测定实验台及其工作原理
进行凸轮机构运动参数的测定实验台有多种形式,现以如图11—1所示的连杆机构与凸轮组合实验台,完成凸轮机构运动参数的测定。
图11—1 连杆机构与凸轮组合实验台
a)b)
图11—2 凸轮机构实验台的运动简图
1--同步脉冲发生器 2—减速器 3--电机 4—传感器
5--光栅盘 6--凸轮 7--平底直动从动件 8--回复弹簧
9--滑块 10--滚子直动从动件
如图11—2a)、b)所示,凸轮机构的实验台是电机、减速器、凸轮、直动从动件、滑块、传感器、同步脉冲发生器、光栅盘和回复弹簧等组成。
通过调速器调节电机的转速输出后,经蜗杆减速器带动凸轮转动,驱动从动件运动,其位移量通过直线位移传感器由模/数转换模块在嵌入式计算机系统的控制下,将位移量转换成数字信号,计算出其往复移动的周期、线速度、线加速度等机构运动参数。
也可更换不同廓线的盘形凸轮,从而调节从动件的偏心距。
2.凸轮机构运动参数的测定实验注意事项
(1) 调节电机的转速时应缓慢转动调速旋钮,在关闭实验台电源前,应将电动机的转速调到最小。
(2) 用手转动凸轮盘1~2 周,检查各运动构件的运行状况,各螺母紧固件应无松动,各运动构件应无卡滞现象。
(3) 测试时,凸轮的转速不应过高,以免产生大的冲击,造成零件损坏。
(4) 调节从动件偏心距时,偏心距不宜过大,否则有可能使凸轮机构卡死,造成零件损坏。
2.凸轮机构运动参数的测定的操作过程
(1) 按要求组装凸轮机构,分析凸轮机构的组成。
(2) 轻轻转动凸轮,分析凸轮机构的运动特性,找出基圆、推程、远休止程、回程、近休止程,并量出对应的推程角、远休止角、回程角、近休止角。
(3) 以从动件在最低位置开始,轻轻转动凸轮,每转5°,量出从
动件尖顶与凸轮中心的距离,通过计算,求出各瞬时从动件的尖顶的位移,在相应的二维图中绘出从动件的位移规律。
根据位移规律分析从动件的运动,特别是在起点、中点、末点的运动。
(4) 在一定的偏心距的情况下,观测凸轮在逆时针、顺时针状态下,机构的运动状况,分析偏心距的方向、大小对凸轮机构运动的影响。
(5) 保持凸轮静止不动,沿原先凸轮回转的反方向转动从动件及导路,思考从动件尖顶轨迹如何。
分析在反转过程中凸轮轮廓曲线与从动件尖顶的关系。
过程质量评定
凸轮机构运动参数的测定实训记录与成绩评定见表10-1。
表10-1 凸轮机构运动参数的测定实训记录与成绩评定
习题:
(一)填空题:
1.凸轮是一种具有_______或_______的构件。
2.凸轮机构由_______、_______和_______三个基本构件组成的。
3.凸轮机构的基本特点在于能使_______获得_______的运动规律。
4.按凸轮的形状分类,凸轮机构可分为_______、_______和_______。
5.按从动件末端形状分类,凸轮机构可分为_______、_______和_______。
6.按从动件的运动形式分类,凸轮机构可分为_______和_______。
7.以凸轮的轮廓曲线的最小向径为半径所作的圆称为凸轮的_______。
8.凸轮机构从动件的常见运动规律主要分为_______、_______和_______。
(二)选择题:
1.凸轮机构从动件的运动规律取决于( )。
A.凸轮的转向 B.凸轮轮廓曲线
C.从动件滚子半径 D.从动件末端形状
2.凸轮与从动件接触处的运动副属于( )。
A.高副 B.转动副 C.移动副
3.要使常用凸轮机构正常工作,必须以凸轮( )。
A.做从动件并匀速转动 B.做从动件并变速转动
C.做主动件并变速转动 D.做主动件并匀速转动
4.在要求( )的凸轮机构中,宜使用滚子式从动件。
A.动力较大 B.传动准确、灵敏 C.转速较高
5. 在凸轮机构的从动件选用等速运动规律时,其从动件的运动(A)
A.将产生刚性冲击
B.将产生柔性冲击
C.没有冲击
D.既有刚性冲击又有柔性冲击
6. 决定了从动杆的运动规律( B)。
A 凸轮转速
B 凸轮轮廓曲线
C 凸轮形状
7.凸轮机构中的压力角是指( A )间的夹角。
A 凸轮上接触点的法线与从动件的运动方向
B 凸轮上接触点的法线与该点线速度
C 凸轮上接触点的切线与从动件的运动方向
8 如图11-3所示,如为以O为圆心的圆弧,此凸轮机构的推程运动角是( )。
A 160°;
B 130°;
C 120°;
D 110°。
9 若要盘形凸轮的从动件在某段时间内停止不动,对应的凸轮轮廓曲线应为( )。
A一段直线; B一段圆弧:
C抛物线; D以凸轮转动中心为圆心的圆弧。
10 如图11-4所示凸轮轮廓是分别以O及O1为圆心的圆弧和直线组成的。
该凸轮机构从动件的运动过程属于( )类型。
A升一停一降一停; B升一停一降;
C升一降一停; D升一降。
图11-3 图11-4
11.凸轮机构从动件的推程采用等速运动规律时,刚性冲击将发生在( )。
A推程的起始点; B推程的中点;
C推程的终点; D推程的始点和终点。
12 如图11--5所示机构中,属空间凸轮机构的是( )。
A a:
B b;
C c;
D d。
图11—5 凸轮机构示意图
13 凸轮从动件与凸轮保持接触的形式也称之为“锁合”,由外力实现接触的锁合称为力锁合,利用结构实现接触的锁合称为形锁合。
图11—5中( )为形锁合。
A a:
B b:
C c;
D d。
14 在图11-5中,( )位置中的从动件压力角最小。
A a:
B b;
C c;
D d。
二、判断题(在括号内。
正确的画“√”,错误的画“×”)
1.凸轮机构是高副机构,易磨损,因此只适用于传递动力不大的场合。
( )
2.在设计凸轮机构时,滚子半径必须大于凸轮理论轮廓外凸部分的最小曲率半径。
( )
3. 凸轮机构中,凸轮的基圆半径越小,则压力角越大,机构的效率就越低。
()
4. 为了保证凸轮机构的从动件不出现运动失真现象,设计时应使
从动件的滚子半径r
r <
min
(理论轮廓外凸部分的最小曲率半径)。
()
5. 当凸轮机构的压力角过大时,机构易出现自锁现象。
()
6.平底直动从动件凸轮机构,其压力角为90︒。
( )
7. 平底从动件凸轮机构的缺点就是平底不能与凹陷凸轮轮廓接触。
( )
8. 凸轮机构的图解法设计原理是采用反转法原理。
( )
9.滚子从动件盘形凸轮的优点是耐磨损,承受载荷大。
( )
10.圆柱凸轮机构为空间凸轮机构。
()(四)、简答题
1.标出图11-6所示位置凸轮机构的压力角。
图11-6 压力角标注
2.设计一对心移动尖底从动件盘形凸轮机构,已知凸轮的基圆半径r0=20mm,凸轮逆时针等速回转。
在推程中,凸轮转过150︒时,从动件等速上升40mm;凸轮继续转过30︒时,从动件保持不动;在回程中,凸轮转过120︒时,从动件以简谐运动规律回到原处;凸轮转过其余60︒时,从动件又保持不动。
要求用图解法:
(1)绘制从动件的位移曲线图;
(2)利用反转法画出凸轮的轮廓曲线;
(3)校验压力角,要求a max≤30︒。