第六章 运筹与优化模型
- 格式:ppt
- 大小:1.54 MB
- 文档页数:65
运输问题的模型建立与优化方法摘要:随着我国市场经济的不断完善和社会经济的发展,运输业在经济生活中的地位越来越重要,同地区、不同地区、甚至跨国间的企业交易活动更加频繁。
运输成本约占10%-30%,所以,开展合理运输,节约运输成本,对于降低社会产品的总成本起着重要作用。
因此,在运输中如何降低运输费用、减少运输路线等问题,已成为交易活动的重点,而线性规划主要应用于解决最优化问题。
本文根据运输问题的基本特征,通过实例对运输问题进行了优化分析,建立了运输问题的线性规划数学模型,并借助于计算机进行求解,而Lingo软件是比较实用,对问题描述清晰,易于掌握。
从而可以得到最优化的方案,提高了实际运输工作中的经济效益。
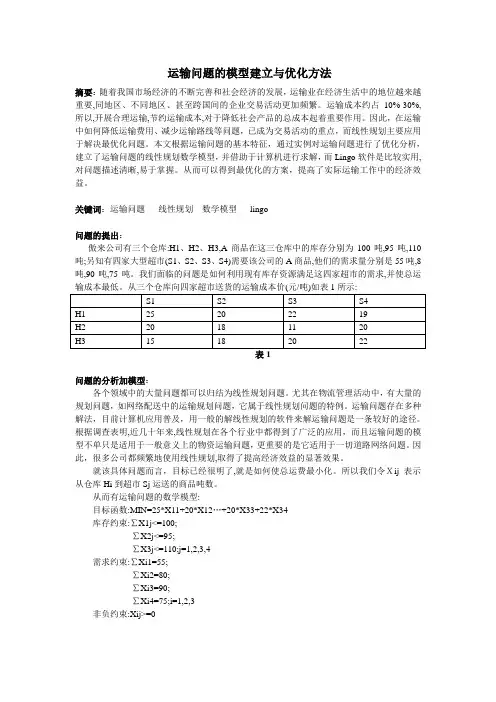
关键词:运输问题线性规划数学模型lingo问题的提出:傲来公司有三个仓库:H1、H2、H3,A商品在这三仓库中的库存分别为100吨,95吨,110吨;另知有四家大型超市(S1、S2、S3、S4)需要该公司的A商品,他们的需求量分别是55吨,8吨,90吨,75吨。
我们面临的问题是如何利用现有库存资源满足这四家超市的需求,并使总运表1问题的分析加模型:各个领域中的大量问题都可以归结为线性规划问题。
尤其在物流管理活动中,有大量的规划问题,如网络配送中的运输规划问题,它属于线性规划问题的特例。
运输问题存在多种解法,目前计算机应用普及,用一般的解线性规划的软件来解运输问题是一条较好的途径。
根据调查表明,近几十年来,线性规划在各个行业中都得到了广泛的应用,而且运输问题的模型不单只是适用于一般意义上的物资运输问题,更重要的是它适用于一切道路网络问题。
因此,很多公司都频繁地使用线性规划,取得了提高经济效益的显著效果。
就该具体问题而言,目标已经很明了,就是如何使总运费最小化。
所以我们令Xij表示从仓库Hi到超市Sj运送的商品吨数。
从而有运输问题的数学模型:目标函数:MIN=25*X11+20*X12…+20*X33+22*X34库存约束:∑X1j<=100;∑X2j<=95;∑X3j<=110;j=1,2,3,4需求约束:∑Xi1=55;∑Xi2=80;∑Xi3=90;∑Xi4=75;i=1,2,3非负约束:Xij>=0编程——数学模型、解答:运输问题是物流系统优化中常见的问题,运输问题是一种特殊的线性规划问题,对它的求解方法本质上也是单纯形法。




运筹与优化模型资料整理1.数学模型是可以详细地描述为对于现实世界的⼀个特定对象,为了⼀个特定的⽬的,根据特有的内在规律,作出⼀些必要的简化假设,运⽤适当的数学⼯具得到的⼀个数学结构。
(1)建模没有唯⼀正确的答案。
模型没有绝对的对与错,评价的唯⼀标准是实践检验。
(2)有不同的建模⽅法。
⽐较常见的是机理分析法、测试分析法、计算机模拟法等,要按照某种确定的准则在某⼀类模型中选出⼀个与数据拟合得最好的模型。
(3)模型与建模⽬的有关。
在建⽴数学模型之前要明确⽬的,对于同⼀个实际对象,建模的⽬的不同将导致建模时考虑的出发点和侧重点都不同,当然作出的模型就不同。
(4)模型具有可移植性。
模型是现实对象抽象化、理想化的产物,因此它并不为对象的所属领域所独有,它可以移植到其它领域,描述其它的实际问题。
(5)建模与建模者的灵性、经验和数学素质有关。
数学建模过程是有⼀定阶段性的。
我们对现实世界的问题进⾏分析、提炼,⽤数学语⾔做出描述,⽤数学⽅法进⾏分析、研究,最后回到现实世界,应⽤于解决、解释实际问题。
⼀般来讲,建模的流程可描述为:问题分析、数据处理、建⽴数学模型、模型分析与检验。
2. 港作拖轮费⽤数据处理(1)营运费⽤的综合分类。
(2)数据可⽐性处理。
(3)数据有效性处理。
3.为了把握模型的整体结构,我们所做的⼯作如下:a.找出与问题有关的各实体(对象)。
b.列出与每个实体有关的因素(属性)。
c.按建模⽬的描述出个实体之间的关系,根据合理的假设略去影响不⼤的实体。
d.将实体之间的关系⽤实体的因素表⽰出来,即建⽴数学关系式。
e.如果满⾜关系的解有多个,则应考虑合理的评价标准求出最优解。
f.对模型加以检验、分析和评价。
4. 设备更新问题的数学模型劣化数值法模型、最⼩平均成本法更新模型、最⼤总收益法、效益分析法、费⽤⽅程法更新模型、MAPI 法更新模型。
①T=sqrt(2k0/⼊)T为经济使⽤寿命k0为设备原值⼊为各种影响因素的费⽤低劣化增长速度③y(t)=y1(t)-y2(t)-k0分别为设备t年内的总收益函数、总收⼊函数、总维持费⽤函数5.最优价格模型为使利润U(P)达到最⼤,可令dU/dP=0,即可求得p*,p= p*时,DR/dP= Dc/dP,在数量经济学中,DR/dP称为边际收⼊,它是价格变动⼀个单位时,收⼊的改变量;Dc/dP是边际成本,他是价格变动⼀个单位时成本的改变量。


运筹与模型优化教案教案标题:运筹与模型优化教案教学目标:1. 了解运筹学和模型优化的基本概念和原理;2. 掌握常见的运筹学方法和模型优化技术;3. 能够应用运筹学方法和模型优化技术解决实际问题;4. 培养学生的逻辑思维能力、问题分析能力和团队合作意识。
教学内容:1. 运筹学基础知识a. 运筹学的定义和发展历程;b. 运筹学在实际问题中的应用领域;c. 运筹学方法的分类和特点。
2. 模型优化基本概念a. 模型优化的定义和基本原理;b. 模型优化在实际问题中的应用价值;c. 模型优化的常用方法和技术。
3. 运筹学方法a. 线性规划i. 线性规划的基本概念和模型形式;ii. 线性规划的求解方法和应用案例。
b. 整数规划i. 整数规划的基本概念和模型形式;ii. 整数规划的求解方法和应用案例。
c. 动态规划i. 动态规划的基本概念和模型形式;ii. 动态规划的求解方法和应用案例。
4. 模型优化技术a. 遗传算法i. 遗传算法的基本原理和流程;ii. 遗传算法的应用案例和优缺点。
b. 蚁群算法i. 蚁群算法的基本原理和流程;ii. 蚁群算法的应用案例和优缺点。
c. 粒子群算法i. 粒子群算法的基本原理和流程;ii. 粒子群算法的应用案例和优缺点。
教学步骤:1. 导入:介绍运筹学和模型优化的基本概念,引发学生对课题的兴趣。
2. 知识讲解:依次介绍运筹学基础知识、模型优化基本概念、运筹学方法和模型优化技术的内容。
3. 示例分析:通过实际问题案例,引导学生分析问题并应用运筹学方法和模型优化技术进行求解。
4. 小组讨论:组织学生分成小组,让他们选择一个实际问题,并运用所学的运筹学方法和模型优化技术进行解决,鼓励团队合作和思维碰撞。
5. 总结归纳:总结运筹学方法和模型优化技术的特点和应用范围,强调其在实际问题中的重要性和价值。
6. 作业布置:布置相关的练习题和实践任务,巩固所学知识。
教学资源:1. 教材:运筹学和模型优化相关的教材,如《运筹学导论》、《模型优化方法与应用》等。



