将A、表B、:C和D连在一起,距离O—A—B—
C—D—O,超过了75千米,不予采纳。
选择另节一约个值最计大的算节表约值10,将B、C
和D连接在一起,距离O—B—C—D—O,
超过了75 千米,仍然不采纳。
选择另O一个A最大B的节C约值D5 ,将A、C
和大于D连A7接5千在—米一,起—不,采距纳2离0。O—5 A—5D—C—O,约值开第始二,步将:客从户最连大接的在节
V5—V7:7+3=10 V7
V6—V7:6+6=12
则标号L7=10,并标记V5—V7。
综上所述,可知V1到V7最短路径为V1—V3— V6—V5—V7(如图中双线所示),距离为
2+4+1+3=10。
如图所示是某地区交通运输的示意图.试问:
从 V1出发,经哪条路线到达V8才能使总行程最 短?
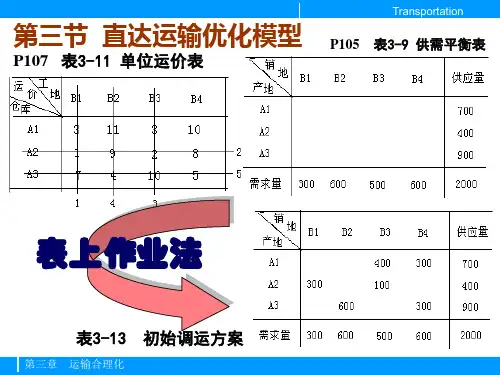
4.图上作业法
因为外圈流向总长超过了全圈总长的1/2( 111km>85km),则可断定初始运输线路存在迂回现象,所 对应的方案不是最优方案。因此,必须进行优化调整。
步骤3 重新去段破圈,调整流向。初始方案中里圈
符合要求,外圈流向总长超过全圈的1/2,故需缩小外圈
。因为外圈流向线中运量最小的是A1到B1的“20”,所以 去掉A1到B1的线路,并在外圈各段流向线上减去“20”的 运量,同时在里圈个流向线上以及原来没有流向线的A1到 B2线上各加上“20”的运量,这样可得到新的运输线路流
步骤2
找出与出发点相邻但未标号点的 最小距离值并在相应点标号。
找出与
已标号点相邻 但未标号点的 最小距离值并 在相应点标号 。
步骤3
步骤4
重复步骤3,直到最后一个未标 号点也标号.