基于MATLAB的判别分析的改进与实现
- 格式:pdf
- 大小:224.81 KB
- 文档页数:4

基于MATLAB的图像识别与处理算法优化研究一、引言图像识别与处理一直是计算机视觉领域的研究热点之一,随着人工智能技术的不断发展,基于MATLAB的图像识别与处理算法优化也成为了当前研究的重要方向。
本文将探讨如何利用MATLAB平台进行图像识别与处理算法的优化研究,以提高算法的准确性和效率。
二、MATLAB在图像处理中的应用MATLAB作为一种强大的科学计算软件,提供了丰富的图像处理工具和函数,广泛应用于图像处理、计算机视觉等领域。
通过MATLAB,我们可以实现图像的读取、显示、编辑、分割、特征提取等操作,为图像识别与处理算法的优化提供了良好的平台。
三、图像识别与处理算法优化方法1. 特征提取与选择在图像识别与处理中,特征提取是至关重要的一步。
通过MATLAB 提供的各种特征提取函数,可以获取图像中的各种特征信息,如颜色、纹理、形状等。
在优化算法时,需要选择合适的特征进行提取,并对特征进行有效筛选,以降低维度和提高分类准确度。
2. 图像增强与去噪图像质量对于识别与处理算法的准确性有着重要影响。
通过MATLAB中的图像增强和去噪技术,可以改善图像质量,提高算法对图像的理解能力。
常用的方法包括直方图均衡化、滤波器去噪等,在优化算法时需要根据具体情况选择合适的方法。
3. 算法调参与优化针对不同的图像识别与处理任务,需要设计相应的算法模型并进行参数调优。
MATLAB提供了丰富的优化工具和函数,如遗传算法、粒子群算法等,可以帮助我们对算法进行自动调参和优化,以提高算法性能和效率。
四、案例分析以人脸识别为例,我们可以通过MATLAB实现人脸检测、特征提取和匹配等功能。
在优化算法过程中,可以结合深度学习技术,设计更加精准和快速的人脸识别系统。
通过不断调整参数和优化算法结构,提高系统在不同场景下的适用性和鲁棒性。
五、总结与展望基于MATLAB的图像识别与处理算法优化研究是一个复杂而又具有挑战性的课题。
通过本文对相关方法和技术进行探讨,我们可以更好地理解如何利用MATLAB平台进行算法优化,并不断提升图像识别与处理系统的性能。

判别分析及MATLAB应用
摘要
本文针对线性判别分析(LDA),总结了LDA的基本原理、求解过程
和MATLAB应用。
首先介绍了LDA的基本原理,即在最大化类内方差和最
小化类间方差之间寻求一个平衡,以作为类间距离的度量;然后,详细介
绍了求解LDA的算法流程,包括LDA的假设、建立数学模型、求解驻点过
程等;最后,结合MATLAB示例,介绍了如何在MATLAB中实现LDA,并介
绍了各种LDA的实现方法。
关键词:线性判别分析(LDA);最大似然估计;MATLAB
1 研究背景
统计学习理论中有两种重要分类模型:支持向量机(Support Vector Machine,SVM)和线性判别分析(Linear Discriminant Analysis,LDA)。
LDA是一种分类模型,它假设每个类别的概率密度函数都是一个
多元正态分布,利用极大似然估计,将各类样本数据的IC。
概率密度函
数的参数估计出来。
LDA可以有效的将特征进行降维,以得到较好的分类
结果。
2 线性判别分析原理
LDA是基于极大似然估计的一种分类模型,假定样本数据服从多元正
态分布,其目的是在最大化类内方差和最小化类间方差之间寻求一个平衡,以作为类间距离的度量。
(1)LDA的假设
LDA的假设有如下几点:
a.样本空间中两类样本具有多元正态分布。

利用Matlab进行模式识别的基本方法与实践引言模式识别是一种重要的人工智能技术,它在许多领域都有广泛应用,如图像识别、声音分析、文本分类等。
利用Matlab进行模式识别研究具有许多优势,因为Matlab提供了丰富的工具和函数库,便于进行数据的处理和分析。
本文将介绍利用Matlab进行模式识别的基本方法与实践。
一、数据预处理数据预处理是进行模式识别前必要的步骤之一。
在真实的应用场景中,我们经常会面临一些棘手的问题,如噪声、缺失值等。
首先,我们需要对数据进行清洗,去除其中的异常值和噪声。
Matlab提供了许多函数,如`median`、`mean`等,可以用于计算中值和均值,帮助我们识别并去除异常值。
其次,对于存在缺失值的情况,我们可以使用插补方法进行填充。
Matlab提供了`interp1`函数,用于进行线性插值,可以帮助我们恢复缺失的数据。
如果缺失值较多,可以考虑使用更高级的插补方法,如多重插补(Multiple Imputation)等。
二、特征提取特征提取是进行模式识别的关键步骤之一。
在实际应用中,原始数据通常具有高维度和冗余性,这对模式识别的算法效率和准确性都会带来很大的负担。
因此,我们需要从原始数据中提取关键特征。
Matlab提供了大量的函数和工具箱,如`wavelet`、`pca`等,可以帮助我们进行特征提取。
例如,对于图像识别任务,我们可以使用小波变换进行特征提取。
Matlab的`wavelet`工具箱提供了丰富的小波函数,可以用于不同类型的特征提取。
另外,主成分分析(Principal Component Analysis, PCA)也是一种常用的特征提取方法。
Matlab提供了`pca`函数,可以用于计算数据的主成分。
三、模型训练模型训练是进行模式识别的核心步骤之一。
在进行模型训练前,我们需要将数据集分为训练集和测试集。
将数据集分为训练集和测试集的目的是为了避免模型的过拟合,并评估模型在未知数据上的泛化能力。

摘要函数序列的一致收敛性理论是数学分析的一个重要内容。
在众多数学分析讲义中给出了函数序列一致收敛的一些判别方法,但是这些方法仍不够全面,并不能解决大多数函数序列的一致收敛问题。
因此,文章简要地阐述了函数序列一致收敛的研究背景以及研究意义,归纳总结了比较实用的六种函数序列一致收敛的判别方法,并对它们的应用做了相应的说明与举例,以便于读者更好的理解这些判别方法,为今后处理函数序列一致收敛的判别提供便利。
同时文章提出MATLAB在函数序列一致收敛判别上的应用,给出解题的程序代码步骤,并通过几个例子说明,实现了信息技术在数学分析中的有效融合,并得到实验的验证。
这对于研究函数序列一致收敛及其收敛区间具有较大的作用。
关键词:函数序列;一致收敛;MATLAB编程AbstractThe theory of uniform convergence of function sequence is an important content of mathematical analysis. In many lecture notes of mathematical analysis, some methods to judge the uniform convergence of function sequences are given, but these methods are still not comprehensive enough to solve the problem of uniform convergence of most function sequences. Consequently,the research background and significance of uniform convergence of function sequences are briefly described in this paper, summarizes six practical methods for judging the uniform convergence of function sequences, and gives corresponding explanations and examples for their applications, so as to facilitate the readers to better understand these methods and provide convenience for dealing with the uniform convergence of function sequences in the future. At the same time, the paper puts forward the application of MATLAB in the judgment of uniform convergence of function sequence, gives the procedure code steps of solving problems, and through several examples, realizes the effective integration of information technology in mathematical analysis, and is verified by experiments. It is important to study the uniform convergence and the convergence interval of function sequences.Key words:Function sequences; Uniform convergence; MATLAB programme and picture.目录1 引言 (1)2 函数序列一致收敛的相关概念 (2)2.1 函数序列的定义 (2)2.2 函数序列收敛的定义 (2)2.3 函数序列一致收敛的定义 (2)3 函数序列一致收敛的判别 (3)3.1 柯西准则 (3)3.2 余项准则 (4)3.3 狄尼(Dini)定理 (5)3.4 海涅定理推广的一致收敛判别 (6)3.5 利普希兹(lipschitz)条件的一致收敛判别 (7)3.6 逐项连续序列的一致收敛判别 (8)4 MATLAB在函数序列一致收敛上的应用 (9)4.1 MATLAB在函数序列一致收敛上的应用举例 (9)4.2 MATLAB在函数序列一致收敛上的编程步骤 (10)4.3 MATLAB在函数序列一致收敛上的几个例子 (11)5 总结 (13)参考文献 (15)致谢 (16)이函数序列一致收敛的判别及MATLAB在其上的应用1 引言古往今来,众多数学家都在函数序列一致收敛方法的研究方面做出了巨大贡献,这些性质早在百多年前就已经研究清楚了。
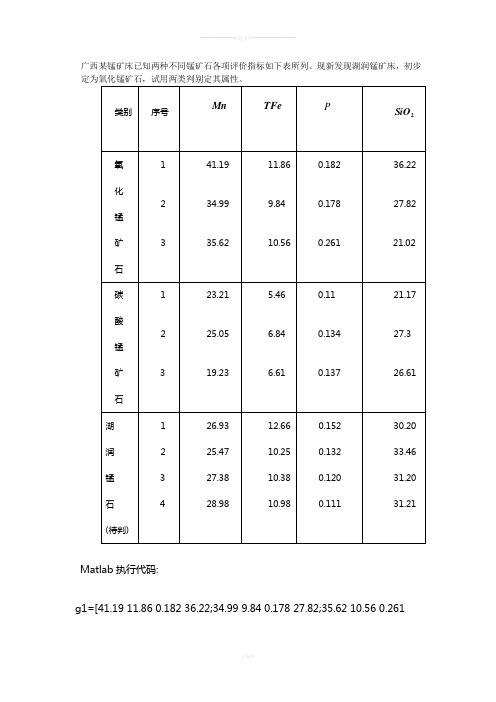
广西某锰矿床已知两种不同锰矿石各项评价指标如下表所列。
现新发现湖润锰矿床,初步Matlab执行代码:g1=[41.19 11.86 0.182 36.22;34.99 9.84 0.178 27.82;35.62 10.56 0.26121.02];g2=[23.21 5.46 0.11 21.17;25.05 6.84 0.134 27.3;19.23 6.61 0.137 26.61]; fprintf('做距离判别分析:\n')fprintf('在两个总体的协方差矩阵相等的假设下进行判别分析:\n')fprintf('两个样本的协方差矩阵s1,s2分别为\n')s1=cov(g1)s2=cov(g2)fprintf('因为两个总体的协方差矩阵相等,所以协方差的联合估计s为:\n') [m1,n2]=size(g1);[m2,n2]=size(g2);s=((m1-1)*s1+(m2-1)*s2)/(m1+m2-2)fprintf('两个总体的马氏平方距离为:\n')sn=inv(s);u1=mean(g1);u2=mean(g2);ucz=(u1-u2)';dmj=(u1-u2)*sn*uczfprintf('该值反映了两个总体的分离程度,线性函数的判别函数为:\n')syms x1;syms x2;syms x3;syms x4;x=[x1;x2;x3;x4];u1z=u1';u2z=u2';a1=(sn*u1z)';b1=(u1*sn*u1z)/2;a2=(sn*u2z)';b2=(u2*sn*u2z)/2;w1=vpa((a1*x-b1),4)w2=vpa((a2*x-b2),4)fprintf('用回代法作出误判率p1为:\n')fprintf('比较gwh1和gwh2大小\n')g=[g1;g2];[m,n]=size(g);for i=1:mghdw1(i,:)=a1.*g(i,:);ghdw2(i,:)=a2.*g(i,:);gwh1(i)=sum(ghdw1(i,:))-b1;gwh2(i)=sum(ghdw2(i,:))-b2;endgwh1gwh2fprintf('经比较得g1中1,2,3号判入g1;g2中1,2,3号判入g2,则误判率的回带估计为:\n')p1=0fprintf('用交叉估计法确认距离判别的误判率:\n')fprintf('依次剔除g1总体中1,2,3号样本是的判别函数值x1w1,x1w2为:')for I=1:3xg1=g1;xg1(I,:)=[];xs1=cov(xg1);x1s=(xs1+2*s2)/3;x1sn=x1s';xu1=mean(xg1);x1w1(I)=sum((x1sn*xu1')'.*g1(I,:))-0.5*xu1*x1sn*xu1';x1w2(I)=sum((x1sn*u2')'.*g1(I,:))-0.5*u2*x1sn*u2';endx1w1x1w2for I1=1:3if(x1w1(I1)>=x1w2(I1))zp1(I1)=1;endendzg1=sum(zp1);fprintf('依次剔除g2总体中1,2,3号样本的判别函数值x2w1,x2w2为:') for J=1:3xg2=g2;xg2(J,:)=[];xs2=cov(xg2);x2s=(2*s1+xs2)/3;x2sn=x2s';xu2=mean(xg2);x2w1(J)=sum((x2sn*xu2')'.*g2(J,:))-0.5*u1*x2sn*u1';x2w2(J)=sum((x2sn*xu2')'.*g2(J,:))-0.5*xu2*x2sn*xu2';endx2w1x2w2for J1=1:3if(x2w1(J1)<x2w2(J1))zp2(J1)=1;endendzg2=sum(zp2);fprintf('由上比较得,交叉法所得的误判率为:\n')zp=zg1+zg2;jwpl=(6-zp)/6fprintf('判别新样品:\n')yp=[26.93 12.66 0.152 30.20;25.47 10.25 0.132 33.46;27.38 10.38 0.120 31.20;28.98 10.98 0.111 31.21];[p,q]=size(yp);for j=1:pw1p(j,:)=a1.*yp(j,:);w2p(j,:)=a2.*yp(j,:);w1pb(j)=sum(w1p(j,:))-b1;w2pb(j)=sum(w2p(j,:))-b2;endw1pbw2pbfor k=1:4if(w1pb(k)>=w2pb(k))fprintf('属于氧化锰矿石的样本序号是%g\n',k)endendfprintf('用贝叶斯判别法分析:\n')fprintf('\n在两个总体的协方差矩阵相等的假设下做贝叶斯判别:\n')fprintf('\n先验概率按比例分配求得总体g1,g2的先验概率分别为:\n')bp1=m1/(m1+m2)bp2=m2/(m1+m2)fprintf('两个正态总体的贝叶斯判别为:\n')bw1=w1+log(bp1);bw2=w2+log(bp2);fprintf('当两个总体的协方差矩阵,误判损失相同且先验概率按比例分配时距离判别与贝叶斯判别等价\n')fprintf('计算广义平方距离函数:')syms bx;syms bx1;syms bx2;syms bx3;syms bx4;bx=[bx1;bx2;bx3;bx4];bdp1=vpa((bx-u1z)'*sn*(bx-u1z)-2*log(bp1),4)bdp2=vpa((bx-u2z)'*sn*(bx-u2z)-2*log(bp2),4)fprintf('后验概率pg1,pg2为:\n')pg1=exp(-0.5*bdp1)/(exp(-0.5*bdp1)+exp(-0.5*bdp2))pg2=exp(-0.5*bdp2)/(exp(-0.5*bdp1)+exp(-0.5*bdp2))fprintf('此时贝叶斯判别法则为:当pg1>=pg2时,属于g1总体;当pg1<pg2时,属于g2总体!!!\n')fprintf('\n贝叶斯判别的回带判别')for t=1:mbdg1(t)=(g(t,:)'-u1z)'*sn*(g(t,:)'-u1z)-2*log(bp1);bdg2(t)=(g(t,:)'-u2z)'*sn*(g(t,:)'-u2z)-2*log(bp2);p1b(t)=exp(-0.5*bdg1(t))/(exp(-0.5*bdg1(t))+exp(-0.5*bdg2(t)));p2b(t)=exp(-0.5*bdg2(t))/(exp(-0.5*bdg1(t))+exp(-0.5*bdg2(t))); endfprintf('回代g1,g2中六个样本,求得的后验概率为:\n')p1bp2bfprintf('经比较得,误判率的回带估计bp为:\n')bp=0fprintf('贝叶斯判别的交叉法确认误判率:\n')fprintf('依次踢除g1总体中1,2,3号样本,所得的广义平方距离b1d1,b1d2为:') for T=1:3bxg1=g1;bxg1(T,:)=[];bju1=mean(bxg1);b1s1=cov(bxg1);b1s=(b1s1+2*s2)/3;bj1p1=2/5 ; bj1p2=3/5;b1d1(T)=(g1(T,:)-bju1)*b1s'*(g1(T,:)'-bju1')-2*log(bj1p1);b1d2(T)=(g1(T,:)-u2)*b1s'*(g1(T,:)'-u2')-2*log(bj1p2);b1p1(T)=exp(-0.5*b1d1(T))/(exp(-0.5*b1d1(T))+exp(-0.5*b1d2(T)));b1p2(T)=exp(-0.5*b1d2(T))/(exp(-0.5*b1d1(T))+exp(-0.5*b1d2(T))); endb1d1b1d2fprintf('依次剔除g2总体中1,2,3号样本,所得的广义平方距离b2d1,b2d2为:') for T1=1:3if(b1d1(T1)<=b1d2(T1))b1zp(T1)=1;endendfor V=1:3bxg2=g2;bxg2(V,:)=[];bju2=mean(bxg2);b2s2=cov(bxg2);b2s=(2*s1+b2s2)/3;bj2p1=3/5;bj2p2=2/5;b2d1(V)=(g2(V,:)-u1)*b2s'*(g2(V,:)'-u1')-2*log(bj2p1);b2d2(V)=(g2(V,:)-bju2)*b2s'*(g2(V,:)'-bju2')-2*log(bj2p2);b2p1(V)=exp(-0.5*b2d1(V))/(exp(-0.5*b2d1(V))+exp(-0.5*b2d2(V)));b2p2(V)=exp(-0.5*b2d2(V))/(exp(-0.5*b2d1(V))+exp(-0.5*b2d2(V))); endb2d1b2d2for V1=1:3if(b2d1(V1)>=b2d2(V1))b2zp(V1)=1;endendfprintf('由上比较贝叶斯判别时,交叉法确认的误判率为:')byp=(6-(sum(b1zp)+sum(b2zp)))/6fprintf('根据以上的贝叶斯判别法则,判别待判样品yp\n')for v=1:pydg1(v)=(yp(v,:)'-u1z)'*sn*(yp(v,:)'-u1z)-2*log(bp1);ydg2(v)=(yp(v,:)'-u2z)'*sn*(yp(v,:)'-u2z)-2*log(bp2);yp1(v)=exp(-0.5*ydg1(v))/(exp(-0.5*ydg1(v))+exp(-0.5*ydg2(v)));yp2(v)=exp(-0.5*ydg2(v))/(exp(-0.5*ydg1(v))+exp(-0.5*ydg2(v))); endfprintf('后验概率yp1,yp2为:\n')yp1yp2fprintf('比较后验概率yp1,yp2知:\n')for w=1:pif(yp1(w)>=yp2(w))fprintf('属于氧化锰矿石总体的待判样品序号为:%g\n',w) endend。

二分法matlab实验原理实验改进意见二分法是一种常用的数值计算方法,可以用于求解函数零点、求解方程、优化问题等。
在matlab中,可以通过编写程序来实现二分法。
本实验将介绍二分法的原理、matlab实现和改进意见。
一、二分法的原理二分法的基本思想是将区间等分,在每个区间中选择一个点作为代表点,判断该点的函数值与零点的符号关系,再将含有零点的区间继续等分,直到所选代表点的函数值与零点的差小于一定的精度要求。
二、matlab实验下面是使用matlab实现二分法的步骤:1.选取初始区间[a,b]和精度要求tol。
2.计算中点c=(a+b)/2。
3.计算代表点f(a),f(c),f(b)的函数值。
4.根据中点函数值与零点的符号关系,缩小区间并更新代表点。
5.如果满足精度要求,则输出结果;否则,返回第三步。
二分法matlab程序:function [c,fc,i] = bisection(f,a,b,tol,max_iter)% f 为函数句柄,a,b为区间端点,tol为精度要求,max_iter 为最大迭代次数fa = f(a); fb = f(b);if fa*fb >= 0error('f(a)与f(b)符号相同')endc = (a+b)/2; fc = f(c);i = 1;while abs(fc) > tol && i <= max_iterif fa*fc < 0b = c;fb = fc;elsea = c;fa = fc;endc = (a+b)/2;fc = f(c);i = i+1;endif i > max_iterwarning('达到最大迭代次数')endend三、实验改进意见1.选择合适的初始区间。
初始区间的选择会影响到二分法的迭代次数和结果的精度。
一般情况下,可以根据函数的取值范围和零点的大致位置来选择初始区间。
实验一基于MATLAB语言的线性离散系统的Z变换分析法一、实验目的1. 学习并掌握 Matlab 语言离散时间系统模型建立方法;2.学习离散传递函数的留数分析与编程实现的方法;3.学习并掌握脉冲和阶跃响应的编程方法;4.理解与分析离散传递函数不同极点的时间响应特点。
二、实验工具1. MATLAB 软件(6.5 以上版本);2. 每人计算机一台。
三、实验内容1. 在Matlab语言平台上,通过给定的离散时间系统差分方程,理解课程中Z变换定义,掌握信号与线性系统模型之间Z传递函数的几种形式表示方法;2. 学习语言编程中的Z变换传递函数如何计算与显示相应的离散点序列的操作与实现的方法,深刻理解课程中Z变换的逆变换;3. 通过编程,掌握传递函数的极点与留数的计算方法,加深理解G(z)/z 的分式方法实现过程;4. 通过系统的脉冲响应编程实现,理解输出响应的离散点序列的本质,即逆变换的实现过程;5. 通过编程分析,理解系统的Z传递函数等于单位脉冲响应的Z变换,并完成响应的脉冲离散序列点的计算;6. 通过程序设计,理解课程中脉冲传递函数极点对系统动态行为的影响,如单独极点、复极点对响应的影响。
四、实验步骤1.创建系统How to create digital system g Four examples are as follows:numg=[0.1 0.03 -0.07];deng=[1 -2.7 2.42 -0.72];g=tf(numg,deng,-1)get(g);[nn dd]=tfdata(g,'v')[zz,pp,kk]=zpkdata(g,'v')Unite circle region with distrbuting zeros points and poles points hold onpzmap(g), hold offaxis equal运行结果:2.转换为零极点标准形式Convert from tf(z-function) to zpk(z-function) Part C exercise form gg=zpk(g)[zz,pp,kk tts]=zpkdata(gg,'v')[z,p k,ts]=zpkdata(g,'v')运行结果:3.四个例子Four examples are as follows:Part A exerciseeg1mun=[1.25 -1.25,0.30];eg1den=[1 -1.05 0.80 -0.10];eg1=tf(eg1mun,eg1den,-1);eg1zpk=zpk(eg1);[zz1,pp1,kk1,tts1]=zpkdata(eg1zpk,'v');Part B exerciseeg2mun=[0.84 -0.062 -0.156 0.058];eg2den=[1 -1.03 0.22 0.094 0.05];eg2=tf(eg2mun,eg2den,-1);eg2zpk=zpk(eg2);[zz2,pp2,kk2,tts2]=zpkdata(eg2zpk,'v');Part C exercisezz3=[-0.2 0.4];pp3=[0.6 0.5+0.75i 0.5-0.75i 0.3];kk3=150;tts3=-1;eg3zpk=zpk(zz3,pp3,kk3,tts3);eg3=tf(eg3zpk);Part D exercisezz4=[-0.3 0.4+0.2i 0.4-0.2i];pp4=[-0.6 -0.3,0.5 0.6];kk4=5;tts4=-1;eg4zpk=zpk(zz4,pp4,kk4,tts4);eg4=tf(eg4zpk);4.留数法Residue method and impluse response numg=[2 -2.2 0.65];deng=[1 -0.6728 0.0463 0.4860]; [rGoz, pGoz,other]=residue(numg,[deng 0]) [mag_pGoz,theta_pGoz] =xy2p(pGoz)[mag-rGoz,theta-rGoz]=xy2p(rGoz)G=tf(numg,deng,-1)impulse(G)[y,k]=impulse(G);stem(k,y,'filled');impulse(G)运行结果:5.复杂极点响应When transfer function is G(Z) with complex ,t=t*ts;pole of z=e^(+-j*30*pi/3) and z=-0.5,as well as its gain value is unit step signal,its collecting cycle is 0.5 second,how to analyze its response.gcfts=0.3;num=[1 0.5];den=conv([1 -exp(i*pi/3)],[1 -exp(-i*pi/3)]);g1=tf(num,den,ts)[y,k]=impulse(g1,20);stem(k,y,'filled'),grid运行结果:6.重极点响应How to analyze response with repeating poles dtime=[0:90];y(k+2)-1.8y(k+1)+0.81y(k)=3u(k+1)-1.2u(k) yi=impulse(gstep,dtime)gcfnum=[3 -1.2];den=[1 -1.8 0.81];[rGoz, pGoz,other]=residue(num,[den 0])t=0:60;y=rGoz(2,1).*(t.*(pGoz(2,1).^(t-1)))+rGoz(1,1).*(pGoz(1,1).^(t)) y1=zeros(1,61);y1(1,1)=rGoz(3,1);y=y+y1;t=ts*t;stem(t,y,'filled'),gridSpecial example about difference real pole tosystem response[rGoz,pGoz,other]=residue(num,[den,0])num1=[rGoz(1) 0];den1=[1 -pGoz(1)]gg1=tf(num1,den1,ts)[y,t]=impulse(gg1,50)stem(t,y,'filled'),grid运行结果:7.阶跃响应numg=[2 -2.2 0.56];deng=[1 -0.6728 0.0463 0.4860];g=tf(numg,deng,1);numgstep=[numg 0];dengstep=conv(deng,[1 -1]);gstep=tf(numgstep,dengstep,1)dtime=[0:90];yi=impulse(gstep,dtime)subplot(2,1,1)stem(dtime,yi,'filled')ys=step(g,dtime);subplot(2,1,2)stem(dtime,ys,'filled')dcgain(g)ys_ss=ys(end)ys_ss=ys(max(dtime))运行结果:Example 1: Analysis of subsection input function subplot(1,1,1)num=[2 -2.2 0.56];den=[1 -0.6728 0.0463 0.4860];ts=0.2;g=tf(num,den,ts);dtime=[0:ts:8]';u=2.0*ones(size(dtime));ii=find(dtime>=2.0); u(ii)=0.5;y=lsim(g,u,dtime);stem(dtime,y,'filled'),gridhold onplot(dtime,u,'o')hold offtext(2.3,-1.8,'output')text(1.6,2.3,'input')运行结果:五、实验思考1、根据实验结果,分析离散传递函数不同极点的时间响应特点。