当前位置：文档之家 › 第3讲__泡点和露点的计算

第3讲__泡点和露点的计算

  • 格式：ppt
  • 大小：373.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

3-2 泡露点计算及图形绘制

3-2 泡露点计算及图形绘制

图 苯、甲苯T-xy图
第 4页
利用闪蒸模块进行V-L相平衡计算
(1) 泡露点的计算
(2) 冷热曲线的绘制
第 5页
例题3-1 通过闪蒸模块求泡露点
【例题】利用闪蒸单元操作，完成以下例题
• 物系：苯，甲苯，其中苯的摩尔分率为0.2,
P=101.325kPa下，（Peng-Rob）求：
1）溶液的泡点温度及平衡气相组成
例题3-1 通过闪蒸模块求泡露点
• 5）定义单元操作
第10页
例题3-1 通过闪蒸模块求泡露点
• 6）运行模拟计算，查看结果
第11页
Flash 题3-6
在压力为106.7kPa下，由摩尔组成为0.3的苯
(C6H6，benzene)、 0.3的甲苯（C7H8，toluene ）和0.4的对二甲苯(C8H10，p-xylene) 所组成 的混合物，存在气液两相区的温度范围为 ( ) K到（ ）K。并计算温度为390K时成平衡 状态的气相和液相的质量组成。采用热力学模 型PENG-ROB方程，
第13页
2）溶液的露点温度及平衡液相组成
第 6页
例题3-1 通过闪蒸模块求泡露点
• 1）添加组分
• 2）选择热力学模型（Peng-Rob）
第 7页
例题 3-1 通过闪蒸模块求泡露点
• 3）绘制模拟流程图（Separators/Flash2）
第 8页
例题3-1 通过闪蒸模块求泡露点
• 4）定义进料流股
第 9页

第12页
Flash 题3-7
• 流量为 1000 mol/hr、压力为 0.11 MPa、含70 mol%乙醇和30mol%水的饱和蒸汽在蒸汽冷凝 器中部分冷凝，冷凝物流的汽/液比（摩尔）为 1/3。则离开冷凝器的汽相流股的流量为多少 kg/h，温度为 K ，需要的热（冷）量 为 kW。并给出液相的摩尔组成。（ 热力学模型NRTL）

四 多组分物系的泡点和露点计算

四 多组分物系的泡点和露点计算

二阶导数 T k1 T k
2
2 f (T k ) f (T k )
f (T k ) f (T k )
T k1 T k 0.0001
收敛快！
Chongqing university of technology
❖ 对与汽相满足理想气体，液相满足理想溶液的体系，
❖ 其平衡常数可以表示为：
迭代3次！ 已达到牛顿法 t5的精度，故t3为所求。
Chongqing university of technology
(2) Ki与组成有关
对于非理想性较强的物系：
Ki = f (T, P, xi , yi )
Ki

i Pisis
ˆ Vi P
expiL

(P R
T
Pi
s
)

例1
计算机计算——按牛顿迭代求解
❖ 牛顿迭代计算结果为：
迭代5次！ 达到迭代精度要求，故泡点温度为99.812℃。
Chongqing university of technology
例1
计算机计算——按牛顿迭代求解
❖ 若用Richmond算法，还需求二阶导数
f ''(t)
Ki
xi
{
2.303Bi
当P不太高时，P的影响不太大，收敛较快。
i ——T, P，xi 一般受压力的影响较小
Chongqing university of technology
泡点温度计算框图

因为

v i

f (T , P, yi ) ，
其中
开始

Ki


i
Pi

泡点和露点计算

泡点和露点计算

正丁烷 （1）
2.1
0.315
正戊烷 （2） 0.71
0.284
正己烷 （3） 0.25
0.1125
∑ 0.7115
传质分离过程
设温度为60℃，查P-T-K 图得K，将K值列于下表
组分 正丁烷 正戊烷 正己烷
∑
Ki
2.8
0.93
0.36
Kixi
0.42
0.372 0.162 0.954
yi
0.42
Ki f T, P, xi , yi
计算步骤：
L i
Pi S
iS
ˆ Vi P
exp ViL
P PiS RT
已知p,假设T 求出（或查出）各组分的相应参数
由已知的 x按i 理想状态求出Ki，初步算出 yi
求出 Ki，由已知的xi yi Ki xi
Ki xi 1 (通常取为0.005) 泡点T
如果 Ki xi 1 ; 升高T,重新计算。 Ki xi 1 ; 降低T,重新计算。
传质分离过程
开始 Y
输入P、y及有关参数
设T并令 1 作第一次迭代
计算PiS ,ViL ,iS ,ˆiV
调整T
计算 K i和xi 计算 xi
是否第一次迭代
圆整 xi
计算 i
Y
N
xi有无变化
N
xi 1 N
第二章 传质分离过程的热力学基础
2.2 多组分物系的泡点和露点的计算
1、定义：泡点Tb、泡点压力P、露点Td、露点压力P 2、泡、露点计算方法：根据相律 f=c-π+2=c。
类型 泡点温度
泡点压力 露点温度 露点压力
规定变量
P, x1 , x2 L L xc

Aspen第三讲要点

Aspen第三讲要点

Aspen第三讲————传热单元模型传热单元属换热器型（Heat Exchanger）共有七种模型，具体如下图所示。

一般用于改变单股物流的温度、压力和相态，比如加热器或冷却器。

Heater模型适用于简单加热，而不需要考虑使用什么样的加热介质时的换热设备类型，其连接图如下：Heater 模型（Block ）需要设定两种参数：（1） 闪蒸指标（flash specification ）所有模块的输入信息均相似进行定义出口流体的温度（Temperature）、压力(Pressure)、温度增量(temperature change)、蒸汽分率(vapor fraction)、过热度(Degree of superheating)、过冷度(Degree of subcooling)、热负荷(Heat duty)等选项需要指定具体数值，但不需要全部指定，通过点击下拉箭头任选2种进行指定即可。

（2）有效相态(valid phase)其中有蒸汽、液体、固体、汽-液、汽-液-液、液-游离水、汽-液-游离水等选项，同上，任选一种即可。

示例：例1: 20℃、0.41MPa、4000kg/hr流量的软水在锅炉中在压力不变的情况下，加热后全部成为饱和的水蒸气进入总管。

求所需的锅炉供热量。

解：第一步：建立换热模型，如下图所示：第二步：进行参数设定;首先是对整个单元进行Set up，如下图所示：在组分(component)中进行组分的定义，根据题意，所加热的组分是水（water）。

在物性（Properties）中，进行物性方法的选择，在本题中，涉及汽-液两相，较为复杂，我们选择“NRTL”物性方法。

在物流（Stream）中，根据题意，将已知条件如温度、压力、流量等信息输入。

在Block中进行该操作单元的相关设置：热焓值热负荷例2: 流量为100kg/hr、压力为0.2MPa、温度为20℃的丙酮通过一电加热器。

当加热功率分别为2kW、5kW、10kW和20kW，且压力不变时，求出口物流的状态。

3.泡、露点计算

3.泡、露点计算

露点温度（压力）
根据相律：
f = c −π + 2 = c
在以上每一类计算中，规定C个参数，必定可求取C个未知数。
2
精馏
2.2.15 多组分系统的泡点计算
1、泡点计算基本方程 相平衡关系 归一方程 相平衡常数式 方程数 变量
∑y =1 ∑x =1
i i i i
yi = Ki xi
(i =1, , c) 2 (i =1, , c)
F(T)＝1－∑ Kixi＝0
泡点方程 新值Tb
参照 Sy ＝∑ Kixi 之值调整。
当P一定，T↑，K↑；T↓，K↓ Sy =∑Kixi > 1，原设 T 过高； Sy =∑Kixi < 1，原设 T 过低。
5
精馏
（2）当 Ki＝f（T，P，x，y）机算 如系统压力P＜1.5Mpa
ˆ f i 0γ i ϕ iL Ki = V = V ˆ ˆ ϕi P ϕi
精馏
x 输入T，
泡点压力计算框图
估计初值Pb和 y
0 ˆV 计算 K i = γ i f i / ϕ i P
ˆ ϕ iL Ki = V ˆ ϕi
计算 yi = K i xi 及 y i = K i xi / ∑ K i xi Pb=Pb(1-F) 否
F =1 − ∑ Ki xi
F ≤ ε ( 如 .0 0 1) ?
F (T ) = 1− ∑ yi Ki = 0
i
F (P) = 1− ∑ yi Ki = 0
i
10
精馏
2.露点计算
给定：P（或T）和汽相组成
ቤተ መጻሕፍቲ ባይዱ
y1 , y2 ,
, yC −1
计算：此P下，凝结出第一滴露珠时的TD及此露珠的组成 xi 此T下，凝结出第一滴露珠时的PD及此露珠的组成 露点压力：计算的迭代式为： 露点压力：

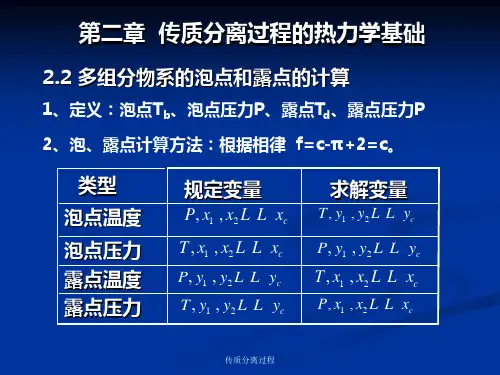
第3讲 泡点和露点的计算

第3讲 泡点和露点的计算
传质分离过程
b、平衡常数与组成有关 计算步骤： 已知T ,假设p 求出（或查出）各组分的相应参数
由已知的 x按i 理想状态求出Ki，初步算出 yi
求出 Ki，由已知的xi yi Ki xi
Ki xi 1 (通常取为0.005) 泡点压力p 如果 Ki xi 1 ; 升高P,重新计算。
点Q~N之间： 气液共存区 分凝器、 再沸器
传质分离过程
3、 泡点温度和泡点压力的计算
(1)、依据的方程：
A、相平衡关系
yi Ki xi （i=1，2，3，……c）
Ki fi P,T, xi , yi (i=1，2，3……c)
B、浓度总和式（归一方程）
xi 1
i
yi 1
第二章 传质分离过程的热力学基础
2.2 多组分物系的泡点和露点的计算
1、定义：泡点Tb、泡点压力P、露点Td、露点压力P 2、泡、露点计算方法：根据相律 f=c-π+2=c。
类型 泡点温度
泡点压力 露点温度 露点压力
规定变量
P, x1 , x2 L L xc
T , x1 , x2 L L xc P, y1 , y2 L L yc T , y1 , y2 L L yc
正丁烷 （1）
2.1
0.315
正戊烷 （2） 0.71
0.284
正己烷 （3） 0.25
0.1125
∑ 0.7115
传质分离过程
设温度为60℃，查P-T-K 图得K，将K值列于下表
组分 正丁烷 正戊烷 正己烷
∑
Ki
2.8
0.93
0.36
Kixi
0.42
0.372 0.162 0.954

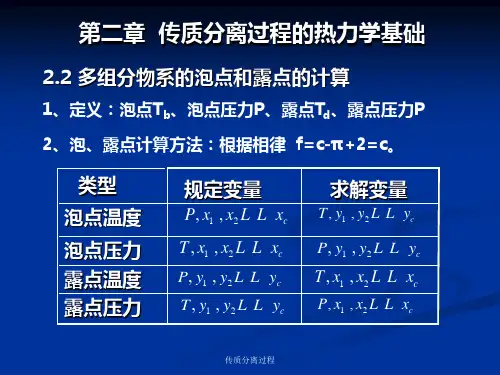
泡点和露点计算

泡点和露点计算

本节内容
气液平衡系统的设计变量 泡露点计算的重点、难点 泡点温度计算 露点温度计算
2.2 多组分物系的泡点和露点计算 Bubble-point and Dew-point Calculation for Multicomponent Systems
分离过程设计中最基本的气液平衡计算。 例如：
练习1
求含乙烷(1)0.15、丙烯(2)0.4、丙烷(3)0.35、 异丁烷(4)0.1（摩尔百分比）的烃类混合物在 300kPa时的泡点温度
问题:
什么样的情况下可认为K与组成无关？
答：1）汽相为理想气体，液相为理想溶液。
Ki pis / p
2）汽相为理想溶液，液相为理想溶液
Ki fiL /fivபைடு நூலகம்
精馏计算： 各塔板温度---泡点计算 操作压力---泡露点压力计算
等温闪蒸计算： 估计闪蒸过程是否可行---泡露点温度计算
一、气液平衡系统设计变量
气相
液相
气液平衡系统
请分析一下上图气液平衡系统的总变量、独立约束方程和 设计变量（10min）
气相 液相 气液平衡系统
？定义哪些变量 称为设计变量
一、气液平衡系统设 计变量
Ki
ˆiL ˆiV
（2-12）
Ki
yi xi
i
Pi
s s i
ˆiV P
exp
viL
(P RT
Pi
s
)
（2-30）
If :
Ki f p,T , c
开始
输入p，x及有关参数
设T并令iV＝1，作第一次迭代
计算pis、ViL、is、i
调整T
N
计算Ki和yi
计算yi

泡点和露点计算 ppt课件

泡点和露点计算 ppt课件
• 取正己烷纯物质的沸点为初始温度 • 查p-T-K图，可得T0=86’C • 计算过程见Excel
ppt课件
14
三、泡点温度的计算（小结）
（1）设定温度T初值
取液相含量最大、或分子量约等于平均分子量的组分 的纯物质沸点作为温度的迭代初值。
（2） 计算或查图得Ki值
1）p-T-K图（烃类物系） 2）简化表达式： K i Pis / P
（3）判断收敛的准则或者是温度的调节方案直接 关系到收敛速度和稳定性。
ppt课件
参见例［2－5］ 22
四、露点温度计算
ppt课件
23
四、露点温度计算
• 类似于泡点温度计算
已知p 设T
计算或查图 得Ki
计算
C
f (T ) yi / Ki 1 i1
调整T
f (T )
是
结束 输出T，x
计算 yi
是否第一次迭代
N
yi有无变化
N
Ln yi
Y
输出p，y
圆整yi，计算iV
Y
Y
Adjust p
结束
ppt课件
Start
Input T, x
Estimate p and ˆ Vi 1 as first iteration
Calculate
pis
,
viL
,

s i
,

i
Calculate Ki , yi
Set T and ˆ Vi 1 as first iteration
Calculate
pis
,
viL
,

s i
,

i
Calculate Ki , yi

分离过程-泡露点

分离过程-泡露点

混合物的逸度系数：
ˆV ln V ln f V ln f i i i 二元：
V 2 （2 B12 B22 B11）py2 RT ln 1 V 2 RT ln （ 2 B B B ） py 2 12 11 22 1 — 参阅《基本有机化工分 离工程》（1 53）式
L 3 . Ki fi
f iL f
V i
一、泡点计算 Tb
1、泡点方程
K x
i i
1
K与p、T的关系
T p Y
K K 结束
2、计算步骤 由T、p 设 Tb 查 说明
Ki
K x
？
i i
1
N
K x
>1 说明所设 Tb高，应降低 Tb 重设 <1 说明所设 Tb低，应提高 Tb 重设
i i
（已知p，x） 计算 变量 与函 数关 系
求泡点压力
（已知T，x）
Ki
i pisfis Vi L ( p pis ) Ki V exp[ ] ˆ p RT f i
与T有关的变量： ˆV ， ，p s，f s，V L f
i i i i i
i
相同
与p有关的变量： ˆv，p f
V ˆ 与yi 有关的变量：f i
p V 2 ˆ ln fi [ Bii （2 B12 B11 B22）y j ] RT — 式中i， j 1， 2
ˆV ln f s 令： i ； 有： ln ln f i i i i fs i 将上式代入（A）： p 1 1 1 2 2 2 （B） 1 2 式中： 2 2B B B ) B（p ps） py（ ii i j 12 11 22 exp[ ] i RT (C ), ( D)

第二章-3 泡露点计算

第二章-3 泡露点计算

• 两相区 ：物系处于泡点露点之间
(1)泡点、露点计算的目的
• 确定气体和液体的饱和条件，及判别平衡位置
(2) 计算类别 • 已知Pv 求 Tv ---求泡、露点温度 • 已知Tv 求Pv ---求泡、露点压力 一类：已知液相组成 xi（或气相组成yi ）和系 统的平衡压力P，求泡点温度T（或露点温度） 和平衡的气相组成yi（液相组成xi ）。 另一类：已知液相组成 xi（或气相组成yi ）和 系统的平衡温度T，求泡点压力P（或露点压力） 和平衡的气相组成yi（液相组成xi ）
泡点方程泡点判别式露点方程露点判别式物系处于露点之上过热蒸汽物系处于泡点之下过冷液体判别是否存在两相区框图小结泡点计算若已知操作压力p液相组成x用试差法求泡点温度的步骤如下
2.5 泡点、露点计算 • • • • 泡点： 形成第一个气泡的温度和压力 露点： 形成第一个液滴的温度和压力: 物系处于露点以上，所有Ki＞1
ri p ki = p
s i
2.6 绝热闪蒸计算 Q=0, 求ϕ ， T 基本闪蒸方程既是ϕ的函数 ，又是 T的函数， 必须建立另外迭代方程 一般做法是：由基本闪蒸方程迭代ϕ，由热平 衡方程迭代T
求解思路： 对宽沸程物系，先假设T，迭代ϕ，再迭代T 对窄沸程物系，先假设ϕ ，迭代T，再迭代ϕ 对ϕ和T均敏感的物系，采用联立方程求解
i i i i
=0
∑z k
i
i
=1
露点时： ϕ=1
z i (1 − k ) z i (1 − k i ) zi zi ∑ 1 + ϕ (k − 1) = ∑ k = ∑ ( k − z i ) = ∑ k − 1 = 0 i i i i
∑
zi = 1 ki
∑z k

2.2多组分物系的泡点和露点计算

2.2多组分物系的泡点和露点计算
给定P
计算中：若 ∑ K i x i > 1, 说明 T偏高； 若 ∑ K i x i < 1, 说明 T偏低。
相平衡常数法－低压下理想混合物
该情形下：
pi Ki = P
s
s
相平衡关系式： 摩尔分率加和方程： N 设T
pi yi = xi P
① ② 缺点是收敛速度较慢
∑y
i
i
i
=1
pis ① yi ②
5
Dew point temperature
Dew Point is the very state at which condensation is about to occur.
Dew Point Temperature Calculation at a Given Pressure Dew Point Pressure Calculation at a Given Temperature Vapor Fraction is ‘1’ at Dew Point
i
②
∑ y = ∑α
i i i
ik
K k xi = 1
故 Kk =
∑ α ik xi
i
1
③
手算：ε =0.5°C
优点：收敛速度较快。 设T pis, pks ① αik ③ Kk pks’ = Kk•P T’
yi
T −T' ≤ ε
N
② Y
例2-4：计算塔釜温度（完全理想系）
已知：1. x i, w S ln Pi、= Ai − Bi (t + Ci ) 2.
• If not =1, then guess another T • If = 1, then yi = Ki(TBP) xi

2.2 多组分物系的泡点和露点计算2007.9.10

2.2 多组分物系的泡点和露点计算2007.9.10

解：
常压
气相—— 气相 为理想气体 液相—— 液相 为理想溶液
•参考解法： 参考解法： 参考解法
Pi Ki = P
s
（1）试差法（手算） 试差法（手算） （2）相对挥发度法 （3）计算机求解
结构相似
例2-4
（1）试差法-计算（见下表） 试差法-计算（见下表）
塔釜温度应为100℃。 ℃ 塔釜温度应为
ˆ υiL ( P − Pi s ) Φ iL γ i Pi Φ Ki = exp = ˆV V ˆ RT Φi P Φi
s s i
1、泡点温度计算 、
严格计算法 ——计算过程 计算过程
xi , P → yi , T
Ki
s i
Pi Φ υ
s
s i
——T, P
(一般受 的影响较小 一般受P的影响较小 一般受 的影响较小)
Ki = f (P, T, xi, yi)
2.2.1 泡点温度和泡点压力计算
总变量：C-xi，C-yi，C-Ki，T，P。共3C+2 总变量： 个 已知C个变量：（ 已知C个变量：（C-1）个组分和T或P ：（C 个组分和T 未知变量为2C+2个 未知变量为2C+2个 由上述2C+2个方程求解 唯一解） 由上述2C+2个方程求解（唯一解） 个方程求解（ 需试差计算
2.2 多组分物系的泡点和露点计算
泡点计算： 泡点计算： 泡点温度计算：已知x 泡点温度计算：已知xi，p，求解T，yi 温度计算 求解T 泡点压力计算：已知x 泡点压力计算：已知xi，T，求解P，yi 压力计算 求解P 露点计算： 露点计算： 露点温度计算：已知y 露点温度计算：已知yi，P， 求解T，xi 温度计算 求解T 露点压力计算：已知y 露点压力计算：已知yi，T， 求解P，xi 压力计算 求解P

2-3泡露点计算

2-3泡露点计算

2.3.1 泡点温度和压力的计算
2.3.2 露点温度和压力的计算

2.3.1 泡点温度和压力的计算
规定液相组成 x 和压力p（或温度T）， 计算汽相组成 y 和温度T（或压力p）。 已知： x 、p 计算： y 、T 已知： x 、T 计算： y 、p 泡点压力计算 泡点温度计算
计算出发点：
输出 p 和 y Y
输入T, x及有关参数， p和y估计值
求iV和iL
调整p
f ' (T0 )
T0
xi Bi Bi f (t ) ( exp(Ai )( )) 2 p Ci t (t Ci )
'
T
Bi f (t ) ( K i xi ) 2 (t Ci )
'
t k 1
f (t ) tk ' tk f (t )
若 t ( k 1) t ( k )
重算Sy得： S y
K x
i 1
4
i i
0.9641
S y 1，应将假设适当温度调高。
③ 再设T=-20℃，查P-T-K图得： K1=4.86，K2=1.01，K3=0.69，K4=0.187
4
重算Sy得：
Sy
K x
i 1
i i
1.0025
Sy比较接近1，可近似认为塔顶产品饱和温度为-20℃。
到泡点温度的数值解。
可选组分 1 或组分 3 的沸点为初值开始计算，若以 t (1) =70 ℃ 作为初值 则 如此进行下去，当迭代至第 6次， ，达到迭代精度
，得泡点温度为 99.81 ℃
若用 Richmond 算法，还需求二阶导数 f'' ( t)

4-2020泡点和露点

4-2020泡点和露点

A T-P-K列线图—适用于烃类体系(p40-41)
B
ki
Pi o P
1 P exp( Ai
Bi ) Ci T
适用于体系为理想气体和 理想溶液的系统
Ai , Bi , Ci
f (物性，T )
可在物性手册中查 取
安托因方程：
log P0 = A - B / T +C
手算方法：
注意：
ε一般取10-3即可 第一次试差温度可取混合物中含量最多的那个组分 在系统压力下的沸点温度左右为第一个试差温度，
比较不变 No
P47，图2-6
露点温度和压力的计算（对汽相而言）：
C
f (T ) xi 1.0 i1
计算机计算泡点和露点：
平衡常数可表示为温度T的函数时，Newton-Raphson,Richmond迭代法 P49 例2-7
3) 四元溶液：三个塔，五种方案 当挥发度：A>B>C>D
A,B,C,D
A B
B,C,D C,D
(Ⅰ)
A,B,C,D
A
B
B,C
C
B,C,D
C
D D
(Ⅱ)
• 总结：若 C---组分数，n---所需塔数 z---可供选择的流程方案数
则有：
C2
3
4
5
6
7
8
n
1
2
3
4
5
6
7

Z
1
2
5
14 42 132 429
(2C+2) ,Xc,,Ki ,Xc,,Ki ,Xc,,Ki ,Xc, ,Ki
泡点温度和压力的计算（对液相而言）：
Ki

泡点和露点计算-PPT

泡点和露点计算-PPT

1. Ki与组成无关：if Ki f(T,P)
泡点方程：
C
fT Kixi 10
i1
计算过程：
已知p 设T
计算或查图 得Ki
计算
C
f (T ) Ki xi 1 i 1
调整T
f (T )
是
结束 输出T，y
否
12
例题2-3
• 例2-3 • 三种组分含量
相差不大，取 分子量居中的 正戊烷在该压 力下的沸点为 初值 • 从p-T-K图上 查得T0=62’C
当汽相为理想气体，液相为非理想溶液时：
c
pb i pis xi i1
当Ki=f(T,p,x,y)时，用活度系数法（压力不太高）或 状态方程法（压力较高）计算泡点压力。
28
开始
输入T，x及有关参数 估计p,并令iV＝1，作第一次迭代
计算pis、ViL、is、i
调整p
N
计算Ki和yi
计算 yi
是否第一次迭代
RCoalucnudlateyiˆ Vi
Whether first Y iteration or not
N
yi Change Y
or not N
n yi
Output p, y
活 度 系 数 法 计 算 泡 点 压 力 的 框 图
End
29
输入T, x及有关参数， p和y估计值
求iV和iL
计算Ki
N
Ln yi
Y
输出T，y
圆整yi，计算iV
Y
Y
结束
Adjust T
Start Input p, x
Set T and ˆ Vi 1 as first iteration

泡点.露点计算简便法举例

泡点.露点计算简便法举例

1、一液体混合物的组成为：苯0.50；甲苯0.25；对二甲苯0.25(摩尔分率)。

分别用平衡常数法和相对挥发度法计算该物系在100kPa 时的平衡温度和汽相组成。

假设为完全理想系。

解1：(1)平衡常数法： 设T=368K 用安托尼公式得：kPa P s 24.1561= ；k P a P s28.632= ；k P a P s 88.263=由式(2-36)得：562.11=K ；633.02=K ；269.03=K 781.01=y ；158.02=y ；067.03=y；006.1=∑i y 由于∑i y >1.001，表明所设温度偏高。

由题意知液相中含量最大的是苯，由式(2-62)得：可得K T 78.367'=重复上述步骤：553.1'1=K ；6284.0'2=K ；2667.0'3=K 7765.0'1=y ；1511.0'2=y ；066675.0'3=y ；0003.1=∑i y所以在温度为367.78K 时，存在与之平衡的汽相， 组成为：苯0.7765、甲苯0.1511、对二甲苯0.066675。

2、含有80%(mol)醋酸乙酯(A)和20%乙醇(E)的二元物系，液相活度系数用V an Laar 方程计算，AE A =0.144，EA A =0.170。

试计算在101.3kPa压力下的泡点温度和露点温度。

安托尼方程为： 醋酸乙酯：()15.5750.27900444.21ln --=T P SA乙醇：()68.4198.38038047.23ln --=T P SE (PS ：Pa ；T ：K)解2：(1)计算活度系数：0075.0)2.017.08.0144.01(144.0}1(ln 22=⨯⨯+=+=EEA A AE AE A x A x A A rA r =1.0075 10137.0}8.0144.02.017.01(17.0}1(ln 22=⨯⨯+=+=AAE E EA EA E x A x A A rE r =1.107(2)计算泡点温度 设T=353.15K(80℃)617.1115.5715.35350.27900444.21ln =--=s A P∴Pa P s A 5101097.1⨯=5917.1168.4115.35398.38088047.23ln =--=s E P∴Pa P s E 510082.1⨯=∴1037.110013.1101097.10075.155=⨯⨯⨯==P P r K S A A A1821.110013.110082.1107.155=⨯⨯⨯==P P r K S E E E∴1194.12.01821.18.01037.1=⨯+⨯=∑i i x K调整98597.01194.11037.12==A K)15.575.27900444.21exp(0075.110013.198597.0522--=⨯⨯==T r P K P A A SA解得T2=349.65，即T2=76.50℃∴s A P ln =11.504 Pa P sA 41091.9⨯=s E P ln =11.453Pa P s E 4104175.9⨯=∴A K =0.9857E K =1.028819943.02.00288.18.09857.0≈=⨯+⨯=∑ii xK故泡点温度为76.5℃ (3)计算露点温度 设T=353.15K(80℃) 由k 'c =k c ⨯i i /k y ∑∴9867.0894.01037.12=⨯=A K)15.575.27900444.21exp(0075.110013.19867.0522--=⨯⨯==T r P K P A A SA解得T2=349.67K(76.52℃)∴sA P ln =11.505Pa P s A 41092.9⨯=s E P ln =11.454Pa P s E 410425.9⨯=9866.0013.1992.00075.1=⨯=A K 03.1013.19425.0107.1=⨯=E K1005.103.12.09866.08.0≈=+=∑ix故露点温度为76.52℃3、某汽相混合物的组成及平衡常数如下：求P=1atm 时，混合物的露点温度，误差判据可取0.001。

【2019年整理】22多组分物系的泡点和露点计算2007910

【2019年整理】22多组分物系的泡点和露点计算2007910
个 已知C个变量：（C-1）个组分和T或P 未知变量为2C+2个 由上述2C+2个方程求解（唯一解）
需试差计算
2.2.1 泡点温度和泡点压力计算
1、泡点温度计算
c
泡点方程： Ki xi 1 i 1
已知 xi, P
c
或 f (T ) Ki xi 1 0 i 1
1、泡点温度计算
计算方法
整采用抛物线法 （Muller）；
开始
因为
v i
f (T , P, yi ) ，
其中
故初次令
v i
1
输入P、ｘ及有关参数
yi 未知，
设定T并令ˆ iv＝1作第一次迭代
设T
计算Pis、ViL、Фis、 i
纯组分i
s i
i
—维里方程，
—wilson(T,P,xｉ)
G （ 1／ T） 线 性 ,P<20ａ ｔｍ，用牛顿－拉普森 （Neuton-Raphson）迭代
例2-3
假设T=50℃,因P=0.2MPa,查图求平衡常数：
组分
xi
Ki
正丁烷
0.15
2.5
正戊烷
0.40
0.76
正己烷
0.45
0.28
yi=Kixi 0.375 0.304 .7℃
Ki xi 0.805 1.00
例2-3
假设T=58.7℃, 查图求平衡常数：
32 33 11322 .895
例2-5
ln
Pi s
A
t
B C
安托尼方程常数
Ps：kPa，t：K
丙酮 丁酮 乙酸乙酯
A 14.6363 14.5836 14.1366
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

已知T , 假设p 求出（或查出）各组分的相应参数
由已知的
yi 按理想状态求出Ki，初步算出 xi
求出 K i， 由已知的yi xi yi / Ki
xi 1 ( 通常取为0. 005) 露点压力p
如果
xi 1 ;
降低P,重新计算。
xi 1 ; 升高P,重新计算。
Ki fi P, T , xi , yi (i=1，2，3……c)
B、浓度总和式（归一方程）
y
i
i
1
x
i
i
1
传质分离过程
(2)、平衡常数与组成无关的露点温度计算
pis ,可简化计算。 若 Ki f T , P p 计算步骤：
S 已知p, 假设T 求出（或查出）各组分的pi
已知T , 假设p 求出（或查出）各组分的相应参数
求出 K i， 由已知的yi xi yi / Ki
xi 1 ( 通常取为0. 005) 露点压力p
如果
xi 1 ;
降低P,重新计算。
xi 1 ; 升高P,重新计算。
传质分离过程
（5）平衡常数与组成有关的露点压力的计算 计算步骤：
a、平衡常数与组成无关
计算步骤：
已知T 求出（或查出）各组分的p
因理想溶液符合拉乌尔定律，即：
S i
p p x
s i i
由已知的xi p
传质分离过程
b、平衡常数与组成有关 计算步骤：
已知T , 假设p 求出（或查出）各组分的相应参数
由已知的
xi 按理想状态求出Ki，初步算出 yi
N
Y
yi 有无变化
ln yi
Y 输出P、y 结束
NБайду номын сангаас
N
计算 Pi
S
,Vi L , iS , i
圆整 y i ˆiV 计算 Y
计算 K i 和yi
调整P 计算 yi 是否第一次迭代
传质分离过程
4、露点温度和压力的计算
(1)、依据的方程： A、相平衡关系
xi yi / Ki （i=1，2，3，……c）
传质分离过程
开始 输入T、y及有关参数 估计P，X值 计算 i 计算 K i 调整P 圆整 x i Y
( yi K i ) 1
Y 输出P、x 结束
N
xi有无变化
N
传质分离过程
泡点压力
露点温度 露点压力
P, y1 , y2
yc
T , x1 , x2
P, x1 , x2
xc
xc
T , y1 , y2
yc
传质分离过程
精馏塔为全凝器时回流最高为何温度？ 分凝器？塔底温度？
D yD,i D xD,i
Fzi
Fzi
W xW,i
W xW,i
传质分离过程
点 Q： 气相点 点N： 液相点
输入P、y及有关参数 设T并令 1 作第一次迭代
S L S ˆV 计算Pi ,Vi , i , i
xi 1
Y 输出T、y
结束
N
N
计算 K i 和xi 调整T 计算 xi 是否第一次迭代
圆整 x i 计算 i Y
传质分离过程
（4）平衡常数与组成无关的露点压力的计算
计算步骤：
求出 K i，由已知的xi yi Ki xi
Ki xi 1 ( 通常取为0. 005) 泡点压力p
如果
Ki xi 1 ;
升高P,重新计算。
Ki xi 1 ; 降低P,重新计算。
传质分离过程
开始 输入T、x及有关参数
V ˆ 估计P并令 i 1作第一次迭代
已知p, 假设T 求出（或查出）各组分的相应参数
由已知的 x 按理想状态求出 Ki，初步算出 i 求出 K i，由已知的xi yi Kixi
yi
Ki xi 1 ( 通常取为0. 005) 泡点T
如果
Ki xi 1 ;
降低T,重新计算。
Ki xi 1 ; 升高T,重新计算。
传质分离过程
(2)、平衡常数与组成无关的泡点温度计算
pis 若 Ki f T , P ,可简化计算。 p 计算步骤：
S 已知p, 假设T 求出（或查出）各组分的pi
pis Ki Ki p
由已知的xi yi Ki xi
Ki xi 1 ( 通常取为0. 005) 泡点T
传质分离过程
开始 输入P、x及有关参数
N Y
yi 有无变化
ˆi 1作第一次迭代 设T并令
V
ln yi
Y 输出T、y 结束
N
N
计算 Pi
S
,Vi L , iS , i
圆整 y i ˆiV 计算 Y
计算 K i 和yi
调整T 计算 yi 是否第一次迭代
传质分离过程
(4)、泡点压力的计算
第二章 传质分离过程的热力学基础
2.2 多组分物系的泡点和露点的计算
1、定义：泡点Tb、泡点压力P、露点Td、露点压力P 2、泡、露点计算方法：根据相律 f=c-π+2=c。
类型
泡点温度
规定变量
P, x1 , x2 T , x1 , x2
P, y1 , y2
求解变量
xc xc
yc
T , y1 , y2 yc
由已知的
yi 按理想状态求出Ki，初步算出 xi
求出 K i， 由已知的yi xi yi / Ki
xi 1 ( 通常取为0. 005) 露点T
如果
Ki xi 1 ;
升高T,重新计算。
Ki xi 1 ; 降低T,重新计算。
传质分离过程
开始
Y
N xi有无变化
pis Ki Ki p
由已知的yi xi yi / Ki
xi 1 ( 通常取为0. 005) 露点T
如果
xi 1 ; xi 1 ;
升高T,重新计算。 降低T,重新计算。
传质分离过程
(3)、平衡常数与组成有关的露点温度计算
计算步骤：
已知p, 假设T 求出（或查出）各组分的相应参数
全凝器
点Q~N之间： 气液共存区 分凝器、 再沸器
传质分离过程
3、
泡点温度和泡点压力的计算
(1)、依据的方程： A、相平衡关系
yi Ki xi
（i=1，2，3，……c）
Ki fi P, T , xi , yi (i=1，2，3……c)
B、浓度总和式（归一方程）
x
i
i
1
y
i
i
1
如果
Ki xi 1 ;
降低T,重新计算。
Ki xi 1 ; 升高T,重新计算。
传质分离过程
例 2－ 3： 求含正丁烷（1）0.15、正戊烷（2）0.4和
正己烷（ 3 ） 0.45 （ mol ）之烃类混合物在 0.2Mpa 压力下 的泡点温度。
解：因各组分均为烷烃，所以汽液两相均可看为理想溶 液可由P-T-K 图求Ki值，设温度为50℃，查P-T-K 图得K， 将K 值列于下表 组分 Ki Ki xi 正丁烷 （1 ） 2.1 0.315 正戊烷 （2） 0.71 0.284 正己烷 （3） 0.25 0.1125 ∑
0.7115
传质分离过程
设温度为60℃，查P-T-K 图得K，将K值列于下表
组分 Ki
K i xi yi 组分 Ki K i xi yi
正丁烷 2.8
0.42 0.42
正戊烷 0.93
0.372 0.372
正己烷 0.36
0.162 0.162
∑
0.954 0.954
设温度为62℃，查P-T-K 图得K，将K 值列于下表 正丁烷 2.9 0.435 0.435 正戊烷 0.98 0.392 0.392
传质分离过程
正己烷 0.39 0.1755 0.1755
∑ 1.0025 1.0025
(3)、平衡常数与组成有关的泡点温度计算
L S V P P P i i Ki f T , P, x, exp i yi ˆ P RT 计算步骤： L S i i V i S i