下载文档原格式
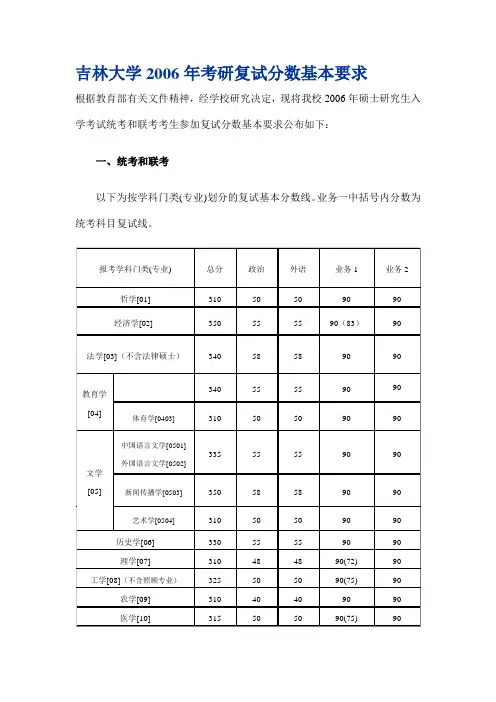
吉林大学2006年考研复试分数基本要求
根据教育部有关文件精神，经学校研究决定，现将我校2006年硕士研究生入学考试统考和联考考生参加复试分数基本要求公布如下：
一、统考和联考
以下为按学科门类(专业)划分的复试基本分数线。
业务一中括号内分数为统考科目复试线。
二、单独考试(含强军计划、援藏计划)、少数民族高层次骨干人才计划：
复试基本分数线根据教育部相关政策另行确定。
三、软件工程硕士：
报考吉林大学软件学院的考生，外语、政治不低于40分，统考数学不低于60分，专业课不低于90分，总分达到295分以上。
四、照顾专业:
报考工学门类中力学[0801]、冶金工程[0806]、动力工程及工程热物理[0807]、水利工程[0815]、地质资源与地质工程[0818]、核科学与技术[0827]、农业工程[0828]专业的考生，外语、政治不低于40分，统考数学不低于60分，专业课不低于90分，总分不低于300分。
五、少数民族政策：
工作单位在国务院公布的民族自治地方，即5个自治区、30个自治州、119个自治县(旗)，并报考为原单位定向或委托培养的少数民族在职人员考生，其复试分数线在我校基本分数线上单科降低5分，总成绩降低20分。
吉林大学2006年攻读硕士学位研究生入学考试试题数学分析卷一、（共30分）判断题1、若函数()f x 在(),a b 上Riemann 可积，则()2f x ⎡⎤⎣⎦在(),a b 也Riemann 可积；2、若级数1n n a ∞=∑收敛，则级数1n n a ∞=∑也收敛；3、任何单调数列必有极限；4、数列(){}1n-的上、下极限都存在； 5、区间(),a b 上的连续函数必能达到最小值； 6、sin x 在整个实轴上是一致连续的；7、若函数(),f x y 沿着任何过原点的直线连续，则(),f x y 在()0,0连续； 8、若函数()f x 在点0x 取极小值，则()00f x '=； 9、若()00f x '=，()00f x ''<，则()f x 在点0x 取极大值； 10、向量场()222222,,x y y z z x ---是无源场。
二、（共20分）填空题1、设()()sin u x y x y z =+++，则grad ()u =；2、设(),,F x y y z z x →=+++，则div ()F →=； 3、设(),,F x yz y zx z xy →=---,则rot ()F →=；4、设s 表示单位球面2221x y z ++=，则第一型曲面积分()2sx ds =⎰⎰；5、数列()2211n n n ⎧⎫+-⎨⎬⎩⎭的下极限为()；三、（共20分）计算下列极限1、1200611lim n n k k →∞=⎛⎫⎪⎝⎭∑；2、01limx x→；3、111lim 200620071n n n n n →∞⎛⎫+++⎪++++⎝⎭L ； 4、120lim 1nn x dx x x→∞++⎰。
四、（共20分）判断下列级数的敛散性1、1200620072005nn nn ∞=-∑； 2、1n n u ∞=∑，其中()2120,,1,2,1n n n u n u n u n ->≤=+L 五、（10分）设函数()f x 在[]0,1两次连续可微，满足()()010f f ==且()10f x dx =⎰。
大学2006年攻读硕士学位研究生入学考试试题数学分析卷一、（共 30 分）判断题1、若函数)(x f 在()b a ,上Riemann 可积，则 []2)(x f 在()b a ,上Riemann 也可积；2、若级数∑∞=1n n a 收敛，则级数∑∞=1n n a 也收敛；3、任何单调数列必有极限；4、数列(){}n1-的上、下极限都存在；5、区间 ()b a , 上的连续函数必能达到最小值；6、x sin 在整个实轴上是一致连续的；7、若函数()y x f ,沿着任何过原点的直线连续，则()y x f ,在()0,0连续； 8、若函数()x f 在点0x 取极小值，则()0x f '=0； 9、若()0x f '=0，()00<''x f ，则()x f 再点0x 取最大值； 10、向量场()222222,,x z z y y x ---是无源场。
二、（共 20 分）填空题1、设))(sin(z y x y x u +++=，则gradu =( );2、设),,(x z z y y x F +++=，则F div =();3、设),,-(xy z zx y yz x F --=，则F rot =( );4、设s 表示单位球面1222=++z y x ，则第一型曲边梯形ds x s⎰⎰2=();5、数列()⎭⎬⎫⎩⎨⎧+2211-n n n 的下极限为( );三、（共 20 分）计算下列极限1、n nk n k 1120061lim ⎪⎭⎫ ⎝⎛∑=∞→；2、()x x xx 31211lim30+-+→；3、()112007120061lim ++++∞→++n n n n n ；4、dx x x x n ⎰++∞→10221lim ； 四、（共 20 分）判断下列级数的敛散性1、∑∞=-1200520072006n n n n； 2、∑∞=1n n u ，其中0>n u ，()2211+≤-n n u u nn ，⋅⋅⋅=2,1n ； 五、（10 分）设函数)(x f 在[]1,0两次连续可微，满足0)1()0(==f f 且()01=⎰dx x f 。
考研已落下帷幕考研虽然已经结束好长时间，而它对于我来说，就像是昨天刚发生一样，清晰且深刻。
回首考研的这段经历，我收获了很多，也成长了许多。
开始基础复习的时候，是在网上找了一下教程视频，然后跟着教材进行学习，先是对基础知识进行了了解，在5月-7月的时候在基础上加深了理解，对于第二轮的复习，自己还根据课本讲义画了知识构架图，是自己更能一目了然的掌握知识点。
8月以后一直到临近考试的状态，开始认真的刷真题，并且对那些自己不熟悉的知识点反复的加深印象，这也是一个自我提升的过程。
考研一路走来，真的很辛苦，考研帮里学长学姐们分享的宝贵经验不仅能让我打起精神背水一战，还使我的复习有条不紊地进行。
初试成绩出来的这两天，酝酿了一下，我也想为将要参加下一届考研的的学弟学妹们写一篇文章，希望你们从复习的开始就运筹帷幄，明年的这个时候旗开得胜。
文章字数很多，大家有时间可以阅读，文末有真题和资料下载分享，谢谢大家。
吉林大学数学的初试科目为：(101)思想政治理论(201)英语一(646)数学分析和(850)空间解析几何与高等代数参考书目为：1.《数学分析》第一册，严子谦、尹景学、张然编，高等教育出版社，2004年5月出版2.《数学分析》第二册，马富明、高文杰编，高等教育出版社，2005年7月出版3.《解析几何》，尤承业编著，北京大学出版社，2004年1月出版4.《空间解析几何》，谢敬然、柯媛元主编，高等教育出版社，2013年5月出版5.《高等代数》，杜现昆、徐晓伟、马晶、孙晓松编，科学出版社，2017年8月出版6.先说英语吧。
7.词汇量曾经是我的一块心病，跟我英语水平差不多的同学，词汇量往往比我高出一大截。
从初中学英语开始就不爱背单词。
在考研阶段，词汇量的重要性胜过四六级，尤其是一些熟词僻义，往往一个单词决定你一道阅读能否做对。
所以，一旦你准备学习考研英语，词汇一定是陪伴你从头至尾的一项工作。
8.考研到底背多少个单词足够？按照大纲的要求，大概是5500多个。
吉林大学2006年攻读硕士学位研究生入学考试试题数学分析卷一、（共 30 分）判断题1、若函数)(x f 在()b a ,上Riemann 可积，则 []2)(x f 在()b a ,上Riemann 也可积；2、若级数∑∞=1n n a 收敛，则级数∑∞=1n n a 也收敛；3、任何单调数列必有极限；4、数列(){}n1-的上、下极限都存在；5、区间 ()b a , 上的连续函数必能达到最小值；6、x sin 在整个实轴上是一致连续的；7、若函数()y x f ,沿着任何过原点的直线连续，则()y x f ,在()0,0连续； 8、若函数()x f 在点0x 取极小值，则()0x f '=0； 9、若()0x f '=0，()00<''x f ，则()x f 再点0x 取最大值； 10、向量场()222222,,x z z y y x ---是无源场。
二、（共 20 分）填空题1、设))(sin(z y x y x u +++=，则gradu =( );2、设),,(x z z y y x F +++=，则F div =();3、设),,-(xy z zx y yz x F --=，则F rot =( );4、设s 表示单位球面1222=++z y x ，则第一型曲边梯形ds x s⎰⎰2=();5、数列()⎭⎬⎫⎩⎨⎧+2211-n n n 的下极限为( );三、（共 20 分）计算下列极限1、nn k n k 1120061lim ⎪⎭⎫ ⎝⎛∑=∞→；2、()x x xx 31211lim30+-+→；3、()112007120061lim ++++∞→++n n n n n ；4、dx x x x n ⎰++∞→10221lim ； 四、（共 20 分）判断下列级数的敛散性1、∑∞=-1200520072006n n nn； 2、∑∞=1n n u ，其中0>n u ，()2211+≤-n n u u n n ，⋅⋅⋅=2,1n ； 五、（10 分）设函数)(x f 在[]1,0两次连续可微，满足0)1()0(==f f 且()01=⎰dx x f 。
