三年高考两年模拟2017版高考数学专题汇编 第八章 立体几何初步5 理

§8.3直线与圆、圆与圆的位置关系Ａ组基础题组1.(2015浙江丽水中学期中)若过点A(a,a)可作圆x2+y2-2ax+a2+2a-3=0的两条切线,则实数a 的取值范围是( )A.(-∞,-3)B.C.(-∞,-3)∪D.(-3,+∞)2.(2015安徽,8,5分)直线3x+4y=b与圆x2+y2-2x-2y+1=0相切,则b的值是( )A.-2或12B.2或-12C.-2或-12D.2或123.(2013陕西,8,5分)已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )A.相切B.相交C.相离D.不确定4.(2013山东,9,5分)过点(3,1)作圆(x-1)2+y2=1的两条切线,切点分别为A,B,则直线AB的方程为( )A.2x+y-3=0B.2x-y-3=0C.4x-y-3=0D.4x+y-3=05.(2015重庆,8,5分)已知直线l:x+ay-1=0(a∈R)是圆C:x2+y2-4x-2y+1=0的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=( )A.2B.4C.6D.26.(2015浙江嘉兴一中一模,6)已知直线Ax+By+C=0(A2+B2=C2≠0)与圆x2+y2=4交于M,N两点,O为坐标原点,则·等于( )A.-2B.-1C.0D.17.(2015重庆,12,5分)若点P(1,2)在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为.8.(2014湖北,12,5分)直线l1:y=x+a和l2:y=x+b将单位圆C:x2+y2=1分成长度相等的四段弧,则a2+b2= .9.(2015山东,13,5分)过点P(1,)作圆x2+y2=1的两条切线,切点分别为A,B,则·= .10.(2015浙江新高考研究卷五(杭州学军中学),12)已知圆C:(x-a)2+(y-2a)2=4(a>0)与直线y=x+2相交于P、Q两点,则当△CPQ的面积最大时,实数a的值为,当a变化时,圆系C的公切线方程为.11.(2015浙江名校(诸暨中学)交流卷四,13)圆心在抛物线y2=2x(y≥0)上,经过点(2,0)且面积最小的圆为☉C,直线y=kx+2与☉C相交于A,B两点,当|AB|取得最小值时,k= .12.(2015辽宁师大附中期中,14)若圆x2+y2-4x-4y-10=0上恰有三个不同的点到直线l:y=kx 的距离为2,则k= .13.(2015课标Ⅰ,20,12分)已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.(1)求k的取值范围;(2)若·=12,其中O为坐标原点,求|MN|.14.(2014课标Ⅰ,20,12分)已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.(1)求M的轨迹方程;(2)当|OP|=|OM|时,求l的方程及△POM的面积.B组提升题组1.(2014浙江,5,5分)已知圆x2+y2+2x-2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a 的值是( )A.-2B.-4C.-6D.-82.(2016超级中学原创预测卷四,4,5分)已知直线x+y-a=0与圆C:(x-2)2+(y+2)2=4相交于A,B两点,且△ABC为等腰直角三角形,则实数a=( )A.±B.C.±2D.23.(2015浙江名校(柯桥中学)交流卷三,2)直线(c-d)(x-a)=(a-b)(y-c)与曲线(x-a)(x-b)+(y-c)(y-d)=0的交点个数为( )A.0B.1C.2D.不确定4.(2014北京,7,5分)已知圆C:(x-3)2+(y-4)2=1和两点A(-m,0),B(m,0)(m>0).若圆C上存在点P,使得∠APB=90°,则m的最大值为( )A.7B.6C.5D.45.(2015山东,9,5分)一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则反射光线所在直线的斜率为( )A.-或-B.-或-C.-或-D.-或-6.(2014江西,9,5分)在平面直角坐标系中,A,B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C面积的最小值为( )A.πB.πC.(6-2)πD.π7.(2015浙江丽水一模,6)已知圆x2+y2=4,过点P(0,)的直线l交该圆于A,B两点,O为坐标原点,则△OAB面积的最大值是( )A. B.2 C.2 D.48.(2016领航高考冲刺卷三,12,4分)已知两圆C1:x2+y2-2ax+4y+a2-5=0和C2:x2+y2+2x-2ay+a2-3=0,则两圆圆心的最短距离为,此时两圆的位置关系是.(填“外离、相交、外切、内切、内含”中的一个)9.(2016领航高考冲刺卷六,14,4分)已知圆M:x2+(y+1)2=4,圆N:(x-4cosθ)2+(y+1-4sinθ)2=1,其中θ∈R,过圆N上任意一点P作圆M的两条切线PA,PB,切点分别为A,B,则与夹角的余弦值的取值范围为.10.(2015浙江测试卷,12,6分)已知过点(1,1)的直线l与圆C:x2+y2-4y+2=0相切,则圆C的半径为,直线l的方程为.11.(2015镇海中学仿真考,10,6分)已知点P(a,b)关于直线l的对称点为P'(b+1,a-1),则圆C:x2+y2-6x-2y=0关于直线l对称的圆C'的方程为;圆C与圆C'的公共弦的长度为.12.(2015湖北,14,5分)如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.(1)圆C的方程为;(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:①=;②-=2;③+=2.其中正确结论的序号是.(写出所有正确结论的序号)13.(2014课标Ⅱ,16,5分)设点M(x0,1),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是.14.(2015浙江镇海中学测试卷三,22)已知圆C:(x-1)2+y2=5.(1)求直线l:4x-3y+1=0被圆C所截得的弦长;(2)过点P(0,3)且斜率为k的直线与圆C相交于A,B两点,若-<k<-,求的取值范围.Ａ组基础题组1.C 圆的方程可化为(x-a)2+y2=3-2a,则3-2a>0①,过点A(a,a)可作圆的两条切线,所以(a-a)2+a2>3-2a②,由①②解得a<-3或1<a<,即a的取值范围为(-∞,-3)∪.故选C.2.D 易知圆心坐标为(1,1),半径r=1,∵直线与圆相切,∴=1,解得b=2或b=12.故选D.3.B 因为M(a,b)在圆O:x2+y2=1外,所以a2+b2>1,而圆心O到直线ax+by=1的距离d==<1.故选B.4.A 如图,圆心坐标为C(1,0),易知A(1,1).又k AB·k PC=-1,且k PC==,∴k AB=-2.故直线AB的方程为y-1=-2(x-1),即2x+y-3=0,故选A.5.C 圆C的标准方程为(x-2)2+(y-1)2=22,圆心为C(2,1),半径r=2,由直线l是圆C的对称轴,知直线l过点C,所以2+a×1-1=0,a=-1,所以A(-4,-1),于是|AC|2=40,所以|AB|===6.故选C.6.A 设M(x1,y1),N(x2,y2),则·=x1x2+y1y2.由消去y得(A2+B2)x2+2ACx+C2-4B2=0.所以x1x2=.同理,消去x可得y1y2=.所以·=x1x2+y1y2=.又C2=A2+B2,所以x1x2+y1y2=-2,即·=-2.故选A.7.答案x+2y-5=0解析设圆的方程为x2+y2=r2,将P的坐标代入圆的方程,得r2=5,故圆的方程为x2+y2=5.设该圆在点P处的切线上的任意一点为M(x,y),则=(x-1,y-2).由⊥(O为坐标原点),得·=0,即1×(x-1)+2×(y-2)=0,即x+2y-5=0.8.答案 22+b2=1+1=2.解析由题意知直线l9.答案解析如图,易得||=||=,又||=1,||=2,所以∠APO=30°,故∠APB=60°.所以·=||·||cos60°=××=.10.答案4;y=2x±2解析设圆心C到直线y=x+2的距离为d,则|PQ|=2,S△CPQ=d|PQ|=d≤=2(当且仅当d2=2时,取等号),由=2⇒a=4(a=0舍去).因为圆心在直线y=2x上,所以公切线方程可设为y=2x+b.由于圆心到直线y=2x+b的距离为2,所以=2,解得b=±2,故公切线方程为y=2x±2.11.答案解析设C(y≥0),则r==.要使圆面积最小,则圆半径最小,则y2=2,又y≥0,得y=,所以圆心C的坐标为(1,),半径r=.直线y=kx+2恒经过点D(0,2),当直线AB垂直于CD时,|AB|最小,而k CD=-2,故k=-=.12.答案2+或2-解析把圆的方程化为标准方程得(x-2)2+(y-2)2=18,圆心坐标为(2,2),半径r=3,根据题意画出图形,如图所示.根据题意和图形可知:圆心到直线l的距离为d==3-2=,化简得k2-4k+1=0,解得k=2±.13.解析(1)由题设,可知直线l的方程为y=kx+1.因为l与C交于两点,所以<1.解得<k<.所以k的取值范围为.(5分)(2)设M(x1,y1),N(x2,y2).将y=kx+1代入方程(x-2)2+(y-3)2=1,整理得(1+k2)x2-4(1+k)x+7=0.所以x1+x2=,x1x2=.(7分)·=x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1=+8.由题设可得+8=12,解得k=1,所以l的方程为y=x+1.故圆心C在l上,所以|MN|=2.(12分)14.解析(1)圆C的方程可化为x2+(y-4)2=16,所以圆心为C(0,4),半径为4.设M(x,y),则=(x,y-4),=(2-x,2-y).由题设知·=0,故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.(2)由(1)可知M的轨迹是以点N(1,3)为圆心,为半径的圆.由于|OP|=|OM|,故O在线段PM的垂直平分线上,又P在圆N上,从而ON⊥PM.因为ON的斜率为3,所以l的斜率为-,故l的方程为y=-x+.又|OM|=|OP|=2,O到l的距离为,|PM|=,所以△POM的面积为.B组提升题组1.B 将圆的方程化为标准方程为(x+1)2+(y-1)2=2-a,所以圆心为(-1,1),半径r=,圆心到直线x+y+2=0的距离d==,故r2-d2=4,即2-a-2=4,所以a=-4,故选B.2.C 由题意得圆的圆心为C(2,-2),半径为2,由△ABC为等腰直角三角形可知圆心C(2,-2)到直线x+y-a=0的距离为,所以=,解得a=±2.3.C(c-d)(x-a)=(a-b) (y-c)表示经过(a,c)、(b,d)两点的直线,(x-a)(x-b)+(y-c)(y-d)=0表示以(a,c)、(b,d)两点为直径两端点的圆,则交点个数为2,故选C.4.B 若∠APB=90°,则点P 的轨迹是以AB 为直径的圆,其方程为x 2+y 2=m 2.由题意知圆C:(x-3)2+(y-4)2=1与圆O:x 2+y 2=m 2有公共点,所以|m-1|≤|OC|≤m+1,易知|OC|=5,所以4≤m ≤6,故m 的最大值为6.选B.5.D 由题意可知反射光线所在直线过点(2,-3),设反射光线所在直线方程为y+3=k(x-2),即kx-y-2k-3=0.∵反射光线所在直线与圆相切,∴=1,解得k=-或k=-.故选D.6.A 由题意得以AB 为直径的圆C 过原点O,圆心C 为AB 的中点,设D 为切点,要使圆C 的面积最小,只需圆的半径最短,也只需OC+CD 最小,其最小值为OE(如图,过原点O 作直线2x+y-4=0的垂线,垂足为E)的长度.由点到直线的距离公式得OE=.∴圆C 面积的最小值为π=π.故选A.7.B 易知直线l 的斜率存在,可设直线l 的方程为y=kx+,则圆心到直线l 的距离d=. 又|AB|=2=2=2, ∴S △OAB =×2×=×=×.∵k 2≥0,∴k 2+1≥1,故0<≤1,故当=时,S △OAB 取到最大值2.故选B. 8.答案 ;内含解析 将圆C1:x 2+y 2-2ax+4y+a 2-5=0化为标准方程得(x-a)2+(y+2)2=9,圆心为C 1(a,-2),半径为r 1=3,将圆C 2:x 2+y 2+2x-2ay+a 2-3=0化为标准方程得(x+1)2+(y-a)2=4,圆心为C 2(-1,a),半径为r 2=2.两圆的圆心距d===,所以当a=-时,d min =,此时<|3-2|,所以两圆内含. 9.答案解析 因为圆心N 的坐标为(4cos θ,4sin θ-1),所以圆心在定圆x 2+(y+1)2=16上.连结MA,MB,MP,设∠MPA=α,则与的夹角为2α,cos2α=1-2sin 2α,因为sin α==,又|MP|∈[3,5],所以sin 2α∈,所以cos2α∈,即与夹角的余弦值的取值范围为.10.答案 ;x-y=0解析 圆C 的标准方程为x 2+(y-2)2=2,则圆C 的半径为,圆心坐标为(0,2).点(1,1)在圆C上,则直线l 的斜率k=-=1,则直线l 的方程为y=x,即x-y=0. 11.答案 (x-2)2+(y-2)2=10;解析将圆C的方程化为标准形式为(x-3)2+(y-1)2=10,由已知结论可得圆心C(3,1)关于直线l的对称点C'为(2,2),故所求圆的方程为(x-2)2+(y-2)2=10.将两圆方程相减消去平方项可得公共弦所在直线的方程为x-y-1=0,故弦长为2=.12.答案(1)(x-1)2+(y-)2=2(2)①②③解析(1)设圆心C(a,b),半径为r,∵圆C与x轴相切于点T(1,0),∴a=1,r=|b|,又圆C与y轴正半轴交于两点,∴b>0,则b=r.∵|AB|=2,∴2=2,∴r=,故圆C的标准方程为(x-1)2+(y-)2=2.(2)设N(x,y),而A(0,-1),B(0,+1),则==,又x2+y2=1,∴==·=(+1)2,∴=+1,同理,=+1.∴=,且-=+1-=2,+=+1+=+1+-1=2,故正确结论的序号是①②③.13.答案[-1,1]解析解法一:当x0=0时,M(0,1),由圆的几何性质得在圆上存在点N(-1,0)或N(1,0),使∠OMN=45°.当x0≠0时,过M作圆的两条切线,切点为A、B.若在圆上存在N,使得∠OMN=45°,应有∠OMB≥∠OMN=45°,∴∠AMB≥90°,∴-1≤x0<0或0<x0≤1.综上,x0的取值范围是-1≤x0≤1.解法二:过O作OP⊥MN,P为垂足,OP=OM·sin45°≤1,∴OM≤,∴OM2≤2,∴+1≤2,∴≤1,∴-1≤x0≤1.14.解析(1)圆心C到直线l的距离d==1,所以弦长=2=4.(2)设A(x1,y1),B(x2,y2),易知x1>0,x2>0,AB:y=kx+3, 联立得消去y,得(k2+1)x2+(6k-2)x+5=0,由根与系数的关系知而|PA|==|x1|,同理,|PB|=|x2|,所以==.由得++2==-·.设t=3k+4,则t∈,==.因为y=t+-8在区间上单调递减,所以y∈.故∈(0,2),所以++2∈.设u=,则即解得<u<1或1<u<5.所以的取值范围是∪(1,5).。

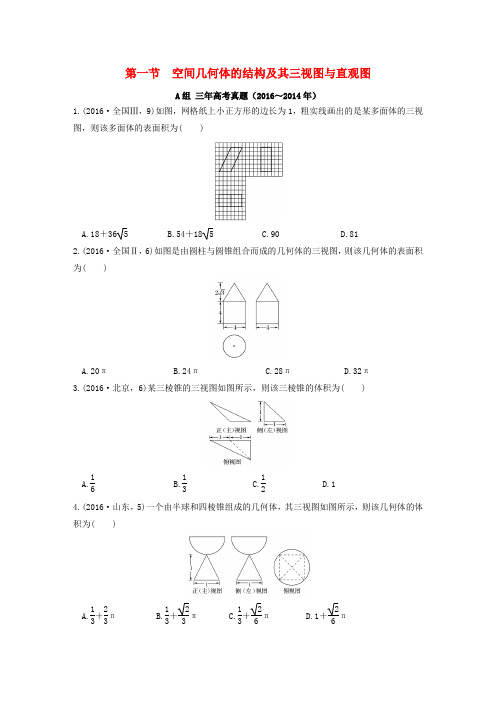
第一节 空间几何体的结构及其三视图与直观图A 组 三年高考真题（2016～2014年）1.(2016·全国Ⅲ，9)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为( )A.18＋365B.54＋18 5C.90D.812.(2016·全国Ⅱ，6)如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )A.20πB.24πC.28πD.32π3.(2016·北京，6)某三棱锥的三视图如图所示，则该三棱锥的体积为( )A.16B.13C.12D.1 4.(2016·山东，5)一个由半球和四棱锥组成的几何体，其三视图如图所示，则该几何体的体积为( )A.13＋23πB.13＋23πC.13＋26πD.1＋26π5.(2015·广东，8)若空间中n 个不同的点两两距离都相等，则正整数n 的取值( )A.大于5B.等于5C.至多等于4D.至多等于36.(2015·北京，5)某三棱锥的三视图如图所示，则该三棱锥的表面积是( )A.2＋ 5B.4＋ 5C.2＋2 5D.57.(2015·浙江，2)某几何体的三视图如图所示(单位：cm)，则该几何体的体积是( )A.8 cm 3B.12 cm 3C.323 cm 3D.403cm 3 8.(2015·新课标全国Ⅰ，11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16＋20π，则r ＝( )A.1B.2C.4D.89.(2014·福建，2)某空间几何体的正视图是三角形，则该几何体不可能是( )A.圆柱B.圆锥C.四面体D.三棱柱10.(2014·江西，5)一几何体的直观图如图，下列给出的四个俯视图中正确的是( )11.(2014·湖北，5)在如图所示的空间直角坐标系Oxyz中，一个四面体的顶点坐标分别是(0,0,2)，(2,2,0)，(1,2,1)，(2,2,2).给出编号为①、②、③、④的四个图，则该四面体的正视图和俯视图分别为( )A.①和②B.③和①C.④和③D.④和②12.(2014·新课标全国Ⅰ，12)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( )A.6 2B.4 2C.6D.413.(2015·天津，10)一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m3.B组两年模拟精选(2016～2015年)1.如图,网格上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( )A.2 2B. 6C.2 3D.32.(2016·广东广州二模)如图，圆锥的底面直径AB ＝2，母线VA ＝3，点C 在母线VB 上，且VC ＝1，有一只蚂蚁沿圆锥的侧面从点A 爬到点C ，则这只蚂蚁爬行的最短路程是( )A.13B.7C.433D.3323.(2016·天津新华中学月考)如图是一个几何体的正视图、侧视图、俯视图，则该几何体的体积是( )A.24B.12C.8D.44.(2015·福建莆田模拟)某几何体的三视图如图所示，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则其侧视图的面积是( )A.12B.32C.1D. 3 5.(2015·山东莱芜模拟)如右图放置的六条棱长都相等的三棱锥，则这个几何体的侧视图是( )A.等腰三角形B.等边三角形C.直角三角形D.无两边相等的三角形6.(2016·河北唐山模拟)在三棱锥P －ABC 中，PB ＝6，AC ＝3，G 为△PAC 的重心，过点G 作三棱锥的一个截面，使截面平行于PB 和AC ，则截面的周长为________.7.(2016·云南师大附中模拟)如图是一几何体的三视图，则该几何体的体积是________.8.(2016·河南洛阳统考)如图是某几何体的三视图，则该几何体的外接球的表面积为________.答案精析A 组 三年高考真题（2016～2014年）(2016年高考题6月底更新)1.B [由题意知，几何体为平行六面体，边长分别为3，3，45，几何体的表面积S ＝3×6×2＋3×3×2＋3×45×2＝54＋18 5.]2.C [由三视图可知，组合体的底面圆的面积和周长均为4π，圆锥的母线长l ＝（23）2＋22＝4，所以圆锥的侧面积为S 锥侧＝12×4π×4＝8π，圆柱的侧面积S 柱侧＝4π×4＝16π，所以组合体的表面积S ＝8π＋16π＋4π＝28π，故选C.]3.A [由三视图知，三棱锥如图所示：由侧视图得高h ＝1，又底面积S ＝12×1×1＝12.所以体积V ＝13Sh ＝16.] 4.C [由三视图知,半球的半径R ＝22,四棱锥为底面边长为1,高为1的正四棱锥, ∴V ＝13×1×1×1＋12×43π×⎝ ⎛⎭⎪⎫223＝13＋26π，故选C.] 5.C [当n ＝3时显然成立，故排除A ，B ；由正四面体的四个顶点，两两距离相等，得n ＝4时成立，故选C.]6.C [该三棱锥的直观图如图所示：过D 作DE ⊥BC ，交BC 于E ，连接AE ，则BC ＝2，EC ＝1，AD ＝1，ED ＝2，S 表＝S △BCD ＋S △ACD ＋S △ABD ＋S △ABC＝12×2×2＋12×5×1＋12×5×1＋12×2×5＝2＋2 5.] 7.C [该几何体是棱长为2 cm 的正方体与一底面边长为2 cm 的正方形，高为2 cm 的正四棱锥组成的组合体，V ＝2×2×2＋13×2×2×2＝323(cm 3).故选C.] 8.B [由题意知，2r ·2r ＋12·2πr ·2r ＋12πr 2＋12πr 2＋12·4πr 2＝4r 2＋5πr 2＝16＋20π，解得r ＝2.]9.A [圆柱的正视图是矩形，则该几何体不可能是圆柱.]10.B [由直观图可知，该几何体由一个长方体和一个截角三棱柱组成.从上往下看，外层轮廓线是一个矩形，矩形内部有一条线段连接的两个三角形.]11.D [在空间直角坐标系O －xyz 中作出棱长为2的正方体，在该正方体中作出四面体，如图所示，由图可知，该四面体的正视图为④，俯视图为②.选D. ]12.C [如图，设辅助正方体的棱长为4，三视图对应的多面体为三棱锥ABCD ，最长的棱为AD ＝（42）2＋22＝6，选C. ]13.83π [由三视图可知，该几何体由相同底面的两圆锥和圆柱组成，底面半径为1，圆锥的高为1，圆柱的高为2，所以该几何体的体积V ＝2×13π×12×1＋π×12×2＝83π m 3.] B 组 两年模拟精选(2016～2015年)1.D [(1)几何体的直观图如图，其中平面ABD ⊥平面BCD ，△ABD 为等腰直角三角形，AB ＝2，BD ＝2，△BCD 是以BD 为底边的等腰三角形，C 到BD 的中点的距离为2，∴BC ＝CD ＝12＋22＝5，AC ＝22＋（5）2＝3.AD ＝22，显然所有棱中，AC 最长，长为3，故选D.]2.B [由题意,圆锥的从VA 到VB 的部分侧面展开图为如图所示的扇形,半径为3,圆心角为π3,连接AC ,在△VAC 中,因为VC ＝1,∠V ＝π3，VA ＝3,所以由余弦定理得AC 2＝32＋12－2×3×1×12＝7. ∴AC ＝7，即蚂蚁爬行最短路程为7，故选B.]3.B [由三视图可知,该几何体由两个相同的直三棱柱构成,三棱柱的高为4,三棱柱的底面三角形为直角三角形,两直角边分别为2，32，所以三棱柱的底面积为12×2×32＝32，所以三棱柱的体积为32×4＝6.即该几何体的体积为2×6＝12，故选B.] 4.B [由三视图可以得到原几何体是以1为半径，母线长为2的半个圆锥，故侧视图的面积是32，故选B.] 5. A [∵六条棱长都相等的三棱锥，它的侧视图是如图所示的等腰三角形(AC ＝AB )，故选A.]6. 8 [过点G 作EF ∥AC ,分别交PA 、PC 于点E 、F ，过E 、F 分别作EN ∥PB 、FM ∥PB ，分别交AB 、BC 于点N 、M ，连接MN ，则四边形EFMN 是平行四边形(面EFMN 为所求截面)，且EF ＝MN ＝23AC ＝2，FM ＝EN ＝13PB ＝2，所以截面的周长为2×4＝8.]7.9 [由三视图知该几何体是一个四棱锥，其体积V ＝13×12×(2＋4)×3×3＝9.] 8. 50 π [由三视图知,该几何体可以由一个长方体截去4个角后得到,此长方体的长、宽、高分别为5、4、3，所以外接球半径R 满足2R ＝42＋32＋52＝52，所以外接球的表面积为S ＝4πR 2＝4π×⎝ ⎛⎭⎪⎫5222＝50π.]。

第六节 空间向量的应用A 组 三年高考真题（2016～2014年）1.(2016·全国Ⅱ,19)如图,菱形ABCD 的对角线AC 与BD 交于点O,AB ＝5,AC ＝6,点E,F 分别在AD,CD 上,AE ＝CF ＝54,EF 交BD 于点H.将△DEF 沿EF 折到△D′EF 的位置.OD ′＝10.(1)证明：D′H⊥平面ABCD ；(2)求二面角B －D′A－C 的正弦值.2.(2015·陕西,18)如图1,在直角梯形 ABCD 中,AD ∥BC,∠BAD ＝π2,AB ＝BC ＝1,AD ＝2,E 是AD的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A1BE 的位置,如图2.(1)证明：CD ⊥平面A1OC ；(2)若平面A1BE ⊥平面BCDE,求平面A1BC 与平面A1CD 夹角的余弦值.3.(2015·天津,17)如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A ⊥底面ABCD,AB ⊥AC,AB ＝1,AC ＝AA1＝2,AD ＝CD ＝5,且点M 和N 分别为B1C 和D1D 的中点. (1)求证：MN ∥平面ABCD ；(2)求二面角D1-AC-B1的正弦值；(3)设E 为棱A1B1上的点,若直线NE 和平面ABCD 所成角的正弦值为13,求线段A1E 的长.B 组 两年模拟精选(2016～2015年)1.(2016·云南丽江模拟)在长方体ABCD －A1B1C1D1中,AB ＝2,AA1＝3,AD ＝22,P 为C1D1的中点,M 为BC 的中点,则AM 与PM 的位置关系为( )A.平行B.异面C.垂直D.以上都不对 2.(2015·长沙模拟)有以下命题：①如果向量a,b 与任何向量不能构成空间向量的一个基底,那么a,b 的关系是不共线； ②O,A,B,C 为空间四点,且向量OA →,OB →,OC →不构成空间的一个基底,那么点O,A,B,C 一定共面； ③已知向量a,b,c 是空间的一个基底,则向量a ＋b,a －b,c 也是空间的一个基底. 其中正确的命题是( )A.①②B.①③C.②③D.①②③3.(2016·莆田模拟)已知a ＝(2,－1,3),b ＝(－1,4,－2),c ＝(7,5,λ),若a,b,c 三向量共面,则实数λ等 于( )A.627B.637C.607D.6574.(2015·福州模拟)若两点的坐标是A(3cos α,3sin α,1),B(2cos β,2sin β,1),则|AB|的取值范围是( )A.[0,5]B.[1,5]C.(0,5)D.[1,25]5.(2016·吉林四平模拟)如图,平面PAC ⊥平面ABC,△ABC 是以AC 为斜边的等腰直角三角形,E,F,O 分别为PA,PB,AC 的中点,AC ＝16,PA ＝PC ＝10.(1)设G 是OC 的中点,证明：FG ∥平面BOE ；(2)证明：在△ABO 内存在一点M,使FM ⊥平面BOE,并求点M 到OA,OB 的距离.6.(2015·河南商丘模拟)如图,在三棱柱ABC －A1B1C1中,已知AB ⊥侧面BB1C1C,AB ＝BC ＝1,BB1＝2,∠BCC1＝60°.(1)求证：C1B ⊥平面ABC ；(2)设CE →＝λCC1→(0≤λ≤1),且平面AB1E 与BB1E 所成的锐二面角的大小为30°,试求λ的值.7.(2015·山东青岛一模)如图,在多面体ABCDEF 中,底面ABCD 是边长为2的的菱形,∠BAD ＝60°,四边形BDEF 是矩形,平面BDEF ⊥平面ABCD,BF ＝3,G 和H 分别是CE 和CF 的中点.(1)求证：平面BDGH ∥平面AEF ；(2)求二面角H －BD －C 的大小.答案精析A 组 三年高考真题（2016～2014年）1.(1)证明 由已知得AC ⊥BD,AD ＝CD.又由AE ＝CF 得AE AD ＝CFCD ,故AC ∥EF.因此EF ⊥HD,从而EF ⊥D′H.由AB ＝5,AC ＝6得DO ＝BO ＝AB2－AO2＝4.由EF ∥AC 得OH DO ＝AE AD ＝14.所以OH ＝1,D ′H ＝DH ＝3.于是D′H 2＋OH2＝32＋12＝10＝D′O 2,故D′H⊥OH.又D′H⊥EF,而OH∩EF＝H, 所以D′H⊥平面ABCD.(2)解 如图,以H 为坐标原点,HF →的方向为x 轴正方向,建立空间直角坐标系H －xyz.则H(0,0,0),A(－3,－1,0),B(0,－5,0),C(3,－1,0),D′(0,0,3),AB →＝(3,－4,0),AC →＝(6,0,0),AD′→＝(3,1,3). 设m ＝(x1,y1,z1)是平面ABD′的法向量,则⎩⎪⎨⎪⎧m·AB →＝0，m·AD′→＝0，即⎩⎪⎨⎪⎧3x1－4y1＝0，3x1＋y1＋3z1＝0，所以可取m ＝(4,3,－5).设n ＝(x2,y2,z2)是平面ACD′的法向量,则⎩⎪⎨⎪⎧n·AC →＝0，n·AD′→＝0，即⎩⎪⎨⎪⎧6x2＝0，3x2＋y2＋3z2＝0，所以可取n ＝(0,－3,1).于是cos 〈m,n 〉＝m·n |m||n|＝－1450×10＝－7525.sin 〈m,n 〉＝29525.因此二面角B －D′A－C 的正弦值是29525.2.(1)证明 在图1中,因为AB ＝BC ＝1,AD ＝2,E 是AD 的中点,∠BAD ＝π2,所以BE ⊥AC,图1即在图2中,BE ⊥OA1,BE ⊥OC,且A1O ∩OC ＝O,图2从而BE ⊥平面A1OC,又在直角梯形ABCD 中,AD ∥BC,BC ＝12AD,E 为AD 中点,所以BC 綉ED,所以四边形BCDE 为平行四边形,故有CD ∥BE,所以CD ⊥平面A1OC. (2)解由已知,平面A1BE ⊥平面BCDE,又由(1)知,BE ⊥OA1,BE ⊥OC, 所以∠A1OC 为二面角A1BEC 的平面角,所以∠A1OC ＝π2,如图,以O 为原点,建立空间直角坐标系, 因为A1B ＝A1E ＝BC ＝ED ＝1,BC ∥ED,所以B ⎝⎛⎭⎪⎫22，0，0,E ⎝ ⎛⎭⎪⎫－22，0，0,A1⎝ ⎛⎭⎪⎫0，0，22,C ⎝ ⎛⎭⎪⎫0，22，0,得BC →＝⎝ ⎛⎭⎪⎫－22，22，0,A1C →＝⎝ ⎛⎭⎪⎫0，22，－22,CD →＝BE →＝(－2,0,0),设平面A1BC 的法向量n1＝(x1,y1,z1),平面A1CD 的法向量n2＝(x2,y2,z2),平面A1BC 与平面A1CD 夹角为θ,则⎩⎪⎨⎪⎧n1·BC →＝0，n1·A1C →＝0，得⎩⎪⎨⎪⎧－x1＋y1＝0，y1－z1＝0，取n1＝(1,1,1)；⎩⎪⎨⎪⎧n2·CD →＝0，n2·A1C →＝0，得⎩⎪⎨⎪⎧x2＝0，y2－z2＝0，取n2＝(0,1,1),从而cos θ＝|cos<n1,n2>|＝23×2＝63, 即平面A1BC 与平面A1CD 夹角的余弦值为63. 3.如图,以A 为原点建立空间直角坐标系,依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,－2,0),A1(0,0,2),B1(0,1,2),C1(2,0,2),D1(1,－2,2),又因为M,N 分别为B1C 和D1D 的中点,得M ⎝ ⎛⎭⎪⎫1，12，1,N(1,－2,1). (1)证明 依题意,可得n ＝(0,0,1)为平面ABCD 的一个法向量,MN →＝⎝⎛⎭⎪⎫0，－52，0,由此可得MN →·n ＝0,又因为直线MN ⊄平面ABCD,所以MN ∥平面ABCD.(2)解 AD1→＝(1,－2,2),AC →＝(2,0,0),设n1＝(x,y,z)为平面ACD1的法向量, 则⎩⎪⎨⎪⎧n1·AD1→＝0，n1·AC →＝0，即⎩⎪⎨⎪⎧x －2y ＋2z ＝0，2x ＝0.不妨设z ＝1,可得n1＝(0,1,1).设n2＝(x,y,z)为平面ACB1的法向量,则⎩⎪⎨⎪⎧n2·AB1→＝0，n2·AC →＝0，又AB1→＝(0,1,2),得⎩⎪⎨⎪⎧y ＋2z ＝0，2x ＝0，不妨设z ＝1,可得n2＝(0,－2,1).因此有cos 〈n1,n2〉＝n1·n2|n1|·|n2|＝－1010,于是sin 〈n1,n2〉＝31010.所以,二面角D1ACB1的正弦值为31010.(3)解 依题意,可设A1E →＝λA1B1→,其中λ∈[0,1],则E(0,λ,2),从而NE →＝(－1,λ＋2,1),又n ＝(0,0,1)为平面ABCD 的一个法向量,由已知,得cos 〈NE →,n 〉＝NE →·n |NE →|·|n|＝1（－1）2＋（λ＋2）2＋12＝13,整理得λ2＋4λ－3＝0,又因为λ∈[0,1],解得λ＝7－2,所以,线段A1E 的长为7－2.B 组 两年模拟精选(2016～2015年)1.C [建立如图所示空间直角坐标系,可得D(0,0,0),P(0,1,3),C(0,2,0),A(22,0,0),M(2,2,0).∴PM →＝(2,1,－3),AM →＝(－2,2,0).∴PM →·AM →＝(2,1,－3)·(－2,2,0)＝0.∴PM →⊥AM →,即AM ⊥PM.]2.C [对于①,“如果向量a,b 与任何向量不能构成空间向量的一个基底,那么a,b 的关系一定是共线”,所以①错误,②③正确.]3. D [由题意得c ＝ta ＋μb ＝(2t －μ,－t ＋4μ,3t －2μ),∴⎩⎪⎨⎪⎧7＝2t －μ，5＝－t ＋4μ，λ＝3t －2μ，解得⎩⎪⎨⎪⎧t ＝337，μ＝177，λ＝657.]4.B[∵A(3cosα,3sinα,1),B(2cosβ,2sinβ,1),|AB|＝（3cos α－2cos β）2＋（3sin α－2sin β）2＋（1－1）2＝9＋4－12（cos αcos β＋sin αsin β）＝13－12cos （α－β）,∴13－12≤|AB|≤13＋12＝5, 即1≤|AB|≤5,故选B.]5.证明 (1)如图,连接OP,易知OB,OC,OP 两两垂直,以点O 为坐标原点,分别以OB,OC,OP 所在直线为x 轴,y 轴,x 轴,建立空间直角坐标系O －xyz,则O(0,0,0),A(0,－8,0),B(8,0,0),C(0,8,0),P(0,0,6),E(0,－4,3),F(4,0,3).由题意,得G(0,4,0)因为OB →＝(8,0,0),OE →＝(0,－4,3), 所以平面BOE 的一个法向量为n ＝(0,3,4). 由FG →＝(－4,4,－3),得n·FG →＝0,即n ⊥FG →. 又直线FG 不在平面BOE 内,所以FG ∥平面BOE.(2)设点M 的坐标为(x0,y0,0),则FM →＝(x0－4,y0,－3).所FM ⊥平面BOE,所以FM →∥n. 因此x0＝4,y0＝－94,即点M 的坐标是(4,－94,0).在平面直角坐标系xOy 中,△AOB 的内部区域可表示为不等式组 ⎩⎪⎨⎪⎧x>0，y<0，x －y<8.经检验,点M 的坐标满足上述不等式组,所以在△AOB 内存在一点M, 使FM ⊥平面BOE.由点M 的坐标得点M 到OA,OB 的距离分别为4,94.6.(1)证明 因为AB ⊥平面BB1C1C,BC1⊂平面BB1C1C,所以AB ⊥BC1, 在△CBC1中,BC ＝1,CC1＝BB1＝2,∠BCC1＝60°, 由余弦定理得：BC21＝BC2＋CC21－2BC·CC1·cos∠BCC1＝12＋22－2×1×2×cos 60°＝3, 所以BC1＝3,故BC2＋BC21＝CC21,所以BC ⊥BC1, 又BC∩AB＝B,∴C1B ⊥平面ABC.(2)解 由(1)可知,AB,BC,BC1两两垂直.以B 为原点,BC,BA,BC1所在直线为x,y,z 轴建立空间直角坐标系. 则B(0,0,0),A(0,1,0),C(1,0,0),C1(0,0,3),B1(－1,0,3).所以CC1→＝(－1,0,3), 所以CE →＝(－λ,0,3λ),∴E(1－λ,0,3λ),则AE →＝(1－λ,－1,3λ),AB1→＝(－1,－1,3).设平面AB1E 的一个法向量为n ＝(x,y,z),则⎩⎪⎨⎪⎧n ⊥AE →，n ⊥AB1→，得⎩⎨⎧（1－λ）x －y ＋3λz ＝0，－x －y ＋3z ＝0，令z ＝3,则x ＝3－3λ2－λ,y ＝32－λ,∴n ＝⎝ ⎛⎭⎪⎫3－3λ2－λ，32－λ，3,∵AB ⊥平面BB1C1C,BA →＝(0,1,0)是平面的一个法向量, ∴|cos 〈n,BA →〉|＝n·BA →|n|·|BA →|＝32－λ1×⎝ ⎛⎭⎪⎫3－3λ2－λ2＋⎝ ⎛⎭⎪⎫32－λ2＋（3）2＝32. 两边平方并化简得2λ2－5λ＋3＝0,所以λ＝1或λ＝32(舍去).∴λ＝1.7. (1)证明 在△CEF 中,因为G,H 分别是CE,CF 的中点.所以GH ∥EF,又因为GH ⊄平面AEF,EF ⊂平面AEF,所以GH ∥平面AEF.设AC∩BD＝O,连接OH,因为ABCD 为菱形,所以O 为AC 中点,所以OH ∥AF, 又因为OH ⊄平面AEF,AF ⊂平面AEF,所以OH ∥平面AEF.又因为OH∩G H ＝H,OH,GH ⊂平面BDGH,所以平面BDGH ∥平面AEF. (2)解 取EF 的中点N,连接ON,因为四边形BDEF 是矩形,O,N 分别为BD,EF的中点,所以ON ∥ED, 因为平面BDEF ⊥平面ABCD,所以ED ⊥平面ABCD, 所以ON ⊥平面ABCD,因为ABCD 为菱形,所以AC ⊥BD,得OB,OC,ON 两两垂直.所以以O 为原点,OB,OC,ON 所在直线分别为x 轴,y 轴,z 轴,如图建立空间直角坐标系.因为底面ABCD 是边长为2的菱形,∠BAD ＝60°,BF＝3,所以B(1,0,0),D(－1,0,0),E(－1,0,3),F(1,0,3),C(0,3,0),H ⎝ ⎛⎭⎪⎫12，32，32,所以BH →＝⎝ ⎛⎭⎪⎫－12，32，32,DB →＝(2,0,0).设平面BDH 的法向量为n ＝(x,y,z),则⎩⎪⎨⎪⎧n·BH →＝0n·DB →＝0⇒⎩⎨⎧－x ＋3y ＋3z ＝0，2x ＝0，令z ＝1,得n ＝(0,－3,1).由ED ⊥平面ABCD,得平面BCD 的法向量为DE →＝(0,0,3), 则cos 〈n,DE →〉＝n·DE →|n||DE →|＝0×0＋（－3）×0＋1×32×3＝12.结合图形知二面角H －BD －C 的大小为60°.。

核 心 八 模2017年普通高等学校招生全国统一考试模拟试题数学（理科）（八）第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.1.若1+是关于x 的实系数方程20x bx c ++=的一个复数根，则A.2,3b c ==B.2,3b c =-=C.2,1b c =-=-D.2,1b c ==-2.已知全集,U R =集合{}{}1|,|21,x M y y x R N x x R -==∈=≥∈，则()U M C N 等于A. []2,2-B. [)2,1-C. []1,4D.[)0,13.若1sin 63πα⎛⎫-= ⎪⎝⎭，则22cos 162πα⎛⎫+-= ⎪⎝⎭ A. 13 B. 13- C. 79 D.79-4.ABC ∆的外接圆圆心为O ，半径为2，OA AB AC ++为零向量，且OA AB =，则CA 在BC 方向上的投影为A. 3-B. 35.秦九韶是我国南北朝时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入,n x 的值分别为3,2，则输出的v 值为A. 9B. 18C. 20D. 356.某几何体的三视图如图所示，则该几何体的表面积是A. (1012π++B. (1112π+C. (1112π++D.136π7.已知函数()()2sin 2cos ,2,2f x x x x x x ππ=+∈-，则其导函数()f x '的图象大致是8.设函数()61,00x x f x x x ⎧⎛⎫-<⎪ ⎪=⎝⎭⎨⎪≥⎩，则当0x >时，表()f f x ⎡⎤⎣⎦达式的展开式中常数项为A. -20B. 20C. -15D. 159.已知函数()()()sin 0f x x ωϕω=+>的部分图象如图所示，下面结论正确的个数是 ①函数()f x 的最小正周期是2π②函数()f x 的图象可由函数()sin 2g x x =的图象向左平移3π个单位长度得到 ③函数()f x 的图象关于直线12x π=对称 ④函数()f x 在区间,126ππ⎡⎤⎢⎥⎣⎦上是增函数 A. 3 B. 2 C. 1 D. 010.如图，在长方体1111ABCD A B C D -中，,E H 分别是棱1111,A B D C 上的动点（点E 与不重合），且11//EH A D ，过EH 的动平面与棱11,BB CC 相交，交点分别为,F G ，设11122,2AB AA a B E B F a ==+=，在长方体1111ABCD A B C D -内随机选取一点，则该点取自几何体11A ABFE D DCGH -内的概率的最小值为， A. 1112 B. 34 C. 1316 D. 7811.已知双曲线()222210,0x y a b a b-=>>的两顶点为12,A A ，虚轴两端点为12,B B ，两焦点12,F F 为，若以12,A A 直径的圆内切于菱形1122F B F B ，则双曲线的离心率为A. 3+12.已知点(),P x y 是平面区域()404y x y x m y ⎧≤⎪-≤⎨⎪≥-⎩内的动点，点()1,1,A O -为坐标原点，设()OP OA R λλ-∈的最小值为M ，若M ≤m 的取值范围是A. 11,35⎡⎤-⎢⎥⎣⎦B. 11,,35⎛⎤⎡⎫-∞+∞ ⎪⎥⎢⎝⎦⎣⎭C. 1,3⎡⎫-+∞⎪⎢⎣⎭D.1,2⎡⎫-+∞⎪⎢⎣⎭第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，共20分.13.设随机变量()10,1X B ，()910P X a ≤<=，其中1419a =⎰，则()11P X ≥= .14.如图，为了测量河对岸A,B 两点间的距离，观察者找到了一个点D ，从D点可以观察到点A,C,找到一个点E ，从E 可以观察到点B,C ，并测量得到一些数据：2,CD CE ==45,105,48.19,75,60D ACD ACB BCD E ∠=∠=∠=∠=∠=,则A,B 两点之间的距离为 .其中cos 48.19取近似值2.315.图中是抛物线形拱桥，当水面在l 时，拱顶离水面2米，水面宽4米，水面下降0.42米后，水面宽为 米.16.已知()y f x =是定义在R 上的奇函数，且()()221,10,10x x f x x ⎧+-<-⎪=⎨-≤≤⎪⎩，当函数()()1122y f x k x =----（其中0k >）的零点个数取得最大值时，实数k 的取值范围为 .三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程.17.（本题满分12分）已知数列{}n a ,n S 是其前n 项和满足，()32.n n a S n n N *=+∈.（1）求证：数列12n a ⎧⎫+⎨⎬⎩⎭是等比数列； （2）记12n n T S S S =+++，求n T 的表达式.18.（本题满分12分） 如图，在等腰梯形ABCD 中，//,1,60AB CD AD DC CB ABC ===∠=四边形ACEF 为矩形，平面A C E F ⊥平面ABCD ,1CF =.（1）求证：EF BC ⊥平面ACEF ；（2）点M 在线段上运动，设平面MAB 与平面FCB 所成的二面角的平面角()90θθ≤为，试求cos θ的取值范围.19.（本题满分12分）根据以往的经验，某工程施工期间的降水量（单位：mm ）对工期的影响如下表：历年气象资料表明，该工程施工期间降水量小于300,700,900的概率分别为0.3,0.7,0.9，求：（1）工期延误天数Y 的均值与方差；（2）在降水量至少是300的条件下，工期延误不超过6天的概率.20.（本题满分12分）已知椭圆()2222:10x y W a b a b+=>>的离心率为2，其左顶点A 在圆22:16O x y +=上. （1）求椭圆W 的方程；（2）若点P 是椭圆W 上不同于点A 的点，直线AP 与圆O 的另一个交点Q ，是否存在点P,使得3PQ AP =？若存在，求出点P 的坐标；若不存在，说明理由.21.（本题满分12分）已知函数()()()()2sin cos ,10x x f x e x x a g x a a e =++=-+（a R ∈且a 为常数）（1）若曲线()y f x =在()()0,0f 处的切线过点()1,2，求实数a 的值；（2）判断函数()()()()()222111ln 110b e g x x x b xa a e x φ+=-++>-+在()0,+∞上的零点的个数，并说明理由.请考生在第22、23两题中任选一题作答，如果两题都做，则按照所做的第一题给分；作答时，请用2B 铅笔将答题卡上相应的题号涂黑。

第五节 直线、平面垂直的判定与性质A 组 三年高考真题（2016～2014年）1.(2014·浙江，6)设m ，n 是两条不同的直线，α，β是两个不同的平面( ) A.若m ⊥n ，n ∥α，则m ⊥α B.若m ∥β，β⊥α，则m ⊥α C.若m ⊥β，n ⊥β，n ⊥α，则m ⊥α D.若m ⊥n ，n ⊥β，β⊥α，则m ⊥α2.(2016·新课标全国Ⅰ，18)如图，已知正三棱锥PABC 的侧面是直角三角形，PA ＝6，顶点P 在平面ABC 内的正投影为点D ，D 在平面PAB 内的正投影为点E ，连接PE 并延长交AB 于点G . (1)证明：G 是AB 的中点；(2)作出点E 在平面PAC 内的正投影F (说明作法及理由)，并求四面体PDEF 的体积. 3.(2016·新课标全国Ⅱ，19)如图，菱形ABCD 的对角线AC 与BD 交于点O ，点E ，F 分别在AD ，CD 上，AE ＝CF ，EF 交BD 于点H ，将△DEF 沿EF 折到△D ′EF 的位置.(1)证明：AC ⊥HD ′；(2)若AB ＝5，AC ＝6，AE ＝54，OD ′＝22，求五棱锥D ′ABCFE 的体积.4.(2016·北京，18)如图，在四棱锥PABCD 中，PC ⊥平面ABCD ，AB ∥DC ，DC ⊥AC .(1)求证：DC ⊥平面PAC ； (2)求证：平面PAB ⊥平面PAC ；(3)设点E 为AB 的中点，在棱PB 上是否存在点F ，使得PA ∥平面CEF ？说明理由. 5.(2016·浙江，18)如图，在三棱台ABCDEF 中，平面BCFE ⊥平面ABC ，∠ACB ＝90°，BE ＝EF ＝FC ＝1，BC ＝2，AC ＝3.(1)求证：BF ⊥平面ACFD ；(2)求直线BD 与平面ACFD 所成角的余弦值.6.(2016·四川，17)如图，在四棱锥PABCD 中，PA ⊥CD ，AD ∥BC ，∠ADC ＝∠PAB ＝90°，BC＝CD ＝12AD .(1)在平面PAD 内找一点M ，使得直线CM ∥平面PAB ，并说明理由. (2)证明：平面PAB ⊥平面PBD .7.(2015·新课标全国Ⅰ，18)如图，四边形ABCD 为菱形，G 是AC 与BD 的交点，BE ⊥平面ABCD .(1)证明：平面AEC ⊥平面BED ；(2)若∠ABC ＝120°，AE ⊥EC ，三棱锥EACD 的体积为63，求该三棱锥的侧面积．8.(2015·安徽，19)如图，三棱锥P ­ABC 中，PA ⊥平面ABC ，PA ＝1，AB ＝1，AC ＝2，∠BAC ＝60°.(1)求三棱锥P ­ABC 的体积；(2)证明：在线段PC 上存在点M ，使得AC ⊥BM ，并求PMMC的值． 9.(2015·湖北，20)《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称 之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．在如图所示的阳马P-ABCD 中，侧棱PD ⊥底面ABCD ，且PD ＝CD ，点E 是PC 的中点，连接DE 、BD 、BE .(1)证明：DE ⊥平面PBC .试判断四面体EBCD 是否为鳖臑．若是，写出其每个面的直角(只需写出结论)；若不是，请说明理由；(2)记阳马P-ABCD 的体积为V 1，四面体EBCD 的体积为V 2，求V 1V 2的值．10.(2015·浙江，18)如图，在三棱柱ABC-A1B 1C 1中，∠BAC ＝90°，AB ＝AC ＝2，A 1A ＝4，A 1在底面ABC 的射影为BC 的中点，D 为B 1C 1的中点．(1)证明：A 1D ⊥平面A 1BC ；(2)求直线A 1B 和平面BB 1C 1C 所成的角的正弦值．11.(2015·天津，17)如图，已知AA 1⊥平面ABC ，BB 1∥AA 1，AB ＝AC ＝3，BC ＝25，AA 1＝7，BB 1＝27，点E 和F 分别为BC 和A 1C 的中点．(1)求证：EF ∥平面A 1B 1BA ； (2)求证：平面AEA 1⊥平面BCB 1； (3)求直线A 1B 1与平面BCB 1所成角的大小．12.(2014·重庆，20)如图，四棱锥P-ABCD 中，底面是以O 为中心的菱形，PO ⊥底面ABCD ，AB ＝2，∠BAD ＝π3，M 为BC 上一点，且BM ＝12.(1)证明：BC ⊥平面POM ；(2)若MP ⊥AP ，求四棱锥PABMO 的体积．13.(2014·新课标全国Ⅰ，19)如图，三棱柱ABC-A 1B 1C 1中，侧面BB 1C 1C 为菱形，B 1C 的中点为O ，且AO ⊥平面BB 1C 1C .(1)证明：B 1C ⊥AB ；(2)若AC ⊥AB 1，∠CBB 1＝60°，BC ＝1，求三棱柱ABCA 1B 1C 1的高．B 组 两年模拟精选(2016～2015年)1.(2016·河南八市重点高中4月质量检测)已知直线l 与平面α相交但不垂直，m 为空间内一条直线，则下列结论可能成立的是( ) A.m ∥l ，m ⊥α B.m ∥l ，m ∥α C.m ⊥l ，m ⊥αD.m ⊥l ，m ∥α2.(2015·泉州模拟)如图所示，AB 是⊙O 的直径，VA 垂直于⊙O 所在的平面，点C 是圆周上不同于A ，B 的任意一点，M ，N 分别为VA ，VC 的中点，则下列结论正确的是( ) A.MN ∥ABB.MN 与BC 所成的角为45°C.OC ⊥平面VACD.平面VAC ⊥平面VBC3.(2015·山东泰安普通高中联考)设α、β、γ是三个互不重合的平面，m 、n 是两条不重合的直线，下列命题中正确的是( ) A.若α⊥β，β⊥γ，则α⊥γ B.若m ∥α，n ∥β，α⊥β，则m ⊥n C.若α⊥β，m ⊥β，则m ∥βD.若α∥β，m ⊄β，且m ∥α，则m ∥β4.(2015·河南六市联考)已知m ，n 分别是两条不重合的直线，a ，b 分别垂直于两个不重合的平面α，β，有以下四个命题：①若m ⊥a ，n ∥b ，且α⊥β，则m ∥n ；②若m ∥a ，n ∥b ，且α⊥β，则m ⊥n ； ③若m ∥a ，n ⊥b ，且α∥β，则m ⊥n ；④若m ⊥a ，n ⊥b ，且α⊥β，则m ∥n . 其中真命题的序号是( ) A.①② B.③④ C.①④D.②③5.(2015·潍坊4月模拟)已知m ，n 为异面直线，α，β为两个不同的平面，m ⊥α，n ⊥β.直线l 满足l ⊥m ，l ⊥n ，l ⊄α，l ⊄β，则( ) A.α∥β，且l ∥α B.α⊥β，且l ⊥βC.α与β相交，且交线垂直于lD.α与β相交，且交线平行于l6.(2015·北京西城区检测)如图，在空间四边形ABCD 中，两条对角线AC ，BD 互相垂直， 且长度分别为4和6，平行于这两条对角线的平面与边AB ，BC ，CD ，DA 分别相交于点E ，F ，G ，H ，记四边形EFGH 的面积为y ，设BEAB＝x ，则( )A.函数y ＝f (x )的值域为(0，4]B.函数y ＝f (x )的最大值为8C.函数y ＝f (x )在⎝ ⎛⎭⎪⎫0，23上单调递减D.函数y ＝f (x )满足f (x )＝f (1－x )7.(2016·河南郑州一中第二次模拟)如图，在梯形ABCD 中，AB ∥CD ，AD ＝DC ＝CB ＝1，∠BCD ＝120°，四边形BFED 为矩形，平面BFED ⊥平面ABCD ，BF ＝1. (1)求证：AD ⊥平面BFED ； (2)已知点P 在线段EF 上，EPPF＝2，求三棱锥EAPD 的体积. 8.(2015·山西康杰中学期中)如图，长方体ABCDA 1B 1C 1D 1中，AD ＝AA 1＝1，AB ＝2，点E是AB 的中点.(1)证明：BD 1∥平面A 1DE ； (2)证明：D 1E ⊥A 1D ； (3)求二面角D 1ECD 的正切值.答案精析A 组 三年高考真题（2016～2014年）1.解析 选项A 、B 、D 中m 均可能与平面α平行、垂直、斜交或在平面α内，故选C. 答案C2.(1)证明 因为P 在平面ABC 内的正投影为D ，所以AB ⊥PD . 因为D 在平面PAB 内的正投影为E ，所以AB ⊥DE . 所以AB ⊥平面PED ，所以AB ⊥PG .又由已知可得PA ＝PB ，从而G 是AB 的中点.(2)解 在平面PAB 内，过点E 作PB 的平行线交PA 于点F ，F 即为E 在平面PAC 内的正投影.理由如下：由已知可得PB ⊥PA ，PB ⊥PC ，又EF ∥PB ， 所以EF ⊥PA ，EF ⊥PC ，所以EF ⊥平面PAC ，即点F 为E 在平面PAC 内的正投影. 连接CG ，因为P 在平面ABC 内的正投影为D ， 所以D 是正三角形ABC 的中心.由(1)知，G 是AB 的中点，所以D 在CG 上，所以CD ＝23CG .由题设可得PC ⊥平面PAB ，DE ⊥平面PAB ， 所以DE ∥PC ，所以PE ＝23PG ，DE ＝13PC .由已知，正三棱锥的侧面是直角三角形且PA ＝6，可得DE ＝2，PE ＝2 2. 在等腰直角三角形EFP 中，可得EF ＝PF ＝2. 所以四面体PDEF 的体积V ＝13×12×2×2×2＝43.3.(1)证明 由已知得AC ⊥BD ，AD ＝CD ，又由AE ＝CF 得AE AD ＝CF CD，故AC ∥EF ， 由此得EF ⊥HD ，折后EF 与HD 保持垂直关系，即EF ⊥HD ′， 所以AC ⊥HD ′.(2)解 由EF ∥AC 得OH DO ＝AE AD ＝14.由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4， 所以OH ＝1，D ′H ＝DH ＝3，于是OD ′2＋OH 2＝(22)2＋12＝9＝D ′H 2， 所以OD ′⊥OH .由(1)知AC ⊥HD ′，又AC ⊥BD ，BD ∩HD ′＝H ， 所以AC ⊥平面DHD ′，于是AC ⊥OD ′，又由OD ′⊥OH ，AC ∩OH ＝O ， 所以OD ′⊥平面ABC . 又由EF AC ＝DH DO 得EF ＝92，五边形ABCFE 的面积S ＝12×6×8－12×92×3＝694，所以五棱锥D ′ABCFE 的体积V ＝13×694×22＝2322.4.(1)证明 ∵PC ⊥平面ABCD ，DC ⊂平面ABCD ， ∴PC ⊥DC .又AC ⊥DC ，PC ∩AC ＝C ，PC ⊂平面PAC ，AC ⊂平面PAC ， ∴CD ⊥平面PAC .(2)证明 ∵AB ∥CD ，CD ⊥平面PAC ， ∴AB ⊥平面PAC ， 又AB ⊂平面PAB ， ∴平面PAB ⊥平面PAC .(3)解 棱PB 上存在点F ，使得PA ∥平面CEF . 证明如下：取PB 的中点F ，连接EF ，CE ，CF ， 又因为E 为AB 的中点， ∴EF 为△PAB 的中位线， ∴EF ∥PA .又PA ⊄平面CEF ，EF ⊂平面CEF ，∴PA ∥平面CEF .5.(1)证明 延长AD ，BE ，CF 相交于一点K ，如图所示，因为平面BCFE ⊥平面ABC ，且AC ⊥BC ， 所以AC ⊥平面BCK ， 所以BF ⊥AC .又因为EF ∥BC ，BE ＝EF ＝FC ＝1，BC ＝2，所以△BCK 为等边三角形，且F 为CK 的中点，则BF ⊥CK . 所以BF ⊥平面ACFD .(2)解 因为BF ⊥平面ACK ，所以∠BDF 是直线BD 与平面ACFD 所成的角. 在Rt △BFD 中，BF ＝3，DF ＝32，得cos ∠BDF ＝217.所以直线BD 与平面ACFD 所成角的余弦值为217. 6.(1)解 取棱AD 的中点M (M ∈平面PAD )，点M 即为所求的一个点，理由如下：因为AD ∥BC ，BC ＝12AD ，所以BC ∥AM ，且BC ＝AM .所以四边形AMCB 是平行四边形，所以CM ∥AB . 又AB ⊂平面PAB ，CM ⊄平面PAB ， 所以CM ∥平面PAB .(说明：取棱PD 的中点N ，则所找的点可以是直线MN 上任意一点) (2)证明 由已知，PA ⊥AB ，PA ⊥CD .因为AD ∥BC ，BC ＝12AD ，所以直线AB 与CD 相交，所以PA ⊥平面ABCD ，所以PA ⊥BD . 因为AD ∥BC ，BC ＝12AD ，所以BC ∥MD ，且BC ＝MD ， 所以四边形BCDM 是平行四边形， 所以BM ＝CD ＝12AD ，所以BD ⊥AB .又AB ∩AP ＝A ，所以BD ⊥平面PAB . 又BD ⊂平面PBD ，所以平面PAB ⊥平面PBD . 7.解 (1)因为四边形ABCD 为菱形，所以AC ⊥BD . 因为BE ⊥平面ABCD ，所以AC ⊥BE . 所以AC ⊥平面BED ，又AC ⊂平面AEC ，所以平面AEC ⊥平面BED .(2)设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，可得AG ＝GC ＝32x ，GB ＝GD ＝x 2. 因为AE ⊥EC ，所以在Rt △AEC 中，可得EG ＝32x . 由BE ⊥平面ABCD ，知△EBG 为直角三角形，可得BE ＝22x . 由已知得，三棱锥EACD 的体积V EACD ＝13×12AC ·GD ·BE ＝624x 3＝63.故x ＝2，从而可得AE ＝EC ＝ED ＝ 6.所以△EAC 的面积为3，△EAD 的面积与△ECD 的面积均为5， 故三棱锥EACD 的侧面积为3＋2 5.8.(1)解 由题设AB ＝1，AC ＝2，∠BAC ＝60°，可得S △ABC ＝12·AB ·AC ·sin 60°＝32.由PA ⊥平面ABC ，可知PA 是三棱锥P ­ABC 的高，又PA ＝1，所以三棱锥P ­ABC 的体积V ＝13·S △ABC ·PA ＝36.(2)证明 在平面ABC 内，过点B 作BN ⊥AC ，垂足为N ， 在平面PAC 内，过点N 作MN ∥PA 交PC 于点M ，连接BM . 由PA ⊥平面ABC 知PA ⊥AC ，所以MN ⊥AC . 由于BN ∩MN ＝N ，故AC ⊥平面MBN ， 又BM ⊂平面MBN ，所以AC ⊥BM .在Rt △BAN 中，AN ＝AB ·cos∠BAC ＝12，从而NC ＝AC －AN ＝32，由MN ∥PA 得PM MC ＝AN NC ＝13.9.解 (1)因为PD ⊥底面ABCD ，所以PD ⊥BC ， 由底面ABCD 为长方形，有BC ⊥CD ， 而PD ∩CD ＝D ，所以BC ⊥平面PCD . 而DE ⊂平面PCD ，所以BC ⊥DE .又因为PD ＝CD ，点E 是PC 的中点，所以DE ⊥PC . 而PC ∩BC ＝C ，所以DE ⊥平面PBC .由BC ⊥平面PCD ，DE ⊥平面PBC ，可知四面体EBCD 的四个面都是直角三角形， 即四面体EBCD 是一个鳖臑，其四个面的直角分别是∠BCD ，∠BCE ，∠DEC ，∠DEB . (2)由已知，PD 是阳马PABCD 的高，所以V 1＝13S ABCD ·PD ＝13BC ·CD ·PD ；由(1)知，DE 是鳖臑DBCE 的高，BC ⊥CE ，所以V 2＝13S △BCE ·DE ＝16BC ·CE ·DE .在Rt △PDC 中，因为PD ＝CD ，点E 是PC 的中点，所以DE ＝CE ＝22CD ， 于是V 1V 2＝13BC ·CD ·PD 16BC ·CE ·DE ＝2CD ·PD CE ·DE＝4.10.(1)证明 设E 为BC 的中点，由题意得A 1E ⊥平面ABC ，所以A 1E ⊥AE ， 因为AB ＝AC ，所以AE ⊥BC ，所以AE ⊥平面A 1BC . 由D ，E 分别为B 1C 1，BC 的中点，得DE ∥B 1B 且DE ＝B 1B ， 从而DE ∥A 1A 且DE ＝A 1A ，所以AA 1DE 为平行四边形，于是A 1D ∥AE . 又因为AE ⊥平面A 1BC ，所以A 1D ⊥平面A 1BC . (2)解 作A 1F ⊥DE ，垂足为F ，连接BF . 因为A 1E ⊥平面ABC ，所以BC ⊥A 1E . 因为BC ⊥AE ，所以BC ⊥平面AA 1DE .所以BC ⊥A 1F ，A 1F ⊥平面BB 1C 1C ，所以∠A 1BF 为直线A 1B 和平面BB 1C 1C 所成的角． 由AB ＝AC ＝2，∠CAB ＝90°，得EA ＝EB ＝ 2. 由A 1E ⊥平面ABC ，得A 1A ＝A 1B ＝4，A 1E ＝14. 由DE ＝BB 1＝4，DA 1＝EA ＝2，∠DA 1E ＝90°，得A 1F ＝72. 所以sin ∠A 1BF ＝78.11.(1)证明 如图，连接A 1B .在△A 1BC 中，因为E 和F 分别是BC 和A 1C 的中点，所以EF ∥BA 1. 又因为EF ⊄平面A 1B 1BA ，所以EF ∥平面A 1B 1BA .(2)证明 因为AB ＝AC ，E 为BC 中点，所以AE ⊥BC ，因为AA 1⊥平面ABC ，BB 1∥AA 1，所以BB 1⊥平面ABC ，从而BB 1⊥AE . 又因为BC ∩BB 1＝B ，所以AE ⊥平面BCB 1， 又因为AE ⊂平面AEA 1，所以平面AEA 1⊥平面BCB 1.(3)解 取BB 1的中点M 和B 1C 的中点N ，连接A 1M ，A 1N ，NE . 因为N 和E 分别为B 1C 和BC 的中点，所以NE ∥B 1B ，NE ＝12B 1B ，故NE ∥A 1A 且NE ＝A 1A ， 所以A 1N ∥AE ，且A 1N ＝AE .又因为AE ⊥平面BCB 1，所以A 1N ⊥平面BCB 1， 从而∠A 1B 1N 为直线A 1B 1与平面BCB 1所成的角． 在△ABC 中，可得AE ＝2，所以A 1N ＝AE ＝2. 因为BM ∥AA 1，BM ＝AA 1，所以A 1M ∥AB ，A 1M ＝AB ， 又由AB ⊥BB 1，有A 1M ⊥BB 1.在Rt △A 1MB 1中，可得A 1B 1＝B 1M 2＋A 1M 2＝4. 在Rt △A 1NB 1中，sin ∠A 1B 1N ＝A 1N A 1B 1＝12，所以∠A 1B 1N ＝30°， 所以直线A 1B 1与平面BCB 1所成的角为30°.12.(1)证明 如图，因为四边形ABCD 为菱形，O 为菱形中心，连接OB ，则AO ⊥OB . 因为∠BAD ＝π3，所以OB ＝AB ·sin∠OAB ＝2sin π6＝1，又因为BM ＝12，且∠OBM ＝π3，在△OBM 中，OM 2＝OB 2＋BM 2－2OB ·BM ·cos∠OBM ＝12＋(12)2－2×1×12×cos π3＝34.所以OB 2＝OM 2＋BM 2，所以OM ⊥BM . 又PO ⊥底面ABCD ，所以PO ⊥BC .从而BC 与平面POM 内两条相交直线OM ，PO 都垂直， 所以BC ⊥平面POM .(2)解 由(1)可得，OA ＝AB ·cos∠OAB ＝2×cos π6＝ 3.设PO ＝a ，由PO ⊥底面ABCD 知，△POA 为直角三角形，故PA 2＝PO 2＋OA 2＝a 2＋3. 由△POM 也是直角三角形，故PM 2＝PO 2＋OM 2＝a 2＋34.连接AM ，在△ABM 中，AM 2＝AB 2＋BM 2－2AB ·BM ·cos∠ABM ＝22＋⎝ ⎛⎭⎪⎫122－2×2×12×cos 2π3＝214. 由已知MP ⊥AP ，故△APM 为直角三角形， 则PA 2＋PM 2＝AM 2，即a 2＋3＋a 2＋34＝214，得a ＝32，a ＝－32(舍去)，即PO ＝32. 此时S 四边形ABMO ＝S △AOB ＋S △OMB ＝12·AO ·OB ＋12·BM ·OM ＝12×3×1＋12×12×32＝538.所以四棱锥PABMO 的体积V PABMO ＝13·S 四边形ABMO ·PO ＝13×538×32＝516.13.(1)证明 连接BC 1，则O 为B 1C 与BC 1的交点． 因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1. 又AO ⊥平面BB 1C 1C ，所以B 1C ⊥AO ， 又因为BC 1∩AO ＝O ，所以B 1C ⊥平面ABO . 由于AB ⊂平面ABO ，故B 1C ⊥AB .(2)解 作OD ⊥BC ，垂足为D ，连接AD .作OH ⊥AD ，垂足为H . 因为BC ⊥AO ，BC ⊥OD ，AO ∩OD ＝O ，所以BC ⊥平面AOD ，所以OH ⊥BC . 又OH ⊥AD ，所以OH ⊥平面ABC .因为∠CBB 1＝60°，所以△CBB 1为等边三角形， 又BC ＝1，可得OD ＝34. 因为AC ⊥AB 1，所以OA ＝12B 1C ＝12.由OH ·AD ＝OD ·OA ，且AD ＝OD 2＋OA 2＝74，得OH ＝2114. 又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为217. 故三棱柱ABCA 1B 1C 1的高为217. B 组 两年模拟精选(2016～2015年)1.解析 由l 与α相交但不垂直知：若m ∥l ，则m 与α相交但不垂直，故A ，B 错误； 若m ⊥l ，则m ⊂α或m ∥α，若m 与α相交但不垂直，故C 错误，D 正确.答案 D2.解析 ∵VM ＝MA ，VN ＝NC ，∴MN ∥AC ，又∵AC ∩AB ＝A ，∴MN 和AB 不可能平行，排除A ；∵VA ⊥面ABC ，∴VA ⊥BC ，又∵BC ⊥AC ，∴BC ⊥面VAC ，∴面VBC ⊥面VAC ，故D 正确，∵BC ⊥MN ，排除B ；∵∠OCA ≠90°，∴OC 和面VAC 不垂直，排除C ，故选D.答案 D3.解析 对于A ，若α⊥β，β⊥γ，α，γ可以平行，也可以相交，对于B ，若m ∥α，n ∥β，α⊥β，则m ，n 可以平行，对于C ，若α⊥β，m ⊥α，则m 可以在平面β内，选项D 正确.答案 D4.解析 ①中m ，n 不一定平行，还可能垂直.④中m ，n 不一定平行，还可能异面. 答案 D5.解析 由于m ，n 为异面直线，m ⊥α，n ⊥β，则α与β必相交，但未必垂直，且交线垂直于直线m ，n ，又直线l 满足l ⊥m ，l ⊥n ，则交线平行于l ，故选D.答案 D6.解析 ∵BE BA ＝EF AC ＝x ，∴EH ＝6(1－x )， ∵AE AB ＝EH BD＝1－x ，∴EF ＝4x ，故y ＝EH ·EF ＝－24x 2＋24x ，x ∈(0，1)，所以y ∈(0，6]，其对称轴为x ＝12，故在⎝ ⎛⎭⎪⎫0，12上单调递增，⎝ ⎛⎭⎪⎫12，1上单调递减， f (1－x )＝－24[(1－x )2－(1－x )]＝f (x ).答案 D7.解 (1)在梯形ABCD 中，∵AB ∥CD ，AD ＝DC ＝CB ＝1，∠BCD ＝120°， ∴AB ＝2，∴BD 2＝AB 2＋AD 2－2AB ·AD ·cos 60°＝3.∴AB 2＝AD 2＋BD 2，∴AD ⊥BD .∵平面BFED ⊥平面ABCD ，平面BFED ∩平面ABCD ＝BD ，DE ⊂平面BEFD ，DE ⊥DB ， ∴DE ⊥平面ABCD ，∴DE ⊥AD ，又DE ∩BD ＝D ，∴AD ⊥平面BFED .(2)由(1)知BD ⊥平面ADE ，∵BD ∥EF ，∴PE ⊥平面ADE ，且PE ＝233，∴V EAPD ＝V PADE ＝13S △ADE |PE |＝13×12×233＝39.8.(1)证明 连接AD 1交A 1D 于O ，连接EO ，则O 为AD 1的中点，又因为E 是AB 的中点，所以OE ∥BD 1，又∵OE ⊂平面A 1DE ，BD 1⊄平面A 1DE ，∴BD 1∥平面A 1DE .(2)证明 由题意可知：四边形ADD 1A 1是正方形，∴A 1D ⊥AD 1，又∵AB ⊥平面ADD 1A 1，A 1D ⊂平面ADD 1A 1，∴AB ⊥A 1D .又∵AB ⊂平面AD 1E ，AD 1⊂平面AD 1E ，AB ∩AD 1＝A ，∴A 1D ⊥平面AD 1E .又∵D 1E ⊂平面AD 1E ，∴A 1D ⊥D 1E .(3)解 在△CED 中，CD ＝2，DE ＝AD 2＋AE 2＝2，CE ＝CB 2＋BE 2＝2， ∴CD 2＝CE 2＋DE 2，∴CE ⊥DE ，又∵D 1D ⊥平面ABCD ，CE ⊂平面ABCD ，∴CE ⊥D 1D ，又∵D 1D ⊂平面D 1DE ，DE ⊂平面D 1DE ，D 1D ∩DE ＝D ，∴CE ⊥平面D 1DE .又∵D 1E ⊂平面D 1DE ，∴CE ⊥D 1E ，∴∠D 1ED 是二面角D 1ECD 的一个平面角，在△D 1ED 中，∠D 1DE ＝90°，D 1D ＝1，DE ＝2，∴tan ∠D 1ED ＝D 1D DE ＝12＝22，∴二面角D 1ECD 的正切值是22.。

第五节空间垂直的判定与性质A组三年高考真题（2016～2014年）1.(2016·浙江,2)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则()A.m∥lB.m∥nC.n⊥lD.m⊥n2.(2015·浙江,8)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′CDB的平面角为α,则()A.∠A′DB≤αB.∠A′DB≥αC.∠A′CB≤αD.∠A′CB≥α3.(2014·广东,7)若空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是()A.l1⊥l4B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定4.(2016·全国Ⅱ,14)α,β是两个平面,m,n是两条直线,有下列四个命题：(1)如果m⊥n,m⊥α,n∥β,那么α⊥β.(2)如果m⊥α,n∥α,那么m⊥n.(3)如果α∥β,m⊂α,那么m∥β.(4)如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________(填写所有正确命题的编号).5.(2016·全国Ⅰ,18)如图,在以A,B,C,D,E,F为顶点的五面体中,平面ABEF为正方形,AF＝2FD,∠AFD＝90°,且二面角D－AF－E与二面角C－BE－F都是60°.(1)证明：平面ABEF⊥EFDC；(2)求二面角E－BC－A的余弦值.6.(2016·江苏，16)如图，在直三棱柱ABC－A1B1C1中，D，E分别为AB，BC的中点，点F 在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1.求证：(1)直线DE∥平面A1C1F；(2)平面B1DE⊥平面A1C1F.7.(2015·新课标全国Ⅱ,19)如图,长方体ABCD－A1B1C1D1中,AB＝16,BC＝10,AA1＝8,点E,F分别在A1B1,D1C1上,A1E＝D1F＝4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由)；(2)求直线AF与平面α所成角的正弦值.8.(2015·新课标全国Ⅰ,18) 如图,四边形ABCD为菱形,∠ABC＝120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE＝2DF,AE⊥EC.(1)证明：平面AEC⊥平面AFC,(2)求直线AE与直线CF所成角的余弦值.9.(2014·新课标全国Ⅰ,19)如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.(1)证明：AC＝AB1；(2)若AC⊥AB1,∠CBB1＝60°,AB＝BC,求二面角AA1B1C1的余弦值.10.(2014·广东,18)如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC＝30°,AF⊥PC于点F,FE∥CD,交PD于点E.(1)证明：CF⊥平面ADF；(2)求二面角DAFE的余弦值.11.(2014·辽宁,19) 如图,△ABC和△BCD所在平面互相垂直,且AB＝BC＝BD＝2,∠ABC＝∠DBC＝120°,E,F分别为AC,DC的中点.(1)求证：EF⊥BC；(2)求二面角EBFC的正弦值.12.(2014·江西,19)如图,四棱锥P-ABCD中,ABCD为矩形,平面P AD⊥平面ABCD.(1)求证：AB⊥PD；(2)若∠BPC＝90°,PB＝2,PC＝2,问AB为何值时,四棱锥P ABCD的体积最大？并求此时平面BPC与平面DPC夹角的余弦值.13.(2014·湖南,19)如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD＝O,A1C1∩B1D1＝O1,四边形ACC1A1和四边形BDD1B1均为矩形.(1)证明：O1O⊥底面ABCD；(2)若∠CBA＝60°,求二面角C1-OB1-D的余弦值.B组两年模拟精选(2016～2015年)1.(2016·湖北天门模拟)如图,在长方体ABCD－A1B1C1D1中,AB＝BC＝2,AA1＝1,则BC1与平面BB1D1D所成角的正弦值为()A.63 B.265 C.155 D.1052.(2016·山东东营模拟) 已知点E,F分别是正方体ABCD－A1B1C1D1的棱AB,AA1的中点,点M,N分别是线段D1E与C1F上的点,则与平面ABCD垂直的直线有()A.0条B.1条C.2条D.无数条3.(2015·豫南五市模拟)m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题中正确的是()①若m、n都平行于平面α,则m、n一定不是相交直线；②若m、n都垂直于平面α,则m、n 一定是平行直线；③已知α、β互相垂直,m、n互相垂直,若m⊥α,则n⊥β；④m、n在平面α内的射影互相垂直,则m、n互相垂直.A.②B.②③C.①③D.②④4.(2015·四川雅安模拟)下列说法错误的是()A.两两相交且不过同一点的三条直线必在同一平面内B.过直线外一点有且只有一个平面与已知直线垂直C.如果共点的三条直线两两垂直,那么它们中每两条直线确定的平面也两两垂直D.如果两条直线和一个平面所成的角相等,则这两条直线一定平行5.(2016·云南玉溪模拟)表面积为60π的球面上有四点S、A、B、C,且△ABC是等边三角形,球心O到平面ABC的距离为3,若平面SAB⊥平面ABC,则三棱锥S－ABC体积的最大值为________.6.(2015·绵阳模拟)在正三棱锥P－ABC中,D,E分别是AB,BC的中点,有下列三个论断：①AC⊥PB；②AC∥平面PDE；③AB⊥平面PDE.其中正确论断的序号为________.7.(2015·山东菏泽二模)如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且AC＝ 6.(1)证明：平面ABEF⊥平面BCDE；(2)求三棱锥E－ABC的体积.答案精析A组三年高考真题（2016～2014年）1.C [由已知,α∩β＝l ,∴l ⊂β,又∵n ⊥β,∴n ⊥l ,C 正确.故选C.]2.B [极限思想：若α＝π,则∠A ′CB ＜π,排除D ；若α＝0,如图,则∠A ′DB ,∠A ′CB 都可以大于0,排除A,C.故选B. ]3.D [构造如图所示的正方体ABCDA 1B 1C 1D 1,取l 1为AD ,l 2为AA 1,l 3为A 1B 1,当取l 4为B 1C 1时,l 1∥l 4,当取l 4为BB 1时,l 1⊥l 4,故排除A 、B 、C ,选D.]4.②③④ [当m ⊥n ,m ⊥α,n ∥β时,两个平面的位置关系不确定,故①错误,经判断知②③④均正确,故正确答案为②③④.]5.(1)证明 由已知可得AF ⊥DF ,AF ⊥FE ,所以AF ⊥平面EFDC ,又AF ⊂平面ABEF ,故平面ABEF ⊥平面EFDC .(2)解 过D 作DG ⊥EF ,垂足为G ,由(1)知DG ⊥平面ABEF .以G 为坐标原点,GF →的方向为x 轴正方向,|GF →|为单位长,建立如图所示的空间直角坐标系G －xyz .由(1)知∠DFE 为二面角D －AF －E 的平面角,故∠DFE ＝60°,则|DF |＝2,|DG |＝3,可得A (1,4,0),B (－3,4,0),E (－3,0,0),D (0,0,3).由已知,AB ∥EF ,所以AB ∥平面EFDC ,又平面ABCD ∩平面EFDC ＝CD ,故AB ∥CD ,CD ∥EF , 由BE ∥AF ,可得BE ⊥平面EFDC ,所以∠CEF 为二面角C －BE －F 的平面角,∠CEF ＝60°,从而可得C (－2,0,3).所以EC →＝(1,0,3),EB →＝(0,4,0),AC →＝(－3,－4,3),AB →＝(－4,0,0).设n ＝(x ,y ,z )是平面BCE 的法向量,则⎩⎪⎨⎪⎧n ·EC →＝0，n ·EB →＝0，即⎩⎨⎧x ＋3z ＝0，4y ＝0.所以可取n ＝(3,0,－3). 设m 是平面ABCD 的法向量,则⎩⎪⎨⎪⎧m ·AC →＝0，m ·AB →＝0. 同理可取m ＝(0,3,4),则cos 〈n ,m 〉＝n ·m |n ||m |＝－21919. 故二面角E －BC －A 的余弦值为－21919. 6.证明 (1)由已知,DE 为△ABC 的中位线,∴DE ∥AC ,又由三棱柱的性质可得AC ∥A 1C 1,∴DE ∥A 1C 1,且DE ⊄平面A 1C 1F ,A 1C 1⊂平面A 1C 1F ,∴DE ∥平面A 1C 1F .(2)在直三棱柱ABC －A 1B 1C 1中,AA 1⊥平面A 1B 1C 1,∴AA 1⊥A 1C 1,又∵A 1B 1⊥A 1C 1,且A 1B 1∩AA 1＝A ,∴A 1C 1⊥平面ABB 1A 1,∵B 1D ⊂平面ABB 1A 1,∴A 1C 1⊥B 1D ,又∵A 1F ⊥B 1D ,且A 1F ∩A 1C 1＝A 1,∴B 1D ⊥平面A 1C 1F ,又∵B 1D ⊂平面B 1DE ,∴平面B 1DE ⊥平面A 1C 1F .7.解 (1)交线围成的正方形EHGF 如图：(2)作EM ⊥AB ,垂足为M ,则AM ＝A 1E ＝4,EM ＝AA 1＝8.因为EHGF 为正方形,所以EH ＝EF ＝BC ＝10.于是MH ＝EH 2－EM 2＝6,所以AH ＝10.以D 为坐标原点,DA →的方向为x 轴正方向,建立如图所示的空间直角坐标系Dxyz ,则A (10,0,0),H (10,10,0),E (10,4,8),F (0,4,8),FE →＝(10,0,0),HE →＝(0,－6,8).设n ＝(x ,y ,z )是平面EHGF 的法向量,则⎩⎪⎨⎪⎧n ·FE →＝0，n ·HE →＝0，即⎩⎪⎨⎪⎧10x ＝0，－6y ＋8z ＝0，所以可取n ＝(0,4,3).又AF →＝(－10,4,8),故|cos 〈n ,AF →〉|＝|n ·AF →||n ||AF →|＝4515. 所以AF 与平面EHGF 所成角的正弦值为4515.8.(1)证明 连接BD ,设BD ∩AC ＝G ,连接EG ,FG ,EF .在菱形ABCD 中,不妨设GB ＝1.由∠ABC ＝120°,可得AG ＝GC ＝ 3. 由BE ⊥平面ABCD ,AB ＝BC ,可知AE ＝EC .又AE ⊥EC ,所以EG ＝3,且EG ⊥AC .在Rt △EBG 中,可得BE ＝2,故DF ＝22. 在Rt △FDG 中,可得FG ＝62. 在直角梯形BDFE 中,由BD ＝2,BE ＝2,DF ＝22,可得EF ＝322, 从而EG 2＋FG 2＝EF 2,所以EG ⊥FG .又AC ∩FG ＝G ,可得EG ⊥平面AFC .因为EG ⊂平面AEC ,所以平面AEC ⊥平面AFC .(2)解 如图,以G 为坐标原点,分别以GB →,GC →的方向为x 轴,y 轴正方向,|GB →|为单位长,建立空间直角坐标系Gxyz ,由(1)可得A (0,－3,0),E (1,0,2),F ⎝⎛⎭⎫－1，0，22,C (0,3,0),所以AE →＝(1,3,2),CF →＝⎝⎛⎭⎫－1，－3，22.故cos 〈AE →,CF →〉＝AE →·CF →|AE →||CF →|＝－33. 所以直线AE 与直线CF 所成角的余弦值为33. 9.(1)证明 连接BC 1,交B 1C 于点O ,连接AO .因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1,且O 为B 1C 及BC 1的中点.又AB ⊥B 1C ,所以B 1C ⊥平面ABO .由于AO ⊂平面ABO ,故B 1C ⊥AO .又B 1O ＝CO ,故AC ＝AB 1.(2)解 因为AC ⊥AB 1,且O 为B 1C 的中点,所以AO ＝CO .又因为AB ＝BC ,所以△BOA ≌△BOC .故OA ⊥OB ,从而OA ,OB ,OB 1两两互相垂直.以O 为坐标原点,OB →的方向为x 轴正方向,|OB →|为单位长,建立如图所示的空间直角坐标系Oxyz .因为∠CBB 1＝60°,所以△CBB 1为等边三角形.又AB ＝BC ,则A ⎝⎛⎭⎫0，0，33,B (1,0,0),B 1⎝⎛⎭⎫0，33，0,C ⎝⎛⎭⎫0，－33，0. AB 1→＝⎝⎛⎭⎫0，33，－33,A 1B 1→＝AB →＝⎝⎛⎭⎫1，0，－33,B 1C 1→＝BC →＝⎝⎛⎭⎫－1，－33，0. 设n ＝(x ,y ,z )是平面AA 1B 1的法向量,则⎩⎪⎨⎪⎧n ·AB 1→＝0，n ·A 1B 1→＝0，即⎩⎨⎧33y －33z ＝0，x －33z ＝0. 所以可取n ＝(1,3,3).设m 是平面A 1B 1C 1的法向量,则⎩⎪⎨⎪⎧m ·A 1B 1→＝0，m ·B 1C 1→＝0. 同理可取m ＝(1,－3,3).则cos 〈n ,m 〉＝n ·m |n||m|＝17. 所以二面角A -A 1B 1­C 1的余弦值为17. 10.(1)证明 ∵PD ⊥平面ABCD ,∴PD ⊥AD .又CD ⊥AD ,PD ∩CD ＝D ,∴AD ⊥平面PCD .∴AD ⊥PC .又AF ⊥PC ,AD ∩AF ＝A ,∴PC ⊥平面ADF ,即CF ⊥平面ADF .(2)解 法一 设AB ＝1,则在Rt △PDC 中,CD ＝1,∵∠DPC ＝30°,∴PC ＝2,PD ＝3,由(1)知CF ⊥DF ,∴DF ＝32,CF ＝12. 又FE ∥CD ,∴DE PD ＝CF PC ＝14,∴DE ＝34.同理EF ＝34CD ＝34. 如图所示,以D 为原点,建立空间直角坐标系,则A (0,0,1),E ⎝⎛⎭⎫34，0，0,F ⎝⎛⎭⎫34，34，0,P (3,0,0),C (0,1,0). 设m ＝(x ,y ,z )是平面AEF 的法向量,则⎩⎪⎨⎪⎧m ⊥AE →，m ⊥EF →.又⎩⎨⎧AE →＝⎝⎛⎭⎫34，0，－1，EF →＝⎝⎛⎭⎫0，34，0， ∴⎩⎨⎧m ·AE →＝34x －z ＝0，m ·EF →＝34y ＝0.令x ＝4,则z ＝3,m ＝(4,0,3).由(1)知平面ADF 的一个法向量为PC →＝(－3,1,0), 设二面角DAFE 的平面角为θ,可知θ为锐角, cos θ＝|cos 〈m ,PC →〉|＝|m ·PC →||m |·|PC →|＝4319×2＝25719. 故二面角DAFE 的余弦值为25719. 法二 设AB ＝1,∵CF ⊥平面ADF ,∴CF ⊥DF .∴在△CFD 中,DF ＝32, ∵CD ⊥AD ,CD ⊥PD ,∴CD ⊥平面ADE .又∵EF ∥CD ,∴EF ⊥平面ADE .∴EF ⊥AE , ∴在△DEF 中,DE ＝34,EF ＝34, 在△ADE 中,AE ＝194,在△ADF 中,AF ＝72. 由V A ­DEF ＝13·S △ADE ·EF ＝13·S △ADF ·h E ­ADF ,解得h E ­ADF ＝38, 设△AEF 的边AF 上的高为h ,由S △AEF ＝12·EF ·AE ＝12·AF ·h ,解得h ＝34×13314, 设二面角D -AF -E 的平面角为θ.则sin θ＝h E -ADF h ＝38×43×14133＝13319,∴cos θ＝25719. 11.(1)证明 法一 过E 作EO ⊥BC ,垂足为O ,连接OF .图1由△ABC ≌△DBC 可证出△EOC ≌△FOC .所以∠EOC ＝∠FOC ＝π2,即FO ⊥BC . 又EO ⊥BC ,因此BC ⊥面EFO ,又EF ⊂面EFO ,所以EF ⊥BC .法二 由题意,以B 为坐标原点,在平面DBC 内过B 作垂直BC 的直线为x 轴,BC 所在直线为y 轴,在平面ABC 内过B 作垂直BC 的直线为z 轴,建立如图所示空间直角坐标系.易得B (0,0,0),A (0,－1,3),D (3,－1,0),C (0,2,0).因而E (0,12,32),F ⎝⎛⎭⎫32，12，0,所以EF →＝⎝⎛⎭⎫32，0，－32,BC →＝(0,2,0),因此EF →·BC →＝0. 从而EF →⊥BC →,所以EF ⊥BC .图2(2)解 法一 在图1中,过O 作OG ⊥BF ,垂足为G ,连接EG .由平面ABC ⊥平面BDC ,从而EO ⊥面BDC ,又OG ⊥BF ,由三垂线定理知,EG ⊥BF . 因此∠EGO 为二面角EBFC 的平面角.在△EOC 中,EO ＝12EC ＝12BC ·cos 30°＝32,由△BGO ∽△BFC 知,OG ＝BO BC ·FC ＝34,因此tan∠EGO ＝EO OG ＝2,从而sin ∠EGO ＝255,即二面角E ­BF ­C 的正弦值为255.法二 在图2中,平面BFC 的一个法向量为n 1＝(0,0,1). 设平面BEF 的法向量n 2＝(x ,y ,z ),又BF →＝⎝⎛⎭⎫32，12，0,BE →＝⎝⎛⎭⎫0，12，32.由⎩⎪⎨⎪⎧n 2·BF →＝0n 2·BE →＝0得其中一个n 2＝(1,－3,1). 设二面角EBFC 大小为θ,且由题意知θ为锐角,则 cos θ＝|cos 〈n 1,n 2〉|＝⎪⎪⎪⎪n 1·n 2|n 1||n 2|＝15, 因此sin θ＝25＝255,即所求二面角的正弦值为255.12.(1)证明 ABCD 为矩形,故AB ⊥AD ；又平面P AD ⊥平面ABCD , 平面P AD ∩平面ABCD ＝AD ,所以AB ⊥平面P AD ,由PD ⊂平面P AD ,故AB ⊥PD .(2)解 过P 作AD 的垂线,垂足为O ,过O 作BC 的垂线,垂足为G ,连接PG .故PO ⊥平面ABCD ,BC ⊥平面POG ,BC ⊥PG . 在Rt △BPC 中,PG ＝233,GC ＝263,BG ＝63.设AB ＝m ,则OP ＝PG 2－OG 2＝43－m 2, 故四棱锥P ABCD 的体积为V ＝13·6·m ·43－m 2＝m 38－6m 2.因为m8－6m 2＝8m 2－6m 4＝－6⎝⎛⎭⎫m 2－232＋83,故当m ＝63,即AB ＝63时,四棱锥P ABCD 的体积最大. 此时,建立如图所示的坐标系,各点的坐标为O (0,0,0),B ⎝⎛⎭⎫63，－63，0,C ⎝⎛⎭⎫63，263，0,D ⎝⎛⎭⎫0，263，0,P ⎝⎛⎭⎫0，0，63.故PC →＝⎝⎛⎭⎫63，263，－63, BC →＝(0,6,0),CD →＝⎝⎛⎭⎫－63，0，0,设平面BPC 的一个法向量n 1＝(x ,y ,1),则由n 1⊥PC →, n 1⊥BC →得⎩⎪⎨⎪⎧63x ＋263y －63＝0，6y ＝0，解得x ＝1,y ＝0,n 1＝(1,0,1). 同理可求出平面DPC 的一个法向量n 2＝⎝⎛⎭⎫0，12，1.从而平面BPC 与平面DPC 夹角θ的余弦值为cos θ＝|n 1·n 2||n 1||n 2|＝12·14＋1＝105. 13.(1)证明 因为四边形ACC 1A 1为矩形,所以CC 1⊥AC ,同理DD 1⊥BD ,因为CC 1∥DD 1,所以CC 1⊥BD ,而AC ∩BD ＝O ,因此CC 1⊥底面ABCD . 由题设知,O 1O ∥C 1C ,故O 1O ⊥底面ABCD .(2)解 法一 如图,过O 1作O 1H ⊥OB 1于H ,连接HC 1.由(1)知,O 1O ⊥底面ABCD ,所以O 1O ⊥底面A 1B 1C 1D 1,于是O 1O ⊥A 1C 1.又因为四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等,所以四边形A 1B 1C 1D 1是菱形, 因此A 1C 1⊥B 1D 1,从而A 1C 1⊥平面BDD 1B 1,所以A 1C 1⊥OB 1,于是OB 1⊥平面O 1HC 1, 进而OB 1⊥C 1H ,故∠C 1HO 1是二面角C 1­OB 1­D 的平面角. 不妨设AB ＝2.因为∠CBA ＝60°,所以OB ＝3,OC ＝1,OB 1＝7.在Rt △OO 1B 1中,易知O 1H ＝OO 1·O 1B 1OB 1＝237,而O 1C 1＝1, 于是C 1H ＝O 1C 21＋O 1H 2＝1＋127＝197. 故cos ∠C 1HO 1＝O 1HC 1H＝237197＝25719.即二面角C 1OB 1D 的余弦值为25719.法二 因为四棱柱ABCDA 1B 1C 1D 1的所有棱长都相等,所以四边形ABCD 是菱形,因此AC ⊥BD .又由(1)知O 1O ⊥底面ABCD ,从而OB ,OC ,OO 1两两垂直.如图,以O 为坐标原点,OB ,OC ,OO 1所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系Oxyz .不妨设AB ＝2,因为∠CBA ＝60°,所以OB ＝3,OC ＝1.于是相关各点的坐标为：O (0,0,0),B 1(3,0,2),C 1(0,1,2). 易知,n 1＝(0,1,0)是平面BDD 1B 1的一个法向量.设n 2＝(x ,y ,z )是平面OB 1C 1的法向量,则⎩⎪⎨⎪⎧n 2·OB 1→＝0，n 2·OC 1→＝0，即⎩⎨⎧3x ＋2z ＝0，y ＋2z ＝0，取z ＝－3,则x ＝2,y ＝23,所以n 2＝(2,23,－3), 设二面角C 1-OB 1-D 的大小为θ,易知θ是锐角,于是 cos θ＝|cos 〈n 1,n 2〉|＝|n 1·n 2|n 1|·|n 2||＝2319＝25719.故二面角C 1-OB 1-D 的余弦值为25719.B 组 两年模拟精选(2016～2015年)1. D [如图,连接A 1C 1,设A 1C 1∩B 1D 1＝O ,连接OB .由已知得C 1O ⊥面BB 1D 1D . ∴∠C 1BO 为所求角,在Rt △C 1OB 中,sin ∠C 1BO ＝OC 1BC 1＝105,故选D.]2.B [如图,设正方体ABCD －A 1B 1C 1D 1的棱长为2,以C 为原点建立空间直角坐标系,则D 1(2,0,2),E (1,2,0),C 1(0,0,2),F (2,2,1),D 1E →＝(－1,2,－2),C 1F →＝(2,2,－1),设D 1M →＝λD 1E →(0≤λ≤1),则M (2－λ,2λ,2－2λ),设C 1N →＝tC 1F →(0≤t ≤1),则N (2t ,2t ,2－t ), ∴MN →＝(2t －2＋λ,2t －2λ,2λ－t ),要使直线MN 与平面ABCD 垂直,则⎩⎪⎨⎪⎧2t －2＋λ＝0，2t －2λ＝0，2λ－t ≠0，解得λ＝t ＝23,∴与平面ABCD 垂直的直线MN 有1条.故选B.] 3. A [①③④错误,②正确,故选A.]4.D [如果两条直线和一个平面所成的角相等,这两条直线可以平行、相交、异面.故选D.]5. 27 [设球O 的半径为R ,则有4πR 2＝60π,解得R ＝15. 由于平面SAB ⊥平面ABC ,平面SAB ∩平面ABC ＝AB ,所以点S 在平面ABC 上的射影D 在AB 上,如图,当球心O 在三棱锥S －ABC 中,且D 为AB 的中点时,SD 最大,三棱锥S －ABC 的体积最大.设O ′为等边三角形ABC 的中心,则OO ′⊥平面ABC ,即有OO ′∥SD .由于OC ＝15,OO ′＝3,则CO ′＝CO 2－OO ′2＝23,则DO ′＝3,则△ABC 是边长为6的等边三角形,则△ABC 的面积为34×62＝9 3. 在直角梯形SDO ′O 中,作OM ⊥SD 于M ,则OM ＝DO ′＝3,DM ＝OO ′＝3,∴SD ＝DM ＋MS ＝3＋（15）2－（3）2＝33,所以三棱锥S －ABC 体积的最大值为13×93×33＝27.]6.①② [如图,∵P －ABC 为正三棱锥,∴PB ⊥AC .又∵DE ∥AC ,DE ⊂平面PDE ,AC ⊄平面PDE ,∴AC ∥平面PDE .故①②正确.]7.(1)证明正六边形ABCDEF 中,连接AC 、BE ,交点为G ,易知AG ⊥BE , 且AG ＝CG ＝3,在多面体中,由AC ＝6,知AG 2＋CG 2＝AC 2,故AG ⊥GC , 又GC ∩BE ＝G ,GC ,BE ⊂平面BCDE ,故AG ⊥平面BCDE, 又AG ⊂平面ABEF ,所以平面ABEF ⊥平面BCDE .(2)解 连接AE 、CE ,则AG 为三棱锥A －BCE 的高,GC 为△BCE 的高.在正六边形ABCDEF 中,BE ＝2AF ＝4,故S △BCE ＝12×4×3＝23,所以V E －ABC ＝V A －BCE ＝13×23×3＝2.。

高考数学（理）真题专项汇编卷（2017—2019）知识点8：立体几何1、中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头，若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是( )A. B. C. D.2、设,αβ为两个平面，则//αβ的充要条件是（）A．α内有无数条直线与β平行B．α内有两条相交直线与β平行C．,αβ平行于同一条直线D．,αβ垂直于同一平面3、如图，点N为正方形ABCD的中心，ECD△为正三角形，平面ECD⊥平面,ABCD M是线段ED的中点，则( )A．BM EN、是相交直线=，且直线BM ENB．BM EN、是相交直线≠，且直线BM ENC．BM EN、是异面直线=，且直线BM END ．BM EN ≠，且直线BM EN 、是异面直线4、某圆柱的高为2，底面周长为16，其三视图如下图.圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为( )A. 17B. 25C.3D. 25、在长方体1111ABCD A B C D -中， 1AB BC ==，13AA 1AD 与1DB 所成角的余弦值为( ) A.1555 D.226、已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，ABC △是边长为2的正三角形，,E F 分别是,PA AB 的中点，90CEF ∠=︒，则球O 的体积为( ) A ．68πB ．64πC ．62πD 6π7、已知正方体的棱长为1，每条棱所在直线与平面a 所成的角相等，则a 截此正方体所得的截面面积的最大值为( ) A 33B 23C ．324D 38、设,,,A B C D 是同一个半径为4的球的球面上四点， ABC △为等边三角形且其面积为93D ABC -体积的最大值为( ) A. 123 B. 183 C. 3 D. 39、学生到工厂劳动实践，利用3D 打印技术制作模型.如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O EFGH -后所得几何体，其中O 为长方体的中心，,,,E F G H 分别为所在棱的中点，16cm 4cm AB =BC =, AA =，3D 打印所用原料密度为30.9 /cm g ，不考虑打印损耗，制作该模型所需原料的质量为___________.10、已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45，若SAB △的面积为515，则该圆锥的侧面积为__________. 11、中国有悠久的金石文化，印信是金石文化的代表之一印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有 个面，其棱长为 .12、如图，在三角锥P ABC -中， 2?2AB BC == 4PA PB PC AC ====，O 为AC 的中点.(1)证明: PO ⊥平面ABC ;(2)若点M 在棱BC 上，且二面角M PA C --为30°，求PC 与平面PAM 所成角的正弦值.13、如图，直四棱柱1111ABCD A B C D -的底面是菱形，14,2,60,,,AA AB BAD E M N ==∠=︒分别是11,,BC BB A D 的中点．(1).证明：//MN 平面1C DE ； (2).求二面角1A MA N --的正弦值．14、图1是由矩形Rt ADEB ABC 、△和菱形BFGC 组成的一个平面图形，其中1,2AB BE BF ===，60FBC ∠=︒，将其沿,AB BC 折起使得BE 与BF 重合，连结DG ，如图2.(1).证明：图2中的,,,A C G D 四点共面，且平面ABC ⊥平面BCGE ； (2).求图2中的二面角B CG A --的大小.15、如图，长方体1111ABCD A B C D -的底面ABCD 是正方形，点E 在棱1AA 上，1BE EC ⊥.(1).证明：BE ⊥平面11EB C ；(2).若1AE A E =，求二面角1––B EC C 的正弦值.答案以及解析1答案及解析：答案：A解析：卯眼是凹进去的部分，因此从上面往下看的俯视图是看不到卯眼的，故卯眼部分为虚线，因为榫头居中，故卯眼也必居中，结合选项A 符合.2答案及解析： 答案：B解析：由面面平行的判定定理知：α内两条相交直线都与β平行是//αβ的充分条件，由面面平行性质定理知，若//αβ，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是//αβ的必要条件，故选B ．3答案及解析： 答案：B解析： 作EO CD ⊥于O ，连接ON ， 过M 作MF OD ⊥于F ．连BF ，平面CDE ⊥平面ABCD ．,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCE ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知012EO N EN ===，5,2MF BF BM ==∴=BM EN ∴≠，故选B ．4答案及解析： 答案：B解析：设过点M 的高与圆柱的下底面交于点 O ，将圆柱沿MO 剪开， 则,M N 的位置如图所示，连接MN ，易知2,4OM ON ==， 则从M 到N 的最短路径的长度为22222425OM ON +=+=.5答案及解析： 答案：C解析：以D 为坐标原点， 1,,DA DC DD 为,,x y z 轴建立空间直角坐标系，则11(0,0,0),(1,0,0),(1,13),3)D A B D 所以: 11(1,0,3),(1,13)AD DB =-= 因为: 1111115cos ,||||25AD DB AD DB AD DB ⋅<>===∈，所以异面直线1AD 与1DB 所5C.6答案及解析： 答案：D解析：方法一：本题也可用解三角形方法，达到求出棱长的目的．适合空间想象能力略差学生．设2PA PB PC x ===，,E F 分别为,PA AB 中点，//EF PB ∴，且12EF PB x ==，ABC ∆为边长为2的等边三角形，3CF ∴又90CEF ∠=︒213,2CE xAE PA x ∴=-== AEC ∆中余弦定理()2243cos 22x x EAC x+--∠=⨯⨯，作PD AC ⊥于D ，PA PC =，D 为AC 中点，1cos 2AD EAC PA x ∠==，2243142x x x x+-+∴=， 22122122x x x ∴+=∴==，2PA PB PC ∴==又===2AB BC AC ，,,PA PB PC ∴两两垂直，22226R ∴++6R ∴=，34466ππ6π33V R ∴===，故选D.方法二：,PA PB PC ABC ==∆为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别PA 、AB 中点，//EF PB ∴，EF AC ∴⊥，又EF CE ⊥，,CEAC C EF =∴⊥平面PAC ，PB ⊥平面PAC ，2PAB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体一部分，22226R =++=，即 364466,ππ6π33R V R =∴==⨯=，故选D ．7答案及解析： 答案：A解析：如图所示平面1AB C 与平面的所有棱缩成角都相等故//α平面1AB C ，构造平面MN ，//PQRS 平面1AB C设1,2A S x SP ==2SR PQ MN x ==，2(1)SM RQ PN x ===- 故=SRQP SMNP S S S +=六边形22(1)6226(1)22x x x x --+2322)x x =+- 当12x =时max 334S =8答案及解析： 答案：B解析：如图所示，点M 为ABC △的重心，E 为AC 中心，当DM ⊥平面ABC 时，三棱锥D ABC -体积最大(O 是球心)此时，4OD OB R ===2393,64ABC S AB AB ∆===∴ ∴22332333BM BE ==⨯=∴Rt ABC △中，有222OM OB BM =-= ∴426DM OD OM =+=+=∴max 1()9361833D ABC V -=⨯=故选B9答案及解析： 答案：118.8解析：由题意得，四棱锥O EFGH -的底面积为2146423122cm ⨯-⨯⨯⨯=，其高为点O 到底面11BB C C 的距离为3cm ，则此四棱锥的体积为211123123V cm =⨯⨯=．又长方体1111ABCD A B C D -的体积为22466144V cm =⨯⨯=，所以该模型体积为22114412132V V V cm =-=-=，其质量为0.9132118.8g ⨯=．10答案及解析：答案：解析：因为母线,SA SB 所成角的余弦值为78，所以母线,SA SB 所成角的正弦值为SAB △的面积为l ，所以212l ⨯=，所以280,l =因为: SA 与圆锥底面所成角为45，所以店面半径为cos ,42l π=因此圆锥的侧面积为22rl l π==11答案及解析： 答案：1解析：由图可知第一层与第三层各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826+=个面．如图，设该半正多面体的棱长为x ，则AB BE x ==，延长BC 与FE 交于点G ，延长BC 交正方体棱于H ，由半正多面体对称性可知，BGE △为等腰直角三角形，BG GE CH x ∴===，21)1GH x x x ∴=+==1x ∴==．12答案及解析：答案：(1)因为4AP CP AC ===，O 为AC 的中点， 所以OP AC ⊥，且OP=23 连结OB ，因为22AB BC AC ==，所以ABC ∆为等腰直角三角形 且OB AC ⊥，122OB AC == 由222OP OB PB +=知PO OB ⊥由OP OB ⊥，OP AC ⊥知PO ⊥平面ABC . (2)如图，以O 为坐标原点， OB 的方向为x 轴正方向，建立空间直角坐标系O xyz - 由已知得(0,0,0),(2,0,0),(0,2,0),(0,2,0),(0,0,23),(0,2,23)O B A C P AP -=， 取平面PAC 的法向量(2,0,0)OB =设(,2,0)(02)M a a a -<≤，则(,4,0)AM a a =- 设平面PAM 的法向量为(,,)n x y z =，由0,0AP n AM n ⋅=⋅=得2230(4)0y z ax a y ⎧+=⎪⎨+-=⎪⎩可取(3(4),3,)n a a a =-- 所以22223(4)cos ,23(4)3a OB a a a -=-++n ，由已知可得3|cos ,|2OB =n 所以22223|4|3=23(4)3a a a a --++，解得4a =- (舍去)， 43a =所以83434(,,)333n =-- 又(0,2,23)PC =-，所以3cos ,PC =n 所以PC 与平面PAM 所成角的正弦值为34. 解析：13答案及解析： 答案：(1).连结1,B C ME ．因为,M E 分别为1,BB BC 的中点，所以1//ME B C ，且112ME B C =． 又因为N 为1A D 的中点，且11//A D B C ，1//ND B C ∴且112ND B C =由题设知11//A B DC ，可得11//B C A D ，故//ME ND ， 因此四边形MNDE 为平行四边形，//MN ED ． 又MN ⊄平面1EDC ，所以//MN 平面1C DE ． (2).由已知可得DE DA ⊥．以D 为坐标原点，DA 的方向为x 轴正方向，建立如图所示的空间直角坐标系D xyz -，则(2,0,0)A ，12,()0,4A ，3,2)M ，(1,0,2)N ，1(0,0,4)A A =-，1(3,2)A M =--，1(1,0,2)A N =--，(0,3,0)MN =-．设(,,)m x y z =为平面1A MA 的法向量，则110m A M m A A ⎧⋅=⎪⎨⋅=⎪⎩，所以320,40x z z ⎧-+-=⎪⎨-=⎪⎩．可取(3,1,0)m =．设(,,)n p q r =为平面1A MN 的法向量，则10,0n MN n A N ⎧⋅=⎪⎨⋅=⎪⎩．所以30,20q p r ⎧-=⎪⎨--=⎪⎩．可取(2,0,1)n =-．于是2315cos ,||||25m n m n m n ⋅〈〉===⨯， 所以二面角1A MA N --10．14答案及解析：答案：(1).由已知得//,//,AD BE CG BE 所以//AD CG ，故,AD CG 确定一个平面，从而,,,A C G D 四点共面．由已知得,AB BE AB BC ⊥⊥，故AB ⊥平面BCGE ． 又因为AB ⊂平面ABC ，所以平面ABC ⊥平面BCGE ．(2).作EH BC ⊥，垂足为H ．因为EH ⊂平面BCGE ，平面BCGE ⊥平面ABC ，所以EH ⊥平面ABC ．由已知，菱形BCGE 的边长为2，60EBC ∠=︒，可求得1,3BH EH ==． 以H 为坐标原点，HC 的方向为x 轴的正方向，建立如图所示的空间直角坐标系H xyz -，则(1,1,0)A -，(1,0,0)C ，3)G ，3)CG =，(2,1,0)AC =-． 设平面ACGD 的法向量为(,,)n x y z =，则0,0,CG n AC n ⎧⋅=⎪⎨⋅=⎪⎩即30,20.x z x y ⎧+=⎪⎨-=⎪⎩所以可取(3,6,3)n ． 又平面BCGE 的法向量可取为(0,1,0)m =，所以3cos ,||||n m n m n m ⋅〈〉==． 因此二面角B CG A --的大小为30︒．15答案及解析：答案：(1).由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ，故11B C BE ⊥．又1BE EC ⊥，所以BE ⊥平面11EB C ．(2).由(1)知190BEB ∠=︒．由题设知11Rt Rt ABE A B E ≅△△，所以45AEB ∠=︒， 故AE AB =，12AA AB =．以D 为坐标原点，DA 的方向为x 轴正方向，DA 为单位长，建立如图所示的空间直角坐标系D xyz -，则(0,1,0),(1,1,0),(0,1,2),(1,0,1),C B E 1(1,1,1),(0,0,2)CE CC =-=． 设平面EBC 的法向量为(,,)n x y x =，则00CB n CE n ⎧⋅=⎪⎨⋅=⎪⎩即0,0,x x y z =⎧⎨-+=⎩所以可取(0,1,1)n =--.设平面1ECC 的法向量为(,,)m x y z =，则10,0,CC m CE m ⎧⋅=⎪⎨⋅=⎪⎩即20,0.z x y z =⎧⎨-+=⎩所以可取(1,1,0)m =． 于是1cos ,2n mn m n m⋅<>==-． 所以，二面角1B EC C --3．。