窄带高斯随机过程的产生

一种窄带高斯白噪声的生成与实现方法窄带高斯白噪声是一种在频率范围较窄的情况下服从高斯分布的信号。

在通信系统中，窄带高斯白噪声经常用于模拟真实的通信环境以进行性能测试。

生成窄带高斯白噪声的一种简单方法是通过随机过程模拟。

下面将详细介绍生成与实现这种噪声的方法。

1.窄带高斯白噪声的特点：窄带高斯白噪声具有以下特点：-平稳性：在时间上是平稳的，即任意时刻的统计特性与时间无关。

-高斯性：噪声样本服从高斯分布，即符合正态分布。

-白噪声：在频率上是平坦的，即在所有频率上的功率谱密度相等。

2.实现窄带高斯白噪声的步骤：为了实现窄带高斯白噪声，我们可以按照以下步骤进行：-生成高斯分布的白噪声信号。

-通过一个窗函数将信号限制在指定的频带内。

接下来对每个步骤进行详细说明。

2.1.生成高斯分布的白噪声信号：生成服从高斯分布的白噪声信号可以通过伪随机数生成器来实现。

伪随机数生成器可以产生类似于高斯分布的随机数，我们可以利用这个特性来生成噪声信号。

生成随机数时需要注意选择合适的随机数生成算法，如Box-Muller变换等。

2.2.通过窗函数限制信号频带：生成的白噪声信号在频率上是平坦的，为了将其转换为窄带的噪声信号，我们需要通过一个窗函数来限制信号的频带。

常用的窗函数有矩形窗、汉宁窗、布莱克曼窗等。

矩形窗函数是一种简单的窗函数，它在指定的频带内给予信号全功率，在其他频带内给予信号零功率。

这样，只要我们选择一个合适的频带，并对生成的白噪声信号进行截断操作，就能获得窄带信号。

在Python中，我们可以使用NumPy和SciPy库中的函数来实现窄带高斯白噪声的生成。

以下是一个简单的示例代码：```pythonimport numpy as npfrom scipy.signal import windows#生成高斯白噪声信号#选择窗函数window = windows.hann(100)#对信号进行窗函数处理，限制在指定的频带内narrowband_noise = white_noise[:100] * window#打印信号的功率谱密度power_spectrum_density =np.abs(np.fft.fft(narrowband_noise))**2print(power_spectrum_density[:50]) # 前50个频率点的功率谱密度```总结：窄带高斯白噪声的生成与实现方法主要包括生成高斯分布的白噪声信号和通过窗函数限制信号频带。

计算机与信息工程学院综合性实验报告一、实验目的1、基于随机过程的莱斯表达式产生窄带随机过程。

2、掌握窄带随机过程的特性，包括均值（数学期望）、方差、概率密度函数、相关函数及功率谱密度等。

3、掌握窄带随机过程的分析方法。

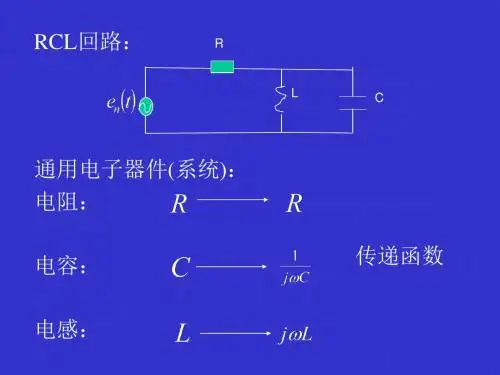
二、实验仪器或设备1、一台计算机2、MATLAB r2013a 三、实验内容及实验原理基于随机过程的莱斯表达式00()()cos ()sin y t a t t b t t ωω=- (3.1)实验过程框图如下：理想低通滤波器如图所示：图1 理想低通滤波器()20AH ∆ω⎧ω≤⎪ω=⎨⎪⎩其它(3.2) 设白噪声的物理谱0=X G N ω（）,则系统输出的物理谱为 220=()=20Y X N AG H G ∆ω⎧0≤ω≤⎪ωωω⎨⎪⎩（）（）其它(3.3) 输出的自相关函数为:01()()cos 2Y Y R G d τωωτωπ∞=⎰ /221cos 2N A d ωωτωπ∆=⎰ (3.4) 20sin 242N A ωτωωτπ∆∆=⋅∆ 可知输出的自相关函数()Y R τ是一个振荡函数。

计算高斯白噪声x(t)、限带白噪声()a t 、()b t 及窄带随机过程()y t 的均值，并绘出随机过程各个随机过程的自相关函数，功率谱密度图形。

四、MATLAB 实验程序function random(p,R,C) %产生一个p 个点的随机过程%--------------------------高斯窄带随机过程代码--------------------------% n=1:p;w=linspace(-pi,pi,p); wn=1/2*pi*R*C;[b,a]=butter(1,wn,'low'); %产生低通滤波器Xt=randn(1,p); %产生p 个点均值为0方差为1的随机数，即高斯白噪声 at=filter(b,a,Xt); %让高斯白噪声通过低通滤波器y_at=at.*cos(w.*n); %产生随机过程a（t）y_bt=at.*sin(w.*n); %产生随机过程b（t）yt=y_at-y_bt; %产生一个p个点的高斯窄带随机过程subplot(211)plot(yt)title('高斯窄带随机过程y(t)')subplot(212)pdf_ft=ksdensity(yt) ;plot(pdf_ft)title('y(t)的概率密度图')disp('均值如下')E_Xt=mean(y_at)E_at=mean(y_at)E_bt=mean(y_bt)E_ft=mean(yt)%-----------------------自相关函数代码如下--------------------------% figure(2)R_Xt=xcorr(Xt); %高斯白噪声X(t)的自相关函数R_at=xcorr(at); %限带白噪声的自相关函数R_y_at=xcorr(y_at); %随机过程a(t).coswt的自相关函数R_y_bt=xcorr(y_bt); %随机过程b(t).coswt的自相关函数R_ft=xcorr(yt);subplot(2,2,1);plot(R_Xt);title('高斯白噪声的自相关函数R_Xt'); %并绘制图形subplot(2,2,2)plot(R_at);title('限带白噪声的自相关函数R_a_bx'); %并绘制图形subplot(2,2,3)plot(R_y_bt);title('随机过程b(t)的自相关函数R_y_bt');subplot(2,2,4)plot(R_ft);title('高斯窄带随机过程y(t)的自相关函数R_yt');%------------------------功率谱密度代码如下---------------------------% figure(3)subplot(1,2,1)periodogram(Xt);title('高斯白噪声功率谱密度S_Xt');subplot(1,2,2)periodogram(at);title('限带白噪声功率谱密度S_a_bt');figure(4)subplot(3,1,1)periodogram(y_at);title('随机过程a(t).coswt概率密度概率密度S_y_at');subplot(3,1,2)periodogram(y_bt);title('随机过程b(t).sinwt功率谱密度S_y_bt');subplot(3,1,3);periodogram(yt);title('高斯窄带随机过程y(t)的功率谱密度S_yt');五、实验结果将上述random 函数放在Path 中后，在Commaod Window 中输入：random(1000,10,0.001)时，输出结果如下：01002003004005006007008009001000-0.50.5高斯窄带随机过程y(t)0102030405060708090100246y(t)的概率密度图0500100015002000-50005001000高斯白噪声的自相关函数R X t 0500100015002000-101020限带白噪声的自相关函数R ab x 0500100015002000-50510随机过程b(t)的自相关函数R yb t 0500100015002000-101020高斯窄带随机过程y(t)的自相关函数R y t00.51-40-30-20-10010Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )高斯白噪声功率谱密度S X t 00.51-80-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )限带白噪声功率谱密度S ab t0.10.20.30.40.50.60.70.80.91-80-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )随机过程a(t).coswt 概率密度概率密度S ya t00.10.20.30.40.50.60.70.80.91-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )随机过程b(t).sinwt 功率谱密度S yb t0.10.20.30.40.50.60.70.80.91-50-40-30-20-10Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )高斯窄带随机过程y(t)的功率谱密度S y t在Commaod Window 中输出的结果如下：E_Xt = 0.0020 E_at= 0.0020 E_bt= -0.0020 E_ft = 0.0040六、实验结果分析：1、由于高斯白噪声Xt是标准正态的，所以均值趋近于零，而at，bt是由Xt通过一个线性系统（低通滤波器）得到的，所以输出均值不变，仍为零，从程序运行结果可以看出，Xt，at，bt均值都趋近于零。

中山大学移动学院本科生实验报告（2015学年春季学期）课程名称：通信原理任课教师：刘洁 教学助理（TA ）：朱焱1、 实验要求1.产生窄带随机过程和其概率谱密度2.产生多个窄带随机过程3.求出窄带随机过程的均值和自相关函数2、 设计思路0sin(2)f t 00)()sin(2)f t b t f t对于第一个实验： 首先便是要搞懂如何产生一个窄带随机过程，按照TA 的提示，循序而进，从定义出发，获得答案。

按照上面的结构框图 ，由公式：t t b t t a t X 00sin )(cos )()(ωω-= 可以较为轻松的得到窄带随机过程（先产生高斯白噪声g =randn(1,1001)，产生低通[b,a] = butter(1,wn)的B/A 系数，由Y = filter （B ，A ,X ），得到a （t ）和 b （t ），之后zt = a(t)cos(wt) - b(t)sin(wt)，通过这个公式就容易了，再通过plot(zt);便可以得到窄带随机过程），后面的两个实验，是基于第一个实验来做的；对第二个实验： 加入for 循环，生成五个窄带随机过程，并且利用subplot 画小图。

对第三个实验： 产生窄带随机过程，利用函数mean 和xcorr 两个函数分别产生均值和自相关函数。

3、运行与测试Lab1：产生窄带随机过程和其概率谱密度在command命令框里写入：zhaidai，这是基于随机过程的莱斯表达式，产生一个1000个点的高斯窄带随机过程，和其概率谱密度（基本呈现正态分布）。

Lab2：产生多个窄带随机过程Subplot（5,2，x）让屏幕中有十个小图，分别为窄带随机过程，和其概率谱密度。

Lab3：求出窄带随机过程的均值和自相关函数分析：各个过程都是实的，中心点上相关程度最高，而且观察到：zt这个过程在中心点位置上有一个峰值，其他位置上，自相关函数会接近于零。

分析：以上是对两次窄带随机过程的均值，对于标准正态的，均值趋近于零，而at，bt是由标准正态通过一个线性系统得到的，所以输出均值不变，仍为零，从程序运行结果可以看出，均值u都趋近于零。

本科实验报告实验名称：窄带高斯随机过程的产生一、实验目的熟悉窄带随机过程的定义，了解窄带随机过程产生的原理与方法，最后估计实验产生的窄带随机过程的功率谱；掌握具有指定功率谱的随机过程产生方法，并以此产生窄带随机过程。

二、实验原理（一）窄带随机过程的产生原理窄带随机过程可以表示为下面的准正弦振荡的形式：cos X t A t ωτϕτ0()=()[+()]或者表示为同相分量与正交分量的合成：00cos sin c s X t A t t A t t ωω()=()-()其中c A t ()与s A t ()均为低频变化的随机过程，可以通过模拟其分布及功率谱特性来实现窄带随机过程的产生。

（二）用频域法模拟任意随机过程模拟一个时长为d T 的高斯随机过程的一个样本函数()X t , 要求功率谱密度满足指定的形式，先将()X t 进行周期性延拓，并做DFS()0201()j k k f kdX e f T X t π∞∞=-==∑% 若k X 是零均值的高斯随机变量，那么()X t %也是零均值的高斯随机过程。

若{}k X 是两两正交的序列()2220()(())k k k k X g f k G f E X f g δ=-∞∞=-=∑%即可以控制k g 得到期望的功率谱。

假定()(0)X G f B f =>，即()X G f 带限，则{}2k g 为有限项，对应的DFS系数{}k X 也为21M +项0()B M f ⎡⎤=⎢⎥⎣⎦，因此只需产生21M +个相互正交的零均值高斯随机变量{}101,,,,,,M M M M X X X X X --+-L L ，其方差为22()k k E X g =。

2k g 应与()0X G kf 成比例，即()20X k G g kf β=，则有()()220()MMMBX XBMk kk k MMk G f G kf df E X g β=-=-=--===∑∑⎰∑即()()BX B MXMk G f G df kf β=--=⎰∑ 产生步骤： i. 根据要求的时长d T 确定01d f T = ，根据功率谱的带宽确定0B M f = ii. 计算系数βiii.产生21M +个独立的高斯随机变量，()0(0,)(,1,,0,,1~,)k X N k M X M G M M kf β=--+-L Liv.构建时域样本函数[]()02()Mf k Mj i t k k X X i i t X e π∆=-=∆=∑（三）用时域滤波法模拟任意随机过程功率谱为1的白噪声通过线性系统，输出的是服从高斯分布的，且输出的功率谱为()()2X G f H f =，因此要产生功率谱为()X G f 的有色高斯噪声，只需设计一个滤波器即可，该滤波器的传递函数应满足()()X H f G f =三、实验内容模拟产生一段时长5ms 的窄带高斯随机过程()X t 的样本函数。

29 窄带实平稳高斯随机过程概述窄带实平稳随机过程的一维包络分布和一维相位分布窄带实平稳随机过程，它的同相分量和正交分量 一个时刻同相分量和正交分量是联合高斯的： 一个时刻包络和相位分量的联合概率密度：一个时刻包络和相位是相互统计独立的随机变量： 窄带实平稳随机过程的二维（两个时刻）包络和相位分布两个时刻信号的表达式：两个时刻同相分量和正交分量是联合高斯的： 两个时刻同相分量和正交分量的协方差矩阵：两个时刻同相分量和正交分量的联合概率密度函数： 两个时刻包络和相位的联合概率密度函数： 两个时刻包络的联合边缘分布：两个相距无穷远时刻的包络联合边缘分布： 一个时刻包络的边缘分布： 两个时刻相位的联合边缘分布：两个时刻相位和两个时刻包络的分布不是统计独立的：29.1 窄带实平稳随机过程的一维包络分布和一维相位分布 29.1.1 窄带实平稳随机过程，它的同相分量和正交分量tf t t f t t x t f t t f t t x c c s cc c πξπξπξπξ2cos )(ˆ2sin )()(2sin )(ˆ2cos )()(−=+=以及t f s t x t f t x t tf t x t f t x t cs c c c s c c ππξππξ2cos )(2sin )()(ˆ2sin )(2cos )()(−=+=因为窄带实平稳高斯随机过程的Hilbert 变换是一个高斯随机过程，它的同相分量与正交分量是它和它的Hilbert 变换的线性变换，同相分量和正交分量也是高斯过程。

上述高斯随机过程是联合高斯的。

29.1.2 一个时刻同相分量和正交分量是联合高斯的：同相分量和正交分量的一维相关矩阵，)(),(t x t x s c 的相关矩阵，⎟⎟⎠⎞⎜⎜⎝⎛=)0(00)0(ξξξξR R R 同相分量和正交分量的联合概率密度是，⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+−=⋅=22222exp 21)()(),(ξξσσπy x y f x f y x f s c s c x x x x 29.1.3 一个时刻包络和相位分量的联合概率密度：同相分量、正交分量与包洛和相位分量的关系是，)(sin )()()(cos )()(t t V t x t t V t x s c φφ⋅=⋅=以及，)()(tan)())(())(()(122t x t x t t x t x t V c s s c −=+=φ同相分量、正交分量到包洛和相位分量的变换行列式是，)()(cos )()(sin )()(sin )(cos ),(),(t V t t V t t V t t V x x s c =⎟⎟⎠⎞⎜⎜⎝⎛−=∂∂φφφφφ 一个时刻包洛和相位分量的联合概率密度是πφσσσσπφφξξξξφ21)(2exp 1)(2exp 21),(),(222222＝f r r r f r r y x f r r f V x x V s c ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧−=⎪⎭⎪⎫⎪⎩⎪⎨⎧−=⋅= 29.1.4 一个时刻包络和相位是相互统计独立的随机变量：)()(),(φφφφf r f r f V V ⋅=一维包洛分量的数字特征是：{}{}{}2222/12222ξξξσπσσπ⋅⎟⎠⎞⎜⎝⎛−==⎟⎠⎞⎜⎝⎛=V D V E V E29.2 窄带实平稳随机过程的二维包络和相位分布 29.2.1 两个时刻信号的表达式：两个时刻信号的同相分量和正交分量表达式11111111112cos )(2sin )()(ˆ2sin )(2cos )()(t f s t x t f t x t t f t x t f t x t c s c c c s c c ππξππξ−=+=22222222222cos )(2sin )()(ˆ2sin )(2cos )()(t f s t x t f t x t t f t x t f t x t c s c c c s c c ππξππξ−=+=两个时刻信号的包络和相位表达式)](2cos[)()(1111t t f t V t c φπξ+= )](2cos[)()(2222t t f t V t c φπξ+=两个时刻同相分量和正交分量是联合高斯的：由于ξ(t)是高斯分布的随机过程，而x c (t 1),x c (t 2),x s (t 1),x s (t 2)都是由ξ(t)经过线性变换得到的，它们是联合高斯分布的随机变量。

随机信号分析目录CONTENTSCONTENTS窄带高斯随机过程的产生窄带高斯随机过程包络的特性窄带高斯随机过程相位的特性小结窄带高斯随机过程的产生用宽带随机过程激励一个高频窄带线性系统，当滤波器的带宽远小于输入过程功率谱的带宽时，根据中心极限定理，滤波器输出端的随机过程可以认为是一个窄带高斯随机过程。

假设X(t)窄带平稳高斯实随机过程，具有零均值和方差。

将X(t)表示为准正弦振荡形式为2σ其中：))(cos()()(0t t t A t X ϕω+=——中心频率或称载波频率()A t ()t ϕ0ω——包络——初相位对任意给定的时刻，对其包络进行采样，得到，其一维概率密度为A t ⎩⎭⎨⎬=−≥⎧⎫σσf A A A A A t t t t 2()exp ,0222称为瑞利（Rayleigh ）概率密度函数，或简称瑞利分布。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）瑞利概率密度函数对任意给定的时刻对其相位进行采样，得到，其一维概率密度为ϕt =≤≤πϕϕπϕf t t 2(),021随机相位在区间内呈均匀分布。

π(0,2)且有，=ϕϕϕϕf A f A f A t t A t t (,)()()即在同一时刻，随机变量和相互独立，但不意味着随机过程和相互独立。

A t ϕt ϕt ()A t ()有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）窄带高斯随机过程包络的一维概率密度满足瑞利分布。

窄带高斯随机过程相位的一维概率密度满足均匀分布。

222()exp ,02tt A t t A A f A A σσ⎧⎫=−≥⎨⎬⎩⎭1(),022t t f ϕϕϕππ=≤≤在同一时刻，窄带高斯随机过程包络和相位的采样相互独立，但包络和相位不相互独立。