(完整版)高三复习专题函数的图像(含答案)

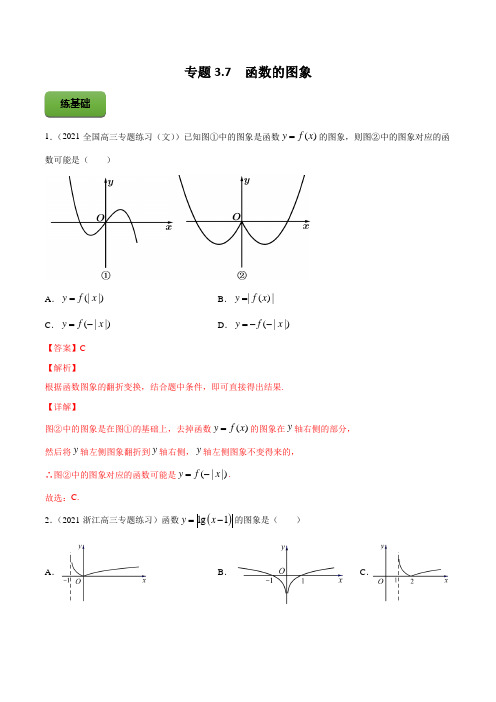
专题3.7 函数的图象1．（2021·全国高三专题练习（文））已知图①中的图象是函数()y f x=的图象，则图②中的图象对应的函数可能是（）A．(||)y f x=B．|()|y f x=C．(||)y f x=-D．(||)y f x=--【答案】C【解析】根据函数图象的翻折变换，结合题中条件，即可直接得出结果.【详解】图②中的图象是在图①的基础上，去掉函数()y f x=的图象在y轴右侧的部分，然后将y轴左侧图象翻折到y轴右侧，y轴左侧图象不变得来的，∴图②中的图象对应的函数可能是(||)y f x=-.故选：C.2．（2021·浙江高三专题练习）函数()lg1y x=-的图象是（）A．B．C．练基础D ．【答案】C【解析】将函数lg y x =的图象进行变换可得出函数()lg 1y x =-的图象，由此可得出合适的选项.【详解】将函数lg y x =的图象先向右平移1个单位长度，可得到函数()lg 1y x =-的图象，再将所得函数图象位于x 轴下方的图象关于x 轴翻折，位于x 轴上方图象不变，可得到函数()lg 1y x =-的图象.故合乎条件的图象为选项C 中的图象.故选：C.3．（2021·全国高三专题练习（理））我国著名数学家华罗庚先生曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔离分家万事休．”在数学的学习和研究中，经常用函数的图象来研究函数的性质，也经常用函数的解析式来研究函数图象的特征．若函数()y fx =在区间[],a b 上的图象如图，则函数()y f x =在区间[],a b 上的图象可能是（ ）A ．B ．C ．D ．【答案】D【解析】先判断出函数是偶函数，根据偶函数的图像特征可得选项．【详解】 函数()y f x =是偶函数，所以它的图象是由()y f x =把0x ≥的图象保留，再关于y 轴对称得到的．结合选项可知选项D 正确，故选：D ．4．（2021·全国高三专题练习（文））函数()5xf x x x e =-⋅的图象大致是（ ）． A ． B ．C ．D ．【答案】B【解析】由()20f >和()20f -<可排除ACD ，从而得到选项.【详解】由()()2223222160f e e =-=->，可排除AD ；由()()2223222160f e e ---=-+=-<，可排除C ；故选：B.5．（2021·陕西高三三模（理））函数x y b a =⋅与()log a y bx =的图像在同一坐标系中可能是（）A ．B ．C ．D ．【答案】C【解析】根据指数函数和对数函数的单调性，以及特殊点函数值的范围逐一判断可得选项．【详解】令x f x b a ，()()log a g x bx =，对于A 选项：由x f xb a 得>1a ，且()00>1f b a b ==⋅，所以log >0a b ，而()1log 0a g b =<，所以矛盾，故A 不正确；对于B 选项：由x f xb a 得>1a ，且()001f b a b ⋅=<=，所以log 0a b <，而()1log >0a g b =，所以矛盾，故B 不正确；对于C 选项：由x f xb a 得>1a ，且()001f b a b ⋅=<=，所以log 0a b <，又()1log 0a g b =<，故C 正确；对于D 选项：由x f xb a 得>1a ，且()00>1f b a b ==⋅，而()()log a g x bx =中01a <<，所以矛盾，故D 不正确；故选：C ． 6．（2021·宁夏吴忠市·高三其他模拟（文））已知函数()()()ln 2ln 4f x x x =-+-，则（ ）． A ．()f x 的图象关于直线3x =对称B ．()f x 的图象关于点()3,0对称C ．()f x 在()2,4上单调递增D ．()f x 在()2,4上单调递减【答案】A【解析】先求出函数的定义域.A ：根据函数图象关于直线对称的性质进行判断即可；B ：根据函数图象关于点对称的性质进行判断即可；C ：根据对数的运算性质，结合对数型函数的单调性进行判断即可；D ：结合C 的分析进行判断即可.【详解】 ()f x 的定义域为()2,4x ∈，A ：因为()()()()3ln 1ln 13f x x x f x +=++-=-，所以函数()f x 的图象关于3x =对称，因此本选项正确；B ：由A 知()()33f x f x +≠--，所以()f x 的图象不关于点()3,0对称，因此本选项不正确；C ：()()()2ln 2ln 4ln(68)x x x f x x =-+-=-+- 函数2268(3)1y x x x =-+-=--+在()2,3x ∈时，单调递增， 在()3,4x ∈时，单调递减，因此函数()f x 在()2,3x ∈时单调递增，在()3,4x ∈时单调递减，故本选项不正确；D ：由C 的分析可知本选项不正确，故选：A7．（2021·安徽高三二模（理））函数()n xf x x a =，其中1a >，1n >，n 为奇数，其图象大致为（ ） A ． B ．C ．D ．【答案】B【解析】分析()f x 在()0,∞+、(),0-∞上的函数值符号，及该函数在()0,∞+上的单调性，结合排除法可得出合适的选项.【详解】对任意x ∈R ，0x a >，由于1n >，n 为奇数，当0x <时，0n x <，此时()0f x <，当0x >时，0n x >，此时()0f x >，排除AC 选项；当0x >时，任取1x 、()20,x ∈+∞且12x x >，则120x x a a >>，120n n x x >>，所以()()12f x f x >，所以，函数()f x 在()0,∞+上为增函数，排除D 选项.故选：B.8．（2021·浙江高三专题练习）已知函数f (x )＝1331,,log 1x x x x ⎧≤⎪⎨>⎪⎩则函数y ＝f (1－x )的大致图象是（ ） A ． B ．C ．D ．【答案】D【解析】由()f x 得到()1f x -的解析式，根据函数的特殊点和正负判断即可.【详解】因为函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩， 所以函数()1f x -()1133,0log 1,0x x x x -⎧≥⎪=⎨-<⎪⎩， 当x ＝0时，y ＝f (1)＝3，即y ＝f (1－x )的图象过点(0，3)，排除A ；当x ＝－2时，y ＝f (3)＝－1，即y ＝f (1－x )的图象过点(－2，－1)，排除B ；当0x <时，()1311,(1)log 10x f x x ->-=-<，排除C ，故选：D ．9.【多选题】（2021·浙江高一期末）如图，某池塘里浮萍的面积y （单位：2m ）与时间t （单位：月）的关系为t y a =．关于下列法正确的是（ ）A ．浮萍每月的增长率为2B ．浮萍每月增加的面积都相等C ．第4个月时，浮萍面积不超过280mD ．若浮萍蔓延到22m 、24m 、28m 所经过的时间分别是1t 、2t 、3t ，则2132t t t =+【答案】AD【解析】根据图象过点求出函数解析式，根据四个选项利用解析式进行计算可得答案.【详解】由图象可知，函数图象过点(1,3)，所以3a =，所以函数解析式为3ty =， 所以浮萍每月的增长率为13323233t t tt t +-⨯==，故选项A 正确； 浮萍第一个月增加的面积为10332-=平方米，第二个月增加的面积为21336-=平方米，故选项B 不正确；第四个月时，浮萍面积为438180=>平方米，故C 不正确；由题意得132t =，234t =，338t =，所以13log 2t =，23log 4t =，33log 8t =，所以2133333332log 2log 8log (28)log 16log 42log 42t t t +=+=⨯====，故D 正确.故选：AD10．（2020·全国高一单元测试）函数()2x f x =和()3g x x =的图象如图所示，设两函数的图象交于点11(,)A x y ，22(,)B x y ，且12x x <．（1）请指出图中曲线1C ，2C 分别对应的函数；（2）结合函数图象，比较(3)f ，(3)g ，(2020)f ，(2020)g 的大小．【答案】（1）1C 对应的函数为()3g x x =，2C 对应的函数为()2x f x =；（2）(2020)(2020)(3)(3)f g g f >>>．【解析】（1）根据指数函数和一次函数的函数性质解题；（2）结合函数的单调性及增长快慢进行比较.【详解】（1）1C 对应的函数为()3g x x =，2C 对应的函数为()2x f x =．（2）(0)1f =，(0)0g =，(0)(0)f g ∴>，又(1)2f =，(1)3g =，(1)(1)f g ∴<，()10,1x ∴∈；(3)8f =，(3)9g =，(3)(3)f g ∴<，又(4)16f =，(4)12g =，(4)(4)f g ∴>，()23,4x ∴∈．当2x x >时，()()f x g x >，(2020)(2020)f g ∴>．(2020)(2020)(3)(3)f g g f ∴>>>．1．（2021·湖南株洲市·高三二模）若函数()2()mx f x e n =-的大致图象如图所示，则（ ）A ．0,01m n ><<B ．0,1m n >>C ．0,01m n <<<D ．0,1m n <>【答案】B【解析】令()0f x =得到1ln x n m =，再根据函数图象与x 轴的交点和函数的单调性判断.【详解】令()0f x =得mx e n =，即ln mx n =，解得1ln x n m =，由图象知1l 0n x m n =>，当0m >时，1n >，当0m <时，01n <<，故排除AD ，当0m <时，易知mx y e =是减函数，当x →+∞时，0y →，()2f x n →，故排除C故选：B2．（2021·甘肃高三二模（理））关于函数()ln |1|ln |1|f x x x =++-有下列结论，正确的是（ ） A ．函数()f x 的图象关于原点对称 B ．函数()f x 的图象关于直线1x =对称 练提升C ．函数()f x 的最小值为0D ．函数()f x 的增区间为(1,0)-，(1,)+∞【答案】D 【解析】A.由函数的奇偶性判断；B.利用特殊值判断；C.利用对数函数的值域求解判断；D.利用复合函数的单调性判断. 【详解】2()ln |1|ln |1|ln |1|f x x x x =++-=-，由1010x x ⎧+>⎪⎨->⎪⎩，解得1x ≠±，所以函数的定义域为{}|1x x ≠±， 因为()ln |1|ln |1|ln |1|ln |1|()f x x x x x f x -=-++--=++-=,所以函数为偶函数，故A 错误. 因为(0)ln |1|0,(3)ln8f f =-==，所以(0)(3)f f ≠，故B 错误；因为 ()2|1|0,x -∈+∞，所以()f x ∈R ，故C 错误；令2|1|t x =-，如图所示：，t 在(),1,[0,1)-∞-上递减，在()(1,0],1,-+∞上递增，又ln y t =在()0,∞+递增，所以函数()f x 的增区间为(1,0)-，(1,)+∞，故D 正确； 故选：D3．（2021·吉林长春市·东北师大附中高三其他模拟（理））函数ln xy x=的图象大致为（ ）A ．B ．C ．D ．【答案】C 【解析】 求出函数ln xy x=的定义域，利用导数分析函数的单调性，结合排除法可得出合适的选项. 【详解】 对于函数ln xy x =，则有0ln 0x x >⎧⎨≠⎩，解得0x >且1x ≠， 所以，函数ln xy x=的定义域为()()0,11,+∞，排除AB 选项；对函数ln x y x =求导得()2ln 1ln x y x -'=.当01x <<或1x e <<时，0y '<；当x e >时，0y '>. 所以，函数ln xy x=的单调递减区间为()0,1、()1,e ，单调递增区间为(),e +∞， 当01x <<时，0ln xy x =<，当1x >时，0ln x y x=>，排除D 选项. 故选：C.4．（2021·海原县第一中学高三二模（文））函数2xx xy e+=的大致图象是（ ）A ．B ．C ．D ．【答案】D 【解析】利用导数可求得2xx xy e+=的单调性，由此排除AB ；根据0x >时，0y >可排除C ，由此得到结果. 【详解】 由题意得：()()222211x xxxx e x x e x x y e e +-+-++'==，令0y '=，解得：1x =，2x =，∴当11,,22x ∞∞⎛⎛⎫+∈-⋃+ ⎪ ⎪⎝⎭⎝⎭时，0y '<；当11,22x ⎛+∈ ⎝⎭时，0y '>；2x x x y e +∴=在1,2⎛--∞ ⎝⎭，1,2⎛⎫++∞ ⎪ ⎪⎝⎭上单调递减，在1122⎛⎫-+ ⎪ ⎪⎝⎭上单调递增，可排除AB ； 当0x >时，0y >恒成立，可排除C. 故选：D.5．（2021·天津高三三模）意大利画家列奥纳多·达·芬奇的画作《抱银鼠的女子》（如图所示）中，女士颈部的黑色珍珠项链与她怀中的白貂形成对比.光线和阴影衬托出人物的优雅和柔美.达·芬奇提出：固定项链的两端，使其在重力的作用下自然下垂，形成的曲线是什么？这就是著名的“悬链线问题”.后人研究得出，悬链线并不是抛物线，而是与解析式为2x x e e y -+=的“双曲余弦函数”相关.下列选项为“双曲余弦函数”图象的是（ ）A ．B ．C ．D ．【答案】C 【解析】分析函数2x xe e y -+=的奇偶性与最小值，由此可得出合适的选项.【详解】令()e e 2x x f x -+=，则该函数的定义域为R ，()()2x xe ef x f x -+-==，所以，函数()e e 2x xf x -+=为偶函数，排除B 选项.由基本不等式可得()112f x ≥⨯=，当且仅当0x =时，等号成立，所以，函数()f x 的最小值为()()min 01f x f ==，排除AD 选项. 故选：C.6．（2021·浙江高三月考）函数()3log 01a y x ax a =-<<的图象可能是（ ）A ．B ．C ．D ．【答案】B 【解析】先求出函数的定义域，判断函数的奇偶性，构造函数，求函数的导数，利用是的导数和极值符号进行判断即可. 【详解】根据题意，()3log a f x x ax =-，必有30x ax -≠，则0x ≠且x ≠即函数的定义域为{|0x x ≠且x ≠，()()()()33log log a a x a x x f f x ax x ---=--==，则函数3log a y x ax =-为偶函数，排除D ，设()3g x x ax =-，其导数()23g x x a '=-，由()0g x '=得x =±，当3x >时，()0g x '>，()g x 为增函数，而()f x 为减函数，排除C ，在区间,33⎛⎫- ⎪ ⎪⎝⎭上，()0g x '<，则()g x 在区间,33⎛⎫- ⎪ ⎪⎝⎭上为减函数，在区间3⎛⎫+∞ ⎪ ⎪⎝⎭上，()0g x '>，则()g x 在区间3⎛⎫+∞ ⎪ ⎪⎝⎭上为增函数，0g=，则()g x 存在极小值33339g a ⎛⎛⎫=-⨯=- ⎪ ⎪⎝⎭⎝⎭，此时()g x ()0,1，此时()0f x >，排除A ， 故选：B.7.（2019·北京高三高考模拟（文））当x∈[0，1]时，下列关于函数y=2(1)mx -的图象与y =的图象交点个数说法正确的是（ ） A ．当[]m 0,1∈时，有两个交点 B ．当(]m 1,2∈时，没有交点 C ．当(]m 2,3∈时，有且只有一个交点 D ．当()m 3,∞∈+时，有两个交点【答案】B 【解析】设f （x ）=2(1)mx -，g （x ） ，其中x∈[0，1]A ．若m=0，则()1f x =与()g x =[0，1]上只有一个交点(1,1)，故A 错误．B ．当m∈（1，2）时，111()(0)1,()(0)1()()2f x f g x g f x g x m<<∴≤=≥=>∴<即当m∈（1，2]时，函数y=2(1)mx -的图象与y =x∈[0，1]无交点，故B 正确，C ．当m∈（2，3]时，2111()(1)(1),()(1)32f x f mg x g m <<∴≤=-≤=2(1)m >-时()()f x g x <，此时无交点，即C 不一定正确．D ．当m∈（3，+∞）时，g （0）1，此时f （1）＞g （1），此时两个函数图象只有一个交点，故D 错误，故选：B．8.（2021·浙江高三专题练习）若关于x的不等式34log2xax-≤在10,2x⎛⎤∈ ⎥⎝⎦恒成立，则实数a的取值范围是（）A．1,14⎡⎫⎪⎢⎣⎭B．10,4⎛⎤⎥⎝⎦C．3,14⎡⎫⎪⎢⎣⎭D．30,4⎛⎤⎥⎝⎦【答案】A 【解析】转化为当10,2x⎛⎤∈ ⎥⎝⎦时，函数342xy=-的图象不在log ay x=的图象的上方，根据图象列式可解得结果.【详解】由题意知关于x的不等式34log2xax-≤在10,2x⎛⎤∈ ⎥⎝⎦恒成立，所以当10,2x⎛⎤∈ ⎥⎝⎦时，函数342xy=-的图象不在log ay x=的图象的上方，由图可知0111log 22a a <<⎧⎪⎨≥⎪⎩，解得114a ≤<. 故选：A9.对a 、b ∈R ，记{},max ,,a a b a b b a b⎧=⎨<⎩≥，函数{}2()max ||,24()f x x x x x =--+∈R ．（1）求(0)f ，(4)f -．（2）写出函数()f x 的解析式，并作出图像．（3）若关于x 的方程()f x m =有且仅有3个不等的解，求实数m 的取值范围．（只需写出结论） 【答案】见解析．【解析】解：（1）∵{},max ,,a a b a b b a b⎧=⎨<⎩≥，函数{}2()max ||,24f x x x x =--+，∴{}(0)max 0,44f ==，{}(4)max 4,44f -=-=．（2）（3）5m =或m 10．（2021·全国高一课时练习）函数()2xf x =和()()30g x xx =≥的图象，如图所示．设两函数的图象交于点()11A x y ，，()22B x y ，，且12x x <．（1）请指出示意图中曲线1C ，2C 分别对应哪一个函数；（2）结合函数图象，比较()8f ，()8g ，()2015f ，()2015g 的大小． 【答案】（1）1C 对应的函数为()()30g x xx =≥，2C 对应的函数为()2x f x =；（2）()()()()2015201588f g g f >>>．【解析】（1）根据图象可得结果；（2）通过计算可知1282015x x <<<，再结合题中的图象和()g x 在()0+∞，上的单调性，可比较()8f ，()8g ，()2015f ，()2015g 的大小.【详解】（1）由图可知，1C 的图象过原点，所以1C 对应的函数为()()30g x xx =≥，2C 对应的函数为()2x f x =．（2）因为11g =（），12f =（），28g =（），24f =（），()9729g =，()9512f =，()101000g =，()101024f =，所以11f g >（）（），22f g <（）（），()()99f g <，()()1010f g >．所以112x <<，2910x <<．所以1282015x x <<<．从题中图象上知，当12x x x <<时，()()f x g x <；当2x x >时，()()f x g x >，且()g x 在()0+∞，上是增函数，所以()()()()2015201588f g g f >>>．1. （2020·天津高考真题）函数241xy x =+的图象大致为（ ） 练真题A ．B ．C ．D ．【答案】A 【解析】由函数的解析式可得：()()241xf x f x x --==-+，则函数()f x 为奇函数，其图象关于坐标原点对称，选项CD 错误； 当1x =时，42011y ==>+，选项B 错误. 故选：A.2.（2019年高考全国Ⅲ卷理）函数3222x xx y -=+在[]6,6-的图像大致为（ ） A ． B ．C ．D ．【答案】B【解析】设32()22x xx y f x -==+，则332()2()()2222x x x x x x f x f x ----==-=-++，所以()f x 是奇函数，图象关于原点成中心对称，排除选项C ．又34424(4)0,22f -⨯=>+排除选项D ； 36626(6)722f -⨯=≈+，排除选项A ， 故选B ．3.（2020·天津高考真题）已知函数3,0,(),0.x x f x x x ⎧=⎨-<⎩若函数2()()2()g x f x kx xk =--∈R 恰有4个零点，则k 的取值范围是（ ） A ．1,(22,)2⎛⎫-∞-+∞ ⎪⎝⎭B ．1,(0,22)2⎛⎫-∞- ⎪⎝⎭C ．(,0)(0,22)-∞D ．(,0)(22,)-∞+∞【答案】D 【解析】注意到(0)0g =，所以要使()g x 恰有4个零点，只需方程()|2|||f x kx x -=恰有3个实根 即可， 令()h x =()||f x x ，即|2|y kx =-与()()||f x h x x =的图象有3个不同交点. 因为2,0()()1,0x x f x h x x x ⎧>==⎨<⎩， 当0k =时，此时2y =，如图1，2y =与()()||f x h x x =有2个不同交点，不满足题意； 当k 0<时，如图2，此时|2|y kx =-与()()||f x h x x =恒有3个不同交点，满足题意； 当0k >时，如图3，当2y kx =-与2yx 相切时，联立方程得220x kx -+=，令0∆=得280k -=，解得k =，所以k >综上，k 的取值范围为(,0)(22,)-∞+∞.故选：D.4.（2019年高考全国Ⅱ卷理）设函数()f x 的定义域为R ，满足(1) 2 ()f x f x +=，且当(0,1]x ∈时，()(1)f x x x =-．若对任意(,]x m ∈-∞，都有8()9f x ≥-，则m 的取值范围是A ．9,4⎛⎤-∞ ⎥⎝⎦B ．7,3⎛⎤-∞ ⎥⎝⎦C ．5,2⎛⎤-∞ ⎥⎝⎦D ．8,3⎛⎤-∞ ⎥⎝⎦【答案】B【解析】∵(1) 2 ()f x f x +=，()2(1)f x f x ∴=-． ∵(0,1]x ∈时，1()(1)[,0]4f x x x =-∈-；∴(1,2]x ∈时，1(0,1]x -∈，1()2(1)2(1)(2),02f x f x x x ⎡⎤=-=--∈-⎢⎥⎣⎦； ∴(2,3]x ∈时，1(1,2]x -∈，()2(1)4(2)(3)[1,0]f x f x x x =-=--∈-，如图：当(2,3]x ∈时，由84(2)(3)9x x --=-解得173x =，283x =，若对任意(,]x m ∈-∞，都有8()9f x ≥-，则73m ≤.则m 的取值范围是7,3⎛⎤-∞ ⎥⎝⎦.故选B.5.（2017·天津高考真题（文））已知函数f(x)={|x|+2,x <1x +2x ,x ≥1．设a ∈R ，若关于x 的不等式f(x)≥|x 2+a|在R 上恒成立，则a 的取值范围是 A ．[−2,2] B ．[−2√3,2] C ．[−2,2√3] D ．[−2√3,2√3] 【答案】A【解析】满足题意时f (x )的图象恒不在函数y =|x2+a|下方，当a =2√3时，函数图象如图所示，排除C,D 选项；当a =−2√3时，函数图象如图所示，排除B 选项，本题选择A 选项.6.（2018·全国高考真题（文））设函数()2010x x f x x -⎧≤=⎨>⎩，，，则满足()()12f x f x +<的x 的取值范围是（ ）A ．(]1-∞-，B ．()0+∞，C ．()10-，D ．()0-∞，【答案】D 【解析】分析：首先根据题中所给的函数解析式，将函数图像画出来，从图中可以发现若有()()12f x f x +<成立，一定会有2021x x x <⎧⎨<+⎩，从而求得结果.详解：将函数()f x 的图像画出来，观察图像可知会有2021x x x <⎧⎨<+⎩，解得0x <，所以满足()()12f x f x +<的x 的取值范围是()0-∞，，故选D .。

专题2 三角函数的图象和性质【老师预测】（1） 三角函数的图象和性质是历年高考中的必考知识点，在高考中，客观题和解答题均会出现，大多以中、低档题为主，主要集中考查三角函数的周期、图象、单调性、值域或最值几个方面，解决此类问题，要求学生熟练地掌握三角函数的图象及其性质，避免失分。

（2）函数sin()y A x ωϕ=+的图象和性质是高考中的必考知识点，在高考中，主要集中考查图象之间的平移伸缩变换、由图象求函数解析式以及利用正余弦型函数解决实际问题为主，常与三角函数的性质、三角恒等变换、向量结合起来综合考查，需多加强数形结合思想的应用意识。

【知识精讲】一、用五点法作正弦函数和余弦函数的简图正弦函数y ＝sin x ，x ∈[0,2π]的图象上，五个关键点是：(0,0)，⎝⎛⎭⎫π2，1，(π，0)，⎝⎛⎭⎫3π2，－1，(2π，0)． 余弦函数y ＝cos x ，x ∈[0,2π]的图象上，五个关键点是：(0,1)，⎝⎛⎭⎫π2，0，(π，－1)，⎝⎛⎭⎫3π2，0，(2π，1)． 二、正弦函数sin y x =,余弦函数cos y x =,正切函数tan y x =的图象与性质三、函数sin()y A x ωϕ=+的图象与性质 1．函数sin()y A x ωϕ=+的图象的画法与变换 （1）变换作图法由函数sin y x =的图象通过变换得到sin()y A x ωϕ=+（A >0,ω>0）的图象，有两种主要途径：“先平移后伸缩”与“先伸缩后平移”.如下图.（2）五点作图法找五个关键点，分别为使y 取得最小值、最大值的点和曲线与x 轴的交点.其步骤为： ①先确定最小正周期T =2ωπ,在一个周期内作出图象；②令=X x ωϕ+,令X 分别取0，2π,π,322ππ,,求出对应的x 值，列表如下：由此可得五个关键点；③描点画图，再利用函数的周期性把所得简图向左右分别扩展，从而得到sin()y A x ωϕ=+的简图. 2．函数sin()y A x ωϕ=+（A >0,ω>0）的性质（1）奇偶性：=k ϕπ时，函数sin()y A x ωϕ=+为奇函数；=2k ϕππ+时，函数sin()y A x ωϕ=+为偶函数.（2）周期性：sin()y A x ωϕ=+存在周期性，其最小正周期为T =2ωπ.（3）单调性：根据y =sin t 和t =x ωϕ+的单调性来研究，由+22,22k x k k ωϕππ-π≤+≤+π∈Z 得单调增区间；由+22,22k x k k ωϕπ3ππ≤+≤+π∈Z 得单调减区间. （4）对称性：利用y =sin x 的对称中心为(,0)()k k π∈Z 求解，令x k k ωϕ+=π(∈)Ζ，求得x .利用y =sin x 的对称轴为()2x k k π=π+∈Z 求解，令+2x k k ωϕπ+=π(∈)Ζ，得其对称轴. 3．函数sin()y A x ωϕ=+（A >0,ω>0）的物理意义当函数sin()y A x ωϕ=+（A >0,ω>0,[0,)x ∈+∞）表示一个简谐振动量时，则A 叫做振幅，T =2ωπ叫做周期，f =12πT ω=叫做频率,x ωϕ+叫做相位，x =0时的相位ϕ叫做初相. 【典例精练】考点一 三角函数的定义域例1．函数y ＝tan ⎝⎛⎭⎫2x －π4的定义域为________________． 【解析】由2x －π4≠k π＋π2，k ∈Z ，得x ≠k π2＋3π8，k ∈Z ，故所求定义域为⎩⎨⎧x ⎪⎪⎭⎬⎫x ≠k π2＋3π8，k ∈Z . 故答案为：⎩⎨⎧x ⎪⎪⎭⎬⎫x ≠k π2＋3π8，k ∈Z 例2．求函数y ＝lg(sin 2x )＋9－x 2的定义域．【解析】由⎩⎪⎨⎪⎧sin 2x ＞0，9－x 2≥0，得⎩⎪⎨⎪⎧k π＜x ＜k π＋π2，k ∈Z ，－3≤x ≤3.∴－3≤x ＜－π2或0＜x ＜π2.∴函数y ＝lg(sin 2x )＋9－x 2的定义域为⎣⎡⎭⎫－3，－π2∪⎝⎛⎭⎫0，π2. 【方法点睛】(1)应用正切函数y ＝tan x 的定义域求函数y ＝A tan(ωx ＋φ)的定义域，要注意本身的要求； (2)求复杂函数的定义域时转化为求解简单的三角不等式． 考点二 三角函数的值域或最值例3．．已知函数f (x )＝sin ⎝⎛⎭⎫x ＋π6，其中x ∈⎣⎡⎦⎤－π3，a ，若f (x )的值域是⎣⎡⎦⎤－12，1，则实数a 的取值范围是________．【解析】由x ∈⎣⎡⎦⎤－π3，a ，知x ＋π6∈⎣⎡⎦⎤－π6，a ＋π6. ∵x ＋π6∈⎣⎡⎦⎤－π6，π2时，f (x )的值域为⎣⎡⎦⎤－12，1， ∴由函数的图象知π2≤a ＋π6≤7π6，所以π3≤a ≤π.故答案为：⎣⎡⎦⎤π3，π例4．求函数y ＝cos 2x ＋sin x ⎝⎛⎭⎫|x |≤π4的最大值与最小值．【解析】令t ＝sin x . ∵|x |≤π4∴t ∈⎣⎡⎦⎤－22，22. ∴y ＝－t 2＋t ＋1＝－⎝⎛⎭⎫t －122＋54， ∴当t ＝12时，y max ＝54，当t ＝－22时，y min ＝1－22.∴函数y ＝cos 2x ＋sin x ⎝⎛⎭⎫|x |≤π4的最大值为54，最小值为1－22. 【方法点睛】三角函数值域或最值的3种求法 (1)直接法：直接利用sin x 和cos x 的值域求解；(2)化一法：把所给三角函数化为y ＝A sin(ωx ＋φ)＋k 的形式，由正弦函数单调性写出函数的值域； (3)换元法：把sin x 、cos x 、sin x cos x 或sin x ±cos x 换成t ，转化为二次函数来求． 考点三 三角函数的图象与性质例5．若函数f (x )＝sin ⎝⎛⎭⎫12x ＋θ－3cos ⎝⎛⎭⎫12x ＋θ⎝⎛⎭⎫|θ|＜π2的图象关于原点对称，则角θ＝________. 【解析】∵f (x )＝2sin ⎝⎛⎭⎫12x ＋θ－π3，且f (x )的图象关于原点对称 ∴f (0)＝2sin ⎝⎛⎭⎫θ－π3＝0，即sin ⎝⎛⎭⎫θ－π3＝0 ∴θ－π3＝k π(k ∈Z)，即θ＝π3＋k π(k ∈Z)．又|θ|＜π2∴θ＝π3.故答案为：π3例6．已知f (x )＝2sin ⎝⎛⎭⎫x ＋π4，x ∈[0，π]，则f (x )的单调递增区间为________． 【解析】由－π2＋2k π≤x ＋π4≤π2＋2k π，k ∈Z ，得－3π4＋2k π≤x ≤π4＋2k π，k ∈Z.又∵x ∈[0，π]∴f (x )的单调递增区间为⎣⎡⎦⎤0，π4. 故答案为：⎣⎡⎦⎤0，π4 例7．若函数f (x )＝sin ωx (ω＞0)在区间⎣⎡⎦⎤0，π3上单调递增，在区间⎣⎡⎦⎤π3，π2上单调递减，则ω＝________. 【解析】∵f (x )＝sin ωx (ω＞0)过原点∴当0≤ωx ≤π2，即0≤x ≤π2ω时，y ＝sin ωx 是增函数；当π2≤ωx ≤3π2，即π2ω≤x ≤3π2ω时，y ＝sin ωx 是减函数． 由f (x )＝sin ωx (ω＞0)在⎣⎡⎦⎤0，π3上单调递增，在⎣⎡⎦⎤π3，π2上单调递减知，π2ω＝π3. ∴ω＝32.故答案为：32【方法点睛】1．函数f (x )＝A sin(ωx ＋φ)的奇偶性、周期性和对称性(1)若f (x )＝A sin(ωx ＋φ)为偶函数，则当x ＝0时，f (x )取得最大或最小值；若f (x )＝A sin(ωx ＋φ)为奇函数，则当x ＝0时，f (x )＝0.(2)对于函数y ＝A sin(ωx ＋φ)，其对称轴一定经过图象的最高点或最低点，对称中心一定是函数的零点，因此在判断直线x ＝x 0或点(x 0,0)是否是函数的对称轴或对称中心时，可通过检验f (x 0)的值进行判断．2．求三角函数单调区间的2种方法(1)代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个角u (或t )，利用基本三角函数的单调性列不等式求解．(2)图象法：画出三角函数的正、余弦曲线，结合图象求它的单调区间． 考点四 函数y ＝A sin(ωx ＋φ)的图象与变换例8．将函数y ＝sin(2x ＋φ)(0＜φ＜π)的图象沿x 轴向左平移π8个单位长度，得到函数y ＝f (x )的图象，若函数y ＝f (x )的图象过原点，则φ＝________.【解析】由题意可得f (x )＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π8＋φ＝sin ⎝⎛⎭⎫2x ＋π4＋φ，因为函数y ＝f (x )的图象过原点，所以sin ⎝⎛⎭⎫π4＋φ＝0，所以π4＋φ＝k π(k ∈Z)，即φ＝k π－π4(k ∈Z)，又因为0＜φ＜π，所以φ＝3π4. 故答案为：3π4.例9．将函数y ＝3sin ⎝⎛⎭⎫2x ＋π3的图象向右平移φ⎝⎛⎭⎫0＜φ＜π2个单位长度后，所得函数为偶函数，则φ＝________.【解析】将函数y ＝3sin ⎝⎛⎭⎫2x ＋π3的图象向右平移φ个单位长度后，所得函数为 3sin 2()3y x πϕ⎡⎤=-+⎢⎥⎣⎦ 3sin ⎝⎛⎭⎫2x ＋π3－2φ. ∵所得的函数为偶函数∴π3－2φ＝k π＋π2(k ∈Z)，解得φ＝－k π2－π12(k ∈Z) ∵0＜φ＜π2∴k ＝－1，得φ＝5π12.故答案为：5π12.【方法点睛】函数y ＝A sin(ωx ＋φ)(A ＞0，ω＞0)的图象的两种作法【注】 平移变换和伸缩变换都是针对x 而言，即x 本身加减多少值，而不是依赖于ωx 加减多少值． 考点五 求函数y ＝A sin(ωx ＋φ)的解析式例10．已知函数f (x )＝A sin(ωx ＋φ)的部分图象如图所示，则f ⎝⎛⎭⎫π2＝________.【解析】由题图知A ＝1，T 2＝π3－⎝⎛⎭⎫－π6＝π2，所以T ＝π＝2πω，得ω＝2，又f ⎝⎛⎭⎫π3＝sin ⎝⎛⎭⎫2π3＋φ＝0，所以φ＝－2π3＋2k π(k ∈Z)或φ＝π3＋2k π(k ∈Z)(舍去，因为f (0)＜0)，所以f (x )＝sin ⎝⎛⎭⎫2x －2π3，故f ⎝⎛⎭⎫π2＝sin ⎝⎛⎭⎫π－2π3＝32. 故答案为：32. 例11．设函数y ＝sin ⎝⎛⎭⎫ωx ＋π3(0＜x ＜π)，当且仅当x ＝π12时，y 取得最大值，则正数ω的值为______． 【解析】∵0＜x ＜π，ω＞0 ∴ωx ＋π3∈⎝⎛⎭⎫π3，ωπ＋π3， 又∵函数当且仅当x ＝π12时取得最大值∴⎩⎨⎧ωπ＋π3≤5π2，πω12＋π3＝π2，解得ω＝2.故答案为：2.【方法点睛】确定y ＝A sin(ωx ＋φ)＋b (A ＞0，ω＞0)中参数的方法（1）求A ，b ：确定函数的最大值M 和最小值m ，则A ＝M －m 2，b ＝M ＋m2；（2）求ω：确定函数的周期T ，则可得ω＝2πT ；（3）求φ：常用的方法有：①代入法：把图象上的一个已知点代入(此时A ，ω，b 已知)或代入图象与直线y ＝b 的交点求解(此时要注意交点在上升区间上还是在下降区间上)．②五点法：确定φ值时，往往以寻找“五点法”中的某一个点为突破口．具体如下：作业：【名校新题】一、填空题1．（2019·常州第一中学高三月考）将函数sin 26y x π⎛⎫=+⎪⎝⎭的图象向右平移(0)2πϕϕ<<个单位后，得到函数()f x 的图像，若函数()f x 是偶函数，则ϕ的值为____． 【解析】由题意，将函数sin 26y x π⎛⎫=+⎪⎝⎭的图象向右平移(0)2πϕϕ<<个单位后，得到函数()()sin 2sin 2266f x x x ππϕϕ⎡⎤⎛⎫=-+=-+ ⎪⎢⎥⎣⎦⎝⎭的图象，若函数()f x 是偶函数，则262k ππϕπ-+=+，即26k ππϕ=--，k Z ∈，所以3πϕ=， 故答案为：3π．2．（2019·南京二模）若函数()()()2sin 0,0f x x ωϕωϕπ=+><<的图象经过点,26π⎛⎫⎪⎝⎭，且相邻两条对称轴间的距离为2π，则4f π⎛⎫⎪⎝⎭的值为______. 【解析】因为相邻两条对称轴间的距离为2π，所以2==2.ππωω∴，所以()()2sin 2f x x ϕ=+. 因为函数的图象经过点,26π⎛⎫⎪⎝⎭，所以sin(=10,36ππϕϕπϕ+<<∴=Q ），.所以()f x =2sin(2)6x π+，所以()2sin()426f πππ=+=3．（2019·高邮期初模拟）函数()πcos 36f x x ⎛⎫=+ ⎪⎝⎭在[]0π，的零点个数为________．【解析】0x πQ ≤≤193666x πππ∴≤+≤由题可知3336262x x ，ππππ+=+=，或5362x ππ+=解得4x ,99ππ=,或79π故有3个零点. 故答案为：3.4．（2018·江苏高考真题）已知函数sin(2)()22y x ϕϕππ=+-<<的图象关于直线3x π=对称，则ϕ的值是________．【解析】由题意可得2sin π13ϕ⎛⎫+=± ⎪⎝⎭，所以2πππππ()326k k k Z ϕϕ+=+=-+∈，，因为ππ22ϕ-<<，所以π0,.6k ϕ==- 故答案为：6π-. 5．（2019·启东中学开学考试）已知函数()2sin (0)f x x ωω=>在区间[,]34ππ-上的最小值是2-，则ω的最小值等于____.【解析】函数()2sin (0)f x x ωω=>在区间[,]34ππ-上的最小值是2-，而x ω的取值范围是[]34ωπωπ-，，当22x k πωπ=-+，k Z ∈时，函数有最小值2-，∴232k ωπππ-≤-+，且 242k ωπππ≥-+，k Z ∈， ∴362k ω-≤，82k ω≥-，k Z ∈， ∵0>ω， ∴ω的最小值等于32， 故答案为：32． 6．（2019·高邮开学考试）设*N ω∈且10ω≤则使函数sin y x ω=在区间,43ππ⎡⎤⎢⎥⎣⎦上不单调的ω的个数是______.【解析】由于函数在区间,43ππ⎡⎤⎢⎥⎣⎦上不单调，故在区间(,)43ππ上有对称轴，由sin y x ω=，有πππ2π,(),()2k x k k Z x k Z ωω+=+∈=∈，故ππππ2,()43k k Z ω+<<∈，由于0>ω，故有42,()332k k Z k ωω<+⎧⎪∈⎨>+⎪⎩，即3342,()0102k k k Z ωω+<<+∈<≤∴Q 1,2k =，求得5,8,9ω=. 故答案为：3.7．（2019·苏锡常第二次调研）函数()cos()(0)3f x x πωω=->的图像关于直线2x π=对称，则ω的最小值为_______．【解析】因为函数()cos (0)3f x x πωω⎛⎫=-> ⎪⎝⎭的图像关于直线2x π=对称， 所以cos 123ππω⎛⎫⨯-=± ⎪⎝⎭，所以()23k k Z ππωπ⨯-=∈. 解得：()223k k Z ω=+∈，又0>ω， 所以当0k =时，ω最小且为23.故答案为：23.8．（2019·常州期末）已知函数f(x)=sin(ωx +φ)(ω>0,φ∈R)是偶函数，点(1,0)是函数y =f(x)图象的对称中心，则ω最小值为________.【解析】∵函数f （x ）＝sin （ωx +φ）（ω＞0，φ∈R ）是偶函数， ∴φ＝k 1π+π2,k 1∈Z ,∵点（1，0）是函数y ＝f （x ）图象的对称中心 ∴sin （ω+φ）＝0，可得ω+φ＝k 2π，k 2∈Z ， ∴ω＝k 2π﹣φ＝（k 2﹣k 1）π﹣π2．又ω＞0，所以当k 2﹣k 1＝1时，ω的最小值为π2． 故答案为：π2．9．（2019·镇江考前模拟）若函数()2sin()f x x ωϕ=+ （01ω<<，02πϕ<<）的图像过点，且关于点(2,0)-对称，则(1)f -=_______.【解析】函数()()2sin f x x ωϕ=+的图像过点( 2sin ϕ∴=sin ϕ=02πϕ<<Q 3πϕ∴=又函数图象关于点()2,0-对称 2sin 203πω⎛⎫∴-+= ⎪⎝⎭，即：23k πωπ-+=，k Z ∈ 126k πωπ∴=-+，k Z ∈01ω<<Q 6πω∴=()2sin 63f x x ππ⎛⎫∴=+⎪⎝⎭，()12sin 2sin 1636f πππ⎛⎫∴-=-+== ⎪⎝⎭故答案为：1.10．（2019·南通3月联考）已知角ϕ的终边经过点(12)P -，，函数()sin()(0)f x x ωϕω=+>图象的相邻两条对称轴之间的距离等于π3，则()π12f 的值为____．【解析】角ϕ终边经过点()1,2P -，则sin5ϕ==-，cos 5ϕ==∵()f x 两条相邻对称轴之间距离为3π∴23T π=，即223T ππω== ∴3ω=，即()()sin 3f x x ϕ=+sin sin cos cos sin 12444f ππππϕϕϕ⎛⎛⎫⎛⎫∴=+=+== ⎪ ⎪ ⎝⎭⎝⎭⎝⎭故答案为：. 11．（2019·南京一模）设函数π()sin()3f x x ω=+，其中0>ω．若函数()f x 在[]0,2π上恰有2个零点，则ω的取值范围是________．【解析】()f x 取零点时x 满足条件()3k x k Z ππωω=-+∈，当0x >时的零点从小到大依次为 123258,,333x x x πππωωω===，所以满足523823ππωππω⎧≤⎪⎪⎨⎪>⎪⎩ ，解得：54,63ω⎡⎫∈⎪⎢⎣⎭ 故答案为：54,63⎡⎫⎪⎢⎣⎭. 12．（2018·无锡期中）已知定义在区间[,]44ππ-上的函数()2sin cos (0)f x a x x b a =+<的最大值为4，最小值为52，则________.a b ⋅= 【解析】因为()()2sin cos sin2f x a x x bf x a x b =+=+，x ,44ππ⎡⎤∈-⎢⎥⎣⎦, 所以2x ,22ππ⎡⎤∈-⎢⎥⎣⎦，()[],f x a b a b ∈+-+, 从而35394.2131644a a b ab a b b ⎧=-⎧⎪+=⎪⎪∴=-⎨⎨⎪⎪-+==⎩⎪⎩， 故答案为：3916-. 13．（2019·盐城期中）若函数()sin3(01)f x x m m =-<<的所有正零点构成公差为d (d ＞0)的等差数列，则d ＝_______．【解析】设第一个正零点为0x ，则第三个正零点为02x d +，由题意得00π3(2)3π.6x d x d +-=∴= 故答案为：6π.14．（2019·徐州期中）已知函数()sin()f x x π=-223，若12()()4f x f x ⋅=-，且[]12,,x x ππ∈-，则12x x -的最大值为______．【解析】1212()()2sin(2)2sin(2)433f x f x x x ππ⋅=-⨯-=-，12sin(2)sin(2)133x x ππ-⨯-=-令1sin(2)3x π-＝1，2sin(2)13x π-=-，则11(2)223x k πππ=++，21(2)223x n πππ=-+.∴12x x -＝1(22)2k n πππ-+＝1[2()]2k n ππ-+＝1(2)2m ππ+，m ，n ，k 都是整数∵[]12,,x x ππ∈- ∴[]122,2x x ππ-∈-， ∴12x x -的最大值为13(2)22πππ+=. 故答案为：32π. 15．（2019·苏北四市期末）将函数()πsin 6f x x ω⎛⎫=- ⎪⎝⎭（0>ω）的图象向左平移π3个单位长度后，所得图象关于直线πx =对称，则ω的最小值为______.【解析】将函数f （x ）＝sin （ωx 6π-）（ω＞0）的图象向左平移3π个单位后，可得函数y ＝sin （ωx 36πωπ+-）的图象，再根据所得图象关于直线x ＝π对称，可得ωπ36πωπ+-=k π2π+，k ∈Z ， ∴当k ＝0时，ω取得最小值为12，故答案为：12．16．（2019·海门第二次调研）将函数f(x)=sin2x 的图像向右平移π6个单位，得到函数g(x)的图像，则函数g(x)在区间[0，π2]上的值域为_____________. 【解析】由题得y=g （x ）=sin2(x −π6)=sin(2x −π3), 因为0≤x ≤π2,∴0≤2x ≤π,∴−π3≤2x −π3≤2π3，所以−√32≤sin(2x −π3)≤1.所以函数y=g(x)的值域为[−√32,1].故答案为：[−√32,1].17．（2018·江苏泰州中学高三月考）将sin 2y x =的图像向右平移ϕ单位（0ϕ>），使得平移后的图像仍过点(3π，则ϕ的最小值为__________．【解析】将sin 2y x =的图像向右平移ϕ单位（0ϕ>）得到sin 2()y x ϕ=-，代入点(3π得：2sin(2)23πϕ=- ，因为0ϕ>，所以当22=33ππϕ-时，第一个正弦值为2的角，此时6π=ϕ. 故答案为：6π. 18．（2019·常州期中）将函数f(x)=sin2x 的图象向右平移φ(0<φ<π2)个单位后得到函数g(x)的图象，若对满足|f(x 1)−g(x 2)|=2的x 1、x 2有|x 1−x 2|min =π3，则φ=______． 【解析】因为函数f(x)=sin2x 的周期为π，函数f(x)=sin2x 的图象向右平移φ(0<φ<π2)个单位后, 得到函数g(x)sin(2x −2φ)的图象．满足|f(x 1)−g(x 2)|=2的可知，f (x 1)、g(x 2)一个取最大值一个取最小值 因为x 1−x 2|min =π3， 若x 1=π4，x 2=7π12，f(x)在x 1=π4取最大值，g(x)在x 2=7π12取得最小值，sin(2×7π12−2φ)=−1， 此时φ=−π6，不合题意， x 1=3π4，x 2=5π12， f(x)在x 1=3π4取最小值，g(x)在x 2=5π12，取得最大值，sin(2×5π12−2φ)=1，此时φ=π6，满足题意．故答案为：π6．二、解答题19．（2019·扬州调研）已知函数f (x )＝1＋3cos 2x －2sin 2⎝⎛⎭⎫π4－x . （1）求f (x )的最小正周期和单调递减区间；（2）若方程f (x )－m ＝0在区间⎣⎡⎦⎤π4，π上有两个不同的实数解，求实数m 的取值范围．【解析】（1）∵f (x )＝1＋3cos 2x －2sin 2⎝⎛⎭⎫π4－x ＝3cos 2x ＋cos ⎝⎛⎭⎫π2－2x ＝3cos 2x ＋sin 2x ＝2sin ⎝⎛⎭⎫2x ＋π3， ∴T ＝2π2＝π.由π2＋2k π≤2x ＋π3≤3π2＋2k π，k ∈Z ，得π12＋k π≤x ≤7π12＋k π，k ∈Z. ∴f (x )的单调递减区间为⎣⎡⎦⎤π12＋k π，7π12＋k π(k ∈Z)． （2）由题意知，函数y ＝f (x )在区间⎣⎡⎦⎤π4，π上的图象与直线y ＝m 有两个不同的交点． 由（1）知，函数f (x )在⎣⎡⎦⎤π4，7π12上单调递减，在⎣⎡⎦⎤7π12，π上单调递增， ∴f (x )min ＝f ⎝⎛⎭⎫7π12＝－2， 又f ⎝⎛⎭⎫π4＝1，f (π)＝3，∴当－2＜m ≤1时，函数y ＝f (x )在区间⎣⎡⎦⎤π4，π上的图象与直线y ＝m 有两个不同的交点，即方程f (x )－m ＝0在区间⎣⎡⎦⎤π4，π上有两个不同的实数解． ∴实数m 的取值范围为(－2,1]．20．（2019·连云港调研）函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫A ＞0，ω＞0，|φ|＜π2的最小正周期为π，点P ⎝⎛⎭⎫π6，2为其图象上一个最高点． （1）求f (x )的解析式；（2）将函数f (x )图象上所有点都向左平移π3个单位长度，得到函数g (x )的图象，求g (x )在区间⎝⎛⎭⎫π2，π上的值域．【解析】（1）∵函数f (x )的最小正周期为π. ∴2πω＝π，解得ω＝2. 又点P ⎝⎛⎭⎫π6，2为其图象上一个最高点， ∴A ＝2，sin ⎝⎛⎭⎫π3＋φ＝1， 又－π2＜φ＜π2，所以φ＝π6，∴f (x )＝2sin ⎝⎛⎭⎫2x ＋π6. （2）由题意得g (x )＝f ⎝⎛⎭⎫x ＋π3＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π3＋π6＝2sin ⎝⎛⎭⎫2x ＋5π6，当x ∈⎝⎛⎭⎫π2，π时，2x ＋5π6∈⎝⎛⎭⎫11π6，17π6， ∴sin ⎝⎛⎭⎫2x ＋5π6∈⎝⎛⎦⎤－12，1，2sin ⎝⎛⎭⎫2x ＋5π6∈(－1,2]， 故g (x )在区间⎝⎛⎭⎫π2，π上的值域为(－1,2]．。

高考数学复习重点知识专题讲解与练习专题05 函数图象的辨析1．（2021·江西赣州·高三期中（文））已知函数||()122x xx f x =+，则函数()y f x =的大致图象为（ ）A ．B ．C ．D ．【答案】D 【分析】函数图像的识别，通常利用性质+排除法进行判断： 利用函数的奇偶性排除B ，利用特殊点的坐标排除A 、C. 【详解】 由||()22x xx f x -=+，得()f x 的定义域为R ，(0)0f =，排除A 选项． 而||()()22x xx f x f x --==+，所以()f x 为偶函数，图像关于y 轴对称，排除B 选项．()1141421,1152522f f ⎛⎫====< ⎪⎝⎭+，排除C 选项． 故选：D ．2．（2021·浙江·高三月考）函数sin 2x y x=的图象可能是（ ）A ．B ．C ．D ．【答案】B 【分析】判断当3,22x x ππ==的符号，可排除AC ，求导，判断函数在()0,π上的单调性，可排除D ，即可得出答案. 【详解】解：由()()sin 02x y f x x x==≠得，1310,0223f f ππππ⎛⎫⎛⎫=>=-< ⎪ ⎪⎝⎭⎝⎭，故排除AC ， ()2cos sin 2x x x f x x -'=，令()cos sin g x x x x =-，则()sin g x x x '=-，当0πx <<时，()0g x '<， 所以函数()g x 在()0,π上递减， 所以()()00g x g <=在()0,π上恒成立， 即()2cos sin 02x x xf x x-'=<在()0,π上恒成立， 所以函数()f x 在()0,π上递减，故排除D. 故选：B.3．（2021·江苏省前黄高级中学高三月考）已知215()sin ,()42f x x x f x π⎛⎫+⎪⎭'=+ ⎝为()f x 的导函数，则()f x '的图象是（ ）A ．B ．C ．D ．【答案】A 【分析】求出导函数，判断导函数的奇偶性，再利用特殊值即可得出选项. 【详解】22co 151()si s n424f x x x x x π⎛⎫=++= +⎪⎝⎭， ()1sin 2f x x x '∴=-，∴函数()f x '为奇函数，排除B 、D.又1024f ππ⎛⎫'=-< ⎪⎝⎭，排除C.故选：A. 【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.4．（2021·浙江·高二开学考试）函数())ln cos f x x x x =+⋅在[]2,2ππ-上的图象可能是（ ）A ．B ．C ．D ．【答案】C 【分析】确定奇偶性，可排除两个选项，然后确定函数在3[,2]2ππ上的单调性可再排除一个选项，从而得正确选项． 【详解】())cos())cos ()f x x x x x x x f x -=-+-=--=-，()f x 是奇函数，排除AB ，在3[,2]2x ππ∈时，由复合函数单调性知)y x =是增函数，且)0y x =>，又cos y x =增函数，且cos 0y x =>，所以)cos y x x =是增函数，而y x =是增函数，所以()f x 是增函数，排除D ． 故选：C ．5．（2021·浙江金华·高三月考）函数|ln()|x ay x a +=-的图象，不可能是（ ）A ．B ．C ．D ．【答案】D 【分析】通过函数的定义域、值域以及特殊值对四个选项中的函数图像一一分析即可判断.【详解】对于A ，当0a =时，ln xy x=，其定义域为{}0,1x x x >≠，且0y >恒成立，故A 正确； 对于B ，由函数定义域可知，0a <，当0y =，x a =-，当x a >-时，0y >，当x a <-时，0y <，故B 正确；对于C ，由函数定义域可知，0a >，当1x a -=时，函数无意义，且0y ≥恒成立，故C 正确；对于D ，由函数定义域可知，0a <，当0y =，x a =-，当x a <-时，0y <，但图中0y >，不满足条件，故D 错误； 故选：D.6．（2021·全国·高三专题练习）函数2x y π=的图像大致是（ ）A ．B ．C ．D ．【答案】A 【分析】由02x <<时()0f x >，排除B 和C ；再探究出函数()f x 的图象关于直线1x =对称，排除D. 【详解】当02x <<时，sin 02x π>，所以()sin02xy f x π==>，故排除B 和C ；又(2)(2)sinsin()22x xf x f x ππ--===，所以函数()f x 的图象关于直线1x =对称，排除D. 故选：A. 【点睛】方法点睛：解决函数图象的识别问题的技巧：一是活用性质，常利用函数的定义域、值域、单调性与奇偶性来排除不合适的选项；二是取特殊点，根据函数的解析式选择特殊点，即可排除不合适的选项，从而得出正确的选项．7．（2021·天津市新华中学高三月考）函数23sin ()x x x x x f x e e--=+的图象大致为（ ）A ．B ．C ．D ．【答案】B 【分析】先判断函数的奇偶性排除A,D,再根据(1)0f >，排除C 即得解. 【详解】解：根据题意，23sin ()x x x x x f x e e--=+，其定义域为R ，有23sin ()()x xx x xf x f x e e---==+，则函数f (x )为偶函数，排除A ，D ， 3sin11(1)01f e e-=>+，排除C ， 故选：B ． 【点睛】方法点睛：根据函数的解析式找图象，一般先找差异，再验证. 8．（2021·全国·高三专题练习）函数2()1cos e 1x f x x ⎛⎫=+⎪-⎝⎭的大致图象为（ ） A ． B ．C ．D ．【答案】B 【分析】判断图像类问题，首先求定义域，其次判断函数的奇偶性()()f x f x -=-；再次通过图像或函数表达式找特殊值代入求值，()0f x =时，即e 1cos 0e 1x x x +⋅=-，此时只能是cos 0x =；也可通过单调性来判断图像.主要是通过排除法得解. 【详解】函数()f x 的定义域为{}0x x ≠，因为2e 12e 1()1cos cos cos e 1e 1e 1x x x x x f x x x x ⎛⎫⎛⎫-++⎛⎫=+⋅=⋅=⋅ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭，并且()()00e 1e e 1e ()cos cos cos e 1e e 1ex x xx x xf x x x x f x --+++-=⋅-=⋅=⋅=----， 所以函数()f x 为奇函数，其图象关于原点对称，可排除A C ，；当()0f x =时，即e 1cos 0e 1x x x +⋅=-，此时只能是cos 0x =，而cos 0x =的根是2x x k k ππ⎧⎫=+∈⎨⎬⎩⎭Z ，，可排除D . 故选:B 【点睛】函数的定义域，奇偶性，特殊值，单调性等是解决这类问题的关键，特别是特殊值的选取很重要，要结合图像的特征来选取.9．（2022·全国·高三专题练习（理））函数()232sin log y x x x π=⋅⋅的图象大致为（ ）A ．B ．C ．D ．【答案】B 【分析】分析函数()232sin log y x x x π=⋅⋅的定义域、奇偶性及其在()0,1上的函数值符号，结合排除法可得出合适的选项. 【详解】设()()()2322sin log sin log f x x x x x x ππ=⋅⋅=⋅，该函数的定义域为{}0x x ≠，()()()()22sin log sin log f x x x x x f x ππ-=-⋅-=⋅=-，函数()f x 为奇函数，排除AC 选项；当01x <<时，0x ππ<<，()sin 0x π>，则()0f x <，排除D 选项. 故选：B. 【点睛】思路点睛：函数图象的辨识可从以下方面入手： （1）从函数的定义域，判断图象的左右位置； （2）从函数的值域，判断图象的上下位置． （3）从函数的单调性，判断图象的变化趋势； （4）从函数的奇偶性，判断图象的对称性； （5）函数的特征点，排除不合要求的图象.10．（2022·全国·高三专题练习）函数()3log 01a y x ax a =-<<的图象可能是（ ）A ．B ．C ．D ．【答案】B 【分析】先求出函数的定义域，判断函数的奇偶性，构造函数，求函数的导数，利用是的导数和极值符号进行判断即可. 【详解】根据题意，()3loga f x x ax =-，必有30x ax -≠，则0x ≠且x ≠， 即函数的定义域为{|0x x ≠且x ≠，()()()()33log log a a x a x x f f x ax x ---=--==，则函数3log a y x ax =-为偶函数，排除D ，设()3g x x ax =-，其导数()23g x x a '=-，由()0g x '=得x =，当x 时，()0g x '>，()g x 为增函数，而()f x 为减函数，排除C ，在区间⎛⎝⎭上，()0g x '<，则()g x 在区间⎛ ⎝⎭上为减函数，在区间⎫+∞⎪⎪⎝⎭上，()0g x '>，则()g x 在区间⎫+∞⎪⎪⎝⎭上为增函数，0g =，则()g x 存在极小值3g a =-=⎝⎭⎝⎭，此时()g x ()0,1，此时()0f x >，排除A ，故选：B. 【点睛】函数图象的辨识可以从以下方面入手：（1）从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置； （2）从函数的单调性，判断图象的变化趋势； （3）从函数的奇偶性，判断图象的对称性； （4）从函数的特征点，排除不合要求的图象.11．（2022·全国·高三专题练习）函数()122cos cos 4421x x f x x x ππ+-⎛⎫⎛⎫=+- ⎪ ⎪+⎝⎭⎝⎭的图象为（ ） A ． B ．C ．D ．【答案】D【分析】先将()f x 的解析式化简，然后判断()f x 的奇偶性，再根据()f π的取值特点判断出对应的函数图象. 【详解】因为()12221cos cos 2442121x x x x f x x x x x x x ππ+⎫⎫--⎛⎫⎛⎫=+-=⋅⋅⋅+⎪⎪ ⎪ ⎪⎪⎪++⎝⎭⎝⎭⎝⎭⎝⎭()222121cos sin cos22121x x x x x x x --=⋅-=⋅++， 所以()()()2112cos 2cos22112x xx x f x x x f x -----=⋅-=⋅=-++且定义域为R 关于原点对称， 所以()f x 为奇函数，排除A 和C ；由()21cos2021f ππππ-=>+，排除B ， 故选：D ． 【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.12．（2021·河南·温县第一高级中学高三月考（理））函数()ln |||sin |,(f x x x x ππ=+-≤≤且0)x ≠的图象大致是（ ）A ．B ．C ．D ．【答案】B 【分析】根据解析式判断奇偶性，在0x π>>上0x +→有()f x →-∞，利用导函数，结合函数图象分析0x π>>内极值点的个数，即可确定正确函数图象. 【详解】函数()ln |||sin()|ln |||sin |()f x x x x x f x -=-+-=+=，(x ππ-≤≤且0)x ≠是偶函数，A 不合要求． 当0x π>>时，()ln sin f x x x =+：当0x +→，()f x →-∞，C 不合要求；而1()cos 0f x x x'=+=时，1,cos y y x x==-在0x π>>上只有一个交点(如下图示)，即区间内只有一个极值点. D不合要求，B 符合要求.故选：B. 【点睛】关键点点睛：利用导函数，应用数形结合分析函数的交点情况，判断函数在区间上极值点个数.13．（2021·全国·高三专题练习（文））已知函数()f x ，()g x 满足()()()()x x f x g x e f x g x e -⎧+=⎪⎨-=⎪⎩，则()()()sin 2x h x f x g x π⎛⎫+ ⎪⎝⎭=⋅的图像大致是（ ） A ． B ．C ．D ．【答案】C 【分析】依题意得()()()221=4x x f x g x e e --⋅，根据奇偶性定义知()h x 为奇函数，再结合特征点即可得答案． 【详解】因为()()()()x x f x g x e f x g x e -⎧+=⎪⎨-=⎪⎩解得()()()()11=,=22x x x xf x e eg x e e --+- 所以()()()221=4x x f x g x e e --⋅，则()()()22sin 4cos 2=x xx x h x f x g x e e π-⎛⎫+ ⎪⎝⎭=⋅- ()h x 定义域为{}0x x ≠因为()()224cos x xxh x h x e e --==--，故()h x 是奇函数，则B ，D 错；当02x π<<时，()224cos 0x xxh x e e -=>-，则C 正确，故选：C 【点睛】思路点睛：函数图象的识别可以以下方面入手： （1）从函数定义域判断； （2）从函数单调性判断； （3）从函数奇偶性判断； （4）从函数特征点判断．14．（2021·湖南·长郡中学二模）函数sin cos 4411()x x f x ee ππ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭的图像可能是（ ）A ．B ．C ．D ．【答案】A 【分析】本题首先可通过()()f x f x -=-判断出函数()f x 为奇函数，C 、D 错误，然后取04x π<≤，通过sin cos 44x x ππ⎛⎫⎛⎫+>+ ⎪ ⎪⎝⎭⎝⎭判断出此时()0f x <，即可得出结果.【详解】 因为sin cos cos sin 44441111()()x x x x f x f x ee e e ππππ⎛⎫⎛⎫⎛⎫⎛⎫-+-+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝==-⎭⎝⎭，x ∈R ，所以函数()f x 为奇函数，C 、D 错误，当04x π<≤，442x πππ<+≤，sin cos 44x x ππ⎛⎫⎛⎫+>+ ⎪ ⎪⎝⎭⎝⎭，sin cos 4411x x e e ππ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭<⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，sin cos 4411()0x x f x ee ππ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎭<⎝，B 错误，故选：A. 【点睛】方法点睛：本题考查函数图像的判断，在判断函数的图像的时候，可以通过函数的单调性、奇偶性、周期性、函数值的大小、是否过定点等函数性质来判断，考查数形结合思想，是中档题.15．（2021·福建龙岩·高一期末）已知函数()cos6x xxf x e e -=-，则()f x 的图象大致是（ ）A ．B ．C ．D ．【答案】C 【分析】分析函数()f x 的奇偶性及其在区间0,12π⎛⎫⎪⎝⎭上的函数值符号，由此可得出合适的选项.【详解】 对于函数()cos6x xxf x e e-=-，0x x e e --≠，解得0x ≠，函数()f x 的定义域为{}0x x ≠， ()()()cos 6cos6x xx xx xf x f x e e e e----==-=---，所以，函数()f x 为奇函数，排除BD 选项， 当0,12x π⎛⎫∈ ⎪⎝⎭时，60,2x π⎛⎫∈ ⎪⎝⎭，则cos60x >且0x x e e -->，此时，()0f x >，排除A 选项. 故选：C. 【点睛】思路点睛：函数图象的辨识可从以下方面入手： （1）从函数的定义域，判断图象的左右位置； （2）从函数的值域，判断图象的上下位置． （3）从函数的单调性，判断图象的变化趋势； （4）从函数的奇偶性，判断图象的对称性； （5）函数的特征点，排除不合要求的图象.16．（2021·湖北武汉·高一期末）函数()32241x xxx y -=+的部分图像大致为（ ）A ．B ．C ．D ．【答案】A 【分析】研究函数奇偶性和区间(的函数值的正负，利用排除法即得结果. 【详解】函数()33222()4122x x xxxx x x y f x ---===++，定义域为R ， 对于任意的自变量x ，()333222()()222222x xx x x x x xx x x x f x f x -------===++-=-+++，故函数()y f x =是奇函数，图象关于原点中心对称，故CD 错误；又(32()2222x x x xx x x x x y f x --+-===++，故(x ∈时，00,0,202x x x x x ->+>+>，，即()0y f x =<，故A 正确，B 错误. 故选：A. 【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性；(4)从函数的特征点，排除不合要求的图象. 17．（2021·全国·高三专题练习（理））函数()x x f x -=的图象大致为（ ）A ．B ．C ．D ．【答案】A 【分析】分析函数()f x 的奇偶性，以及当0x >时，()f x 的符号，进而可得出合适的选项. 【详解】 设())lng x x =，对任意的x ∈Rx x >≥-0x >，则函数()g x 的定义域为R ，())ln xxg x x-==)()lnx g x ==-=-，所以，函数())ln g x x =为奇函数，令())ln0g x x ==1x =1x =-，所以，10x -≥，可得1x ≤1x =-可得()2211x x +=-，解得0x =. 所以，函数()x x f x -=的定义域为{}0x x ≠，()()()()2222x x x xf x f xg x g x --++-==-=--，所以，函数()f x 为奇函数，排除BD 选项，当0x >时，)ln ln10x >=，220x x -+>，所以，()0f x >，排除C 选项.故选：A. 【点睛】思路点睛：函数图象的辨识可从以下方面入手： （1）从函数的定义域，判断图象的左右位置； （2）从函数的值域，判断图象的上下位置． （3）从函数的单调性，判断图象的变化趋势； （4）从函数的奇偶性，判断图象的对称性； （5）函数的特征点，排除不合要求的图象.18．（2021·全国全国·高三月考（理））已知函数()31sin f x x x x ⎛⎫=-⋅ ⎪⎝⎭，则其图象为（ ） A ． B ．C ．D ．【答案】A 【分析】分析函数()f x 的定义域、奇偶性以及该函数在()0,1上的函数值符号，结合排除法可得出合适的选项. 【详解】 函数()31sin f x x x x ⎛⎫=-⋅ ⎪⎝⎭的定义域为{}0x x ≠，排除D 选项； ()()()()()()333111sin sin sin f x x x x x x x f x x x x ⎡⎤⎛⎫⎛⎫⎢⎥-=--⋅-=-+⋅-=-⋅= ⎪ ⎪⎝⎭⎝⎭⎢⎥-⎣⎦， 所以，函数()f x 为偶函数，排除B 选项；当01x <<时，433110x x x x--=<，sin 0x >，此时()0f x <，排除C 选项.故选：A. 【点睛】思路点睛：函数图象的辨识可从以下方面入手： （1）从函数的定义域，判断图象的左右位置； （2）从函数的值域，判断图象的上下位置． （3）从函数的单调性，判断图象的变化趋势； （4）从函数的奇偶性，判断图象的对称性； （5）函数的特征点，排除不合要求的图象.19．（2020·全国全国·模拟预测（文））函数()()ee sin 32xx xf x -+⋅=在55,22⎡⎤-⎢⎥⎣⎦上的图象大致是（ ）A ．B ．C ．D ．【答案】B 【分析】先判断函数奇偶性得函数为奇函数，故排除A,再结合π0,3x ⎛⎫∈ ⎪⎝⎭时，()0f x >排除C ，最后讨论函数在对应区间内的零点个数即可得答案. 【详解】∵()()()()()e e sin 3e e sin 322xx xx x f f xx x --+⋅-+⋅==-=--，∴()f x 是奇函数，排除A ．当π0,3x ⎛⎫∈ ⎪⎝⎭时，()0f x >，排除C ．由()0f x =得sin30x =，又15153,22x ⎡⎤∈-⎢⎥⎣⎦， ∴30x =或π±或2π±，∴()f x 在55,22⎡⎤-⎢⎥⎣⎦上有5个零点，排除D ．故选：B ． 【点睛】本题考查利用函数性质确定函数图象，考查了函数的奇偶性，考查数形结合思想，属于基础题．思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势； (3)从函数的奇偶性，判断图象的对称性； (4)从函数的特征点，排除不合要求的图象.20．（2020·山西·河津中学高三月考（理））函数(),()sin f x x g x x x ==+，则()()()h x f x g x =的图象大致为（ ）A ．B ．C ．D ．【答案】A 【分析】由()h x 为偶函数，故排除选项B ，当0x >时，()0,f x >且()f x 为增函数，()g x 在(0,)+∞上为增函数，所以当0x >时，()()00g x g >=，所以当0x >时，()()()0h x f x g x =>，排除选项D ，从而可得出()h x 在(0,)+∞上为增函数，排除选项C ，得到答案.【详解】()(sin )h x x x x =+，则()()()()sin sin h x x x x x x x h x -=---=+=，所以()h x 为偶函数，故排除选项B. 当0x >时，()0,f x >且()f x 为增函数.()1cos 0g x x '=+≥恒成立，所以()g x 在(0,)+∞上为增函数，所以当0x >时，()()00g x g >=所以当0x >时，()()()0h x f x g x =>，排除选项D. 设120x x <<，则()()120f x f x <<，()()120g x g x << 则()()()()()()121122g g h x h x f x x f x x -=-()()()()()()()()11121222g g g g f x x f x x f x x f x x =-+- ()()()()()()()()112212g g g f x x x x f x f x =-+- ()()()()()()()()112212g g g f x x x x f x f x =-+-由条件()10f x >，()()12g g 0x x -<，则()()()()112g g 0f x x x -<()2g 0x >，()()120f x f x -<，则()()()()212g 0x f x f x -<所以()()()()()()()()112212g g g 0f x x x x f x f x -+-<，即()()12h x h x < 因此()h x 在(0,)+∞上为增函数，排除选项C 故选：A 【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置． (2)从函数的单调性，判断图象的变化趋势；(3)从函数的奇偶性，判断图象的对称性；(4)从函数的特征点，排除不合要求的图象.。

高三数学函数图像试题答案及解析1.函数在上的图像大致为（）【答案】A【解析】函数是奇函数，所以C,D被排除；当时，，,由此判断，函数原点右侧开始时应该是正数，所以选A.【考点】函数的图像与性质2.如图，已知l1⊥l2，圆心在l1上、半径为1 m的圆O在t＝0时与l2相切于点A，圆O沿l1以1m/s的速度匀速向上移动，圆被直线l2所截上方圆弧长记为x，令y＝cos x，则y与时间t(0≤t≤1，单位：s)的函数y＝f(t)的图象大致为( )【答案】B【解析】通过圆心角α将弧长x与时间t联系起来．圆半径为1，设弧长x所对的圆心角为α，则α＝x，如图所示，cos＝1－t，即cos＝1－t，则y＝cos x＝2cos2－1＝2(1－t)2－1＝2(t－1)2－1(0≤t≤1)．其图象为开口向上，在[0,1]上的一段抛物线．3.若函数的图像如右图所示，则下列函数图像正确的是（）【答案】B【解析】由题意可得.所以函数是递减的即A选项不正确.B正确. 是递减,所以C不正确. 图象与关于y轴对称，所以D不正确.故选B.【考点】函数的图象.4.已知函数f(x)＝|lgx|，若a≠b，且f(a)＝f(b)，则a＋b的取值范围是()A．(1，＋∞)B．[1，＋∞)C．(2，＋∞)D．[2，＋∞)【答案】C【解析】函数f(x)＝|lgx|的图象如图所示，由图象知a，b一个大于1，一个小于1，不妨设a>1,0<b<1.∵f(a)＝f(b)，∴f(a)＝|lga|＝lga＝f(b)＝|lgb|＝－lgb＝lg.∴a＝.∴a＋b＝b＋>2＝2.5.设f(x)与g(x)是定义在同一区间[a，b]上的两个函数，若函数y＝f(x)－g(x)在x∈[a，b]上有两个不同的零点，则称f(x)和g(x)在[a，b]上是“关联函数”，区间[a，b]称为“关联区间”．若f(x)＝x2－3x＋4与g(x)＝2x＋m在[0,3]上是“关联函数”，则m的取值范围为________．【答案】【解析】由题意知，y＝f(x)－g(x)＝x2－5x＋4－m在[0,3]上有两个不同的零点．在同一直角坐标系下作出函数y＝m与y＝x2－5x＋4(x∈[0,3])的图像如图所示，结合图像可知，当x∈[2,3]时，y＝x2－5x＋4∈，故当m∈时，函数y＝m与y＝x2－5x＋4(x∈[0,3])的图像有两个交点．6.函数y=2a x﹣1（0＜a＜1）的图象一定过点（）A．（1，1）B．（1，2）C．（2，0）D．（2，﹣1）【答案】B【解析】因为函数y=a x（0＜a＜1）的图象一定经过点（0，1），而函数y=2a x﹣1（0＜a＜1）的图象是由y=a x（0＜a＜1）的图象向右平移1个单位，然后把函数y=a x﹣1（0＜a＜1）的图象上所有点的横坐标不变，纵坐标扩大到原来的2倍得到的，所以函数y=2a x﹣1（0＜a＜1）的图象一定过点（1，2）．故选B．7.函数y=2x﹣x2的图象大致是（）【答案】A【解析】因为当x=2或4时，2x﹣x2=0，所以排除B、C；当x=﹣2时，2x﹣x2=，故排除D，所以选A．8.函数f（x）的图象向右平移1个单位长度，所得图象与曲线y=e x关于y轴对称，则f（x）=（）A．e x+1B．e x﹣1C．e﹣x+1D．e﹣x﹣1【答案】D【解析】函数y=e x的图象关于y轴对称的图象的函数解析式为y=e﹣x，而函数f（x）的图象向右平移1个单位长度，所得图象与曲线y=e x的图象关于y轴对称，所以函数f（x）的解析式为y=e﹣（x+1）=e﹣x﹣1．即f（x）=e﹣x﹣1．故选D．9.已知，则函数的零点个数为（）A．1B．2C．3D．4【答案】D【解析】由题意可知，要研究函数的零点，只要研究函数与函数的交点个数，画出两个函数的图象，如图，很明显是4个交点.【考点】1.函数的零点；2.函数的图象.10.函数的图象大致是()．【答案】C【解析】不难知道，函数是奇函数，故排除A;又，令得，而此方程有无穷个解，且在每个解的两边函数值不同号，所以函数有无穷多个极值点，故可排除B，D．11.已知，点在曲线上，若线段与曲线相交且交点恰为线段的中点，则称为曲线关于曲线的一个关联点.记曲线关于曲线的关联点的个数为，则( ) A．B．C．D．【答案】B【解析】设则的中点为所以有，因此关联点的个数就为方程解得个数，由于函数在区间上分别单调增及单调减，所以只有一个交点，即.【考点】函数图像12.如图，不规则四边形ABCD中，AB和CD是线段，AD和BC是圆弧，直线于E，当从左至右移动（与线段AB有公共点）时，把四边形ABCD分成两部分，设，左侧部分面积为，则关于的图像大致为( )【答案】C【解析】由直线的变化可知，开始时圆弧那段变化较慢，所以排除A,B选项，由于左边的面积始终在增大，所以D选项不正确.【考点】1.图形的变化规律.2.关注局部图形的变化.13.已知函数y＝f(x)的图象如图所示，请根据已知图象作出下列函数的图象：①y＝f(x＋1)；②y＝f(x)＋2；【答案】【解析】(1)将函数y＝f(x)的图象向左平移一个单位得到y＝f(x＋1)的图象(如图①所示)，将函数y＝f(x)的图象向上平移两个单位得到y＝f(x)＋2的图象(如图②所示)．14.已知函数，，若在区间内，函数与轴有3个不同的交点，则实数的取值范围是（）A．B．C．D．【答案】C【解析】∵，∴，∴，∴，∴，∴当时，，∵函数与x轴有3个不同交点，∴函数与有3个不同的交点，函数的图像如图所示，直线与相切是一个边界情况，直线过时是一个边界情况，符合题意的直线需要在这2条直线之间，∵，∴，∴，所以切线方程为，与相同，即，当过点时，，综上可得：，故选C.【考点】1.导数的运算；2.函数图像；3.曲线的切线.15.函数y=lnx－1的图象关于直线y=x对称的图象大致是 ( )A. B. C. D.【答案】A【解析】因为关于直线y=x对称点的关系为，所以函数y=lnx－1的关于直线y=x对称的函数的解析式为.即相当于将函数的图像向左平移一个单位，显然B,D不正确，C 选项中的图像在y轴的交点过低，所以不正确.故选A.【考点】1.函数的对称性.2.指数函数的图像.3.函数图像的平移知识.16.下列函数图象与x轴均有公共点，其中能用二分法求零点的是()．【答案】C【解析】只有零点两侧的函数值符号相反且在零点附近连续时才可用二分法．17.函数y＝的图象大致是()．【答案】D【解析】由y＝知为奇函数，排除A，B.根据函数有两个零点x＝±1，排除C.18.函数y＝－2sin x的图象大致是 ()．【答案】C【解析】当x＝0时，y＝0－2sin 0＝0，故函数图象过原点，可排除A.又∵y′＝－2cos x，当x在y轴右侧趋向0时，f′(x)＜0，此时函数为减函数；当x＝2 π时，f′(2 π)＝－2 cos 2 π＝－＜0，所以x＝2 π应在函数的减区间上，故选C19.函数的图象大致是( )【答案】D【解析】因为的定义域为，且，故可排除,所以应选D.【考点】1、函数的定义域；2、函数的性质；函数的图象.20.函数的图象大致是( )【答案】A【解析】,故此函数在上为增函数,在为减函数;且只有一个根,故只有一个零点.所以选A.【考点】函数的性质与图像.21.随着生活水平的提高，私家车已成为许多人的代步工具。

高考专题《函数图像问题》考题归纳及详解一．选择题（共34小题）1．函数f（x）=（x2﹣2x）e x的图象大致是（）A． B．C．D．2．函数y=x+cosx的大致图象是（）A．B．C．D．3．函数y=的图象大致是（）A． B．C．D．4．函数y=xln|x|的大致图象是（）A．B．C．D．5．函数f（x）=x2﹣2|x|的图象大致是（）A． B．C．D．6．函数f（x）=+ln|x|的图象大致为（）A．B．C．D．7．在下列图象中，二次函数y=ax2+bx及指数函数y=（）x的图象只可能是（）A．B． C．D．8．函数y=xln|x|的图象大致是（）A．B．C．D．9．f（x）=的部分图象大致是（）A．B．C． D．10．函数的图象大致为（）A． B． C． D．11．函数f（x）=（其中e为自然对数的底数）的图象大致为（）A． B．C．D．12．函数f（x）=（2x﹣2﹣x）cosx在区间[﹣5，5]上的图象大致为（）A． B．C．D．13．函数的部分图象大致为（）A．B．C．D．14．函数f（x）=的部分图象大致为（）A．B．C．D．15．函数的部分图象大致为（）A．B．C．D．16．函数y=x（x2﹣1）的大致图象是（）A．B． C． D．17．函数y=x﹣2sinx，x∈[﹣，]的大致图象是（）A．B．C．D．18．函数f（x）=的部分图象大致是（）A．． B．.C．.D．.19．函数y=﹣2x2+2|x|在[﹣2，2]的图象大致为（）A．B．C．D．20．函数的图象大致是（）A．B．C．D．21．函数f（x）=（x∈[﹣2，2]）的大致图象是（）A．B．C．D．22．函数的图象大致是（）A．B．C．D．23．函数y=的大致图象是（）A．B．C．D．24．函数y=sinx（1+cos2x）在区间[﹣2，2]上的图象大致为（）A．B．C．D．25．函数f（x）=（x2﹣3）•ln|x|的大致图象为（）A． B． C． D．26．函数f（x）=﹣e﹣ln|x|+x的大致图象为（）A．B．C．D．27．函数y=1+x+的部分图象大致为（）A．B．C．D．28．函数y=的部分图象大致为（）A．B．C．D．29．函数f（x）=x•ln|x|的图象可能是（）A．B．C．D．30．函数f（x）=e ln|x|+的大致图象为（）A．B．C．D．31．函数y=的一段大致图象是（）A． B．C．D．32．函数的图象大致是（）A．B．C．D．33．函数的大致图象是（）A．B．C．D．34．函数的图象大致为（）A．B．C．D．二．解答题（共6小题）35．在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρcosθ=4．（1）M为曲线C1上的动点，点P在线段OM上，且满足|OM|•|OP|=16，求点P的轨迹C2的直角坐标方程；（2）设点A的极坐标为（2，），点B在曲线C2上，求△OAB 面积的最大值．36．在直角坐标系xOy中，曲线C1的参数方程为（t 为参数，a＞0）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=4cosθ．（Ⅰ）说明C1是哪种曲线，并将C1的方程化为极坐标方程；（Ⅱ）直线C3的极坐标方程为θ=α0，其中α0满足tanα0=2，若曲线C1与C2的公共点都在C3上，求a．37．在直角坐标系xOy中，曲线C1的参数方程为（α为参数），以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为ρsin（θ+）=2．（1）写出C1的普通方程和C2的直角坐标方程；（2）设点P在C1上，点Q在C2上，求|PQ|的最小值及此时P 的直角坐标．38．在直角坐标系xOy中，曲线C的参数方程为，（θ为参数），直线l的参数方程为，（t为参数）．（1）若a=﹣1，求C与l的交点坐标；（2）若C上的点到l距离的最大值为，求a．39．在平面直角坐标系xOy中，已知直线l的参数方程为（t为参数），曲线C的参数方程为（s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．40．在直角坐标系xOy中，直线l1的参数方程为，（t为参数），直线l2的参数方程为，（m为参数）．设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．（1）写出C的普通方程；（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ（cosθ+sinθ）﹣=0，M为l3与C的交点，求M的极径．函数图像问题高考试题精选参考答案与试题解析一．选择题（共34小题）1．函数f（x）=（x2﹣2x）e x的图象大致是（）A． B．C．D．【解答】解：因为f（0）=（02﹣2×0）e0=0，排除C；因为f'（x）=（x2﹣2）e x，解f'（x）＞0，所以或时f（x）单调递增，排除B，D．故选A．2．函数y=x+cosx的大致图象是（）A．B．C．D．【解答】解：由于f（x）=x+cosx，∴f（﹣x）=﹣x+cosx，∴f（﹣x）≠f（x），且f（﹣x）≠﹣f（x），故此函数是非奇非偶函数，排除A、C；又当x=时，x+cosx=x，即f（x）的图象与直线y=x的交点中有一个点的横坐标为，排除D．故选：B．3．函数y=的图象大致是（）A． B．C．D．【解答】解：当x＞0时，y=xlnx，y′=1+lnx，即0＜x＜时，函数y单调递减，当x＞，函数y单调递增，因为函数y为偶函数，故选：D4．函数y=xln|x|的大致图象是（）A．B．C．D．【解答】解：令f（x）=xln|x|，易知f（﹣x）=﹣xln|﹣x|=﹣xln|x|=﹣f（x），所以该函数是奇函数，排除选项B；又x＞0时，f（x）=xlnx，容易判断，当x→+∞时，xlnx→+∞，排除D选项；令f（x）=0，得xlnx=0，所以x=1，即x＞0时，函数图象与x轴只有一个交点，所以C选项满足题意．故选：C．5．函数f（x）=x2﹣2|x|的图象大致是（）A． B．C．D．【解答】解：∵函数f（x）=x2﹣2|x|，∴f（3）=9﹣8=1＞0，故排除C，D，∵f（0）=﹣1，f（）=﹣2=0.25﹣＜﹣1，故排除A，故选：B当x＞0时，f（x）=x2﹣2x，∴f′（x）=2x﹣2x ln2，故选：B6．函数f（x）=+ln|x|的图象大致为（）A．B．C．D．【解答】解：当x＜0时，函数f（x）=，由函数y=、y=ln（﹣x）递减知函数f（x）=递减，排除CD；当x＞0时，函数f（x）=，此时，f（1）==1，而选项A的最小值为2，故可排除A，只有B正确，故选：B．7．在下列图象中，二次函数y=ax2+bx及指数函数y=（）x的图象只可能是（）A．B． C．D．【解答】解：根据指数函数y=（）x可知a，b同号且不相等则二次函数y=ax2+bx的对称轴＜0可排除B与D选项C，a﹣b＞0，a＜0，∴＞1，则指数函数单调递增，故C 不正确故选：A8．函数y=xln|x|的图象大致是（）A．B．C．D．【解答】解：∵函数f（x）=xln|x|，可得f（﹣x）=﹣f（x），f（x）是奇函数，其图象关于原点对称，排除A，D，当x→0时，f（x）→0，故排除B又f′（x）=lnx+1，令f′（x）＞0得：x＞，得出函数f（x）在（，+∞）上是增函数，故选：C．9．f（x）=的部分图象大致是（）A．B．C． D．【解答】解：∵f（﹣x）=f（x）∴函数f（x）为奇函数，排除A，∵x∈（0，1）时，x＞sinx，x2+x﹣2＜0，故f（x）＜0，故排除B；当x→+∞时，f（x）→0，故排除C；故选：D10．函数的图象大致为（）A． B． C． D．【解答】解：函数是非奇非偶函数，排除A、B，函数的零点是x=e﹣1，当x=e时，f（e）=，排除选项D．故选：C．11．函数f（x）=（其中e为自然对数的底数）的图象大致为（）A． B．C．D．【解答】解：f（﹣x）====f（x），∴f（x）是偶函数，故f（x）图形关于y轴对称，排除B，D；又x→0时，e x+1→2，x（e x﹣1）→0，∴→+∞，排除C，故选A．12．函数f（x）=（2x﹣2﹣x）cosx在区间[﹣5，5]上的图象大致为（）A． B．C．D．【解答】解：当x∈[0，5]时，f（x）=（2x﹣2﹣x）cosx=0，可得函数的零点为：0，，，排除A，B，当x=π时，f（π）=﹣2π+2﹣π，＜0，对应点在x轴下方，排除选项C，故选：D．13．函数的部分图象大致为（）A．B．C．D．【解答】解：∵f（﹣x）=﹣f（x），可得f（x）为奇函数，排除B，∵＜1，排除A．当x＞0时，，，∴在区间（1，+∞）上f （x）单调递增，排除D，故选C．14．函数f（x）=的部分图象大致为（）A．B．C．D．【解答】解：函数f（x）==﹣，当x=0时，可得f（0）=0，f（x）图象过原点，排除A．当﹣＜x＜0时；sin2x＜0，而|x+1|＞0，f（x）图象在上方，排除C．当x＜﹣1，x→﹣1时，sin（﹣2）＜0，|x+1|→0，那么f（x）→∞，当x=﹣时，sin2x=﹣，y=﹣=，对应点在第二象限，排除D，B满足题意．故选：B．15．函数的部分图象大致为（）A．B．C．D．【解答】解：∵f（﹣x）=﹣f（x），可得f（x）为奇函数，排除B，∵＜1，排除A．当x＞0时，，，∴在区间（1，+∞）上f （x）单调递增，排除D，故选C．16．函数y=x（x2﹣1）的大致图象是（）A．B． C． D．【解答】解：∵函数y=x（x2﹣1），令f（x）=x（x2﹣1），则f（﹣x）=﹣x（x2﹣1）=﹣f（x），故函数f（x）为奇函数，又当0＜x＜1时，f（x）＜0，综上所述，函数y=x（x2﹣1）的大致图象是选项A．故选：A．17．函数y=x﹣2sinx，x∈[﹣，]的大致图象是（）A．B．C．D．【解答】解：f（﹣x）=﹣x+2sinx=﹣（x﹣2sinx）=﹣f（x），所以函数为奇函数，故函数的图象关于原点对称，只有CD适合，y′=1﹣2cosx，由y′=0解得x=，∴当x=时，函数取极值，故D适合，故选：D．18．函数f（x）=的部分图象大致是（）A．． B．.C．.D．.【解答】解：由x2+|x|﹣2=0，解得x=﹣1或x=1，∴函数的定义域为（﹣∞，﹣1）∪（﹣1，1）∪（1，+∞），∵f（﹣x）==﹣f（x），∴f（x）为奇函数，∴f（x）的图象关于原点对称，故排除A，令f（x）=0，解得x=0，故排除C，当x=时，f（）=＜0，故排除B，故选：D19．函数y=﹣2x2+2|x|在[﹣2，2]的图象大致为（）A．B．C．D．【解答】解：由y=﹣2x2+2|x|知函数为偶函数，即其图象关于y 轴对称，故可排除B，D．又当x=2时，y=﹣2•（﹣2）2+22=﹣4．所以，C是错误的，故选：A．20．函数的图象大致是（）A．B．C．D．【解答】解：解：定义域为（﹣∞，0）∪（0，+∞），f（x）=）=﹣，∴f（﹣x）=f（x），f（x）为偶函数，．∴其图象关于y轴对称，可排除A、C，；又当x→0时，cos（πx）→1，x2→0，∴f（x）→﹣∞．故可排除B；而D均满足以上分析．故选：D．21．函数f（x）=（x∈[﹣2，2]）的大致图象是（）A．B．C．D．【解答】解：函数f（x）=（x∈[﹣2，2]）满足f（﹣x）=﹣f（x）是奇函数，排除D，x=1时，f（1）=＞0，对应点在第一象限，x=2时，f（2）=＜0，对应点在第四象限；所以排除B，C；故选：A．22．函数的图象大致是（）A．B．C．D．【解答】解：函数满足f（﹣x）=﹣f（x），故函数图象关于原点对称，排除A、B，当x∈（0，）时，，故排除D，故选：C23．函数y=的大致图象是（）A．B．C．D．【解答】解：函数y=的导数为，令y′=0，得x=，时，y′＜0，时，y′＞0，时，y′＜0．∴函数在（﹣），（）递减，在（）递增．且x=0时，y=0，故选：C24．函数y=sinx（1+cos2x）在区间[﹣2，2]上的图象大致为（）A．B．C．D．【解答】解：函数y=sinx（1+cos2x），定义域为[﹣2，2]关于原点对称，且f（﹣x）=sin（﹣x）（1+cosx）=﹣sinx（1+cosx）=﹣f（x），则f（x）为奇函数，图象关于原点对称，排除D；由0＜x＜1时，y=sinx（1+cos2x）=2sinxcos2x＞0，排除C；又2sinxcos2x=0，可得x=±（0＜x≤2），则排除A，B正确．故选B．25．函数f（x）=（x2﹣3）•ln|x|的大致图象为（）A． B． C． D．【解答】解：函数f（x）=（x2﹣3）•ln|x|是偶函数；排除选项A，D；当x→0时，f（x）→+∞，排除选项B，故选：C．26．函数f（x）=﹣e﹣ln|x|+x的大致图象为（）A．B．C．D．【解答】解：函数f（x）=﹣e﹣ln|x|+x是非奇非偶函数，排除A，D；当x＞0时，f（x）=﹣e﹣lnx+x=x﹣，函数是增函数，排除C；故选：B．27．函数y=1+x+的部分图象大致为（）A．B．C．D．【解答】解：函数y=1+x+，可知：f（x）=x+是奇函数，所以函数的图象关于原点对称，则函数y=1+x+的图象关于（0，1）对称，当x→0+，f（x）＞0，排除A、C，点x=π时，y=1+π，排除B．故选：D．28．函数y=的部分图象大致为（）A．B．C．D．【解答】解：函数y=，可知函数是奇函数，排除选项B，当x=时，f（）==，排除A，x=π时，f（π）=0，排除D．故选：C．29．函数f（x）=x•ln|x|的图象可能是（）A．B．C．D．【解答】解：函数f（x）=x•ln|x|是奇函数，排除选项A，C；当x=时，y=，对应点在x轴下方，排除B；故选：D．30．函数f（x）=e ln|x|+的大致图象为（）A．B．C．D．【解答】解：∵f（x）=e ln|x|+∴f（﹣x）=e ln|x|﹣f（﹣x）与f（x）即不恒等，也不恒反，故函数f（x）为非奇非偶函数，其图象不关于原点对称，也不关于y轴对称，可排除A，D，当x→0+时，y→+∞，故排除B故选：C．31．函数y=的一段大致图象是（）A． B．C．D．【解答】解：f（﹣x）=﹣=﹣f（x），∴y=f（x）为奇函数，∴图象关于原点对称，∴当x=π时，y=﹣＜0，故选：A．32．函数的图象大致是（）A．B．C．D．【解答】解：由题意，函数在（﹣1，1）上单调递减，在（﹣∞，﹣1），（1，+∞）上单调递减，故选A．33．函数的大致图象是（）A．B．C．D．【解答】解：f（﹣x）===﹣f（x），∴f（x）是奇函数，图象关于原点对称，故A，C错误；又当x＞1时，ln|x|=lnx＞0，∴f（x）＞0，故D错误，故选B．34．函数的图象大致为（）A．B．C．D．【解答】解：f（﹣x）==﹣=﹣f（x），∴函数f（x）为奇函数，则图象关于原点对称，故排A，B，当x=时，f（）==故选：D二．解答题（共6小题）35．在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C1的极坐标方程为ρcosθ=4．（1）M为曲线C1上的动点，点P在线段OM上，且满足|OM|•|OP|=16，求点P的轨迹C2的直角坐标方程；（2）设点A的极坐标为（2，），点B在曲线C2上，求△OAB 面积的最大值．【解答】解：（1）曲线C1的直角坐标方程为：x=4，设P（x，y），M（4，y0），则，∴y0=，∵|OM||OP|=16，∴=16，即（x2+y2）（1+）=16，∴x4+2x2y2+y4=16x2，即（x2+y2）2=16x2，两边开方得：x2+y2=4x，整理得：（x﹣2）2+y2=4（x≠0），∴点P的轨迹C2的直角坐标方程：（x﹣2）2+y2=4（x≠0）．（2）点A的直角坐标为A（1，），显然点A在曲线C2上，|OA|=2，∴曲线C2的圆心（2，0）到弦OA的距离d==，∴△AOB的最大面积S=|OA|•（2+）=2+．36．在直角坐标系xOy中，曲线C1的参数方程为（t 为参数，a＞0）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=4cosθ．（Ⅰ）说明C1是哪种曲线，并将C1的方程化为极坐标方程；（Ⅱ）直线C3的极坐标方程为θ=α0，其中α0满足tanα0=2，若曲线C1与C2的公共点都在C3上，求a．【解答】解：（Ⅰ）由，得，两式平方相加得，x2+（y﹣1）2=a2．∴C1为以（0，1）为圆心，以a为半径的圆．化为一般式：x2+y2﹣2y+1﹣a2=0．①由x2+y2=ρ2，y=ρsinθ，得ρ2﹣2ρsinθ+1﹣a2=0；（Ⅱ）C2：ρ=4cosθ，两边同时乘ρ得ρ2=4ρcosθ，∴x2+y2=4x，②即（x﹣2）2+y2=4．由C3：θ=α0，其中α0满足tanα0=2，得y=2x，∵曲线C1与C2的公共点都在C3上，∴y=2x为圆C1与C2的公共弦所在直线方程，①﹣②得：4x﹣2y+1﹣a2=0，即为C3 ，∴1﹣a2=0，∴a=1（a＞0）．37．在直角坐标系xOy中，曲线C1的参数方程为（α为参数），以坐标原点为极点，以x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为ρsin（θ+）=2．（1）写出C1的普通方程和C2的直角坐标方程；（2）设点P在C1上，点Q在C2上，求|PQ|的最小值及此时P 的直角坐标．【解答】解：（1）曲线C1的参数方程为（α为参数），移项后两边平方可得+y2=cos2α+sin2α=1，即有椭圆C1：+y2=1；曲线C2的极坐标方程为ρsin（θ+）=2，即有ρ（sinθ+cosθ）=2，由x=ρcosθ，y=ρsinθ，可得x+y﹣4=0，即有C2的直角坐标方程为直线x+y﹣4=0；（2）由题意可得当直线x+y﹣4=0的平行线与椭圆相切时，|PQ|取得最值．设与直线x+y﹣4=0平行的直线方程为x+y+t=0，联立可得4x2+6tx+3t2﹣3=0，由直线与椭圆相切，可得△=36t2﹣16（3t2﹣3）=0，解得t=±2，显然t=﹣2时，|PQ|取得最小值，即有|PQ|==，此时4x2﹣12x+9=0，解得x=，即为P（，）．另解：设P（cosα，sinα），由P到直线的距离为d==，当sin（α+）=1时，|PQ|的最小值为，此时可取α=，即有P（，）．38．在直角坐标系xOy中，曲线C的参数方程为，（θ为参数），直线l的参数方程为，（t为参数）．（1）若a=﹣1，求C与l的交点坐标；（2）若C上的点到l距离的最大值为，求a．【解答】解：（1）曲线C的参数方程为（θ为参数），化为标准方程是：+y2=1；a=﹣1时，直线l的参数方程化为一般方程是：x+4y﹣3=0；联立方程，解得或，所以椭圆C和直线l的交点为（3，0）和（﹣，）．（2）l的参数方程（t为参数）化为一般方程是：x+4y﹣a ﹣4=0，椭圆C上的任一点P可以表示成P（3cosθ，sinθ），θ∈[0，2π），所以点P到直线l的距离d为：d==，φ满足tanφ=，且的d 的最大值为．①当﹣a﹣4≤0时，即a≥﹣4时，|5sin（θ+4）﹣a﹣4|≤|﹣5﹣a﹣4|=5+a+4=17解得a=8≥﹣4，符合题意．②当﹣a﹣4＞0时，即a＜﹣4时|5sin（θ+4）﹣a﹣4|≤|5﹣a﹣4|=5﹣a﹣4=1﹣a=17解得a=﹣16＜﹣4，符合题意．39．在平面直角坐标系xOy中，已知直线l的参数方程为（t为参数），曲线C的参数方程为（s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．【解答】解：直线l的直角坐标方程为x﹣2y+8=0，∴P到直线l的距离d==，∴当s=时，d取得最小值=．40．在直角坐标系xOy中，直线l1的参数方程为，（t为参数），直线l2的参数方程为，（m为参数）．设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．（1）写出C的普通方程；（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ（cosθ+sinθ）﹣=0，M为l3与C的交点，求M的极径．【解答】解：（1）∵直线l1的参数方程为，（t为参数），∴消掉参数t得：直线l1的普通方程为：y=k（x﹣2）①；又直线l2的参数方程为，（m为参数），同理可得，直线l2的普通方程为：x=﹣2+ky②；联立①②，消去k得：x2﹣y2=4，即C的普通方程为x2﹣y2=4；（2）∵l3的极坐标方程为ρ（cosθ+sinθ）﹣=0，∴其普通方程为：x+y﹣=0，联立得：，∴ρ2=x2+y2=+=5．∴l3与C的交点M的极径为ρ=．。

高考数学复习考点知识与题型专题讲解训练专题04 函数的图象、零点及应用考点1 作函数的图象 1.作出下列函数的图象． (1)y ＝⎩⎨⎧－2x ＋3，x ≤1，－x 2＋4x －2，x >1；(2)y ＝2x ＋2；【解析】(1)分段分别画出函数的图象，如图①所示．(2)y ＝2x ＋2的图象是由y ＝2x 的图象向左平移2个单位长度得到的，其图象如图②所示．考点2 识图与辨图2.已知定义在区间[0,4]上的函数y ＝f (x )的图象如图所示，则y ＝－f (2－x )的图象为( )【答案】D【解析】法一：先作出函数y ＝f (x )的图象关于y 轴的对称图象，得到y ＝f (－x )的图象； 然后将y ＝f (－x )的图象向右平移2个单位，得到y ＝f (2－x )的图象；再作y ＝f (2－x )的图象关于x 轴的对称图象，得到y ＝－f (2－x )的图象．故选D. 法二：先作出函数y ＝f (x )的图象关于原点的对称图象，得到y ＝－f (－x )的图象；然后将y ＝－f (－x )的图象向右平移2个单位，得到y ＝－f (2－x )的图象．故选D.3．（2021·浙江省诸暨市第二高级中学高三模拟）函数()21xy x e =-的图象是（ ）A ．B ．C ．D ．【答案】A【解析】因为()21xy x e =-，则()21xy x e '=+，1,2x ⎛⎫∈-∞- ⎪⎝⎭时，()210x y x e '=+<，所以函数()21x y x e =-在1,2⎛⎫-∞- ⎪⎝⎭上单调递减，1,2x ⎛⎫∈+∞ ⎪⎝⎭时，()210x y x e '=+>，所以函数()21x y x e =-在1,2⎛⎫-∞- ⎪⎝⎭上单调递增，且12x <时，()210xy x e =-<，所以BCD 均错误，故选：A.4．（2021·吉林高三模拟）函数()6cos 2sin xf x x x=-的图象大致为（ ）．A ．B ．C ．D ．【答案】A 【解析】函数()6cos 2sin xf x x x=-为奇函数，所以排除选项BC ，又当0x >时，()f x 第一个零点为2x π=，所以令4x π=，则有222sin 0,cos0242x x ππ--=>=>，所以排除D.故选：C 考点3 函数图象的应用 考向1 研究函数的性质5.已知函数f (x )＝x |x |－2x ，则下列结论正确的是( ) A ．f (x )是偶函数，递增区间是(0，＋∞) B ．f (x )是偶函数，递减区间是(－∞，1) C ．f (x )是奇函数，递减区间是(－1,1) D ．f (x )是奇函数，递增区间是(－∞，0) 【答案】C【解析】将函数f (x )＝x |x |－2x 去掉绝对值得f (x )＝⎩⎨⎧x 2－2x ，x ≥0，－x 2－2x ，x <0，画出函数f (x )的图象，如图，观察图象可知，函数f (x )的图象关于原点对称，故函数f (x )为奇函数，且在(－1,1)上单调递减．6．（2021·山东烟台高三模拟）设函数()2,01,0x x f x x -⎧≤=⎨>⎩，则满足()()12f x f x +<的x 的取值范围是（ ） A ．(],1-∞- B ．()0,∞+ C ．()1,0- D ．(),0-∞【答案】D【解析】作出函数()f x 的图象如下图所示：所以，函数()f x 在(),0-∞上为减函数，且当0x ≥时，()1f x =， 因为()()12f x f x +<，观察图象可得2021x x x <⎧⎨<+⎩，解得0x <，所以满足()()12f x f x +<的x 的取值范围是(),0-∞.故选：D. 考向2 求不等式解集7.若不等式(x －1)2<log a x (a >0，且a ≠1)在x ∈(1,2)内恒成立，则实数a 的取值范围为( ) A ．(1,2] B.)1,22(C ．(1，2) D ．(2，2) 【答案】A【解析】要使当x ∈(1,2)时，不等式(x －1)2<log a x 恒成立，只需函数y ＝(x －1)2在(1,2)上的图象在y ＝log a x 的图象的下方即可．当0<a <1时，显然不成立；当a >1时，如图，要使x ∈(1,2)时，y ＝(x －1)2的图象在y ＝log a x 的图象的下方，只需(2－1)2≤log a 2，即log a 2≥1，解得1<a ≤2，故实数a 的取值范围是(1,2]．8.（2021·甘肃省会宁县第一中学高三模拟）已知)(f x 在R 上是可导函数，)(f x 的图象如图所示，则不等式)()(2230x x f x '-->解集为（ ）A ．)()(,21,-∞-⋃+∞B ．)()(,21,2-∞-⋃C ．)()()(,11,02,-∞-⋃-⋃+∞D ．)()()(,11,13,-∞-⋃-⋃+∞ 【答案】D【解析】原不等式等价于()22300x x f x '⎧-->⎪⎨>⎪⎩或()22300x x f x '⎧--<⎪⎨<⎪⎩，结合)(f x 的图象可得，3111x x x x ><-⎧⎪⎨-⎪⎩或或或1311x x -<<⎧⎨-<<⎩，解得1x <-或3x >或11x -<<．故选：D ． 考点4 函数图象对称性的应用9.已知lga ＋lgb ＝0，函数f(x)＝a x 与函数g(x)＝－log b x 的图像可能是( )【答案】B【解析】∵lga ＋lgb ＝0，∴lgab ＝0，ab ＝1，∴b ＝1a .∴g(x)＝－log b x ＝log a x ，∴函数f(x)与g(x)互为反函数，图像关于直线y ＝x 对称，故选B.10．（2021·云南高三模拟）已知函数()f x 是R 上的奇函数，且满足()()11f x f x =+-，当(]0,1x ∈，()ln f x x =，则下列关于函数()f x 叙述正确的是（ ）A ．函数()f x 的最小正周期为1B ．函数()f x 在()0,2021内单调递增C ．函数()f x 相邻两个对称中心的距离为2D ．函数()ln y f x x =+在区间()0,2021内有1010个零点 【答案】D【解析】由()()11f x f x =+-得：()()2f x f x +=，()f x ∴最小正周期为2，A 错误； 当(]0,1x ∈时，()ln f x x =，又()f x 为R 上的奇函数，则()00f =， 可得()f x 大致图象如下图所示：由图象可知：()f x 在()0,2021上没有单调性，B 错误；()f x 的对称中心为()()0,k k Z ∈，则相邻的对称中心之间距离为1，C 错误；()ln y f x x =+在区间()0,2021内的零点个数等价于()f x 与ln y x =-在()0,2021内的交点个数，在平面直角坐标系中画出()f x 与ln y x =-大致图象如下图所示：由图象可知：()f x 与ln y x =-在每个()()2,22k k k Z +∈内都有1个交点，且在区间内的交点横坐标等于或小于21k +，∴两个函数在()0,2021内有1010个交点，即()ln y f x x =+在区间()0,2021内有1010个零点，D正确.故选：D.11．（2021·山东淄博高三模拟）已知函数()y f x =的定义域为{|0}x x x ∈≠R ，，且满足()()0f x f x --=，当0x >时，()ln 1f x x x =-+，则函数()y f x =的大致图象为（）．A ．B ．C ．D ．【答案】D【解析】由()()0f x f x --=得函数()f x 为偶函数，排除A 、B 项， 又当0x >时，()ln 1f x x x =-+，∴(1)0f =，()20f e e =-<.故选:D 考点5 判断函数零点所在的区间12.设函数f (x )＝13x －ln x ，则函数y ＝f (x )( )A ．在区间)1,1(e，(1，e)内均有零点B ．在区间)1,1(e，(1，e)内均无零点C ．在区间)1,1(e 内有零点，在区间(1，e)内无零点D ．在区间)1,1(e内无零点，在区间(1，e)内有零点【答案】D【解析】法一：图象法 令f (x )＝0得13x ＝ln x ．作出函数y ＝13x 和y ＝ln x 的图象，如图， 显然y ＝f (x )在)1,1(e内无零点，在(1，e)内有零点．法二：定理法当x ∈),1(e e 时，函数图象是连续的，且f ′(x )＝13－1x ＝x －33x <0，所以函数f (x )在),1(e e 上单调递减．又f )1(e ＝13e ＋1>0，f (1)＝13>0，f (e)＝13e －1<0，所以函数有唯一的零点在区间(1，e)内．13．（2021·黑龙江高三模拟）函数()1293xf x x ⎛⎫=-- ⎪⎝⎭的零点所在的一个区间是（）A ．()1,2B ．()1,0-C ．()0,1D ．()2,1--【答案】D【解析】如图，绘出函数13xy ⎛⎫= ⎪⎝⎭与函数29y x =+的图像，结合图像易知，函数()1293xf x x ⎛⎫=-- ⎪⎝⎭的零点所在的一个区间是()2,1--，故选：D.考点6 判断函数零点(或方程根)的个数14.(2021·福建期末)已知函数f (x )＝⎩⎪⎨⎪⎧x 2－2x ，x ≤0，1＋1x ，x >0，则函数y ＝f (x )＋3x 的零点个数是( )A ．0B ．1C ．2D ．3【答案】C【解析】解方程法，令f (x )＋3x ＝0， 则⎩⎨⎧x ≤0，x 2－2x ＋3x ＝0或⎩⎪⎨⎪⎧x >0，1＋1x ＋3x ＝0，解得x ＝0或x ＝－1，所以函数y ＝f (x )＋3x 的零点个数是2.15．（2021·山东潍坊高三模拟）已知函数221,0()2,0x x f x x x x ⎧->=⎨--≤⎩，若函数()()g x f x m =-有3个零点，则实数m 的取值范围（ ） A ．()1,0- B ．[]1,0-C ．（0，1）D ．[]0,1【答案】C【解析】因为函数()()g x f x m =-有3个零点，所以()()0g x f x m =-=有三个实根，即直线y m =与函数()y f x =的图象有三个交点．作出函数()y f x =图象，由图可知，实数m 的取值范围是(0,1)．故选：C ．16．（2021·浙江镇海中学高三模拟）函数4()log (||1)cos f x x x π=+-的零点个数为（ ） A ．9 B ．8C ．7D ．6【答案】D【解析】令()4log (||1)x g x =+ ，因为10x +>恒成立，则()g x 的定义域为R ， 由()()44log (||1)log (||1)x g x x g x --+=+==，所以()g x 为偶函数， 当0x >时，()4log (1)g x x +=，在()0,∞+上单调递增，令()cos h x x π=， 分别画出()g x 与()h x 的函数图象，由图可知，()g x 与()h x 有六个交点， 即函数4()log (||1)cos f x x x π=+-有六个零点.故选: D.考点7 函数零点的应用 考向1 根据零点的范围求参数17.若函数f(x)＝2x －2x －a 的一个零点在区间(1，2)内，则实数a 的取值范围是( ) A ．(1，3) B ．(1，2) C ．(0，3) D ．(0，2) 【答案】C【解析】由条件可知f(1)f(2)<0，即(2－2－a)(4－1－a)<0，即a(a －3)<0，解之得0<a<3.18．（2021·浙江高一期末）已知函数()()2log 1,1212,1x x x f x x ⎧-<-⎪=⎨-+≥-⎪⎩，若函数()()F x f x k =- 恰有3个零点，则实数k 的取值范围是（ ）A ．52,2⎛⎤⎥⎝⎦B ．()2,3C ．(]3,4D ．()2,+∞【答案】A【解析】函数()()F x f x k =- 恰有3个零点，即函数()y f x =与()h x k =的图象有三个交点，分别画出()y f x =与()h x k =的图象，如图所示，5(1)2f -=，观察图象可得，当522k <≤时，两图象有3个交点，即函数()()F x f x k =-恰有3个零点.故选：A.19．（2021·江西高三模拟）设函数,10()11,01(1)x x f x x f x -<≤⎧⎪=⎨+<<⎪-⎩，若函数()4y f x t =-在区间()1,1-内有且仅有一个零点，则实数的取值范围是（ ）A ．1,4⎛⎫-+∞ ⎪⎝⎭B ．1,04⎛⎫- ⎪⎝⎭C ．1,4⎛⎫-∞- ⎪⎝⎭D ．1,{0}4⎛⎤-∞- ⎥⎝⎦【答案】D【解析】因为()(),1011,011x x f x x f x -<≤⎧⎪=⎨+<<⎪-⎩所以(),1011,011x x f x x x -<≤⎧⎪=⎨+<<⎪-⎩，其图象如下：函数()4y f x t =-在区间()1,1-内有且仅有一个零点，等价于()40f x t -=在区间()1,1-内有且仅有一个实数根，又等价于函数()y f x =的图象与直线4y t =在区间()1,1-内有且仅有一个公共点. 于是41t ≤-或40t =，解得14t ≤-或0t =.故选：D 考向2 已知函数零点或方程根的个数求参数20．（2020·湖南高三模拟）已知函数2141,0()1,02x x x x f x x +⎧-+≥⎪=⎨⎛⎫<⎪ ⎪⎝⎭⎩，若()()g x f x a =-恰好有3个零点，则实数a 的取值范围为（ ） A ．[0,1) B ．(0,1)C ．1,12⎡⎫⎪⎢⎣⎭D ．1,12⎛⎤ ⎥⎝⎦【答案】D【解析】由条件可知()0f x a -=()a f x ⇒=()()g x f x a =-恰好有3个零点，等价于y a =与()y f x =有3个交点，如图画出函数的图象，由图象可知112a <≤.故选：D21.(2021·安庆摸底)若函数f (x )＝4x －2x －a ，x ∈[－1,1]有零点，则实数a 的取值范围是________．【答案】]2,41[-【解析】∵函数f (x )＝4x －2x －a ，x ∈[－1,1]有零点， ∴方程4x －2x －a ＝0在[－1,1]上有解， 即方程a ＝4x －2x 在[－1,1]上有解． 方程a ＝4x －2x 可变形为a ＝2)412(-x －14，∵x ∈[－1,1]，∴2x ∈]2,21[，∴2)412(-x －14∈]2,41[-∴实数a 的取值范围是]2,41[-考点8 用函数图象刻画变化过程22.甲、乙二人同时从A 地赶往B 地，甲先骑自行车到两地的中点再改为跑步，乙先跑步到中点再改为骑自行车，最后两人同时到达B 地．已知甲骑车比乙骑车的速度快，且两人骑车速度均大于跑步速度．现将两人离开A 地的距离s 与所用时间t 的函数关系用图象表示，则下列给出的四个函数图象中，甲、乙的图象应该是( )A ．甲是图①，乙是图②B ．甲是图①，乙是图④C ．甲是图③，乙是图②D ．甲是图③，乙是图④ 【答案】B【解析】由题知速度v ＝st 反映在图象上为某段图象所在直线的斜率．由题知甲骑自行车速度最大，跑步速度最小，甲与图①符合，乙与图④符合．23．（2021·重庆高三模拟）匀速地向一底面朝上的圆锥形容器注水，则该容器盛水的高度h 关于注水时间t 的函数图象大致是（ ）A ．B ．C ．D ．【答案】A【解析】设圆锥PO 底面圆半径r ，高H ，注水时间为t 时水面与轴PO 交于点O '，水面半径AO x '=，此时水面高度PO h '=，如图：由垂直于圆锥轴的截面性质知，xhr H =，即r x h H=⋅，则注入水的体积为2223211()333r r V x h h h h H H πππ==⋅⋅=⋅，令水匀速注入的速度为v ，则注水时间为t 时的水的体积为V vt =，于是得2223333222333r H vt H v h vt h h t H r r πππ⋅=⇒=⇒=⋅，而,,r H v 都是常数，即2323H v r π是常数，所以盛水的高度h 与注水时间t 的函数关系式是23323H v h tr π=⋅，203r H t v π≤≤，223323103H v h t r π-'=⋅>，函数图象是曲线且是上升的，随t 值的增加，函数h 值增加的幅度减小，即图象是先陡再缓，A 选项的图象与其图象大致一样，B ，C ，D 三个选项与其图象都不同.故选：A 24．（2021·浙江高三模拟）如图，设有圆O 和定点C ，当l 从0l 开始在平面上绕O 匀速旋转（旋转角度不超过90︒）时，它扫过圆内阴影部分面积S 是时间t 的函数，它的图像大致是如下哪一种（ ）A ．B ．C ．D ．【答案】C【解析】当直线l 从初始位置0l 转到经过点C 的过程中阴影部分面积增加的越来越快，图像越来越“陡峭”；l 从过点C 的位置转至结束时阴影部分面积增加的越来越慢，图像越来越“平缓”，故选：C.考点9 应用所给函数模型解决实际问题25.某市家庭煤气的使用量x (m 3)和煤气费f (x )(元)满足关系f (x )＝⎩⎨⎧C ，0<x ≤A ，C ＋B x －A ，x >A .已知某家庭2018年前三个月的煤气费如表： 月份 用气量 煤气费 一月份 4 m 3 4元 二月份 25 m 3 14元 三月份35 m 319元若四月份该家庭使用了20 m 3的煤气，则其煤气费为( ) A ．11.5元 B ．11元 C ．10.5元 D ．10元 【答案】A【解析】根据题意可知f (4)＝C ＝4，f (25)＝C ＋B (25－A )＝14，f (35)＝C ＋B (35－A )＝19，解得A ＝5，B ＝12，C ＝4，所以f (x )＝⎩⎪⎨⎪⎧4，0<x ≤5，4＋12x －5，x >5，所以f (20)＝4＋12×(20－5)＝11.5.26．（2021·湖南高三期末）某工厂8年来某种产品年产量C 与时间t (年)的函数关系如图所示.以下四种说法：①前三年产量增长的速度越来越快； ②前三年产量增长的速度越来越慢； ③第三年后这种产品停止生产； ④第三年到第八年每年的年产量保持不变. 其中说法正确的序号是________. 【答案】②④【解析】由图可知，前3年的产量增长的速度越来越慢，故①错误，②正确； 第三年后这种产品的产量保持不变，故③错误，④正确； 综合所述，正确的为：②④. 故答案为：②④.27．（【百强校】福建师范大学附属中学2020-2021学年高一上学期期末考试数学试题）如图所示，边长为 1的正方形PABC 沿 x 轴从左端无穷远处滚向右端无穷远处，点B 恰好能经过原点．设动点P 的纵坐标关于横坐标的函数解析式为()y f x =，则对函数()y f x =有下列判断：①函数()y f x = 是偶函数； ②()y f x =是周期为 4 的函数；③函数 ()y f x =在区间[10，12] 上单调递减； ④函数 ()y f x = 在区间[1，1] 上的值域是[1，2] 其中判断正确的序号是_______．(写出所有正确结论的序号) 【答案】①②④【解析】当2x 1-≤<-时，P 的轨迹是以A 为圆心，半径为1的14圆当1x 1-≤<时，P 的轨迹是以B 为圆心，半径为2的14圆 当1x 2≤<时，P 的轨迹是以C 为圆心，半径为1的14圆当2x 3≤≤时，P 的轨迹是以A 为圆心，半径为1的14圆 故函数的周期为4因此最终构成图象如下所示：①根据图象的对称性可知函数()y f x =是偶函数；故正确②由图可得()f x 的周期为4，故正确③函数()y f x =在区间[2，4]上为增函数，故在区间[10，12]上也是增函数，故错误 ④在区间[1，1]上的值域是[1，2]，故正确 综上，正确的序号是①②④考点10 构建函数模型解决实际问题 考向1 构建二次函数模型28.有一批材料可以建成200 m 长的围墙，如果用此材料在一边靠墙的地方围成一块矩形场地，中间用同样的材料隔成三个面积相等的矩形(如图所示)，则围成的矩形场地的最大面积为________ m 2.(围墙厚度不计) 【答案】2 500【解析】设围成的矩形场地的长为x m ，则宽为200－x4 m ，则S ＝x ·200－x 4＝14(－x 2＋200x )． 当x ＝100时，S max ＝2 500 (m 2)．29．（2021·四川高三模拟）某市出租车的计价标准为1.2元/km ，起步价为6元，即最初3km （不含3km ）计费6元.若某人乘坐该市的出租车去往13km 处的目的地，且一路畅通，等候时间为0，那么他需要支付的车费为_____. 【答案】19.2【解析】乘车距离为x km ，车费为y 元，由题意得：6,036 1.2,346 1.22,456 1.23,56x x y x x <<⎧⎪+≤<⎪⎪=+⨯≤<⎨⎪+⨯≤<⎪⎪⎩， 所以当13x =时，()6132 1.219.2y =+-⨯=元，所以他需要支付的车费为19.2元，故答案为：19.230（2021·河南郑州一中高三模拟）在“绿水青山就是金山银山”的环保理念指引下，结合最新环保法规和排放标准，各企业单位勇于担起环保的社会责任，采取有针对性的管理技术措施，开展一系列卓有成效的改造．已知某化工厂每月收入为100万元，若不改善生产环节将受到环保部门的处罚，每月处罚20万元．该化工厂一次性投资500万元建造垃圾回收设备，一方面可以减少污染避免处罚，另一方面还能增加废品回收收入．据测算，投产后的累计收入是关于月份x 的二次函数，前1月、前2月、前3月的累计收入分别为100.5万元、202万元和304.5万元．当改造后累计纯收入首次多于不改造的累计纯收入时，x =（ ）A ．18B ．19C ．20D ．21【答案】A【解析】不妨设投产后的累计收入2y ax bx c =++，则100.520242304.593a b c a b c a b c =++⎧⎪=++⎨⎪=++⎩，解得1,100,02a b c ===， 211002y x x ∴=+， ∴改造后累计纯收入为215001005002y x x -=+-， 不改造的累计纯收入为()10020x -，令()21100500100202x x x +->-， 即212050002x x +->， 解得201014x >-+201014x <--，20101417.4x ∴>-+，x N *∈，x 的最小值为18.故选：A 考向2 构建指数函数、对数函数模型31.某位股民购进某支股票，在接下来的交易时间内，他的这支股票先经历了n 次涨停(每次上涨10%)，又经历了n 次跌停(每次下跌10%)，则该股民这支股票的盈亏情况(不考虑其他费用)为( )A ．略有盈利B ．略有亏损C ．没有盈利也没有亏损D ．无法判断盈亏情况【答案】B【解析】设该股民购进这支股票的价格为a 元，则经历n 次涨停后的价格为a (1＋10%)n ＝a ×1.1n 元，经历n 次跌停后的价格为a ×1.1n ×(1－10%)n ＝a ×1.1n ×0.9n ＝a ×(1.1×0.9)n ＝0.99n ·a <a ，故该股民这支股票略有亏损．32.声强级1L （单位：dB ）与声强I 的函数关系式为：11210lg 10I L -⎛⎫= ⎪⎝⎭.若普通列车的声强级是95dB ，高速列车的声强级为45dB ，则普通列车的声强是高速列车声强的（ ） A ．610倍B ．510倍C ．410倍D ．310倍【答案】B【解析】设普通列车的声强为1I ，高速列车的声强为2I ，因为普通列车的声强级是95dB ，高速列车的声强级为45dB ，所以1129510lg 10I -⎛⎫= ⎪⎝⎭，2124510lg 10I -⎛⎫= ⎪⎝⎭， ()11129510lg 10lg 1210I I -⎛⎫==+ ⎪⎝⎭，解得12.5lg I -=，所以 2.5110I -=， ()22124510lg 10lg 1210I I -⎛⎫==+ ⎪⎝⎭，解得27.5lg I -=，所以7.5210I -=， 两式相除得 2.5517.52101010I I --==， 则普通列车的声强是高速列车声强的510倍.故选：B.33．（2020·重庆市酉阳第一中学校高三月考）为了衡量星星的明暗程度，古希腊天文学家喜帕恰斯（Hipparchus ，又名依巴谷）在公元前二世纪首先提出了星等这个概念.星等的数值越小，星星就越亮；星等的数值越大它的光就越暗.到了1850年，英国天文学家普森又提出了亮度的概念，并提出著名的普森公式：22112.51g E m m E -=-，联系两个天体的星等1m ､2m 和它们对应的亮度1E ､2E .这个星等尺度的定义一直沿用至今.已知南十字星座的“十字架三”星等是1.26，猎户星座的“参宿一”星等是1.76，则“十字架三”的亮度大约是“参宿一”的（ ）倍.（当x 较小时，2101 2.3 2.7x x x ≈++）A ．1.567B ．1.568C ．1.569D ．1.570 【答案】B【解析】设“十字架三”的星等是1m ，“参宿一”的星等是2m ，“十字架三”的亮度是1E ，“参宿一”的亮度是2E ，则1 1.26m =，2 1.76m =，设12E rE =， 两颗星的星等与亮度满足22112.51gE m m E -=-， 211.76 1.26 2.51g E E ∴-=-，0.21210E E =0.22101 2.30.2 2.7(0.2) 1.568r ∴=≈+⨯+⨯=，∴与r 最接近的是1.568，故选B ． 考向3 构建分段函数模型34（2021·广东江门市·高三模拟）某医药研究所开发一种新药，如果成年人按规定的剂量服用，据监测，服药后每毫升血液中的含药量（微克）与时间（时）之间近似满足如图所示的图象．据进一步测定，每毫升血液中含药量不少于0.25微克时，治疗疾病有效，则服药一次治疗疾病有效的时间为___________小时．【答案】7916【解析】当01t ≤≤时，函数图象是一个线段，由于过原点与点()1,4，故其解析式为4,01y t t =≤≤，当 1t ≥时，函数的解析式为12t a y -⎛⎫= ⎪⎝⎭，因为()1,4M 在曲线上，所以1142a -⎛⎫= ⎪⎝⎭，解得 3a =， 所以函数的解析式为31,12t y t -⎛⎫=≥ ⎪⎝⎭， 综上，34(01)()1(1)2t t t y f t t -≤<⎧⎪==⎨⎛⎫≥ ⎪⎪⎝⎭⎩，由题意有340.2510.252t t -≥⎧⎪⎨⎛⎫≥ ⎪⎪⎝⎭⎩，解得1165t t ⎧≥⎪⎨⎪≤⎩，所以1516t ≤≤， 所以服药一次治疗疾病有效的时间为17951616-=个小时，故答案为：7916． 35．（2020·福建三明市·三明一中高三期中）某在校大学生提前创业，想开一家服装专卖店，经过预算，店面装修费为10000元，每天需要房租水电等费用100元，受营销方法、经营信誉度等因素的影响，专卖店销售总收入P 与店面经营天数x 的关系是21300,0300()245000,300x x x P x x ⎧-≤<⎪=⎨⎪≥⎩，则总利润最大时店面经营天数是__________，最大总利润是__________．【答案】200 10000元【解析】由题意，0300x ≤<时，221130010010000(200)1000022y x x x x =---=--+，200x ∴=时，10000max y =；300x ≥时，4500010010000350001005000y x x =--=-≤，200x ∴=天时，总利润最大为10000元 故答案为：200, 10000元。

2022版新高考数学总复习--§2.5函数的图象—五年高考—考点1函数的图象1.(2021浙江,7,4分)已知函数f(x)=x2+14,g(x)=sin x,则图象为下图的函数可能是()A.y=f(x)+g(x)-14B.y=f(x)-g(x)-14C.y=f(x)g(x)D.y=g(x)f(x)答案D2.(2020浙江,4,4分)函数y=x cos x+sin x在区间[-π,π]上的图象可能是()答案A3.(2020天津,3,5分)函数y=4xx2+1的图象大致为()答案A4.(2019课标Ⅰ,文5,理5,5分)函数f(x)=sinx+xcosx+x2在[-π,π]的图象大致为()答案D5.(2019浙江,6,4分)在同一直角坐标系中,函数y=1a x ,y=log a(x+12)(a>0,且a≠1)的图象可能是()答案D6.(2018课标Ⅱ,文3,理3,5分)函数f(x)=e x-e-xx2的图象大致为()答案B7.(2018课标Ⅲ理,7,5分)函数y=-x4+x2+2的图象大致为()答案D8.(2018浙江,5,4分)函数y=2|x|sin 2x的图象可能是()答案D以下为教师用书专用(1—8)的部分图象大致为() 1.(2017课标Ⅰ文,8,5分)函数y=sin2x1-cosx答案 C 本题考查函数图象的识辨. 易知y =sin2x1-cosx 为奇函数,图象关于原点对称,故排除B 选项;sin 2≈sin 120°=√32,cos 1≈cos 60°=12,则f (1)=sin21-cos1=√3,故排除A 选项;f (π)=sin2π1-cos π=0,故排除D 选项,故选C .方法总结 已知函数解析式判断函数图象的方法:(1)根据函数的定义域判断图象的左右位置,根据函数的值域判断图象的上下位置; (2)根据函数的单调性判断图象的变化趋势; (3)根据函数的奇偶性判断图象的对称性; (4)根据函数的周期性判断图象的循环往复.2.(2017课标Ⅲ文,7,5分)函数y =1+x +sinxx 2的部分图象大致为( )答案 D 当x ∈(0,1)时,sin x >0,∴y =1+x +sinxx 2>1+x >1,排除A 、C . 令f (x )=x +sinx x 2,则f (-x )=-x +sin (-x )(-x )2=-f (x ),∴f (x )=x +sinxx 2是奇函数, ∴y =1+x +sinxx 2的图象关于点(0,1)对称,故排除B .故选D .解后反思 函数图象问题,一般从定义域、特殊点的函数值、单调性、奇偶性等方面入手进行分析.选择题通常采用排除法.3.(2016课标Ⅰ,理7,文9,5分)函数y =22-e |x |在[-2,2]的图象大致为( )答案 D 当x =2时,y =8-e 2∈(0,1),排除A ,B ;易知函数y =2x 2-e |x |为偶函数,当x ∈[0,2]时,y =2x 2-e x,求导得y'=4x -e x ,当x =0时,y'<0,当x =2时,y'>0,所以存在x 0∈(0,2),使得y'=0,故选D .4.(2016浙江,3,5分)函数y =sin x 2的图象是 ( )答案 D 排除法.由y =sin x 2为偶函数判断函数图象的对称性,排除A ,C ;当x =π2时,y =sin (π2)2=sin π24≠1,排除B ,故选D .5.(2015课标Ⅱ,理10,文11,5分)如图,长方形ABCD 的边AB =2,BC =1,O 是AB 的中点.点P 沿着边BC ,CD 与DA 运动,记∠BOP =x.将动点P 到A ,B 两点距离之和表示为x 的函数f (x ),则y =f (x )的图象大致为( )答案 B 当点P 与C 、D 重合时,易求得PA +PB =1+√5;当点P 为DC 的中点时,有OP ⊥AB ,则x =π2,易求得PA +PB =2PA =2√2.显然1+√5>2√2,故当x =π2时, f (x )没有取到最大值,则C 、D 选项错误.当x ∈[0,π4)时, f (x )=tan x +√4+tan 2x ,不是一次函数,排除A ,故选B .6.(2015安徽文,10,5分)函数f (x )=ax 3+bx 2+cx +d 的图象如图所示,则下列结论成立的是 ( )A.a >0,b <0,c >0,d >0B.a >0,b <0,c <0,d >0C.a <0,b <0,c >0,d >0D.a >0,b >0,c >0,d <0答案 A 由f (x )的图象易知d >0,且f '(x )=3ax 2+2bx +c 的图象是开口向上的抛物线,与x 轴正半轴有两个不同的交点,则{a >0,-b 3a>0,c >0,即{a >0,b <0,c >0,故选A .评析 本题考查导数的应用及运用图象解题的能力.7.(2015浙江,5,5分)函数f (x )=(x -1x )cos x (-π≤x ≤π且x ≠0)的图象可能为 ( )答案 D 因为f (-x )=(-x +1x )cos (-x )=-(x -1x )cos x =-f (x ),所以函数f (x )为奇函数,排除A 、B .当0<x <1时,x -1x <0,cos x >0,所以f (x )<0,排除C ,故选D .8.(2012课标理,10,5分)已知函数f (x )=1ln (x+1)-x ,则y =f (x )的图象大致为( )答案 B 令g (x )=ln (x +1)-x ,则g'(x )=1x+1-1=-xx+1, ∴当-1<x <0时,g'(x )>0,当x >0时,g'(x )<0,∴g (x )max =g (0)=0.∴f (x )<0,排除A 、C ,又由定义域可排除D ,故选B .评析 本题考查了函数的图象,考查了利用导数判断函数单调性,求值域,考查了数形结合的数学思想.考点2 函数图象的应用1.(2020北京,6,4分)已知函数f (x )=2x-x -1,则不等式f (x )>0的解集是 ( )A.(-1,1)B.(-∞,-1)∪(1,+∞)C.(0,1)D.(-∞,0)∪(1,+∞) 答案 D2.(2017天津文,8,5分)已知函数f (x )={|x |+2,x <1,x +2x,x ≥1.设a ∈R ,若关于x 的不等式f (x )≥|x2+a|在R 上恒成立,则a 的取值范围是 ( )A.[-2,2]B.[-2√3,2]C.[-2,2√3]D.[-2√3,2√3] 答案 A以下为教师用书专用(1—2)1.(2016课标Ⅱ,12,5分)已知函数f (x )(x ∈R )满足f (-x )=2-f (x ),若函数y =x+1x与y =f (x )图象的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则∑i=1m(x i +y i )=( )A.0B.mC.2mD.4m答案 B 由f (-x )=2-f (x )可知f (x )的图象关于点(0,1)对称,又易知y =x+1x =1+1x的图象关于点(0,1)对称,所以两函数图象的交点成对出现,且每一对交点都关于点(0,1)对称,∴∑i=1m(x i +y i )=0×m2+2×m 2=m.故选B .思路分析 分析出函数y =f (x )和y =x+1x的图象都关于点(0,1)对称,进而得两函数图象的交点成对出现,且每一对交点都关于点(0,1)对称,从而得出结论.2.(2015安徽文,14,5分)在平面直角坐标系xOy 中,若直线y =2a 与函数y =|x -a |-1的图象只有一个交点,则a 的值为 . 答案 -12解析 若直线y =2a 与函数y =|x -a |-1的图象只有一个交点,则方程2a =|x -a |-1只有一解,即方程|x -a |=2a +1只有一解,故2a +1=0,所以a =-12.— 三年模拟 —A 组 考点基础题组考点1 函数的图象1.(2020河北新时代NT 教育模拟)已知函数f (x )={e x -4,x ≥0,e -x -4,x <0,则函数g (x )=x 2f (x )的大致图象是 ( )答案 A2.(2020湖南炎陵一中仿真考试)函数f (x )=x 4e x -e -x 的部分图象可能是( )答案 B3.(2021湖南岳阳一模,3)函数f (x )=x +ln |x |x的图象大致为 ( )A BCD答案 A4.(2021辽宁沈阳市郊联体一模,4)函数f (x )=xcosx -1的部分图象大致是 ( )A BCD答案 D5.(2021山东德州二模,5)函数f (x )=2x+1·ln |x |4x +1的部分图象大致为 ( )A BCD答案 A6.(2020普通高等学校招生全国统一考试考前演练)某函数的部分图象如图,则下列函数中可以作为该函数的解析式的是 ( )A.y =sin2xe sin2xB.y =cos2xe cos2x C.y =|cos2x |e cos2xD.y =|cosx |e cosx答案 C7.(2021福建三明三模,5)若函数y =f (x )的大致图象如图所示,则f (x )的解析式可能是 ( )A. f (x )=x|x |-1 B. f (x )=x1-|x | C. f (x )=xx 2-1 D. f (x )=x1-x 2答案Ce|x|在[-32,32]上的图象大致为()8.(2020山东百师联盟自测,7)函数f(x)=2|x|cos x-12答案A考点2函数图象的应用(多选题)(2021江苏南通一模,12)已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=e x(x+1),则下列命题正确的是()A.当x>0时,f(x)=-e-x(x-1)B.函数f(x)有3个零点C. f(x)<0的解集为(-∞,-1)∪(0,1)D.∀x1,x2∈R,都有|f(x1)-f(x2)|<2答案BCDB组综合应用题组时间:30分钟分值:30分一、单项选择题(每小题5分,共20分)1.(2021山东日照一模,6)如图所示,单位圆上一定点A与坐标原点重合.若单位圆从原点出发沿x轴正向滚动一周,则A点形成的轨迹为()A BCD 答案 A2.(2021上海普陀二模,16)已知函数f (x )=3x 1+3x ,设x i (i =1,2,3)为实数,且x 1+x 2+x 3=0.给出下列结论: ①若x 1·x 2·x 3>0,则f (x 1)+f (x 2)+f (x 3)<32;②若x 1·x 2·x 3<0,则f (x 1)+f (x 2)+f (x 3)>32.其中正确的是 ( ) A.①与②均正确 B.①正确,②不正确C.①不正确,②正确D.①与②均不正确答案 A3.(2020河北邯郸备考检测,8)函数f (x )=e x +1e x -1·cos x 的部分图象大致为 ( )答案 A4.(2020普通高等学校招生全国统一考试考前演练,9)设符号min {x ,y ,z }表示x ,y ,z 中的最小者,已知函数f (x )=min {|x -2|,x 2,|x +2|},则下列结论正确的是 ( )A.∀x ∈[0,+∞), f (x -2)>f (x )B.∀x ∈[1,+∞), f (x -2)>f (x )C.∀x ∈R , f (f (x ))≤f (x )D.∀x ∈R , f (f (x ))>f (x )答案 C二、多项选择题(每小题5分,共10分)5.(2021江苏七市第二次调研,10)已知函数f (x )=√|x 2-a |(a ∈R ),则y =f (x )的大致图象可能为 ( )AB C D答案 ABD 6.(2021山东聊城二模,12)用符号[x ]表示不超过x 的最大整数,例如:[0.6]=0,[2.3]=2.设f (x )=(1-ln x )(ax 2+2ln x )有3个不同的零点x 1,x 2,x 3,则 ( )A.x =e 是f (x )的一个零点B.x 1+x 2+x 3=2√e +eC.a 的取值范围是(-1e ,0)D.若[x 1]+[x 2]+[x 3]=6,则a 的范围是[-2ln39,-ln24) 答案 AD — 一年原创 —1.(2021 5·3原创题)已知某函数图象如图所示,则该函数有可能是 ( )A.f (x )=(x 2-cx )e xB.f (x )=(x 2-cx )ln (x +3) C.f (x )=13x 3-cx D.f (x )=x 2-cx e x答案 A2.(2021 5·3原创题)若偶函数f (x )=ax 2+(b -2)x 的图象过点A (1,2),则函数g (x )=bx +a x ,x ∈[-3,-12]的值域为 .答案 [-203,-4]。

三角函数的图像和性质学校:___________姓名：___________班级：___________考号：___________1.函数y＝lgcos x的定义域为( )A. (2k π，＋2kπ)(k∈Z)B. (－＋2k π，＋2kπ)(k∈Z)C. (k π，＋kπ)(k∈Z)D. (－＋k π，＋kπ)(k∈Z)2.将函数的图象向左平移个单位长度，再将得到的图象上的全部点的横坐标变为原来的2倍（纵坐标不变），最终得到函数的图象，则（）A. B. C. D.3.将函数的图象上各点向右平行移动个单位长度，再把横坐标缩短为原来的一半，纵坐标伸长为原来的4倍，则所得到的图象的函数解析式是（）A. B.C. D.4.函数y＝cos－2x的单调递增区间是()A. (k∈Z)B. (k∈Z)C. (k∈Z)D. (k∈Z)5.函数的单调递减区间为（）A. B.C. D.6.函数在定义域内零点的个数为A. 3B. 4C. 6D. 77.下列函数中最小值为8的是（）A. B. C . D.18.函数的图象向右平移个单位长度后得到函数g(x)的图象，且g(x)的图象的一条对称轴是直线，则ω的最小值为．9.函数的单调减区间为（）A. B.C. D.10.已知函数．（1）求的最小正周期和单调递减区间；（2）试比较与的大小．1.【答案】B2.【答案】C3.【答案】A4.【答案】B5.【答案】B6.【答案】C7.【答案】D8.【答案】9.【答案】A10.【答案】解：（1），∴函数的最小正周期为．令，得，函数的单调增区间为，函数的单调减区间为，（2），．，且在上单调递增，，即．3。

高三数学函数图像试题答案及解析1.设函数f(x)＝x＋的图象为C1，C1关于点A(2,1)对称的图象为C2，C2对应的函数为g(x)．(1)求g(x)的解析式；(2)若直线y＝m与C2只有一个交点，求m的值和交点坐标．【答案】（1）g(x)＝x－2＋.（2）当m＝0时，经检验合理，交点为(3,0)；当m＝4时，经检验合理，交点为(5,4)．【解析】解：(1)设点P(x，y)是C2上的任意一点，则P(x，y)关于点A(2,1)对称的点为P′(4－x,2－y)，代入f(x)＝x＋，可得2－y＝4－x＋，即y＝x－2＋，∴g(x)＝x－2＋.(2)由消去y得x2－(m＋6)x＋4m＋9＝0，Δ＝[－(m＋6)]2－4(4m＋9)，∵直线y＝m与C2只有一个交点，∴Δ＝0，解得m＝0或m＝4.当m＝0时，经检验合理，交点为(3,0)；当m＝4时，经检验合理，交点为(5,4)．2.如图，是张大爷晨练时所走的离家距离(y)与行走时间(x)之间的函数关系的图象．若用黑点表示张大爷家的位置，则张大爷散步行走的路线可能是()【答案】D【解析】根据图象可知在第一段时间张大爷离家距离随时间的增加而增加，在第二段时间内，张大爷离家的距离不变，第三段时间内，张大爷离家的距离随时间的增加而减少，最后回到始点位置，对比各选项，只有D正确．3.已知函数f(x)＝x1，x2，x3，x4，x5是方程f(x)＝m的五个不等的实数根，则x1＋x2＋x3＋x4＋x5的取值范围是()A．(0，π)B．(－π，π)C．(lg π，1)D．(π，10)【答案】D【解析】函数f(x)的图象如图所示，结合图象可得x1＋x2＝－π，x3＋x4＝π，若f(x)＝m有5个不等的实数根，需lg π<lg x5<1，得π<x5<10，又由函数f(x)在[－π，π]上对称，所以x1＋x2＋x3＋x4＝0，故x1＋x2＋x3＋x4＋x5的取值范围为(π，10)．4.若函数满足，当x∈[0，1]时，，若在区间(-1，1]上，方程有两个实数解，则实数m的取值范围是A．0<m≤B．0<m<C．<m≤l D．<m<1【答案】【解析】有两个零点，即曲线有两个交点.令，则，所以.在同一坐标系中，画出的图象（如图所示）：直线过定点，所以，满足即选.【考点】分段函数，函数的图象，函数的零点.5.已知函数对任意的满足，且当时，．若有4个零点，则实数的取值范围是．【答案】【解析】由题意得函数为偶函数，因此当有4个零点时，在上有且仅有两个零点，所以即【考点】二次函数的图象与性质，零点问题6.已知函数的最小正周期为，为了得到函数的图象，只要将的图象（）A．向左平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向右平移个单位长度【答案】B【解析】由于函数的最小正周期为，所以.所以函数.所以将函数向右平移即可得到.故选B.【考点】1.函数的平移.2.函数的诱导公式.7.已知函数f(x)=，若，则a的取值范围是（）A．B．C．[－2，1]D．[－2，0]【答案】D【解析】由题意作出的图象(如图)当a>0时直线y=ax过一、三象限（如图），必与y=ln(x+1)相交，所以a≤0当a≤0时，直线y=ax过三、四象限对x>0，|f(x)|=ln(x+1)> ax成立;对x<0，由|f(x)|=x2－2x≥ax a≥x－2，而当x<0时x－2<－2，所以a≥－2综合知－2≤a≤08.已知函数f(x)＝若|f(x)|≥ax，则a的取值范围是________．【答案】[－2，0]【解析】作出函数y＝|f(x)|的图象，当|f(x)|≥ax时，必有k≤a≤0，其中k是y＝x2－2x(x≤0)在原点处的切线斜率，显然k＝－2.所以a的取值范围是[－2，0]．9.若函数f(x)＝的图象如图，则m的取值范围是________．【答案】(1,2)【解析】∵函数f(x)的定义域为R，∴x2＋m恒不等于零，∴m＞0.由题图知，当x＞0时，f(x)＞0，∴2－m＞0⇒m＜2.又∵在(0，＋∞)上函数f(x)在x＝x0(x＞1)处取得最大值，而f(x)＝，∴x＝＞1⇒m＞1.综上，1＜m＜2.10.若函数满足，且时，，函数，则函数在区间内的零点的个数为____.【答案】9【解析】因为，所以函数是周期为2函数．因为时，，所以作出它的图象，利用函数是周期为2函数，可作出在区间上的图象，如图所示：故函数在区间内的零点的个数为9，故答案为9．【考点】函数的零点；函数的周期性．11.已知函数，则不等式的解集为．【答案】【解析】函数的图象如图，由不等式知，，从而得到不等式的解集为.【考点】函数的图象和性质的综合运用..12.设D＝{(x,y)|(x－y)(x＋y)≤0}，记“平面区域D夹在直线y＝－1与y＝t(t∈[－1,1])之间的部分的面积”为S，则函数S＝f(t)的图象的大致形状为（）【答案】C【解析】由题意，有二次函数图像可得，答案选Ｃ．【考点】函数的图象与图象变化．13.已知函数，若方程有且只有两个不相等的实数根，则实数a的取值范围为（）A、 B、Ｃ、 D、。