当前位置：文档之家 › 拉氏变换详解ppt课件

拉氏变换详解ppt课件

  • 格式：ppt
  • 大小：1.73 MB
  • 文档页数：86

下载文档原格式

  / 86

合集下载

高数第10章 拉普拉斯变换PPT课件

高数第10章 拉普拉斯变换PPT课件

L [sit]n dtarc t t an arc stan
t s t2 1
s2
或
L [stit]n s t2 d 1 令 tt u 11 s 0 1 d u 2u 0 1 s1 d u 2u aru c0 1 s ta arnc 1 st
第三节 拉氏逆变换的运算
❖ 重点：拉氏逆变换的求法 ❖难点：拉氏逆变换的求法
5. 积分性质: L[f(t)]F(s) ,( s 0 ) ，且 f ( t ) 连续，则
L[1f(x)dx]L[f(t)]F(s)
0
s
s
性质5表明，一个函数积分后取拉氏变换，等于这个函数
的拉氏变换除以参数 s .
性质5可以推广到有限次积分的情形：
n次
t t
L[ dt dt 00
t 0
f(t)dt]Fs(ns)
(s1)2 3
(s1)2 3
24
24
f(t)e2 t co3 st3e2 t sin 3t
2
2
例2
求
F(s)s2
s3 3ss
的拉氏逆变换。
解： 先将F (s) 分解为两个简单分式之和，
s 3 s 3 AB s2 3 ss (s 1 )s( 2 ) s 1s 2
其中AB为待定的常数，上式两边同乘以(s1)s(2)，得
1 s
1 ss
e as
1 s
n!
(s ) n1
13
et sin t
14
et cost
15
tet sint
16
tet cost
17
sht
(s )2 2
s (s )2 2
2(s ) [(s )2 2 ]2

《拉氏变换详解》课件

《拉氏变换详解》课件

积分性质
积分性质
若 $f(t)$ 的拉普拉斯变换为 $F(s)$， 则 $int_{0}^{infty} f(t) dt$ 的拉普拉 斯变换为 $- frac{1}{s} F(s)$。
应用
积分性质在求解初值问题和极值问题 时非常有用，可以方便地得到原函数 的表达式。
微分性质
微分性质
若 $f(t)$ 的拉普拉斯变换为 $F(s)$，则 $f^{(n)}(t)$ 的拉普拉斯变换为 $s^{n} F(s) - s^{n-1} f(0-) - s^{n-2} f'(0-) - ldots - f^{(n-1)}(0-)$。
卷积定理
总结词
卷积定理是拉普拉斯变换的一个重要特性， 它描述了函数与其导数之间的卷积关系。
详细描述
卷积定理表明，对于任意实数t，如果函数 f(t)与其导数f'(t)的拉普拉斯变换都存在，则 它们之间的卷积结果等于零。这个定理在信 号处理、控制系统等领域有着广泛的应用， 可以帮助我们更好地理解和分析函数的性质
，再通过反变换得到 (y(t))。
控制系统的稳定性分析
总结词
通过拉普拉斯变换，可以分析控制系统的稳定性，为系 统设计和优化提供依据。
详细描述
对于线性时不变控制系统，通过拉普拉斯变换，可以将 其转化为传递函数的形式。根据传递函数的极点和零点 分布，可以判断系统的稳定性。如果所有极点都在复平 面的左半部分，则系统是稳定的。如果极点在右半部分 或等于零，则系统是不稳定的。此外，系统的动态性能 也可以通过传递函数的极点和零点分布进行分析和优化 。
03
动态行为。
2023
PART 02
拉普拉斯变换的应用
REPORTING
在微分方程中的应用

二章2拉氏变换ppt课件

二章2拉氏变换ppt课件

五、拉氏变换求解线性微分方程
➢将微分方程通过拉氏变换变为 s 的代数方程； ➢解代数方程，得到有关变量的拉氏变换表达式； ➢应用拉氏反变换，得到微分方程的时域解。
A1 A2 A3 S S2 S3
A1
S S
1
2S
3
S
S 0
1 6
A2
S S
1
2S
3 S
2
S 2
1 2
A3
S S
1
2S
3 S
3
S 3
1 3
1
Y(S) 6
1 2
1 3
S S2 S3
yt 1 1 e2t 1 e3t
62 3
1 e2t 1 e3t
2
3
1
S 0.5
0.57 0.866
S S 0.52 0.8662 S 0.52 0.8662
f t 1 e0.5t cos 0.866 t 0.57e0.5t sin 0.866 t
３、A(S)=0有重极点
设A(S)=0有r个重极点，将F（Ｓ）展开成下列形式：
FS
S
A01
P0 r
1 !
例3：求
F
S
S
S 3
22 S
1
的反变换
将F（Ｓ）展开成下列形式：
FS
S
A01
22
A02
S 2
A3
S 1
A01
S
S 3
22 S
1 S
22
S 2
1
A02
d
ds
S
S 3
22 S
1 S
22
S
2
2

自动控制原理课件-拉氏变换专讲

自动控制原理课件-拉氏变换专讲

a3 an a1s a2 F ( s) s p1 s p2 s p3 s pn
1
a1s a2 s p
F ( s )s p1 s p2 s p
1
根据上述方程，令实部=实部，虚部= 虚部，可解出a1，a2
s 1 例: 求 F ( s ) 2 s s s 1 的部分分式 a3 a1 s a2 解: F ( s ) 2 s s 1 s
用拉氏变换法求解微分方程(2)
1 A a b
1 B a b
1 1 1 ba ba s a s b s a sb
用拉氏变换法求解微分方程(2)
留数法（适用于复杂函数)
s z1 s zm B( s ) 设 F ( s) A( s) s p1 s pn
a1 F (s)s 1
3 s 1
s 2s 3
2


s 1
2
用拉氏变换法求解微分方程(6)
d F ( s )s 1 a2 ds
2

3

s 1
2 s 2 s 1 0
3
1 d F ( s )s 1 a3 2 3 1! ds
2


令
A B C Y ( s) s s2 s3
2 1
0.866a1 a2 0.866
2
0.5
用拉氏变换法求解微分方程(5)
化简: a1 a2 1 求解得:
a1 a2 1
a2 0
a1 1
s 1 a3 s 1 2 s s s 1 s 0

拉氏变换详解ppt课件

拉氏变换详解ppt课件
a

0
a
令t / a , 则原式 f ( )e
0

sa
ad aF (as)
9
(8)卷积定理 两个原函数的卷积的拉氏变换等于两个象函 数的乘积。 t 即 L[ f (t ) f ( )d ] F ( s) Nhomakorabea ( s)
0 1 2 1 2
证明： L[ f1 (t ) f 2 ( )d ] [ f1 (t ) f 2 ( )d ]e dt
原函数之和的拉氏变换等于各原函数的拉 氏变换之和。 (2)微分性质 若 L[ f (t )] F ( s) ，则有 L[ f (t )] sF (s) f (0) f(0)为原函数f(t) 在t=0时的初始值。
3
证：根据拉氏变换的定义有
L[ f (t )] f (t )e dt s f (t )e dt f (t )e
st st 0 0


st 0
sF ( s) f (0)
原函数二阶导数的拉氏变换
L[ f (t )] sL[ f (t )] f (0) s[ sF ( s) f (0)] f (0) s 2 F ( s) sf (0) f (0)
14
2. 拉式反变换——部分分式展开式的求法
M (s) b0 s b1s bm1s bm F ( s) n (m n) n 1 D(s) s a1s an1s an
m
m1

（1）情况一:F(s) 有不同极点,这时,F(s) 总能展开成如下简单的部分分式之和
f (t ) L [ F ( s)] t 1 e

信号与系统课件11-拉氏变换

信号与系统课件11-拉氏变换

求其拉普拉斯变换。
解 其双边拉普拉斯变换 F (s)=F (s)+F (s) b b1 b2
jω
仅当>时，其收敛域为 <Re[s]<的一个带状区域， 如图所示。
α
0
β
σ
例4 求下列信号的双边拉氏变换。 f1(t)= e-3t (t) + e-2t (t) f2(t)= – e -3t (–t) – e-2t (–t) f3(t)= e -3t (t) – e-2t (– t) 解
二、收敛域
只有选择适当的值才能使积分收敛，信号f(t) 的双边拉普拉斯变换存在。
使 f(t)拉氏变换存在的取值范围称为Fb(s)的
收敛域。
二．拉氏变换的收敛域
•收敛域：使F(s)存在的s 的区域称为收敛域。
•记为：ROC(region of convergence)
•实际上就是拉氏变换存在的条件；
拉氏变换对
F ( s) L f (t )
1


f (t ) e s t d t
正变换 反变换
1 σ j st f (t ) L f (t ) F ( s ) e ds σ j 2π j
记作 f (t ) F ( s )， f
(t ) 称为原函数， F ( s) 称为象函数
连续系统的复频域分析
引 言
频域分析以虚指数信号ejωt为基本信号，任意 信号可分解为众多不同频率的虚指数分量之和。使 响应的求解得到简化。物理意义清楚。
傅里叶正变换F ( j ) F f (t ) f (t ) e jt d t 1 1 傅里叶逆变换f (t ) F F ( j ) F ( j ) e jt d 2

拉普拉斯积分变换 PPT课件

拉普拉斯积分变换 PPT课件

记为 F(s) L f (t)
F(s)称为 f (t)的拉氏变换（或称为象函数）。
2
若F(s)是f (t) 的拉氏变换，则称 f (t) 为F(s)的拉 氏逆变换（或称为象原函数），记为
f (t) L1F(s)
可以看出，f (t) (t 0)的拉氏变换，实际上就是 f (t)u(t)e t 的傅氏变换。
解 Lsin kt sin ktestdt 0
e st s2 k2
(s sin
kt
k
cos kt)
0
s2
k
k2
(Re(s) 0)
同样可得余弦函数的拉氏变换：
Lcoskt
s2
s
k2
(Re(s) 0)
9
例6 求单位脉冲函数 (t) 的拉氏变换。
解
利用性质： f (t) (t)dt f (0) ，有
即
L
t 0
f
(t )dt
1 s
L
f
(t)
1 s
F (s)
这个性质表明：一个函数积分后再取拉氏 变换等于这个函数的拉氏变换除以复参数s。
20
重复应用积分性质可得：
L
t
dt
t
dt
0
0
n次
t 0
f
(t)dt
1 sn
F (s)
此外，由拉氏变换存在定理，还可以得到象函数 的积分性质：
L
7
则 f (t) 的拉氏变换
F (s) f (t) est dt 0
在半平面 Re(s) c上一定存在，右端的积分在 Re(s) c1 c 上绝对收敛而且一致收敛，并且在 Re(s) c 的半平面内，F(s)为解析函数。

数学基础-拉普拉斯变换PPT课件

数学基础-拉普拉斯变换PPT课件

es F (s)
f (t )
t
拉氏变换性质
(d)微分定理
L[df (t)] L[ f '(t)] sF (s) f (0) dt
d 2 f (t) L[ dt 2 ]
L[
f
''(t )]
s2F(s)
sf
(0)
f
'(0)
f (0)
其中：
f (t)
t 0
f '(0) f '(t) t0
1
(t)dt 1(t 0)
f(t)
0 L[ (t)]
(t )estdt
lim 1estdt (t)0(t 0)
0
0 0
t
eL[e ] lim 1 (1 S) lijmt(1
0 S
0
(2)单位阶跃函数u(t)
e( S)'
S
)'
s
11 j
f(t)
L[u(t)]
0
10
21 [
e
0
[
( s j
e(s
)t dt
j )t dt
2 j 0
e ( s j )t dt ]
0
e( s j )t dt ]
21j[ 01
1
0
]
21 s j1 s j1
L[cost]
2 j [ss
s2 2
j
s
]
j
L[sint]
s2
2
拉普拉斯变换
（5）et sint，et sint，et cost，et cost
欧拉 e jt cost j sint
公式

自动控制原理拉氏变换课件

自动控制原理拉氏变换课件
可以证明:若f (t) 是周期 T 的周期函数,即
为
f (t T ) f (t) (t 0)
当 f (t) 在一个周期上连续或分段连续时,则有
1
ℒ f (t) 1 es T
T f (t)es tdt
0
这是求周期函数拉氏变换公式
三 拉氏变换的几个重要定理
（1）线性性质
（2）微分定理
精品ppt所确定的某一域内收敛则由此积分所确定的函数可写为设函数称上式为函数的拉普拉斯变换式叫做的拉氏逆变换象原函数精品ppt二一些常用函数的拉普拉斯变换求单位阶跃函数的拉氏变换求单位脉冲函数的拉氏变换求函数的拉氏变换ktstdtre求单位斜坡函数的拉氏变换tedttedtre精品ppt例5正弦函数精品ppt是周期为在一个周期上连续或分段连续时则有周期函数的拉普拉斯变换这是求周期函数拉氏变换公式精品ppt1线性性质拉氏变换的几个重要定理2微分定理3积分定理4实位移定理5复位移定理6初值定理7终值定理终值确实存在时精品ppt自动控制原理国家精品课程浙江工业大学自动化研究所19应用拉氏变换的终值定理求注意拉氏变换终值定理的适用条件
1 (s a)-s a s(s a)

1 a
1 s

s
1
a

f(t) 1 1 eat a
1 利用拉普拉斯变换表和性质求拉普拉斯逆变换
一些常用函数的 拉氏变换
典型信号的拉氏变换（2）
《自动控制原理》国家精品课程 浙江工业大学自动化研究所 23
2.用留数法分解部分分式
s p1
d (m1) ds m 1
(s
p1 )m .F(s)
n

Cie pit
im1

课件_拉氏变换

课件_拉氏变换

1 na 2 2 p ( ) l na 1 l l na l L[sin t] na 2 na 2 na 2 na l 2 p ( ) p ( ) l l ~ T ( p) F ( p)
l na ~ T ( p) F ( p) L[sin t] na l
§5.5 应用举例: 例1：利用Laplace变换求解
na 2 T (t ) ( l ) T (t ) f (t ) T( 0 ) 0 T (0) 0
L[ f (t )] F[ p]
t0
解：两边关于t 实施Laplace变换，并记
~ L[T (t )] T ( p)
x u ( x, t ) 2 sin t 2 sin (t ) 2 2 a 2 x 2 2 2 [sin t sin (t )] 2 2 a
2 2
2

2

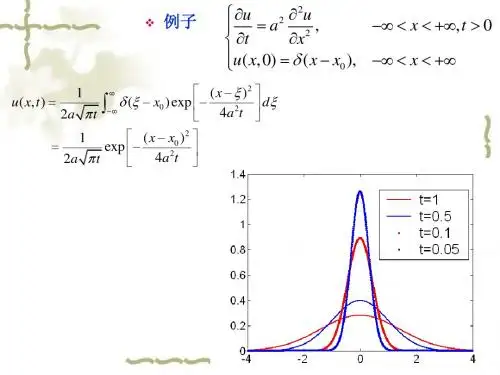
例3：求解一维半无限的热传导问题
u t a 2 u xx 0 (0 x , lim u ( x, t ) 0 u (0, t ) u 0 , x u ( x,0) 0 (0 x ) 解：关于t 实施 Laplace 变换并记
由上式知特征方程为：
p r 2 0 a
2
r1, 2
p a x
p a
p a x
~ u ( x, p) c1e
~ lim u ( x, p ) 0
x
c2 e
c2 0
又
~(0, p) u 0 u p
u0 c1 p
p a x
~ ( x, p ) u 0 e u p
拉氏变换
f ( x) F ( p )

拉普拉斯变换及反变换ppt课件

拉普拉斯变换及反变换ppt课件
补充 拉普拉斯变换及反变换 重点 知识
一、拉氏变换及其特性 1、 拉氏变换定义
如果有一个以时间 t为自变量的实变函数 f t ，它的定义域是 t 0 ，那么 f t 的拉普
拉斯变换定义为
F
s
L
f
t
0
f
t estdt
式中，s是复变数，s j（ 、
均为实数）， est 称为拉普拉斯积分；F s 0
>> p=[1 -120 25 126
用num和den分别表示F(s)的分子和分母多项式， 即：num = [b0 b1 … bm]
den = [a0 a1 … an] MATLAB提供函数residue用于实现部分分式展 开，其句法为：
[r, p, k] = residue(num, den)
f (t) L1(F (s)) 1
c
j
F
(s)e
st
ds
2j c j
式中 L1 表示拉普拉斯反变换的符号
2、拉氏反变换的计算方法 由象函数求原函数的方法：
方法一：利用拉氏反变换定义求 ——不常用解
方法二：查拉氏变换表求解——对简单的象函数适用 方法三：部分分式法——象函数为有理分式函数时适用
p1)r ]}s p1
br j
1 dj
{ j!
ds
j
[F
s
(s
p1)r ]}s p1
b1
1
d r1
(r
{ 1)!
ds
r
1
[
F
s
(s
p1)r ]}s p1
例
F(s)
(s
s 1 2)3 ( s
3)
解：F (s)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

0
0
f ( 2
) e s d
f ( 1
) e s d
0
0
即得证。
精选ppt
F (s)F (s)
2
1
11
二.拉氏反变换
1. 定义：从象函数F(s)求原函数f(t)的运算 称为拉氏反变换。记为 L1[F(s)] 。 由F(s)可按下式求出
f(t) L 1 [F (s) ] 1C j F (s)e sd t (ts 0 ) 2jC j
两个原函数的卷积的拉氏变换等于两个象函 数的乘积。
即 L [t f1(t)f2()d]F 1(s)F 2(s)
0
t
t
证明： L[ f1(t)f2()d] [ f1(t)f2()d]estdt
0
00
t时，f1(t)1(t)0
t
f1(t)f2()d f1(t)1(t) f2()d
0
精选pp0t
1est
0
0 0
0 s 0
lim lim 0
1 (1es)
s
0
1 s(111!s2 2s!2 )1
精选ppt
1
e （3）例3.求指数函数f(t)= at 的拉氏变换
F (s) e ae t sd t te (a s)td t 1e (s a )t1
0
0
s a 0 s a
同理，对f(t)的二重积分的拉氏变换为
L [ f ( t ) d 2 ] ts 1 2 F ( s ) s 1 2f( 1 )( 0 ) 1 s f( 2 )( 0 )
若原函数f(t)及其各重积分的初始值都等于0
则有 L[ f(t)dnt]s1 nF(s)
即原函数 f(t)的n重积分的拉氏变换等于其象
证：设 h(t)f(t)dt则有 h(t)f(t) 由上述微分定理，有
L [ h ( t) ] s[ h L ( t) ] h ( 0 )
L[h(t)]1L[h(t)]1h(0)1L[f(t)]1h(0)
s
s
s
s
1F(s)1f1(0)
s
s
精选ppt
5
即： L[ f(t)d]tF(s)f1(0) ss
式中C是实常数，而且大于F(s)所有极点的 实部。
直接按上式求原函数太复杂，一般都用查 拉氏变换表的方法求拉氏反变换，但F(s)必 须是一种能直接查到精选的ppt 原函数的形式。 12
若F(s)不能在表中直接找到原函数，则需要 将F(s)展开成若干部分分式之和，而这些部 分分式的拉氏变换在表中可以查到。
依次类推，可以得到原函数n阶导数的拉氏
变换 L [ fn ( t ) s ] n F ( s ) s n 1 f( 0 ) s n 2 f( 0 ) fn 1 ( 0 )
精选ppt
4
(3)积分性质 若 L[f(t) ]F(s)
则
L[ f(t)d]tF(s)f1(0) ss
式中 f 1 (0) 为积分 f (t)dt 当t=0时的值。
函数除以 s n 。
精选ppt
6
（4）终值定理 lim f(t)lim sF (s)
t
s 0
原函数的终值等于其象函数乘以s的初值。
证：由微分定理，有
L[f(t)] f(t)esd t tsF (s)f(0)
0
等式两边对s趋向于0取极限
左边
lim
f
(t)estdt
lim
f
(t)estdt
s0 0
即： L [e af t(t) ]F (s a )
(7)时间比例尺定理
原函数在时间上收缩（或展宽）若干倍，
则象函数及其自变量都增加（或减小）同
样倍数。即：L[f(t)]aF (as)
证：
a
L[f
(t
)]
f
(t
)estd
t
a 0a
令t/a,则原式 精选pfpt()esaad aF(as)
9
0
(8)卷积定理
10
t
L[
f (t 1
)
f ( 2
)d
]
0
[
f ( t )1 ( t ) f ( ) d ]e st dt
1
2
00
f ( 2
)d
f ( t ) 1 ( t ) e st dt 1
0
0
令 t ,则
t
L[
f (t 1
)
f ( 2
)d
]
0
f ( 2
)d
f ( 1
) e d s ( )
精选ppt
3
证：根据拉氏变换的定义有
L [f(t) ] 0 f(t)esd t ts 0 f(t)esd t tf(t)est0 s(F s)f(0)
原函数二阶导数的拉氏变换
L [f( t) ]s[L f( t) ]f( 0 ) s [s( F s ) f( 0 ) ]f( 0 )
s 2 F (s ) s( 0 f) f( 0 )
2.常用函数的拉氏变换
数学知识回顾
(1)例1.求阶跃函数f(t)=A·1(t)的拉氏变换。
F(s) Asetd t AestA
0
s
0
s
1
单位阶跃函数f(t)=1(t)的拉氏变换为 s 。
(2)例2.求单位脉冲函数f(t)=δ(t)的拉氏变换。
lim lim
F(s) (t)estd t
1estd t
(5)初值定理：lim f(t)lim sF (s)
t 0
s
证明方法同上。只是要将 s取极限。
(6)位移定理：
a.实域中的位移定理，若原函数在时间上延 迟 ，则其象函数应乘以 es
L [f(t) ]e sF (s)
精选ppt
8
b.复域中的位移定理，象函数的自变量延迟a，
原函数应乘以 e at
L [ a ( t ) b f( t ) f a ] [ f ( t ) L b ] [ f ( t ) L
1
2
1
2
原函数之和的拉氏变换等于各原函数的拉 氏变换之和。
(2)微分性质
若 L[f(t) ]F(s) ，则有 L [f(t) ]s(F s) f(0 ) f(0)为原函数f(t) 在t=0时的初始值。
几个重要的拉氏变换
f(t)
F(s) f(t)
F(s)
δ(t) 1
sinwt
w (s2 w2 )
1(t)
1/s
coswt s
(s2 w2 )
t
1 s2
eatsinwt w
(s a)2 w2
e at
1/(s+a)
e精a选tcppot ws t
(s
sa a)2
w2
2
❖ 3.拉氏变换的基本性质 (1)线性性质
0 s0
0
f
(t)dt
f (t) 0
lim f t
(t)
f (0)
右边 lim[sF(s) f (0)] limsF(s) f (0)
s0
s0
精选ppt
7
lim f (t) limsF(s)
t
s0
注：若 t 时f(t)极限 lim f (t) 不存在， t 则不能用终值定理。如对正弦函数和余弦 函数就不能应用终值定理。