当前位置：文档之家 › 算法导论-第一章-导论

算法导论-第一章-导论

  • 格式：ppt
  • 大小：635.50 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

算法导论笔记

算法导论笔记

第一章算法在计算中的应用第九章中位数和顺序统计学9.1-11.将数组中的元素分组，每组两个元素，然后比较每组中的两个元素得到最小值，重新得到包含原来一半元素的数组，继续重复上述过程，那么最后一个元素必然为最小值。

如图所示，数组为{2, 1, 4, 3, 5}2.上述过程形成的是一个二叉树，其中叶子节点都为数组元素，非叶子节点刚好4个，这是二叉树的性质。

3.然后我们来找第二小元素，第二小元素必然跟着1，首先赋值为5，然后再赋值为3，然后赋值为2，即为所求。

【运行结果】：1.我们先将N个数配对，每两个数一对，每对之间进行互相比较得出小值。

2.对得出的N/2个元素重复第一步，直至得出最小值。

到这儿我们得出了最小值，实际上比较的次数为n-1次。

不难发现上面的过程实际上可以演示为一个二叉树。

例如在5,8,11,18四个数找出最小值，二叉树演示如下（每个节点相当于一次比较）：观察二叉树，可以得出这样一个结论，所有与最小值比较过的数中的最小值纪即为第二小的的值。

二叉树的高度为lgn，因此与最小值比较的数的数目为lgn,在lgn个数中找出最小值要进行lgn-1次比较。

9.1-29.3节的方法可以在最坏情况下的线性复杂度的算法来求顺序统计量.其核心思想在于获得一个更好的中枢值来更好地划分数组.然而题中给了我们一个"黑盒子"来以线性复杂度获取一个真正好的中枢值，那么再好不过了。

在同时找到最大值和最小值时，每个元素都参与了与最大值和最小值的比较，比较了两次。

将数组成对处理。

两两互相比较，将大的与最大值比较，小的与最小值比较。

每两个元素需要的比较次数是，两两比较一次，大者与最大值比较一次，小者与最小值比较一次，共三次。

9.2-1长度为0的数组，RANDOMIZED-SELECT直接返回，当然不会递归调用。

9.2-29.2-3 写出RANDOMIZED-SELECT的一个迭代版本【算法思想】：递归：在函数中调用自身的程序过程。

算法导论第1次课

算法导论第1次课

n
Βιβλιοθήκη n最好情况：输入数据状态为升序，此时A[i]≤key，所以tj=1 T(n) = C1n+C2(n-1)+C3(n-1)+C4(n-1)+C7(n-1) = (C1+C2+C3+C4+C7)n-(C2+C3+C4+C7) = An+B 最坏情况：输入数据状态为倒序，此时A[i]>key，所以tj=j T(n) = C1n+C2(n-1)+C3(n-1)+C4 = ½(C4+C5+C6)n2+(C1+C2+C3+½C4-½C5 -½C6+C7)n-(C2+C3+C4+C7) = An2+Bn+C
特别提示，大O既可表示紧上界也可表示松上界。
2.3 Ω符号(渐进下界) def: Ω(g(n)={f(n):存在正常数C和n0，使得对于所有 的n≥n0，都有0≤Cg(n)≤f(n)} 记为：f(n) = Ω(g(n))
例5：证明f(n)=3n2 = Ω(n) proof: 即要证 Cn≤3n2 Θ,O,Ω符号之间存在关系如下： 定理3.1（P29） 对于任意的函数f(n)和g(n)，当且仅当f(n)=O(g(n))且 f(n)=Ω(g(n))时，f(n)=Θ(g(n))。
1 例6：f (n ) n(n 1), g(n ) n 2 2 例7：f (n ) l g n, g(n ) n
第二章 渐进符号(Asympototic notation)
2.1 Θ符号(渐近符号)
def: Θ(g(n)) = { f(n):存在大于0的常数C1、C2和n0，使得

计算机算法基础(第一章)

计算机算法基础(第一章)
·作为算法分析的数据集：典型特征 ·作为程序性能测试的数据集：对执行指标产生影响的性质
3. 如何进行算法分析？
对算法进行全面分析，可分两个阶段进行：
事前分析：就算法本身，通过对其执行性能的理论分析， 得出关于算法特性——时间和空间的一个特征 函数（Ο 、Ω）——与计算机物理软硬件没有 直接关系。
目的：运行程序，确定程序实际耗费的时间与空 间，验证先前的分析结论——包括正确性、执行 性能等，比较、优化所设计的算法。
分析手段：作时、空性能分布图
4. 计算时间的渐近表示
记：算法的计算时间为f(n) 数量级限界函数为g(n)
其中，
n是输入或输出规模的某种测度。 f(n)表示算法的“实际”执行时间—与机器及语言有关。 g(n)是形式简单的函数，如nm，logn，2n，n!等。是事
在事前分析中，只限于确定与所使用的机器及其他环境因 素无关的频率计数，依此建立理论分析模型。
数量级
语句的数量级：语句的执行频率
例：1，n ，n2
算法的数量级：算法所包含的所有语句的执 行频率之和。
算法的数量级从本质上反映了一个算法的执行特性。
例：假如求解同一个问题的三个算法分别具有n， n2 ， n3数 量级。 若n=10，则可能的执行时间将分别是10，100，1000个单 位时间——与环境因素无关。
计算机算法基础
参考书目
算法导论（第二版 影印版）Introduction to Algorithms(Second Edition )
（美）Thomas H.Cormen等 高等教育出版社
计算机程序设计艺术（英文影印版）（1-3卷精装 全套）The Art of Computer Programming Volumes 1-3 Boxed Set （美）Donald E.Knuth 清华大学出版社

算法导论复习资料

算法导论复习资料

算法导论复习资料一、选择题：第一章的概念、术语。

二、考点分析：1、复杂度的渐进表示，复杂度分析。

2、正确性证明。

考点：1）正确性分析（冒泡，归并，选择）；2）复杂度分析（渐进表示O，Ｑ，©，替换法证明，先猜想，然后给出递归方程）。

循环不变性的三个性质：1）初始化：它在循环的第一轮迭代开始之前，应该是正确的；2）保持：如果在循环的某一次迭代开始之前它是正确的，那么，在下一次迭代开始之前，它也应该保持正确；3）当循环结束时，不变式给了我们一个有用的性质，它有助于表明算法是正确的。

插入排序算法：【INSERTION-SORT(A)1 for j ←2 to length[A]2 do key ←A[j]3 ▹Insert A[j] into the sorted sequence A[1，j - 1].4 i ←j - 15 while i > 0 and A[i] > key6 do A[i + 1] ←A[i]7 i ←i - 18 A[i + 1] ←key插入排序的正确性证明：课本11页。

》归并排序算法：课本17页及19页。

归并排序的正确性分析：课本20页。

3、分治法（基本步骤，复杂度分析）。

——许多问题都可以递归求解考点：快速排序，归并排序，渐进排序，例如：12球里面有一个坏球，怎样用最少的次数找出来。

（解：共有24种状态，至少称重3次可以找出不同的球）不是考点：线性时间选择，最接近点对，斯特拉算法求解。

解：基本步骤：一、分解：将原问题分解成一系列的子问题；二、解决：递归地解各子问题。

若子问题足够小，则直接求解；三、合并：将子问题的结果合并成原问题的解。

复杂度分析：分分治算法中的递归式是基于基本模式中的三个步骤的，T(n)为一个规模为n的运行时间，得到递归式、T(n)=Q(1) n<=cT(n)=aT(n/b)+D(n)+C(n) n>c附加习题：请给出一个运行时间为Q(nlgn)的算法，使之能在给定的一个由n个整数构成的集合S 和另一个整数x时，判断出S中是否存在有两个其和等于x的元素。

算法导论详解PPT课件

算法导论详解PPT课件

computing
“计算机算法的圣经”
Bibliography
《Introduction to Algorithms》(Second Edition),
T. H. Cormen, C. E. Leiserson, R. L. Rivest (2002, Turing Award),
The MIT Press
}
利用此界面使 方法sum通用化
18
第18页/共25页
1.3 描述算法
6.通用方法
（2）parable 界面 Java的Comparable 界面中惟一的方法头compareTo用于比较
2个元素的大小。例如pareTo(y) 返回x-y的符号，当x<y时返回负数，当x=y时返回0，当x>y时返 回正数。 （3）Operable 界面
8
第8页/共25页
1.2 表达算法的抽象机制
2.抽象数据类型
抽象数据类型是算法的一个数据模型连同定义在该模型上 并作为算法构件的一组运算。
抽象数据类型带给算法设计的好处有：
（1）算法顶层设计与底层实现分离； （2）算法设计与数据结构设计隔开，允许数据结构自由选择； （3）数据模型和该模型上的运算统一在ADT中，便于空间和时间耗费的折衷； （4）用抽象数据类型表述的算法具有很好的可维护性； （5）算法自然呈现模块化； （6）为自顶向下逐步求精和模块化提供有效途径和工具； （7）算法结构清晰，层次分明，便于算法正确性的证明和复杂性的分析。
期末闭卷考试：
about 70%
课程安排
课堂讲解：基本理论讲解，基本方法的介绍分析
上机实践：基本习题和经典习题的上机实践
第4页4 /共25页
主要内容介绍

算法导论

算法导论

算法1算法导论 15-3 动态规划求最短编辑距离(2010-07-15 19:35:23)转载▼描述：设A和B是2个字符串。

要用最少的字符操作将字符串A转换为字符串B。

这里所说的字符操作包括:(1)删除一个字符;(2)插入一个字符；(3)将一个字符改为另一个字符。

将字符串A变换为字符串B所用的最少字符操作数称为字符串A到B的编辑距离,记为d(A,B)。

试设计一个有效算法,对任给的2个字符串A和B,计算出它们的编辑距离d(A,B)。

(2)7要求：输入：第1行是字符串A,第2行是字符串B。

输出：字符串A和B的编辑距离d(A,B)思路：开一个二维数组d[i][j]来记录a0-ai与b0-bj之间的编辑距离，要递推时，需要考虑对其中一个字符串的删除操作、插入操作和替换操作分别花费的开销，从中找出一个最小的开销即为所求具体算法：首先给定第一行和第一列，然后，每个值d[i,j]这样计算：d[i][j] = min(d[i-1][j]+1,d[i][j-1]+1,d[i-1][j-1]+(s1[i] == s2[j]?0:1));最后一行，最后一列的那个值就是最小编辑距离poj3356类似题目：/JudgeOnline/problem?id=3356c++代码：#include <iostream>using namespace std;int len1,len2;//分别代表原string与目标string的长度char s[1005],d[1005];//分别存储原string与目标stringint dp[1001][1001];inline int Max(int a,int b){return a>b?a:b;}inline int Min(int a,int b){return a<b?a:b;}void Dp(){int i,j;for (i = 0; i <= Max(len1,len2); i++){dp[i][0] = i;dp[0][i] = i;}for (i=1; i<=len1; i++)for (j=1; j<=len2; j++){if (s[i-1]==d[j-1])dp[i][j]=dp[i-1][j-1];//不需操作elsedp[i][j]=Min(dp[i][j-1]+1,Min(dp[i-1][j]+1,dp[i-1][j-1]+1)); }cout<<dp[len1][len2]<<endl;}int main(void){//freopen("in.txt","r",stdin);while (cin>>len1>>s){cin>>len2>>d;Dp();}return 0;}动态规划求编辑距离http://qinxuye.me/article/get-edit-distance-by-dynamic-programming/发表于2011年4月21日8:12 p.m. 位于分类一箩筐这两天在写一个简单的单词拼写检查器（Spell checker），本来求编辑距离只是其中的一个子问题，现在把它罗列出来，是因为鉴于看到一些书，把本来不是很难的问题讲得很复杂，而且不知道是不是一些作者，为了显得自己水平之高，几乎没有任何的推导，只有一堆结果罗列。

算法导论中文版

补充递归和分治策略•通过例子理解递归的概念；•掌握设计有效算法的分治策略；•通过下面的范例学习分治策略设计技巧：过的范例学分策略技¾Merge sort¾Multiplication of two numbers¾Multiplication of two matrices¾Finding Minimum and Maximumj y p¾Majority problem (多数问题)算法总体思想对这k个子问题分别求解。

如果子问题的规模仍然不够z 将要求解的较大规模的问题分割成k个更小规模的子问小，则再划分为k个子问题，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止。

题。

nT(n)=T(n/2)T(n/2)T(n/2)T(n/2)算法总体思想将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。

nT(n)=n/2n/2n/2n/2T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4) T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)T(/4)算法总体思想将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。

分治法的设计思想是将个难以直接解决的大问题n T(n)=分治法的设计思想是，将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之分而治之。

n/2n/2n/2n/2T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4)T(n/4递归的概念直接或间接地调用自身的算法称为z递归算法。

第1讲算法导论讲述

• 什么是算法？ • 算法是解决一个计算问题的一系列计算步骤有序、 合理的排列。对一个具体问题（有确定的输入数 据）依次执行一个正确的算法中的各操作步骤， 最终将得到该问题的解（正确的输出数据）。
广州大学华软软件学院
第3页
算法分析与设计 3
算法(Algorithm)
• 算法是指解决问题的一种方法或一个过程。 • 算法是若干指令的有穷序列，满足性质： • (1)输入：有外部提供的量作为算法的输入。 • (2)输出：算法产生至少一个量作为输出。
lim
n
• 若λ=非零常数，则称Ỹ（n）是T（n）的渐近表达式， 或称T（n）渐近等于Ỹ（n），记为 T（n）=Θ（Ỹ（n）），这个记号称为算法运 行时间的渐近Θ-记号，简称为Θ-记号。
T ( n)

广州大学华软软件学院
第11页
算法分析与设计 11
5．有效算法
• 如果两个算法运行时间的渐近表达式相同，则将 它们视为具有相同时间复杂度的算法。显然，渐 近时间为对数幂的算法优于渐近时间为幂函数的 算法，而渐近时间为幂函数的算法则优于渐近时 间为指数函数的算法。我们把渐近时间为幂函数 的算法称为是具有多项式时间的算法，渐近时间 不超过多项式的算法则称其为有效的算法。
广州大学华软软件学院
第9页
算法分析与设计 9
3．实例
• 在线性表A中查找。 • （a）查找值为x=1的元素， 从A[1]起依次要进行5次检测， 第一次找到值为1的元素。 • （b）查找值为x=11的元素， 从A[1]起依次检测完所有元素 （进行10次检测），没有找到 值为11的元素——最坏情形。 • （c）查找值为x=3的元素， 从A[1]起仅进行一次检测就找 到值为3的元素——最好情形。

算法导论

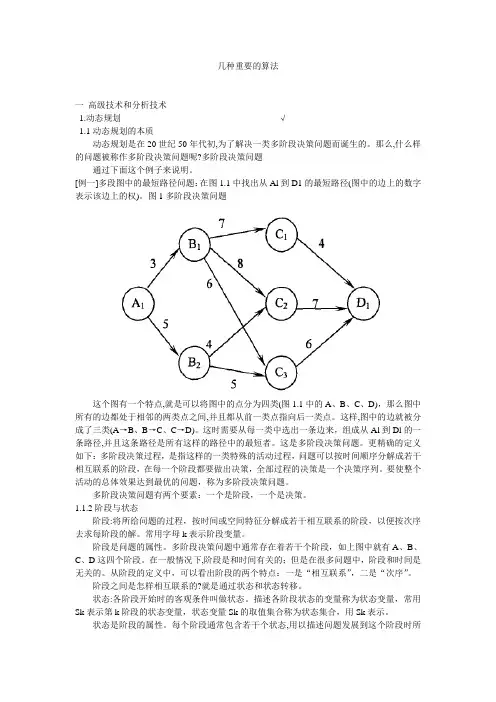
几种重要的算法一高级技术和分析技术1.动态规划------------------------------------------------------√1.1动态规划的本质动态规划是在20世纪50年代初,为了解决一类多阶段决策问题而诞生的。

那么,什么样的问题被称作多阶段决策问题呢?多阶段决策问题通过下面这个例子来说明。

[例一]多段图中的最短路径问题：在图1.1中找出从Al到D1的最短路径(图中的边上的数字表示该边上的权)。

图1多阶段决策问题这个图有一个特点,就是可以将图中的点分为四类(图1.1中的A、B、C、D)，那么图中所有的边都处于相邻的两类点之间,并且都从前一类点指向后一类点。

这样,图中的边就被分成了三类(A→B、B→C、C→D)。

这时需要从每一类中选出一条边来，组成从Al到Dl的一条路径,并且这条路径是所有这样的路径中的最短者。

这是多阶段决策问题。

更精确的定义如下：多阶段决策过程，是指这样的一类特殊的活动过程，问题可以按时间顺序分解成若干相互联系的阶段，在每一个阶段都要做出决策，全部过程的决策是一个决策序列。

要使整个活动的总体效果达到最优的问题，称为多阶段决策问题。

多阶段决策问题有两个要素：一个是阶段，一个是决策。

1.1.2阶段与状态阶段:将所给问题的过程，按时间或空间特征分解成若干相互联系的阶段，以便按次序去求每阶段的解。

常用字母k表示阶段变量。

阶段是问题的属性。

多阶段决策问题中通常存在着若干个阶段，如上图中就有A、B、C、D这四个阶段。

在一般情况下,阶段是和时间有关的；但是在很多问题中，阶段和时间是无关的。

从阶段的定义中，可以看出阶段的两个特点：一是“相互联系”，二是“次序”。

阶段之间是怎样相互联系的?就是通过状态和状态转移。

状态:各阶段开始时的客观条件叫做状态。

描述各阶段状态的变量称为状态变量，常用Sk表示第k阶段的状态变量，状态变量Sk的取值集合称为状态集合，用Sk表示。

状态是阶段的属性。

算法导论中文版答案


24.2-3
24.2-4
24.3-1 见图 24-6 24.3-2
24.3-3
24.3-4 24.3-5 24.3-6
24.3-7
24.3-8 这种情况下不会破坏已经更新的点的距离。 24.4**** 24.5****
25.1-1 见图 25-1 25.1-2 为了保证递归定义式 25.2 的正确性 25.1-3
8.3-3 8.3-4
8.3-5(*) 8.4-1 见图 8-4 8.4-2
8.4-3 3/2，1/2 8.4-4(*) 8.4-5(*)
9.1-1
9.1-2 9.2-1 9.3-1
第九章
9.3-2 9.3-3
9.3-4 9.3-5
9.3-6 9.3-7
9.3-8
9.3-9
15.1-1
6.4-4
6.4-5
6.5-1 据图 6-5 6.5-2
6.5-3 6.5-4 6.5-5
6.5-6 6.5-7
6.5-8
7.1-1 见图 7-1 7.1-2
7.1-3 7.1-4 7.2-1 7.2-2
7.2-3 7.2-4 7.2-5
第七章
7.2-6 7.3-1
7.3-2
7.4-1 7.4-2
5.3-6
6.1-1 6.1-2 6.1-3 6.1-4 6.1-5 6.1-6
第6章
6.1-7
6.2-1 见图 6-2 6.2-2
6.2-3
6.2-4
6.2-5 对以 i 为根结点的子树上每个点用循环语句实现 6.2-6
6.3-1
见图 6-3 6.3-2
6.3-3
6.4-1 见图 6-4 6.4-2 HEAPSORT 仍然正确，因为每次循环的过程中还是会运行 MAX-HEAP 的过程。 6.4-3
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Analysis of insertion sort
cost c1 c2 0 c4 c5
c6
times
n
n-1
n-1 n-1
t n j2 j
n j2
(t
j
1)
c7
n j2
(t
j
1)
c8
n-1
tj : the number of times the while loop test in line 5 is executed for the j value第5行中while循环所做的测试次数
j2
j2
n
c7 (t j 1) c8 (n 1) j2
The best-case if the array is already sorted最好情况是数组
已经有序tj=1
T (n) c1n c2 (n 1) c4 (n 1) c5(n 1) c8(n 1)
假设每行代码花费的时间是常量Ci ，但每一 行代码花费的时间可能不同
Running time(运行时间)
Worst-case: (usually) --T(n) = maximum time of algorithm on any input of size n.
最坏情况下的运行时间，指的是size给定，任何输入实例的 最长运行时间
Ignore not only the actual statement costs, but also the
Ch1 导论
Alogrithm算法
A well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output. （良定义的计算过程，良定义指的是 满足五个要素:有穷性、确定性、可行性、有输入和输出，计 算过程指的是一系列的计算步骤）
元素个数n即为输入规模(Input size)
对另外一些问题，例如两个整数相乘，其输入规 模是输入在二进制表示下的位数
有时候用二个数来表示输入，例如输入是一个图
因此需要确定每个问题的输入规模
Running time(运行时间)
运行时间是指执行的基本操作数（步数）， 基本操作独立于具体机器
Main fact impacting on running time (影响运行时间的主要因素)
Numbers of inputs输入规模
The distribution of input, some (not all) algorithms can take different amounts of time to sort two different input sequence of the same size输入构成
Best-case: (bogus) --Cheat with a slow algorithm that works fast on some
input. 最好情况下的运行时间，指的是size给定，输入实例的最短 运行时间
Running time(运行时间)
The average running time is usually very hard to compute, we usually strive to analyze the worst case running time. The average case is often roughly as bad as the worst case平均情况难以分析，经常分析 最坏情况
Average-case: (sometimes) --T(n) = expected time of algorithm over all inputs of size n. --Need assumption of statistics distribution of inputs.
平均情况下的运行时间，指的是size给定，不同的实例分布 的平均所需的运行时间
The average-case:与输入的概率分布有关，假设
对所有的数据出现的概率相等，tj=(j+1)/2
T (n) c1n c2 (n 1) c4 (n 1) c5 (n2 3n 2) / 4 c6 (n2 3n 2) / 4 c7 (n2 3n 2) / 4 c8 (n 1)
函数
n
n
t j ( j 1) / 2 (n2 3n 4) / 4
j2
j2
n
n
(t j 1) ( j / 2 1) (n2 3n 2) / 4
j2
j2
Order of growth增长率
在算法分析过程中，通过抽象来简化分析过程，忽 略每个语句的实际开销，代之以抽象的尝试Ci
数组是逆序tj=j
T (n) c1n c2(n 1) c4(n 1) c5(n(n 1) / 2 1) c6(n(n 1) / 2)
c7 (n(n 1) / 2) c8(n 1)
(c5 / 2 c6 / 2 c7 / 2)n2
(c1 c2 c4 c5 / 2 c6/ 2 c7 / 2 c8 )n (c2 c4 c5 c8 )
Analysis of algorithm 算法分析---估 计算法所需要的资源
We shall assume a generic one-processor, random-access machine (RAM) model of computation随机存储器作为计算模型
指令一条接一条执行，没有并发操作 指令作为一个原子操作被执行，指令包括算术操 作、逻辑操作、数据移动和控制操作 指令需要一个定量的执行时间 RAM容量足够大 ……
(c5 / 4 c6 / 4 c7 / 4)n2 (c1 c2 c4 3c5 / 4 3c 6 /4 3c7 / 4 c8)n (c2 c4 c5 c6 / 2 c7 / 2 c8)
The running time is a quadratic function of n二次
Analysis of insertion sort
To compute T(n), the running time of Insertion-sort, we
sum the products of the cost and times columns, obtaining
n
n
T (n) c1n c2 (n 1) c4 (n 1) c5 t j c6 (t j 1)
Under RAM model: count fundamental operations计算基本操作数目
RAM model (RAM 模型)
为了在RAM模型上分析算法，我需要：
Combinatorics组合
Probability theory概率
Algebra代数
The ability to identify the most significant terms in a formula找出最重要项的能力
(c1 c2 c4 c5 c8 )n (c2 c4 c5 c8 )
--The running time is a linear function of n线性函数
Analysis of insertion sort
The worst-case results if the array is in reverse sorted order- that is, in decreasing order最坏情况是
Usually describe the running time of a program as a function of the input size通常 将运行时间表示为输入的函数
Main fact impacting on running time (影响运行时间的主要因素)
The running time of an algorithm may depending on how the algorithm is implemented as well as what kind of data structure is used有 时候运行时间和算法采用的数据结构有关系
Input
Algorithm
Output
Note ：实例-------计算一个解（输出）所有的输入
Application of algorithm
人类基因组计划
互联网
路由问题：寻找数据由源节点到达目的节点的路径 搜索问题
制造业
电子商务
The problem of sorting
Generally, we seek upper bounds on the running time, because everybody likes a guarantee
Input size(输入规模)
输入规模依赖所研究的问题
对许多计算问题，其输入规模就是输入项的个数， 例如排序和计算傅里叶变换(DFT)，输入数组的
The running time is a quadratic function of n二次
函数
n
n
t j j n(n 1) / 2 1
j2
j2
n
n
(t j 1) ( j 1) n(n 1) / 2rtion sort
Example of insertion sort
Example of insertion sort