11-1 低通模拟信号的抽样定理
- 格式:pdf
- 大小:335.97 KB
- 文档页数:9



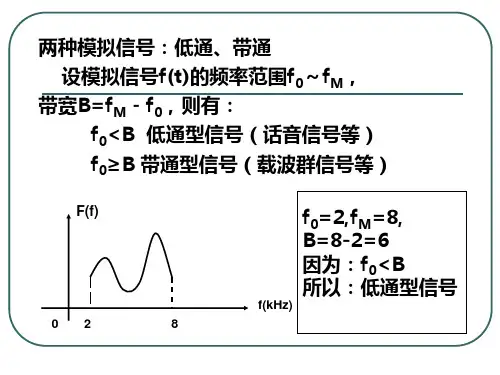
实验一抽样定理一.概述抽样的分类:(1) 根据信号是低通型的还是带通型的,抽样定理分低通抽样定理和带通抽样定理。
(2) 根据用来抽样的脉冲序列是等间隔的还是非等同隔的,又分均匀抽样定理和非均匀抽样。
(3) 根据抽样的脉冲序列是冲击序列还是非冲击序列,又可分理想抽样和实际抽样。
二.实验原理及其框图抽样定理是通信原理中十分重要的定理之一,是模拟信号数字化的理论基础。
低通型连续信号的抽样定理一个频带限制在内的时间连续信号,若以的间隔对它进行等间隔抽样,则将被所得到的抽样值完全确定。
原理框图图1 抽样说明:抽样过程中满足抽样定理时,PCM系统应无失真。
这一点与量化过程有本质区别。
量化是有失真的,只不过失真的大小可以控制。
三.实验步骤1、根据抽样原理,用Systemview 软件建立一个仿真电路,如下图所示:图2 仿真电路元件参数配制Token 0: 被采样的模拟信号—正弦波(频率=100Hz,电平=1V,相位=0)Token 2: 乘法器Token 5 抽样脉冲——窄脉宽矩形脉冲(脉宽=1us )Token1,3: 模拟低通滤波器(截止频率=100 Hz )Token 4,6,7: 观察点—分析窗(6频率=100Hz 电压=-1V)2、运行时间设置运行时间=0.3 秒采样频率=10,00 赫兹3、运行系统在Systemview 系统窗内运行该系统后,转到分析窗观察Token 5,6,8三个点的波形。
4、功率谱在分析窗绘出该系统调制后的功率谱。
四、实验报告1)观察实验波形:Token 0-被采样的模拟信号波形;Token 2-采样后波形;Token 3-恢复信号的波形。
2)整理波形,存入文档。
3)观察采样前后各信号的功率谱,结果存入文档,进行比较。
4)分析说明实验结果与理论值之间的差别。
5)改变参数配置,将所得不同结果存档后,与实验结果进行比较,说明参数改变对结果的影响。

模拟信号幅值,时间,且直接与消息相对应;数字信号幅值,时间,且不直接与消息相对应。
模拟通信系统是利用来传递信息的通信系统。
原始电信号通常称为,基带的含义是信号的频谱从附近开始。
基带信号是未经过的信号,其频带从或附近开始。
调制是指把变换为适宜在信道中传输的信号。
调制的逆过程是。
已调信号又称为或或。
未经过调制的信号称为,也可以成为基带信号。
信源编码的作用是和。
信道编码的功能是,目的是进步通信系统的。
是指人为地按一定规律参加多余的数字码以到达接收端可以发现和的目的。
其最主要的目的是进步数字通信的。
数字调制的功能是把的频谱搬移到高频处,形成适宜在中传输的。
同步的功能是使收发两端的信号在保持,是保证数字通信系统有序、准确、可靠工作的前提条件。
与模拟通信系统相比,数字通信的优点和缺点分别是什么?通信系统按调制方式分类,分为系统和传输系统;按信号特征分类,分为系统和系统;按传输媒介分类,分为通信系统和通信系统。
说出几种模拟通信系统:、、、、、。
说出几种数字通信系统:、、。
通信的目的是传递消息中所包含的。
按照数据传输的流向和时间关系,通信方式可分为:、和。
信息量是对信息发生的的度量。
信息量的单位是。
一个二进制码元含的信息量;一个M进制码元含有比特的信息量。
符号集为A、B、C、D,它们互相独立,相应概率为、、、,其中包含信息量最小的符号是。
信息源的熵,即每个符号的,其公式为。
情况下,信息源的熵有最大值。
符号集为A、B、C、D,互相独立,相应概率为1/2、1/5、1/8、7/40,其平均信息量为。
某二进制信源,0符号出现概率为1/4,该信源的平均信息量为比特/符号。
衡量一个通信系统的主要性能指标是和;其中模拟通信系统是用和来衡量;数字通信系统是用和来衡量。
有效性是指传输一定信息量时所占用的信道资源〔频带宽度和时间间隔〕,是“〞问题;可靠性是指接收信息的准确程度,也就是传输的“〞问题。
码元传输速率R B,又称为或,其定义为单位时间〔每秒〕传送的数目,单位为;信息传输速率R b,又称为或,定义为单位时间内传递的或,单位为。

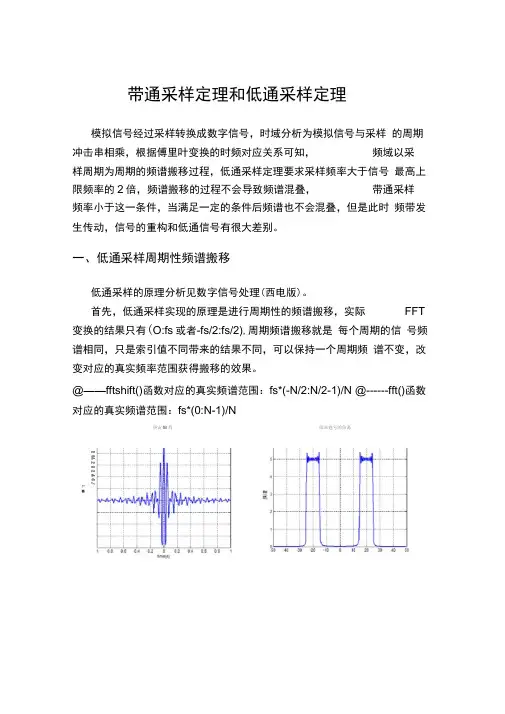
带通采样定理和低通采样定理模拟信号经过采样转换成数字信号,时域分析为模拟信号与采样的周期冲击串相乘,根据傅里叶变换的时频对应关系可知,频域以采样周期为周期的频谱搬移过程,低通采样定理要求采样频率大于信号最高上限频率的2倍,频谱搬移的过程不会导致频谱混叠,带通采样频率小于这一条件,当满足一定的条件后频谱也不会混叠,但是此时频带发生传动,信号的重构和低通信号有很大差别。
一、低通采样周期性频谱搬移低通采样的原理分析见数字信号处理(西电版)。
首先,低通采样实现的原理是进行周期性的频谱搬移,实际FFT 变换的结果只有(O:fs或者-fs/2:fs/2),周期频谱搬移就是每个周期的信号频谱相同,只是索引值不同带来的结果不同,可以保持一个周期频谱不变,改变对应的真实频率范围获得搬移的效果。
@——fftshift()函数对应的真实频谱范围:fs*(-N/2:N/2-1)/N @------fft()函数对应的真实频谱范围:fs*(0:N-1)/N庚宙IB茸障站霆号的魚谒E 64 2 Q 24€B .:1.■U的耳 IS r/电 £写抽Mil保持原始信号的频谱不变,转换频谱搬移周期,刚好达到两倍采 样频率,谱结构如下:结论:(1) 低通采样定理的周期性频谱搬移以采样频率为周期,采样频率 必须大于信号最高上限的二倍,否则就会导致频谱混叠。
(2) 低通采样后的信号重构只需要经过低通滤波器即可。
二、带通采样定理原理和重构分析 1、带通采样定理原理带通采样定理:一个频带限制在f L ,f H 内的连续时间信号X t ,信号带宽B f H f L ,令N 为不大于f H B 的最大正整数,当采样频率f s 满足一 下条件-]I -1 ir■ qr n 11I 1 : !i i…-一.....r1i ii ii :1 11 1iiJLJi L i*L1JiL ] JL€则可以由采样后的序列无失真的重构原始信号 x t 原理分析:X(f)Xs(f)采样后的信号在频域变现为周期性的频谱搬移,为了能够重构原 始信号,选择合适的采样频率,使f H ,f L 和f L ,f H 的频带分量不会 和延拓分量出现混叠,这样通过升采样后经过带通滤波器即可恢复原 始信号,分析正频率附近无混叠的条件:保证延拓的频谱分量f H mf s , f L mf s 和 f H (m 1)f s , h (m 1)f s 与无拓展频率分量不会混叠,即满足以下关系:整理可得,2f Hf 2fL m 1 s m当m 0时,f s 2f H ,此时为低通采样定理(奈奎斯特采样定理) 延拓周期还要保证f s 2B ,f s2f LfHfL 01)fsf H m 1 f s f H2f L f Lf s B带通采样定理由此而来2、重构分析低通采样后的信号经过低通滤波器后即可恢复原始信号,低通信号的抽样和恢复比起带通信号来要简单。

什么是PCM ?这种将模拟信号经过抽样、量化、编码三个处理步骤变成数字信号的A/D 转换方式称为脉冲编码调制(PCM,Pulse Code Modulation )。
说说“抽样”所谓抽样就是不断地以固定的时间间隔采集模拟信号当时的瞬时值低通模拟信号的抽样定理:设一个连续模拟信号m (t)中的最高频率 < f H ,则以间隔时间为T 1/2f H 的周期性冲激脉冲对它抽样时,m (t )将被这些抽样值所完全确定 恢复原信号的条件是: 即抽样频率f s 应不小于f H 的两倍。
这一最低抽样速率2f H 称为奈奎斯特速率。
与此相应的最小抽样时间间隔称为奈奎斯特间隔。
例如,典型电话信号的最高频率通常限制在3400 Hz ,而抽样频率通常采用8000 Hz 。
说说“量化”量化就是把一个连续函数的无限个数值的集合映射为一个离散函数的有限个数值的集合。
通常采用“四舍五入”的原则进行数值量化确定的量化后的取值叫量化值(有的书籍也称量化电平),s s s s s s s s s s(a) 抽样脉冲(c) PCM 量化(b) PCM 抽样(d) PCM 编码量化值的个数称为量化级量化间隔——相邻两个量化值之差就是量化间隔(也称量化台阶)存在于收、发信号之间的误差是由量化造成的,我们称其为量化误差或量化噪声。
比如在上例中,量化间隔为1,由于采用“四舍五入”进行量化,因此量化噪声的最大值是0.5。
一般地说,量化噪声的最大绝对误差是0.5个量化间隔。
这种量化间隔都一样的量化叫做均匀量化。
均匀量化的缺点:比如上例中,信号最大值为6,绝对量化噪声为0.5,而相对误差为0.5/6=1/12,即量化误差是量化值的1/12;而当信号为1时,绝对量化噪声仍为0.5,但相对误差却为0.5/1=1/2,量化误差达到量化值的一半。
那么如果我们在一定的取值范围内把量化值多取几个(量化级增多),也就是把量化间隔变小,则量化噪声就会减小。

(初级)通信专业综合能力-通信系统-第2节信源编码[单选题]1.对于给定的信号最大幅度,量化电平数越(),量化噪声越(),量化信噪比越高。
A.多,小B.少(江南博哥),小C.多,大D.少,大正确答案:A参考解析:对于给定的信号最大幅度,量化电平数越多,量化噪声越小,量化信噪比越高。
【知识点:脉冲编码调制】[单选题]2.把离散时间连续幅度的抽样信号转换为离散时间离散幅度的数字信号的过程是()。
A.抽样B.编码C.调制D.量化正确答案:D参考解析:量化把离散时间连续幅度的抽样信号转换为离散时间离散幅度的数字信号的过程。
抽样是把连续时间模拟信号转换为离散时间连续幅度的抽样信号。
编码是把量化后的信号编码形成一个二进制码组输出的过程。
【知识点:脉冲编码调制】[单选题]4.脉冲编码调制(PCM)的实现过程不包括()。
A.抽样B.量化C.编码D.放大正确答案:D参考解析:脉冲编码调制简称脉码调制,它是一种将模拟语音信号变换成数字信号的编码方式。
脉码调制的过程如图4-8所示。
【知识点:脉冲编码调制】[单选题]5.抽样是指在()上的离散化。
A.时间B.幅值C.相位D.频率正确答案:A参考解析:PCM主要包括抽样、量化与编码3个过程。
抽样是把连续时间模拟信号转换成离散时间连续幅度的抽样信号;量化是把离散时间连续幅度的抽样信号转换成离散时间离散幅度的数字信号;编码是将量化后的信号编码形成一个二进制码组输出。
【知识点:脉冲编码调制】[单选题]6.下列不属于脉冲编码调制(PCM)的过程的是()。
A.抽样B.量化C.解调D.编码正确答案:C参考解析:PCM主要包括抽样、量化与编码3个过程。
抽样是把连续时间模拟信号转换成离散时间连续幅度的抽样信号;量化是把离散时间连续幅度的抽样信号转换成离散时间离散幅度的数字信号;编码是将量化后的信号编码形成一个二进制码组输出。
【知识点:脉冲编码调制】[单选题]7.()是用脉冲调制的方法使不同信号占据不同的时间区间。

第10章信源编码思考题10-1 模拟信号在抽样后,是否变成时间离散和取值离散的信号了?答:模拟信号在进行抽样后变成时间离散信号,其取值仍然是连续的。
10-2 试述模拟信号抽样和PAM的异同点。
答:模拟信号抽样和PAM的异同点:(1)相同点:两者都是时间离散取值连续的信号;(2)不同点:抽样信号的频谱是周期延拓,幅度不下降,而PAM频谱是周期延拓,但幅度下降。
10-3 对于低通模拟信号而言,为了能无失真恢复,理论上对于抽样频率有什么要求?答:对于低通模拟信号而言,为了能无失真恢复,理论上需要采样频率大于等于信号最高频率的两倍,即满足奈奎斯特抽样定理。
10-4 试说明什么是奈奎斯特抽样速率和奈奎斯特抽样间隔?答:对无失真恢复低通信号所要求的最低采样速率称为奈奎斯特速率,与此相对的最小抽样时间间隔称为奈奎斯特间隔。
10-5 试说明抽样时产生频谱混叠的原因。
答:抽样时产生频谱混叠的原因:在信号域内的采样,会造成信号频谱的周期延拓,当采样频率小于两倍的信号最高频率时,就会造成不同周期的混叠。
10-6 对于带通信号而言,若抽样频率高于教材图10-3所示曲线,是否就能保证不发生频谱混叠?答:对于带通信号而言,若抽样频率高于教材图10-3所示曲线,不能保证不发生频谱混叠。
对于带通信号,若要求抽样后的频谱不产生重叠,需要满足221s s n k B nf f B k n ++()=或=(/)10-7 PCM 电话通信通常用的标准抽样频率等于多少?答:PCM 电话通信通常用的标准抽样频率等于8000Hz 。
10-8 信号量化的目的是什么?答:信号量化的目的是使信号取值离散,是把模拟信号变成数字信号过程中重要的一部分。
10-9 量化信号有哪些优点和缺点?答:量化信号的优点和缺点:(1)优点:抗干扰能力强、无噪声积累;便于传输、存储和加密。
(2)缺点:量化会产生量化误差和引入量化噪声。
10-10 对电话信号进行非均匀量化有什么优点?答:对电话信号进行非均匀量化的优点:电话信号主要集中在小幅度区间,故采用非均匀量化能够改善信号量噪比和传输比特数。

一、基本原理1.1抽样定理抽样时时间上连续的模拟信号变成一系列时间上离散的抽样序列的过程。
抽样定理要解决的事,能否由此抽样序列无失真的恢复出模拟信号。
对一个频带受限的、时间连续的模拟信号抽样,当抽样速度达到一定的数值时,那么根据它的抽样值就能无失真恢复原模拟信号。
也就是说,若要传输模拟信号,不一定要传输模拟信号本身,只需要传输由抽样得到的抽样即可。
因此,抽样定理是模拟信号数字化的理论依据。
抽样的过程是将输入的模拟信号与抽样信号相乘,通常抽样信号时一个周期为T 的周期脉冲信号,抽样后得到的信号称为抽样信号。
理想的抽样为()∑⎪⎪⎭⎫ ⎝⎛-=nT t s nT t δδ其中(){ss t t T f t 1,0010===≠δ称为抽样速率。
因此抽样后信号为 ()()()()()sk sT s nT t nT x t t x t x -==∑∞-∞=δδ1.2低通抽样定理一个频带限制在()H f ,0内的连续信号()t x ,如果以()H sf T 2\1≤ 秒的时间间隔对它进行均匀抽样,则()t x 将被所得到的抽样值完全确定,可以由抽样值序列无失真地重建原始信号。
()H s f T 2\1=是抽样的最大间隔,称为奈奎斯特间隔。
低通信号的抽样可以从频域来理解,抽样的时域、频域对照如图4-3所示,根据频域卷积定理,()t x 的频域表达式为()()()[]()()()∑∑∞-∞=∞-∞=-=⎥⎦⎤⎢⎣⎡-*=*=n ssn s sT s n X T n X T X X ωωωωδωωδωπω1121由上式可见,在s ω的整数倍(n=⋅⋅⋅±±,,21)处存在()ωX 的复制谱。
如图4—3(c )所示,抽样后信号的频谱是原信号频谱平移s nf 后叠加而成,因此如果不发生频谱重叠,可以通过低通滤出原信号。
如果抽样频率H s ωω2<,即抽样间隔()H s f T 2/1>,则抽样信号的频谱会发生混叠现象,此时不可能无失真地重建原始信号。
2019年通信工程师考试中级综合真题解析1、职业道德在形式上具有()。
A多样性和适用性B稳定性和连续性C专业性和具体性D特殊性和一般性正确答案A答案解析:所谓职业道德,就是人们从事正当的社会职业,并在其履行职责的过程中,在思想和行为上应当遵循的具有自身职业特征的道德准则和规范。
职业道德的特点主要体现在三个方面:职业道德在形式上具有多样性和适用性;职业道德具有较强的稳定性和连续性;职业道德具有很强的专业性和具体性。
故本题选A2、在科技工作者道德行为的选择中,既受着客观条件的制约,又有()的自由。
A主观条件B个人意志C选择行为D主观意志支配正确答案D答案解析:在科技工作者道德行为的选择中,既受着客观条件的制约,又有主观意志支配的自由。
这主要取决于科技工作者依据何种道德原则和规范,去选择自己的行为。
故本题选D3、从通信科技的劳动的特点看,通信科技职业具有()。
A实践性、应用性B严谨性、准确性C高度集中的统一性D“广”和“远”的特性正确答案A答案解析:通信科技是科学技术在通信中的运用,它受到通信职业特点的制约。
与其他科技职业相比,有一般科技职业的特点,更具有其自身的特点。
主要体现在以下四个方面:(1)从通信科技劳动的特点看,具有实践性,应用性。
(2)从通信科技劳动的目的和结果看,具有严谨性、准确性。
(3)从通信科技全网、联合作业的劳动过程看,具有高度的集中统一性。
(4)从通信科技劳动的人际关系看,具有“广”和“远”的特点。
A选项从通信科技劳动的特点看,B选项是从通信科技劳动的目的和结果看,C选项从通信科技全网、联合作业的劳动过程看,D选项是从劳动的人际关系看。
故本题选A4、()反对本位主义,是通信科技职业道德的重要规范。
A发扬民主精神B加强纪律组织C树立全程全网观念D从部门利益触发正确答案C答案解析:着眼全程全网,反对本位主义,是社会主义集体主义思想在通信科技职业活动中的重要体现,是通信科技职业道德的重要规范,主要应从三个方面努力:树立整体观念;发扬协作精神和高度的组织纪律性,强烈的社会责任感。
低通抽样定理的理解带通信号抽样速率的一统性研究(篇一):低通抽样定理的理解写在前:这是笔者第一篇CSDN博客,希望未来保持更新和分享,督促自己学习和思考,也希望能有助于小伙伴们的解惑,内容是关于通信和信号处理方面的。
我现在基本还是通信和信息的小白,会不断学习。
如果内容有出错或者不够严谨的地方希望指正,相互交流,共同进步。
本篇是《带通信号抽样速率的一统性研究》的篇一,基础知识部分。
从频域和时域两个角度对低通抽样定理进行了探讨和理解。
在通信与信息系统中需要将一个时间连续信号(模拟信号,时间和幅度上均连续)通过抽样(或称为采样)来转换为时间离散信号(时间离散,幅度不离散),继而通过量化、编码得到数字信号(时间离散,幅度离散)。
数字信号相对于模拟信号具有便于存储、处理、传输等优点。
我们只探讨抽样过程和其对应的信号恢复过程。
经过抽样得到的离散序列需要能够还原出原来的模拟信号,这也就意味着抽样过程完整地保留了原信号的信息。
抽样过程追求高效,离散序列的长度被期待尽量短(对应抽样速率尽量低)。
抽样定理包含两个内容:低通抽样定理和带通抽样定理。
我们先从低通抽样定理入手。
低通抽样定理:给定最高非零频率为fH f_HfH的带限信号m(t) m(t)m(t),如果取抽样间隔Ts<1/(2fH) T_s<1/(2f_H)Ts<1/(2fH )(即抽样速率fs>2fH f_s>2f_Hfs>2fH,有些资料的表达为fs≥2f H f_s\ge2f_Hfs≥2fH),则m(t) m(t)m(t)由其样值序列{mn=m(nTs),n为整数} \big\{m_n=m(nT_s),n为整数\big\}{mn=m(nTs),n为整数}唯一确定,即m(t)⟷只要fs>2fH{mn,n=0,±1,±2,…} m(t)\stackrel{只要f_s>2f_H}{\longleftrightarrow}\big\{m_n,n=0,\pm1,\pm2,…\big\}m(t)⟷只要fs>2fH{mn,n=0,±1,±2,…}低通抽样定理中,抽样速率必须大于2fH 2f_H2fH,该频率2fH 2f_H2fH通常称为奈奎斯特频率。
低通型采样定理低通型采样定理是数字信号处理中的一个重要理论基础,它规定了对连续时间信号进行采样时的最低采样频率。
根据低通型采样定理,如果一个连续时间信号的最高频率为Fmax,那么在进行采样时,至少需要以2Fmax的采样频率进行采样,才能保证采样后的离散信号能够完整地还原原始信号。
低通型采样定理的基本原理是基于奈奎斯特定理,也称为奈奎斯特-香农采样定理。
奈奎斯特定理指出,如果一个信号的最高频率为Fmax,那么至少需要以2Fmax的采样频率进行采样,才能够完全还原原始信号。
而低通型采样定理则是奈奎斯特定理在实际应用中的一种具体形式。
为了更好地理解低通型采样定理,我们可以通过一个简单的例子来说明。
假设有一个连续时间信号,其最高频率为10kHz,那么根据低通型采样定理,我们需要以至少20kHz的采样频率对该信号进行采样,才能够完整地还原原始信号。
如果采样频率低于20kHz,则会出现采样失真,导致还原的离散信号与原始信号存在差异。
低通型采样定理的应用非常广泛,特别是在音频和视频信号处理领域。
在音频播放器中,为了能够准确地还原音频信号,通常会使用44.1kHz的采样频率进行采样,这是因为人耳的听觉范围大约在20Hz到20kHz之间,而根据低通型采样定理,最高频率为20kHz的音频信号至少需要以40kHz的采样频率进行采样,才能够完整还原原始信号。
类似地,在视频播放器中,为了能够准确地还原图像信号,通常会使用至少两倍于图像最高频率的采样频率进行采样。
除了音频和视频信号处理领域,低通型采样定理还在通信系统中发挥着重要作用。
在数字通信中,为了传输连续时间信号,通常需要先对信号进行采样,然后通过调制和编码等处理将其转换为数字信号进行传输。
在采样过程中,低通型采样定理的应用可以确保采样后的离散信号能够完整还原原始信号,从而保证传输的准确性和可靠性。
低通型采样定理是数字信号处理中一个重要的理论基础,它规定了对连续时间信号进行采样时的最低采样频率。
问题
问题
抽样信号
x t
()
模拟信号的数字化
主要内容
第十一讲模拟信号的抽样
第十二讲抽样信号的量化
第十三讲脉冲编码调制
第十四讲差分脉码调制与增量调制
第十五讲时分复用
低通模拟信号的抽样定理
低通模拟信号的抽样定理
低通模拟信号的抽样定理
收端重建的模当抽样频率f s (=1/T s ) 满足低通抽样定理(f s ≥2f H )时
T s
低通模拟信号的抽样定理低通模拟信号的抽样定理
低通模拟信号的抽样定理低通模拟信号的抽样定理
低通模拟信号的抽样定理
低通模拟信号的抽样定理
Harry Nyquist Claude Elwood Shannon
(1916−2001)
14
低通模拟信号的抽样定理
低通模拟信号的抽样定理
n
实际应用中,抽样频率f必须比2f大一些。
低通模拟信号的抽样定理。