带通抽样定理带通抽样定理

带通采样编辑带通采样又叫IF采样、调和采样、下奈奎斯特采样和下采样等[1]。

实际中遇到的许多信号是带通型信号?这种信号的带宽往往远小于信号中心频率。

若带通信号的上截止频率为fH,下截止频率为fL, 这时并不需要抽样频率高于两倍上截止频率fH,可按照带通抽样定理确定抽样频率。

带通采样定理：设带通信号m(t),其频率限制在fL与fH之间，带宽为B=fH-fL，如果最小抽样速率fs=2fH/m,m是一个不超过fH/B的最大整数，那么m(t),可以完全由其抽样值确定。

降采样：2048HZ对信号来说是过采样了，事实上只要信号不混叠就好（满足尼奎斯特采样定理），所以可以对过采样的信号作抽取，即是所谓的“降采样”。

在现场中采样往往受具体条件的限止，或者不存在300HZ的采样率，或调试非常困难等等。

若R>>1，则Rfs/2就远大于音频信号的最高频率fm，这使得量化噪声大部分分布在音频频带之外的高频区域，而分布在音频频带之内的量化噪声就会相应的减少，于是，通过低通滤波器滤掉fm以上的噪声分量，就可以提高系统的信噪比。

原采样频率为2048HZ，这时信号允许的最高频率是1024HZ（满足尼奎斯特采样定理），但当通过滤波器后使信号的最高频率为16HZ，这时采样频率就可以用到32HZ（满足尼奎斯特采样定理，最低为32HZ，比32HZ高都可以）。

从2048HZ降到32HZ，便是每隔64个样本取1个样本。

这种把采样频率降下来，就是降采样downsample）。

这样做的好处是减少数据样点，也就是减少运算时间，在实时处理时常采用的方法。

过采样：过采样定义：就是用高于nyquist频率进行采样，好处是可以提高信噪比，缺点是处理数据量大。

过采样是使用远大于奈奎斯特采样频率的频率对输入信号进行采样。

设数字音频系统原来的采样频率为fs，通常为44.1kHz或48kHz。

若将采样频率提高到R×fs，R称为过采样比率，并且R>1。

带通抽样定理《信号与系统A（2）》课程自学报告实施报告题目：带通采样定理与软件无线电带通抽样定理实际中遇到的许多信号是带通型信号，这种信号的带宽往往远小于信号中心频率。

若带通信号的上截止频率为H f ，下截止频率为L f ，这时并不需要抽样频率高于两倍上截止频率H f ，可按照带通抽样定理确定抽样频率。

[定理] 带通抽样定理：一个频带限制在),(H L f f 内的时间连续信号)(t x ，信号带宽L H f f B -=，令N B f M H -=/，这里N 为不大于B f H /的最大正整数。

如果抽样频率s f 满足条件，10-≤≤N m （3.1-9） )(t x 。

对信号)(t x 以频率s f 抽样后，得到的采样信号)(s nT x 的频谱是)(t x 的频谱经过周期延拓而成，延拓周期为s f ，如图3-3所示。

为了能够由抽样序列无失真的重建原始信号)(t x ，必须选择合适的延拓周期（也就是选择采样频率），使得位于),(H L f f 和),(L H f f --的频带分量不会和延拓分量出现混叠，这样使用带通滤波器就可以由采样序列重建原始信号。

由于正负频率分量的对称性，我们仅考虑),(H L f f 的频带分量不会出现混叠的条件。

在抽样信号的频谱中，在),(H L f f 频带的两边，有着两个延拓频谱分量：),(s L s H mf f mf f +-+-和))1(,)1((s L s H f m f f m f ++-++-。

为了避免混叠，延拓后的频带分量应满足）3.1-11）综合式（3.1-103.1-12） 这里mH s f f 2≥（3.1-13）这时实际上是把带通信号看作低通信号进行采样。

m 取得越大，则符合式（3.1-12）的采样频率会越低。

但是m 有一个上限，因为mff L s 2≤，而为了避免混叠，延拓周期要大于两倍的信号带宽，即B f s 2≥。

因此3.1-14） 由于N 为不大于B f H /B f L /的最大正整数为1-N ，故有10-≤≤N m综上所述，要无失真的恢复原始信号)(t x ，采样频率s f 应满足mff m f L s H 212≤≤+，10-≤≤N m （3.1-15） ffLf Hf H f -Lf -Lf Hf H f -Lf -图3-3 带通采样信号的频谱带通抽样定理在频分多路信号的编码、数字接收机的中频采样数字化中有重要的应用。

数字化的重要理论：带通采样定理
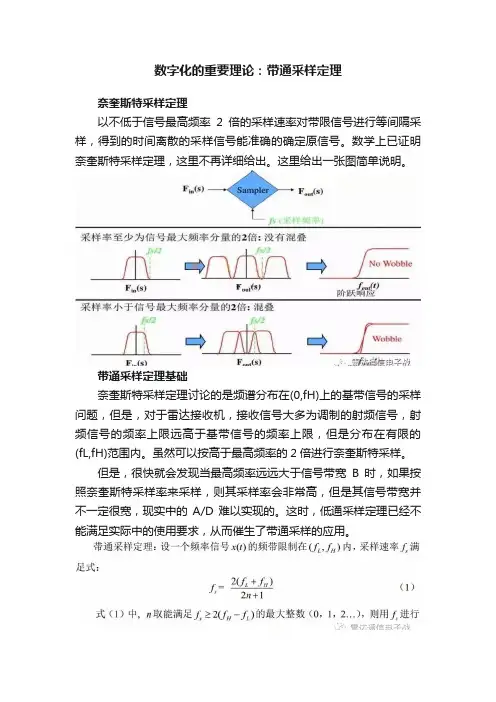
奈奎斯特采样定理
以不低于信号最高频率2倍的采样速率对带限信号进行等间隔采样，得到的时间离散的采样信号能准确的确定原信号。

数学上已证明奈奎斯特采样定理，这里不再详细给出。

这里给出一张图简单说明。

带通采样定理基础
奈奎斯特采样定理讨论的是频谱分布在(0,fH)上的基带信号的采样问题，但是，对于雷达接收机，接收信号大多为调制的射频信号，射频信号的频率上限远高于基带信号的频率上限，但是分布在有限的(fL,fH)范围内。

虽然可以按高于最高频率的2倍进行奈奎斯特采样。

但是，很快就会发现当最高频率远远大于信号带宽B时，如果按照奈奎斯特采样率来采样，则其采样率会非常高，但是其信号带宽并不一定很宽，现实中的A/D难以实现的。

这时，低通采样定理已经不能满足实际中的使用要求，从而催生了带通采样的应用。

带通采样的限制条件
带通采样定理使用的前提条件是：只允许在其中一个频带上存在信号，而不允许在不同的频带同时存在信号，否则将会引起信号混叠。

如下图所示，为满足这一条件，可采用跟踪滤波器的办法来解决，即在采样前先进行滤波。

这样的跟踪滤波器称之为抗混叠滤波器。

带通采样理论的应用大大降低了所需的采样频率，为后面的实时处理奠定了基础。

另外，当对于一个频率很高的射频信号采样时，如果采样频率设的太低，对提高采样量化的信噪比是不利的。

所以，在可能的情况下，带通采样频率应该尽可能选的高一些，使瞬时采样带宽尽可能宽。

《信号与系统A（2）》课程自学报告实施报告题目：带通采样定理与软件无线电带通抽样定理实际中遇到的许多信号是带通型信号，这种信号的带宽往往远小于信号中心频率。

若带通信号的上截止频率为H f ，下截止频率为L f ，这时并不需要抽样频率高于两倍上截止频率H f ，可按照带通抽样定理确定抽样频率。

[定理] 带通抽样定理：一个频带限制在),(H L f f 内的时间连续信号)(t x ，信号带宽L H f f B -=，令N B f M H -=/，这里N 为不大于B f H /的最大正整数。

如果抽样频率f，10-≤≤N m （3.1-9） )(t x 。

对信号)(t x 以频率s f 抽样后，得到的采样信号)(s nT x 的频谱是)(t x 的频谱经过周期延拓而成，延拓周期为s f ，如图3-3所示。

为了能够由抽样序列无失真的重建原始信号)(t x ，必须选择合适的延拓周期（也就是选择采样频率），使得位于),(H L f f 和),(L H f f --的频带分量不会和延拓分量出现混叠，这样使用带通滤波器就可以由采样序列重建原始信号。

由于正负频率分量的对称性，我们仅考虑),(H L f f 的频带分量不会出现混叠的条件。

在抽样信号的频谱中，在),(H L f f 频带的两边，有着两个延拓频谱分量：),(s L s H mf f mf f +-+-和))1(,)1((s L s H f m f f m f ++-++-。

为了避免混叠，延） 3.1-11）综合式（3.1-12） 这里m m 取零，则上述条件化为 H s f f 2≥（3.1-13）这时实际上是把带通信号看作低通信号进行采样。

m 取得越大，则符合式（3.1-12）的采样频率会越低。

但是m 有一个上限，因为mf f Ls 2≤，而为了避免混叠，延拓周期要大于两倍的信号带宽，即B f s 2≥。

因此3.1-14） 由于N 为不大于B f H /B f L /的最大正整数为1-N ，故有10-≤≤N m综上所述，要无失真的恢复原始信号)(t x ，采样频率s f 应满足mff m f L s H 212≤≤+，10-≤≤N m （3.1-15） ffLf Hf H f -Lf -Lf Hf H f -Lf -图3-3 带通采样信号的频谱带通抽样定理在频分多路信号的编码、数字接收机的中频采样数字化中有重要的应用。

低通与带通抽样定理验证【分析内容】按照低通抽样定理与带通抽样定理，分别对构造的低通型信号和带通型信号、两种抽样后的信号及滤波重建信号进行时域和频域观察，形象地给出低通抽样定理与带通抽样定理（带通部分选做）。

【分析目的】通过分析验证低通抽样定理与带通抽样定理。

【系统组成】抽样定理实质上研究的是随时间连续变化的模拟信号经抽样变成离散序列后，能否由此离散序列值重建原始模拟信号的问题。

对于低通型和带通型模拟信号，分别对应不同的抽样定理，抽样定理是模拟信号数字化的理论基础。

对上限频率为f H 的低通型信号，低通抽样定理要求抽样频率应满足： 对下限频率为f L 、上限频率为f H 的带通型信号，带通抽样定理要求抽样频率满足：其中， 为信号带宽，n 为正整数， 。

应该注意的是，当 时，无论带通型信号的f L 和f H 为何值，只需将抽样频率设定在2B ，理论上就不会发生抽样后的频谱重叠，而不像低通抽样定理要求的必须为上限频率的2倍以上。

仿真分析系统将按照图1所示结构创建。

其中，对于恒定频谱的冲激函数，通过低通滤波产生低通型信号，再进行低通抽样；通过带通滤波产生带通型信号，再进行带通滤波产生带通抽样，最后分别滤波重建原始信号。

仿真分析时，设低通滤波器的上限频率为10Hz ，带通滤波器下限频率为100Hz 、上限频率为120Hz ，低通抽样频率选为30Hz ；带通型信号上限频率f H = 6×20=120Hz （B=20Hz ，n=6），带通抽样频率至少应取40Hz ，现取60 Hz的带通抽样频率。

【创建分析】第1步：进入SystemView 系统视窗，设置“时间窗”参数如下：① 运行时间：Start Time: 0秒；StopTime: 0.4秒；② 采样频率：Sample Rate= 10000Hz 。

第2步：在SystemView 系统窗下，创Hs f f 2≥]1[2nk B f s +⋅≥L H f f B -=10<≤k nBf H =冲激函数 发生器 低通 滤波 低通抽样带通 滤波 带通 抽样 低通 重建 带通 重建 图1 仿真分析系统结构图2 SystemView 仿真分析系统建的仿真分析系统如图2所示。

带通采样定理3.1.3 带通抽样定理实际中遇到的许多信号是带通型信号，这种信号的带宽往往远小于信号中心频率。

若带通信号的上截止频率为H f ，下截止频率为L f ，这时并不需要抽样频率高于两倍上截止频率H f ，可按照带通抽样定理确定抽样频率。

[定理3-2] 带通抽样定理：一个频带限制在),(H L f f 内的时间连续信号)(t x ，信号带宽L H f f B -=，令N B f M H -=/，这里N 为不大于B f H /的最大正整数。

如果抽样频率s f 满足条件mf f m f L s H 212≤≤+，10-≤≤N m （3.1-9） 则可以由抽样序列无失真的重建原始信号)(t x 。

对信号)(t x 以频率s f 抽样后，得到的采样信号)(s nT x 的频谱是)(t x 的频谱经过周期延拓而成，延拓周期为s f ，如图3-3所示。

为了能够由抽样序列无失真的重建原始信号)(t x ，必须选择合适的延拓周期（也就是选择采样频率），使得位于),(H L f f 和),(L H f f --的频带分量不会和延拓分量出现混叠，这样使用带通滤波器就可以由采样序列重建原始信号。

由于正负频率分量的对称性，我们仅考虑),(H L f f 的频带分量不会出现混叠的条件。

在抽样信号的频谱中，在),(H L f f 频带的两边，有着两个延拓频谱分量：),(s L s H mf f mf f +-+-和))1(,)1((s L s H f m f f m f ++-++-。

为了避免混叠，延拓后的频带分量应满足L s L f mf f ≤+- （3.1-10）H s H f f m f ≥++-)1( （3.1-11）综合式（3.1-10）和式（3.1-11）并整理得到mf f m f L s H 212≤≤+ （3.1-12） 这里m 是大于等于零的一个正数。

如果m 取零，则上述条件化为H s f f 2≥ （3.1-13）这时实际上是把带通信号看作低通信号进行采样。

带通采样定理和频谱混叠关系【引言】在数字信号处理领域，通采样定理和频谱混叠关系是两个重要的概念。

通采样定理指出，如果一个连续时间信号的频率小于采样频率的一半，那么可以通过采样和重构恢复原始信号。

而频谱混叠则是在采样时没有满足通采样条件导致出现的混叠，即被采样信号的频谱被复制到了不同的频率位置上，影响了信号的恢复。

本文将详细介绍通采样定理和频谱混叠关系，并给出相关例子分析。

【正文】在信号处理中，我们经常会遇到连续时间信号采样的问题。

连续时间信号是一种在每个时间点都有定义的信号，而数字信号是在有限的时间范围内离散的信号。

为了将连续时间信号转换成数字信号，我们需要对其进行采样。

通采样定理是由萨奇-托洛茨基（Shannon-Tellegen）在1949年提出的，它指出，如果一个连续时间信号的频率小于采样频率的一半，那么可以通过采样和重构来准确地恢复原始信号。

通采样定理的证明思路如下：在连续时间信号中，将其分解成一系列不同频率的正弦波，然后对每一个正弦波进行采样。

根据采样频率和采样周期的关系，可以用离散时间的正弦波去逼近连续时间的正弦波。

这样，我们就可以通过对每一个频率成分都进行采样和重构，来重建原始信号。

然而，在实际应用中，往往无法满足通采样定理的条件，即采样频率必须大于信号频率的两倍，否则就会出现频谱混叠的问题。

频谱混叠是由于原始信号频谱被复制到了不同的频率位置上而产生的，这会导致重构的信号不再准确。

具体来说，当采样频率小于信号频率的两倍时，原始信号的高频部分会被复制到低频部分的位置上，从而导致低频成分在频谱中出现了多余的能量。

为了更好地理解频谱混叠的问题，我们可以通过一个简单的例子进行分析。

假设原始信号的频率为10Hz，采样频率为15Hz。

根据通采样定理，我们应该至少以20Hz的频率进行采样。

然而，由于采样频率小于信号频率的两倍，就会出现频谱混叠。

首先，我们可以将原始信号表示为一个简单的正弦波：x(t) = sin(2π10t)。