必修2 第1章 立体几何初步.

数学：第一章《立体几何初步》学案（新人教版B 版必修2）第一章《立体几何初步》单元小结导航知识链接点击考点（1）了解柱，锥，台，球及简单组合体的结构特征。

（2） 能画出简单空间图形的三视图，能识别三视图所表示的立体模型，并会用斜二测法画出它们的直观图。

（3） 通过观察用平行投影与中心投影这两种方法画出的视图与直观图，了解空间图形的不同表示形式。

（4） 理解柱，锥，台，球的表面积及体积公式。

（5） 理解平面的基本性质及确定平面的条件。

（6） 掌握空间直线与直线，直线与平面，平面与平面平行的判定及性质。

（7） 掌握空间直线与平面，平面与平面垂直的判定及性质。

名师导航1.学习方法指导 （1） 空间几何体①空间图形直观描述了空间形体的特征，我们一般用斜二测画法来画空间图形的直观图。

②空间图形可以看作点的集合，用符号语言表述点，线，面的位置关系时，经常用到集合的有关符号，要注意文字语言，符号语言，图形语言的相互转化。

③柱，锥，台，球是简单的几何体，同学们可用列表的方法对它们的定义，性质，表面积及体积进行归纳整理。

④对于一个正棱台，当上底面扩展为下底面的全等形时，就变为一个直棱柱；当上底面收缩为中心点时，就变为一个正棱锥。

由1()2S c c h ''=+正棱台侧和()3hV s s '=正棱台，就可看出它们的侧面积与体积公式的联系。

（2） 点，线，面之间的位置关系①“确定平面”是将空间图形问题转化为平面图形问题来解决的重要条件，这种转化最基本的就是三个公理。

②空间中平行关系之间的转化：直线与直线平行 直线与平面平行平面与平面平行。

③空间中垂直关系之间的转化：直线与直线垂直 直线与平面垂直平面与平面垂直。

2.思想方法小结在本章中需要用到的数学思想方法有：观察法，数形结合思想，化归与转化思想等。

主要是立体几何问题转化为平面几何问题，平行与垂直的相互转化等。

3.综合例题分析例1：如图，P 是∆ABC 所在平面外一点，A '，B '，C '分别是PBC ∆，PCA ∆，PAB ∆的重心。

第一章立体几何初步二、重点难点重点：空间直线，平面的位置关系。

柱、锥、台、球的表面积和体积的计算公式。

平行、垂直的定义，判定和性质。

难点：柱、锥、台、球的结构特征的概括。

文字语言，图形语言和符号语言的转化。

平行，垂直判定与性质定理证明与应用。

第一课时棱柱、棱锥、棱台【学习导航】学习要求1．初步理解棱柱、棱锥、棱台的概念。

掌握它们的形成特点。

2．了解棱柱、棱锥、棱台中一些常用名称的含义。

3．了解棱柱、棱锥、棱台这几种几何体简单作图方法4．了解多面体的概念和分类．【课堂互动】自学评价1．棱柱的定义：表示法：思考:棱柱的特点：.【答】2．棱锥的定义：表示法：思考:棱锥的特点：. 【答】3．棱台的定义：表示法：思考:棱台的特点：.【答】4．多面体的定义：5．多面体的分类：⑴棱柱的分类⑵棱锥的分类⑶棱台的分类【精典范例】例1：设有三个命题：甲：有两个面平行，其余各面都是平行四边形所围体一定是棱柱；乙：有一个面是四边形，其余各面都三角形所围成的几何体是棱锥；丙：用一个平行与棱锥底面的平面去截棱锥，得到的几何体叫棱台。

以上各命题中，真命题的个数是（A）A．0 B. 1 C. 2 D. 3例2：画一个四棱柱和一个三棱台。

【解】四棱柱的作法：⑴画上四棱柱的底面----画一个四边形；⑵画侧棱-----从四边形的每一个顶点画平行且相等的线段；⑶画下底面------顺次连结这些线段的另一个端点互助参考７页例１⑷画一个三棱锥，在它的一条侧棱上取一点，从这点开始，顺次在各个侧面画出与底面平行的线段，将多余的线段檫去．互助参考７页例１点评：(1)被遮挡的线要画成虚线(2)画台由锥截得思维点拔：解柱、锥、台概念性问题和画图需要：(1).准确地理解柱、锥、台的定义(2).灵活理解柱、锥、台的特点：例如：棱锥的特点是：⑴两个底面是全等的多边形；⑵多边形的对应边互相平行；⑶棱柱的侧面都是平行四边形。

反过来，若一个几何体，具有上面三条，能构成棱柱吗？或者说，上面三条能作为棱柱的定义吗？答：不能．点评:就棱柱来验证这三条性质，无一例外，能不能找到反例，是上面三条能作为棱柱的定义的关键。

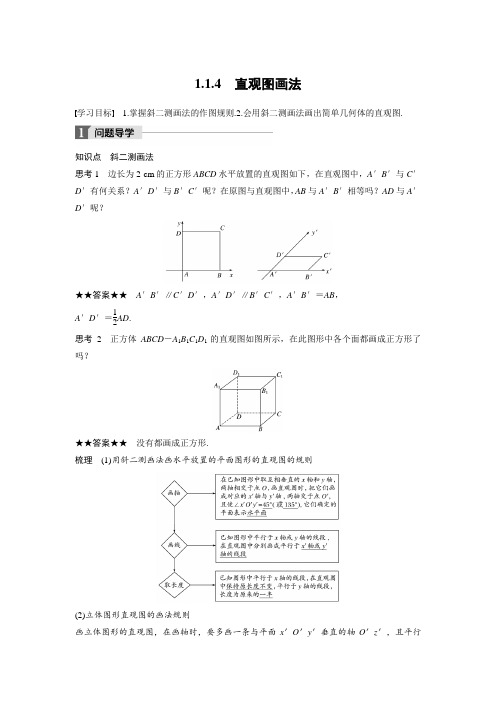
1.1.4 直观图画法学习目标 1.掌握斜二测画法的作图规则.2.会用斜二测画法画出简单几何体的直观图.知识点 斜二测画法思考1 边长为2 cm 的正方形ABCD 水平放置的直观图如下，在直观图中，A ′B ′与C ′D ′有何关系？A ′D ′与B ′C ′呢？在原图与直观图中，AB 与A ′B ′相等吗？AD 与A ′D ′呢？★★答案★★ A ′B ′∥C ′D ′，A ′D ′∥B ′C ′，A ′B ′＝AB ， A ′D ′＝12AD .思考2 正方体ABCD －A 1B 1C 1D 1的直观图如图所示，在此图形中各个面都画成正方形了吗？★★答案★★ 没有都画成正方形.梳理 (1)用斜二测画法画水平放置的平面图形的直观图的规则(2)立体图形直观图的画法规则画立体图形的直观图，在画轴时，要多画一条与平面x ′O ′y ′垂直的轴O ′z ′，且平行于O ′z ′的线段长度不变，其他同平面图形的画法.类型一 平面图形的直观图例1 画出如图水平放置的直角梯形的直观图.解 (1)在已知的直角梯形OBCD 中，以底边OB 所在直线为x 轴，垂直于OB 的腰OD 所在直线为y 轴建立平面直角坐标系.画出对应的x ′轴和y ′轴，使∠x ′O ′y ′＝45°，如图①②所示.(2)在x ′轴上截取O ′B ′＝OB ，在y ′轴上截取O ′D ′＝12OD ，过点D ′作x ′轴的平行线l ，在l 上沿x ′轴正方向取点C ′使得D ′C ′＝DC .连结B ′C ′，如图②. (3)所得四边形O ′B ′C ′D ′就是直角梯形OBCD 的直观图，如图③.引申探究若将本例中的直角梯形改为等腰梯形，其直观图如何？解 画法：(1)如图①所示，取AB 所在直线为x 轴，AB 中点O 为原点，建立直角坐标系，画出对应的坐标系x ′O ′y ′，使∠x ′O ′y ′＝45°.(2)以O ′为中点在x ′轴上取A ′B ′＝AB ，在y 轴上取O ′E ′＝12OE ，以E ′为中点画出C ′D ′∥x ′轴，并使C ′D ′＝CD . 连结B ′C ′，D ′A ′，如图②所示.(3)所得的四边形A ′B ′C ′D ′就是水平放置的等腰梯形ABCD 的直观图，如图③所示.反思与感悟 在画水平放置的平面图形的直观图时，选取适当的直角坐标系是关键之一，一般要使平面多边形尽可能多的顶点落在坐标轴上，以便于画点.原图中不平行于坐标轴的线段可以通过作平行于坐标轴的线段来作出其对应线段.确定多边形顶点的位置是关键之二，借助于平面直角坐标系确定顶点后，只需把这些顶点顺次连结即可.跟踪训练1如图所示，为一个水平放置的正方形ABCO，它在直角坐标系xOy中，点B的坐标为(2,2)，则在用斜二测画法画出的正方形的直观图中，顶点B′到x′轴的距离为________.★★答案★★2 2解析正方形的直观图如图所示.由直观图的画法知，O′A′＝1，又∠A′O′C′＝45°，过点A′作A′D′⊥O′C′，垂足为D′，∴点A′到x′轴的距离为A′D′＝O′A′·sin 45°＝2 2.又A′B′∥x′轴，∴点B′到x′轴的距离也是2 2.类型二直观图的还原与计算命题角度1由直观图还原平面图形例2如图所示，△A′B′C′是水平放置的平面图形的斜二测直观图，将其还原成平面图形.解①画出直角坐标系xOy，在x轴的正方向上取OA＝O′A′，即CA＝C′A′；②过B′作B′D′∥y′轴，交x′轴于点D′，在OA上取OD＝O′D′，过D作DB∥y 轴，且使DB＝2D′B′；③连结AB，BC，得△ABC.则△ABC即为△A′B′C′对应的平面图形，如图所示.反思与感悟 由直观图还原平面图形的关键(1)平行x ′轴的线段长度不变，平行y ′轴的线段扩大为原来的2倍.(2)对于相邻两边不与x ′、y ′轴平行的顶点可通过作x ′轴，y ′轴的平行线确定其在xOy 中的位置.跟踪训练2 如图所示，矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图，其中O ′A ′＝6 cm ，C ′D ′＝2 cm ，则原图形是________.★★答案★★ 菱形解析 如图所示，在原图形OABC 中，应有OD ＝2O ′D ′＝2×22＝42(cm)，CD ＝C ′D ′＝2(cm)，∴OC ＝OD 2＋CD 2＝(42)2＋22＝6(cm)， ∴OA ＝OC ，故四边形OABC 是菱形.命题角度2 原图形与直观图的面积的计算例3 如图所示，梯形A 1B 1C 1D 1是一平面图形ABCD 的直观图.若A 1D 1∥O ′y ′，A 1B 1∥C 1D 1，A 1B 1＝23C 1D 1＝2，A 1D 1＝O ′D 1＝1.试画出原四边形的形状，并求出原图形的面积.解 如图，建立直角坐标系xOy ，在x 轴上截取OD ＝ O ′D 1＝1，OC ＝O ′C 1＝2.在过点D 的y 轴的平行线上截取DA ＝2D 1A 1＝2. 在过点A 的x 轴的平行线上截取AB ＝A 1B 1＝2.连结BC ，即得到了原图形.由作法可知，原四边形ABCD 是直角梯形，上、下底长度分别为AB ＝2，CD ＝3，直角腰的长度AD ＝2，所以面积为S ＝2＋32×2＝5.反思与感悟 (1)由原图形求直观图的面积，关键是掌握斜二测画法，明确原来实际图形中的高，在直观图中变为与水平直线成45°角且长度为原来一半的线段，这样可得出所求图形相应的高.(2)若一个平面多边形的面积为S ，它的直观图面积为S ′，则S ′＝24S . 跟踪训练3 如图所示，一个水平放置的三角形的斜二测直观图是等腰直角三角形A ′B ′O ′，若O ′B ′＝1，那么原三角形ABO 的面积是________.★★答案★★2解析 直观图中等腰直角三角形的直角边长为1，因此面积为12.又直观图与原平面图形面积比为2∶4，所以原图形的面积为 2. 类型三 简单几何体的直观图例4 用斜二测画法画长、宽、高分别为4 cm 、3 cm 、2 cm 的长方体ABCD —A ′B ′C ′D ′的直观图.解 (1)画轴.如图，画x 轴、y 轴、z 轴，三轴相交于点O ，使∠xOy ＝45°，∠xOz ＝90°.(2)画底面.以点O 为中点，在x 轴上取线段MN ，使MN ＝4 cm ；在y 轴上取线段PQ ，使PQ ＝32 cm.分别过点M 和N 作y 轴的平行线，过点P 和Q 作x 轴的平行线，设它们的交点分别为A ，B ，C ，D ，四边形ABCD 就是长方体的底面ABCD .(3)画侧棱.过A ，B ，C ，D 各点分别作z 轴的平行线，并在这些平行线上分别截取2 cm 长的线段AA ′，BB ′，CC ′，DD ′.(4)成图.顺次连结A ′，B ′，C ′，D ′(去掉辅助线，将被遮挡的部分改为虚线)，就得到长方体的直观图.反思与感悟 直观图中应遵循的基本原则(1)用斜二测画法画空间图形的直观图时，图形中平行于x 轴、y 轴、z 轴的线段在直观图中应分别画成平行于x ′轴、y ′轴、z ′轴的线段.(2)平行于x 轴、z 轴的线段在直观图中长度保持不变，平行于y 轴的线段长度变为原来的12.(3)直观图画法口诀“一斜、二半、三不变”.跟踪训练4 用斜二测画法画出六棱锥P －ABCDEF 的直观图，其中底面ABCDEF 为正六边形，点P 在底面上的投影是正六边形的中心O .(尺寸自定)解 (1)画出六棱锥P －ABCDEF 的底面.①在正六边形ABCDEF 中，取AD 所在的直线为x 轴，对称轴MN 所在的直线为y 轴，两轴相交于点O ，如图(1)，画出相应的x ′轴、y ′轴、z ′轴，三轴相交于O ′，使∠x ′O ′y ′＝45°，∠x ′O ′z ′＝90°，如图(2)；②在图(2)中，以O ′为中点，在x ′轴上取A ′D ′＝AD ，在y ′轴上取M ′N ′＝12MN ，以点N ′为中点，画出B ′C ′平行于x ′轴，并且等于BC ，再以M ′为中点，画出E ′F ′平行于x ′轴，并且等于EF ；③连结A ′B ′，C ′D ′，D ′E ′，F ′A ′，得到正六边形ABCDEF 水平放置的直观图A ′B ′C ′D ′E ′F ′.(2)画出正六棱锥P －ABCDEF 的顶点.在z ′轴正半轴上截取点P ′，点P ′异于点O ′. (3)成图.连结P ′A ′，P ′B ′，P ′C ′，P ′D ′，P ′E ′，P ′F ′，并擦去x ′轴、y ′轴和z ′轴，便可得到六棱锥P －ABCDEF 的直观图P ′－A ′B ′C ′D ′E ′F ′，如图(3).1.利用斜二测画法画出边长为3 cm 的正方形的直观图，正确的是图中的________.(填序号)★★答案★★ ③解析 正方形的直观图应是平行四边形，且相邻两边的边长之比为2∶1.2.已知一个正方形的直观图是一个平行四边形，其中有一边长为4，则此正方形的面积为__________.★★答案★★ 16或64解析 等于4的一边在原图形中可能等于4，也可能等于8，所以正方形的面积为16或64. 3.已知两个底面半径相等的圆锥，底面重合在一起(底面平行于水平面)，其中一个圆锥顶点到底面的距离为2 cm ，另一个圆锥顶点到底面的距离为3 cm ，则其直观图中这两个顶点之间的距离为________ cm. ★★答案★★ 5解析 圆锥顶点到底面的距离即圆锥的高，故两顶点间距离为2＋3＝5(cm)，在直观图中与z 轴平行的线段长度不变，仍为5 cm.4.如图所示为一平面图形的直观图，则此平面图形可能是下图中的________.(填序号)★★答案★★ ③解析 在x 轴上或与x 轴平行的线段在新坐标系中的长度不变，在y 轴上或与y 轴平行的线段在新坐标系中的长度变为原来的12，并注意到∠xOy ＝90°，∠x ′O ′y ′＝45°，因此由直观图还原成原图形为③.5.画出一个正三棱台的直观图.(尺寸：上，下底面边长分别为1 cm,2 cm ，高为2 cm) 解 (1)作水平放置的下底面等边三角形的直观图△ABC ，其中O 为△ABC 的重心，BC ＝2 cm ，线段AO 与x 轴的夹角为45°，AO ＝2OD .(2)过O 作z 轴，使∠xOz ＝90°，在z 轴上截取OO ′＝2 cm ，作上底面等边三角形的直观图△A ′B ′C ′，其中B ′C ′＝1 cm ，连结AA ′，BB ′，CC ′，得正三棱台的直观图.1.画水平放置的平面图形的直观图，关键是确定直观图的顶点.确定点的位置，可采用直角坐标系.建立恰当的坐标系是迅速作出直观图的关键，常利用图形的对称性，并让顶点尽量多地落在坐标轴上或与坐标轴平行的直线上.2.用斜二测画法画图时要紧紧把握住：“一斜”、“二测”两点：(1)一斜：平面图形中互相垂直的Ox、Oy轴，在直观图中画成O′x′、O′y′轴，使∠x′O′y′＝45°或135°.(2)二测：在直观图中平行于x轴的长度不变，平行于y轴的长度取一半，记为“横不变，纵折半”.课时作业一、填空题1.在斜二测画法中，位于平面直角坐标系中的点M(4,4)在直观图中的对应点是M′，则点M′的坐标为________.★★答案★★(4,2)解析由直观图画法“横不变，纵折半”可得点M′的坐标为(4,2).2.如图，△A′B′C′是水平放置的△ABC的直观图，A′B′∥y′轴，B′C′∥x′轴，则△ABC的形状是______三角形.★★答案★★直角解析∵A′B′∥y′轴，B′C′∥x′轴，∴在原图形中，AB∥y轴，BC∥x轴，故△ABC为直角三角形.3.给出以下说法，其中不正确的是________.(填序号)①水平放置的矩形的直观图可能是梯形；②水平放置的梯形的直观图可能是平行四边形；③水平放置的平行四边形的直观图可能是矩形；④水平放置的菱形的直观图可能是平行四边形.★★答案★★①②解析由斜二测画法规则可知①②不正确.4.下面各组图形中2个边长为1的正△ABC的直观图不是全等三角形的一组是________.(填序号)★★答案★★③解析可分别画出各组图形的直观图，观察可得结论.5.如图，用斜二测画法画一个水平放置的平面图形的直观图为一个正方形，则原来图形的形状是________.(填序号)★★答案★★①解析直观图中正方形的对角线长为2，故在平面图形中平行四边形的高为22，只有①满足条件，故①正确.6.如图所示，△A′B′O′为水平放置的△ABO的直观图，由图判断△ABO中，AB，BO，BD，OD由小到大的顺序是____________.★★答案★★OD，BD，AB，BO解析由题图可知，在△ABO中，OD＝2，BD＝4，AB＝17，BO＝25，故OD<BD<AB<BO.7.用斜二测画法画水平放置的平面图形的直观图，对其中的线段说法正确的是________.(填序号)①原来相交的仍相交；②原来垂直的仍垂直；③原来平行的仍平行；④原来共点的仍共点.★★答案★★ ①③④解析 根据斜二测画法，原来互相垂直的线段未必垂直.8.一个长方体的长，宽，高分别是4,8,4，则画其直观图时对应的长度依次为____________. ★★答案★★ 4,4,4解析 根据斜二测画法规则可知，水平线段长度不变，平行于y 轴的线段长度减半，竖直线段长度不变，所以其长度分别为4,4,4.9.在如图所示的直观图中，四边形O ′A ′B ′C ′为菱形且边长为2 cm ，则在坐标系xOy 中，原四边形OABC 为______(填形状)，面积为________ cm 2.★★答案★★ 矩形 8解析 由题意并结合斜二测画法，可得四边形OABC 为矩形，其中OA ＝2 cm ，OC ＝4 cm ，∴四边形OABC 的面积为S ＝2×4＝8(cm 2).10.如图所示，四边形OABC 是上底为2，下底为6，底角为45°的等腰梯形，用斜二测画法画出这个梯形的直观图O ′A ′B ′C ′，则在直观图中，梯形的高为________.★★答案★★ 1解析 作CD 、BE ⊥OA 于点D 、E ，则OD ＝EA ＝OA －BC 2＝2(cm)，∴OD ＝CD ＝2 cm ，∴在直观图中梯形的高为12×2＝1(cm).二、解答题11.如图所示，画出水平放置的四边形OBCD 的直观图.解 (1)过点C 作CE ⊥x 轴，垂足为E ，如图①所示.画出对应的x ′轴，y ′轴，使∠x ′O ′y ′＝45°，如图②所示.(2)如图②所示，在x ′轴的正半轴上取点B ′，E ′，使得O ′B ′＝OB ，O ′E ′＝OE ；在y ′轴的正半轴上取一点D ′，使得O ′D ′＝12OD ；过E ′作E ′C ′∥y ′轴，使E ′C ′＝12EC . (3)连结B ′C ′，C ′D ′，并擦去x ′轴与y ′轴及其他一些辅助线，如图③所示，四边形O ′B ′C ′D ′就是所求作的直观图.12.如图，△A ′B ′C ′是水平放置的平面图形的直观图，试画出原平面图形△ABC .解 (1)过C ′，B ′分别作y ′轴的平行线交x ′轴于点D ′，E ′.(2)在直角坐标系xOy 中，在x 轴上取两点E ，D ，使OE ＝O ′E ′，OD ＝O ′D ′，再分别过E ，D 作y 轴的平行线，取EB ＝2E ′B ′，DC ＝2D ′C ′，连结OB ，OC ，BC ，并擦出辅助线及x 轴，y 轴，即求出原△ABC .13.如图所示，在△ABC 中，AC ＝12 cm ，AC 边上的高BD ＝12 cm ，求其水平放置的直观图的面积.解 方法一 画x ′轴，y ′轴，两轴交于O ′，使∠x ′O ′y ′＝45°，作△ABC 的直观图如图所示，则A ′C ′＝AC ＝12 cm ，B ′D ′＝12BD ＝6 cm ， 故△A ′B ′C ′的高为22B ′D ′＝3 2 cm ， 所以S △A ′B ′C ′＝12×12×32＝182(cm 2). 即水平放置的直观图的面积为18 2 cm 2.方法二 △ABC 的面积为12AC ·BD ＝12×12×12＝72(cm 2). 由平面图形的面积与直观图的面积间的关系，可得△ABC 水平放置的直观图的面积是24×72＝182(cm 2).三、探究与拓展14.水平放置的△ABC ，有一边在水平线上，用斜二测画法作出的直观图是正三角形A ′B ′C ′，则△ABC 是______三角形.★★答案★★ 钝角解析 将△A ′B ′C ′还原，由斜二测画法知，△ABC 为钝角三角形.15.用斜二测画法画出正三棱柱ABC —A ′B ′C ′的直观图.解 (1)画轴.如图，画出x 轴，y 轴，z 轴，三轴相交于点O ，使∠xOy ＝45°，∠xOz ＝90°.(2)画底面.作水平放置的三角形的直观图△ABC .(3)画侧棱.过A ，B ，C 各点分别作z 轴的平行线，并在这些平行线上分别截取线段AA ′，BB ′，CC ′，使得AA ′＝BB ′＝CC ′.(4)成图.顺次连结A ′，B ′，C ′，并擦去辅助线，将被遮住的部分改为虚线，得到的图形就是几何体的直观图.。

1高中数学 第1章《立体几何初步》垂直关系的判定导学案北师大版必修2你的 疑惑3.（1）半平面：一个平面内的一条直线，把这个平面分成 _________，其中的________都叫作半平面.（2）二面角：从一条直线出发的___________所组成的图形叫作二面角，___________叫做二面角的棱，______________叫作二面角的面.（3）二面角的记法：以直线AB 为棱，半平面α、β为面的二面角，记作________________.（如下图（1））（4）二面角的平面角：以二面角的棱上_________为端点，在两个半平面内分别作___________的两条射线，这两条射线所组成的角叫作二面角的平面角. 如下图（2）中的AOB ∠. ______________的二面角叫作直二面角.（5）两个平面相交，如果所成的二面角是__________，就说这两个平面互相垂直.4. 将一支铅笔垂直于桌面，再用一本书紧贴着铅笔转动，你能观察到书本和桌面的关系吗？再观察下图（1）（2）中的长方体，可以发现：平面α内的直线a 与平面β________，这时，α____β.抽象概括平面和平面垂直的判定定理：如果一个平面经过另一个平面的一条_______，那么这两个平面互相垂直.图形语言： 符号语言：若直线AB ____平面β，AB ______平面α，策略与反思 纠错与归纳【学习目标】 1. 理解直线和平面、平面和平面垂直的判定定理，并能进行简单应用. 2. 通过垂直关系判定定理的探究和应用过程，进一步提高空间想象能力和逻辑思维能力. 3. 通过垂直关系判定定理的探究和应用过程，体会数学和生活的紧密联系. 【重点难点】 重点：直线和平面、平面和平面垂直的判定定理及应用. 难点：对直线和平面、平面和平面垂直判定定理的理解. 【使用说明】 1. 认真阅读课本第35—37页的内容，独立完成自主学习内容. 2. 在自主学习的基础上，通过小组讨论，完成合作探究内容. 【自主学习】 1. 如右图，拿一块教学用的直角三角板，放在墙角，使三角板的 直角顶点C 与墙角重合，直角边AC 所在直线与墙角所在直线重合，将三角板绕AC 转动，在转动过程中，直角边CB 与地面紧贴，这就表示，AC 与地面垂直.抽象概括 直线和平面垂直的定义：如果一条直线和一个平面内的___________直线都_________，那么称这条直线和这个平面垂直. 2. 观察上图（1）的长方体，c b ,是平面α内的两条_______直线，直线a __b ，a __c ，这时，a __α. 观察上图（2）的长方体，平面α内的两条直线c b ,不相交，虽然直线a 与c b ,都______，但是a 与α_________. 抽象概括 直线和平面垂直的判定定理：如果一条直线和一个平面内的_______________都垂直，那么该直线与此平面垂直. 图形语言： 符号语言：若直线a ____平面α，直线b _____平面α， 直线l ____a ， 直线l ____b ，a ____A b =， 则α⊥l .天才在于积累 聪明在于勤奋。

第5课时线面垂直的综合应用学习目标 1.理解斜线在平面内的射影及与平面所成角的概念，会求简单的线面角.2.理解点到平面的距离的概念，会求简单的点面距离.3.线面平行与垂直的有关定理的综合运用．知识点一直线与平面所成的角思考直线与平面所成的角是如何定义的？取值范围是什么？★★答案★★平面的一条斜线与它在这个平面内的射影所成的锐角，叫做这条直线与这个平面所成的角．规定：一条直线垂直于平面，我们说它们所成的角是直角；一条直线与平面平行或在平面内，我们说它们所成的角是0°的角．直线与平面所成的角θ的取值范围是[0°，90°]．梳理有关概念对应图形斜线一条直线与一个平面相交，但不和这个平面垂直，图中直线P A斜足斜线与平面的交点，图中点A射影过平面外一点P向平面α引斜线和垂线，那么过斜足A和垂足O的直线就是斜线在平面内的正投影(简称射影)，线段OA 就是斜线段P A在平面α内的射影直线与平面所成的角定义：平面的一条斜线与它在这个平面内的射影所成的锐角，图中为∠P AO，规定：一条直线垂直于平面，它们所成的角是直角；一条直线与平面平行或在平面内，它们所成的角是0°的角取值范围设直线与平面所成的角为θ，则0°≤θ≤90°知识点二两种距离1．点到平面的距离从平面外一点引平面的垂线，这个点和垂足间的距离，叫做这个点到这个平面的距离．2．直线和平面的距离一条直线和一个平面平行，这条直线上任意一点到这个平面的距离，叫做这条直线和这个平面的距离．类型一 与线面角有关的问题例1 已知∠BAC 在平面α内，P ∉α，∠P AB ＝∠P AC .求证：点P 在平面α内的射影在∠BAC 的平分线上．证明 如图所示，作PO ⊥α，PE ⊥AB ，PF ⊥AC ，垂足分别为O ，E ，F ，连结OE ，OF ，OA.⎭⎪⎬⎪⎫PE ⊥AB ，PF ⊥AC ∠P AE ＝∠P AF P A ＝P A⇒Rt △P AE ≌Rt △P AF ⇒AE ＝AF .⎭⎪⎬⎪⎫PO ⊥αAB ⊂α⇒⎭⎪⎬⎪⎫AB ⊥POAB ⊥PE PO ∩PE ＝P⇒AB ⊥平面PEO ⇒AB ⊥OE .同理，AC ⊥OF .在Rt △AOE 和Rt △AOF 中，AE ＝AF ，OA ＝OA ， 所以Rt △AOE ≌Rt △AOF . 于是∠EAO ＝∠F AO ，因此，点P 在α内的射影O 在∠BAC 的平分线上． 反思与感悟 (1)求直线和平面所成角的步骤 ①寻找过斜线上一点与平面垂直的直线；②连结垂足和斜足得到斜线在平面上的射影，斜线与其射影所成的锐角或直角即为所求的角；③把该角归结在某个三角形中，通过解三角形，求出该角．(2)在上述步骤中，其中作角是关键，而确定斜线在平面内的射影是作角的关键，几何图形的特征是找射影的依据，图形中的特殊点是突破口．跟踪训练1 如图所示，在斜三棱柱ABC —A 1B 1C 1中，∠BAC ＝90°，BC 1⊥AC ，C 1H ⊥AB ，证明：点H 是C 1在平面ABC 内的射影．证明连结AC1.∵∠BAC＝90°，∴AB⊥AC，又AC⊥BC1，BC1∩AB＝B，∴AC⊥平面ABC1.又∵C1H⊂平面ABC1，∴AC⊥C1H.又AB⊥C1H，AB∩AC＝A，∴C1H⊥平面ABC，∴点H是C1在平面ABC上的射影．类型二直线与平面垂直的判定与性质的综合应用例2如图，在四棱锥P—ABCD中，P A⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，P A＝AB＝BC，E是PC的中点．求证：(1)CD⊥AE；(2)PD⊥平面ABE.证明(1)在四棱锥P—ABCD中，∵P A⊥底面ABCD，CD⊂平面ABCD，∴P A⊥CD.∵AC⊥CD，P A∩AC＝A，∴CD⊥平面P AC.而AE⊂平面P AC，∴CD⊥AE.(2)由P A＝AB＝BC，∠ABC＝60°，可得AC＝P A.∵E是PC的中点，∴AE⊥PC.由(1)知，AE⊥CD，又PC∩CD＝C，∴AE⊥平面PCD.而PD⊂平面PCD，∴AE⊥PD.∵P A⊥底面ABCD，∴PD在底面ABCD内的射影是AD，又∵AB⊥AD，∴AB⊥PD.又AB∩AE＝A，∴PD⊥平面ABE.反思与感悟证明线面垂直的核心是证明线线垂直，而证明线线垂直又可借助于线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．跟踪训练2如图，直三棱柱ABC－A1B1C1中，∠BAC＝90°，AB＝AC＝a，AA1＝2a，D为棱B1B的中点．(1)证明：A1C1∥平面ACD；(2)求异面直线AC与A1D所成角的大小；(3)证明：直线A1D⊥平面ADC.(1)证明在直三棱柱ABC－A1B1C1中，AC∥A1C1.又A1C1⊄平面ACD，AC⊂平面ACD，∴A1C1∥平面ACD.(2)解在直三棱柱ABC－A1B1C1中，AA1⊥平面ABC，∴A1A⊥AC.又∠BAC＝90°，∴AC⊥AB.∵AA1∩AB＝A，∴AC⊥平面A1ABB1，又A1D⊂平面A1ABB1，∴AC⊥A1D.∴异面直线AC与A1D所成的角为90°.(3)证明∵△A1B1D和△ABD都为等腰直角三角形，∴∠A1DB1＝∠ADB＝45°，∴∠A1DA＝90°，即A1D⊥AD.由(2)知，A1D⊥AC，且AD∩AC＝A，∴A1D⊥平面ADC.1．下列说法：①平面的斜线与平面所成的角的取值范围是0°<θ<90°；②直线与平面所成的角的取值范围是0°<θ≤90°；③若两条直线与一个平面所成的角相等，则这两条直线互相平行；④若两条直线互相平行，则这两条直线与一个平面所成的角相等．其中正确的是________．(填序号)★★答案★★①④解析②应为0°≤θ≤90°；③中这两条直线可能平行，也可能相交或异面．2．AB是平面α的斜线段，其长为a，它在平面α内的射影A′B的长为b，则垂线A′A的长为________．★★答案★★a2－b23．在长方体ABCD—A1B1C1D1中，MN在平面BCC1B1内，MN⊥BC于M，则MN与AB的位置关系为______．★★答案★★垂直解析AB⊥平面BCC1B1，又MN⊂平面BCC1B1，∴AB⊥MN.4.若长方体ABCD—A1B1C1D1的底面边长为1，AB1与底面ABCD成60°角，则A1C1到底面ABCD的距离为________．★★答案★★ 3解析依题可知∠B1AB＝60°，A1C1∥平面ABCD，A1A⊥平面ABCD，∴A1A即为A1C1到底面ABCD的距离．由题意得A1A＝B1B＝ 3.5.如图所示，平面ABB1A1为圆柱OO1的轴截面，点C为底面圆周上异于A，B的任意一点．(1)求证：BC⊥平面A1AC；(2)若D为AC的中点，求证：A 1D ∥平面O 1BC .证明 (1)∵AB 为⊙O 的直径，点C 为⊙O 上的任意一点，∴BC ⊥AC . 又在圆柱OO 1中，AA 1⊥底面⊙O ，∴AA 1⊥BC ， 又AA 1∩AC ＝A ， ∴BC ⊥平面A 1AC .(2)取BC 的中点E ，连结DE ，O 1E ，∵D 为AC 的中点，∴在△ABC 中，DE ∥AB ，且DE ＝12AB ，又在圆柱OO 1中，A 1O 1∥AB ，且A 1O 1＝12AB ，∴DE ∥A 1O 1，DE ＝A 1O 1，∴四边形A 1DEO 1为平行四边形，∴A 1D ∥EO 1. 而A 1D ⊄平面O 1BC ，EO 1⊂平面O 1BC ， ∴A 1D ∥平面O 1BC .立体几何中经常遇到由一个点向一个平面引垂线的问题，垂线的位置是由这个点在平面内的射影来确定的，因此这个点的射影就是一个关键量，一般来说，可以直接由这个点作平面的垂线，然后通过证明或计算说明垂足的位置，也可以借助一些常见结论进行确定，如： (1)如果一个角所在平面外一点到角的两边距离相等，那么这一点在平面内的射影在这个角的平分线上．(2)经过一个角的顶点引这个角所在平面的斜线，如果斜线与这个角的两边的夹角相等，那么斜线在平面内的射影是这个角的平分线所在的直线．课时作业一、填空题1．如图，在△ABC 中，∠BAC ＝90°，P A ⊥平面ABC ，AB ＝AC ，D 是BC 的中点，则图中直角三角形的个数是____．★★答案★★ 8解析 在Rt △ABC 中，∠BAC ＝90°， P A ⊥平面ABC ，∴AB ⊥P A ，P A ⊥DA ，P A ⊥AC . ∵AB ＝AC ，D 是BC 的中点，∴AD ⊥BC ，∴BP ＝CP ，可得PD ⊥BC ，∴图中直角三角形有△P AC ，△P AB ，△P AD ，△ABC ，△ABD ，△ADC ，△BPD ，△DPC ，共8个． 2．下列命题：①⎭⎪⎬⎪⎫a ⊥αb ⊂α⇒a ⊥b; ② ⎭⎪⎬⎪⎫a ⊥αa ∥b ⇒b ⊥α； ③ ⎭⎪⎬⎪⎫a ⊥αb ∥α⇒a ⊥b; ④ ⎭⎪⎬⎪⎫a ⊥b b ⊂α⇒a ⊥α； ⑤⎭⎪⎬⎪⎫a ∥αa ⊥b ⇒b ⊥α；⑥⎭⎪⎬⎪⎫a ⊥αb ⊥a ⇒b ∥α或b ⊂α. 其中正确的命题是________．(填序号) ★★答案★★ ①②③⑥3．已知△ABC 的三条边长分别是5,12,13，点P 到A ，B ，C 三点的距离都等于7，则点P 到平面ABC 的距离为________．★★答案★★332解析 由点P 到△ABC 三个顶点的距离相等可知，P 在平面ABC 上的射影为△ABC 的外心． ∵△ABC 为直角三角形，∴其外心是斜边的中点，即点P 在平面ABC 上的射影是△ABC 斜边的中点D ，如图． ∴点P 到平面ABC 的距离为PD ＝72－⎝⎛⎭⎫1322＝332.4．下列四个正方体图形中，l 是正方体的一条体对角线，点M ，N ，P 分别为其所在棱的中点，能得出l ⊥平面MNP 的图形的序号是________．(写出所有符合要求的图形的序号)★★答案★★①④解析设定正方体的顶点如图，连结DB，AC，∵M，N分别为中点，∴MN∥AC.∵四边形ABCD为正方形，∴AC⊥BD.∵BB′⊥平面ABCD，AC⊂平面ABCD，∴BB′⊥AC.∵BB′∩DB＝B，BB′⊂平面DBB′，DB⊂平面DBB′，∴AC⊥平面DBB′，∵DB′⊂平面DBB′，∴AC⊥DB′.∵MN∥AC，∴DB′⊥MN，同理可证DB′⊥MF，DB′⊥NF，∵MF∩NF＝F，MF⊂平面MNF，NF⊂平面MNF，∴DB′⊥平面MNF，即l垂直于平面MNP，故①正确；④中由①证明可知l⊥MP，∵MN∥AC，AC⊥l，∴l⊥MN，∴l⊥平面MNP.5.如图，ABCD—A1B1C1D1为正方体，下列结论中正确的是________．(填序号)①BD∥平面CB1D1；②AC1⊥平面CB1D1；③过点A1与异面直线AD和CB1成90°角的直线有2条．★★答案★★①②解析由题图可知，在正方体ABCD—A1B1C1D1中，由于BD∥B1D1，由直线和平面平行的判定定理可得BD∥平面CB1D1，故①正确；由正方体的性质可得B1D1⊥A1C1，CC1⊥B1D1，故B1D1⊥平面ACC1A1，故B1D1⊥AC1.同理可得B1C⊥AC1.再根据直线和平面垂直的判定定理可得AC1⊥平面CB1D1，故②正确；过点A1与直线AD成90°角的直线必和BC也垂直，过点A1与CB1成90°角的直线必和CB1垂直，则该直线必和平面B1C1CB垂直，满足条件的只有直线A1B1，故③不正确．6．已知平面α外两点A、B到平面α的距离分别是2和4，则A，B的中点P到平面α的距离是________．★★答案★★3或1解析若A，B在α同侧，如图①，则P到α的距离为3；若A，B在α异侧，如图②，则P到α的距离为PO′－OO′＝3－2＝1.7．如图，直线P A垂直于圆O所在的平面，△ABC内接于圆O，且AB为圆O的直径，点M为线段PB的中点．现有以下命题：①BC⊥PC；②OM∥平面APC；③点B到平面P AC的距离等于线段BC的长．其中正确的命题为________．(填序号)★★答案★★①②③解析∵P A⊥平面ABC，BC⊂平面ABC，∴P A⊥BC，∵AB是圆O的直径，∴AC⊥BC，又∵P A⊂平面P AC，AC⊂平面P AC，P A∩AC＝A，∴BC⊥平面P AC，∵PC⊂平面P AC，∴BC⊥PC，故①③正确．∵M是PB的中点，O是AB的中点，∴OM∥P A，∵P A⊂平面P AC，OM⊄平面P AC，∴OM∥平面P AC.故②正确．8.如图，四棱锥S—ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中正确的有________个．①AC⊥SB；②AB∥平面SCD；③SA与平面ABCD所成的角是∠SAD；④AB与SC所成的角等于DC与SC所成的角．★★答案★★ 4解析∵AC⊥BD，SD⊥AC，BD与AC相交，∴AC⊥平面SBD，∴AC⊥SB，故①正确；∵AB∥CD，∴AB∥平面SCD，故②正确；∵SD⊥平面ABCD，∴SA在平面ABCD的射影是AD，故③正确；∵AB∥CD，故④正确．9.如图所示，在直四棱柱ABCD—A1B1C1D1中，当底面四边形A1B1C1D1满足条件________时，有A1C⊥B1D1.(注：填上你认为正确的一种情况即可，不必考虑所有可能的情况)★★答案★★B1D1⊥A1C1(★★答案★★不惟一)解析由直四棱柱可知CC1⊥面A1B1C1D1，所以CC1⊥B1D1，要使B1D1⊥A1C，只要B1D1⊥平面A1CC1，所以只要B1D1⊥A1C1，还可以填写四边形A1B1C1D1是菱形、正方形等条件．10.如图是底面边长为a的正三棱柱(侧棱与底面垂直且底面为正三角形的棱柱)，则AA1到平面BB1C1C的距离为________．★★答案★★3 2a解析∵AA1∥BB1，∴AA1∥平面BB1C1C，∴AA1到平面BB1C1C的距离等于A到平面BB1C1C的距离．取BC的中点D，连结AD，则AD⊥BC.又AD⊥BB1.∴AD⊥平面BB1C1C.∴AD＝32a，∴AA1到平面BB1C1C的距离为3 2a.11．如图，在正方体ABCD—A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总是保持AP与BD1垂直，则动点P的轨迹为________．★★答案★★线段CB1解析如图，先找到一个平面总是保持与BD1垂直，连结AC，AB1，B1C，在正方体ABCD—A1B1C1D1中，易得BD1⊥CB1，BD1⊥AC.则BD1⊥平面ACB1，又点P在侧面BCC1B1及其边界上运动，根据平面的基本性质，得点P的轨迹为平面ACB1与平面BCC1B1的交线段CB1.二、解答题12．如图，在边长为2的正方形ABCD中，点E，F分别是AB，BC的中点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点A′，求证：A′D⊥EF.证明在正方形ABCD中，有AD⊥AE，CD⊥CF，则A′D⊥A′E，A′D⊥A′F.又A′E∩A′F＝A′，∴A′D⊥平面A′EF，又EF⊂平面A′EF，∴A′D⊥EF.13．如图，在正三棱柱ABC—A1B1C1中，点D是BC的中点，BC＝2，BB1＝2，求证：(1)A1C∥平面AB1D；(2)BC1⊥平面AB1D.证明(1)连结A1B，交AB1于点O，连结OD，则点O是A1B的中点．又点D是BC的中点，所以A1C∥OD.又OD⊂平面AB1D，A1C⊄平面AB1D，所以A1C∥平面AB1D.(2)因为D为BC的中点，所以AD⊥BC.在正三棱柱ABC—A1B1C1中，BB1⊥平面ABC，AD⊂平面ABC，所以AD⊥BB1.又BC∩BB1＝B，BC⊂平面BCC1B1，BB1⊂平面BCC1B1，所以AD⊥平面BCC1B1.又BC1⊂平面BCC1B1，所以AD⊥BC1.设B1D∩BC1＝F，在Rt△DBB1和Rt△BB1C1中，BD BB1＝12，BB1B1C1＝22，所以△DBB1∽△BB1C1，所以∠BDF＝∠C1BB1.又∠C1BB1＋∠FBD＝90°，所以∠BDF＋∠FBD＝90°，所以BC1⊥B1D.又BC1⊥AD，AD∩B1D＝D，AD⊂平面AB1D，B1D⊂平面AB1D，所以BC1⊥平面AB1D.三、探究与拓展14.如图，已知AB是圆O的直径，C为圆上一点，AB＝2，AC＝1，P为⊙O所在平面外一点，且P A垂直于圆O所在平面，PB与平面ABC所成的角为45°.(1)求证：BC⊥平面P AC；(2)求点A到平面PBC的距离．(1)证明∵P A⊥平面ABC，∴P A⊥BC.∵AB是圆O的直径，C为圆上一点，∴BC⊥AC.又∵P A∩AC＝A，∴BC⊥平面P AC.(2)解如图，过点A作AD⊥PC于点D，∵BC⊥平面P AC，AD⊂平面P AC，∴BC⊥AD，∴AD⊥平面PBC.∴AD即为点A到平面PBC的距离，∵∠PBA为PB与平面ABC所成的角，即∠PBA＝45°，∴P A＝AB＝2，AC＝1，可得PC＝ 5.∵AD·PC＝P A·AC，∴AD＝2×15＝255，即点A到平面PBC的距离为25 5.15.如图，三棱柱ABC—A1B1C1的底面是边长为4的正三角形，侧棱AA1⊥底面ABC，M为A1B1的中点．(1)证明：MC ⊥AB ；(2)若AA 1＝26，侧棱CC 1上是否存在点P 使得MC ⊥平面ABP ？若存在，求出PC 的长；若不存在，请说明理由．(1)证明 取AB 的中点N ，连结MN ，CN ，则MN ⊥底面ABC ，MN ⊥AB .因为△ABC 是正三角形，所以NC ⊥AB ，由MN ∩NC ＝N ，MN ⊂平面MNC ，NC ⊂平面MNC ，可得AB ⊥平面MNC ，从而AB ⊥MC .(2)解 由(1)知，MC ⊥AB ，若存在点P 使得MC ⊥平面ABP ，则必有MC ⊥BP . 过M 作MQ ⊥B 1C 1，垂足为Q ，连结QC ，则QC 是MC 在平面BCC 1B 1内的射影，只需QC ⊥BP 即可，此时Rt △QC 1C 与Rt △PCB 相似，QC 1C 1C ＝PC CB， 所以PC ＝QC 1·CB C 1C ＝3×426＝6，点P 恰好是CC 1的中点．。