高中数学竞赛试题及答案

2024年全国中学生数学奥林匹克竞赛（预赛）暨2024年全国高中数学联合竞赛一试（A 卷）参考答案及评分标准说明：1. 评阅试卷时，请依据本评分标准. 填空题只设8分和0分两档；其他各题的评阅，请严格按照本评分标准的评分档次给分，不得增加其他中间档次.2. 如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，解答题中第9小题4分为一个档次，第10、11小题5分为一个档次，不得增加其他中间档次．一、填空题：本大题共8小题，每小题8分，满分64分．1. 若实数1m 满足98log (log )2024m ，则32log (log )m 的值为 ． 答案：4049．解：323898log (log )log (3log )12log (log )1220244049m m m ．2. 设无穷等比数列{}n a 的公比q 满足01q ．若{}n a 的各项和等于{}n a 各项的平方和，则2a 的取值范围是 ．答案：1,0(0,2)4． 解：因为数列{}n a 的各项和为11a q，注意到{}n a 各项的平方依次构成首项为21a 、公比为2q 的等比数列，于是2{}n a 的各项和为2121a q． 由条件知211211a a q q，化简得11a q ． 当(1,0)(0,1)q 时，22111(1),0(0,2)244a q q q ． 3. 设实数,ab 满足：集合2{100}A x x x a R 与3{}B x bx b R 的交集为[4,9]，则a b 的值为 ．答案：7．解：由于2210(5)25x x a x a ，故A 是一个包含[4,9]且以5x 为中点的闭区间，而B 是至多有一个端点的区间，所以必有[1,9]A ，故9a ．进一步可知B 只能为[4,) ，故0b 且34b b ，得2b ．于是7a b ．4. 在三棱锥P ABC 中，若PA 底面ABC ，且棱,,,AB BP BC CP 的长分别为1,2,3,4，则该三棱锥的体积为 ．答案：34． 解：由条件知PA AB ，PA AC ．因此PA AC ．在ABC 中，22219131cos 22132AB BC AC B AB BC ，故sin B ．所以1sin 2ABC S AB BC B 又该三棱锥的高为PA ，故其体积为1334ABC V S PA ． 5. 一个不均匀的骰子，掷出1,2,3,4,5,6点的概率依次成等差数列．独立地先后掷该骰子两次，所得的点数分别记为,a b ．若事件“7a b ”发生的概率为17，则事件“a b ”发生的概率为 ． 答案：421． 解：设掷出1,2,,6 点的概率分别为126,,,p p p ．由于126,,,p p p 成等差数列，且1261p p p ，故16253413p p p p p p ． 事件“7a b ”发生的概率为1162561P p p p p p p ． 事件“a b ”发生的概率为2222126P p p p ． 于是22221216253411()()()333P P p p p p p p ． 由于117P ，所以21143721P ． 6. 设()f x 是定义域为R 、最小正周期为5的函数．若函数()(2)x g x f 在区间[0,5)上的零点个数为25，则()g x 在区间[1,4)上的零点个数为 ．答案：11．解：记2x t ，则当[0,5)x 时，[1,32)t ，且t 随x 增大而严格增大．因此，()g x 在[0,5)上的零点个数等于()f t 在[1,32)上的零点个数．注意到()f t 有最小正周期5，设()f t 在一个最小正周期上有m 个零点，则()f t 在[2,32)上有6m 个零点，又设()f t 在[1,2)上有n 个零点，则625m n ，且0n m ，因此4,1m n ．从而()g x 在[1,4)上的零点个数等于()f t 在[2,16)[1,16)\[1,2) 上的零点个数，即311m n ．7. 设12,F F 为椭圆 的焦点，在 上取一点P （异于长轴端点），记O 为12PF F 的外心，若12122PO F F PF PF ，则 的离心率的最小值为 ．答案 解：取12F F 的中点M ，有12MO F F ，故120MO F F ． 记1212,,PF u PF v F F d ，则121212PO F F PM F F MO F F 12211()()2PF PF PF PF 222v u ， 222121222cos PF PF uv F PF u v d ，故由条件知222222v u u v d ，即22232u v d ． 由柯西不等式知222281(3)1()33d u v u v （当3v u 时等号成立）．所以 的离心率d e u v ．当::u v d 时， 的离心率e 取到最小值8. 若三个正整数,,a b c 的位数之和为8，且组成,,a b c 的8个数码能排列为2,0,2,4,0,9,0,8，则称(,,)a b c 为“幸运数组”，例如(9,8,202400)是一个幸运数组．满足10a b c 的幸运数组(,,)a b c 的个数为 ．答案：591．解：对于幸运数组(,,)a b c ，当10a b c 时，分两类情形讨论． 情形1：a 是两位数，,b c 是三位数．暂不考虑,b c 的大小关系，先在,,a b c 的非最高位（五个位置）中选三个位置填0，剩下五个位置还未填，任选其中两个填2，最后三个位置填写4,8,9，这样的填法数为3255C C 3!600 ．再考虑其中,b c 的大小关系，由于不可能有b c ，因此b c 与b c 的填法各占一半，故有300个满足要求的幸运数组．情形2：,a b 是两位数，c 是四位数．暂不考虑,a b 的大小关系，类似于情形1，先在,,a b c 的非最高位（五个位置）中选三个位置填0，剩下五个位置填2,2,4,8,9，这样的填法数为600．再考虑其中,a b 的大小关系．若a b ，则必有20a b ，c 的四个数字是0,4,8,9的排列，且0不在首位，有33!18 种填法，除这些填法外，a b 与a b 的填法各占一半，故有600182912个满足要求的幸运数组． 综上，所求幸运数组的个数为300291591 ．二、解答题：本大题共3小题，满分56分．解答应写出文字说明、证明过程或演算步骤．9. （本题满分16分） 在ABC 中，已知sin cos sin cos cos 22A AB B C，求cos C 的值．解：由条件知cos 44C A B． …………4分 假如44A B，则2C ，cos 0C ，但sin 04A ，矛盾． 所以只可能44A B ．此时0,2A B ，2C A ． …………8分注意到cos 04C A ，故2C ，所以,42A B ，结合条件得cos cos 2sin 22sin cos 244C A A A A2C ，又cos 0C ，化简得28(12cos )1C ，解得cos C…………16分 10.（本题满分20分）在平面直角坐标系中，双曲线22:1x y 的右顶点为A ．将圆心在y 轴上，且与 的两支各恰有一个公共点的圆称为“好圆”．若两个好圆外切于点P ，圆心距为d ，求d PA 的所有可能的值． 解：考虑以0(0,)y 为圆心的好圆2220000:()(0)x y y r r ．由0 与 的方程消去x ，得关于y 的二次方程2220002210y y y y r ．根据条件，该方程的判别式22200048(1)0y y r ，因此220022y r ．…………5分对于外切于点P 的两个好圆12, ，显然P 在y 轴上．设(0,)P h ，12, 的半径分别为12,r r ，不妨设12, 的圆心分别为12(0,),(0,)h r h r ，则有2211()22h r r ，2222()22h r r ．两式相减得2212122()h r r r r ，而120r r ，故化简得122r r h． …………10分 进而221211222r r r r ，整理得 221122680r r r r ．① 由于12d r r ，(1,0)A ，22212()114r r PA h ，而①可等价地写为2212122()8()r r r r ，即228PA d ，所以d PA…………20分 11.（本题满分20分）设复数,z w 满足2z w ，求2222S z w w z 的最小可能值．解法1：设i (,)z a b a b R ，则2i w a b ，故2222242(1)i 642(3)i S a a b b a a a b b a ，22222464a a b a a b2222(1)5(3)5a b a b ． ①…………5分记1t a ．对固定的b ，记255B b ，求22()(4)f t t B t B 的最小值．由()(4)f t f t ，不妨设2t ．我们证明0()()f t f t ，其中0t ． 当0[2,]t t 时，04[2,4]t t ，22200()()()((4))((4))f t f t B t B t B t2222220000(4)((4))(28)(28)t t t t t t t t0 （用到02t t 及228y x x 在[2,) 上单调增）． …………10分当0[,)t t 时，22200()()(4)(4)f t f t t B t B t B222200(4)(4)t t t t 000()8t t t t t t0 （用到04t t ）． …………15分所以200()(4)1616S f t B t ．当0b （①取到等号），011a t 时，S 取到最小值16．…………20分解法2：设1i,1i (,)R z x y w x y x y ，不妨设其中0x ． 计算得2222(41)(24)i z w x x y x y ，2222(41)(24)i w z x x y x y ．所以22Re(2)Re(2)S z w w z 22224141x x y x x y ． …………5分利用a b a b ，可得8S x ，① 亦有22222212(1)2(1)S x y x y x ． ②…………10分注意到方程282(1)x x 2．当2x 时，由①得816S x ．当02x 时，由②得222(1)2(12))16S x ．因此当2,0x y 时，S 取到最小值16． …………20分 解法3：因为2w z =−，所以我们有222(2)2411z z z z z22(2)26411z z z z z从而上两式最右边各项分别是z 到复平面中实轴上的点1−1−，33+的距离，所以把i z x y =+换成其实部x 时，都不会增大.因此只需 考虑函数22()2464f x x x x x +−+−+在R 上的最小值.…………10分因为1313−−<<−+<，因此我们有以下几种情况：1.若1x≤−,则2()24f x x x=−,在这一区间上的最小值为(116f−=+；2.若(13x∈−−，则()88f x x=−+，在这一区间上的最小值为(316f=−+…………15分3.若31x∈−，则2()24f x x x=−+，在这一区间上的最小值为((3116f f=−+=−+；4.若13x∈− ，则()88f x x=−，在这一区间上的最小值为(116f−+=−+；5.若3x≥+，则2()24f x x x=−，在这一区间上的最小值为(316f=+.综上所述，所求最小值为((3116f f=−+=−.…………20分。

全国高中数学联合竞赛（9月19日上午9：00～11：00）一、选择题（本题共6个小题，每小题5分满分30分）（1）若函数x x x f 2sin 2cos 811)(--=的最大值为a ，最小值为b ，则ba 1-等于（ ） （A ）18 （B ）6 （C ）5 （D ）0 （2）若b a <<0，且1=+b a ，则下列各式中最大的是（ ） （A ）1- （B ）1log log 22++b a（C ）b 2log（D ）)(log 32232b ab b a a +++（3）已知数列2004，2005，1，2004-，2005-，…，这个数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前2004项之和2004S 等于（ ） （A ）2005（B ）2004 （C ）1 （D ）0（4）已知函数xx xx ee e e xf --+-=)(的反函数是)(1x f -，且k f f =---|)6.0(||)8.0(|11，则（ ） （A ）)21,0(∈k （B ）)1,21(∈k（C ）)23,1(∈k（D ）)2,23(∈k（5）正四棱锥ABCD S -中，侧棱与底面所成的角为α，侧面与底面所成的角为β，侧面等腰三角形的底角为γ，相邻两侧面所成的二面角为θ，则α、β、γ、θ的大小关系是（ ） （A ）θγβα<<< （B ）γθβα<<< （C ）βγαθ<<<（D ）θβγα<<<（6）若对任意的长方体A ，都存在一个与A 等高的长方体B ，使得B 与A 的侧面积之比和体积之比都等于k ，则k 的取值范围是（ ） （A ）0>k （B ）10≤<k （C ）1>k（D ）1≥k二、填空题（本题共6个小题，每小题5分，满分30分）1P 2P 3P AO BC4P 5P 6P（7）若关于x 的方程x ax a x =+-lg 1lg 2只有一个实数解，则a 的值等于 ．（8）在ABC ∆中，若21tan =A ，31tan =B ，且最长的边的长为1，则最短的边的的长等于 ．（9）若正奇数n 不能表示为三个不相等的合数之和，则满足条件的n 的最大值为 ． （10）设a 、b 、c 是直角三角形的三条边长，且)(2)(2222n n n n n n c b a c b a ++=++，其中*N n ∈，2≥n ，则n 的值等于 ．（11）连接正文体各个顶点的所有直线中，异面直线共有 对．（12）如图，以)0,0(O 、)0,1(A 为顶点作正1OAP ∆，再以1P 和A P 1的中点B 为顶点作正21BP P ∆，再以2P 和B P2的中点C 为顶点作正32CP P ∆，…，如此继续下去．有如下结论：①所作的正三角形的边长构成公比为21的等比数列；②每一个正三角形都有一个顶点在直线2AP （1=x ）上；③第六个正三角形的不在第五个正三角形边上的顶点6P 的坐标是)36421,6463(； ④第2004个正三角形的不在第2003个正三角形边上的顶点2004P 的横坐标是20042004211-=x ．其中正确结论的序号是 （把你认为正确结论的序号都填上）．三、解答题（本题共3小题，每小题20分，满分60分）（13）已知函数a a x f x3)(+=（0>a ，1≠a ）的反函数是)(1x fy -=，而且函数)(x g y =的图象与函数)(1x f y -=的图象关于点)0,(a 对称．（Ⅰ）求函数)(x g y =的解析式； （Ⅱ）若函数)()()(1x g x f x F --=-在]3,2[++∈a a x 上有意义，求a 的取值范围．（14）设边长为1的正ABC ∆的边BC 上有n 等分点，沿点B 到点C 的方向，依次为1P ，2P ，…，1-n P ，若AC AP AP AP AP AB S n n ⋅++⋅+⋅=-1211 ，求证：nn S n 62112-=．（15）已知}{n a 是等差数列，d 为公差且不等于0，1a 和d 均为实数，它的前n 项和记作n S ，设集合}|),{(*N n nS a A n n ∈=，},,141|),{(22R y x y x y x B ∈=-=，试问下列结论是否正确，如果正确，请给予证明；如果不正确，请举例说明．（Ⅰ）若以集合A 中的元素作为点的坐标，则这些点都在一条直线上； （Ⅱ）B A 至多有一个元素；（Ⅲ）当01≠a 时，一定有∅≠B A ．全国高中数学联合竞赛 试题参考答案及评分标准一、选择题（本题共6个小题，每小题5分满分30分）（1）B （2）C （3）D （4）D （5）A （6）D 二、填空题（本题共6个小题，每小题5分，满分30分） （7）100 （8）55（9）17 （10）4 （11）174 （12）①②③④ 三、解答题（本题共3小题，每小题20分，满分60分）（13）【解】（Ⅰ）由a a x f x3)(+=（0>a ，1≠a ），得)3(log )(1a x x fa -=-…………5分又函数)(x g y =的图象与函数)(1x fy -=的图象关于点)0,(a 对称，则)()(1x a f x a g --=+-，于是，)(lo g)2()(1a x x a f x g a---=--=-．（a x -<）…………………………………10分 （Ⅱ）由（Ⅰ）的结论，有)(log )3(log )()()(1a x a x x g x fx F a a -+-=--=-．要使)(x F 有意义，必须⎩⎨⎧>->-.0,03a x a x又0>a ，故a x 3>． (15)分由题设)(x F 在]3,2[++∈a a x 上有意义，所以a a 32>+，即1<a ．于是，10<<a ． ……………………………………………………………………… 20分14．【证明】如图，设c AB =，b AC =，a BC =， 令n=1，则p k c BP AB AP k k +=+=（0=k ，1，2，…，n ） 其中，AP =0，AP n =． ∴)(])1([1p k c p k c AP AP k k +⋅-+=⋅-22)1()12(k k k -+⋅-+=（0=k ，1，2，…，n ） ……………5分又∵AC AP AP AP AP AB S n n ⋅++⋅+⋅=-1211 ， ∴2112)]1([)]12([p k k p c k c n S nk n k n ∑∑==-+⋅-+=222)(3)1)(1(n n n n n n -++⋅+= ……………………………………………10分22222231)(31)(nn n n n n n n n n -+⋅+=-+⋅+=． ………………………15分又∵1||||||===，与的夹角为60，∴nn n n n n S n 6211312122-=-++=． ……………………………………………………20分15．【解】（Ⅰ）正确．因为，在等差数列}{n a 中，2)(1n n a a n S +=，所以，21nn a a n S +=． 这表明点),(nS a n n 的坐标适合方程)(211a x y +=．所以，点),(nS a n n 均在直线)(211a x y +=上． ……………………………………………5分 （Ⅱ）正确．设B A y x ∈),(，则),(y x 坐标中的x 、y 应是方程组⎪⎩⎪⎨⎧=-+=14,2121221y x a x y 的解． 解这个方程组，消去y ，得42211-=+a x a ．（﹡）当01=a 时，方程（﹡）无解，此时，∅=B A ． …………………………………10分当01≠a 时，方程（﹡）只有一个解12124a a x --=，此时方程组也只有一个解，即⎪⎪⎩⎪⎪⎨⎧-=--=.44,24121121a a y a a x 故上述方程组至多有一解，所以B A 至多有一个元素． ………………………………15分（Ⅲ）不正确．取11=a ，1=d ，对一切*N n ∈，有0)1(1>=-+=n d n a a n ，0>nS n． 这时集合A 中的元素的点的横、纵坐标均为正．另外，由于011≠=a ，如果∅≠B A ，那么根据（Ⅱ）的结论，B A 至多有一个元素（00,y x ），而025241210<-=--=a a x ，043441210<-=-=a a y ．这样的A y x ∉),(00，产生矛盾．所以，11=a ，1=d 时，∅=B A ，故01≠a 时，一定有∅=B A 是不正确的． ……………………………………20分。

高中数学竞赛试题及答案一、选择题（每题5分，共20分）1. 下列哪个数是无理数？A. 2B. πC. 0.5D. √4答案：B2. 已知函数f(x) = x^2 - 4x + 4，求f(2)的值。

A. 0B. 4C. -4D. 8答案：A3. 一个等差数列的前三项分别为1, 4, 7，求第四项的值。

A. 10B. 11C. 13D. 15答案：A4. 计算复数z = 1 + i的模。

A. √2B. 2C. 1D. √3答案：A二、填空题（每题5分，共20分）5. 已知等比数列的公比为2，首项为1，求第5项的值。

答案：326. 已知向量a = (3, -4)，向量b = (-2, 3)，求向量a与向量b的点积。

答案：-67. 计算函数y = x^3 - 6x^2 + 11x - 6在x = 2处的导数值。

答案：18. 已知圆的方程为(x - 2)^2 + (y - 3)^2 = 9，求圆心坐标。

答案：(2, 3)三、解答题（每题10分，共60分）9. 求证：对于任意正整数n，n^2 + 3n + 2总是能被3整除。

证明：设n = 3k, 3k + 1, 3k + 2，其中k为整数。

当n = 3k时，n^2 + 3n + 2 = 9k^2 + 9k + 2 = 3(3k^2 + 3k + 1)，能被3整除。

当n = 3k + 1时，n^2 + 3n + 2 = 9k^2 + 6k + 1 + 9k + 3 + 2 =3(3k^2 + 5k + 2)，能被3整除。

当n = 3k + 2时，n^2 + 3n + 2 = 9k^2 + 12k + 4 + 9k + 6 + 2 = 3(3k^2 + 7k + 4)，能被3整除。

因此，对于任意正整数n，n^2 + 3n + 2总是能被3整除。

10. 已知函数f(x) = x^3 - 3x^2 + 2x，求f(x)的单调区间。

解：首先求导数f'(x) = 3x^2 - 6x + 2。

高中的数学竞赛试题及答案高中数学竞赛试题一、选择题（每题5分，共20分）1. 下列哪个数不是有理数？A. πB. √2C. 0.333...（无限循环）D. 1/32. 如果函数f(x) = 2x^2 - 5x + 3在x = 2时取得最小值，那么f(2)的值是多少？A. -1B. 1C. 3D. 53. 已知等差数列的前三项分别为3, 8, 13，求第10项的值。

A. 43B. 48C. 53D. 584. 若sinx = 1/2，求cosx的值（假设x在第一象限）。

A. √3/2B. -√3/2C. 1/2D. -1/2二、填空题（每题4分，共12分）5. 计算(2x^3 - 3x^2 + 4x - 5) / (x - 1)的商式和余数。

商式为：________余数为：______6. 已知复数z = 3 + 4i，求其共轭复数。

共轭复数为：______7. 一个圆的半径为5，求其内接正六边形的边长。

边长为：______三、解答题（每题18分，共54分）8. 证明：对于任意正整数n，n^5 - n 总是能被30整除。

9. 已知函数g(x) = x^3 - 6x^2 + 11x - 6，求其导数g'(x)，并找出g(x)的极值点。

10. 解不等式：|x + 2| + |x - 3| > 4。

四、证明题（每题10分，共10分）11. 证明：对于任意实数a和b，(a^2 + b^2)(1/a^2 + 1/b^2) ≥ 2。

五、附加题（每题15分，共15分）12. 一个圆的半径为r，圆内接正n边形的边长为s。

证明：s =2r*sin(π/n)。

高中数学竞赛试题答案一、选择题1. A（π是无理数）2. B（f(2) = 4 - 10 + 3 = -3，但题目要求最小值，故应为B）3. C（公差d = 13 - 8 = 5，第10项a_10 = 3 + 9*5 = 53）4. A（根据勾股定理，cosx = √3/2）二、填空题5. 商式为：2x^2 - x - 5，余数为：-36. 共轭复数为：3 - 4i7. 边长为：10三、解答题8. 证明略。

数学竞赛试题及答案高中生试题一：代数问题题目：已知\( a, b \) 是方程 \( x^2 + 5x + 6 = 0 \) 的两个实根，求 \( a^2 + 5a + 6 \) 的值。

解答：根据韦达定理，对于方程 \( x^2 + bx + c = 0 \)，其根\( a \) 和 \( b \) 满足 \( a + b = -b \) 和 \( ab = c \)。

因此，对于给定的方程 \( x^2 + 5x + 6 = 0 \)，我们有 \( a + b =-5 \) 和 \( ab = 6 \)。

由于 \( a \) 是方程的一个根，我们可以将 \( a \) 代入方程得到 \( a^2 + 5a + 6 = 0 \)。

所以 \( a^2 + 5a + 6 = 0 \)。

试题二：几何问题题目：在一个直角三角形中，已知直角边长分别为 3 厘米和 4 厘米，求斜边的长度。

解答：根据勾股定理，直角三角形的斜边长度 \( c \) 可以通过直角边 \( a \) 和 \( b \) 计算得出，公式为 \( c = \sqrt{a^2 + b^2} \)。

将给定的边长代入公式，我们得到 \( c = \sqrt{3^2 + 4^2} =\sqrt{9 + 16} = \sqrt{25} = 5 \) 厘米。

试题三：数列问题题目：一个等差数列的首项 \( a_1 = 3 \)，公差 \( d = 2 \)，求第 10 项 \( a_{10} \) 的值。

解答：等差数列的通项公式为 \( a_n = a_1 + (n - 1)d \)，其中\( n \) 是项数。

将给定的值代入公式，我们得到 \( a_{10} = 3 + (10 - 1) \times 2 = 3 + 9 \times 2 = 3 + 18 = 21 \)。

试题四：组合问题题目：从 10 个不同的球中选取 5 个球，求不同的选取方式有多少种。

竞赛数学高中试题及答案试题一：多项式问题题目：已知多项式 \( P(x) = x^3 - 3x^2 + 2x - 5 \)，求 \( P(2) \) 的值。

解答：将 \( x = 2 \) 代入多项式 \( P(x) \) 中，得到：\[ P(2) = 2^3 - 3 \times 2^2 + 2 \times 2 - 5 = 8 - 12 + 4 -5 = -5 \]试题二：几何问题题目：在直角三角形 ABC 中，角 C 是直角，若 \( AB = 10 \) 且\( AC = 6 \)，求斜边 BC 的长度。

解答：根据勾股定理，直角三角形的斜边 \( BC \) 可以通过以下公式计算：\[ BC = \sqrt{AB^2 - AC^2} = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8 \]试题三：数列问题题目：给定数列 \( a_n = 2n - 3 \)，求数列的前 5 项。

解答：根据数列公式 \( a_n = 2n - 3 \)，我们可以计算出前 5 项：\[ a_1 = 2 \times 1 - 3 = -1 \]\[ a_2 = 2 \times 2 - 3 = 1 \]\[ a_3 = 2 \times 3 - 3 = 3 \]\[ a_4 = 2 \times 4 - 3 = 5 \]\[ a_5 = 2 \times 5 - 3 = 7 \]数列的前 5 项为：-1, 1, 3, 5, 7。

试题四：概率问题题目：一个袋子里有 5 个红球和 3 个蓝球，随机抽取 2 个球，求抽到一个红球和一个蓝球的概率。

解答：首先计算总的可能组合数，即从 8 个球中抽取 2 个球的组合数：\[ \text{总组合数} = \binom{8}{2} = \frac{8 \times 7}{2} = 28 \]然后计算抽到一个红球和一个蓝球的组合数：\[ \text{有利组合数} = \binom{5}{1} \times \binom{3}{1} = 5 \times 3 = 15 \]所以，抽到一个红球和一个蓝球的概率为：\[ P = \frac{\text{有利组合数}}{\text{总组合数}} =\frac{15}{28} \]试题五：函数问题题目：若函数 \( f(x) = x^2 - 4x + 4 \)，求 \( f(x) \) 的最小值。

高中数学竞赛试题附详细答案一选择题(每题5分,满分60分)1. 如果a,b,c 都是实数，那么P ∶ac<0,是q ∶关于x 的方程ax 2+bx+c=0有一个正根和一个负根的（ ）（A ）必要而不充分条件 （B ）充要条件（C ）充分而不必要条件 （D ）既不充分也不必要条件2. 某种放射性元素，100年后只剩原来质量的一半，现有这种元素1克，3年后剩下（ ）。

（A ）1005.03⨯克 （B ）(1－0.5%)3克 （C ）0.925克 （D ）100125.0克 3. 由甲城市到乙城市t 分钟的电话费由函数g (t )=1.06×(0.75[t ]+1)给出，其中t >0，[t ]表示大于或等于t 的最小整数，则从甲城市到乙城市5.5分钟的电话费为（ ）。

（A ）5.83元 （B ）5.25元 （C ）5.56元 （D ）5.04元4. 已知函数>0，则的值A 、一定大于零B 、一定小于零C 、等于零D 、正负都有可能 5. 已知数列3，7，11，15，…则113是它的（ ） （A ）第23项 （B ）第24项 （C ）第19项 （D ）第25项6. 已知等差数列}{n a 的公差不为零，}{n a 中的部分项 ,,,,,321n k k k k a a a a 构成等比数列，其中,17,5,1321===k k k 则n k k k k ++++ 321等于（ ） (A) 13--n n(B) 13-+n n(C) 13+-n n(D)都不对 7. 已知函数x b x a x f cos sin )(-=（a 、b 为常数，0≠a ，R x ∈）在4π=x 处取得最小值，则函数)43(x f y -=π是（ ） A ．偶函数且它的图象关于点)0,(π对称 B ．偶函数且它的图象关于点)0,23(π对称 C ．奇函数且它的图象关于点)0,23(π对称 D ．奇函数且它的图象关于点)0,(π对称 8. 如果A A tan 1tan 1+-= 4+5，那么cot （A +4π）的值等于 ( )A -4-5B 4+5C -541+ D541+9. 已知︱︱=1，︱︱=3,∙=0,点C 在∠AOB 内，且∠AOC =30°，设=m +n (m 、n ∈R )，则nm等于A.31 B.3 C.33 D.3 10. 等边△ABC 的边长为，AD 是BC 边上的高，将△ABD 沿AD 折起，使之与△ACD 所在平面成1200的二面角，这时A 点到BC 的距离是A 、B 、C 、3D 、211. 抛两个各面上分别标有1，2，3，4，5，6的均匀的正方体玩具，“向上的两个数之和为3”的概率是（ ）A ．31 B ．61 C ．361 D ．181 12. 对于直角坐标平面内的任意两点A (x 1,y 1)、B (x 2，y 2)，定义它们之间的一种“距离”：‖AB ‖=︱x 1－x 2︱+︱y 1－y 2︱.给出下列三个命题： ①若点C 在线段AB 上，则‖AC ‖+‖CB ‖=‖AB ‖;②在△ABC 中，若∠C =90°，则‖AC ‖2+‖CB ‖2=‖AB ‖2； ③在△ABC 中，‖AC ‖+‖CB ‖>‖AB ‖. 其中真命题的个数为A.0B.1C.2D.3 二填空题:(每题5分,满分30分)13棱锥的底面面积为150cm 2,平行于底面的截面面积为54cm 2底面和截面距离为14cm,则这个棱锥高为_________14函数y=x －2+的最小值是________;最大值是________.15. 若数列｛a n ｝由a 1=2，a n+1=a n +2n(n ≥1)确定，求通项公式a n ==________.16. 有一公用电话亭，在观察使用这个电话的人的流量时，设在某一个时刻，有n 个人正在使用电话或等待使用的概率为)(n P ，且)(n P 与时刻t 无关，统计得到⎪⎩⎪⎨⎧≥≤≤⋅=6,051,)0()21()(n n P n P n，那么在某一时刻这个公用电话亭里一个人也没有的概率P (0)的值是 ．17. 定义在N ＋上的函数f(x)，满足f (1 )＝1，且f(n+1)=⎪⎩⎪⎨⎧.),(,),(21为奇数　为偶数n n f n n f 则f (22) = ．18. 定义在R 上的函数)(x f y =，它同时满足具有下述性质： ①对任何);()(33x f x f R x =∈均有②对任何).()(,,212121x f x f x x R x x ≠≠∈均有则=-++)1()1()0(f f f ．三解答题(每题15分,满分60分)19. 三角形ABC 中，三个内角A 、B 、C 的对边分别为，若，求角C 的大小。

高中数学竞赛初赛试题(含答案)高中数学竞赛初赛试题(含答案)一、选择题1. 设函数 f(x) = 2x^3 - 3x^2 + 2ax + b，如果 f(1) = 3 且 f'(1) = 4，那么常数 a 和 b 的值分别是多少？A) a = 2, b = 4 B) a = 2, b = 3 C) a = 3, b = 4 D) a = 3, b = 32. 在平面直角坐标系中，点 P(-3,4) 和点 Q(1,-2) 的连线所在直线的斜率是多少？A) -1/4 B) 2/3 C) 2 D) -3/23. 若 a, b, c 是等差数列的前三项，且 a + b + c = 9，那么 a 的值是多少？A) 1 B) 3/2 C) 2 D) 34. 若函数 f(x) = 2x^3 + ax^2 + bx + 2 的图像经过点 (2, 8)，那么常数a 和b 的值之和为多少？A) 6 B) 8 C) 10 D) 125. 已知等比数列的首项为 4，公比为 2，前 n 项和为 S_n。

下列哪个等式是正确的？A) S_n = 4(2^n - 1) B) S_n = 2(2^n - 1) C) S_n = 2^n + 2 D) S_n = 2^n二、填空题1. 若 3/4 张纸能折成 2^7 层，那么一张纸最多能折成多少层？答案：2^10 层2. 若 1/3 张纸能折成 2^8 层，那么一张纸最多能折成多少层？答案：3 × 2^8 层3. 一条长杆分成三段，第一段比第二段长 2cm，第二段比第三段长4cm，三段的长度之和是 50cm。

请分别求出第一段、第二段和第三段的长度。

答案：第一段：12cm，第二段：14cm，第三段：24cm4. 若 a 和 b 是互质的整数，并且 a × b = 147，那么 a 和 b 的值分别是多少？答案：a = 1，b = 147 或 a = 147，b = 15. 在平面直角坐标系中，顶点为 (0,0)，椭圆的长轴在 x 轴上，短轴在 y 轴上，且长轴长为 8，短轴长为 6。

全国高中数学联合竞赛一、选择题（本题满分30分，每小题5分）本题共有6小题，每题均给出（A ）、（B ）、（C ）、（D ）四个结论，其中有且只有一个是正确的。

请将正确答案的代表字母填在题后的括号内。

每小题选对得5分；不选、选错或选出的代表字母超过一个（不论是否写在括号内），一律得0分。

1.函数()142-+=x x x x f 是（ ） （A ）是偶函数但不是奇函数 （B ）是奇函数但不是偶函数（C ）既是奇函数又是偶函数 （D ）既不是奇函数也不是偶函数2. 已知()x f 对任意整数x 都有()()22-=+x f x f ，若()20030=f ，则()2004f =（ ）（A ）2002 （B ）2003 （C ）2004 （D ）20053. 已知不等式()θθ222sin 45cos +-+m m ≥0恒成立，则实数m 的取值范围是（ ）（A ）0≤m ≤4 （B ）1≤m ≤4 （C ）m ≥4或m ≤0 （D ）m ≥1或m ≤0 4. 母线长为6的圆锥中，体积最大的那一个的底面圆的半径为（ ）（A ）1 （B ）2 （C ）3 （D ）45. 正三棱锥相邻侧面所成二面角，等于侧面与底面所成二面角的两倍，则侧棱与底面边长之比为（ ）（A ）23 （B ）34 （C ）43 （D ）32 6. 函数x x x y cos sin cos 23-+=的最大值等于（ ）（A ）2732 （B ）2716 （C ）278 （D ）274 二、填空题（本题满分30分，每小题5分）本题共6小题，要求直接将答案写在横线上。

7. 已知函数()x xx f 22333+=，则⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛1011010121011f f f = . 8. 不等式22-x ≤12+x 的解集为 .9. 某城市的机动车牌照是从“10000”到“99999”连续编号，则在这90000个牌照中数字9至少出现一个，并且各数字之和是9的倍数的车牌照共有 个.10. 若0<a ，b ，c <1满足1=++ca bc ab ，则cb a -+-+-111111的最小值是 . 11. 已知正四棱锥V －ABCD 的棱长都等于a ，侧棱VB ，VD 的中点分别为H 和K ，若过A 、H 、K 三点的平面交侧棱VC 于L ，则四边形AHLK 的面积为 .12. 已知a 、b 、x 是实数，函数()122+-=ax x x f 与函数()()x a b x g -=2的图象不相交。

2023年全国中学生数学奥林匹克(预赛) 暨2023年全国高中数学联合竞赛一试试题(A 卷)一、填空题：本大题共8小题，每小题8分，满分64分 1.设复数z =9+10i ((i 为虚数单位)，若正整数n 满足|z n |≤2023，则n 的最大值为(((((((((((.2.若正实数a ，b 满足a lgb =2,a lga ∙b lgb =5.则(ab)lgab 的值为((((((((((((.3.将一枚均匀的骰子独立投掷三次，所得的点数依次记为x 、y 、z ，则事件“C 7x<C 7y <C 7z ”发生的概率为(((((((((((.4.若平面上非零向量α⃗，β⃗，γ⃗满足α⃗⊥β⃗，β⃗∙γ⃗=2|α⃗|，γ⃗∙α⃗=3|β⃗|，则|γ⃗|的最小值为(((((((((((.5.方程sinx =cos2x 的最小的20个正实数解之和为((((((((((((((((.6.设a ，b ，c 为正数，a < b ，若a 、b 为一元二次方程ax 2−bx +c =0的两个根，且a 、b 、c 是一个三角形的三边长，则a +b −c 的取值范围是(((((((((((((((.7.平面直角坐标系xOy 中，已知圆Ω与x 轴、y 轴均相切，圆心在椭圆Γ:x 2a2+y 2b 2=1(a (>(b (>(0)内，且Ω与Γ有唯一的公共点(8,9).则Γ的焦距为(((((((((((((.8.八张标有A 、B 、C 、D 、E 、F 、G 、H 的正方形卡片构成下图，现逐一取走这些卡片，要求每次取走一张卡片时，该卡片与剩下的卡片中至多有一张有公共边(例如可按D 、A 、B 、E 、C 、F 、G 、H 的次序取走卡片，但不可按D 、B 、A 、E 、C 、F 、G 、H 的次序取走卡片)，则的不同次序的取走这八张卡片的不同次序的数目为((((((((((((((.二、解答题：本大题共3小题，满分56分，解答应写出文字说明、证明过程或演算步骤.9.(本题满分16分)(平面直角坐标系xOy 中，抛物线Γ:y 2=4x ，F 为Γ的焦点，A 、B 为Γ上的两个不重合的动点，使得线段AB 的一个三等分点P 位于线段OF 上(含端点)，记Q 为线段AB 的另一个三等分点.求点Q 的轨迹方程.10.（本题满分20分）已知三棱柱Ω：ABC-A 1B 1C 1的9条棱长均相等，记底面ABC 所在平面为α(.若Ω的另外四个面(即面A 1B 1C 1,ABB 1A 1,ACC 1A 1,BCC 1B 1()在α上投影面积从小到大重排后依次为2√3，3√3，4√3，5√3.求Ω的体积.11. （本题满分20分）求出所有满足下面要求的不小于1的实数t ：对任意a,b ∈[−1,t ]，总存在c,d ∈[−1,t ]，使得(a +c )(b +d )=1.HGFED CB A2023年全国中学生数学奥林匹克竞赛（预赛）暨2023年全国高中数学联合竞赛 一试（A 卷）参考答案及评分标准说明：1. 评阅试卷时，请依据本评分标准. 填空题只设8分和0分两档；其他各题的评阅，请严格按照本评分标准的评分档次给分，不得增加其他中间档次.2. 如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，解答题中第9小题4分为一个档次，第10、11小题5分为一个档次，不得增加其他中间档次．一、填空题：本大题共8小题，每小题8分，满分64分．1. 设复数910i z （i 为虚数单位），若正整数n 满足2023n z ，则n 的最大值为 ． 答案：2．解：22910181nnnnz z．因21812023z ，而当3n 时，181132023nn n z，故n 的最大值为2．2. 若正实数,a b 满足lg 2b a ，lg lg 5a b a b ，则lg ()ab ab 的值为 ． 答案：20．解：因为lg lg lg lg 102a a b b b a ，所以lg lg lg lg lg lg lg ()()()52220ab a b a b b a ab ab a b a b ．3. 将一枚均匀的骰子独立投掷三次，所得的点数依次记为,,x y z ，则事件“777C C C x y z”发生的概率为 ． 答案：127．解：由于162534777777C C C C C C ，因此当,,{1,2,3,4,5,6}x y z 时，事件“777C C C x y z”发生当且仅当“{1,6},{2,5},{3,4}x y z ”成立，相应的概率为321627． 4. 若平面上非零向量,, 满足 ，2|| ，3|| ，则||的最小值为 ．答案：23．解：由 ，不妨设(,0),(0,)a b ，其中,0a b ，并设(,)x y，则由2||得2by a ，由3|| 得3ax b ．所以2232||2223b ax y xy a b． 取3,2a b ，此时6x y ，||取到最小值23．5. 方程sin cos2x x 的最小的20个正实数解之和为 ． 答案：130 ．解：将2cos212sin x x 代入方程，整理得(2sin 1)(sin 1)0x x ，解得532,2,2()662Z x k k k k．上述解亦可写成2()36Z k x k，其中0,1,,19k 对应最小的20个正实数解，它们的和为192219202013036326k k． 6. 设,,a b c 为正数，a b ．若,a b 为一元二次方程20ax bx c 的两个根，且,,a b c 是一个三角形的三边长，则a b c 的取值范围是 ．答案：7,518． 解：由条件知2222()()()ax bx c a x a x b ax a ab x a b ，比较系数得22,b a ab c a b ，故24,11a a b c a a，从而 24231a a a b c a a a a a ．由于201a a b a，故112a ．此时显然0b c ．因此，,,a b c 是一个三角形的三边长当且仅当a c b ，即4211a a a a a，即2(1)0a a a ，结合112a ，解得15122a ．令23()f x x x x ，则()a b c f a ．显然当0x 时()f x 连续且严格递增，故a b c 的取值范围是151,22f f，即7,518 ． 7. 平面直角坐标系xOy 中，已知圆 与x 轴、y 轴均相切，圆心在椭圆2222:1(0)x y a b a b内，且 与 有唯一的公共点(8,9)．则 的焦距为 ．答案：10．解：根据条件，可设圆心为(,)P r r ，则有222(8)(9)r r r ，解得5r 或29r ．因为P 在 内，故5r ．椭圆 在点(8,9)A 处的切线为2289:1x y l a b ，其法向量可取为2289,n a b． 由条件，l 也是圆 的切线，故n 与PA 平行，而(3,4)PA ，所以223227a b．又2264811a b ，解得22160,135a b ．从而 的焦距为22210a b ．8. 八张标有,,,,,,,A B C D E F G H 的正方形卡片构成下图．现逐一取走这些卡片，要求每次取走一张卡片时，该卡片与剩下的卡片中至多一张有公共边（例如可按,,,,,,,D A B E C F G H 的次序取走卡片，但不可按,,,,,,,D B A E C F G H 的次序取走卡片），则取走这八张卡片的不同次序的数目为 ．AB C D EFGH答案：392．解：如左下图重新标记原图中的八张卡片．现将每张卡片视为顶点，有公共边的两张卡片所对应的顶点之间连一条边，得到一个八阶图，该图可视为右下图中的2m n 阶图(,)G m n 在3,3m n 时的特殊情况．231-3-20P-1 G (m , n )Pn...210-1-2-m ...取卡片（顶点）的规则可解释为：(i) 若顶点P 已取走，则以下每步取当前标号最小或最大的顶点，直至取完； (ii) 若顶点P 未取走，则必为某个(,)(,0)G m n m n 的情形，此时若0m ，则将P 视为1 号顶点，归结为(i)的情形；若0,0m n ，则将P 视为1号顶点，归结为(i)的情形；若,1m n ，则当前可取P 或m 号顶点或n 号顶点，分别归结为(i)或(1,)G m n 或(,1)G m n 的情形．设(,)G m n 的符合要求的顶点选取次序数为(,)f m n ，本题所求即为(3,3)f ．由(i)、(ii)知1(,0)2(0)m f m m ，1(0,)2(0)n f n n ，且(,)2(1,)(,1)(,1)m n f m n f m n f m n m n ．由此可依次计算得(1,1)12f ，(1,2)(2,1)28f f ，(1,3)(3,1)60f f ，(2,2)72f ，(2,3)(3,2)164f f ，(3,3)392f ，即所求数目为392．二、解答题：本大题共3小题，满分56分．解答应写出文字说明、证明过程或演算步骤．9. （本题满分16分）平面直角坐标系xOy 中，抛物线2:4y x ，F 为 的焦点，,A B 为 上的两个不重合的动点，使得线段AB 的一个三等分点P 位于线段OF 上（含端点），记Q 为线段AB 的另一个三等分点．求点Q 的轨迹方程．解：设1122(,),(,)A x y B x y ．不妨设AP PQ QB ，则121222,33x x y y P． 易知(1,0)F ．由于点P 位于线段OF 上，故122[0,1]3x x ，12203y y ． ……………4分可设12,2y t y t ，则2212,4t x x t ．此时有2122[0,1]32x x t ，且由,A B 不重合知0t ，所以2(0,2]t ． ……………8分设(,)Q Q Q x y ，则21212232,343Q Q x x y y x t y t，有243Q Q y x ． 注意到2330,42Q x t ，故点Q 的轨迹方程为243(0)32y x x ．……………16分10.（本题满分20分）已知三棱柱111:ABC A B C 的9条棱长均相等．记底面ABC 所在平面为 ．若 的另外四个面（即面111111111,,,A B C ABB A ACC A BCC B ）在 上投影的面积从小到大重排后依次为23,33,43,53，求 的体积．解：设点111,,A B C 在平面 上的投影分别为,,D E F ，则面11111,,A B C ABB A 1111,ACC A BCC B 在 上的投影面积分别为,,,DEF ABED ACFD BCFE S S S S ．由已知及三棱柱的性质，DEF 为正三角形，且,,ABED ACFD BCFE 均为平行四边形．由对称性，仅需考虑点D 位于BAC 内的情形（如图所示）． 显然此时有ABED ACFD BCFE S S S ． ……………5分XFEB DCA由于,,,23,33,43,53DEF ABED ACFD BCFE S S S S ，故,ABED ACFD S S 必为23,33的排列，53BCFE S ，进而43DEF S ，得DEF 的边长为4，即正三棱柱 的各棱长均为4． ……………10分不妨设23,33ABED ACFD S S ，则333,2ABD ACD S S ．取射线AD 与线段BC 的交点X ，则23ABD ACD BX S CX S ，故85BX ．因此2242cos60195AX AB BX AB BX ， 而58ABD ACD ABC AD S S AX S ，故192AD． ……………15分 于是 的高221352h AA AD． 又43ABC S ，故 的体积615ABC V S h ． ……………20分11.（本题满分20分）求出所有满足下面要求的不小于1的实数t ：对任意,[1,]a b t ，总存在,[1,]c d t ，使得()()1a c b d ．解：记[1,]t I t ，()()S a c b d ．假如2t ，则当a b t 时，对任意,t c d I ，均有2(1)1S t ，不满足要求．假如312t，则当1,2a b t 时，对任意,t c d I ，均有 21a c t ，12t b d ．若,a c b d 同正或同负，则2(1)1S t ，其余情况下总有01S ，不满足要求． ……………5分以下考虑322t 的情形．为便于讨论，先指出如下引理．引理：若1,2u v ，且52u v ，则1uv ．事实上，当32u v 时，22225312244u v u v uv ． 当32u v 时，1131222uv ．引理得证． 下证对任意,t a b I ，可取11,t c d I ，使得111()()1S a c b d ．① 若12a b ，则取111c d ，此时1(1)(1)(1)(1)S a b a b ，其中31311,12222a b b a ，且5(1)(1)2()2a b a b ，故由引理知11S ．若12a b ，则取1132t c d I ，此时13322S a b， 其中331,222a b ，且3353222a b a b ，故由引理知11S ． ……………15分 注意到，当,t a b I 时，可取2t c I ，使得21a c （例如，当[1,1]a 时取20c ，当(1,]a t 时取21c ），同理，可取2t d I ，使得21b d ．此时22222()()1S a c b d a c b d ．②根据①、②，存在一个介于12,c c 之间的实数c ，及一个介于12,d d 之间的实数d ，使得()()1a c b d ，满足要求．综上，实数t 满足要求当且仅当322t ． ……………20分2023年全国中学生数学奥林匹克(预赛)暨2023年全国高中数学联合竞赛加试试题(A卷)一、(本题满分40分)如图，Ω是以AB为直径的固定的半圆弧，ω是经过点A及Ω上另一定点T的定圆，且ω的圆心位于△ABT内，设P是Ω的弧TB̂(不含端点)上的动点，C、D 是ω上的两动点，满足：C在线段AP上，C、D在直线AB的异侧，且CD⊥AB.记△CDP 的外心为K.证明：(1)点K在△TDP的外接圆上；(2)K为定点.(答题时请将图画在答卷纸上)二、(本题满分40分)正整数n称为“好数”，如果对任意不同于n的正整数m，均有{2n n2}≠{2mm2}，这里{x}表示x的小数部分.证明：存在无穷多个两两互素的合数均为好数.三、(本题满分50分)求具有下述性质的最小正整数k：若将1,2，…，k中的每个数任意染成红色或蓝色，则或者存在9个互不相同的红色的数x1,x2,⋯,x9满足x1+x2+⋯+x8< x9，或者存在10个互不相同的蓝色的数y1,y2,⋯,y10满足y1+y2+⋯+y9<y10.四、(本题满分50分)设a=1+10−4.在2023×2023的方格表的每一个小方格中填入区间[1，a]中的一个实数.设第i行的总和为x i，第i列的总和为y i，1≤i≤2023.求y1y2⋯y2023 x1x2⋯x2023的最大值(答案用含a的式子表示).A2023年全国中学生数学奥林匹克竞赛（预赛）暨2023年全国高中数学联合竞赛 加试（A 卷）参考答案及评分标准说明：1．评阅试卷时，请严格按照本评分标准的评分档次给分．2．如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，10分为一个档次，不得增加其他中间档次．一．（本题满分40分）如图， 是以AB 为直径的固定的半圆弧， 是经过点A 及 上另一个定点T 的定圆，且 的圆心位于ABT 内．设P 是 的弧 TB （不含端点）上的动点，,C D 是 上的两个动点，满足：C 在线段AP 上，,C D位于直线AB 的异侧，且CD AB ．记CDP 的外心为K ．证明：(1) 点K 在TDP 的外接圆上； (2) K 为定点．ΩωP DABTC证明：(1) 易知PCD 为钝角，由K 为CDP 的外心知2(180)2PKD PCD ACD ．由于90APB ，CD AB ，故PBA ACD ATD ．……………10分 所以2180PTD PKD PTA ATD ACD PTA PBA ． 又,K T 位于PD 异侧，因此点K 在TDP 的外接圆上． ……………20分 (2) 取 的圆心O ，过点O 作AB 的平行线l ，则l 为CD 的中垂线，点K 在直线l 上． ……………30分由,,,T D P K 共圆及KD KP ，可知K 在DTP 的平分线上，而9090DTB ATD PBA PAB PTB ，故TB 为DTP 的平分线．所以点K 在直线TB 上．显然l 与TB 相交，且l 与TB 均为定直线，故K 为定点． ……………40分ωΩl DP OK BA TC二．（本题满分40分）正整数n 称为“好数”，如果对任意不同于n 的正整数m ，均有2222n m n m ⎧⎫⎧⎫⎪⎪⎪⎪≠⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭，这里，{}x 表示实数x 的小数部分．证明：存在无穷多个两两互素的合数均为好数．证明：引理：设n 是正奇数，且2模n 的阶为偶数，则n 是好数．引理的证明：反证法．假设n 不是好数，则存在异于n 的正整数m ，使得2222n m n m ．因此22n n 与22m m 写成既约分数后的分母相同．由n 为奇数知22n n 是既约分数，故2m 的最大奇因子为2n ，从而m 的最大奇因子为n ．设2tm n ，其中t 为正整数（从而m 是偶数）．于是22222m m t m n．由22222m t n n n可得2222(mod )m t n n ，故 222(mod )m t n n ． （*） 设2模n 的阶为偶数d ．由（*）及阶的基本性质得2(mod )m t n d ，故2m t n 是偶数．但2m t 是偶数，n 是奇数，矛盾．引理得证．……………20分回到原问题．设221(1,2,)kk F k ．由于1221k k F ，而k F 221k，因此2模k F 的阶为12k ，是一个偶数．对正整数l ，由221(mod )l k F 可知21(mod )l k F ，故由阶的性质推出，2模2k F 的阶被2模k F 的阶整除，从而也是偶数．因2k F 是奇数，由引理知2k F 是好数．……………30分对任意正整数,()i j i j ，211(,)(,(21)2)(,2)1ii j i i i j i F F F F F F F ，故123,,,F F F 两两互素．所以222123,,,F F F 是两两互素的合数，且均为好数． ……………40分三．（本题满分50分） 求具有下述性质的最小正整数k ：若将1,2,,k 中的每个数任意染为红色或者蓝色，则或者存在9个互不相同的红色的数129,,,x x x 满足1289x x x x +++< ，或者存在10个互不相同的蓝色的数1210,,,y y y 满足12910y y y y +++< ．解：所求的最小正整数为408．一方面，若407k =时，将1,55,56,,407 染为红色，2,3,,54 染为蓝色，此时最小的8个红数之和为1555661407++++= ，最小的9个蓝数之和为231054+++= ，故不存在满足要求的9个红数或者10个蓝数．对407k <，可在上述例子中删去大于k 的数，则得到不符合要求的例子． 因此407k ≤不满足要求． ……………10分 另一方面，我们证明408k =具有题述性质．反证法．假设存在一种1,2,,408 的染色方法不满足要求，设R 是所有红数的集合，B 是所有蓝数的集合．将R 中的元素从小到大依次记为12,,,m r r r ，B 中的元素从小到大依次记为12,,,n b b b ，408m n +=．对于R ，或者8R ≤，或者128m r r r r +++≥ ；对于B ，或者9B ≤，或者129n b b b b +++≥ ．在1,2,,16 中至少有9个蓝色的数或至少有8个红色的数． 情形1：1,2,,16 中至少有9个蓝色的数．此时916b ≤．设区间9[1,]b 中共有t 个R 中的元素12,,,(08)t r r r t ≤< ．记12t x r r r =+++ ，则112(1)2x t t t ≥+++=+ ．因为12912,,,,,,,t b b b r r r 是9[1,]b 中的所有正整数，故{}{}12912,,,,,,,1,2,,9t b b b r r r t =+ ．于是 12912(9)n b b b b t x ≤+++=++++- 1(9)(10)2t t x =++-． （*） ……………20分特别地，116171362n b ≤⨯⨯=．从而9R ≥．对任意(1)i i m t ≤≤-，由（*）知1(9)(10)2t i n r b i t t x i +≤+≤++-+．从而811811(9)(10)2t m t t i r r r r r x t t x i -+=⎛⎫⎪≤+++++≤+++-+ ⎪⎝⎭∑11(9)(10)(8)(8)(9)(7)22t t t t t t x =++-+---- 111(9)(10)(8)(8)(9)(7)(1)222t t t t t t t t ≤++-+----⋅+ 2819396407t t =-++≤（考虑二次函数对称轴，即知1t =时取得最大）． 又136n b ≤，这与,n m b r 中有一个为408矛盾． ……………40分情形2：1,2,,16 中至少有8个红色的数． 论证类似于情形1．此时816r ≤．设区间8[1,]r 中共有s 个B 中的元素12,,,(09)s b b b s ≤< ．记1s y b b =++ ，则1(1)2y s s ≥+．因为12128,,,,,,,s b b b r r r 是8[1,]r 中的所有正整数，故{}{}12128,,,,,,,1,2,,8s b b b r r r s =+ ．于是1(8)(9)2m r s s y ≤++-．特别地，116171362m r ≤⨯⨯=．从而10B ≥．对任意(1)i i n s ≤≤-，有1(8)(9)2s i m b r i s s y i +≤+≤++-+．从而911911(8)(9)2s n s s i b b b b b y s s y i -+=⎛⎫ ⎪≤+++++≤+++-+ ⎪⎝⎭∑ 11(9)(8)(9)(8)(9)(10)22s s s s y s s =-++--+--111(9)(8)(9)(8)(1)(9)(10)222s s s s s s s s ≤-++--⋅++-- 2727369395s s =-++≤（在2s =时取得最大）， 又136m r ≤，这与,n m b r 中有一个为408矛盾．由情形1、2知408k =具有题述性质．综上，所求最小正整数k 为408． ……………50分四．（本题满分50分）设4110a -=+．在20232023⨯的方格表的每个小方格中填入区间[1,]a 中的一个实数．设第i 行的总和为i x ，第i 列的总和为i y ，12023i ≤≤．求122023122023y y y x x x 的最大值（答案用含a 的式子表示）． 解：记2023n =，设方格表为(),1,ij a i j n ≤≤，122023122023y y y x x x λ= ． 第一步：改变某个ij a 的值仅改变i x 和j y ，设第i 行中除ij a 外其余1n -个数的和为A ，第j 列中除ij a 外其余1n -个数的和为B ，则jij i ij y B a x A a +=+．当A B ≥时，关于ij a 递增，此时可将ij a 调整到,a λ值不减．当A B ≤时，关于ij a 递减，此时可将ij a 调整到1,λ值不减．因此，为求λ的最大值，只需考虑每个小方格中的数均为1或a 的情况． ……………10分第二步：设{}1,,1,ij a a i j n ∈≤≤，只有有限多种可能，我们选取一组ij a 使得λ达到最大值，并且11n nij i j a ==∑∑最小．此时我们有,,1,.i j ij i j a x y a x y ⎧>⎪=⎨≤⎪⎩（*） 事实上，若i j x y >，而1ij a =，则将ij a 改为a 后，行和及列和变为,i j x y ''，则11j j j i i iy y a y x x a x '+-=>'+-， 与λ达到最大矛盾，故ij a a =．若i j x y ≤，而ij a a =，则将ij a 改为1后，λ不减，且11n nij i j a ==∑∑变小，与ij a 的选取矛盾．从而（*）成立．通过交换列，可不妨设12n y y y ≤≤≤ ，这样由（∗）可知每一行中a 排在1的左边，每一行中的数从左至右单调不增．由此可知12n y y y ≥≥≥ ．因而只能12n y y y === ，故每一行中的数全都相等（全为1或全为a ）.……………20分 第三步：由第二步可知求λ的最大值，可以假定每一行中的数全相等.设有k 行全为a ,有n k -行全为1,0k n ≤≤．此时()()()n nk k n k n k ka n k ka n k na nn a λ-+-+-==． 我们只需求01,,,n λλλ 中的最大值． ()11(1)1111()(1)nn n k k n k n kk a n k a n a ka n k a k a n n a λλ++++--⎛⎫- ⎪==+ ⎪+--+⎝⎭． 因此1111(1)n k k a a k a n λλ+⎛⎫- ⎪≥⇔+≥ ⎪-+⎝⎭ 11(1)n n x x k x n-⇔+≥-+（记n x a =） 2111(1)n n x x x k x n-++++⇔≥-+ 2111n n x x x n k x -++++-⇔≤- 211(1)(1)1n n x x x x x--+++++++=+++ ． 记上式右边为y ,则211(2)1n n n n x x y x x ---+-++=+++ ． 下面证明(1010,1011)y ∈． ……………30分 首先证明1011y <．1011y < 2021202220222021101110111011x x x x ⇔+++<+++1010101210132021202210111010210101011x x x x x x ⇔+++<++++ ．由于220221x x x <<<< ，故101010101012011(1011)101110121011101222k k k x x x =-<⋅⋅<⋅⋅∑101110110k k kx +=<∑． ……………40分 再证明1010y >，等价于证明2021202200(2022)1010kk k k k x x ==->∑∑． 由于2021202100(2022)(2022)10112023k k k k x k ==->-=⨯∑∑， 20222022010101010202310102023k k x x a =<⨯<⨯∑，只需证明1011202310102023a ⨯>⨯，而410111101010a -=+<，故结论成立． 由上面的推导可知1k k λλ+≥当且仅当1010k ≤时成立，从而1011λ最大．故 2023max 101120231011(10111012)2023a aλλ+==． ……………50分。

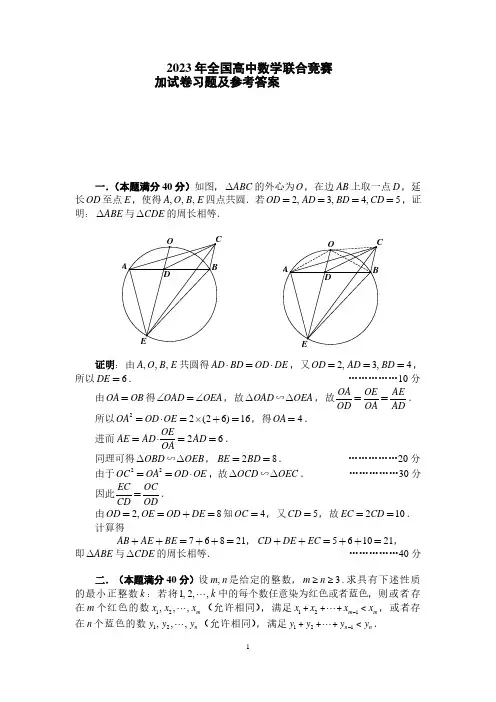
2023年全国高中数学联合竞赛加试卷习题及参考答案一．（本题满分40分）如图，ABC 的外心为O ，在边AB 上取一点D ，延长OD 至点E ，使得,,,A O B E 四点共圆．若2,3,4,5OD AD BD CD ，证明：ABE 与CDE 的周长相等．证明：由,,,A O B E 共圆得AD BD OD DE ，又2,3,4OD AD BD ，所以6DE ． ……………10分由OA OB 得OAD OEA ，故OAD OEA ∽，故OA OE AEOD OA AD． 所以22(26)16OA OD OE ，得4OA ．进而26OEAE AD AD OA．同理可得OBD OEB ∽ ，28BE BD ． ……………20分 由于22OC OA OD OE ，故OCD OEC ∽． ……………30分因此EC OC CD OD． 由2,8OD OE OD DE 知4OC ，又5CD ，故210EC CD ． 计算得76821AB AE BE ，561021CD DE EC ，即ABE 与CDE 的周长相等． ……………40分二．（本题满分40分）设,m n 是给定的整数，3m n ≥≥.求具有下述性质的最小正整数k ：若将1,2,,k 中的每个数任意染为红色或者蓝色，则或者存在m 个红色的数12,,,m x x x （允许相同），满足121m m x x x x -+++< ，或者存在n 个蓝色的数12,,,n y y y （允许相同），满足121n n y y y y -+++< ．C E O A BD C EO A B D解：答案是1mn n -+．若k mn n =-，将1,2,,1n - 染为蓝色，,1,,n n mn n +- 染为红色．则对任意m 个红色的数12,,,m x x x ，有121(1)m m x x x n m x -+++≥-≥ ，对任意n 个蓝色的数12,,,n y y y ，有1211n n y y y n y -+++≥-≥ ，上述例子不满足要求．对k mn n <-，可在上述例子中删去大于k 的数，则得到不符合要求的例子．因此所求1k mn n ≥-+． ………………10分下面证明1k mn n =-+具有题述性质．假设可将1,2,,1mn n -+ 中的每个数染为红色或蓝色，使得结论不成立． 情形一：若1是红色的数，则红色的数均不超过1m -，否则可取一个红色的数m x m ≥，再取1211m x x x -==== ，则11m m x x x -++< ，与假设矛盾． ………………20分故,1,,1m m mn n +-+ 均为蓝色的数，此时取121,1n n y y y m y mn n -=====-+ ，有121(1)11n n y y y m n mn m mn n y -+++=-<-+≤-+= ，（*） 与假设矛盾． ………………30分情形二：若1是蓝色的数，则同情形一可知蓝色的数均不超过1n -，故,1,,1n n mn n +-+ 均是红色的数．此时取121,1m m x x x n x mn n -=====-+ ，与（*）类似，可得矛盾．故1k mn n =-+时结论成立．综上，所求最小的正整数1k mn n =-+． ………………40分三．（本题满分50分）是否存在2023个实数122023,,,(0,1]a a a ，使得20236120231110i j i j k ka a a证明你的结论．解：记20231202311i j i j k kS a a a． 假设存在122023,,,(0,1]a a a ，使得610S ． 不妨设12202301a a a ，则将12023i j i j a a去掉绝对值后，k a 的系数为22024k ，从而202311(22024)k k kS k a a． ……………10分 当11011k 时，由基本不等式知 11(22024)(20242)220242k k kkk a k a k a a． ……………20分当10122023k 时，由于1()(22024)k f x k x x在(0,1]上单调增，故1(22024)(1)22025k k kk a f k a． 从而1011202311012220242(22025)k k S k k1011110101012202422k k k． ……………30分注意到202422(20242)2202444k k k k ，故61010101210114410S ，这意味者不存在122023,,,a a a 满足条件． ……………50分四．（本题满分50分）设正整数,,,a b c d 同时满足： (1) 2023a b c d +++= ； (2) ab ac ad bc bd cd +++++ 是2023的倍数； (3) abc bcd cda dab +++是2023的倍数． 证明：abcd 是2023的倍数． 证明：易知22023717=⨯． 首先，由(1)，(3)知2()()()()() a b a c a d a a b c d abc bcd cda dab +++=+++++++是2023的倍数，故,,a b a c a d +++中至少有一个是 7的倍数． ……………10分由对称性，不妨设a b +是7的倍数，则) 2023( c d a b +=-+也是7的倍数，()()ac ad bc bd a b c d +++=++也是7的倍数，故结合(2)知ab cd +是7的倍数，因此22) (()()a c a a b c c d ab cd +=+++-+也是 7的倍数．又平方数除以 7的余数只能是0,1,2,4，因此22,a c 只能同时是 7的倍数， 这表明,,,a b c d 都是 7的倍数． ………………20分同上面分析可知：) ()()( a b a c a d +++是217的倍数，故或者其中有一个因子是217的倍数，或者其中有两个因子是 17的倍数．如果有一个因子是217的倍数，不妨设a b +是217的倍数，结合 ,a b 都是7的倍数知，a b +是 22023717=⨯的倍数，但这与2023a b c d +++=及,,,a b c d 是正整数相矛盾！ ………………30分因此,,a b a c a d +++中至少有两个是17的倍数．不妨设,a b a c ++都是17的倍数，那么b d +也是17的倍数，由2()()(2)()ab ac ad bc bd cd a b d b d c a a b a a c a +++++=+++++++-知，22a 是17的倍数，故a 是17的倍数．因此,,,a b c d 都是17的倍数，这就说明了abcd 是44717⨯的倍数，也就是2023的倍数．………………50分。

全国高中数学竞赛试题及答案试题一：函数与方程1. 已知函数\( f(x) = 2x^3 - 3x^2 + x - 5 \)，求\( f(x) \)的极值点。

2. 求解方程\( x^2 - 4x + 3 = 0 \)的所有实根。

3. 判断函数\( g(x) = \frac{1}{x} \)在区间\( (0, +\infty) \)上的单调性。

试题二：解析几何1. 已知椭圆\( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \)，其中\( a > b > 0 \)，求椭圆的焦点坐标。

2. 求圆\( (x - h)^2 + (y - k)^2 = r^2 \)的切线方程，已知切点坐标为\( (m, n) \)。

3. 证明点\( P(x_1, y_1) \)和点\( Q(x_2, y_2) \)的连线\( PQ \)的中点坐标为\( \left(\frac{x_1 + x_2}{2}, \frac{y_1 +y_2}{2}\right) \)。

试题三：数列与级数1. 已知等差数列的首项\( a_1 = 3 \)，公差\( d = 2 \)，求第10项\( a_{10} \)。

2. 求等比数列\( b_1, b_2, b_3, \ldots \)的前\( n \)项和，其中\( b_1 = 1 \)，公比\( r = 3 \)。

3. 判断数列\( c_n = \frac{1}{n(n + 1)} \)的收敛性。

试题四：概率与统计1. 从5个红球和3个蓝球中随机抽取3个球，求至少有2个红球的概率。

2. 抛掷一枚均匀硬币4次，求正面朝上的次数为2的概率。

3. 某工厂生产的产品中有2%是次品，求从一批产品中随机抽取10个产品，至少有1个是次品的概率。

试题五：组合与逻辑1. 有5个不同的球和3个不同的盒子，将球分配到盒子中，每个盒子至少有一个球，求不同的分配方法总数。

2. 证明：对于任意的正整数\( n \)，\( 1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n + 1)(2n + 1)}{6} \)。

高中数学竞赛赛题精选一、选择题（共12题）1．定义在R 上的函数()y f x =的值域为［m,n ］,则)1(-=x f y 的值域为（ ） A ．［m,n ］B ．［m-1,n-1］C ．［)1(),1(--n f m f ］D ．无法确定解：当函数的图像左右平移时，不改变函数的值域.故应选A.2．设等差数列{n a }满足13853a a =，且n S a ,01>为其前n 项之和，则)(*∈N n S n 中最大的是( ) A. 10S B. 11S C. 20S D. 21S 解：设等差数列的公差为d,由题意知3(1a +7d)=5(1a +12d),即d=-3921a , ∴n a = 1a +( n-1)d= 1a -3921a (n-1)= 1a (3941-392n),欲使)(*∈N n S n 最大，只须n a ≥0，即n ≤20.故应选C.3．方程log 2x=3cosx 共有（ ）组解．A ．1B ．2C ．3D ．4解：画出函数y=log 2x 和y=3cosx 的图像，研究其交点情况可知共有3组解．应选C ．4．已知关于x 的一元二次方程()02122=-+-+a x a x 的一个根比1大，另一个根比1小，则（）Ａ．11<<-a Ｂ．1-<a 或1>aＣ．12<<-aＤ．2-<a 或1>a解：令f(x)= ()2122-+-+a x a x ，其图像开口向上，由题意知f(1)＜0，即 ()211122-+⨯-+a a ＜0，整理得022<-+a a ，解之得12<<-a ，应选C ．5．已知βα,为锐角，,cos ,sin y x ==βα53)cos(-=β+α，则y 与x 的函数关系为（ ） A ．1)x 53( x 54x 153y 2<<+--= B ．1)x (0 x 54x 153y 2<<+--=C ．)53x (0 x 54x 153y 2<<---= D ．1)x (0 x 54x 153y 2<<---= []xx y 54153sin )sin(cos )cos()(cos cos 2+-⋅-=⋅+++=-+==αβααβααβαβ解： 而)1,0(∈y 15415302<+-⋅-<∴x x ， 得)1,53(∈x .故应选A. 6．函数sin y x =的定义域为[],a b ，值域为11,2⎡⎤-⎢⎥⎣⎦，则b a-的最大值是（ ）A. πB. π2C.34πD. 35π解：如右图，要使函数sin y x =在定义域[],a b 上，值域为11,2⎡⎤-⎢⎥⎣⎦，则b a -的最大值是74()663πππ--=.故应选C. 7．设锐角使关于x 的方程x 2+4x cos+cot =0有重根，则的弧度数为 ( )A ．6B ．12或512C ．6或512D ．12解：由方程有重根，故14=4cos 2－cot =0，∵ 0<<2，2sin2=1，=12或512．选B ． 8．已知M={(x ，y )|x 2+2y 2=3}，N={(x ，y )|y=mx+b }．若对于所有的m ∈R ，均有M ∩N ，则b 的取值范围是 ( )A ．[－62，62] B ．(－62，62) C ．(－233，233] D ．[－233，233] 解：点(0，b )在椭圆内或椭圆上，2b 2≤3，b ∈[－62，62]．选A ．9．不等式log 2x －1+12log 12x 3+2>0的解集为A ．[2，3)B ．(2，3]C ．[2，4)D ．(2，4] 解：令log 2x=t ≥1时，t －1>32t －2．t ∈[1，2)，x ∈[2，4)，选C ．10．设点O 在ABC 的内部，且有+2+3=，则ABC 的面积与AOC 的面积的比为( )A ．2B ．32C ．3D ．53解：如图，设AOC=S ，则OC 1D=3S ，OB 1D=OB 1C 1=3S ，AOB=OBD=1.5S ．OBC=0.5S ，ABC=3S ．选C ．11．设三位数n=，若以a ，b ，c 为三条边长可以构成一个等腰(含等边)三角形，则这样的三位数n 有( )A ．45个B ．81个C ．165个D ．216个 解：⑴等边三角形共9个；⑵ 等腰但不等边三角形：取两个不同数码(设为a ，b )，有36种取法，以小数为底时总能构成等腰三角形，而以大数为底时，b <a <2b ．a=9或8时，b=4，3，2，1，(8种)；a=7，6时，b=3，2，1(6种)；a=5，4时，b=2，1(4种)；a=3，2时，b=1(2种)，共有20种不能取的值．共有236－20=52种方法，而每取一组数，可有3种方法构成三位数，故共有523=156个三位数即可取156+9=165种数．选C ．12．顶点为P 的圆锥的轴截面是等腰直角三角形，A 是底面圆周上的点，B 是底面圆内的点，O 为底面圆圆心，AB ⊥OB ，垂足为B ，OH ⊥PB ，垂足为H ，且PA=4，C 为PA 的中点，则当三棱锥O －HPC 的体积最大时，OB 的长为 ( )A ．53 B ．253 C ．63 D ．263解：AB ⊥OB ，PB ⊥AB ，AB ⊥面POB ，面PAB ⊥面POB ．OH ⊥PB ，OH ⊥面PAB ，OH ⊥HC ，OH ⊥PC ，又，PC ⊥OC ，PC ⊥面OCH ．PC 是三棱锥P －OCH 的高．PC=OC=2．而OCH 的面积在OH=HC=2时取得最大值(斜边=2的直角三角形)．当OH=2时，由PO=22，知∠OPB=30，OB=PO tan30=263．又解：连线如图，由C 为PA 中点，故V O －PBC =12V B －AOP ，S B 11OABCABPO H C而V O －PHC ∶V O －PBC =PH PB =PO 2PB2(PO 2=PH ·PB )．记PO=OA=22=R ，∠AOB=，则V P —AOB =16R 3sin cos =112R 3sin2，V B －PCO =124R 3sin2． PO 2PB 2=R 2R 2+R 2cos 2=11+cos 2=23+cos2．V O －PHC =sin23+cos2112R 3． ∴ 令y=sin23+cos2，y=2cos2(3+cos2)－(－2sin2)sin2(3+cos2)2=0，得cos2=－13，cos =33， ∴ OB=263，选D ．二、填空题（共10题）13. 设n S 为等差数列{}n a 的前n 项和，若510S =，105S =-，则公差为 解：设等差数列{}n a 的首项为1a ，公差为d .由题设得⎩⎨⎧-=+=+，，545101010511d a d a 即 ⎩⎨⎧-=+=+，，1922211d a d a 解之得1-=d .14. 设()log ()a f x x b =+(0a >且1)a ≠的图象经过点(21)，，它的反函数的图象经过点(28)，，则b a +等于 4 .解：由题设知 log (2)1log (8)2a a b b +=⎧⎨+=⎩，， 化简得 2(2)(8).b a b a +=⎧⎨+=⎩，解之得 1131a b =⎧⎨=⎩，； 2224.a b =-⎧⎨=-⎩，（舍去）. 故a b +等于4.15．已知函数()y f x =的图象如图，则满足22221()(lg(620))021x x f f x x x x --⋅-+≤-+的 x 的取值范围为 [21)x ∈-， ．解： 因为 ()()22lg 620lg (3)11lg111x x x -+=-+≥>，所以()2lg 6200x x -+<. 于是，由图象可知，2111x x +≤-，即 201x x +≤-，解得 21x -≤<. 故x 的取值范围为 [21)x ∈-，．16．圆锥曲线0|3|102622=+--+-++y x y x y x 的离心率是 2 ．解：原式变形为|3|)1()3(22+-=-++y x y x ，即=2|3|2+-y x ．所以动点),(y x 到定点(31)-，的距离与它到直线03=+-y x 的距离之比为2．故此动点轨迹为双曲线，离心率为2．17．在ABC ∆中，已知3tan =B ，322sin =C ，63=AC ，则ABC ∆的面积为ABC S ∆=解：在ABC ∆中，由3tan =B 得︒=60B ．由正弦定理得sin 8sin AC CAB B⋅==．因为︒>60322arcsin，所以角C 可取锐角或钝角，从而31cos ±=C ．sin sin()sin cos cos sin A B C B C B C =+=+=sin 2ABC AC ABS A ∆⋅== 18. 设命题P :2a a <，命题Q : 对任何x ∈R ，都有2410x ax ++>. 命题P 与Q 中有 且仅有一个成立，则实数a 的取值范围是 021≤<-a 或 121<≤a . 解：由a a <2得10<<a ．由0142>++ax x 对于任何x ∈R 成立，得04162<-=∆a ，即2121<<-a ．因为命题P 、Q 有且仅有一个成立，故实数 a 的取值范围是 021≤<-a 或 121<≤a ．19.22cos 75cos 15cos75cos15++⋅的值是 ． 解：22cos 75cos 15cos75cos15++⋅ =cos²75°+sin²75°+sin15°·cos15° =1+°30sin 21=5420.定义在R 上的函数()f x 满足(1)2f =，且对任意的x R ∈，都有1()2f x '<，则不等式22log 3(log )2x f x +>的解集为 ． 解：令g ﹙x ﹚=2f ﹙x ﹚－x ，由f '(x ) <1/2得，2f '(x ) -1<0，即'g ﹙x ﹚<0，g(x)在R 上为减函数，且g(1)=2f(1)-1=3，不等式f(log2X)>2log 2X化为2f(log2X)—log2X≥3，即g(log2X)>g(1),由g(x)的单调性得：log2X<1,解得，0<x<2. 21.圆O 的方程为221x y +=，(1,0)A ，在圆O 上取一个动点B ，设点P 满足()AP OB R λλ=∈且1AP AB ⋅=．则P 点的轨迹方程为 ．解：设P(x,y), AB =λOB (λϵR)得B(k(x —1)，ky)，（λ=k1）。

2024年全国中学生数学奥林匹克竞赛（预赛）暨2024年全国高中数学联合竞赛加试（A 卷）参考答案及评分标准说明：1．评阅试卷时，请严格按照本评分标准的评分档次给分．2．如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，10分为一个档次，不得增加其他中间档次．一．（本题满分40分）给定正整数r ．求最大的实数C ，使得存在一个公比为r 的实数等比数列1{}n n a ，满足n a C 对所有正整数n 成立．（x 表示实数x 到与它最近整数的距离．）解：情形1：r 为奇数．对任意实数x ，显然有12x ，故满足要求的C 不超过12． 又取{}n a 的首项112a ，注意到对任意正整数n ，均有1n r 为奇数，因此1122n n r a ．这意味着12C 满足要求．从而满足要求的C 的最大值为12． …………10分 情形2：r 为偶数．设*2()r m m N ．对任意实数 ，我们证明1a 与2a 中必有一数不超过21m m ，从而21m C m ． 事实上，设1a k ，其中k 是与1a 最近的整数（之一），且102． 注意到，对任意实数x 及任意整数k ，均有x k x ，以及x x ．若021m m ，则121m a k m ． 若1212m m ，则22221m m m m ，即21m m r m m ，此时 2121m a a r kr r r m ． …………30分 另一方面，取121m a m ，则对任意正整数n ，有1(2)21n n m a m m ，由二项式展开可知11(211)(1)2121n n n m m a m K m m ，其中K 为整数，故21n m a m ．这意味着21m C m 满足要求． 从而满足要求的C 的最大值为212(1)m r m r ．综上，当r 为奇数时，所求C 的最大值为12；当r 为偶数时，所求C 的最大值为2(1)r r ． …………40分二．（本题满分40分）如图，在凸四边形ABCD 中，AC 平分BAD ，点,E F 分别在边,BC CD 上，满足||EF BD ．分别延长,FA EA 至点,P Q ，使得过点,,A B P 的圆1 及过点,,A D Q 的圆2 均与直线AC 相切．证明：,,,B P Q D 四点共圆．（答题时请将图画在答卷纸上）证明：由圆1 与AC 相切知180BPA BAC CAD CAF PAC ，故,BP CA 的延长线相交，记交点为L ．由||EF BD 知CE CF CB CD．在线段AC 上取点K ，使得CK CE CF CA CB CD ，则||,||KE AB KF AD ． …………10分由ABL PAL KAF ，180180BAL BAC CAD AKF ，可知ABL KAF ∽，所以KF AB AL KA． …………20分 同理，记,DQ CA 的延长线交于点L ，则KE AD AL KA． 又由||,||KE AB KF AD 知KE CK KF AB CA AD，即KE AD KF AB ． 所以AL AL ，即L 与L 重合．由切割线定理知2LP LB LA LQ LD ，所以,,,B P Q D 四点共圆．…………40分三．（本题满分50分）给定正整数n .在一个3n ×的方格表上，由一些方格构成的集合S 称为“连通的”，如果对S 中任意两个不同的小方格,A B ，存在整数2l ≥及S 中l 个方格12,,,lA C C CB ==，满足iC 与1i C +有公共边(1,2,,1i l −).求具有下述性质的最大整数K ：若将该方格表的每个小方格任意染为黑色或白色，总存在一个连通的集合S ，使得S 中的黑格个数与白格个数之差的绝对值不小于K .解：所求最大的K n =.对一个由小方格构成的集合S ，记b S 是S 中的黑格个数，w S 是S 中的白格个数. 用[,]i j 表示第i 行第j 列处的方格，这里13i ≤≤,1j n ≤≤.对于两个方格[,]A i j =，[,]B i j ′′=, 定义它们之间的距离为(,)||||d A B i i j j ′′=−+−.首先，如果将方格表按国际象棋棋盘一样黑白间隔染色，我们证明对任意连通的集合S ，均有||b w S S n −≤，这表明K n ≤.设[1,1]是黑格，并记{0,1}ε∈，满足(mod 2)n ε≡.先证b w S S n −≤.可不妨设S 包含所有黑格，这是因为若S 不包含所有黑格， 取不属于S 的黑格A 满足(,)d A S 最小，这里(,)min (,)B Sd A S d A B ∈=.易知(,)1d A S =或2.若(,)1d A S =，取{}S S A ′=，则S 仍是连通的，且b w S S ′′−更大. 若(,)2d A S =，则存在与A 相邻的白格C ，而C 与S 中某个方格B 相邻，取{,}S S A B ′= ，则S 仍是连通的，且bw S S ′′−不变. 因而可逐步扩充S ，使得S 包含所有黑格，保持S 的连通性，且b w S S −不减.考虑白格集合{[,]|}k W i j i j k =+=，3,5,,1k n ε++，每个k W 中至少有一个方格属于S ，否则不存在从黑格[1,1]A S =∈到黑格[3,1]B n ε=−+的S 中路径.故1()2w S n ε≥+，而1(3)2b S n ε=+，故b w S S n −≤. …………10分 类似可证w b S S n −≤.同上，可不妨设S 包含所有白格, 从而1(3)2w S n ε=−. 再考虑黑格集合{[,]|}k B i j i j k =+=, 4,6,,2k n ε+−，每个k B 中至少有一个黑格属于S ，否则不存在从白格[1,2]A =到白格[3,]B n ε=−的S 中路径. 从而1()2b S n ε≥−，故w b S S n −≤. …………20分 下面证明K n =具有题述性质，即对任意的染色方案，总存在连通的集合S ， 使得b w S S n −≥.设表格中共有X 个黑格和Y 个白格，在第二行中有x 个黑格和y 个白格. 于是3X Y n +=, x y n +=.故()()()()2X y Y x X Y x y n −+−=+−+=.由平均值原理可知max{,}X y Y x n −−≥.不妨设X y n −≥.取S 为第二行中的y 个白格以及所有X 个黑格.由于S 包含第二行中所有方格，因而S 是连通的. 而b S X =，w S y =，b w S S X y n −=−≥.综上所述，max K n =. …………50分四．（本题满分50分）设,A B 为正整数，S 是一些正整数构成的一个集合，具有下述性质：(1) 对任意非负整数k ，有k A S ；(2) 若正整数n S ，则n 的每个正约数均属于S ；(3) 若,m n S ，且,m n 互素，则mn S ；(4) 若n S ，则An B S ．证明：与B 互素的所有正整数均属于S ．证明：先证明下述引理．引理：若n S ，则n B S ．引理的证明：对n S ，设1n 是n 的与A 互素的最大约数，并设12n n n ，则2n 的素因子均整除A ，从而12(,)1n n ．由条件(1)及(2)知，对任意素数|p A 及任意正整数k ，有k p S ．因此，将11k A n 作标准分解，并利用(3)知11k A n S ．又2|n n ，而n S ，故由(2)知2n S ．因112(,)1k A n n ，故由(3)知112k A n n S ，即1k A n S ．再由(4)知k A n B S （对任意正整数k ）． ① …………10分 设n B C D ，这里正整数C 的所有素因子均整除A ，正整数D 与A 互素，从而(,)1C D ．由(1)及(2)知C S （见上面1k A n S 的证明）． 另一方面，因(,)1D A ，故由欧拉定理知()1D D A ．因此()()(1)()0(mod )D D A n B A n n B D ，但由①知()D A n B S ，故由(2)知D S ．结合C S 及(,)1C D 知CD S ，即n B S ．引理证毕． …………40分回到原问题．由(1)，取0k 知1S ，故反复用引理知对任意正整数y ，有1By S ．对任意*,(,)1n n B N ，存在正整数,x y 使得1nx By ，因此nx S ，因|n nx ，故n S ．证毕． …………50分。

数学竞赛高中试题入门及答案一、选择题（每题5分，共20分）1. 下列哪个数不是整数？A. -3B. 0C. 5D. 2.52. 如果函数\( f(x) = 3x^2 - 5x + 2 \)，那么\( f(-1) \)的值是多少？A. 10B. 8C. 6D. 43. 圆的半径为3，圆心在原点，那么圆上任意一点到圆心的距离是多少？A. 1B. 2C. 3D. 44. 已知三角形ABC的三个内角A、B、C，且A + B + C = 180°，如果角A = 60°，角B = 50°，那么角C是多少度？A. 70°B. 80°C. 90°D. 100°二、填空题（每题5分，共20分）5. 若\( a \)，\( b \)，\( c \)为三角形的三边，且\( a^2 + b^2 = c^2 \)，则该三角形是________。

6. 一个数的平方根是4，那么这个数是________。

7. 一个圆的面积为28.26平方厘米，那么它的半径是________厘米。

8. 已知等差数列\( 3, 7, 11, ... \)，第5项的值是________。

三、解答题（每题15分，共30分）9. 证明：如果\( a \)，\( b \)，\( c \)是正实数，且\( a + b +c = 1 \)，那么\( \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \geq9 \)。

10. 一个直角三角形的两条直角边长分别为6厘米和8厘米，求斜边的长度。

（使用勾股定理）四、证明题（每题15分，共15分）11. 证明：对于任意正整数\( n \)，\( 1^3 + 2^3 + ... + n^3 = (1 + 2 + ... + n)^2 \)。

五、结束语本试题旨在为高中数学竞赛入门者提供一个基础的练习平台，通过这些题目，学生可以检验自己的数学基础知识和解题技巧。

高中数学竞赛试题及答案一、选择题1.若直线l1:y = -2x + 3，直线l2过点(1,5)且与l1垂直，则l2的方程是：A. y = x + 4B. y = -x + 6C. y = x - 4D. y = -x + 4答案：C2.已知集合A = {x | |x - 3|< 2}，则A的值是： A. (-∞, 1) U (5, ∞) B. (-∞,1) U (3, ∞) C. (1, 5) D. (1, 5] U (5, ∞)答案：D二、填空题1.若a、b满足a+b=5，且ab=6，则a和b的值分别是____。

答案：2和32.若某几何体的体积V和表面积S满足S=3V，且V>0，则该几何体的体积V的值为____。

答案：1/3三、解答题1.设数列{an}满足a1=1，a2=2，an+2 = an + 2n，求数列的通项公式。

解答：首先给出数列的前几项： a1 = 1 a2 = 2 a3 = 1 + 2 × 1 = 3 a4 = 2 + 2 × 2 =6 a5 = 3 + 2 × 3 = 9 … 从数列的前几项可以观察到，第n项的值为n^2 - 1。

所以数列的通项公式为an = n^2 - 1。

2.已知函数f(x) = x^3 - 3x^2 + 4x - 2，求f(x)的最小值及取得最小值时的x值。

解答：对于任意x，有f’(x) = 3x^2 - 6x + 4。

令f’(x) = 0，可以解得x = 1。

再求f’‘(x) = 6x - 6，当x = 1时，f’’(x) = 0。

所以x = 1是f(x)的极小值点。

代入f(x) = x^3 - 3x^2 + 4x - 2计算得最小值为-2。

所以f(x)的最小值是-2，取得最小值时的x值为1。

四、简答题1.数列的极限是什么？如何判断一个数列的极限存在？答：数列的极限是指当项数趋向无穷大时，数列的项的值趋向的一个确定的数。

高中数学竞赛试题及答案试题（一）一、 ABC ∆为等边三角形，P 为其内一动点，且120APC ∠=。

AP 交BC 于N 、CP交AB 于M 。

求BMN ∆外心O 的轨迹。

(12分)二、 任意选24个相异且小于88的正奇数，试证：其中必有两个数它们的和是90。

(12分)三、 试证：对实数,,,0a b c d ≥，()()()()()()()()222222224a b c d a b b c c d d a ++++≥++++。

(12分) 四、定义：设A 是二阶整系数方阵，若存在二阶整系数方阵B ，使得1001AB BA I ⎡⎤===⎢⎥⎣⎦，则称A 可逆。

(13分) (1) A 是二阶整系数方阵。

试证：A 可逆的充要条件为A 的行列式||1A =±。

(2) 设A , B 均为二阶整系数方阵，且,,2,3,4A A B A B A B A B ++++均可逆，试证：5A B +亦可逆。

试题（二） 一、设(1)2(,,)(1)2,,,(1)2x x yz A x y y z z x y y zx x y z z z xy ⎧⎫-+⎪⎪=---=-+∈⎨⎬⎪⎪=-+⎩⎭，试求A 。

(5分)二、记不大于t 的整数中最大的整数为[]t 。

求方程 22[2]2[][]x x x x -+=在03x ≤<内所有实数解。

(5分)三、设a 和b 为实数，且使方程43210x ax bx ax ++++=至少有一个实根，对所有这种数对(,)a b ，求出22a b +的最小可能值。

(6分)四、令N 为自然数集，若函数:f N N →满足(1)()f n f n +>且(())3f f n n =，求(54)f 。

(5分)试题（一）解答一、 【解】令G 为ABC ∆的外心。

因120MPN APC ∠=∠=与B ∠互补，P 在BMN ∆的外接圆上。

因120APC AGC ∠=∠=，A 、P 、G 、C 共圆，且30CPG CAG ∠=∠=。

2023年全国中学生数学奥林匹克竞赛（预赛）暨2023年全国高中数学联合竞赛加试（A 卷）参考答案及评分标准说明：1．评阅试卷时，请严格按照本评分标准的评分档次给分．2．如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，10分为一个档次，不得增加其他中间档次．一．（本题满分40分）如图， 是以AB 为直径的固定的半圆弧， 是经过点A 及 上另一个定点T 的定圆，且 的圆心位于ABT 内．设P 是 的弧 TB（不含端点）上的动点，,C D 是 上的两个动点，满足：C 在线段AP 上，,C D 位于直线AB 的异侧，且CD AB ．记CDP 的外心为K ．证明：(1) 点K 在TDP 的外接圆上；(2) K 为定点． ΩωPD ABT C证明：(1) 易知PCD 为钝角，由K 为CDP 的外心知2(180)2PKD PCD ACD ．由于90APB ，CD AB ，故PBA ACD ATD ．……………10分 所以2180PTD PKD PTA ATD ACD PTA PBA ． 又,K T 位于PD 异侧，因此点K 在TDP 的外接圆上． ……………20分(2) 取 的圆心O ，过点O 作AB 的平行线l ，则l 为CD 的中垂线，点K 在直线l 上． ……………30分由,,,T D P K 共圆及KD KP ，可知K 在DTP 的平分线上，而9090DTB ATD PBA PAB PTB ，故TB 为DTP 的平分线．所以点K 在直线TB 上．显然l 与TB 相交，且l 与TB 均为定直线，故K 为定点． ……………40分 ωΩl D P OK B ATC二．（本题满分40分）正整数n 称为“好数”，如果对任意不同于n 的正整数m ，均有2222n m n m ⎧⎫⎧⎫⎪⎪⎪⎪≠⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎩⎭，这里，{}x 表示实数x 的小数部分． 证明：存在无穷多个两两互素的合数均为好数．证明：引理：设n 是正奇数，且2模n 的阶为偶数，则n 是好数．引理的证明：反证法．假设n 不是好数，则存在异于n 的正整数m ，使得2222n m n m ．因此22n n 与22m m 写成既约分数后的分母相同．由n 为奇数知22n n 是既约分数，故2m 的最大奇因子为2n ，从而m 的最大奇因子为n ．设2t m n ，其中t 为正整数（从而m 是偶数）．于是22222m m t m n． 由22222m t n n n可得2222(mod )m t n n ，故 222(mod )m t n n ． （*）设2模n 的阶为偶数d ．由（*）及阶的基本性质得2(mod )m t n d ，故2m t n 是偶数．但2m t 是偶数，n 是奇数，矛盾．引理得证．……………20分回到原问题．设221(1,2,)k k F k ．由于1221k k F ，而k F 221k，因此2模k F 的阶为12k ，是一个偶数．对正整数l ，由221(mod )l k F 可知21(mod )l k F ，故由阶的性质推出，2模2k F 的阶被2模k F 的阶整除，从而也是偶数．因2k F 是奇数，由引理知2k F 是好数．……………30分对任意正整数,()i j i j ，211(,)(,(21)2)(,2)1i i j i i i j i F F F F F F F ，故123,,,F F F 两两互素．所以222123,,,F F F 是两两互素的合数，且均为好数． ……………40分三．（本题满分50分） 求具有下述性质的最小正整数k ：若将1,2,,k 中的每个数任意染为红色或者蓝色，则或者存在9个互不相同的红色的数129,,,x x x 满足1289x x x x +++< ，或者存在10个互不相同的蓝色的数1210,,,y y y 满足12910y y y y +++< ．解：所求的最小正整数为408．一方面，若407k =时，将1,55,56,,407 染为红色，2,3,,54 染为蓝色，此时最小的8个红数之和为1555661407++++= ，最小的9个蓝数之和为231054+++= ，故不存在满足要求的9个红数或者10个蓝数．对407k <，可在上述例子中删去大于k 的数，则得到不符合要求的例子． 因此407k ≤不满足要求． ……………10分 另一方面，我们证明408k =具有题述性质．反证法．假设存在一种1,2,,408 的染色方法不满足要求，设R 是所有红数的集合，B 是所有蓝数的集合．将R 中的元素从小到大依次记为12,,,m r r r ，B 中的元素从小到大依次记为12,,,n b b b ，408m n +=．对于R ，或者8R ≤，或者128m r r r r +++≥ ；对于B ，或者9B ≤，或者129n b b b b +++≥ ．在1,2,,16 中至少有9个蓝色的数或至少有8个红色的数．情形1：1,2,,16 中至少有9个蓝色的数．此时916b ≤．设区间9[1,]b 中共有t 个R 中的元素12,,,(08)t r r r t ≤< ．记12t x r r r =+++ ，则112(1)2x t t t ≥+++=+ ． 因为12912,,,,,,,t b b b r r r 是9[1,]b 中的所有正整数，故{}{}12912,,,,,,,1,2,,9t b b b r r r t =+ ．于是 12912(9)n b b b b t x ≤+++=++++- 1(9)(10)2t t x =++-． （*） ……………20分 特别地，116171362n b ≤⨯⨯=．从而9R ≥． 对任意(1)i i m t ≤≤-，由（*）知1(9)(10)2t i n r b i t t x i +≤+≤++-+．从而 811811(9)(10)2t m t t i r r r r r x t t x i -+=⎛⎫ ⎪≤+++++≤+++-+ ⎪⎝⎭∑ 11(9)(10)(8)(8)(9)(7)22t t t t t t x =++-+---- 111(9)(10)(8)(8)(9)(7)(1)222t t t t t t t t ≤++-+----⋅+ 2819396407t t =-++≤（考虑二次函数对称轴，即知1t =时取得最大）． 又136n b ≤，这与,n m b r 中有一个为408矛盾． ……………40分情形2：1,2,,16 中至少有8个红色的数．论证类似于情形1．此时816r ≤．设区间8[1,]r 中共有s 个B 中的元素12,,,(09)s b b b s ≤< ．记1s y b b =++ ，则1(1)2y s s ≥+． 因为12128,,,,,,,s b b b r r r 是8[1,]r 中的所有正整数，故 {}{}12128,,,,,,,1,2,,8s b b b r r r s =+ ． 于是1(8)(9)2m r s s y ≤++-． 特别地，116171362m r ≤⨯⨯=．从而10B ≥． 对任意(1)i i n s ≤≤-，有1(8)(9)2s i m b r i s s y i +≤+≤++-+．从而 911911(8)(9)2s n s s i b b b b b y s s y i -+=⎛⎫ ⎪≤+++++≤+++-+ ⎪⎝⎭∑ 11(9)(8)(9)(8)(9)(10)22s s s s y s s =-++--+--111(9)(8)(9)(8)(1)(9)(10)222s s s s s s s s ≤-++--⋅++-- 2727369395s s =-++≤（在2s =时取得最大）， 又136m r ≤，这与,n m b r 中有一个为408矛盾．由情形1、2知408k =具有题述性质．综上，所求最小正整数k 为408． ……………50分四．（本题满分50分）设4110a -=+．在20232023⨯的方格表的每个小方格中填入区间[1,]a 中的一个实数．设第i 行的总和为i x ，第i 列的总和为i y ，12023i ≤≤．求122023122023y y y x x x 的最大值（答案用含a 的式子表示）． 解：记2023n =，设方格表为(),1,ij a i j n ≤≤，122023122023y y y x x x λ= ． 第一步：改变某个ij a 的值仅改变i x 和j y ，设第i 行中除ij a 外其余1n -个数的和为A ，第j 列中除ij a 外其余1n -个数的和为B ，则jij i ij y B a x A a +=+．当A B ≥时，关于ij a 递增，此时可将ij a 调整到,a λ值不减．当A B ≤时，关于ij a 递减，此时可将ij a 调整到1,λ值不减．因此，为求λ的最大值，只需考虑每个小方格中的数均为1或a 的情况． ……………10分第二步：设{}1,,1,ij a a i j n ∈≤≤，只有有限多种可能，我们选取一组ij a 使得λ达到最大值，并且11n nij i j a ==∑∑最小．此时我们有,,1,.i j ij i j a x y a x y ⎧>⎪=⎨≤⎪⎩（*） 事实上，若i j x y >，而1ij a =，则将ij a 改为a 后，行和及列和变为,i j x y ''，则11j j j i i iy y a y x x a x '+-=>'+-， 与λ达到最大矛盾，故ij a a =．若i j x y ≤，而ij a a =，则将ij a 改为1后，λ不减，且11n nij i j a ==∑∑变小，与ij a 的选取矛盾．从而（*）成立．通过交换列，可不妨设12n y y y ≤≤≤ ，这样由（∗）可知每一行中a 排在1的左边，每一行中的数从左至右单调不增．由此可知12n y y y ≥≥≥ ．因而只能12n y y y === ，故每一行中的数全都相等（全为1或全为a ）.……………20分 第三步：由第二步可知求λ的最大值，可以假定每一行中的数全相等.设有k 行全为a ,有n k -行全为1,0k n ≤≤．此时()()()n nk k n k n k ka n k ka n k na nn a λ-+-+-==． 我们只需求01,,,n λλλ 中的最大值． ()11(1)1111()(1)nn n k k n k n kk a n k a n a ka n k a k a n n a λλ++++--⎛⎫- ⎪==+ ⎪+--+⎝⎭． 因此1111(1)n k k a a k a n λλ+⎛⎫- ⎪≥⇔+≥ ⎪-+⎝⎭ 11(1)n n x x k x n-⇔+≥-+（记n x a =） 2111(1)n n x x x k x n-++++⇔≥-+ 2111n n x x x n k x -++++-⇔≤- 211(1)(1)1n n x x x x x--+++++++=+++ ． 记上式右边为y ,则211(2)1n n n n x x y x x ---+-++=+++ ． 下面证明(1010,1011)y ∈． ……………30分 首先证明1011y <．1011y < 2021202220222021101110111011x x x x ⇔+++<+++1010101210132021202210111010210101011x x x x x x ⇔+++<++++ ．由于220221x x x <<<< ，故101010101012011(1011)101110121011101222k k k x x x =-<⋅⋅<⋅⋅∑101110110k k kx +=<∑． ……………40分 再证明1010y >，等价于证明2021202200(2022)1010kk k k k x x ==->∑∑． 由于2021202100(2022)(2022)10112023k k k k x k ==->-=⨯∑∑， 20222022010101010202310102023k k x x a =<⨯<⨯∑，只需证明1011202310102023a ⨯>⨯，而410111101010a -=+<，故结论成立． 由上面的推导可知1k k λλ+≥当且仅当1010k ≤时成立，从而1011λ最大．故 2023max 101120231011(10111012)2023a aλλ+==． ……………50分。