下载文档原格式
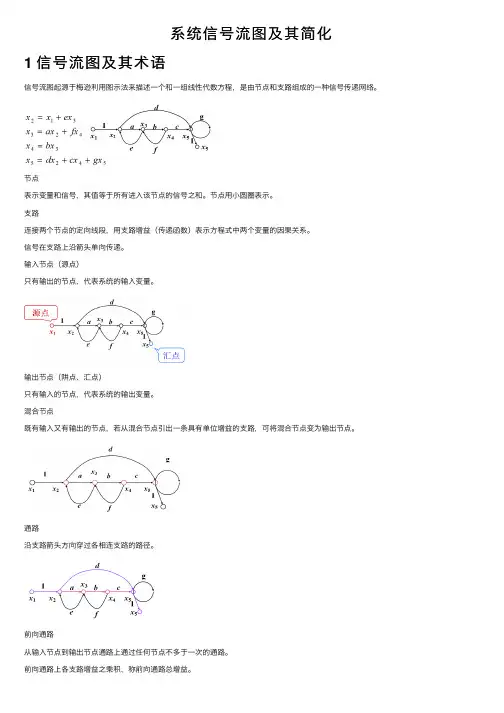
系统信号流图及其简化1 信号流图及其术语信号流图起源于梅逊利⽤图⽰法来描述⼀个和⼀组线性代数⽅程，是由节点和⽀路组成的⼀种信号传递⽹络。
节点表⽰变量和信号，其值等于所有进⼊该节点的信号之和。
节点⽤⼩圆圈表⽰。
⽀路连接两个节点的定向线段，⽤⽀路增益（传递函数）表⽰⽅程式中两个变量的因果关系。
信号在⽀路上沿箭头单向传递。
输⼊节点（源点）只有输出的节点，代表系统的输⼊变量。
输出节点（阱点、汇点）只有输⼊的节点，代表系统的输出变量。
混合节点既有输⼊⼜有输出的节点，若从混合节点引出⼀条具有单位增益的⽀路，可将混合节点变为输出节点。
通路沿⽀路箭头⽅向穿过各相连⽀路的路径。
前向通路从输⼊节点到输出节点通路上通过任何节点不多于⼀次的通路。
前向通路上各⽀路增益之乘积，称前向通路总增益。
回路起点与终点重合且通过任何节点不多于⼀次的闭合通路，回路中所有⽀路增益之乘积称为回路增益。
不接触回路相互之间没有任何公共节点的回路。
2 信号流图的绘制两种⽅法：1. 由系统微分⽅程绘制信号流图。
根据微分⽅程绘制信号流图的步骤与绘制⽅框图的步骤类似。
例：取Ui(s)、I1(s)、U A(s)、I2(s)、Uo (s)作为信号流图的节点，其中，Ui(s)、Uo(s)分别为输⼊及输出节点。
按上述⽅程绘制出各部分的信号流图，再综合后即得到系统的信号流图。
2. 由系统⽅框图绘制信号流图。
例：3 梅逊公式例：⽤梅逊公式求传递函数对于该RC电路⽹络，输⼊与输出之间只有⼀条前向通路，其传递函数为：三个不同回路的传递函数分别为：流图特征式为：前向通路特征式的余因⼦为：所以：。
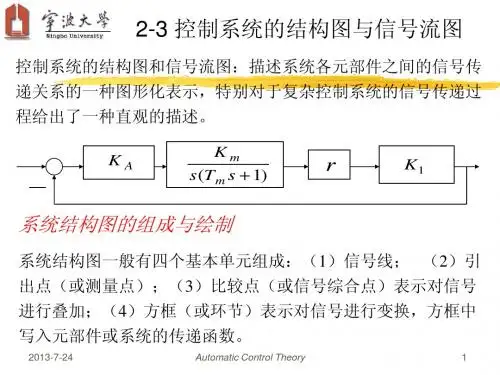
信号流图及其术语与图3.55所示系统方框图对应的系统信号流图如图3.56所示。
由图可以看出，信号流图中的网络是由一些定向线段将一些节点连接起来组成的。
下面说明这些线段和节点的含义。
(1)节点表示变量或信号，其值等于所有进入该节点的信号之和。
例如：是图3.56中的节点。
(2)输入节点它是只有输出的节点，也称源点。
例如，图3.56中是一个输入节点。
(3)输出节点它是只有输入的节点，也称汇点。
然而这个条件并不总是能满足的。
为了满足定义的要求可引进增益为1的线段。
例如，图3.56中右端点为输出节点。
(4)混和节点它是既有输入又有输出的节点。
例如，图3.56中是一个混和节点。
(5)支路定向线段称为支路，其上的箭头表明信号的流向，各支路上还标明了增益，即支路的传递函数。
例如，图3.56中从节点到为一支路，其中为该支路的。
(6)通路沿支路箭头方向穿过各相连支路的路径称为通路。
(7)前向通道从输入节点到输出节点的通路上通过任何节点不多于一次的通路称为前向通道。
例如，图3.56中的——是前向通道。
(8)回路始端与终端重合且与任何节点相交不多于一次的通道称为回路。
例如，图3.56中——是一条回路。
(9)不接触回路没有任何公共节点的回路称为不接触回路。
信号流图的绘制绘制系统的信号流图，首先必须将描述系统的线性微分方程变换成以为变量的信号流图代数方程；其次，线性代数方程组中每一个方程都要写成因果关系式。
且在书写时，将作为“因”的一些变量写在等式右端，而把“果”的变量写在等式左端。
下面以图3.57所示的二级电路网络为例说明信号流图的绘制步骤。
对于由两个环节（这里是两个电路）串联而成的系统，由于后一环节的存在，影响前一环节的输出，因此两相邻环节间存在着负载效应。
这时必须将它们视为一个整体来考虑。
所以，根据基尔霍夫定律，可写出下列原始方程将以上各式作拉氏变换，得方程组取、、、、为信号流图的节点，其中把作为输入节点，作为输出节点。
