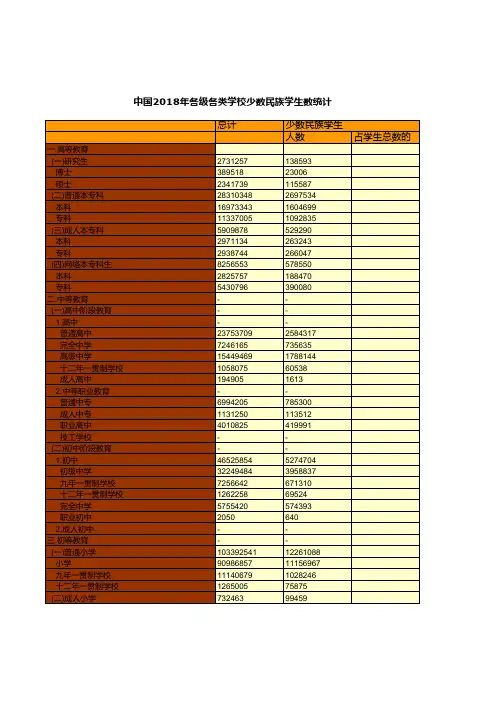
教育事业发展全国及各地省市区统计数据:中国2018年普通高中学生数统计(总计)
- 格式:xls
- 大小:14.50 KB
- 文档页数:2

河南省南阳市2024高三冲刺(高考数学)人教版模拟(评估卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知,函数在区间上单调递增,则的取值范围是()A.B.C.D.第(2)题双曲线左、右焦点坐标分别是()A.,B.,C.,D.,第(3)题已知函数,若对任意、、,总有、、为某一个三角形的边长,则实数的取值范围是A.B.C.D.第(4)题在复数范围内方程的解为()A.B.C.D.第(5)题已知,为锐角,,,则()A.B.C.D.第(6)题设集合,,,则A.B.C.D.第(7)题设全集,集合,则()A.B.C.D.第(8)题已知函数,若,则的取值范围是()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题下图是《2018年全国教育事业发展统计公报》中1949-2018年我国高中阶段在校生数条形图和毛入学率的折线图,根据下图可知在1949-2018年()高中阶段在校生数和毛入学率A.1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高B.从1990年开始,我国高中阶段的在校生数和毛入学率在逐年增高C.2010年我国高中阶段在校生数和毛入学率均达到了最高峰D.2018年高中阶段在校生数比2017年下降了约0.91%,而毛入学率提高了0.5个百分点第(2)题设函数,则()A.有三个零点B .是的极大值点C.曲线为轴对称图形D .为曲线的对称中心第(3)题已知函数在上有且仅有5个零点,则( )A .的取值范围是B .的图象在上有且仅有3个最高点C.的图象在上最多有3个最低点D .在上单调递增三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题某学校每天安排4项课后服务供学生自愿选择参加.学校规定:(1)每位学生每天最多选择1项;(2)每位学生每项一周最多选择1次.学校提供的安排表如下:时间周一周二周三周四周五课后服务音乐、阅读、体育、编程口语、阅读、编程、美术手工、阅读、科技、体育口语、阅读、体育、编程音乐、口语、美术、科技若某学生在一周内共选择了阅读、体育、编程3项,则不同的选择方案共有______种.(用数值表示)第(2)题执行如图所示的程序框图,输入l=2,m=3,n=5,则输出的y 的值____第(3)题已知为虚数单位,复数,则______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题某学校有1000人,想通过验血的方式筛查出某种病毒的携带者,如果对每个人的血样逐一化验,需要化验1000次,统计专家提出了一种方法:随机地按10人一组分组,然后将各组10个人的血样混合再化验,如果混合血样呈阴性,说明这10个人全部阴性;如果混合血样呈阳性,说明其中至少有一个人呈阳性,就需要对这组的每个人再分别化验一次.假设某学校携带病毒的人数有10人.()(1)用样本的频率估计概率,若5个人一组,求一组混合血样呈阳性的概率;(2)用统计专家这种方法按照5个人一组或10个人一组,问哪种分组方式筛查出这1000人中该病毒携带者需要化验次数较少?为什么?第(2)题在直角坐标系中,圆的参数方程为(为参数).以坐标原点为极点,轴的正半轴为极轴建立极坐标系,直线的极坐标方程为.(1)求圆的普通方程和直线的直角坐标方程;(2)若直线与圆相交于两点,点的直角坐标为,求的值.第(3)题已知点在抛物线上,且到抛物线的焦点的距离为2.(1)求抛物线的标准方程;(2)过点向抛物线作两条切线,切点分别为,若直线与直线交于点,且点到直线、直线的距离分别为.求证:为定值.第(4)题新冠病毒奥密克戎毒株开始流行后,为了控制新冠肺炎疫情,杭州某高中开展了每周核酸检测工作.周一至周五,每天中午13:30开始,安排位师生进行核酸检测,教职工每天都要检测,用五天时间实现全员覆盖.(1)该校教职工有人,高二学生有人,高三学生有人.①用分层抽样的方法,求高一学生每天的检测人数.②高一年级共个班,该年级每天进行核酸检测的学生有两种安排方案.方案一:集中来自部分班级;方案二:分散来自所有班级.你认为哪种方案更合理?给出理由.(2)学校开展核酸检测的第一周,周一至周五核酸检测用时记录如下表.第天用时①计算变量和的相关系数(精确到),并说明两变量的线性相关程度;②根据①中的计算结果,判定变量和是正相关还是负相关,并给出可能的原因.参考数据和公式:,相关系数.第(5)题已知数列的前项和为,,.(1)求数列的通项公式;(2)若,求数列的前项和.。
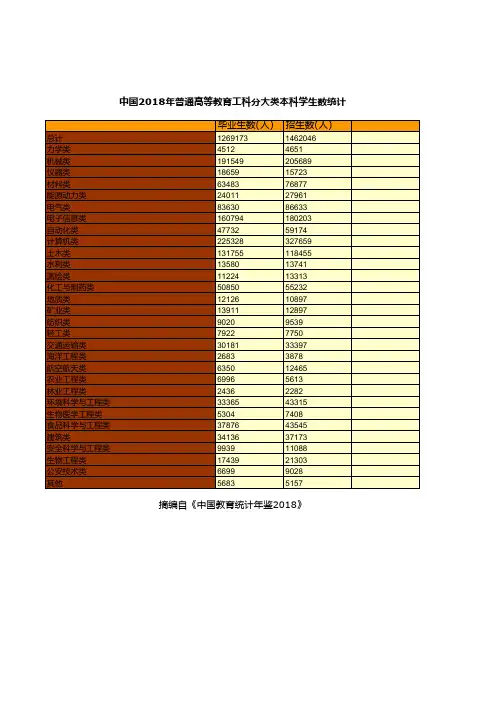

2018年中国教育数据报告2018年,全国共有各级各类学校251.88万所,比上年增加5017所。
全国各级各类学历教育在校生2.76亿人,比上年增加539.40万人,增长2.0%。
全国各级各类学校专任教师1672.85万人,比上年增加45.96万人,增长2.8%。
全国各级各类学校共拥有校舍建筑面积335.73亿平方米,比上年增加1.54亿平方米,增长4.5%;全国各级各类学校教学、科研仪器设备资产总值10218.21亿元,比上年增加1027.26亿元,增长11.2%。
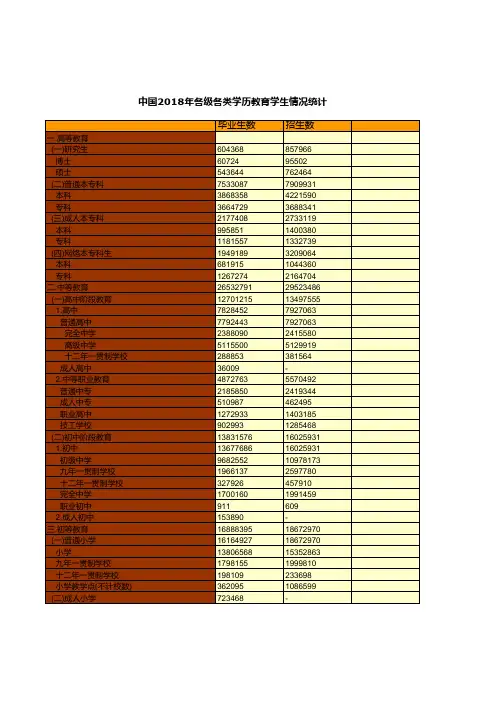
义务教育(一)义务教育规模2018年,全国共有义务教育阶段学校21.38万所,比上年减少5110所;义务教育阶段招生3469.89万人,比上年增加156.11万人,增长4.7%;在校生1.50亿人,比上年增加456.08万人,增长3.1%。
小学招生、在校生人数继续增长,城市小学招生增长较快。
2018年,全国共有普通小学16.18万所,比上年减少5198所;小学招生1867.30万人,比上年增加100.74万人,增长5.7%。
其中,城市小学招生713.51万人,同比增长13.2%,农村小学招生1153.79万,同比增长1.5%。
全国普通小学在校生规模继续增加,为10339.25万人,比上年增加245.56万人,增长2.4%。
初中招生、在校生规模持续增长,城市初中增长较快。
2018全国共有初中阶段学校5.20万所,比上年增加88所。
初中招生1602.59万人,比上年增加55.37万人,增长3.6%。
其中,城市初中招生581.56万人,同比增长5.7%,农村初中招生1021.03万人,同比增长2.4%。
初中阶段在校生4652.59万人,比上年增加210.52万人,增长4.7%。
受在校生规模增长影响,每十万人口中小学在校生人数比上年增加138人,为7438人;每十万人口中初中阶段在校生人数比上年增加134人,为3347人。
(二)义务教育普及与巩固水平2018年,小学学龄儿童净入学率达99.95%,全国及绝大多数省份男女童入学率性别差异已经消除;全国初中阶段毛入学率为100.9% 。

江苏省南京市(新版)2024高考数学统编版真题(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知球与圆台的上下底面和侧面都相切.若圆台的侧面积为;上、下底面的面积之比为,则球的表面积为().A.B.C.D.第(2)题已知函数,若对任意,恒成立,则实数的取值范围为()A.B.C.D.第(3)题设等差数列的前n项和为,若,则当取得最小值时,n的值为()A.11B.10C.9D.8第(4)题平面直角坐标系中,点、是方程表示的曲线上不同两点,且以为直径的圆过坐标原点,则到直线的距离为( )A.2B.C.3D.第(5)题已知复数满足,则在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限第(6)题点在同一个球的球面上,,若四面体体积的最大值为,则该球的表面积为A.B.C.D.第(7)题“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件第(8)题已知椭圆C:()的左、右焦点分别为,,P为C上一点,满足,以C的短轴为直径作圆O,截直线的弦长为,则C的离心率为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题在对具有相关关系的两个变量进行回归分析时,若两个变量不呈线性相关关系,可以建立含两个待定参数的非线性模型,并引入中间变量将其转化为线性关系,再利用最小二乘法进行线性回归分析.下列选项为四个同学根据自己所得数据的散点图建立的非线性模型,且散点图的样本点均位于第一象限,则其中可以根据上述方法进行回归分析的模型有()A.B.C.D.第(2)题已知,则()A.的最大值为B.的最小值为C.的最大值为2D.的最小值为第(3)题下图是《2018年全国教育事业发展统计公报》中1949-2018年我国高中阶段在校生数条形图和毛入学率的折线图,根据下图可知在1949-2018年()高中阶段在校生数和毛入学率A.1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高B.从1990年开始,我国高中阶段的在校生数和毛入学率在逐年增高C.2010年我国高中阶段在校生数和毛入学率均达到了最高峰D.2018年高中阶段在校生数比2017年下降了约0.91%,而毛入学率提高了0.5个百分点三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知数列的前n项和,记,则数列的前n项和_______.第(2)题随机变量分布列如下表,则______;______.012第(3)题若函数的图象关于点对称,且关于直线对称,则______(写出满足条件的一个函数即可).四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题正四棱锥中,,,其中为底面中心,为上靠近的三等分点.(1)求证:平面;(2)求四面体的体积.第(2)题第22届亚运会在中国杭州举行,中国代表团斩获201枚金牌,稳居榜首.为了普及亚运会知识,某校组织了亚运会知识竞赛,设置了A,B,C三套不同试卷.现将每份试卷分别装入大小、外观均相同的竹筒中,再放入甲、乙两个抽题箱内,其中甲箱装有A卷竹筒4个、B卷竹筒3个、C卷竹筒2个、乙箱装有A卷竹筒2个、B卷竹筒2个、C卷竹筒5个.(1)若从甲箱中取出一个竹筒,求该竹筒装有A卷的概率.(2)若从甲、乙箱中各取出一个竹筒,记取出的装有B卷的竹筒数为随机变量,求的分布列与数学期望.(3)若先从甲箱中随机取出一个竹筒放入乙箱,再从乙箱中随机取出一个竹筒,求从乙箱取出的竹筒装有C卷的概率.第(3)题已知双曲线的右焦点为,过与轴垂直的直线交于两点,且,离心率为.(1)求的方程;(2)已知圆上点处的切线方程是,利用类比思想可知双曲线上点处的切线方程为.过点分别作双曲线的左、右两支的切线,切点分别为,连接,并过线段的中点分别再作双曲线左、右两支的切线,切点分别为,证明:点在同一条直线上.第(4)题记为数列的前n项和,时,满足,.(1)求的通项公式;(2)求.第(5)题已知函数的一个极值点是.(1)求a与b的关系式,并求的单调区间;(2)设,,若存在,,使得成立,求实数a的范围.。