下载文档原格式
模型一、鸟头模型：两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在△ABC中，D，E分别是AB，AC上的点如图(或D在BA的延长线上，E在AC上)，则:():()ABC ADES S AB AC AD AE=⨯⨯△△(2007年”走美”五年级初赛试题)如图所示，正方形ABCD边长为6厘米，13AE AC=，13CF BC=。
三角形DEF的面积为_______平方厘米。
如图，已知三角形ABC面积为1，延长AB至D，使BD＝AB；延长BC至E，使CE＝2BC；延长CA至F，使AF＝3AC，求三角形DEF的面积。
例2例1小升初——五大模型如图，将四边形ABCD的四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H，若四边形ABCD的面积为5，则四边形EFGH的面积是____。
模型二、任意四边形中的比例关系(“蝴蝶定理”)，如图所示。
①S1∶S2＝S4∶S3或者S1×S3＝S2×S4②AO∶CO＝(S1＋S2)∶(S4＋S3)蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径，通过构造模型，一方面我们可以使不规则四边形的面积关系与四边形内的三角形相联系，另一方面，我们也可以得到与面积对应的对角线的比例关系。
如图平行四边形ABCD的对角线相交于O点，三角形CEF，OEF，ODF，BOE的面积依次是2、4、4、6。
求三角形OCF的面积，三角形GCE的面积。
例4例3例5如图边长为1的正方形ABCD中，BE＝2CE，F为DC的中点，求三角形AGE的面积。
模型三、梯形中的蝴蝶定理①S1：S3＝a2：b2②S1：S3：S2：S4＝a2：b2：ab：ab③S的对应份数为(a＋b)2梯形蝴蝶定理，给我们提供了解决梯形面积与上下底之间关系互相转换的渠道。
构造模型，例6长方形ABCD分别被CE、DF分成四块，其中三块的面积分别是2、5、8平方厘米，那么余下的OFBC的面积是多少？如图所示，在边长为1的正方形ABCD中，BE＝2EC，DF＝2FC，求四边形ABGD的面积。
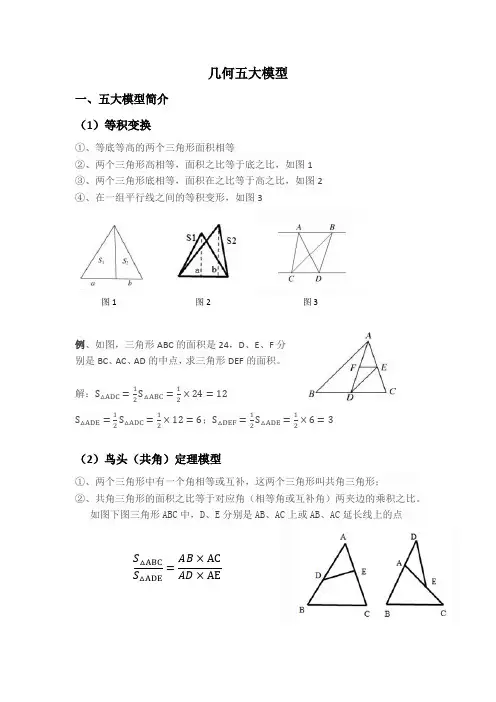
几何五大模型一、五大模型简介（1）等积变换①、等底等高的两个三角形面积相等②、两个三角形高相等，面积之比等于底之比，如图1③、两个三角形底相等，面积在之比等于高之比，如图2④、在一组平行线之间的等积变形，如图3图1 图2 图3例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。
解：S△ADC=12S△ABC=12×24=12S△ADE=12S△ADC=12×12=6；S△DEF=12S△ADE=12×6=3（2）鸟头（共角）定理模型①、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；②、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。
如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点S△ABC S△ADE =AB×AC AD×AE例、如图在ΔABC中，D在BA的延长线上，E在AC上，且AB：AD=5:2，AE：EC=3:2，△ADE的面积为12平方厘米，求ΔABC 的面积。
解：由题意知：S△ABCS△ADE =AB×ACAD×AE=52×53=256∴S△ABC=256×S△ADE=256×12=50(平方厘米)（3）蝴蝶模型1、梯形中比例关系(“梯形蝴蝶定理”)①S2=S4(梯形两翼相等)②S1:S3:S2:S4=a2:b2:ab:ab③梯形S对应的分数为（a+b)2例、如图，梯形ABCD，AB与CD平行，对角线AC、BD交于点O，已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米，求梯形ABCD的面积。
解：S△AOB:S△BOC=25:35=5:7S△AOB:S△DOC=AB2:DC2=52:72=25：49∴S△DOC=49又S△AOD=S△BOC=35∴S ABCD=25+35+35+49=144(平方厘米)2、任意四边形中的比例关系(“蝴蝶定理”)：①S1:S2=S4:S3或S1×S3=S2×S4②AO:OC=S1:S4=S2:S3=(S1+S2):(S4+S3)例、如图，四边形ABCD的对角线AC、BD交于点O，如果三角形ABD的面积等于三角形BCD面积的1/3，且AO=2，求OC解：AO:OC=S△ABD:S△BCD=1:3OC=2×3=6（4）相似模型1、相似三角形：形状相同,大小不相等的两个三角形相似；2、寻找相似模型的大前提是平行线：平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似。
几何五大模型一、五大模型简介(1)等积变换模型1 、等底等高的两个三角形面积相等；2 、两个三角形高相等，面积之比等于底之比，如图①所示，S[sub]1[/sub] : S[sub]2[/sub]=a:b ；3 、两个三角形底相等，面积在之比等于高之比，如图②所示,S[sub]1[/sub] : S[sub]2[/sub]=a:b ；4 、在一组平行线之间的等积变形，如图③所示，S[sub] △ ACD[/sub]=S[sub] △ BCD[/sub];反之，如果S[sub] △ ACD[/sub]=S[sub] △ BCD[/sub]，则可知直线AB平行于CD点，求三角形DEF的面积。
例、如图，三角形ABC的面积是24，D、E、F分别是BC AC AD的中【详解】根据等积变换知，5^=15^ = 1x24=12,]$丄攻=斥卅1匚=6 • EggF = Q6 - 3（2）鸟头（共角）定理模型1 、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；2 、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。
如图下图三角形ABC中，D、E分别是AB AC上或AB AC延长线上的点A D则有：S[sub] △ ABC[/sub] : S[sub] △ ADE[/sub]= (ABX AC (ADX AE我们现在以互补为例来简单证明一下共角定理!p _AB AC . 亨尹Z （平方厘料如图连接BE 根据等积变化模型知，S[sub] △ ADE[/sub]:S[sub] △ ABE[/sub] =AD AB S[sub] △ ABE[/sub]:S[sub] △ CBE[/sub]=AE : CE 所以 S[sub] △ ABE[/sub]:S[sub] △ ABC[/sub]=S[sub] △ ABE[/sub]:(S[sub] △ ABE[/sub]+S[sub] △ CBE[/sub] ) =AE AC,因此 S[sub] △ ADE[/sub] : S[sub] △ ABC[/sub]= (S[sub] △ ADE[/sub]: S[sub] △ ABE[/sub] ) x( S[sub] △ ABE[/sub] : S[sub] △ ABC[/sub])= (AD AB x ( AE AC 。
人教版小升初数学复习专项《几何的五大模型之鸟头模型》能力达标卷一、基础题1、如图，在△ABC中，AB的长度是BD的4倍，AC的长度是EC的3倍，如果△ABC 的面积是20平方厘米，那么△ADE的面积是多少平方厘米？2、如图在△ABC中，D、E分别是AB、AC上的点，其中EC＝3AE，AD＝2DB，且△ABC的面积是1平方厘米，求△ADE的面积是多少平方厘米？3、如图，在平行四边形ABCD中，AF的长度是FD的2倍，CE的长度等于ED，如果平行四边形ABCD的面积是120平方厘米，那么△FE D的面积是多少平方厘米？4、如图，在平行四边形ABCD中，AD：AF＝3：2，CD：CE＝2：1。
如果平行四边形ABCD 的面积为150平方厘米，那么△FDE的面积是多少平方厘米？二、提高题1、如图，在△ABC中，E是AC上的点，D是BA延长线上的一点，其中EC＝2AE，AB＝2AD，△ABC的面积是2平方厘米，求△ADE的面积是多少平方厘米？2、如图，在△ABC中，D是BC的中点，AE＝3ED，△ABC的面积是96平方厘米，求△ABE的面积是多少平方厘米？3、三角形ABC中，AB的长度是DB的4倍，E点是AC的三等分点，BF：FC＝3：2。
若三角形ABC的面积等于30平方厘米，则三角形DEF的面积是多少平方厘米？4、如图，在△ABC中，AD的长度是DB的2倍，AC的长度是EC的4倍。
如果四边形DBEC的面积为60平方厘米，那么△ABC的面积是多少平方厘米？5、如图，在△ABC中，FD＝2AF，FC＝2FE，CD＝2BD，△ABC的面积是54平方厘米，求阴影部分△DEF的面积是多少平方厘米？☆☆☆竞赛题1、如图，三角形ABC中，D是BC的中点，E、F是AC上的三等分点，已知三角形ABC的面积是108平方厘米，求三角形CDE的面积？2、如图所示，CF＝5AC，BE＝3BC，B是AD的中点，那么三角形DEF的面积是三角形ABC面积的几倍？3、如图，把三角形DEF的边DF、EF、DE依次向外延长1、2、3倍后等到三角形ABC，若三角形DEF的面积是4平方米，则三角形ABC的面积是的多少平方米？4、把四边形BADC的各边向外延长2倍后得到四边形FEHG，四边形BADC的面积为2平方米．那么阴影部分的面积是多少？5、把四边形ABCD的各边向外延长后得到四边形FGHE，若AB＝BF，CG＝2BC，CD ＝DH，AE＝2DA，且四边形ABCD的面积为6平方米．那么四边形FGHE的面积是多少？几何的五大模型之鸟头模型能力达标卷一、基础题1、答案：10平方厘米解析：根据鸟头原理：321432 ADEABCS AD AE AD AES AB AC AB AC⨯⨯⨯⨯△△＝＝＝＝所以S△ADE＝12S△ABC＝12×20＝10（平方厘米）答：△ADE的面积是10平方厘米。
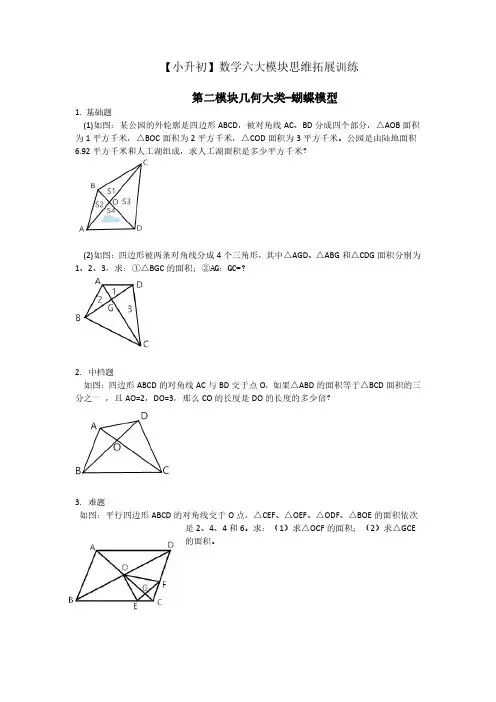
第二模块几何大类-蝴蝶模型1.基础题(1)如图：某公园的外轮廓是四边形ABCD，被对角线AC、BD分成四个部分，△AOB面积为1平方千米，△BOC面积为2平方千米，△COD面积为3平方千米。
公园是由陆地面积6.92平方千米和人工湖组成，求人工湖面积是多少平方千米？(2)如图：四边形被两条对角线分成4个三角形，其中△AGD、△ABG和△CDG面积分别为1、2、3，求：①△BGC的面积；②AG：GC=?2.中档题如图：四边形ABCD的对角线AC与BD交于点O，如果△ABD的面积等于△BCD面积的三分之一，且AO=2，DO=3，那么CO的长度是DO的长度的多少倍？3.难题如图：平行四边形ABCD的对角线交于O点，△CEF、△OEF、△ODF、△BOE的面积依次是2、4、4和6。
求：（1）求△OCF的面积；（2）求△GCE的面积。
蝴蝶模型--答案1.基础题（1）如图：某公园的外轮廓是四边形ABCD，被对角线AC、BD 分成四个部分，△AOB 面积为1平方千米，△BOC 面积为2平方千米，△COD 面积为3平方千米。
公园是由陆地面积6.92平方千米和人工湖组成，求人工湖面积是多少平方千米？解：根据蝴蝶模型定理：()（平方千米）（平方千米）得：湖58.092.6-5.1321s 5.1s s s s s 44321=+++===答：人工湖面积是0.58平方千米。
（2）如图：四边形被两条对角线分成4个三角形，其中△AGD 、△ABG 和△CDG 面积分别为1、2、3，求：①△BGC 的面积；②AG：GC=?解：①根据蝴蝶模型：②根据蝴蝶模型：2.中档题如图：四边形ABCD 的对角线AC 与BD 交于点O ，如果△ABD 的面积等于△BCD 面积的三分之一，且AO=2，DO=3，那么CO 的长度是DO的长度的多少倍？1:23:6:63231313131===⨯=====OD OC CO CO AO S S CG AH S S GBD CG H BD AH DOC AOD BCD ABD 得到得到由题意知：于垂直，于垂直解：作△△△△3.难题如图：平行四边形ABCD 的对角线交于O 点，△CEF 、△OEF 、△ODF 、△BOE 的面积依次是2、4、4和6。
第二讲 几何之五大模型及其应用1． 回顾几何图形中的倍比关系； 2． 精讲五大模型及其应用。
【例1】 ★★★（思维训练导引）如图，平行四边形ABCD 周长为75厘米，以BC 为底时高是14厘米；以CD 为底时高是16厘米。
求平行四边形ABCD 的面积。
解：BC ×14=CD ×16，BC ：CD=16：14， BC+CD=752，BC=752×161614=20 ABCD 面积=14×20=280（平方厘米）【例2】 ★★★（小学数学奥林匹克）如图，一个长方形被切成8块，其中三块的面积分别为12，23，32，则图中阴影部分的面积为（ ）ABCDEF平面几何也是小升初考试的必考内容，而且常常以大题形式出现（分值一般在10分～16分），名牌中学的选拔考试面积题目，有逐步增加难度的趋势，这一部分的分值又较高，希望同学们重视并好好总结归纳，本讲重点研讨几何问题中直线型面积问题，尤其强调奥数几何题中的五大模型及应用。
教学目标专题回顾【解】如右图，已知a+b+x=23+a+32+12+b 所以 x=23+32+12x=67.【点评】本题渗透等量代换思想，方程中有相抵成份，不必害怕未知数太多。
【例3】 三个正方形ABCD ，BEFG ，HKPF 如图所示放置在一起，图中正方形BEFG 的周长等于14厘米。
求图中阴影部分的面积。
【解】如图，连接KF ，EG ，BD 。
设KG ，EF 相交于O ，DE ，BG 相交于V ，由KF ∥EG ∥BD ， S △KEG =S △FGE ，S △DEG =S △BGE 。
设阴影阴影的面积为S,则S= S △KGE + S △DEG = S △FGE + S △BGE = S BEFG正方形BEFG 的周长为14厘米，边长为3.5厘米。
所以S BEFG =3.52=12.25(平方厘米)【点评】等积变形方法的最常见形式是在一组平行线内，两个三角形同底等高的情况。
第16讲小升初专项训练平面几何五种模型－答案一、知识要点1、三角形的等积变形1、两个三角形的底高相等，则它们面积相等。
2、①两个三角形高相等，面积比等于它们的底之比；②两个三角形底相等，面积比等于它们的高之比；3、推广到平行四边形。
2、等分点结论( 共角模型、鸟头模型或鸟头定理)两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．3、蝴蝶定理1、任意四边形中的比例关系S1∶S2=S4∶S3或 S1×S3= S2×S4上、下部分的面积之积等于左、右部分的面积之积2、梯形中的比例关系3、长方形或正方形中的比例关系4、相似三角形性质：金字塔模型和沙漏模型。
5、共边：燕尾模型（燕尾定理）和风筝模型附：中间桥梁及“差不变”二、典型问题【典型问题－1：三角形的等积变形】1、两个三角形的底高相等，则它们面积相等。
①平行线间的三角形：底等则面积相等。
反之，则两线为平行线。
②两个相邻的长方形，对角线间的三角形。
③正方形或长方形中的三角形——拉窗帘。
2、①两个三角形高相等，面积比等于它们的底之比；S1 : S2 = a : b②两个三角形底相等，面积比等于它们的高之比；S1 : S2 = h1 : h23、推广到平行四边形。
①三角形面积等于与它等底等高的平行四边形面积的一半；②等底等高的两个平行四边形面积相等(长方形和正方形是特殊的平行四边形)；③两个平行四边形高相等，面积比等于它们的底之比；④两个平行四边形底相等，面积比等于它们的高之比。
练习一：1、如图，ABCD是直角梯形，求阴影部分的面积和。
（单位：厘米）解：连结AC。
则S阴=6×3÷2=9（平方厘米）答：求阴影部分的面积和9平方厘米。
2、如图，ABCD是直角梯形，AD=5厘米，DC=3厘米，三角形DOC的面积是5平方厘米，则阴影部分的面积是_________平方厘米。
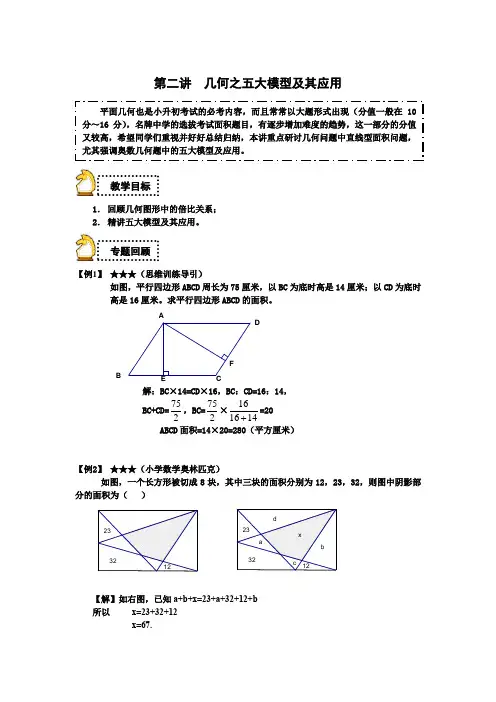
第二讲 几何之五大模型及其应用1． 回顾几何图形中的倍比关系； 2． 精讲五大模型及其应用。
【例1】 ★★★（思维训练导引）如图，平行四边形ABCD 周长为75厘米，以BC 为底时高是14厘米；以CD 为底时高是16厘米。
求平行四边形ABCD 的面积。
解：BC ×14=CD ×16，BC ：CD=16：14， BC+CD=752，BC=752×161614=20 ABCD 面积=14×20=280（平方厘米）【例2】 ★★★（小学数学奥林匹克）如图，一个长方形被切成8块，其中三块的面积分别为12，23，32，则图中阴影部分的面积为（ ）【解】如右图，已知a+b+x=23+a+32+12+b 所以 x=23+32+12 x=67.ABCDE F233212123223dc bax平面几何也是小升初考试的必考内容，而且常常以大题形式出现（分值一般在10分～16分），名牌中学的选拔考试面积题目，有逐步增加难度的趋势，这一部分的分值又较高，希望同学们重视并好好总结归纳，本讲重点研讨几何问题中直线型面积问题，尤其强调奥数几何题中的五大模型及应用。
教学目标专题回顾【点评】本题渗透等量代换思想，方程中有相抵成份，不必害怕未知数太多。
【例3】三个正方形ABCD，BEFG，HKPF如图所示放置在一起，图中正方形BEFG的周长等于14厘米。
求图中阴影部分的面积。
【解】如图，连接KF，EG，BD。
设KG，EF相交于O，DE，BG相交于V，由KF∥EG∥BD，S△KEG=S△FGE，S△DEG=S△BGE。
设阴影阴影的面积为S,则S= S△KGE+ S△DEG= S△FGE+ S△BGE= S BEFG正方形BEFG的周长为14厘米，边长为3.5厘米。
所以S BEFG=3.52=12.25(平方厘米)【点评】等积变形方法的最常见形式是在一组平行线内，两个三角形同底等高的情况。
【例4】如图，有四个长方形的面积分别是1平方厘米、2平方厘米、3平方厘米和4平方厘米，组合成一个大的长方形，求图中阴影部分的面积。
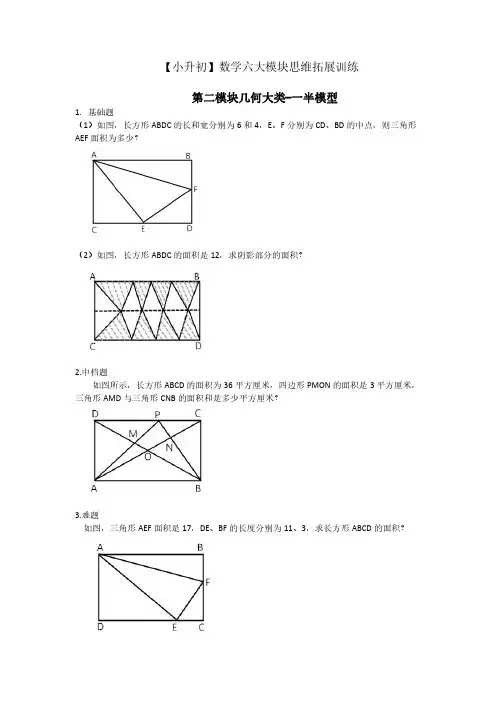
第二模块几何大类-一半模型1.基础题（1）如图，长方形ABDC的长和宽分别为6和4，E、F分别为CD、BD的中点，则三角形AEF面积为多少？（2）如图，长方形ABDC的面积是12，求阴影部分的面积？2.中档题如图所示，长方形ABCD的面积为36平方厘米，四边形PMON的面积是3平方厘米，三角形AMD与三角形CNB的面积和是多少平方厘米？3.难题如图，三角形AEF面积是17，DE、BF的长度分别为11、3，求长方形ABCD的面积？一半模型--答案1.基础题（1）如图，长方形ABDC 的长和宽分别为6和4，E 、F 分别为CD 、BD 的中点，则三角形AEF 面积为多少？（2）如图，长方形ABDC 的面积是12，求阴影部分的面积？2.中档题如图所示，长方形ABCD 的面积为36平方厘米，四边形PMON 的面积是3平方厘米，三角形AMD 与三角形CNB 的面积和是多少平方厘米？3.难题如图，三角形AEF 面积是17，DE 、BF 的长度分别为11、3，求长方形ABCD的面积？()9214632121=⨯⨯+⨯==AEF AEDB AEF S S S △梯形△即知解：由梯形一半模型可6122121=⨯==阴影长方形阴影即解：S S S ABDC ()()21-S S S S S BOC AOD ++=△△阴影解：()()()平方厘米四边形△△12391818---3621=---=⨯=PMON AOB ABP S S S ()6734332332113222=+=+=+++⨯=+++⨯=AFEAME MFE AMF AMEMFE AMF S S S S S S S HM GM △△△△△△△MEDHMFCE GMFB AHMG ABCD S S S S S +++=长方形解：。
小学奥数几何篇五大模型蝴蝶定理一、蝴蝶定理的定义与公式蝴蝶定理是小学奥数几何篇中的一个重要模型，它描述了在等腰三角形中，一条平行于底边的线段将底边平分，并且这条线段与等腰三角形的两腰相交于同一点时，该线段的中点与等腰三角形的顶点、底边的中点以及两腰上的交点形成一个等腰三角形。
蝴蝶定理的公式如下：设等腰三角形ABC中，AB=AC，底边BC的长度为2a，点D在BC上，且BD=DC=a，点E在AB上，点F在AC上，DE平行于BC，交AB于点E，交AC于点F，点G为DE的中点，连接AG、BG、CG，则AG=BG=CG。
二、蝴蝶定理的应用1. 在等腰三角形中求边长：通过蝴蝶定理，可以快速求出等腰三角形中未知边的长度。
例如，已知等腰三角形ABC中，AB=AC，底边BC 的长度为2a，点D在BC上，且BD=DC=a，点E在AB上，点F在AC上，DE平行于BC，交AB于点E，交AC于点F，点G为DE的中点，连接AG、BG、CG，求AG的长度。
解答：根据蝴蝶定理，AG=BG=CG，又因为AB=AC，所以AG=AB/2=a。
2. 在等腰三角形中求角度：通过蝴蝶定理，可以求出等腰三角形中未知角的度数。
例如，已知等腰三角形ABC中，AB=AC，底边BC的长度为2a，点D在BC上，且BD=DC=a，点E在AB上，点F在AC上，DE平行于BC，交AB于点E，交AC于点F，点G为DE的中点，连接AG、BG、CG，求∠AGB的度数。
解答：由于AG=BG=CG，所以△AGB是等边三角形，∠AGB=60°。
3. 在等腰三角形中求面积：通过蝴蝶定理，可以求出等腰三角形中未知部分的面积。
例如，已知等腰三角形ABC中，AB=AC，底边BC的长度为2a，点D在BC上，且BD=DC=a，点E在AB上，点F在AC上，DE平行于BC，交AB于点E，交AC于点F，点G为DE的中点，连接AG、BG、CG，求△AGB的面积。
解答：由于△AGB是等边三角形，所以△AGB的面积=（a^2 √3）/ 4。
几何五大模型
1、如图，在三角形ABC 中，，D 为BC 的中点，E 为AB 上的一点，且BE=
1
3
AB,已知四边形EDCA 的面积是35，求三角形ABC 的面积. （
【解】根据定理：
ABC BED ∆∆=3211⨯⨯=6
1
，所以四边形ACDE 的面积就是6-1=5份，这样三角形
35÷5×6=42。
2、四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米，大正方形面积是5平方米，那麽直角三角形中，最短的直角边长度是______米.
【解】小正方形面积是1平方米，大正方形面积是5平方米，所以外边四个面积和是5-1=4，
所以每个三角形的面积是1，这个图形是“玄形”，所以长直角边和短直角边差就是中间正方形的边长，所以求出短边长就是1。
3、如图在长方形ABCD 中，△ABE 、△ADF 、四边形AECF 的面积相等。
△AEF 的面积是长
方形ABCD 面积的______ (填几分之几)。
【解】连接AC ，首先△ABC 和△ADC 的面积相等，又△ABE 和△ADF 的面积相等，则△AEC 和△AFC 的面积也相等且等于ABCD 的1/6，不难得△AEC 与△ABE 的面积之比为1/2，由于这两个三角形同高，则EC 与BE 之比为1/2，同理FC 与DF 之比也为1/2。
从而△ECF 相当于ABCD 面积的1/18，而四边形AECF 相当于ABCD 面积的1/3，从而答案为1/3-1/18=5/18。
F
D
C
4、如图1，一个长方形被切成8块，其中三块的面积分别为12，23，32，则图中阴影部分的面积为_____
（01年同方杯）【解】设图示两个三角形的面积分别为a和b，因为△AED面积等于ABCD的一半，则△ABE 加上△DEC的面积也等于ABCD的一半。
而△FDC的面积也等于ABCD的一半，即23+a+32+12+b=a+b+阴影面积，可见阴影面积=23+32+12=67。
D
C
B
F
5、右图中
AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE的面积是平方厘米．
【解】：四边形AFDC的面积=三角形AFD+三角形ADC=（
2
1
×FD×AF）+（
2
1
×AC×CD）=
2
1
（FE+ED）×AF+
2
1
（AB+BC）×CD= （
2
1
×FE×AF+
2
1
×ED×AF）+（
2
1
×AB×CD+
2
1
×BC ×CD）。
所以阴影面积=四边形AFDC-三角形AFE—三角形BCD=（
2
1
×FE×AF+
2
1
×ED×AF）+（
2
1
×
AB×CD+
2
1
×BC×CD）-
2
1
×FE×AF-
2
1
×BC×CD=
2
1
×ED×AF+
2
1
×AB×CD=
2
1
×8×7+
2
1
×3×12=28+18=46。
练习题
1、（★★）如右图所示，已知三角形ABC 面积为1，延长AB 至D ，使BD=AB ；延长BC 至E ，使CE=2BC ；延长CA 至F ，使AF=3AC ，求三角形DEF 的面积。
解：作辅助线FB ，则S ΔBAF ＝3×S ΔABC ＝1/2×S ΔDAF ；则有S ΔABC ＝1/6×S ΔDAF ；作辅助线AE ，则S ΔACE ＝2×S ΔABC ＝1/4×S ΔCEF ；则S ΔABC ＝1/8×S ΔCEF ；作辅助线CD ，则有：
S ΔCBD ＝S ΔABC ＝1/3×S ΔCEF ；综上，三角形DEF 由这四个三角形构成，那么由已求出的比例关系可知，三角形DEF 的面积为1+6+8+3＝18。
2、（★★）右图是一块长方形耕地，它由四个小长方形拼合而成，其中三个小长方形的面积分别为15、18、30公顷，问图中阴影部分的面积是多少？ 解：设定阴影部分面积为X,则不难由长方形面积公式看出比例关系为：X/30=15/18，则X=25。
3、（★★★）如下图，已知D 是BC 的中点，E 是CD 的中点，F 是AC 的中点，且ADG ∆的
面积比EFG ∆的面积大6平方厘米。
?的面积是多少平方厘米
ABC ∆ A
B
C
D
E
F G
解：因为6,6+=+=∆∆∆∆D EF AD E EFG AD G S S S S 所以。
根据已知条件：D EF ECF AEC AD E S S S S ∆∆∆∆===22。
所以三角形DEF 的面积为6。
因此三角形ABC 的面积为48平方厘米。
4、（★★）长方形ABCD 的面积为36平方厘米，E 、F 、G 分别为边AB 、BC 、CD 的中点，H 为AD 边上的任一点。
求图中阴影部分的面积是多少？
【解答1】极限考虑，若H 点动到D 点，那么阴影面积为四边形BEFH ， 所以面积占总共的一半为18。
【解答2】过H 作HI 垂直BC ，这样四边形FCGH 的面积就分成三角形FHI 和 梯形ICGH ，所以空白部分的总面积为： （CG+HI ）×IC ÷2+FI ×HI ÷2+AE ×AH ÷2=2
1
×（CG ×IC+HI ×IC+FI ×HI+AE ×AH ） (CG=AE)
=
2
1×[CG ×(IC+AH)+HI ×(IC+FI)]
(HI=CD)
=
21×(CG ×BC+CD ×FC)= 2
1
四边形ABCD 的面积=18.
5、（★★）如图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米，求阴影部分的面积。
解：我们要得到阴影部分，只要两个正方形的面积和扣除三个三角形的面积即可。
那么正方形面积和为：10×10＋12×12＝244。
三角形ABG 面积为50；三角形ABD 面积为1/2×22×12＝132；三角形AFG 面积为1/2×2×12＝12。
则阴影部分面积为244－50－132－12＝50。
6、正方形ABFD 的面积为100平方厘米，直角三角形ABC 的面积，比直角三角形（CDE 的面积大30平方厘米，求DE 的长是多少？ 【解答】：公共部分的运用，三角形ABC 面积-三角形CDE 的面积=30，
两部分都加上公共部分（四边形BCDF ），正方形ABFD-三角形BFE=30， 所以三角形BFE 的面积为70，所以FE 的长为70×2÷10=14，所以DE=4。
