离散系统的Z域分析
- 格式：doc
- 大小：101.52 KB
- 文档页数：6
下载文档原格式
合集下载
离散系统的Z域分析法
X(z)
D z-1
X(k-1)
z-1X(z)
X
注意:z域框图只能求系统零状态响应 注意 域框图只能求系统零状态响应
第
例题
1.求如图系统的单位响应 求如图系统的单位响应h(k)和单位阶跃响应 和单位阶跃响应g(k) 求如图系统的单位响应 和单位阶跃响应
8 页
2. 知 阶 散 统 初 条 为 zi (0) = 2, yzi (1) =1 已 二 离 系 的 始 件 y , 当 入 (k) = ε (k)时 输 f , 1 5 k k 输 全 应 (k) =[ + 4⋅ 2 − ⋅ 3 ]ε (k), 出 响 y 2 2 求 差 方 .， 画 系 框 。 此 分 程 并 出 统 图
求解线性时不变离散系统的差分方程有两种方法： 求解线性时不变离散系统的差分方程有两种方法： •时域方法: y(k) =y zi (k) + yzs (k) yzs (k) = h(k) ∗ x(k) 时域方法: 时域方法 •z变换方法: 变换方法: 变换方法 Yzs (z) = H(z) ⋅ X(z)
X
第
二.系统框图的z域分析法
基本思路: 基本思路 时域框图 z域框图 域框图 z域代数方程 域代数方程 Yzs(z)
7 页
yzs(k)
x(k) ⇒ X (z) yzs (k) ⇒ Yzs (z) 延迟单元 x(k)
x(k)ε (k) ↔ X(z) x(k −1)ε (k) ↔ z−1X(z) + x(−1)
y(k)
X
第 5 页
优点: 优点:
•差分方程经 变换→代数方程； 差分方程经z变换 代数方程； 差分方程经 变换→ •将时域卷积→z域乘积； 将时域卷积→ 域乘积； 将时域卷积 域乘积 •部分分式展开后求解z逆变换较容易； 部分分式展开后求解z 部分分式展开后求解 逆变换较容易； •z变换过程自动引入了系统初始状态（相当于0变换过程自动引入了系统初始状态（相当于0 变换过程自动引入了系统初始状态 的条件） 可同时求出零输入和零状态响应。 的条件）,可同时求出零输入和零状态响应。 ， 注意：z域求解系统只需 －状态[y(-1)，y(-2), …,] 注意： 域求解系统只需0 状态 域求解系统只需 时域求解系统要递推出0 状态确定待定系数。 时域求解系统要递推出 ＋状态确定待定系数。
D z-1
X(k-1)
z-1X(z)
X
注意:z域框图只能求系统零状态响应 注意 域框图只能求系统零状态响应
第
例题
1.求如图系统的单位响应 求如图系统的单位响应h(k)和单位阶跃响应 和单位阶跃响应g(k) 求如图系统的单位响应 和单位阶跃响应
8 页
2. 知 阶 散 统 初 条 为 zi (0) = 2, yzi (1) =1 已 二 离 系 的 始 件 y , 当 入 (k) = ε (k)时 输 f , 1 5 k k 输 全 应 (k) =[ + 4⋅ 2 − ⋅ 3 ]ε (k), 出 响 y 2 2 求 差 方 .， 画 系 框 。 此 分 程 并 出 统 图
求解线性时不变离散系统的差分方程有两种方法： 求解线性时不变离散系统的差分方程有两种方法： •时域方法: y(k) =y zi (k) + yzs (k) yzs (k) = h(k) ∗ x(k) 时域方法: 时域方法 •z变换方法: 变换方法: 变换方法 Yzs (z) = H(z) ⋅ X(z)
X
第
二.系统框图的z域分析法
基本思路: 基本思路 时域框图 z域框图 域框图 z域代数方程 域代数方程 Yzs(z)
7 页
yzs(k)
x(k) ⇒ X (z) yzs (k) ⇒ Yzs (z) 延迟单元 x(k)
x(k)ε (k) ↔ X(z) x(k −1)ε (k) ↔ z−1X(z) + x(−1)
y(k)
X
第 5 页
优点: 优点:
•差分方程经 变换→代数方程； 差分方程经z变换 代数方程； 差分方程经 变换→ •将时域卷积→z域乘积； 将时域卷积→ 域乘积； 将时域卷积 域乘积 •部分分式展开后求解z逆变换较容易； 部分分式展开后求解z 部分分式展开后求解 逆变换较容易； •z变换过程自动引入了系统初始状态（相当于0变换过程自动引入了系统初始状态（相当于0 变换过程自动引入了系统初始状态 的条件） 可同时求出零输入和零状态响应。 的条件）,可同时求出零输入和零状态响应。 ， 注意：z域求解系统只需 －状态[y(-1)，y(-2), …,] 注意： 域求解系统只需0 状态 域求解系统只需 时域求解系统要递推出0 状态确定待定系数。 时域求解系统要递推出 ＋状态确定待定系数。
数字信号处理实验离散系统的Z域分析
数字信号处理实验报告实验名称：离散系统的Z 域分析学号：姓名： 评语： 成绩： 一、实验目的1、掌握离散序列z 变换的计算方法。
2、掌握离散系统系统函数零极点的计算方法和零极点图的绘制方法，并能根据零极点图分析系统的因果性和稳定性。
3、掌握利用MATLAB 进行z 反变换的计算方法。
二、实验原理与计算方法1、z 变换离散序列x (n )的z 变换定义为：。
∑∞-∞=-=n n z n x Z X )()(在MATLAB 中可以利用符号表达式计算一个因果序列的z 变换。
其命令格式为：syms n; f=(1/2)^n+(1/3)^n;ztrans(f)2、离散系统的系统函数及因果稳定的系统应满足的条件一个线性移不变离散系统可以用它的单位抽样响应h (n )来表示其输入与输出关系，即y (n )= x (n )* h (n )对该式两边取z 变换，得： Y (z )= X (z )· H (z )则： )()()(z X z Y z H =将H (z )定义为系统函数，它是单位抽样响应h (n )的z 变换，即∑∞-∞=-==n n z n h n h Z z H )()]([)(对于线性移不变系统，若n <0时，h (n )=0，则系统为因果系统；若，则系统稳∞<∑∞-∞=n n h |)(|定。
由于h (n )为因果序列，所以H (z )的收敛域为收敛圆外部区域，因此H (z )的收敛域为收敛圆外部区域时，系统为因果系统。
因为，若z =1时H (z )收敛，即∑∞-∞=-=n n z n h z H )()(，则系统稳定，即H(z)的收敛域包括单位圆时，系统稳定。
∞<=∑∞-∞==n z n h z H |)(||)(1因此因果稳定系统应满足的条件为：，即系统函数H (z )的所有极点全部落在1,||<∞≤<ααz z 平面的单位圆之内。
3、MATLAB 中系统函数零极点的求法及零极点图的绘制方法MATLAB 中系统函数的零点和极点可以用多项式求根函数roots ()来实现，调用该函数的命令格式为：p=roots(A)。
信号与系统第8章 离散时间系统的z域分析
零状态响应为
Yf
(z)
(1 z 1 z 2 ) 2 3z 1 z 2
1 1 z 1
1/ 6 0.5 5 / 6 1 z1 1 z1 1 0.5z1
yf [k] Z 1{Yf (z)}{1/ 6 0.5(1)k (5/ 6)(0.5)k}u[k]
y[k] yx[k] yf [k] {1/ 6 3.5(1)k (4 / 3)(0.5)k}u[k]
离散时间信号与系统的Z域分析
• 离散时间信号的Z域分析 • 离散时间系统的Z域分析 • 离散时间系统函数与系统特
性
离散时间信号的Z域分析
• 理想取样信号的拉普拉斯变换 • 单边Z变换定义 • 单边Z变换的收敛域 • 常用序列的Z变换 • 单边Z变换的性质 • Z反变换
理想取样信号的拉普拉斯变换
fs (t) f (t) (t kT) f (kT) (t kT)
Re(z)
三、常用序列的Z变换
1) Z{ (k)} 1, z 0
2) 3)
Z{u(k)} 1 1 z
Z{aku(k)}
1 , 1
1 a
z
z
1
1 z
a
4)
Z{e
j0k
u(k
)}
1
e
1
j0
z
1
z z e j0
5)
Z{e-
j0k u (k
)}
1
1 e- j0
z
1
z z e- j0
z e j0 z e j0
解代数方程
二阶系统响应的z域求解
y[k] a1 y[k 1] a2 y[k 2] b0 f [k] b1 f [k 1] k 0
初始状态为y[1], y[2] 对差分方程两边做Z变换，利用
7.离散时间信号与系统的z域分析
第七章离散时间系统的Z域分析7.1 学习要求1.熟练掌握信号的Z域分析方法：Z变换的定义、收敛区及基本性质，能够应用长除法和部分分式分解法求Z反变换。
2.掌握序列的傅里叶变换的定义和基本性质，并了解Z变换与拉普拉斯变换、傅里叶变换的关系。
3.掌握离散系统响应的Z变换分析方法：深刻理解离散系统的系统函数的概念，掌握离散时间系统的时域和Z域框图与流图描述形式。
7.2 学习重点1.z变换,z反变换定义、基本性质、计算方法。
2.离散时间系统的z域分析。
3.离散时间系统的频率响应特性。
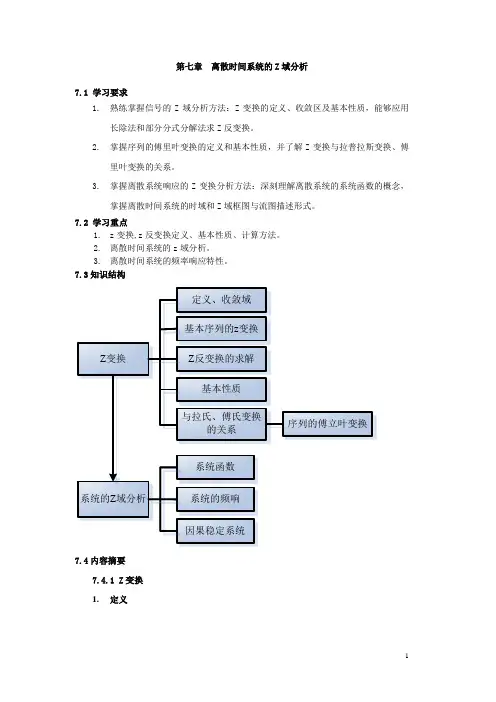
7.3知识结构7.4内容摘要7.4.1 Z变换1.定义∑∞-∞=-=n nz n x z X )()( 表示为：)()]([z X n x Z =。
2. 收敛域 (1) 有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他当0,021>>n n 时，收敛条件为0>z ；当0,021<<n n 时，收敛条件为∞<z ；当0,021><n n 时，收敛条件为∞<<z 0。
(2) 右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩当01>n 时，收敛域为1x R z >，1x R 为最小收敛半径；当01<n 时，收敛域为∞<<z R x 1。
(3) 左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他 当02<n ，收敛域为2x R z <，2x R 为最大收敛半径； 当02>n ，收敛域为20x R z <<。
(4) 双边序列双边序列指n 为任意值时,)(n x 皆有值的序列，即左边序列和右边序列之和。
其z 变换：∑∑∑∞=--∞=--∞-∞=-+==1)()()()(n n nnn nzn x zn x zn x z X双边序列的收敛域为一环形区域21x x R z R <<。
第6章 离散时间系统的z域分析
1 | z | 1 2 | z | 2
例 求序列f (k ) cosh (2k ) (k )的z变换。
1 2k 由于 cosh ( k ) (e e 2 k ) 2 2 在单边指数序列a k ( k )的z变换中令a e 2 , 可得 z e (k ) , | z || e 2 | z e2 根据z变换的线性性质可得
f (k )
3
f ( k ) ( k ) 3
2
2
1
1 o 1 2
f ( k 1) 3 2
k
1 o 1 2
f ( k 1) ( k ) 3 2
1
k
1
1 o 1 2
f ( k 1)
k
1 o 1 2
f ( k 1) ( k )
3
k
3
2 1
1 o 1 2
k
1 o 1 2
k
(1)双边Z变换的移位 若 f (k ) F ( z )
k 0
该式称为单边Z变换。
将f ( k )的Z变换简记为Z [ f ( k )] ，象函数F ( z )的逆z变换 简记为Z
1
[ F ( z )] f ( k )与F ( z )两者间的关系简记为 ，
f (k ) F ( z )
在拉普拉斯变换分析中重点讨论了单边拉普拉斯 变换，这是由于在连续时间系统中，非因果信号 的应用较少。 对于离散系统，非因果信号也有一定的应用范围， 因此对单、双边z变换都进行讨论。
a
b
O
Re(z )
6.1.3 常见序列的Z变换
(k )
1
O
k
(k ) 1
离散系统的Z域分析
z
k
cos(
0
k
)
k
z
z2 z2 z cos 2z2 2z cos 0
0
1
2
..........
k
sin 0k
k
z
2z2
z 2
sin 0 z cos 0
1 2
.........
k k
k
z (z )2k kk Nhomakorabea1
五、ZT & DTFT
求和收敛
设f(k)
为因果序列、则
F (e j ) f k e jk
Z eS Ts e e Ts jTs e j
k
F (z) f (k)zk k 0
e Ts
Ts
2 s
S 域中的一点→ → Z 域中的一点；Z 域中的一点→ → S 域中的无穷个点。
S 1 Ln z 1 Ln(e j ) 1 Ln j
Ts
Ts
Ts
Ts
三、收敛域: F (z) f k zk
ak (k) bk (k 1) z z ∣a∣< |z|< |b|
za zb
jIm[z]
|b|
|a|
o
Re[z]
四、常用 z 变换
(k+1) ←→z; (k-1) ←→z-1;……
(k) ←→1 (k) ←→z/(z-1) ←→ - (- k-1)
零、极 点分布
k k z k k 1
F(z)
K1 e j z
z e j
K1 e j z
z e j
若z> , f(k)=2K1kcos(k+)(k)，… …
(3) F(z)有重极点 推导记忆：
k
cos(
0
k
)
k
z
z2 z2 z cos 2z2 2z cos 0
0
1
2
..........
k
sin 0k
k
z
2z2
z 2
sin 0 z cos 0
1 2
.........
k k
k
z (z )2k kk Nhomakorabea1
五、ZT & DTFT
求和收敛
设f(k)
为因果序列、则
F (e j ) f k e jk
Z eS Ts e e Ts jTs e j
k
F (z) f (k)zk k 0
e Ts
Ts
2 s
S 域中的一点→ → Z 域中的一点；Z 域中的一点→ → S 域中的无穷个点。
S 1 Ln z 1 Ln(e j ) 1 Ln j
Ts
Ts
Ts
Ts
三、收敛域: F (z) f k zk
ak (k) bk (k 1) z z ∣a∣< |z|< |b|
za zb
jIm[z]
|b|
|a|
o
Re[z]
四、常用 z 变换
(k+1) ←→z; (k-1) ←→z-1;……
(k) ←→1 (k) ←→z/(z-1) ←→ - (- k-1)
零、极 点分布
k k z k k 1
F(z)
K1 e j z
z e j
K1 e j z
z e j
若z> , f(k)=2K1kcos(k+)(k)，… …
(3) F(z)有重极点 推导记忆：
第六章 离散系统的z域分析
3z 例： 2δ(k)+ 3ε(k) ←→ 2 + δ ε z −1
第1-12页 12页
z > 1
青岛科技大学信息科学技术学院
信号与系统 电子教案
6.2
z变换的性质 z变换的性质
二、移位特性
双边z 双边z变换
若： f (k) ←→F (z) ， α<z<β，且有整数 β 且有整数m>0， ， 则： f(k±m) ←→ z±mF(z)， α<z<β ± ， β
2 2
z > a
青岛科技大学信息科学技术学院
信号与系统 电子教案
6.2
z变换的性质 z变换的性质
四、卷积定理
若： f1 (k) ←→F1(z) ， α1<z<β1 β f2 (k) ←→F2(z) ， α2<z<β2 β 则： f1(k) * f2(k) ←→ F1(z)F2(z)， ， 例 收敛域至少为 相交部分 求单边序列 (k+1)akε(k)的z变换，(0<a<1)。 的 变换， 。 变换
三、z域尺度变换(序列乘ak) 域尺度变换(序列乘a
若： f (k) ←→F (z) ， α<z<β，且对整数m>0， β 且对整数 ， 则： ak f(k) ←→ F(z/a)， αa<z<βa ， β 变换。 例：求指数衰减正弦序列 aksin(βk)ε(k) 的z变换。 β 解:
6.1 z 变 换
b k , k < 0 f 2 (k ) = b k ε (−k − 1) = 0, k ≥ 0
解: 反因果序列的 变换为： 反因果序列的z变换为 变换为：
第1-12页 12页
z > 1
青岛科技大学信息科学技术学院
信号与系统 电子教案
6.2
z变换的性质 z变换的性质
二、移位特性
双边z 双边z变换
若： f (k) ←→F (z) ， α<z<β，且有整数 β 且有整数m>0， ， 则： f(k±m) ←→ z±mF(z)， α<z<β ± ， β
2 2
z > a
青岛科技大学信息科学技术学院
信号与系统 电子教案
6.2
z变换的性质 z变换的性质
四、卷积定理
若： f1 (k) ←→F1(z) ， α1<z<β1 β f2 (k) ←→F2(z) ， α2<z<β2 β 则： f1(k) * f2(k) ←→ F1(z)F2(z)， ， 例 收敛域至少为 相交部分 求单边序列 (k+1)akε(k)的z变换，(0<a<1)。 的 变换， 。 变换
三、z域尺度变换(序列乘ak) 域尺度变换(序列乘a
若： f (k) ←→F (z) ， α<z<β，且对整数m>0， β 且对整数 ， 则： ak f(k) ←→ F(z/a)， αa<z<βa ， β 变换。 例：求指数衰减正弦序列 aksin(βk)ε(k) 的z变换。 β 解:
6.1 z 变 换
b k , k < 0 f 2 (k ) = b k ε (−k − 1) = 0, k ≥ 0
解: 反因果序列的 变换为： 反因果序列的z变换为 变换为：
差分方程离散系统的z域分析法稳定性
A/D：模拟信号→数字信号，图中还包括 连续信号→离散信号的采样过程
D/A：数字信号→模拟信号，图中还包括 离散信号→连续信号的保持过程 计算机
r
e
数字
控制器
u(t) 执行
D/A
机构
受控 y(t)对象A/D Nhomakorabea测量
计算机控制系统原理图
4
计算机控制系统的主要特点
修改控制器结构及参数很方便（改变控制程序）； 便于实现各种先进控制，能完成复杂的控制任务； 控制精度高，抗干扰能力强，能有效抑制噪声； 有显示、报警等多种功能。 有利于实现“智能化”、“网络化”、“管控一体 化”、多级分布式控制等；
表示为为便于数学处理将2t2t实际上被保持器抵消了该系数在有保持器的系统中率特性系统的传递函不影响离散信号的频系数相差一个变换的角度看两者只脉冲为时刻的单位幅值时刻的单位幅值脉冲表示ntsst二采样信号的数学表达式变换即得到z变换是离散信号拉氏变换的有理式表达形式个采样时刻的取值的系数为信号在第n10仿真实验
z-n的系数为信号在第n个采样时刻的取值
Z变换只表达了连续函数在采样时刻的特性，不包含采样 时刻之间的信息。
对f(t) 采样后的 f (t) 是唯一的，但 f (t) 所对应的 f(t) 不 唯一； f (t) 与 F(z) 之间的变换是唯一的。
19
S平面与Z平面的对应关系：
根据Z变换定义，有 z eTs
而 uh( t ) 1( t ) - 1( t - T )
U( s ) ,
Uh(
s
)
1
- e-Ts s
零阶保持器实际的传递函数为
Gh (
s
)
离散信号与系统的Z域分析
序列相加减（线性加权）后，所得序列z变换的ROC，有 可能比原序列z变换的ROC大。位移特性常用来分析单边 周期信号，单边周期信号总具有相似的形式。
8 离散信号与系统的 Z 域分析 p 16
例： F(z) = 1/(za) |z| a 求f [k]。 解：
1 F ( z) z 1 1 az
z 例： (3) u[k ] , z 3 z 3
k
类似于傅氏、拉氏变换的尺度变换特性。
1 1 s L f (at ) F ( j ) f (at ) F ( ), a a a a
F
8 离散信号与系统的 Z 域分析 p 18
a 0, a 0
例*：求aksin(0k) u[k] 的z变换及收敛域
1 cos 0 z 1 1 2 z 1 cos 0 z 2 sin 0 z 1 1 2 z 1 cos 0 z 2
五、单边z变换的主要性质
f [k ] F ( z), z R f
f1[k ] F1 ( z), z R f 1
1 2
sin 0 z 1 za 2 2 z 1 cos 0 z 2
8 离散信号与系统的 Z 域分析 p 19
五、单边z变换的主要性质
4. z域微分特性（时域线性加权）
dF ( z ) kf [k ] z dz
Z
Z Rf
m d m d F ( z) Z m m 或写成 : ( z ) F ( z ) k f [k ] ( z ) m dz dz
2 2
8 离散信号与系统的 Z 域分析 p 13
五、单边z变换的主要性质
2. 位移特性(记忆)
因果序列的位移
8 离散信号与系统的 Z 域分析 p 16
例： F(z) = 1/(za) |z| a 求f [k]。 解：
1 F ( z) z 1 1 az
z 例： (3) u[k ] , z 3 z 3
k
类似于傅氏、拉氏变换的尺度变换特性。
1 1 s L f (at ) F ( j ) f (at ) F ( ), a a a a
F
8 离散信号与系统的 Z 域分析 p 18
a 0, a 0
例*：求aksin(0k) u[k] 的z变换及收敛域
1 cos 0 z 1 1 2 z 1 cos 0 z 2 sin 0 z 1 1 2 z 1 cos 0 z 2
五、单边z变换的主要性质
f [k ] F ( z), z R f
f1[k ] F1 ( z), z R f 1
1 2
sin 0 z 1 za 2 2 z 1 cos 0 z 2
8 离散信号与系统的 Z 域分析 p 19
五、单边z变换的主要性质
4. z域微分特性（时域线性加权）
dF ( z ) kf [k ] z dz
Z
Z Rf
m d m d F ( z) Z m m 或写成 : ( z ) F ( z ) k f [k ] ( z ) m dz dz
2 2
8 离散信号与系统的 Z 域分析 p 13
五、单边z变换的主要性质
2. 位移特性(记忆)
因果序列的位移
离散信号与系统的 Z 域分析
第 六 章 离散信号与系统的 Z 域分析引言与线性连续系统的频域分析和复频域分析类似，线性离散系统的频域分析是输入信号分解为基本信号e jΩk 之和,则系统的响应为基本信号的响应之和。
这种方法的数学描述是离散时间傅里叶变换和逆变换。
如果把复指数信号e jΩk 扩展为复指数信号Z k ,Z=re jΩ ,并以Zk 为基本信号， 把输入信号分解为基本信号Z k 之和， 则响应为基本信号Z k 的响应之和。
这种方法的数学描述为Z 变换及其逆变换,这种方法称为离散信号与系统的Z 域分析法.如果把离散信号看成连续时间信号的 抽样值序列，则Z 变换可由拉普拉斯变换引入.因此离散信号与系统的Z 域分析 和连续时间信号与系统的复频域分析有许多相似之处.通过Z 变换，离散时间信 号的卷积运算变成代算,离散时间系统的差分方程变成Z 域的代数方程,因此可 以比较方便的分析系统的响应。
Z 变换从拉普拉斯变换到Z 变换对连续信号f(t)进行理想抽样，即f（t）乘以单位冲击序列δT （t），T 为 抽样间隔，得到抽样信号为f s （t）=f（t）δT （t）= =对fs（t）取双边拉普拉斯变换，得F s （s）=￡[fs（t）]=令z=e sT , 则Fs（s）=F(z) ,得F（z）=因为T为常数,所以通常用f(k)表示f(kT),于是变为F(z)=称为f(k)的双边Z变换,z为复变量。
z和s的关系为:z=e sTs=（1/T）㏑z由复变函数理论,可以得到f(k)= ∮cF(z)z k-1 dz式(7.1-5)称为F(z)的双边Z逆变换(后面讨论).双边Z变换的定义和收敛域§双边 Z 变换的定义对于离散序列f(k)(k=0,±1,±2,┄),函数(z的幂级数)F(z)=称为f(k)的双边Z变换,记为F(z)=Z[f(k)].F(z)又称为f(k)的象函数,f(k)又 称为F(z)的原函数.为了表示方便,f(k)与F(z)之间的对应关系可表示为 f(k) F(z)§双边 Z 变换的收敛域f(k)的双边Z变换为一无穷级数,因此存在级数是否收敛的问题.只有当 (7.1-6)式的级数收敛,F(z)才存在.F(z)存在或级数收敛的充分条件是 ∞在f(k)给定的条件下,式(7.1-6)级数是否收敛取决于z的取值.在z复平面上, 使级数收敛的z取值区域称为F(Z)的收敛域。
北京理工大学信号与系统实验报告6离散时间系统的z域分析
北京理工大学信号与系统实验报告6-离散时间系统的z域分析————————————————————————————————作者：————————————————————————————————日期：实验6 离散时间系统的z 域分析（综合型实验）一、 实验目的1） 掌握z 变换及其反变换的定义,并掌握ＭAT ＬＡＢ实现方法。
2） 学习和掌握离散时间系统系统函数的定义及z 域分析方法。
3） 掌握系统零极点的定义,加深理解系统零极点分布与系统特性的关系。
二、 实验原理与方法 1. z 变换序列(n)x 的z 变换定义为(z)(n)znn X x +∞-=-∞=∑ (1）Z 反变换定义为11(n)(z)z 2n rx X dz jπ-=⎰(2）MA ＴＬA Ｂ中可采用符号数学工具箱z ｔrans 函数和ｉz ｔｒans 函数计算z 变换和z 反变换： Z=ztran ｓ（Ｆ）求符号表达式Ｆ的z 变换。
Ｆ=iztra ｎｓ（Z)求符号表达式Z 的ｚ 反变换 2. 离散时间系统的系统函数离散时间系统的系统函数H(z)定义为单位抽样响应ｈ(n)的z 变换(z)(n)znn H h +∞-=-∞=∑ (３）此外连续时间系统的系统函数还可由系统输入与输出信号z 变换之比得到(z)(z)/X(z)H Y = (4)由(4）式描述的离散时间系统的系统时间函数可以表示为101101...(z)...MM NN b b z b z H a a z a z----+++=+++ (5） 3. 离散时间系统的零极点分析ＭＡTLAB 中可采用roots 来求系统函数分子多项式和分母多项式的根，从而得到系统的零极点。
此外还可采用MATL ＡB 中zpl ａne 函数来求解和绘制离散系统的零极点分布图,zp ｌane 函数的调用格式为：zplane(b,a) ｂ、a 为系统函数分子分母多项式的系数向量(行向量) zplane （z,p) z 、ｐ为零极点序列(列向量) 系统函数是描述系统的重要物理量，研究系统函数的零极点分布不仅可以了解系统单位抽样响应的变化,还可以了解系统频率特性响应以及判断系统的稳定性; 系统函数的极点位置决定了系统的单位抽样响应的波形，系统函数零点位置只影响冲激响应的幅度和相位，不影响波形。
第五章 Z域分析
m
m 1
x(k ) z
max( R 11 , R 21 ) z
2. 位移性
a. 双边Z变换
则
x(n) X ( z )
m
x(n m ) z
X ( z ), m 为整数
收敛域：1）不包括
0，
处，收敛域不变 处，需重新判断
2） 包括 0，
证明: z [ x ( n m )] 令k=n+m
z [ x ( n m )] z
x ( n )u ( n ) x ( z )
m
则
x ( n m )u ( n ) z [ X ( z )
m 1
x(k ) z
k
]
k 0
证明：
z [ x ( n m ) u ( n )]
x(n m ) z
n
n0
令k=n+m 则：
z [ x ( n m ) u ( n )] z [ X ( z )
a. X(z)/z 有N个单极点
则：
Z1 Z N
X z
N
Ai z z zi
i0
Ai
X (z) z
( z zi )
z zi
b X(z)有一个r阶重极点
X z A0
Z1
j
d
r
Ajz ( z z1 )
(r j) (r j)
j 1
z
1<|z|<2
k2
k 1
( k 1)
z ( z 2)
2
|z|<2
2 ( k 1)
m 1
x(k ) z
max( R 11 , R 21 ) z
2. 位移性
a. 双边Z变换
则
x(n) X ( z )
m
x(n m ) z
X ( z ), m 为整数
收敛域：1）不包括
0，
处，收敛域不变 处，需重新判断
2） 包括 0，
证明: z [ x ( n m )] 令k=n+m
z [ x ( n m )] z
x ( n )u ( n ) x ( z )
m
则
x ( n m )u ( n ) z [ X ( z )
m 1
x(k ) z
k
]
k 0
证明：
z [ x ( n m ) u ( n )]
x(n m ) z
n
n0
令k=n+m 则：
z [ x ( n m ) u ( n )] z [ X ( z )
a. X(z)/z 有N个单极点
则：
Z1 Z N
X z
N
Ai z z zi
i0
Ai
X (z) z
( z zi )
z zi
b X(z)有一个r阶重极点
X z A0
Z1
j
d
r
Ajz ( z z1 )
(r j) (r j)
j 1
z
1<|z|<2
k2
k 1
( k 1)
z ( z 2)
2
|z|<2
2 ( k 1)
信号与系统 第六章离散系统的Z域分析
j
Z平面
k 1 k (1 z ) ( 3z ) 3 k 1 k 0
0
|z|<3时，第一项收敛于
z ，对应于左边序列。 z 3 z |z|>1/3时，第二项收敛于 ，对应于右边序列。 1 收敛域 z3
1 3
3
1 当 | z | 3 时, 3
8 z z 3 z F ( z) 1 z 3 z 3 ( z 3)( z 1 3)
应用尺度变换:
k
sin k (k )
z a
z sin z 2 2 z cos 1
0< a <1
sin a z sin a sin k (k ) z 2 z ( a ) 2( a ) cos 1 z 2 2 a z cos a 2
§6.2
Z变换的性质
| k-3|(k)
解：（1） F z
k k k z 1
k 1
（2） 双边z变换： F z
k
f k z
k
2 1 z 2z 3 2 z z
2
0 z
单边z变换： F z f k z
k 0
长春理工大学
零点：0 极点：3，1/3
§6.1
Z 变换
Z变换的收敛域
收敛域内不包含任何极点，在极点处，F(z)为无穷大， Z变换不收敛。 有限长序列的收敛域为整个Z平面, 可能不含z=0, z=。 因果有限长序列： F(z)=f (1)z -1+ f (2)z -2+· · · · |z|>0 反因果有限长序列： F(z)=f (-1)z 1+ f (-2)z2+· · · · |z|< 如果是因果序列，收敛域为|z|>0圆的外部。 如果是左边序列，收敛域为|z|<0 。 如果是双边序列，收敛域由圆环组成。
Z平面
k 1 k (1 z ) ( 3z ) 3 k 1 k 0
0
|z|<3时，第一项收敛于
z ，对应于左边序列。 z 3 z |z|>1/3时，第二项收敛于 ，对应于右边序列。 1 收敛域 z3
1 3
3
1 当 | z | 3 时, 3
8 z z 3 z F ( z) 1 z 3 z 3 ( z 3)( z 1 3)
应用尺度变换:
k
sin k (k )
z a
z sin z 2 2 z cos 1
0< a <1
sin a z sin a sin k (k ) z 2 z ( a ) 2( a ) cos 1 z 2 2 a z cos a 2
§6.2
Z变换的性质
| k-3|(k)
解：（1） F z
k k k z 1
k 1
（2） 双边z变换： F z
k
f k z
k
2 1 z 2z 3 2 z z
2
0 z
单边z变换： F z f k z
k 0
长春理工大学
零点：0 极点：3，1/3
§6.1
Z 变换
Z变换的收敛域
收敛域内不包含任何极点，在极点处，F(z)为无穷大， Z变换不收敛。 有限长序列的收敛域为整个Z平面, 可能不含z=0, z=。 因果有限长序列： F(z)=f (1)z -1+ f (2)z -2+· · · · |z|>0 反因果有限长序列： F(z)=f (-1)z 1+ f (-2)z2+· · · · |z|< 如果是因果序列，收敛域为|z|>0圆的外部。 如果是左边序列，收敛域为|z|<0 。 如果是双边序列，收敛域由圆环组成。
离散系统的Z域分析
F(z)
2、系统函数的求解 （1）由定义求 （2）已知差分方程 y(n) a1y(n 1) aN y(n N ) b0 f (n) b1 f (n 1) bM f (n M )
离散时间信号与系统的Z域分析
在零状态条件下有：
Yf (z) a1z1Yf (z) aN zNYf (z)
y1(n) D
2
+
6 _
y(n)
解： 由框图得
y1(n) f (n) 2 y1(n 1)
y(n) y1(n) 6 y1(n 1)
离散时间信号与系统的Z域分析
在零状态下，取Z变换得
Y1(z) F (z) 2z1Y1(z)
Yf (z) Y1(z) 6z1Y1(z)
F (z) (2z1 1)Y1(z) Yf (z) (1 6z1)Y1(z)
b0F (z) b1z1F (z) bM zM F (z)
6-19
源码
故：
H
(z)
Yf (z) F(z)
b0 b1z1 ... bM zM 1 a1z1 ... aN zN
6-20 源码
（3）已知 h(n)
6-21
源码
h(n) H (z)
6-22
源码
离散时间信号与系统的Z域分析
例2 系统框图如图所示，
离散时间信号与系统的Z域分析
信号与系统分析
（2）由于
H (z) z2 z[ z ] z[ 1 1 ]
z2 2z 1 (z 1)2
(z 1)2 z 1
故 h(n) (n 1)(1)nU (n)
离散时间信号与系统的Z域分析
例3 如图所示离散系统，当输入f (n) (2)nU (n)
求其零状态响应 y f (n)
2、系统函数的求解 （1）由定义求 （2）已知差分方程 y(n) a1y(n 1) aN y(n N ) b0 f (n) b1 f (n 1) bM f (n M )
离散时间信号与系统的Z域分析
在零状态条件下有：
Yf (z) a1z1Yf (z) aN zNYf (z)
y1(n) D
2
+
6 _
y(n)
解： 由框图得
y1(n) f (n) 2 y1(n 1)
y(n) y1(n) 6 y1(n 1)
离散时间信号与系统的Z域分析
在零状态下，取Z变换得
Y1(z) F (z) 2z1Y1(z)
Yf (z) Y1(z) 6z1Y1(z)
F (z) (2z1 1)Y1(z) Yf (z) (1 6z1)Y1(z)
b0F (z) b1z1F (z) bM zM F (z)
6-19
源码
故：
H
(z)
Yf (z) F(z)
b0 b1z1 ... bM zM 1 a1z1 ... aN zN
6-20 源码
（3）已知 h(n)
6-21
源码
h(n) H (z)
6-22
源码
离散时间信号与系统的Z域分析
例2 系统框图如图所示，
离散时间信号与系统的Z域分析
信号与系统分析
（2）由于
H (z) z2 z[ z ] z[ 1 1 ]
z2 2z 1 (z 1)2
(z 1)2 z 1
故 h(n) (n 1)(1)nU (n)
离散时间信号与系统的Z域分析
例3 如图所示离散系统，当输入f (n) (2)nU (n)
求其零状态响应 y f (n)
第七章 离散信号与系统的Z域分析
f (k ) 3k (k 1) 3k (k 2)
31 3k 1 (k 1) 32 3k 2 (k 2)
由表7.1
根据双边Z变换位移性质，得： z z2 3k 1 (k 1) z z 3 z 3
z 3 (k ) z 3
(2) 无限长因果序列双边Z变换的收敛域为|z|>|z0|，z0为复数、虚数或实数， 即收敛域为半径为|z0|的圆外区域。 (3) 无限长反因果序列双边Z变换的收敛域为|z|<|z0|，即收敛域为以|z0|为 半径的圆内区域。
(4) 无限长双边序列双边Z变换的收敛域为|z1|<|z|<|z2|，即收敛域位于以|z1| 为半径和以|z2|为半径的两个圆之间的环状区域。
k 0
f (i) z
( i m )
z
1
m
i m
f (i) z
i
z [ f (i) z
m i i 0
i m
f (i) z
1
i
]
z m [ F ( z )
i m
f (i) z i ]
z
7.2 Z变换的性质
例 7.2-3 已知f(k)=3k［ε(k+1)-ε(k-2)］，求f(k)的双边Z变换 及其收敛域。 解： f(k)可以表示为
(5) 不同序列的双边Z变换可能相同，即序列与其双边Z变换不是一一对 应的。序列的双边Z变换连同收敛域一起与序列才是一一对应的。
7.1 Z 变 换
7.1.3 常用序列的双边Z变换
(1) f (k ) (k )
F ( z)
k
(k ) z k (0) z 0 1
第六章离散系统的Z域分析
z z F (z) （ a z b ） za zb
a z 当 1且 1即a z b 收敛 z b
j Im [z ]
b
0
a
Re [ z ]
5
由上可知 （1） z变换的收敛域与f(k) 与z值的范围有关，两 个不同的序列由于收敛域不同可能对应于同一个z 变换，为了单值的确定z变换对应的序列，在给出 序列的z变换式的同时，必须明确其收敛域。
m
n m
f (n)z
1
n m
f (n)z
n
1
n
]
]
14
z f ( k m ) ( k ) f ( k m )z
k 0
k
z
m
f (k m )z
k 0
( k m )
z
m
z [ f ( n)z
n 0
m m 1 n 0
据定义
zkf ( k )
k 1
z ( kz
k
d k d z z f (k ) z F ( z ) dz k dz
时域序列线性加权的z变换为原序列象函数微 20 分后乘以（z）
kf (k )z dz ) f ( k ) z [ dz
k k
k
k
] f (k )
推广：
m
d m k f ( k ) ( z ) F ( z ) ( 1 z 2 ) dz
d m ( z ) F ( z )表示对F ( z )求导并乘以 ( z )共m次 dz
z 例4、 若 已 知 z[ ( k )] ,求 斜 变 序 列 k ( k )的z变 换 z 1
第10章 离散时间信号与系统的Z域分析
例： 已知 f (n) a 解
n m 1
n
n
u (m 1),
m 1
n
求f(n)的双边Z变换F(z)。
u (m 1) u (m 1)
m
n
z 1 u ( n 1) z z 1 z 1
1
|z|>1
根据部分和性质，则
z u (m 1) m u (m 1) ( z 1) 2 m 1
x( n)un
4 4 x( n 2)u( n) 4 x ( n 2)u( n)
1O 1
n
1O 1
n
1O 1
n
xn mun, xn mun较xnun的长度有所增减。
若x(n)为双边序列，并 x(n)U(n) X(z)，则
1 n x(n m)U (n) z X ( z ) x(n) z n m m
12
4、时域卷积定理：
若
f1 (n) F1 ( z )
f 2 ( n) F2 ( z )
R x1 Z R x 2
R y1 Z R y 2
则 f1 (n) * f 2 (n) F1 ( z ) F2 ( z )
max( R x 1 , R y 1 ) z min( R x 2 , R y 2 )
f ( n) z n
收敛域
不同f(n)的z变换，由于收敛域不同，可能对应于相同的z变换，故在
确定z变换时，必须指明收敛域。
例：
a n f1 (n) 0
n n 0
n0 n0
a z
n n 0 n
j Im( z )
n m 1
n
n
u (m 1),
m 1
n
求f(n)的双边Z变换F(z)。
u (m 1) u (m 1)
m
n
z 1 u ( n 1) z z 1 z 1
1
|z|>1
根据部分和性质，则
z u (m 1) m u (m 1) ( z 1) 2 m 1
x( n)un
4 4 x( n 2)u( n) 4 x ( n 2)u( n)
1O 1
n
1O 1
n
1O 1
n
xn mun, xn mun较xnun的长度有所增减。
若x(n)为双边序列，并 x(n)U(n) X(z)，则
1 n x(n m)U (n) z X ( z ) x(n) z n m m
12
4、时域卷积定理：
若
f1 (n) F1 ( z )
f 2 ( n) F2 ( z )
R x1 Z R x 2
R y1 Z R y 2
则 f1 (n) * f 2 (n) F1 ( z ) F2 ( z )
max( R x 1 , R y 1 ) z min( R x 2 , R y 2 )
f ( n) z n
收敛域
不同f(n)的z变换，由于收敛域不同，可能对应于相同的z变换，故在
确定z变换时，必须指明收敛域。
例：
a n f1 (n) 0
n n 0
n0 n0
a z
n n 0 n
j Im( z )
§6.4 离散系统的Z域分析
z 2z 9z 8z z2 z z4 2 Y ( z) 1 2 z 5z 6 z 4 z 2 z 3 z 4 1 5z 6 z
y(k ) [2(2) k 9(3) k 8(4) k ]U (k )
1 k 例2： 已知h(k ) ( ) U (k ), f (k ) G5 (k ), 求系统零状态响应 f (k ). y 2 z z z 2z z 5 解： H ( z ) )(1 z ) [ ](1 z 5 ) Y ( z) H ( z) F ( z) ( )( 1 z 1 z 1 z 1 z 1 z 2 2 2
i N
1
y (i) z i
a N a N 1 z 1 a0 z N
3）求反变换，得差分方程时域解。
Y ( z ) y (k )
信号与系统
例： 已知某线性时不变系统数学模型如下： y(k)-5y(k-1)+6y(k-2)=0 初始状态y(-1)=4，y(-2)=1，求零输入响应y(k)。 解： 对差分方程进行Z变换(用移序性质) ；
z z 5 F ( z) z z 1 z 1
1 k 1 k 5 y f (k ) [2 ( ) ]U (k ) [2 ( ) ]U (k 5) 2 2
信号与系统
3、全响应Z域求解： y (k ) y x (k ) y f (k ) 例1： 已知系统框图，列出系统的差分方程；
2
4
信号与系统
y(n) x(n) 2 y(n 1) 4 y(n 2) y(n) 2 y(n 1) 4 y(n 2) x(n) n (n 2) 2为二阶差分方程 后向差分方程
第五章 离散系统的z域分析
(3) ZT[δ (n +1)] = ∑δ (n +1)z + ∑δ (n +1)z
n=−∞ n=0
= z1 + 0 = z
(0 ≤ z < ∞)
Lanzhou University of Technology
ZT [u (n)] = ∑ u (n) z
单位阶跃序列 ∞
n =0
−n
斜变序列
1 z = = −1 1− z z −1
k
(k )
2k k p 0 = 1 k k ≥ 0 2
变换。 求 f (k ) = f1 ( k ) − f2 ( k ) 的Z变换。 变换
Lanzhou University of Technology
z f 1 (k ) = ε (k ) ↔ z −1 z 1 ε (k ) ↔ z− 2
*即满足均匀性与叠加性； 即满足均匀性与叠加性； 均匀性 收敛域为两者重叠部分。 重叠部分 *收敛域为两者重叠部分。
Lanzhou University of Technology
例： 设有阶跃序列 f 1 ( k ) = ε ( k ) 和双边指数衰 减序列
f2
(k ) = (2 )
k
1 ε (− k − 1 ) + ε 2
k k 1 2
z f1 1 z f 2 z p 2
−z (2 ) ε (− k − 1 ) ↔ z−2 利用线性性质
k
z −z 1 k f 2 (k ) = ε (k ) + (2 ) ε (− k − 1 ) ↔ + 1 z− 2 z−2 2 − 3z 2 = (z − 1 )(z − 2 ) 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验名：离散系统的Z 域分析一、实验目的1、掌握离散序列z 变换的计算方法。
2、掌握离散系统系统函数零极点的计算方法和零极点图的绘制方法，并能根据零极点图分析系统的因果性和稳定性。
3、掌握利用MATLAB 进行z 反变换的计算方法。
二、实验原理与计算方法1、z 变换离散序列x (n )的z 变换定义为：∑∞-∞=-=n nzn x Z X )()(。
在MA TLAB 中可以利用符号表达式计算一个因果序列的z 变换。
其命令格式为： syms n;f=(1/2)^n+(1/3)^n; ztrans(f)2、离散系统的系统函数及因果稳定的系统应满足的条件一个线性移不变离散系统可以用它的单位抽样响应h (n )来表示其输入与输出关系，即y (n )= x (n )* h (n )对该式两边取z 变换，得： Y (z )= X (z )· H (z )则： )()()(z X z Y z H =将H (z )定义为系统函数，它是单位抽样响应h (n )的z 变换，即∑∞-∞=-==n nzn h n h Z z H )()]([)(对于线性移不变系统，若n <0时，h (n )=0，则系统为因果系统；若∞<∑∞-∞=n n h |)(|，则系统稳定。
由于h (n )为因果序列，所以H (z )的收敛域为收敛圆外部区域，因此H (z )的收敛域为收敛圆外部区域时，系统为因果系统。
因为∑∞-∞=-=n nzn h z H )()(，若z =1时H (z )收敛，即∞<=∑∞-∞==n z n h z H |)(||)(1，则系统稳定，即H(z)的收敛域包括单位圆时，系统稳定。
因此因果稳定系统应满足的条件为：1,||<∞≤<ααz ，即系统函数H (z )的所有极点全部落在z 平面的单位圆之内。
3、MA TLAB 中系统函数零极点的求法及零极点图的绘制方法MATLAB 中系统函数的零点和极点可以用多项式求根函数roots ()来实现，调用该函数的命令格式为：p=roots(A)。
其中A 为待求根多项式的系数构成的行向量，返回向量p 是包含该多项式所有根位置的列向量。
如：求多项式8143)(2++=z z z A 的根的MA TLAB 命令为：A=[1 3/4 1/8]; p=roots(A) 运行结果为： p=-0.5000 -0.2500 也可以用[z,p,k]=tf2zp(B,A)函数求得。
其中z 为由系统的零点构成的向量，p 为由系统的极点构成的向量，k 表示系统的增益；B 、A 分别为系统函数中分子分母多项式的系数向量。
离散系统的系统函数可能有两种形式，一种是分子和分母多项式均按z 的正次幂降幂排列，如12232)(23431+++++=z z z z zz z H ，另一种是分子分母多项式均按z 的负次幂升幂排列，如2112412111)(---+++=z z z z H ，在构造多项式系数向量时，分子和分母多项式系数向量的维数一定要相同，缺项用0补齐。
对于H 1(z )其分子多项式的系数向量应为：B=[0 1 0 2 0]；分母多项式的系数向量应为：A=[1 3 2 2 1]。
对于H 2(z )其分子多项式的系数向量应为：B=[1 1 0]；分母多项式的系数向量应为：A=[1 1/2 1/4]。
绘制系统函数的零极点图可由MATLAB 中的zplane 函数实现。
该函数的调用方法为：zplane(B,A)或者zplane(z,p,k)，其中B ，A ，z ，p ，k 的含义与tf2zp 函数相同。
若调用zplane(B,A)绘图，则首先将系统函数中分子分母多项式变换成按z 的正次幂降幂排列的系数向量，再求零极点。
4、z 反变换的计算方法z 反变换可由部分分式展开法求得。
由于指数序列a n u (n )的z 变换为az z-，因此求反变换时，通常对zz X )(进行展开：kk z z A z z A z z A z z X -+-+-=Λ2211)( 其中),2,1()()(k i z z X z z A i z z i i Λ=-==称为有理函数zz X )(的留数。
分两种情况进行讨论：（1）X (z )的所有极点均为单实极点此时kk z z z A z z zA z z z A z X -+-+-=Λ2211)(，则X (z )的z 反变换为： ∑=⋅+=ki n i i z A A n x 10)()(（2）X (z )有共轭极点设X (z )有一对共轭极点βαj e p ±=2,1，则k k z z z A z z zA p z z r p z z r z X -+-+--=Λ112211)(，其中留数的计算方法与单极点相同，即θj p z e r zz X p z r ||)()(1111=-==，r 2=r 1 *因此，只要求出zz X )(部分分式展开的系数（留数），就可以直接求出X (z )的z 反变换x (n )。
在MA TLAB 中可利用函数residue()求解。
令B 和A 分别是zz X )(的分子和分母多项式构成的系数向量，则函数[r,p,k]=residue (B,A)将产生三个向量r 、p 、k ，其中r 为包含zz X )(部分分式展开系数r i (i =1,2,…,N )的列向量，p 为包含zz X )(所有极点的行向量，k 为包含zz X )(部分分式展开的多项式项的系数c j (j =1,2,…,M -N )的列向量，若M ≤N ，则k 为空阵。
用residue()函数求出zz X )(部分分式展开的系数后，便可根据其极点位置分布情况直接求出X (z )的反变换x (n )。
如：已知23)(22++=z z z z X ，求其z 反变换x (n )。
首先利用residue()函数求出23)(2++=z z zz z X 的部分分式展开的系数和极点，相应的MATLAB 命令为： B=[0 1 0]; A=[1 3 2];[r,p,k]=residue (B,A) 运行结果为： r = 2 -1 p = -2 -1 k =[ ]由以上结果可得：1122)(+-++=z z z X ；即X (z )只有两个单极点，其z 反变换为：[])()1()2(2)(n u n x nn ---=。
已知122)(232-+-+=z z z zz z X ，求其z 反变换x (n )。
利用residue()函数求出1221)(23-+-+=z z z z z z X 的部分分式展开的系数和极点，可得：B=[0 0 1 1]; A=[1 -2 2 -1];[r,p,k]=residue (B,A) r =2.0000 -1.0000 + 0.0000i -1.0000 - 0.0000i p =1.0000 0.5000 + 0.8660i 0.5000 - 0.8660i k =[ ]可见，zz X )(包含一对共轭极点，用abs()和angle()函数即可求出共轭极点的模和相位，相应命令为： p1=abs(p') p1 =1.0000 1.0000 1.0000 a1=angle(p')/pi a1 =0 -0.3333 0.3333即共轭极点为：32,1πjep ±=，则12)(33-+--+--=-z z ez z ez z z X jjππ，其z 反变换为：)(23cos 2)(n u n n x ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=π三、实验内容（1）求下列序列的z 变换：2-n u (n )；-(1/2)n u (n )；(1/2)n +(1/3)n u (n )①2-n u (n )的Z 变换程序如下：syms n ; f=(1./2)^(n) ztrans(f)结果为：f = (1/2)^n ans =2*z/(2*z-1) ②-(1/2)nu (n )的Z 变换程序为：syms n ; f=-(1./2)^(n) ztrans(f)结果为：f = -(1/2)^n ans =-2*z/(2*z-1) ③(1/2)n+(1/3)n u (n )因为是非因果系统，所以Z[(1/2)n +(1/3)n u (n )]=()()23nn n n u n z ∞---=-∞+∑=331zz - （2）已知两个离散因果系统的系统函数分别为：142)(2321+-++=z z z z z z H ；2132122112)(-----+++-=zz z z z z H 分别求出各系统的零极点，绘制零极点图，分析系统的稳定性；求出各系统单位抽样响应。
① 程序为：A=[1 2 -4 1] B=[0 1 1 0][z,p,k]=tf2zp(B,A)%求零极点[r,p,k]=residue (B,A)%部分分式展开的系数和极点 zplane(B,A)零极点为 ：z = 0 -1 p =-3.3028 1.0000 0.3028零极图为：稳定性：由上图看出收敛域不包括单位圆，即不是稳定系统 系统抽样响应： 由下得r =0.4902 0.6667 -0.1569 p =-3.3028 1.0000 0.3028 k = []3028.01569.016667.03028.30.4902)(1--+-++=z z z z H 系统抽样响应为：h （n ）=()()[])(3028.01569.06667.0)3028.3(4902.0)(n u n h nn-+-=② 程序为：A=[1 1 1/2 0] B=[0 2 -1 1][z,p,k]=tf2zp(B,A)%求零极点[r,p,k]=residue (B,A)%部分分式展开的系数和极点 p1=abs(p') a1=angle(p')/pi zplane(B,A)零极点为 ： z =0.2500 + 0.6614i 0.2500 - 0.6614i p =0 -0.5000 + 0.5000i -0.5000 - 0.5000i k = 2 零极图为：稳定性：由上图看出收敛域包括单位圆，所以系统稳定 系统抽样响应： 由r =-0.0000 + 3.0000i -0.0000 - 3.0000i 2.0000 p =-0.5000 + 0.5000i -0.5000 - 0.5000i 0含一对共轭极点，用abs()和angle()函数即可求出共轭极点的模和相位 p1 =0.7071 0.7071 0 a1 =-0.7500 0.7500 0 即共轭极点为：432,1πj ep ±=，则12)(4343-+--+--=-z z ez z ez z z X j j ππ，其z 反变换为：)(243cos 2)(n u n n x ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=π及为系统的抽样响应。