纯弯曲梁的正应力试验

实验二、纯弯曲梁正应力电测实验一、 实验目的1、 电测法测定纯弯曲梁正应力分布规律。

2、验证纯弯曲梁正应力计算公式。

二、 实验装置与仪器1、 纯弯曲梁实验装置。

2、 数字式电阻应变仪。

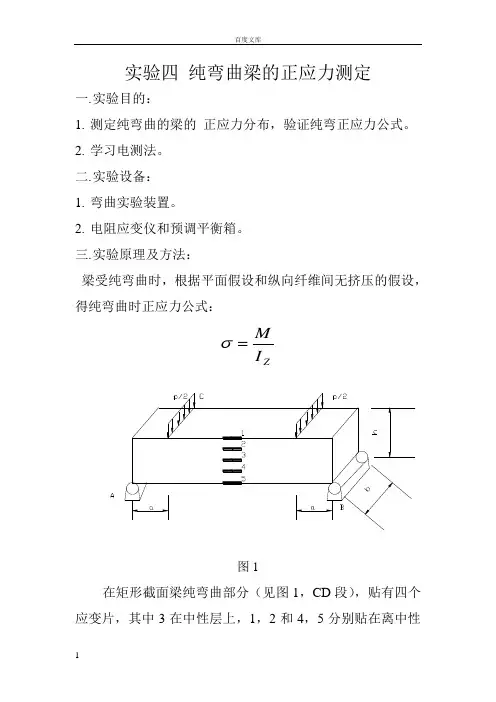
三、 实验装置与实验原理1、实验装置弯曲梁试验装置如图1所示。

它有弯曲梁1，定位板2，支座3，试验机架4，加载系统5，两端带万向接头的加载杆6，加载压头（包括φ16钢珠）7，加载横梁8，载荷传感器9和测力仪10等组成。

该装置有已粘贴好应变片的钢梁（其弹性模量2210m GNE =）用来完成纯弯曲梁正应变分布规律试验。

纯弯曲梁正应变分布规律试验纯弯曲梁受力状态及有关尺寸见图2。

图 2在梁的纯弯曲段内已粘贴好两组应变片，每组8片，分别为1～8号片和1*～8*号片，各片距中心层的距离在图3中已标出。

当梁受力变形后，可由应变仪测出每片应变片产生的应变，这样就可得到实测的沿梁横截面高度的正应变分布规律。

根据材料力学中纯弯曲梁的平面假设，沿梁横截面高度的正应变分布规律应当是直线。

另外材料力学中还假设梁在纯弯曲段内是单向应力状态，为此，我们在梁的下表面粘贴有与7号片和7*号片垂直的8号片和8*号片，当梁受力变形后，可测得8ε和*8ε，根 据泊松比纵横εεμ=，可由78εε或**78εε计算得到 'μ，若'μ近似等于μ时，则证明梁纯弯曲段内近似于单向应力状态。

2、实验原理梁的纯弯曲段内，每片应变片所处状态是单向应力状态。

根据单向应力状态的虎克定律：σ = E ε可以计算出梁的纯弯曲段内每片应变片所处的应力。

注：该装置只允许加4KN 载荷，超载会损坏传感器。

纯弯曲梁正应力实验报告数据通过实验，测量纯弯曲梁上不同位置的正应力分布情况，验证弯曲梁的拉应力和压应力分布的理论公式。

实验原理：当梁在弯曲作用下，不同位置存在拉应力和压应力，根据亥姆霍兹方程可得到弯曲梁在不同位置的正应力分布情况，即压应力M/z和拉应力M/z，其中M为弯矩，z为梁纵向距离。

实验中通常采用张力应变计和屈服应变计来测量梁上不同位置的正应力。

实验设备和材料：1. 弯曲梁样品：选取一根长度较长、宽度和厚度相对较小的金属样品；2. 悬挂装置：用于悬挂样品并施加弯矩；3. 应变计：用于测量样品上不同位置的应变。

实验步骤：1. 将弯曲梁样品固定在悬挂装置上，并调整悬挂装置，使得梁样品呈现凸起形状；2. 使用应变计测量梁上不同位置的应变，记录下对应的位置和应变数值；3. 变动悬挂装置的位置，重复步骤2，记录更多位置的应变数值；4. 将测得的应变数值转化为正应力数值，并绘制应力-位置曲线。

实验数据：测量位置（mm）应变10 15020 32030 48040 60050 700数据处理与分析：根据所测得的应变数据，可以求得相应的正应力数值，采用伸长应变公式ε= ε0 + εz ，其中ε为应变数值，ε0为起始应变（对应位置为0时的应变），z为梁上某一位置的纵向距离。

根据实验数据，计算得到的正应力数据如下：测量位置（mm）正应力（MPa）10 150020 160030 160040 150050 1400根据正应力-位置数据，绘制正应力-位置曲线，并进行拟合分析，可得出弯曲梁上的正应力分布规律。

实验结果与讨论：通过实验测量，我们得到了纯弯曲梁上不同位置的正应力分布情况。

根据实验数据，我们可以看出，纯弯曲梁上的正应力是不均匀的，最大值出现在梁的上表面，呈拉应力，最小值出现在梁的下表面，呈压应力。

这符合我们的理论预期。

在实验过程中，可能存在一些误差。

一方面，样品的准备和测量过程中可能存在一些不均匀性，导致测得的应变和正应力数值存在一定的误差。

纯-弯曲梁的正应力实验本实验旨在研究弯曲梁在受力时的正应力分布情况，通过实验数据的测量及分析，探讨影响梁正应力分布的因素，并对梁的强度进行评估。

1. 实验原理1.1 弯曲梁正应力分析弯曲梁是一种常用的结构元件，例如桥梁、楼层结构等，她受到外力的作用会发生弯曲形变，产生正应力和剪应力。

弯曲梁的正应力是沿着截面法向的应力，在梁的顶部为拉应力，底部为压应力。

正应力的计算公式如下：$$\sigma = \frac{My}{I}$$其中，$\sigma$为正应力，$M$为弯矩，$y$为受力点到截面重心的距离，$I$为截面惯性矩。

弯曲梁正应力的分布情况受到多种因素的影响，主要包括：① 梁材料的弹性模量：弹性模量越大，弯曲梁的刚度越大，相同外力作用下，梁的形变和正应力都会相应减小。

② 梁截面形状和尺寸：梁截面的惯性矩影响正应力的大小和分布情况。

截面抗弯性能越强，正应力越小。

③ 受力位置和方向：受力位置和作用方向是影响正应力大小和分布情况的重要因素。

不同位置和方向的外力作用会导致不同的正应力分布规律。

2. 实验设备和方法本实验采用的主要设备有：弯曲梁试验机、电子天平、千分尺等。

2.2 实验步骤1. 准备弯曲梁样品，将其加工成常用的矩形截面和半圆形截面，分别测量其截面形状和尺寸。

2. 调整弯曲梁试验机，设置好取样位置和取样方式。

3. 将弯曲梁放入试验机，设置试验参数，包括荷重大小、位移速率等。

4. 开始试验，记录每个荷载下的跨中挠度和荷载大小，并计算出弯矩大小。

5. 在试验过程中，用电子天平测量梁的重量，并用千分尺对梁的跨中直径和截面高度进行测量，计算出截面惯性矩。

6. 根据测量数据，计算出每个荷载下的正应力，并绘制出正应力分布图。

3. 结果分析3.1 实验数据记录本实验用常见的矩形和半圆形弯曲梁进行了试验，记录了不同工况下的荷载和跨中挠度等数据。

根据数据计算得出弯矩以及正应力等数据，具体数据结果如下表：1. 矩形截面弯曲梁（1）弯曲梁在起始荷载下出现了微小的振动，但并未发生失稳。

梁纯弯曲正应力测定实验（一）实验目的*在承受纯弯曲的钢梁上，测取其横截面上各点的正应力，验证梁的正应力公式和观察应力的分布规律；*熟悉电测初步知识和测量方法。

（二）实验原理*试件、尺寸、设备——见系网页中“教学资源栏目”之“实验指导” *操作步骤、仪器使用（同上） （三）数据处理 *测量过程记录表*注：应力平均值（增量）计算：=E 理论值计算：zM yI σ∆⋅∆=，对应载荷增量∆F 所产生的弯矩：∆M=0.5∆F .a （四）思考题*弯曲正应力的大小与材料的弹性模量E 是否有关？*分析理论值计算与实验值产生的误差原因。

（列出可能的几种） *若在实验中出现与中性层对应的点的数值为“非零”，是什么原因？临床实验室定量测定室内质量控制一术语和定义1偏倚 bias试验结果偏离可接受参考值的系统偏离（带有正负号）。

2不精密度 imprecision一组重复测定结果的随机离散，其值由统计量定量表示为标准差或变异系数。

3质量控制quality control质量管理的一部分，致力于满足质量要求。

[GB/T 19000-2000，]4 质量控制策略 quality control strategy质控品种类、每种检测频次、放置的位置，以及用于质控数据解释和确定分析批是在控还是失控的规则。

5 随机误差 random error测量结果与在重复性条件下对同一被测量进行无限多次测量所得结果的平均值之差。

6 系统误差 systematic error在重复性条件下，对同一被测量进行无限多次测量所得结果的平均值与被测量的真值之差。

7 可报告范围 reportable range在仪器、试剂盒或系统的测定响应之间的关系,显示是有效的期间内试验值范围。

8 标准差 standard deviation观察值或测定结果中不精密度的统计度量。

变异性/离散的度量是总体方差的正平方根。

二质量控制的目的质量控制方法是用来监测检验方法的分析性能，警告检验人员存在的问题。

纯弯曲梁正应力实验报告数据纯弯曲梁正应力实验报告数据引言：纯弯曲梁正应力实验是结构力学实验中的一项重要内容，通过对材料的弯曲变形进行测试，可以得到材料在不同载荷下的正应力分布情况。

本文将介绍一项纯弯曲梁正应力实验的数据结果，并对实验结果进行分析和讨论。

实验装置与方法：本次实验使用了一台万能材料试验机，悬臂梁的试件采用了标准的矩形截面，材料为钢。

实验过程中，通过加载试件的两端，使其产生弯曲变形，并通过应变计和测力计等传感器测量试件在不同载荷下的应变和力的变化。

实验结果：在不同的载荷下，测得悬臂梁试件的应变和力的变化数据如下：载荷（N）应变（με）力（N）100 500 10200 1000 20300 1500 30400 2000 40500 2500 50数据分析与讨论：通过对实验结果的分析，可以得到以下几个方面的结论：1. 应变与载荷的关系：从实验数据可以看出，应变随着载荷的增加而线性增加。

这是由于在纯弯曲梁实验中，试件的上表面受到拉应力，下表面受到压应力，而应变计测量的是试件的表面应变，因此随着载荷的增加，试件的弯曲变形增大，表面应变也相应增加。

2. 力与载荷的关系：实验数据表明，力与载荷之间呈线性关系，即力随着载荷的增加而增加。

这是因为在纯弯曲梁实验中，试件受到的弯曲力矩与载荷成正比，而力是力矩除以试件的截面积，因此力与载荷之间呈线性关系。

3. 正应力分布：根据弯曲梁的受力分析理论，试件上表面受到拉应力，下表面受到压应力。

通过实验数据可以得到，试件上表面的正应力随着载荷的增加而增大，而下表面的正应力随着载荷的增加而减小。

这与弯曲梁的受力分布规律一致。

结论：通过纯弯曲梁正应力实验的数据分析与讨论，可以得出以下结论：1. 在纯弯曲梁实验中，应变与载荷呈线性关系，力与载荷呈线性关系；2. 试件上表面的正应力随着载荷的增加而增大，下表面的正应力随着载荷的增加而减小。

这些结论对于理解材料在弯曲变形下的应力分布规律具有重要意义，对于结构设计和工程实践具有指导作用。

实验三 纯弯曲梁正应力测定一、 实验目的1．测定梁在纯弯曲时横截面上的正应力分布，验证平面假设理论和弯曲正应力公式。

2．学习电测应力实验方法。

二、 实验设备1．简支梁及加载装置。

2． YJ-31型静态电阻应变仪。

3．游标卡尺。

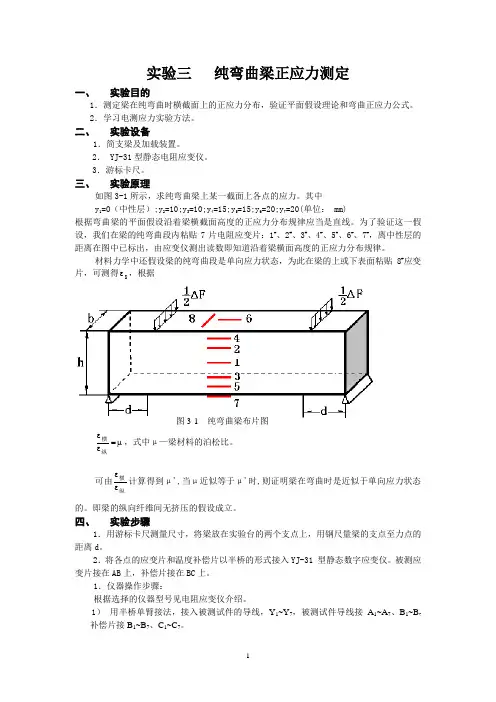
三、 实验原理如图3-1所示，求纯弯曲梁上某一截面上各点的应力。

其中y 1=0（中性层）;y 2=10;y 3=10;y 4=15;y 5=15;y 6=20;y 7=20(单位： mm)根据弯曲梁的平面假设沿着梁横截面高度的正应力分布规律应当是直线。

为了验证这一假设，我们在梁的纯弯曲段内粘贴7片电阻应变片：1#、2#、3#、4#、5#、6#、7#，离中性层的距离在图中已标出，由应变仪测出读数即知道沿着梁横面高度的正应力分布规律。

材料力学中还假设梁的纯弯曲段是单向应力状态，为此在梁的上或下表面粘贴8#应变片，可测得8ε，根据μ=εε纵横，式中μ—梁材料的泊松比。

可由纵横εε计算得到μ',当μ近似等于μ'时,则证明梁在弯曲时是近似于单向应力状态的。

即梁的纵向纤维间无挤压的假设成立。

四、 实验步骤1．用游标卡尺测量尺寸，将梁放在实验台的两个支点上，用钢尺量梁的支点至力点的距离d 。

2．将各点的应变片和温度补偿片以半桥的形式接入YJ-31 型静态数字应变仪。

被测应变片接在AB 上，补偿片接在BC 上。

1．仪器操作步骤：根据选择的仪器型号见电阻应变仪介绍。

1） 用半桥单臂接法，接入被测试件的导线，Y 1~Y 7，被测试件导线接A 1~A 7、B 1~B 7补偿片接B 1~B 7、C 1~C 7。

图3-1 纯弯曲梁布片图被测点 6 4 2 1 3 5 7接线端子 1 2 3 4 5 6 72）分别调（1~7点）电阻平衡。

面板显示为0000（每次转换一个测量点，必须稳定2分钟后再调平衡或读出测量值）。

3）采用增量法加载，每次0.5kN。

注意不能超载。

0.5 kN 初载荷调零1.0 kN 读出应变值1.5 kN 读出应变值2.0 kN 读出应变值2.5 kN 读出应变值4）实验结束。