线性回归分析练习题

一、是非题1．单个自变量的线性回归就是直线回归。

2．直线回归就是指自变量和应变量的观察值落在在一条直线上。

3．直线回归中预测值Y 是固定某个X 值，Y 的总体均数估计值。

4．用逐步回归的方法评价自变量与应变量之间的关联性，只能推断某个自变量与应变量有关联性，不能推断无它们之间无关联性。

二、选择题1．用最小二乘法确定直线回归方程的原则是各观察点（）A ． 距直线的纵向距离相等B ． 距直线的纵向距离的平方和最小C ． 与直线的垂直距离相等D ． 与直线的垂直距离的平方和最小 2．直线回归的系数假设检验（）E ． 只能利用相关系数r 的检验方法进行检验F ． 只能用t 检验G ． 只能用F 检验H ． 三者均可3．Y ˆ=7+2X 是1~7岁儿童以年龄(岁)估计体重(公斤)的回归方程，若把体重的单位换成市斤，则此方程（ ）A ．截矩改变B ．回归系数改变C ． 截矩与回归系数都改变D ．回归系数不变E ．截矩不变 4．直线回归系数的假设检验，其自由度为（ ）A ．nB ．n-1C ．n-2D ．2n-1E ．2n-25．对应变量Y 的离均差平方和，下列哪个分解是正确的？（ ）A ．SS 剩=SS 回B ．SS 总=SS 剩C ．SS 总=SS 回D ．SS 总＋SS 剩=SS 回E ．SS 总＋SS 回=SS 剩三、计算分析题1．15名儿童的身高与肺死腔容积的观察值如表15-3所示。

表15-3 儿童身高与肺死腔容积的观测数据对象号 身高(cm)X 肺死腔容积(ml)Y 对象号 身高(cm)X 肺死腔容积(ml)Y 1 110 45 9 175 102 2 116 32 10 167 111 3 123 41 11 165 88 4 130 45 12 160 65 5 129 43 13 157 79 6 142 67 14 156 92 7 147 58 15 149 58 815357试用该资料进行回归分析：（1）计算样本回归方程的截矩与回归系数； （2）进行回归系数等于0的假设检验； （3）验证是否存在F t b =的关系；（4）估计回归系数β的95%置信区间。

第9章一元线性回归练习题一．选择题1．具有相关关系的两个变量的特点是（）A．一个变量的取值不能由另一个变量唯一确定B．一个变量的取值由另一个变量唯一确定C．一个变量的取值增大时另一个变量的取值也一定增大D．一个变量的取值增大时另一个变量的取值肯定变小2．下面的各问题中，哪个不是相关分析要解决的问题A．判断变量之间是否存在关系B．判断一个变量数值的变化对另一个变量的影响C．描述变量之间的关系强度 D.判断样本所反映的变量之间的关系能否代表总体变量之间的关系3.根据下面的散点图，可以判断两个变量之间存在（）A.正线性相关关系B. 负线性相关关系C. 非线性关系D. 函数关系4.下面的陈述哪一个是错误的（）A. 相关系数是度量两个变量之间线性关系强度的统计量B．相关系数是一个随机变量C．相关系数的绝对值不会大于1D．相关系数不会取负值5.根据你的判断，下面的相关系数取值哪一个是错误的（）A. -0.86B. 0.78C. 1.25D. 06.如果相关系数r=0,则表明两个变量之间（）A.相关程度很低B. 不存在任何关系C．不存在线性相关关系D.存在非线性关系7.下列不属于相关关系的现象是（）A.银行的年利息率与贷款总额B.居民收入与储蓄存款C.电视机的产量与鸡蛋产量D.某种商品的销售额与销售价格8.设产品产量与产品单位成本之间的线性相关系数为-0.87，这说明二者之间存在着（）A. 高度相关B.中度相关C.低度相关D.极弱相关9.在回归分析中，被预测或被解释的变量称为（）A.自变量B.因变量C.随机变量D.非随机变量10.对两变量的散点图拟合最好的回归线，必须满足一个基本的条件是（）A.2ˆ()yy∑-最小B.2)(ˆyy∑-最大C.2ˆ()yy∑-最大D.2)(ˆyy∑-最小11. 下列哪个不属于一元回归中的基本假定（）A.误差项i ε服从正态分布B. 对于所有的X ，方差都相同C. 误差项i ε相互独立D. 0)ˆ=-i i yy E （ 12.如果两个变量之间存在着负相关，指出下列回归方程中哪个肯定有误（ ）A.x y75.025ˆ-= B. x y 86.0120ˆ+-= C. x y 5.2200ˆ-= D. x y 74.034ˆ--= 13.对不同年份的产品成本拟合的直线方程为,75.1280ˆx y-=y 表示产品成本，x 表示不同年份，则可知（ ）A.时间每增加一个单位，产品成本平均增加1.75个单位B. 时间每增加一个单位，产品成本平均下降1.75个单位C.产品成本每变动一个单位，平均需要1.75年时间D. 产品成本每减少一个单位，平均需要1.75年时间 14.在回归分析中，F 检验主要是用来检验（ ）A ．相关关系的显著性 B.回归系数的显著性 C. 线性关系的显著性D.估计标准误差的显著性15.说明回归方程拟合优度的统计量是（ ）A. 相关系数B.回归系数C. 判定系数D. 估计标准误差16.已知回归平方和SSR=4854,残差平方和SSE=146,则判定系数R 2=( ) A.97.08% B.2.92% C.3.01% D. 33.25% 17. 判定系数R2值越大，则回归方程（ ）A 拟合程度越低B 拟合程度越高C 拟合程度有可能高，也有可能低D 用回归方程进行预测越不准确 18. 居民收入与储蓄额之间的相关系数可能是（ ） A -0.9247 B 0.9247 C -1.5362 D 1.536219.在对一元回归方程进行显著性检验时，得到判定系数R 2=0.80,关于该系数的说法正确的是（ ）A. 该系数越大，则方程的预测效果越好B. 该系数越大，则由回归方程所解释的因变量的变差越多C. 该系数越大，则自变量的回归对因变量的相关关系越显著D. 该回归方程中自变量与因变量之间的相关系数可能小于0.8 20.下列方程中肯定错误的是（ ）A. x y48.015ˆ-=，r=0.65 B. x y 35.115ˆ--=, r= - 0.81 C. x y85.025ˆ+-=, r=0.42 D. x y 56.3120ˆ-=, r= - 0.96 21. 若两个变量存在负相关关系，则建立的一元线性回归方程的判定系数R 2的取值范围是（ ）A.【0，1】B. 【-1，0】C. 【-1，1】D.小于0的任意数二． 填空题1.当从某一总体中抽取了一样本容量为30的样本，并计算出某两个变量的相关系数为0.8时，我们是否可认为这两个变量存在着强相关性（不能 ） ，理由是（因为该相关系数为样本计算出的相关系数，它的大小受样本数据波动的影响，它是否显著尚需检验 ）。

§1回归分析一、基础过关1．下列变量之间的关系是函数关系的是() A．已知二次函数y＝ax2＋bx＋c，其中a，c是已知常数，取b为自变量，因变量是这个函数的判别式Δ＝b2－4acB．光照时间和果树亩产量C．降雪量和交通事故发生率D．每亩施用肥料量和粮食产量2．在以下四个散点图中，其中适用于作线性回归的散点图为()A．①②B．①③C．②③D．③④3．下列变量中，属于负相关的是() A．收入增加，储蓄额增加B．产量增加，生产费用增加C．收入增加，支出增加D．价格下降，消费增加4．已知对一组观察值(x i，y i)作出散点图后确定具有线性相关关系，若对于y＝bx＋a，求得b＝0.51，x＝61.75，y＝38.14，则线性回归方程为A．y＝0.51x＋6.65 B．y＝6.65x＋0.51C．y＝0.51x＋42.30 D．y＝42.30x＋0.515．对于回归分析，下列说法错误的是()A．在回归分析中，变量间的关系若是非确定关系，那么因变量不能由自变量唯一确定B．线性相关系数可以是正的，也可以是负的C．回归分析中，如果r2＝1，说明x与y之间完全相关D．样本相关系数r∈(－1,1)6．下表是x和y之间的一组数据，则y关于x的回归方程必过() ArrayA.点(2,3) B．点(1.5,4)C．点(2.5,4) D．点(2.5,5)7．若线性回归方程中的回归系数b＝0，则相关系数r＝________.二、能力提升8．若施化肥量x(kg)与小麦产量y(kg)之间的线性回归方程为y＝250＋4x，当施化肥量为50 kg时，预计小麦产量为________ kg.9．某车间为了规定工时定额，需确定加工零件所花费的时间，为此做了4次试验，得到的数据如下：若加工时间y(1)求加工时间与零件个数的线性回归方程；(2)试预报加工10个零件需要的时间．10．在一段时间内，分5次测得某种商品的价格x (万元)和需求量y (t)之间的一组数据为：已知∑5i ＝1x i y i ＝62，∑i ＝1x 2i ＝16.6. (1)画出散点图；(2)求出y 对x 的线性回归方程；(3)如果价格定为1.9万元，预测需求量大约是多少？(精确到0.01 t)． 11．某运动员训练次数与运动成绩之间的数据关系如下：(1)(2)求出回归方程；(3)计算相关系数并进行相关性检验； (4)试预测该运动员训练47次及55次的成绩．答案1．A 2.B 3.D 4.A 5.D 6.C 7．0 8.y ＝－11.3＋36.95x 9．45010．解 (1)由表中数据，利用科学计算器得x ＝2＋3＋4＋54＝3.5， y ＝2.5＋3＋4＋4.54＝3.5，∑4i ＝1x i y i ＝52.5，∑4i ＝1x 2i ＝54， b ＝∑4i ＝1x i y i －4x y ∑4i ＝1x 2i －4x 2＝52.5－4×3.5×3.554－4×3.52＝0.7，a ＝y －b x ＝1.05，因此，所求的线性回归方程为y ＝0.7x ＋1.05.(2)将x ＝10代入线性回归方程，得y ＝0.7×10＋1.05＝8.05(小时)，即加工10个零件的预报时间为8.05小时．11．解 (1)散点图如下图所示：(2)因为x ＝15×9＝1.8，y ＝15×37＝7.4，∑5i ＝1x i y i ＝62，∑5i ＝1x 2i ＝16.6， 所以b ＝∑5i ＝1x i y i －5x y ∑5i ＝1x 2i －5x 2＝62－5×1.8×7.416.6－5×1.82＝－11.5，a ＝y －b x ＝7.4＋11.5×1.8＝28.1， 故y 对x 的线性回归方程为y ＝28.1－11.5x . (3)y ＝28.1－11.5×1.9＝6.25(t)．所以，如果价格定为1.9万元，则需求量大约是6.25 t.12．解 (1)作出该运动员训练次数x 与成绩y 之间的散点图，如下图所示，由散点图可知，它们之间具有线性相关关系．(2)列表计算：次数x i 成绩y i x 2i y 2i x i y i 30 30 900 900 900 33 34 1 089 1 156 1 122 35 37 1 225 1 369 1 295 37 39 1 369 1 521 1 443 39 42 1 521 1 764 1 638 44 46 1 936 2 116 2 024 46 48 2 116 2 304 2 208 50512 5002 6012 550由上表可求得x ＝39.25，y ＝40.875，∑8i ＝1x 2i ＝12 656，∑8i ＝1y 2i ＝13 731， ∑8i ＝1x i y i ＝13 180，∴b ＝∑8i ＝1x i y i －8x y∑8i ＝1x 2i －8x2≈1.041 5，a ＝y －b x ＝－0.003 88，∴线性回归方程为y ＝1.041 5x －0.003 88.(3)计算相关系数r ＝0.992 7，因此运动员的成绩和训练次数两个变量有较强的相关关系． (4)由上述分析可知，我们可用线性回归方程y ＝1.041 5x －0.003 88作为该运动员成绩的预报值． 将x ＝47和x ＝55分别代入该方程可得y ＝49和y ＝57.故预测该运动员训练47次和55次的成绩分别为49和57. 13．解 ∵s x ＝l xyn，s y ＝l xy n， ∴l xyn＝r l xy n ·l yyn ＝0.5×7.6×15.2＝57.76.∴β1＝l xyn l xy n＝57.767.62＝1， β0＝y －β1x ＝72－1×172＝－100.故由身高估计平均体重的回归方程为y ＝x －100.由x ，y 位置的对称性，得b ＝l xyn l xy n ＝57.7615.22＝0.25，∴a ＝x －b y ＝172－0.25×72＝154.故由体重估计平均身高的回归方程为x ＝0.25y ＋154.1.3 可线性化的回归分析一、基础过关1． 某商品销售量y (件)与销售价格x (元/件)负相关，则其线性回归方程可能是( )A ．y ＝－10x ＋200B ．y ＝10x ＋200C ．y ＝－10x －200D ．y ＝10x －200 2． 在线性回归方程y ＝a ＋bx 中，回归系数b 表示( )A ．当x ＝0时，y 的平均值B ．x 变动一个单位时，y 的实际变动量C ．y 变动一个单位时，x 的平均变动量D ．x 变动一个单位时，y 的平均变动量3． 对于指数曲线y ＝a e bx ，令u ＝ln y ，c ＝ln a ，经过非线性化回归分析之后，可以转化成的形式为 ( )A ．u ＝c ＋bxB ．u ＝b ＋cxC ．y ＝b ＋cxD ．y ＝c ＋bx4． 下列说法错误的是( )A ．当变量之间的相关关系不是线性相关关系时，也能直接用线性回归方程描述它们之间的相关关系B ．把非线性回归化为线性回归为我们解决问题提供一种方法C ．当变量之间的相关关系不是线性相关关系时，也能描述变量之间的相关关系D ．当变量之间的相关关系不是线性相关关系时，可以通过适当的变换使其转换为线性关系，将问题化为线性回归分析问题来解决5． 每一吨铸铁成本y c (元)与铸件废品率x %建立的回归方程y c ＝56＋8x ，下列说法正确的是 ( )A ．废品率每增加1%，成本每吨增加64元B ．废品率每增加1%，成本每吨增加8%C ．废品率每增加1%，成本每吨增加8元D ．如果废品率增加1%，则每吨成本为56元 6． 为了考察两个变量x 和y 之间的线性相关性，甲、乙两个同学各自独立地做10次和15次试验，并且利用线性回归方法，求得回归直线分别为l 1和l 2.已知在两个人的试验中发现对变量x 的观测数据的平均值恰好相等，都为s ，对变量y 的观测数据的平均值也恰好相等，都为t .那么下列说法正确的是 ( ) A ．直线l 1和l 2有交点(s ，t ) B ．直线l 1和l 2相交，但是交点未必是点(s ，t ) C ．直线l 1和l 2由于斜率相等，所以必定平行 D ．直线l 1和l 2必定重合 二、能力提升7． 研究人员对10个家庭的儿童问题行为程度(X )及其母亲的不耐心程度(Y )进行了评价结果如下，家庭1,2,3,4,5,6,7,8,9,10，儿童得分：72,40,52,87,39,95,12,64,49,46，母亲得分：79,62,53,89,81,90,10,82,78,70. 下列哪个方程可以较恰当的拟合( )A．y＝0.771 1x＋26.528 B．y＝36.958ln x－74.604C．y＝1.177 8x1.014 5 D．y＝20.924e0.019 3x8．已知x，y之间的一组数据如下表：则y与x9．已知线性回归方程为y＝0.50x－0.81，则x＝25时，y的估计值为________．10．在一次抽样调查中测得样本的5个样本点，数值如下表：（1）建立y与xx 时，y大约是多少（2）当811．某地区六年来轻工业产品利润总额y与年次x的试验数据如下表所示：y关于x的回归方程．(保留三位有效数字)三、探究与拓展12．某商店各个时期的商品流通率y(%)和商品零售额x(万元)资料如下：散点图显示出x 与y y 决定于商品的零售额x ，体现着经营规模效益，假定它们之间存在关系式：y ＝a ＋bx .试根据上表数据，求出a 与b 的估计值，并估计商品零售额为30万元时的商品流通率．答案1．A 2.D 3.A 4.A 5.C 6.A 7.B 8．(1.16,2.4) 9.11.6910．解 画出散点图如图(1)所示，观察可知y 与x 近似是反比例函数关系．设y ＝k x (k ≠0)，令t ＝1x，则y ＝kt .可得到y 关于t 的数据如下表：t 4 2 1 0.5 0.25 y1612521画出散点图如图(2)得：b ＝∑5i ＝1t i y i －5t y ∑5i ＝1t 2i －5t 2≈4.134 4，a ＝y －b t ≈0.791 7， 所以y ＝4.134 4t ＋0.791 7， 所以y 与x 的回归方程是y ＝4.134 4x＋0.791 7. 11．解 对y ＝ab x e 0两边取对数，得ln y ＝ln a e 0＋x ln b ，令z ＝ln y ， 则z 与x 的数据如下表：x 1 2 3 4 5 6 z2.432.472.522.572.612.67由z ＝ln a e 0＋x ln b 0即z ＝2.38＋0.047 7x ，所以y ＝10.8×1.05x . 12．解 设u ＝1x，则y ≈a ＋bu ，得下表数据：进而可得n ＝10，u ≈0.060 4，y ＝3.21，∑i ＝110u 2i －10u 2≈0.004 557 3， ∑i ＝110u i y i －10u y ≈0.256 35，b ≈0.256 350.004 557 3≈56.25， a ＝y －b ·u ≈－0.187 5，所求的回归方程为y ＝－0.187 5＋56.25x.当x ＝30时，y ＝1.687 5，即商品零售额为30万元时，商品流通率为1.687 5%.。

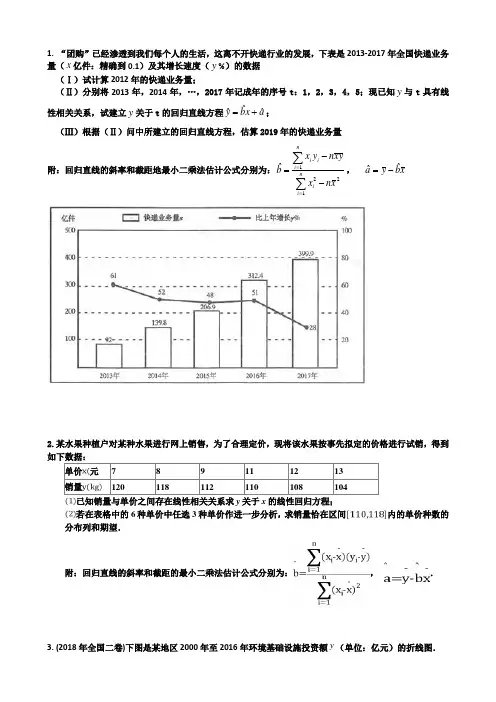
1. “团购”已经渗透到我们每个人的生活，这离不开快递行业的发展，下表是2013-2017年全国快递业务量（x 亿件：精确到0.1）及其增长速度（y %）的数据（Ⅰ）试计算2012年的快递业务量；（Ⅱ）分别将2013年，2014年，…，2017年记成年的序号t ：1，2，3，4，5；现已知y 与t 具有线性相关关系，试建立y 关于t 的回归直线方程a x b yˆˆˆ+=； （Ⅲ）根据（Ⅱ）问中所建立的回归直线方程，估算2019年的快递业务量附：回归直线的斜率和截距地最小二乘法估计公式分别为：∑∑==--=ni ini ii x n xy x n yx b1221ˆ， x b y aˆˆ-=2.某水果种植户对某种水果进行网上销售，为了合理定价，现将该水果按事先拟定的价格进行试销，得到如下数据：单价元 7 8 9 11 12 13 销量120118112110108104已知销量与单价之间存在线性相关关系求y 关于x 的线性回归方程； 若在表格中的6种单价中任选3种单价作进一步分析，求销量恰在区间内的单价种数的分布列和期望．附：回归直线的斜率和截距的最小二乘法估计公式分别为：， ．3. (2018年全国二卷)下图是某地区2000年至2016年环境基础设施投资额y （单位：亿元）的折线图．为了预测该地区2018年的环境基础设施投资额，建立了y 与时间变量t 的两个线性回归模型．根据2000年至2016年的数据（时间变量t 的值依次为1217，，…，）建立模型①：ˆ30.413.5y t =-+；根据2010年至2016年的数据（时间变量t 的值依次为127，，…，）建立模型②：ˆ9917.5y t =+． （1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值； （2）你认为用哪个模型得到的预测值更可靠？并说明理由．4.(2014年全国二卷) 某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：年份 2007 2008 2009 2010 2011 2012 2013 年份代号t 1 2 3 4 5 6 7 人均纯收入y 2.93.33.64.44.85.25.9（Ⅰ）求y 关于t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121niii ni i t t y y b t t ∧==--=-∑∑，ˆˆay bt =-5（2019 2卷）18．11分制乒乓球比赛，每赢一球得1分，当某局打成10∶10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束．甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立．在某局双方10∶10平后，甲先发球，两人又打了X 个球该局比赛结束．(1)求P(X＝2)；(2)求事件“X＝4且甲获胜”的概率．。

多元线性回归模型练习一、单项选择题1.在由30n =的一组样本估计的、包含3个解释变量的线性回归模型中，计算得可决系数为0.8500，则调整后的可决系数为（ D ）A. 0.8603B. 0.8389C. 0.8655D.0.8327 2.用一组有30个观测值的样本估计模型01122t t t t y b b x b x u =+++后，在0.05的显著性水平上对1b 的显著性作t 检验，则1b 显著地不等于零的条件是其统计量t 大于等于（ C ）A. )30(05.0tB. )28(025.0tC. )27(025.0tD. )28,1(025.0F 3.线性回归模型01122......t t t k kt t y b b x b x b x u =+++++ 中，检验0:0(0,1,2,...)t H b i k ==时，所用的统计量 服从( C )A.t(n-k+1)B.t(n-k-2)C.t(n-k-1)D.t(n-k+2) 4. 调整的可决系数 与多元样本判定系数 之间有如下关系( D )A.2211n R R n k -=-- B. 22111n R R n k -=---C.2211(1)1n R R n k -=-+-- D. 2211(1)1n R R n k -=----5.对模型Y i =β0+β1X 1i +β2X 2i +μi 进行总体显著性F 检验，检验的零假设是( A ) A. β1=β2=0B. β1=0C. β2=0D. β0=0或β1=06．设k 为回归模型中的参数个数，n 为样本容量。

则对多元线性回归方程进行显著性检验时，所用的F 统计量可表示为（ B ）A. )1()(--k RSS k n ESS B ．C ．)1()1()(22---k R k n R D ．)()1/(k n TSS k ESS -- 7．多元线性回归分析中（回归模型中的参数个数为k ），调整后的可决系数2R 与可决系数2R 之间的关系（ A ）) 1 ( ) 1 ( 2 2 - - k R k R - nA.B. 2R ≥2RC. 02>R D.1)1(122----=n k n R R8．已知五元线性回归模型估计的残差平方和为8002=∑t e，样本容量为46，则随机误差项t u 的方差估计量2ˆσ为( D ) A. 33.33 B. 40 C. 38.09 D. 209．多元线性回归分析中的 ESS 反映了（ C ）A.因变量观测值总变差的大小B.因变量回归估计值总变差的大小C.因变量观测值与估计值之间的总变差D.Y 关于X 的边际变化23．在古典假设成立的条件下用OLS 方法估计线性回归模型参数，则参数估计量具有（ C ）的统计性质。

1. 从20的样本中得到的有关回归结果是：SSR=60，SSE=40。

要检验x 与y 之间的线性关系是否显著，即检验假设：01:0H β=。

(1)线性关系检验的统计量F 值是多少? (2)给定显著性水平a ＝0.05，F a 是多少? (3)是拒绝原假设还是不拒绝原假设?(4)假定x 与y 之间是负相关，计算相关系数r 。

(5)检验x 与y 之间的线性关系是否显著?解：（1）SSR 的自由度为k=1；SSE 的自由度为n-k-1=18；因此：F=1SSR k SSE n k --=6014018=27 （2）()1,18F α=()0.051,18F =4.41 （3）拒绝原假设，线性关系显著。

（4），由于是负相关，因此r=-0.7746（5）从F 检验看线性关系显著。

2. 某汽车生产商欲了解广告费用(x)对销售量(y)的影响，收集了过去12年的有关数据。

通过计算得到下面的有关结果：(1)完成上面的方差分析表。

(2)汽车销售量的变差中有多少是由于广告费用的变动引起的?(3)销售量与广告费用之间的相关系数是多少?(4)写出估计的回归方程并解释回归系数的实际意义。

(5)检验线性关系的显著性(a＝0.05)。

（2）R2=0.9756，汽车销售量的变差中有97.56%是由于广告费用的变动引起的。

（3）r=0.9877。

（4）回归系数的意义：广告费用每增加一个单位，汽车销量就增加1.42个单位。

（5）回归系数的检验：p=2.17E—09＜α，回归系数不等于0，显著。

回归直线的检验：p=2.17E—09＜α，回归直线显著。

3. 根据两个自变量得到的多元回归方程为12ˆ18.4 2.014.74yx x =-++，并且已知n ＝10，SST ＝6 724.125，SSR ＝6 216.375，1ˆ0.0813s β=，2ˆs β＝0.056 7。

要求：(1)在a=0.05的显著性水平下，12,x x 与y 的线性关系是否显著? (2)在a ＝0.05的显著性水平下，1β是否显著?(3)在a ＝0.05的显著性水平下，2β是否显著?解（1）回归方程的显著性检验：假设：H 0：1β=2β=0 H 1：1β，2β不全等于0 SSE=SST-SSR=6 724.125-6 216.375=507.75 F=1SSR p SSE n p --=6724.1252507.751021--=42.85()2,7F α=4.74，F>()2,7F α，认为线性关系显著。

统计学一元线性回归分析练习题一、内容提要本章介绍了回归分析的基本思想与基本方法。

首先，本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始，建立了回归分析的基本思想。

总体回归函数是对总体变量间关系的定量表述，由总体回归模型在若干基本假设下得到，但它只是建立在理论之上，在现实中只能先从总体中抽取一个样本，获得样本回归函数，并用它对总体回归函数做出统计推断。

本章的一个重点是如何获取线性的样本回归函数，主要涉及到普通最小二乘法的学习与掌握。

同时，也介绍了极大似然估计法以及矩估计法。

本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断，即进行所谓的统计检验。

统计检验包括两个方面，一是先检验样本回归函数与样本点的“拟合优度”，第二是检验样本回归函数与总体回归函数的“接近”程度。

后者又包括两个层次：第一，检验解释变量对被解释变量是否存在着显著的线性影响关系，通过变量的t检验完成；第二，检验回归函数与总体回归函数的“接近”程度，通过参数估计值的“区间检验”完成。

本章还有三方面的内容不容忽视。

其一，若干基本假设。

样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。

其二，参数估计量统计性质的分析，包括小样本性质与大样本性质，尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。

Goss-markov定理表明OLS估计量是最佳线性无偏估计量。

其三，运用样本回归函数进行预测，包括被解释变量条件均值与个值的预测，以及预测置信区间的计算及其变化特征。

二、典型例题分析例1、令kids表示一名妇女生育孩子的数目，educ 表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为kids??0??1educ??随机扰动项?包含什么样的因素？它们可能与教育水平相关吗？上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。

线性回归习题答案线性回归是统计学中一种常见的数据分析方法，用于建立自变量与因变量之间的线性关系模型。

在实际应用中，线性回归模型常用于预测、趋势分析和关联度分析等领域。

下面将通过一些典型的线性回归习题来探讨其应用。

习题一：某公司根据过去几年的销售数据，建立了一个线性回归模型来预测未来的销售额。

已知公司的广告费用与销售额之间存在着一定的线性关系。

根据模型，当广告费用为1000元时，预测的销售额为15000元。

求该模型的回归方程。

解答：假设回归方程为y = a + bx，其中y表示销售额，x表示广告费用。

根据已知条件，可以得到一个方程：15000 = a + 1000b。

进一步，如果再给出另外一个广告费用与销售额的数据点，就可以求解出回归方程的具体参数a和b。

习题二：某城市的房价与房屋面积之间存在一定的线性关系。

已知一套房子的面积为120平方米，根据线性回归模型预测其价格为80万元。

求该模型的回归方程。

解答：假设回归方程为y = a + bx，其中y表示房价，x表示房屋面积。

根据已知条件，可以得到一个方程：80 = a + 120b。

同样地，如果再给出另外一个房屋面积与价格的数据点，就可以求解出回归方程的具体参数a和b。

习题三：某公司根据市场调研数据，建立了一个线性回归模型来分析产品销售量与价格之间的关系。

已知当产品价格为10元时，预测的销售量为1000个。

根据该模型，求当产品价格为15元时的预测销售量。

解答：假设回归方程为y = a + bx，其中y表示销售量，x表示产品价格。

根据已知条件，可以得到一个方程：1000 = a + 10b。

根据该方程，可以求解出参数a和b的具体值。

然后，将x取15，代入回归方程中，即可得到当产品价格为15元时的预测销售量。

通过以上习题的解答，我们可以看到线性回归模型在实际问题中的应用。

通过建立合适的回归方程，我们可以通过已知的自变量值来预测因变量的取值。

这对于企业决策、市场分析以及经济预测等方面都具有重要意义。

X 8.12, Y 7.28,
X
2 i
330.62
XiYi 296.37,
n 1 n
X iYi
X
2 i
(
Xi Yi Xi )2
0.846
ˆ0 Y ˆ1X 0.411
Y关于X的样本回归方程为：
Yi 0.411 0.846 X i
2、下列方程哪些是正确的？哪些是错误的？为什么？
Yt X t
Yt X t t
Yt ˆ ˆ Xt t Yˆt ˆ ˆ Xt t
t 1,2,, n t 1,2,, n
t 1,2,,n t 1,2,,n
Yt ˆ ˆ Xt Yˆt ˆ ˆ Xt Yt ˆ ˆ Xt ˆt Yˆt ˆ ˆ Xt ˆt
率项将会成为原回归系数的1/10。同样地，记Y*为原变量Y的
单位扩大10倍的变量，则Y=Y*/10，于是
Y 10
0
1 X ,
Y 100 101 X
可见，被解释变量的单位扩大10倍时，截距项与斜率项都会比 原回归系数扩大10倍。
（2）假定给X的每个观测值都增加2，对原回归的斜率和截距 会有什么样的影响？如果给Y的每个观测值都增加2，又会怎样？
4.对线性回归模型进行最小二乘估计，最小二乘准则是 __残_差_平_方__和_最_小___________。
5. 普通最小二乘法得到的参数估计量具有___线_性_性_____、 __无_偏__性_____、__有__效_性_____统计性质。
6.对计量经济学模型作统计检验包括___似_合_优_度____检验、 __变_量__的_显_著_性__检验、__方__程_的_显_著_性__检验。
归方程为
，这说明（）。
A.产量每Yˆ 增 加35一6 台1，.5X单位产品成本增加356元

简单线性回归分析思考与练习参考答案第10章简单线性回归分析思考与练习参考答案⼀、最佳选择题1．如果两样本的相关系数21r r =，样本量21n n =，那么（ D ）。

A. 回归系数21b b = B ．回归系数12b b < C. 回归系数21b b > D ．t 统计量11r b t t = E. 以上均错2．如果相关系数r =1，则⼀定有（ C ）。

A ．总SS =残差SSB ．残差SS =回归SSC ．总SS =回归SSD ．总SS ＞回归SS E.回归MS =残差MS3．记ρ为总体相关系数，r 为样本相关系数，b 为样本回归系数，下列（ D ）正确。

A ．ρ=0时，r =0B ．|r |＞0时，b ＞0C ．r ＞0时，b ＜0D ．r ＜0时，b ＜0 E. |r |=1时，b =14．如果相关系数r =0，则⼀定有（ D ）。

A ．简单线性回归的截距等于0B ．简单线性回归的截距等于Y 或XC ．简单线性回归的残差SS 等于0D ．简单线性回归的残差SS 等于SS 总E ．简单线性回归的总SS 等于05．⽤最⼩⼆乘法确定直线回归⽅程的含义是（ B ）。

A ．各观测点距直线的纵向距离相等B ．各观测点距直线的纵向距离平⽅和最⼩C ．各观测点距直线的垂直距离相等D ．各观测点距直线的垂直距离平⽅和最⼩E ．各观测点距直线的纵向距离等于零⼆、思考题1．简述简单线性回归分析的基本步骤。

答：①绘制散点图，考察是否有线性趋势及可疑的异常点；②估计回归系数；③对总体回归系数或回归⽅程进⾏假设检验；④列出回归⽅程，绘制回归直线；⑤统计应⽤。

2．简述线性回归分析与线性相关的区别与联系。

答：区别：（1）资料要求上，进⾏直线回归分析的两变量，若X 为可精确测量和严格控制的变量，则对应于每个X 的Y 值要求服从正态分布；若X 、Y 都是随机变量，则要求X 、Y 服从双变量正态分布。

直线相关分析只适⽤于双变量正态分布资料。

《9.1 线性回归分析》同步训练(答案在后面)一、单选题（本大题有8小题，每小题5分，共40分）1、某地区近五年内每年的GDP（单位：亿元）如下表所示：年份 | GDP–|—– 2016 | 300 2017 | 320 2018 | 350 2019 | 370 2020 | 400若要用线性回归分析预测该地区2021年的GDP，以下哪项说法是正确的？A、根据2016年到2020年的数据，拟合直线y=10x+290，则预测2021年GDP为410亿元B、根据2016年到2020年的数据，拟合直线y=10x+280，则预测2021年GDP为420亿元C、根据2016年到2020年的数据，拟合直线y=10x+280，则预测2021年GDP为400亿元D、根据2016年到2020年的数据，拟合直线y=10x+290，则预测2021年GDP为400亿元2、已知一组数据的线性回归方程为(y=1.5x+20)，若将(x)的值增加 2，则(y)的值将（）。

A、减少 3B、减少 2C、增加 3D、增加 23、（单选题）若线性回归方程为y = 3x + 1，当x增加1个单位时，y大约增加多少个单位？A. 1个单位B. 3个单位C. 4个单位D. 2个单位4、给定一组数据点((x1,y1),(x2,y2),...,(x n,y n))，假设我们已经计算出了线性回归方程(y=ax+b)中的斜率(a)和截距(b)。

如果增加一个新数据点((x n+1,y n+1))到这组数据中，那么新的线性回归方程中的斜率(a′)相对于原来的斜率(a)：A. 一定会变大B. 一定会变小C. 可能会变大，可能会变小，也可能会不变D. 一定不会改变5、某校为研究学生身高与体重之间的关系，随机抽取了10名学生的身高和体重数据，并建立了线性回归方程y=50x+35（其中x为身高，y为体重），若某学生的身高为1.75米，则该学生的预测体重约为：A. 70千克B. 75千克C. 80千克D. 85千克6、某研究机构对两种不同品牌的学习卡片销售情况进行了统计，得到了两组数据，为了找到哪种学习卡片的销售趋势更好的线性回归方程，第一组（品牌A）的广告费用与销售额数据如下：广告费用x（元）分别为100、200、300、400、500，对应的销售额y（万元）分别为15、25、35、45、55。

第9章一元线性回归练习题一．选择题1．具有相关关系的两个变量的特点是（）A．一个变量的取值不能由另一个变量唯一确定B．一个变量的取值由另一个变量唯一确定C．一个变量的取值增大时另一个变量的取值也一定增大D．一个变量的取值增大时另一个变量的取值肯定变小2．下面的各问题中，哪个不是相关分析要解决的问题A．判断变量之间是否存在关系B．判断一个变量数值的变化对另一个变量的影响C．描述变量之间的关系强度 D.判断样本所反映的变量之间的关系能否代表总体变量之间的关系3.根据下面的散点图，可以判断两个变量之间存在（）A.正线性相关关系B. 负线性相关关系C. 非线性关系D. 函数关系4.下面的陈述哪一个是错误的（）A. 相关系数是度量两个变量之间线性关系强度的统计量B．相关系数是一个随机变量C．相关系数的绝对值不会大于1D．相关系数不会取负值5.根据你的判断，下面的相关系数取值哪一个是错误的（）A. -0.86B. 0.78C. 1.25D. 06.如果相关系数r=0,则表明两个变量之间（）A.相关程度很低B. 不存在任何关系C．不存在线性相关关系D.存在非线性关系7.下列不属于相关关系的现象是（）A.银行的年利息率与贷款总额B.居民收入与储蓄存款C.电视机的产量与鸡蛋产量D.某种商品的销售额与销售价格8.设产品产量与产品单位成本之间的线性相关系数为-0.87，这说明二者之间存在着（）A. 高度相关B.中度相关C.低度相关D.极弱相关9.在回归分析中，被预测或被解释的变量称为（）A.自变量B.因变量C.随机变量D.非随机变量10.对两变量的散点图拟合最好的回归线，必须满足一个基本的条件是（）A.2ˆ()yy∑-最小B.2)(ˆyy∑-最大C.2ˆ()yy∑-最大D.2)(ˆyy∑-最小11. 下列哪个不属于一元回归中的基本假定（）A.误差项i ε服从正态分布B. 对于所有的X ，方差都相同C. 误差项i ε相互独立D. 0)ˆ=-i i yy E （ 12.如果两个变量之间存在着负相关，指出下列回归方程中哪个肯定有误（ ）A.x y75.025ˆ-= B. x y 86.0120ˆ+-= C. x y 5.2200ˆ-= D. x y 74.034ˆ--= 13.对不同年份的产品成本拟合的直线方程为,75.1280ˆx y-=y 表示产品成本，x 表示不同年份，则可知（ ）A.时间每增加一个单位，产品成本平均增加1.75个单位B. 时间每增加一个单位，产品成本平均下降1.75个单位C.产品成本每变动一个单位，平均需要1.75年时间D. 产品成本每减少一个单位，平均需要1.75年时间 14.在回归分析中，F 检验主要是用来检验（ ）A ．相关关系的显著性 B.回归系数的显著性 C. 线性关系的显著性D.估计标准误差的显著性15.说明回归方程拟合优度的统计量是（ ）A. 相关系数B.回归系数C. 判定系数D. 估计标准误差16.已知回归平方和SSR=4854,残差平方和SSE=146,则判定系数R 2=( ) A.97.08% B.2.92% C.3.01% D. 33.25% 17. 判定系数R2值越大，则回归方程（ ）A 拟合程度越低B 拟合程度越高C 拟合程度有可能高，也有可能低D 用回归方程进行预测越不准确 18. 居民收入与储蓄额之间的相关系数可能是（ ） A -0.9247 B 0.9247 C -1.5362 D 1.536219.在对一元回归方程进行显著性检验时，得到判定系数R 2=0.80,关于该系数的说法正确的是（ ）A. 该系数越大，则方程的预测效果越好B. 该系数越大，则由回归方程所解释的因变量的变差越多C. 该系数越大，则自变量的回归对因变量的相关关系越显著D. 该回归方程中自变量与因变量之间的相关系数可能小于0.8 20.下列方程中肯定错误的是（ ）A. x y48.015ˆ-=，r=0.65 B. x y 35.115ˆ--=, r= - 0.81 C. x y85.025ˆ+-=, r=0.42 D. x y 56.3120ˆ-=, r= - 0.96 21. 若两个变量存在负相关关系，则建立的一元线性回归方程的判定系数R 2的取值范围是（ ）A.【0，1】B. 【-1，0】C. 【-1，1】D.小于0的任意数二． 填空题1.当从某一总体中抽取了一样本容量为30的样本，并计算出某两个变量的相关系数为0.8时，我们是否可认为这两个变量存在着强相关性（不能 ） ，理由是（因为该相关系数为样本计算出的相关系数，它的大小受样本数据波动的影响，它是否显著尚需检验 ）。

线性回归分析法例题一、单选题1.相关分析研究的是（）A、变量间相互关系的紧密程度B、变量之间因果关系C、变量之间严苛的相依关系D、变量之间的线性关系2．若变量X的值减少时，变量Y的值也减少，那么变量X和变量Y之间存有着（）。

A、正相关关系B、负相关关系C、直线有关关系D、曲线有关关系3．若变量X的值增加时，变量Y的值随之下降，那么变量X和变量Y之间存在着（）。

A、正有关关系B、负相关关系C、直线相关关系D、曲线相关关系4．相关系数等于零说明两变量（）。

A.是严格的函数关系B.不存在相关关系C.不存有线性相关关系D.存在曲线线性相关关系5．有关关系的主要特征就是（）。

A、某一现象的标志与另外的标志之间的关系是不确定的B、某一现象的标志与另外的`标志之间存有着一定的依存关系，但它们不是确认的关系C、某一现象的标志与另外的标志之间存在着严格的依存关系D、某一现象的标志与另外的标志之间存有着不确认的直线关系6．时间数列自身相关是指（）。

A、两变量在相同时间上的依存关系B、两变量静态的依存关系C、一个变量随其时间相同其前后期变量值之间的依存关系D、一个变量的数值与时间之间的依存关系7．如果变量X和变量Y之间的相关系数为负1，表明两个变量之间（）。

A、不存在相关关系B、相关程度很低C、有关程度很高D、全然负相关8．若物价上涨，商品的需求量愈小，则物价与商品需求量之间（）。

A、并无有关B、存有正有关C、存在负相关D、无法判断是否相关9．有关分析对资料的建议就是（）。

A.两变量均为随机的B.两变量均不是随机的C、自变量就是随机的，因变量不是随机的D、自变量不是随机的，因变量是随机的10．重回分析中直观重回就是指（）。

A.时间数列自身回归B.两个变量之间的回归C.变量之间的线性重回D.两个变量之间的线性重回11.已知某工厂甲产品产量和生产成本有直线关系，在这条直线上，当产量为时，其生产成本为元，其中不随产量变化的成本为元，则成本总额对产量的回归方程为（）A. y=+24xB. y=6+0.24xC. y=+6xD. y=24+x12.直线回归方程中，若回归系数为负，则（）A.表明现象正相关B.表明现象负相关C.说明有关程度较弱D.无法表明有关方向和程度二、多项选择题1．以下属有关关系的存有（）。

回归分析的基本思想及其初步应用一、选择题 1. 某同学由x 与y 之间的一组数据求得两个变量间的线性回归方程为y bx a =+，已知：数据x 的平均值为2，数据y 的平均值为3，则 ( )A ．回归直线必过点（2，3）B ．回归直线一定不过点（2，3）C ．点（2，3）在回归直线上方D ．点（2，3）在回归直线下方2. 在一次试验中，测得(x,y)的四组值分别是A(1,2),B(2,3),C(3,4),D(4,5)，则Y 与X 之间的回归直线方程为（ ）A ．yx 1=+ B ．y x 2=+ C ．y 2x 1=+ Ｄ．y x 1=-3. 在对两个变量x ，y 进行线性回归分析时，有下列步骤：①对所求出的回归直线方程作出解释； ②收集数据(i x 、i y ），1,2i =，…，n ；③求线性回归方程； ④求未知参数； ⑤根据所搜集的数据绘制散点图如果根据可行性要求能够作出变量,x y 具有线性相关结论，则在下列操作中正确的是（ ） A ．①②⑤③④ B ．③②④⑤① C ．②④③①⑤ D ．②⑤④③①4. 下列说法中正确的是（ ）A ．任何两个变量都具有相关关系B ．人的知识与其年龄具有相关关系C ．散点图中的各点是分散的没有规律D ．根据散点图求得的回归直线方程都是有意义的5. 给出下列结论：（1）在回归分析中，可用指数系数2R 的值判断模型的拟合效果，2R 越大，模型的拟合效果越好； （2）在回归分析中，可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好； （3）在回归分析中，可用相关系数r 的值判断模型的拟合效果，r 越小，模型的拟合效果越好； （4）在回归分析中，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适．带状区域的宽度越窄，说明模型的拟合精度越高． 以上结论中，正确的有（ ）个．A ．1B ．2C ．3D ．4 6. 已知直线回归方程为2 1.5y x =-，则变量x 增加一个单位时（）A.y 平均增加1.5个单位B.y 平均增加2个单位C.y 平均减少1.5个单位D.y 平均减少2个单位7. 下面的各图中，散点图与相关系数r 不符合的是（ ）8. 一位母亲记录了儿子3～9岁的身高，由此建立的身高与年龄的回归直线方程为ˆ7.1973.93yx =+，据此可以预测这个孩子10岁时的身高，则正确的叙述是（ ）A ．身高一定是145.83cmB ．身高超过146.00cmC ．身高低于145.00cmD ．身高在145.83cm 左右9. 在画两个变量的散点图时，下面哪个叙述是正确的( ) (A)预报变量在x 轴上，解释变量在y 轴上 (B)解释变量在x 轴上，预报变量在y 轴上(C)可以选择两个变量中任意一个变量在x 轴上 (D)可以选择两个变量中任意一个变量在y 轴上10. 两个变量y 与x 的回归模型中，通常用2R 来刻画回归的效果，则正确的叙述是（ ）A. 2R 越小，残差平方和小B. 2R 越大，残差平方和大C. 2R 于残差平方和无关 D. 2R 越小，残差平方和大 11. 两个变量y 与x 的回归模型中，分别选择了4个不同模型，它们的相关指数2R 如下 ，其中拟合效果最好的模型是( )A.模型1的相关指数2R 为B.模型2的相关指数2R 为C.模型3的相关指数2R 为 D.模型4的相关指数2R 为12. 在回归分析中，代表了数据点和它在回归直线上相应位置的差异的是( ) A.总偏差平方和 B.残差平方和 C.回归平方和 D.相关指数R 213.工人月工资（元）依劳动生产率（千元）变化的回归直线方程为ˆ6090y x =+，下列判断正确的是（ ） A.劳动生产率为1000元时，工资为50元 B.劳动生产率提高1000元时，工资提高150元 C.劳动生产率提高1000元时，工资提高90元 D.劳动生产率为1000元时，工资为90元14. 下列结论正确的是（ ）①函数关系是一种确定性关系；②相关关系是一种非确定性关系；③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法． Ａ．①② Ｂ．①②③ Ｃ．①②④ Ｄ．①②③④15. 已知回归直线的斜率的估计值为，样本点的中心为（4，5），则回归直线方程为（ ） Ａ． 1.234y x =+ Ｂ． 1.235y x =+ Ｃ． 1.230.08y x =+ Ｄ．0.08 1.23y x =+二、填空题16. 在比较两个模型的拟合效果时，甲、乙两个模型的相关指数2R 的值分别约为和，则拟合效果好的模型是 ．17. 在回归分析中残差的计算公式为 ．18. 线性回归模型y bx a e =++（a 和b 为模型的未知参数）中，e 称为 ．19. 若一组观测值（x 1,y 1）（x 2,y 2）…（x n ,y n ）之间满足y i =bx i +a+e i (i=1、2.…n)若e i 恒为0，则R 2为_____三、解答题20. 调查某市出租车使用年限x 和该年支出维修费用y （万元），得到数据如下：（2）由（1）中结论预测第10年所支出的维修费用．（121()()()ni i i ni i x x y y b x x a y bx==⎧-⋅-⎪⎪=⎨-⎪⎪=-⎪⎩∑∑）21. 以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据：（1）画出数据对应的散点图；（2）求线性回归方程，并在散点图中加上回归直线；150m时的销售价格.（3）据（2）的结果估计当房屋面积为2（4）求第2个点的残差。

竞赛班高考数学练习（9）——线性回归分析1.在两个变量的回归分析中，作散点图是为了（ ）A. 直接求出回归直线方程B. 直接求出回归方程C. 根据经验选定回归方程的类型D. 估计回归方程的参数 2.下列四个结论：①在回归分析模型中，残差平方和越大，说明模型的拟合效果越好；②某学校有男教师60名、女教师40名，为了解教师的体育爱好情况，在全体教师中抽取20名调查，则宜采用的抽样方法是分层抽样；③线性相关系数|r|越大，两个变量的线性相关性越弱；反之，线性相关性越强；④在回归方程0.52y x =+中，当解释变量x 每增加一个单位时，预报变量y 增加0.5个单位. 其中正确的结论是（ ） A. ①② B. ①④C. ②③D. ②④3.某同学在只听课不做作业的情况下，数学总不及格.后来他终于下定决心要改变这一切，他以一个月为周5一个月内每天做题数x 5 8 6 4 7 数学月考成绩y8287848186ˆˆ1.6yx a =+题数为（ ） A. 8 B. 9 C. 10 D. 11 4.下列关于回归分析的说法中错误的有（ ）个(1).残差图中残差点所在的水平带状区域越宽，则回归方程的预报精确度越高.(2).回归直线一定过样本中心(),x y 。

(3)两个模型中残差平方和越小的模型拟合的效果越好。

(4) 甲、乙两个模型的2R 分别约为0.88和0.80，则模型乙的拟合效果更好。

A. 4 B. 3 C. 2 D. 15.两个变量y 与x 的回归模型中，分别选择了4个不同模型，它们的相关指数2R 如下，其中拟合效果最好的模型是（ ）A. 模型3的相关指数2R 为0.50B. 模型2的相关指数2R 为0.80C. 模型1的相关指数2R 为0.98D. 模型4的相关指数2R 为0.256.相关变量x ，y 的散点图如图所示，现对这两个变量进行线性相关分析，方案一：根据图中所有数据，得到线性回归方程11y b x a =+，相关系数为1r ；方案二：剔除点(10,21)，根据剩下数据得到线性回归直线方程：22y b x a =+，相关系数为2r .则（ ） A. 1201r r <<< B. 2101r r <<< C. 1210r r -<<<D. 2110r r -<<<7(补).2019年是新中国成立七十周年，新中国成立以来，我国文化事业得到了充分发展，尤其是党的十八大以来，文化事业发展更加迅速，下图是从2013 年到 2018 年六年间我国公共图书馆业机构数（个）与对应年份编号的散点图（为便于计算，将 2013 年编号为 1，2014 年编号为 2，…，2018年编号为 6，把每年的公共图书馆业机构个数作为因变量，把年份编号从 1 到 6 作为自变量进行回归分析），得到回归直线ˆ13.7433095.7yx =+，其相关指数2R 0.9817=，给出下列结论，其中正确的个数是( D )①公共图书馆业机构数与年份的正相关性较强 ②公共图书馆业机构数平均每年增加13.743个 ③可预测 2019 年公共图书馆业机构数约为3192个 A. 0 B. 1 C. 2 D. 37.某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示，该地周光照量X(小时)都在30小时以上，其中不足50小时的周数有5周，不低于50小时且不超过70小时的周数有35周，超过70小时的周数有10周.根据统计，该基地的西红柿增加量y(百斤)与使用某种液体肥料x(千克)之间对应数据为如图所示的折线图．（1）依据数据的折线图，是否可用线性回归模型拟合y 与x 的关系？请计算相关系数r 并加以说明(精确到0.01)(若0.75r >，则线性相关程度很高，可用线性回归模型拟合)（2）蔬菜大棚对光照要求较大，某光照控制仪商家为该基地提供了部分光照控制仪，但每周光照控制仪最多可运行台数受周光照量X 限制，并有如表关系：周光照量X （单位：小时） 3050X <<5070X ≤≤70X >光照控制仪最多可运行台数321若某台光照控制仪运行，则该台光照控制仪周利润为元；若某台光照控制仪未运行，则该台光照控制仪周亏损1000元.以过去50周的周光照量的频率作为周光照量发生的概率，商家欲使周总利润的均值达到最大，应安装光照控制仪多少台？附：相关系数12211()()()()niii nniii i x x yy r x x yy ===--=--∑∑∑，参考数据：51()()6i i i x x y y =--=∑，521()25ii x x =-=∑，521()2,0.30.55ij y y =-=≈∑，0.90.95≈8.东莞市公交公司为了方便广大市民出行，科学规划公交车辆的投放，计划在某个人员密集流动地段增设一个起点站，为了研究车辆发车的间隔时间x 与乘客等候人数y 之间的关系，选取一天中的六个不同的调查小组先从这组数据中选取其中的组数据求得线性回归方程，再用剩下的组数据进行检验，检验方法如下：先用求得的线性回归方程计算间隔时间对应的等候人数ˆy，再求ˆy 与实际等候人数y 的差，若两组差值的绝对值均不超过1，则称所求的回归方程是“理想回归方程”.（1）若选取的是前4组数据，求y 关于x 的线性回归方程ˆy bxa =+； （2）判断（1）中的方程是否是“理想回归方程”：（3）为了使等候的乘客不超过38人，试用（1）中方程估计间隔时间最多可以设置为多少分钟？ 参考公式：用最小二乘法求线性回归方程˙ˆˆˆy bx a =+的系数公式：()()()1122211ˆˆˆ,n niii ii i nnii i ix x y y x y n x ybay bx x x xnx ====---••===---∑∑∑∑，9.某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局和某医院抄录了1至该兴趣小组确定的研究方案是先从这组数据中选取组，用剩下的组数据求线性回归方程，再用被选出的2组数据进行检验.（1）若选取的是1月和6月的两组数据，请根据2月至5月的数据求出y 关x 于的线性回归方程；（2）若由线性回归方程得到的估计数，与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的.试问：该小组所得的线性回归方程是否理想？附;()()()1122211=nni i i ii i nni i i i x x y y x y nxyb x x x nx a y bx====⎧---⎪⎪=⎪⎨--⎪⎪=-⎪⎩∑∑∑∑10.某羽绒服卖场为了解气温对营业额的影响，随机记录了该店3月份上旬中某5天的日营业额y(单元：千元)与该地当日最低气温x(单位：°C)的数据，如表：（1）求y 关于x 的回归直线方程ˆˆˆybx a =+； （2）设该地3月份的日最低气温2~(,)X N μσ，其中μ近似为样本平均数，2σ近似为样本方差，求()0.6 3.8P X <<参考公式：()()()1122211ˆnni iiii i nniii i x ynxyx x yy bxnx x x ====---==--∑∑∑∑，ˆˆay bx =- 计算参考值：22222258911295,2125108898117287++++=⨯+⨯+⨯+⨯+⨯=.3.2,()0.6827,(22)0.9545P X P X μσμσμσμσ≈-<<+=-<<+=.竞赛班高考数学练习（9）——参考答案更正第7题第（2）问答案选择题1--6 CDC CCD解答题7.【详解】（1）由已知数据可得2456855x++++==，3444545y++++==所以相关系数()()0.95ni ix x y yr--===≈∑因为0.75r>，所以可用线性回归模型拟合y与x的关系。

第11章 一元线性回归练习题一、填空题1、拟合简单回归直线最常用的方法是 ，其基本要求是使 达到最小。

2、在简单回归分析中，因变量y 的总离差可以分解为 和 。

3、设SSR=36，SSE=4，n=18，判定系数2R = 。

4、在判定现象相关关系密切程度时，主要用 进行一般性判断，用 进行数量上的说明。

5、在线性回归方程 2.87X 48.53Yˆ+=中，截距项系数48.53的含义是 ，斜率项系数2.87的含义是 。

6、如果从图形上看，两变量之间的关系近似地表现为直线形式，则称这两变量之间存在 关系。

7、回归模型中，对参数β进行显著性检验时，原假设H 是 ，备择假设1H 是 。

8、判定系数的取值范围是 。

9、按某产品产量（千件）与生产费用（万元）之间的相关关系，求得回归方程满足：产量每增加1千件，生产费用将增加2.5万元，当产量为8千件时，生产费用将为26万元。

则直线回归方程为 。

10、反映y 的总变差中由x 和y 的线性关系解释的部分的平方和是 。

二、判断题（共10题，每题1分，共计10分） 1、222i i i i ˆˆ(y y )(y y )(y y )-=-+-∑∑∑，反映了因变量y 的总变异可以分解为两部分，一个好的回归应使等式右端的两部分都小。

( ) 2、用一元线性回归模型中，随机误差项反映的是除了自变量X 以外其他所有因素对因变量Y 的影响。

( ) 3、在一元线性回归模型中对回归系数显著性检验的t 统计量和对因变量与自变量相关系数检验的t 统计量没有关系。

( ) 4、相关系数与回归系数的正负方向是一致的。

( ) 5、根据航班正点率（%）与旅客投诉率（次/万名）建立的回归方程为ˆ 6.020.07yx =-，其中回归系数-0.07，表示航班正点率与旅客投诉率之间是低度相关。

( ) 6、相关系数有正负、有大小，因而它反映的是两现象之间具体的数量变动关系。

( ) 7、当相关系数0r =时，表明现象之间完全无关。