线性回归方程练习题

回归方程例题
回归方程是一种用于预测因变量与自变量之间的关系的数学模型。

在例题中，我们可以使用线性回归方程来预测某个因变量的值，该因变量的值受多个自变量的影响。

下面是一个简单的线性回归方程例题:
假设有一组数据点，其横轴为自变量 x1、x2、x3 等，纵轴为因变量 y。

我们希望建立一个线性回归方程，来预测 y 的值。

首先，我们需要计算出每个数据点的平均值。

例如，对于自变量x1，我们可以计算所有数据点中 x1 的平均值，即:
mean(x1) = (x11 + x12 + x13 + ... + x1n) / n
接着，我们可以计算出每个自变量对因变量的影响。

例如，对于自变量 x1，我们可以计算 y 关于 x1 的线性回归系数，即:
b1 = (y - mean(y)) / std(x1)
其中，std(x1) 表示 x1 的标准差，mean(y) 表示 y 的平均值，std(y) 表示 y 的标准差。

最后，我们可以使用计算出的回归系数来构建线性回归方程，例如:
y = b0 + b1*x1 + b2*x2 + b3*x3 + ... + bnxn
其中，b0、b1、b2、b3 等为常数，x1、x2、x3 等为自变量。

在实际问题中，我们需要根据具体问题来选择适当的回归方程类型，并计算出相应的回归系数。

然后，我们可以使用这些系数来预测因变量的值。

一、是非题1．单个自变量的线性回归就是直线回归。

2．直线回归就是指自变量和应变量的观察值落在在一条直线上。

3．直线回归中预测值Y 是固定某个X 值，Y 的总体均数估计值。

4．用逐步回归的方法评价自变量与应变量之间的关联性，只能推断某个自变量与应变量有关联性，不能推断无它们之间无关联性。

二、选择题1．用最小二乘法确定直线回归方程的原则是各观察点（）A ． 距直线的纵向距离相等B ． 距直线的纵向距离的平方和最小C ． 与直线的垂直距离相等D ． 与直线的垂直距离的平方和最小 2．直线回归的系数假设检验（）E ． 只能利用相关系数r 的检验方法进行检验F ． 只能用t 检验G ． 只能用F 检验H ． 三者均可3．Y ˆ=7+2X 是1~7岁儿童以年龄(岁)估计体重(公斤)的回归方程，若把体重的单位换成市斤，则此方程（ ）A ．截矩改变B ．回归系数改变C ． 截矩与回归系数都改变D ．回归系数不变E ．截矩不变 4．直线回归系数的假设检验，其自由度为（ ）A ．nB ．n-1C ．n-2D ．2n-1E ．2n-25．对应变量Y 的离均差平方和，下列哪个分解是正确的？（ ）A ．SS 剩=SS 回B ．SS 总=SS 剩C ．SS 总=SS 回D ．SS 总＋SS 剩=SS 回E ．SS 总＋SS 回=SS 剩三、计算分析题1．15名儿童的身高与肺死腔容积的观察值如表15-3所示。

表15-3 儿童身高与肺死腔容积的观测数据对象号 身高(cm)X 肺死腔容积(ml)Y 对象号 身高(cm)X 肺死腔容积(ml)Y 1 110 45 9 175 102 2 116 32 10 167 111 3 123 41 11 165 88 4 130 45 12 160 65 5 129 43 13 157 79 6 142 67 14 156 92 7 147 58 15 149 58 815357试用该资料进行回归分析：（1）计算样本回归方程的截矩与回归系数； （2）进行回归系数等于0的假设检验； （3）验证是否存在F t b =的关系；（4）估计回归系数β的95%置信区间。

线性回归练习一、选择题1.下列两个变量之间的关系中，哪个是函数关系 （ ） A.学生的性别与他的数学成绩 B.人的工作环境与健康状况 C.女儿的身高与父亲的身高 D. 正三角形的边长与面积2．从某大学随机选取8名女大学生，其身高x (cm)和体重y (kg)的回归方程为 ˆ0.84985.712yx =-，则身高172cm 的女大学生，由回归方程可以预报其体重 （ ）A.为6 0.316kgB. 约为6 0.316kgC.大于6 0.316kgD.小于6 0.316kg3. 工人月工资（元）依劳动生产率（千元）变化的回归直线方程为ˆ160180yx =+，下列判断正确的是 （ ）A ．劳动生产率为1000元时，工资为340元B ．劳动生产率提高1000元时，工资提高180元C ．劳动生产率提高1000元时，工资平均提高180元 D.工资为520元时，劳动生产率为2000元 4．由右表可计算出变量,x y 的线性回归方程为（ ） A. ˆ0.350.15y x =-+ B. ˆ0.350.25y x =-+ C. ˆ0.350.15y x =+ D. ˆ0.350.25y x =+ 二、填空题5．下列说法中正确的是 （填序号）①回归分析就是研究两个相关事件的独立性；②回归模型都是确定性的函数；③回归模型都是线性的；④回归分析的第一步是画散点图或求相关系数r ；⑤回归分析就是通过分析、判断，确定相关变量之间的内在的关系的一种统计方法. 6．三点()3,10,(7,20),(11,24)的线性回归方程是三、解答[2016高考新课标Ⅲ文数]下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图（I ）由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明；（II ）建立y 关于t 的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量． 附注： 参考数据：719.32ii y==∑，7140.17i i i t y ==∑0.55=，7≈2.646.参考公式：相关系数r =回归方程y a b =+中斜率和截距的最小二乘估计公式分别为：121()()()nii i nii tt y y b tt ==--=-∑∑，a y bt =-【2015高考重庆，文17】随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款（年底余额）如下表：(Ⅰ)求y 关于t 的回归方程^^^t y b a =+(Ⅱ)用所求回归方程预测该地区2015年（6t =）的人民币储蓄存款. 附：回归方程^^^t yb a=+中1122211()(),().nniii ii i nniii i x x y y x y nx yb x x xnxa y bx ====⎧---⎪⎪==⎪⎨--⎪⎪=-⎪⎩∑∑∑∑8、这个世界并不是掌握在那些嘲笑者的手中，而恰恰掌握在能够经受得住嘲笑与批忍不断往前走的人手中。

第9章一元线性回归练习题一．选择题1．具有相关关系的两个变量的特点是（）A．一个变量的取值不能由另一个变量唯一确定B．一个变量的取值由另一个变量唯一确定C．一个变量的取值增大时另一个变量的取值也一定增大D．一个变量的取值增大时另一个变量的取值肯定变小2．下面的各问题中，哪个不是相关分析要解决的问题A．判断变量之间是否存在关系B．判断一个变量数值的变化对另一个变量的影响C．描述变量之间的关系强度 D.判断样本所反映的变量之间的关系能否代表总体变量之间的关系3.根据下面的散点图，可以判断两个变量之间存在（）A.正线性相关关系B. 负线性相关关系C. 非线性关系D. 函数关系4.下面的陈述哪一个是错误的（）A. 相关系数是度量两个变量之间线性关系强度的统计量B．相关系数是一个随机变量C．相关系数的绝对值不会大于1D．相关系数不会取负值5.根据你的判断，下面的相关系数取值哪一个是错误的（）A. -0.86B. 0.78C. 1.25D. 06.如果相关系数r=0,则表明两个变量之间（）A.相关程度很低B. 不存在任何关系C．不存在线性相关关系D.存在非线性关系7.下列不属于相关关系的现象是（）A.银行的年利息率与贷款总额B.居民收入与储蓄存款C.电视机的产量与鸡蛋产量D.某种商品的销售额与销售价格8.设产品产量与产品单位成本之间的线性相关系数为-0.87，这说明二者之间存在着（）A. 高度相关B.中度相关C.低度相关D.极弱相关9.在回归分析中，被预测或被解释的变量称为（）A.自变量B.因变量C.随机变量D.非随机变量10.对两变量的散点图拟合最好的回归线，必须满足一个基本的条件是（）A.2ˆ()yy∑-最小B.2)(ˆyy∑-最大C.2ˆ()yy∑-最大D.2)(ˆyy∑-最小11. 下列哪个不属于一元回归中的基本假定（）A.误差项i ε服从正态分布B. 对于所有的X ，方差都相同C. 误差项i ε相互独立D. 0)ˆ=-i i yy E （ 12.如果两个变量之间存在着负相关，指出下列回归方程中哪个肯定有误（ ）A.x y75.025ˆ-= B. x y 86.0120ˆ+-= C. x y 5.2200ˆ-= D. x y 74.034ˆ--= 13.对不同年份的产品成本拟合的直线方程为,75.1280ˆx y-=y 表示产品成本，x 表示不同年份，则可知（ ）A.时间每增加一个单位，产品成本平均增加1.75个单位B. 时间每增加一个单位，产品成本平均下降1.75个单位C.产品成本每变动一个单位，平均需要1.75年时间D. 产品成本每减少一个单位，平均需要1.75年时间 14.在回归分析中，F 检验主要是用来检验（ ）A ．相关关系的显著性 B.回归系数的显著性 C. 线性关系的显著性D.估计标准误差的显著性15.说明回归方程拟合优度的统计量是（ ）A. 相关系数B.回归系数C. 判定系数D. 估计标准误差16.已知回归平方和SSR=4854,残差平方和SSE=146,则判定系数R 2=( ) A.97.08% B.2.92% C.3.01% D. 33.25% 17. 判定系数R2值越大，则回归方程（ ）A 拟合程度越低B 拟合程度越高C 拟合程度有可能高，也有可能低D 用回归方程进行预测越不准确 18. 居民收入与储蓄额之间的相关系数可能是（ ） A -0.9247 B 0.9247 C -1.5362 D 1.536219.在对一元回归方程进行显著性检验时，得到判定系数R 2=0.80,关于该系数的说法正确的是（ ）A. 该系数越大，则方程的预测效果越好B. 该系数越大，则由回归方程所解释的因变量的变差越多C. 该系数越大，则自变量的回归对因变量的相关关系越显著D. 该回归方程中自变量与因变量之间的相关系数可能小于0.8 20.下列方程中肯定错误的是（ ）A. x y48.015ˆ-=，r=0.65 B. x y 35.115ˆ--=, r= - 0.81 C. x y85.025ˆ+-=, r=0.42 D. x y 56.3120ˆ-=, r= - 0.96 21. 若两个变量存在负相关关系，则建立的一元线性回归方程的判定系数R 2的取值范围是（ ）A.【0，1】B. 【-1，0】C. 【-1，1】D.小于0的任意数二． 填空题1.当从某一总体中抽取了一样本容量为30的样本，并计算出某两个变量的相关系数为0.8时，我们是否可认为这两个变量存在着强相关性（不能 ） ，理由是（因为该相关系数为样本计算出的相关系数，它的大小受样本数据波动的影响，它是否显著尚需检验 ）。

线性回归方程高考题1、下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（吨）与相应的生产能耗（吨标准煤）的几组对照数据：3 4 5 62.5 3 4 4.5（1）请画出上表数据的散点图；（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；（3）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? （参考数值：）2、假设关于某设备的使用年限x和所支出的维修费用y(万元)统计数据如下:使用年限x 2 3 4 5 6维修费用y 2.2 3.8 5.5 6.5 7.0若有数据知y对x呈线性相关关系.求:(1) 填出下图表并求出线性回归方程=bx+a的回归系数,;序号x y xy x21 2 2.22 3 3.83 4 5.54 5 6.55 6 7.0∑(2) 估计使用10年时,维修费用是多少.3、某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四实试验，得到的数据如下：零件的个数x（个） 2 3 4 5加工的时间y（小时） 2.5 3 4 4.5（1）在给定的坐标系中画出表中数据的散点图；（2）求出y关于x的线性回归方程，并在坐标系中画出回归直线；（3）试预测加工10个零件需要多少时间？（注：4、某服装店经营的某种服装，在某周内获纯利(元)与该周每天销售这种服装件数之间的一组数据关系如下表：3 4 5 6 7 8 966 69 73 81 89 90 91已知：．(Ⅰ)画出散点图；(1I)求纯利与每天销售件数之间的回归直线方程．5、某种产品的广告费用支出与销售额之间有如下的对应数据：2 4 5 6 830 40 60 50 70(1)画出散点图：(2)求回归直线方程；(3)据此估计广告费用为10时，销售收入的值．6、下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据：ｘ 3 4 5 6ｙ 2.5 3 4 4.5（I）请画出上表数据的散点图；（II）请根据上表提供的数据，求出ｙ关于ｘ的线性回归方程；（III）已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据（II）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？（参考公式及数据: ,）7、以下是测得的福建省某县某种产品的广告费支出x与销售额y（单位：百万元）之间，有如下的对应数据：广告费支出x 2 4 5 6 8销售额y 30 40 60 50 70（1）画出数据对应的散点图，你能从散点图中发现福建省某县某种产品的广告费支出x与销售额y（单位：百万元）之间的一般规律吗？（2）求y关于x的回归直线方程；（3）预测当广告费支出为2（百万元）时，则这种产品的销售额为多少？（百万元）8、在某种产品表面进行腐蚀线实验，得到腐蚀深度y与腐蚀时间t之间对应的一组数据：时间t(s) 5 10 15 20 306 10 10 13 16深度y(m)(1)画出散点图；(2)试求腐蚀深度y对时间t的回归直线方程。

13．(09·江苏理)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习，每人投1021．(本题满分12分)下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x (吨)与相应的生产能耗(1)(2)请根据上表提供的数据，求出y 关于x 的回归直线方程； (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的回归直线方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？13．(09·江苏理)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习，每人投10[答案] 25[解析] x 甲＝6＋7＋7＋8＋75＝7，x 乙＝6＋7＋6＋7＋95＝7，∴s 2甲＝(6－7)2＋(7－7)2＋(7－7)2＋(8－7)2＋(7－7)25＝25， s 2乙＝(7－6)2＋(7－7)2＋(7－6)2＋(7－7)2＋(7－9)25＝65， 21．(本题满分12分)下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x (吨)与相应的生产能耗(1)(2)请根据上表提供的数据，求出y 关于x 的回归直线方程；(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的回归直线方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？[解析] (1)散点图如图．(2)x －＝4.5，y －＝3.5，b ^＝∑x i y i －4x － y －∑x 2i －4x －2＝66.5－6386－81＝0.7，a ^＝3.5－0.7×4.5＝0.35，∴回归直线方程为y ^＝0.7x ＋0.35. (3)90－(0.7×100＋0.35)＝19.65(t) ∴降低了19.65吨．教你如何用WORD 文档标签： 杂谈1. 问：WORD答：分节，不同。

2. 问：请问word 部改了？答：在插入分隔符里，个字来。

线性回归方程一．选择题（共11小题）1．（2017•山东）为了研究某班学生的脚长x （单位：厘米）和身高y （单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y 与x 之间有线性相关关系，设其回归直线方程为ˆˆˆybx a =+，已知101225ii x==∑，1011600i i y ==∑，ˆ4b=，该班某学生的脚长为24，据此估计其身高为( ) A ．160 B ．163 C ．166 D ．1702．（2015•福建）为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程ˆˆy bx a =+，其中ˆˆ0.76,b a y bx ==-，据此估计，该社区一户收入为15万元家庭年支出为( ) A ．11.4万元B ．11.8万元C ．12.0万元D ．12.2万元3．（2014•重庆）已知变量x 与y 正相关，且由观测数据算得样本平均数3x =， 3.5y =，则由该观测数据算得的线性回归方程可能是( ) A ．ˆ0.4 2.3yx =+ B ．ˆ2 2.4yx =- C ．ˆ29.5yx =-+ D ．ˆ0.3 4.4yx =-+ 4．（2014•湖北）根据如下样本数据：得到了回归方程ˆˆy bx a =+，则( ) A ．ˆ0a>，ˆ0b < B ．ˆ0a>，ˆ0b > C ．ˆ0a<，ˆ0b < D ．ˆ0a<，ˆ0b > 5．（2014•湖北）根据如下样本数据，得到回归方程ˆybx a =+，则( )6．（2013•湖北）四名同学根据各自的样本数据研究变量x ，y 之间的相关关系，并求得回归直线方程，分别得到以下四个结论：①y 与x 负相关且ˆ 2.347 6.423yx =-； ②y 与x 负相关且ˆ 3.476 5.648yx =-+； ③y 与x 正相关且ˆ 5.4378.493yx =+； ④y 与x 正相关且ˆ 4.326 4.578yx =--． 其中一定不正确的结论的序号是( )A ．①②B ．②③C ．③④D ．①④7．（2013•福建）已知x 与y 之间的几组数据如表：假设根据上表数据所得线性回归直线方程为ˆˆy bx a =+，若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y b x a ='+'，则以下结论正确的是( ) A ．ˆbb >'，ˆa a >' B ．ˆbb >'，ˆa a <' C ．ˆbb <'，ˆa a >' D ．ˆbb <'，ˆa a <' 8．（2011•陕西）设1(x ，1)y ，2(x ，2)y ，⋯，(n x ，)n y 是变量x 和y 的n 次方个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论正确的是( )A ．直线l 过点(,)x yB ．x 和y 的相关系数为直线l 的斜率C ．x 和y 的相关系数在0到1之间D ．当n 为偶数时，分布在l 两侧的样本点的个数一定相同9．（2011•江西）为了解儿子身高与其父亲身高的关系，随机抽取5对父子身高数据如下A ．1y x =-B ．1y x =+C ．1882y x =+D ．176y =10．（2011•陕西）设1(x ，1)y ，2(x ，2)y ，⋯，(n x ，)n y 是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是( )A ．x 和y 的相关系数为直线l 的斜率B ．x 和y 的相关系数在0到1之间C ．当n 为偶数时，分布在l 两侧的样本点的个数一定相同D ．直线l 过点(x ，)y11．（2011•山东）某产品的广告费用x 与销售额y 的统计数据如下表根据上表可得回归方程ˆˆybx a =+的b 为9.4，据此模型预报广告费用为6万元时销售额为( ) A ．63.6万元 B ．65.5万元 C ．67.7万元 D ．72.0万元二．填空题（共3小题）12．（2011•辽宁）调查了某地若干户家庭的年收x （单位：万元）和年饮食支出y （单位：万元），调查显示年收入x 与年饮食支出y 具有线性相关关系，并由调查数据得到y 对x 的回归直线方程ˆ0.2540.321yx =+．由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加 万元．13．（2011•广东）某数学老师身高176cm ，他爷爷、父亲和儿子的身高分别是173cm 、170cm 和182cm ．因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为 cm ．14．（2011•广东）工人月工资y （元)与劳动生产率x （千元）变化的回归方程为ˆ5080yx =+，下列判断正确的是 ①劳动生产率为1千元时，工资为130元；②劳动生产率提高1千元，则工资提高80元；③劳动生产率提高1千元，则工资提高130元；④当月工资为210元时，劳动生产率为2千元．三．解答题（共2小题）15．（2013•重庆）从某居民区随机抽取10个家庭，获得第i 个家庭的月收入i x （单位：千元）与月储蓄i y （单位：千元）的数据资料，算得10180i i x ==∑，10120i i y ==∑，101184i i i x y ==∑，1021720i i x ==∑．（Ⅰ）求家庭的月储蓄y 对月收入x 的线性回归方程y bx a =+； （Ⅱ）判断变量x 与y 之间是正相关还是负相关；（Ⅲ）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．附：线性回归方程y bx a =+中，1221ni ii nii x ynxyb xnx ==-=-∑∑，a y bx =-，其中x ，y 为样本平均值，线性回归方程也可写为ˆˆˆybx a =+． 16．（2012•福建）某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：bx （Ⅱ）预计在今后的销售中，销量与单价仍然服从()I 中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）线性回归方程参考答案与试题解析一．选择题（共11小题）1．（2017•山东）为了研究某班学生的脚长x （单位：厘米）和身高y （单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y 与x 之间有线性相关关系，设其回归直线方程为ˆˆˆybx a =+，已知101225ii x==∑，1011600i i y ==∑，ˆ4b=，该班某学生的脚长为24，据此估计其身高为( ) A ．160 B ．163 C ．166 D ．170【解答】解：由线性回归方程为ˆˆ4y x a =+， 则101122.510i i x x ===∑，101116010i i y y ===∑，则数据的样本中心点(22.5,160)，由回归直线方程样本中心点，则ˆˆ4160422.570ay x =-=-⨯=， ∴回归直线方程为ˆ470yx =+， 当24x =时，ˆ42470166y=⨯+=， 则估计其身高为166， 故选：C ．2．（2015•福建）为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程ˆˆy bx a =+，其中ˆˆ0.76,b a y bx ==-，据此估计，该社区一户收入为15万元家庭年支出为( ) A ．11.4万元B ．11.8万元C ．12.0万元D ．12.2万元【解答】解：由题意可得1(8.28.610.011.311.9)105x =++++=，1(6.27.58.08.59.8)85y =++++=，代入回归方程可得ˆ80.76100.4a=-⨯=， ∴回归方程为ˆ0.760.4yx =+， 把15x =代入方程可得0.76150.411.8y =⨯+=， 故选：B ．3．（2014•重庆）已知变量x 与y 正相关，且由观测数据算得样本平均数3x =， 3.5y =，则由该观测数据算得的线性回归方程可能是( )A ．ˆ0.4 2.3y x =+B ．ˆ2 2.4y x =-C ．ˆ29.5y x =-+D ．ˆ0.3 4.4yx =-+ 【解答】解：变量x 与y 正相关， ∴可以排除C ，D ；样本平均数3x =， 3.5y =，代入A 符合，B 不符合， 故选：A ．4．（2014•湖北）根据如下样本数据：得到了回归方程ˆˆy bx a =+，则( ) A ．ˆ0a>，ˆ0b < B ．ˆ0a>，ˆ0b > C ．ˆ0a<，ˆ0b < D ．ˆ0a<，ˆ0b > 【解答】解：样本平均数 5.5x =，0.25y =，∴61()()24.5i i i x x y y =--=-∑，621()17.5i i x x =-=∑，24.51.417.5b ∴=-=-， 0.25( 1.4)5.57.95a ∴=--=，故选：A ．5．（2014•湖北）根据如下样本数据，得到回归方程ˆybx a =+，则( )【解答】解：由题意可知：回归方程经过的样本数据对应的点附近，是减函数，所以0b <，且回归方程经过(3,4)与(4,2.5)附近，所以0a >． 故选：B ．6．（2013•湖北）四名同学根据各自的样本数据研究变量x ，y 之间的相关关系，并求得回归直线方程，分别得到以下四个结论：①y 与x 负相关且ˆ 2.347 6.423yx =-； ②y 与x 负相关且ˆ 3.476 5.648yx =-+； ③y 与x 正相关且ˆ 5.4378.493yx =+； ④y 与x 正相关且ˆ 4.326 4.578yx =--． 其中一定不正确的结论的序号是( ) A ．①②B ．②③C ．③④D ．①④【解答】解：①y 与x 负相关且ˆ 2.347 6.423yx =-；此结论误，由线性回归方程知，此两变量的关系是正相关； ②y 与x 负相关且ˆ 3.476 5.648yx =-+；此结论正确，线性回归方程符合负相关的特征； ③y 与x 正相关且ˆ 5.4378.493yx =+； 此结论正确，线性回归方程符合正相关的特征； ④y 与x 正相关且ˆ 4.326 4.578yx =--．此结论不正确，线性回归方程符合负相关的特征．综上判断知，①④是一定不正确的 故选：D ．7．（2013•福建）已知x 与y 之间的几组数据如表：假设根据上表数据所得线性回归直线方程为ˆˆy bx a =+，若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y b x a ='+'，则以下结论正确的是( ) A ．ˆbb >'，ˆa a >' B ．ˆbb >'，ˆa a <' C ．ˆbb <'，ˆa a >' D ．ˆbb <'，ˆa a <' 【解答】解：由题意可知6n =，1121762n ii x x n ====∑，11136n i i y y n ===∑， 故22217916()222nii x nx =-=-⨯=∑，171325586262ni i i x y nxy =-=-⨯⨯=∑，故可得12215ˆ7ni ii nii x ynxybxnx ==-==-∑∑，13571ˆ6723a y bx =-=-⨯=-， 而由直线方程的求解可得02212b -'==-，把(1,0)代入可得2a '=-， 比较可得?b b <'，?a a >'， 故选：C ．8．（2011•陕西）设1(x ，1)y ，2(x ，2)y ，⋯，(n x ，)n y 是变量x 和y 的n 次方个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论正确的是( )A ．直线l 过点(,)x yB ．x 和y 的相关系数为直线l 的斜率C ．x 和y 的相关系数在0到1之间D ．当n 为偶数时，分布在l 两侧的样本点的个数一定相同 【解答】解：回归直线一定过这组数据的样本中心点，故A 正确， 两个变量的相关系数不是直线的斜率，而是需要用公式做出，故B 不正确， 直线斜率为负，相关系数应在(1,0)-之间，故C 不正确，所有的样本点集中在回归直线附近，不一定两侧一样多，故D 不正确， 故选：A ．9．（2011•江西）为了解儿子身高与其父亲身高的关系，随机抽取5对父子身高数据如下A ．1y x =-B ．1y x =+C ．1882y x =+D ．176y =【解答】解：1741761761761781765x ++++==，1751751761771771765y ++++==，∴本组数据的样本中心点是(176,176)，根据样本中心点一定在线性回归直线上，把样本中心点代入四个选项中对应的方程，只有1882y x =+适合， 故选：C ．10．（2011•陕西）设1(x ，1)y ，2(x ，2)y ，⋯，(n x ，)n y 是变量x 和y 的n 个样本点，直线l 是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是( )A ．x 和y 的相关系数为直线l 的斜率B ．x 和y 的相关系数在0到1之间C ．当n 为偶数时，分布在l 两侧的样本点的个数一定相同D ．直线l 过点(x ，)y【解答】解：直线l 是由这些样本点通过最小二乘法得到的线性回归直线，回归直线方程一定过样本中心点， 故选：D ．11．（2011•山东）某产品的广告费用x 与销售额y 的统计数据如下表根据上表可得回归方程ˆˆybx a =+的b 为9.4，据此模型预报广告费用为6万元时销售额为( ) A ．63.6万元 B ．65.5万元 C ．67.7万元D ．72.0万元【解答】解：42353.54x +++==， 49263954424y +++==，数据的样本中心点在线性回归直线上， 回归方程ˆˆˆybx a =+中的ˆb 为9.4， ˆ429.4 3.5a ∴=⨯+， ∴ˆ9.1a=， ∴线性回归方程是9.49.1y x =+，∴广告费用为6万元时销售额为9.469.165.5⨯+=，故选：B ．二．填空题（共3小题）12．（2011•辽宁）调查了某地若干户家庭的年收x （单位：万元）和年饮食支出y （单位：万元），调查显示年收入x 与年饮食支出y 具有线性相关关系，并由调查数据得到y 对x 的回归直线方程ˆ0.2540.321yx =+．由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加 0.254 万元． 【解答】解：对x 的回归直线方程ˆ0.2540.321y x =+． ∴1ˆ0.254(1)0.321yx =++， ∴1ˆˆ0.254(1)0.3210.2540.3210.254yy x x -=++--=． 故答案为：0.254．13．（2011•广东）某数学老师身高176cm ，他爷爷、父亲和儿子的身高分别是173cm 、170cm 和182cm ．因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高为 185 cm ．【解答】解：设X 表示父亲的身高，Y 表示儿子的身高则Y 随X 的变化情况如下；建立这种线性模型：求解得线性回归方程3y x =+ 当182x =时，185y = 故答案为：185．14．（2011•广东）工人月工资y （元)与劳动生产率x （千元）变化的回归方程为ˆ5080yx =+，下列判断正确的是 ②①劳动生产率为1千元时，工资为130元；②劳动生产率提高1千元，则工资提高80元；③劳动生产率提高1千元，则工资提高130元；④当月工资为210元时，劳动生产率为2千元． 【解答】解：：对x 的回归直线方程ˆ5080y x =+， ∴1ˆ80(1)50yx =++， ∴1ˆˆ80(1)50805080yy x x -=++--=．所以劳动生产率提高1千元，则工资提高80元，②正确，③不正确． ①④不满足回归方程的意义． 故答案为：②．三．解答题（共2小题）15．（2013•重庆）从某居民区随机抽取10个家庭，获得第i 个家庭的月收入i x （单位：千元）与月储蓄i y （单位：千元）的数据资料，算得10180i i x ==∑，10120i i y ==∑，101184i i i x y ==∑，1021720i i x ==∑．（Ⅰ）求家庭的月储蓄y 对月收入x 的线性回归方程y bx a =+； （Ⅱ）判断变量x 与y 之间是正相关还是负相关；（Ⅲ）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．附：线性回归方程y bx a =+中，1221ni ii nii x ynxyb xnx==-=-∑∑，a y bx =-，其中x ，y 为样本平均值，线性回归方程也可写为ˆˆˆybx a =+． 【解答】解：（Ⅰ）由题意可知10n =，1180810n ii x x n ====∑，1120210n i i y y n ====∑， 故222172010880nxx ii l x nx ==-=-⨯=∑，1184108224nxy i i i l x y nxy ==-=-⨯⨯=∑，故可得240.380xy xxl b l ====，20.380.4a y bx =-=-⨯=-， 故所求的回归方程为：0.30.4y x =-；（Ⅱ）由（Ⅰ）可知0.30b =>，即变量y 随x 的增加而增加，故x 与y 之间是正相关；（Ⅲ）把7x =代入回归方程可预测该家庭的月储蓄为0.370.4 1.7y =⨯-=（千元）．16．（2012•福建）某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：bx （Ⅱ）预计在今后的销售中，销量与单价仍然服从()I 中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本） 【解答】解：88.28.48.68.89()8.56I x +++++==，1(908483807568)806y =+++++=20b =-，a y bx =-，11 / 11 80208.5250a ∴=+⨯=∴回归直线方程ˆ20250yx =-+； ()II 设工厂获得的利润为L 元，则233(20250)4(20250)20()361.254L x x x x =-+--+=--+ ∴该产品的单价应定为334元，工厂获得的利润最大．。

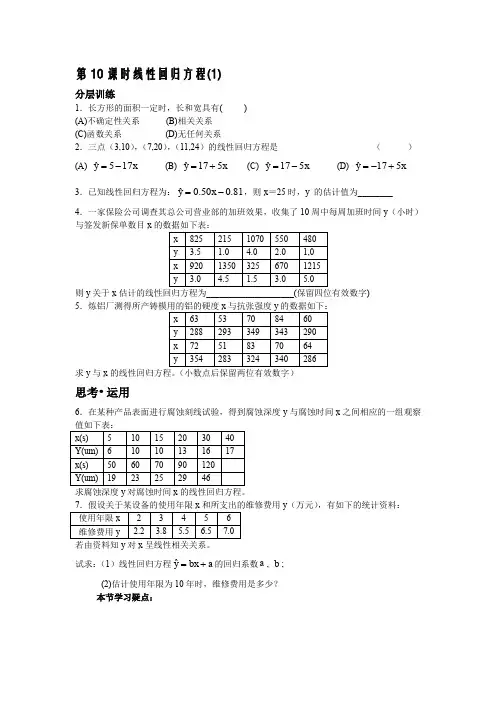
第10课时线性回归方程(1)
分层训练
1．长方形的面积一定时，长和宽具有( ) (A)不确定性关系 (B)相关关系 (C)函数关系 (D)无任何关系 2．三点（3,10），（7,20），（11,24）的线性回归方程是 （ ）
(A) x y
175ˆ-= (B) x y 517ˆ+= (C) x y 517ˆ-= (D) x y 517ˆ+-= 3．已知线性回归方程为：81.050.0ˆ-=x y
，则x ＝25时，y 的估计值为________ 4．一家保险公司调查其总公司营业部的加班效果，收集了10周中每周加班时间y （小时）与签发新保单数目x
则y 关于x 估计的线性回归方程为____________________(保留四位有效数字) 5
求y 与x 的线性回归方程。

（小数点后保留两位有效数字）
思考∙运用
6．在某种产品表面进行腐蚀刻线试验，得到腐蚀深度y 与腐蚀时间x 之间相应的一组观察值如下表：
y （万元），有如下的统计资料：
试求：（1）线性回归方程a bx y
+=ˆ的回归系数a , b ; (2)估计使用年限为10年时，维修费用是多少？
本节学习疑点：
6.4.1 线性回归方程(1)
1．C 2．D 3．11.69
4．x y
003585.01181.0ˆ+= 5．x y
96.168.183ˆ+= 6．x y
304.036.5ˆ+= 7．(1) 23.1=b , 08.0=a
(2) 线性回归方程是 08.023.1ˆ+=x y
当x=10时，38.1208.01023.1ˆ=+⨯=y
即估计使用10年时的维修费用是12.38万元。

第二章 简单线性回归模型练习题一、术语解释 1 解释变量 2 被解释变量 3 线性回归模型 4 最小二乘法 5 方差分析 6 参数估计 7 控制 8 预测 二、填空1 在经济计量模型中引入反映（ ）因素影响的随机扰动项t ξ，目的在于使模型更符合（ ）活动。

2 在经济计量模型中引入随机扰动项的理由可以归纳为如下几条：（1）因为人的行为的（ ）、社会环境与自然环境的（ ）决定了经济变量本身的（ ）；（２）建立模型时其他被省略的经济因素的影响都归入了（ ）中；（３）在模型估计时，（ ）与归并误差也归入随机扰动项中；（4）由于我们认识的不足，错误的设定了（ ）与（ ）之间的数学形式，例如将非线性的函数形式设定为线性的函数形式，由此产生的误差也包含在随机扰动项中了。

3 （ ）是因变量离差平方和，它度量因变量的总变动。

就因变量总变动的变异来源看，它由两部分因素所组成。

一个是自变量，另一个是除自变量以外的其他因素。

（ ）是拟合值的离散程度的度量。

它是由自变量的变化引起的因变量的变化，或称自变量对因变量变化的贡献。

（ ）是度量实际值与拟合值之间的差异，它是由自变量以外的其他因素所致，它又叫残差或剩余。

4 回归方程中的回归系数是自变量对因变量的（ ）。

某自变量回归系数β的意义，指的是该自变量变化一个单位引起因变量平均变化（ ）个单位。

5 模型线性的含义，就变量而言，指的是回归模型中变量的（ ）；就参数而言，指的是回归模型中的参数的（ ）；通常线性回归模型的线性含义是就（ ）而言的。

6 样本观察值与回归方程理论值之间的偏差，称为（ ），我们用残差估计线性模型中的（ ）。

三、简答题1 在线性回归方程中，“线性”二字如何理解？2 用最小二乘法求线性回归方程系数的意义是什么？3 一元线性回归方程的基本假设条件是什么？4 方差分析方法把数据总的平方和分解成为两部分的意义是什么？5 试叙述t 检验法与相关系数检验法之间的联系。

高二第二学期第一章线性回归方程同步练习题（文科）（1）一、选择题1 . 下列两个变量之间的关系哪个不是函数关系（ D ） A ．角度和它的余弦值 B.正方形边长和面积 C ．正ｎ边形的边数和它的内角和 D.人的年龄和身高2．某市纺织工人的月工资（元）依劳动生产率（千元）变化的回归方程为y=50+80x ，则下列说法中正确的是（ C ）A ．劳动生产率为1000元时，月工资为130元B ．劳动生产率提高1000元时，月工资提高约为130元C ．劳动生产率提高1000元时，月工资提高约为80元D ．月工资为210元时，劳动生产率为2000元 3．设有一个回归方程为y=2-1.5x ，则变量x 每增加一个单位时，y 平均 （ C ） A ．增加1.5单位 B ．增加2单位 C ．减少1.5单位 D ．减少2单位4．实验测得四组(x ，y )的值为(1,2)，(2,3)，(3,4)，(4,5)，则y 与x 之间的回归直线方程为( A )A.y ^＝x ＋1 B.y ^＝x ＋2 C.y ^＝2x ＋1 D.y ^＝x －15．由一组样本(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )得到的回归直线方程y ^＝a ＋bx ，下面有四种关于回归直线方程的论述：(1)直线y ^＝a ＋bx 至少经过点(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )中的一个点；(2)直线y ^＝a ＋bx 的斜率是∑ni ＝1x i y i －n x y ∑ni ＝1x 2i －n x 2；(3)直线y ^＝a ＋bx 必过(x ，y )点； (4)直线y ^＝a ＋bx 和各点(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )的偏差∑ni ＝1 (y i －a －bx i )2是该坐标平面上所有的直线与这些点的偏差中最小的直线．其中正确的论述有( D )A ．0个 B ．1个C ．2个 D ．3个解析 线性回归直线不一定过点(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )中的任何一点；b ＝∑ni ＝1x i y i －n x y∑ni ＝1x 2i －n x 2就是线性回归直线的斜率，也就是回归系数；线性回归直线过点(x ，y )；线性回归直线是平面上所有直线中偏差∑ni ＝1(y i －a －bx i )2取得最小的那一条．故有三种论述是正确的，选D. 6．某化工厂为预测产品的回收率y ，需要研究它和原料有效成分含量x 之间的相关关系，现取8对观测值，计算，得∑8i ＝1x i ＝52，∑8i ＝1y i ＝228，∑8i ＝1x 2i ＝478，∑8i ＝1x i y i ＝1849，则其线性回归方程为( A ) A.y ^＝11.47＋2.62x B.y ^＝－11.47＋2.62x C.y ^＝2.62＋11.47x D.y ^＝11.47－2.62x解析 利用回归系数公式计算可得a ＝11.47，b ＝2.62，故y ^＝11.47＋2.62x . 7. 下列变量之间的关系是函数关系的是（ A ）A ．已知二次函数c bx ax y ++=2，其中a ，b 是已知常数，取b 为自变量，因变量是这个函数的判别式ac b Δ42-=B ．光照时间和果树的亩产量C ．降雪量和交通事故发生率D ．每亩用肥料量和粮食亩产量 8. 列有关线性回归的说法，不正确是（ D ）A.变量取值一定时，因变量的取值带有一定的随机性的两个变量之间的关系叫做相关关系B.在平面直角坐标系中用描点的方法得到表示具有相关关系的两个变量的一组数据的图形叫做散点图C.线性回归直线方程最能代表观测值x ，y 之间的关系D.任何一组观测值都能得到具有代表意义的回归直线方程 9.已知x 与y 之间的一组数据：则y 对x 的线性回归方程y ＝bx ＋A. (2,2) B. (1.5,3.5) C. (1,2) D. (1.5,4)10. 设回归直线方程为y ＝2－1.5x ，若变量x 增加1个单位，则( C )． A. y 平均增加1.5个单位 B. y 平均增加2个单位 C. y 平均减少1.5个单位 D. y 平均减少2个单位二、填空题11.下列关系中，是相关关系的为 （填序号）.①学生的学习态度与学习成绩之间的关系；②教师的执教水平与学生的学习成绩之间的关系； ③学生的身高与学生的学习成绩之间的关系；④家庭的经济条件与学生的学习成绩之间的关系. 答案 ①②12.下列有关线性回归的说法，正确的是 （填序号）.①相关关系的两个变量不一定是因果关系②散点图能直观地反映数据的相关程度 ③回归直线最能代表线性相关的两个变量之间的关系④任一组数据都有回归直线方程 答案 ①②③13.下列命题：①线性回归方法就是由样本点去寻找一条贴近这些样本点的直线的数学方法； ②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示；③通过回归直线yˆ=b ˆx +a ˆ及回归系数b ˆ,可以估计和预测变量的取值和变化趋势. 其中正确命题的序号是 .答案 ①②③14．下列关系：①人的年龄与其拥有的财富之间的关系；②曲线上的点与该点的坐标之间的关系；③苹果的产量与气候之间的关系；④森林中的同一树木，其截面直径与高度之间的关系；⑤学生的身高与其学号之间的关系，其中有相关关系的是___①③④_____(填序号)．15.已知回归方程为yˆ=0.50x-0.81,则x=25时，y ˆ的估计值为 .答案 11.69 16．下表是某厂1～4由散点图可知，用水量y 与月份x 之间有较好的线性相关关系，其线性回归直线方程是y ^＝－0.7x ＋a ，则a 等于______．解析 x ＝2.5，y ＝3.5，∵回归直线方程过定点(x ，y )，∴3.5＝－0.7×2.5＋a .∴a ＝5.25. 17．某服装商场为了了解毛衣的月销售量y (件)与月平均气温x (℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：由表中数据算出线性回归方程y ＝bx ＋a 中的b ≈－2，气象部门预测下个月的平均气温约为6℃，据此估计，该商场下个月毛衣的销售量约为________件．答案 46解析 由所提供数据可计算得出x ＝10，y ＝38，又b ≈－2代入公式a ＝y －b x 可得a ＝58，即线性回归方程y ^＝－2x ＋58，将x ＝6代入可得．18．正常情况下，年龄在18岁到38岁的人们，体重y （kg ）依身高x （cm ）的回归方程为y=0.72x-58.5。

线性回归习题答案线性回归是统计学中一种常见的数据分析方法，用于建立自变量与因变量之间的线性关系模型。

在实际应用中，线性回归模型常用于预测、趋势分析和关联度分析等领域。

下面将通过一些典型的线性回归习题来探讨其应用。

习题一：某公司根据过去几年的销售数据，建立了一个线性回归模型来预测未来的销售额。

已知公司的广告费用与销售额之间存在着一定的线性关系。

根据模型，当广告费用为1000元时，预测的销售额为15000元。

求该模型的回归方程。

解答：假设回归方程为y = a + bx，其中y表示销售额，x表示广告费用。

根据已知条件，可以得到一个方程：15000 = a + 1000b。

进一步，如果再给出另外一个广告费用与销售额的数据点，就可以求解出回归方程的具体参数a和b。

习题二：某城市的房价与房屋面积之间存在一定的线性关系。

已知一套房子的面积为120平方米，根据线性回归模型预测其价格为80万元。

求该模型的回归方程。

解答：假设回归方程为y = a + bx，其中y表示房价，x表示房屋面积。

根据已知条件，可以得到一个方程：80 = a + 120b。

同样地，如果再给出另外一个房屋面积与价格的数据点，就可以求解出回归方程的具体参数a和b。

习题三：某公司根据市场调研数据，建立了一个线性回归模型来分析产品销售量与价格之间的关系。

已知当产品价格为10元时，预测的销售量为1000个。

根据该模型，求当产品价格为15元时的预测销售量。

解答：假设回归方程为y = a + bx，其中y表示销售量，x表示产品价格。

根据已知条件，可以得到一个方程：1000 = a + 10b。

根据该方程，可以求解出参数a和b的具体值。

然后，将x取15，代入回归方程中，即可得到当产品价格为15元时的预测销售量。

通过以上习题的解答，我们可以看到线性回归模型在实际问题中的应用。

通过建立合适的回归方程，我们可以通过已知的自变量值来预测因变量的取值。

这对于企业决策、市场分析以及经济预测等方面都具有重要意义。

《线性回归方程》强化训练1、（门槛题） 某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：零件的个数x （个） 23 4 5 加工的时间y （小时）2.5344.5（Ⅰ）在给定的坐标系中画出表中数据的散点图；（Ⅱ）求出y 关于x 的线性回归方程ˆˆˆybx a =+，并在坐标系中画出回归直线； （Ⅲ）试预测加工10个零件需要多少时间？附录：参考公式：()()()121ˆniii nii x x y y bx x ==--=-∑∑ ，ˆˆay bx =-.2、（泸州市2017届高三一诊第20题） 某班主任为了解本班学生的数学和物理考试成绩间关系，在某次阶段性测试中，他在全班学生中随机抽取一个容量(Ⅱ)建立y 与x 的线性回归方程（系数精确到0.01），并预测该班数学分数为88的学生的物理分数.附录：参考数据：51450i i y ==∑，5141880i i i x y ==∑ 4.90=；参考公式：相关系数()()niix x y y r --=∑； 回归直线的方程是ˆˆˆybx a =+， 其中对应的回归估计值：()()()121ˆniii ni i x x y y bx x==--=-∑∑ ，ˆˆay bx =- 3.87=.3、（2016年全国新课标高考Ⅲ卷第18题） 下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图.（Ⅰ）由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明； （Ⅱ）建立y 关于t 的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量. 附注：参考数据：，2.646≈. 参考公式：相关系数()()nii y y r t t --=∑，回归方程中斜率和截距的最小二乘估计公式分别为：719.32ii y==∑7140.17i i i t y ==∑0.55=y a bt =+)))121()()()nii i nii tt y y b tt ==--=-∑∑)，=.a y bt -)))4、（2015年全国新课标高考Ⅰ卷第19题）某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x （单位：千元）对年销售量y （单位：t ）和年利润z （单位：千元）的影响，对近8年的宣传费i x 和年销售量()1,2,,8i y i =L 数据作了初步处理，得到下面的散点图及一些统计量的值.x ry u r w u r821()ii x x =-∑821()ii w w =-∑81()()iii x x y y =--∑ 81()()iii w w yy =--∑46.6 563 6.8289.8 1.6 1469 108.8表中i i w x =，w u r =811.8i i w =∑（Ⅰ）根据散点图判断，y a bx =+与y c d x =+，哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型？（给出判断即可，不必说明理由）（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y 关于x 的回归方程；（Ⅲ）已知这种产品的年利润z 与x ，y 的关系为0.2z y x =- ，根据（Ⅱ）的结果回答下列问题：（ⅰ）年宣传费49x =时，年销售量及年利润的预报值是多少？（ⅱ）年宣传费x 为何值时，年利润的预报值最大？ 附：对于一组数据11(,)u v ,22(,)u v ，…，(,)n n u v ,其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为：µ121()()=()niii ni i u u v v u u β==---∑∑，µµ=v u αβ-.。

线性回归方程高考题1、下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量（吨）与相应的生产能耗（吨标准煤）的几组对照数据：（1）请画出上表数据的散点图；（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；（3）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? （参考数值：）2、假设关于某设备的使用年限x和所支出的维修费用y(万元)统计数据如下:若有数据知y对x呈线性相关关系.求:(1) 填出下图表并求出线性回归方程=bx+a的回归系数,;(2) 估计使用10年时,维修费用是多少.3、某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四实试验，得到的数据如下：（1）在给定的坐标系中画出表中数据的散点图；（2）求出y关于x的线性回归方程，并在坐标系中画出回归直线；（3）试预测加工10个零件需要多少时间？（注：4、某服装店经营的某种服装，在某周内获纯利(元)与该周每天销售这种服装件数之间的一组数据关系如下表：已知：．(Ⅰ)画出散点图；(1I)求纯利与每天销售件数之间的回归直线方程．5、某种产品的广告费用支出与销售额之间有如下的对应数据：(1)画出散点图：(2)求回归直线方程；(3)据此估计广告费用为10时，销售收入的值．6、下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据：（I）请画出上表数据的散点图；（II）请根据上表提供的数据，求出ｙ关于ｘ的线性回归方程；（III）已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据（II）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？（参考公式及数据: ,）7、以下是测得的福建省某县某种产品的广告费支出x与销售额y（单位：百万元）之间，有如下的对应数据：（1）画出数据对应的散点图，你能从散点图中发现福建省某县某种产品的广告费支出x与销售额y（单位：百万元）之间的一般规律吗？（2）求y关于x的回归直线方程；（3）预测当广告费支出为2（百万元）时，则这种产品的销售额为多少？（百万元）8、在某种产品表面进行腐蚀线实验，得到腐蚀深度y与腐蚀时间t之间对应的一组数据：(1)画出散点图；(2)试求腐蚀深度y对时间t的回归直线方程。

第9章一元线性回归练习题一．选择题1．具有相关关系的两个变量的特点是（）A．一个变量的取值不能由另一个变量唯一确定B．一个变量的取值由另一个变量唯一确定C．一个变量的取值增大时另一个变量的取值也一定增大D．一个变量的取值增大时另一个变量的取值肯定变小2．下面的各问题中，哪个不是相关分析要解决的问题A．判断变量之间是否存在关系B．判断一个变量数值的变化对另一个变量的影响C．描述变量之间的关系强度 D.判断样本所反映的变量之间的关系能否代表总体变量之间的关系3.根据下面的散点图，可以判断两个变量之间存在（）A.正线性相关关系B. 负线性相关关系C. 非线性关系D. 函数关系4.下面的陈述哪一个是错误的（）A. 相关系数是度量两个变量之间线性关系强度的统计量B．相关系数是一个随机变量C．相关系数的绝对值不会大于1D．相关系数不会取负值5.根据你的判断，下面的相关系数取值哪一个是错误的（）A. -0.86B. 0.78C. 1.25D. 06.如果相关系数r=0,则表明两个变量之间（）A.相关程度很低B. 不存在任何关系C．不存在线性相关关系D.存在非线性关系7.下列不属于相关关系的现象是（）A.银行的年利息率与贷款总额B.居民收入与储蓄存款C.电视机的产量与鸡蛋产量D.某种商品的销售额与销售价格8.设产品产量与产品单位成本之间的线性相关系数为-0.87，这说明二者之间存在着（）A. 高度相关B.中度相关C.低度相关D.极弱相关9.在回归分析中，被预测或被解释的变量称为（）A.自变量B.因变量C.随机变量D.非随机变量10.对两变量的散点图拟合最好的回归线，必须满足一个基本的条件是（）A.2ˆ()yy∑-最小B.2)(ˆyy∑-最大C.2ˆ()yy∑-最大D.2)(ˆyy∑-最小11. 下列哪个不属于一元回归中的基本假定（）A.误差项i ε服从正态分布B. 对于所有的X ，方差都相同C. 误差项i ε相互独立D. 0)ˆ=-i i yy E （ 12.如果两个变量之间存在着负相关，指出下列回归方程中哪个肯定有误（ ）A.x y75.025ˆ-= B. x y 86.0120ˆ+-= C. x y 5.2200ˆ-= D. x y 74.034ˆ--= 13.对不同年份的产品成本拟合的直线方程为,75.1280ˆx y-=y 表示产品成本，x 表示不同年份，则可知（ ）A.时间每增加一个单位，产品成本平均增加1.75个单位B. 时间每增加一个单位，产品成本平均下降1.75个单位C.产品成本每变动一个单位，平均需要1.75年时间D. 产品成本每减少一个单位，平均需要1.75年时间 14.在回归分析中，F 检验主要是用来检验（ ）A ．相关关系的显著性 B.回归系数的显著性 C. 线性关系的显著性D.估计标准误差的显著性15.说明回归方程拟合优度的统计量是（ ）A. 相关系数B.回归系数C. 判定系数D. 估计标准误差16.已知回归平方和SSR=4854,残差平方和SSE=146,则判定系数R 2=( ) A.97.08% B.2.92% C.3.01% D. 33.25% 17. 判定系数R2值越大，则回归方程（ ）A 拟合程度越低B 拟合程度越高C 拟合程度有可能高，也有可能低D 用回归方程进行预测越不准确 18. 居民收入与储蓄额之间的相关系数可能是（ ） A -0.9247 B 0.9247 C -1.5362 D 1.536219.在对一元回归方程进行显著性检验时，得到判定系数R 2=0.80,关于该系数的说法正确的是（ ）A. 该系数越大，则方程的预测效果越好B. 该系数越大，则由回归方程所解释的因变量的变差越多C. 该系数越大，则自变量的回归对因变量的相关关系越显著D. 该回归方程中自变量与因变量之间的相关系数可能小于0.8 20.下列方程中肯定错误的是（ ）A. x y48.015ˆ-=，r=0.65 B. x y 35.115ˆ--=, r= - 0.81 C. x y85.025ˆ+-=, r=0.42 D. x y 56.3120ˆ-=, r= - 0.96 21. 若两个变量存在负相关关系，则建立的一元线性回归方程的判定系数R 2的取值范围是（ ）A.【0，1】B. 【-1，0】C. 【-1，1】D.小于0的任意数二． 填空题1.当从某一总体中抽取了一样本容量为30的样本，并计算出某两个变量的相关系数为0.8时，我们是否可认为这两个变量存在着强相关性（不能 ） ，理由是（因为该相关系数为样本计算出的相关系数，它的大小受样本数据波动的影响，它是否显著尚需检验 ）。

线性回归方程一、解答题1.为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取20名学生的成绩进行以上的把握认为“成绩优秀与教学方式有关”?2.现从上述样本“成绩不优秀”的学生中,抽取3?人进行考核,记“成绩不优秀”的乙班人数为X,求X的分布列和期望.参考公式:22()()()()()n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.100?名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”。

:附:随机变量22()()()()()n ad bcKa b c d a c b d-=++++(其中n a b c d=+++为样本总量).参考数据2()P K k≥0.150 0.100 0.050 0.025k 2.072 2.706 3.841 5.024.2.在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的22⨯列联表,并?非手机迷手机迷合计男女合计3.某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20?名学生,对他们的课外阅读时间进行问卷调查。

现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B 类(参加课外阅读,但平均每周参加课外阅读的时间不超过3?小时),C类(参加课外阅读,且平均每周参加课外阅读的A类B类C类男生x 5 3女生y 3 390%的把握认为“参加课外阅读与否”与性别有关;男生女生总计不参加课外阅读参加课外阅读总计,记X为抽取的这3?名女生中A类人数和C类人数差的绝对值,求X的数学期望。

附:2 2()n ad bc k-=2()P k k≥0.10 0.05 0.01k 2.706 3.841 6.635模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1500名学生(其中男生900人,女生600 人)中,采用分层抽样的方法从中抽取n 名学生进行调查. 1.已知抽取的n 名学生中含女生20人,求n 的值及抽取到的男生人数;2.学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在1的条件下抽取到的n 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的22⨯列联表. 请将列联表补充完整,并判断是否有99%的把握认为选择科目与性别有关?说名,再从这5名学生中抽取2人了解学生对“地理”的选课意向情况,求2人中至少有1名男生的概率. 附:参考公式及数据()()()()()22n ad bc k a b c d a c b d -=++++2男性且休闲方式都是读书的概率是多少? .()()()()()2n ad bc k a b c d a c b d -=++++,其中n a b c d =+++.6.某市春节期间7家超市的广告费支出 x (万元)和销售额y (万元)数据如下:;2.用对数回归模型拟合y 与x 的关系,可得回归方程: 12l 22ˆn yx =+,经计算得出线性回归模型和对数模型的2R 分别约为0.75和0.97,请用说明选择哪个回归模型更合适,并用此模型预测A 超市广告费支出为8万元时的销售额.参数数据及公式: 772118,42,2794,708,i i i i i x y x y x ======∑∑1221,,l ˆˆˆn 20.7ni ii nii x y n xybay bx xnx ==--==-≈-∑∑ 7.一只药用昆虫的产卵数y 与一定范围内的温度x 有关, 现收集了该种药用昆虫的6组观测数据如下表:经计算得: 1266i i x x ===∑,1336i i y y ===∑,1()()557i i i x x y y =--=∑,621()84i i x x =-=∑,621()3930i i y y =-=∑线性回归模型的残差平方和621()236.64iii y y =-=∑,8.06053167e ≈,其中,i i x y 分别为观测数据中的温度和产卵数, 1,2,3,4,5,6i =1.若用线性回归模型,求y 关于x 的回归方程ˆˆˆybx a =+ (精确到0.1); 2.若用非线性回归模型求得y 关于x 的回归方程为0.23030.06ˆxye =,且相关指数20.9522.R =①试与1中的回归模型相比,用2R 说明哪种模型的拟合效果更好.②用拟合效果好的模型预测温度为35C 时该种药用昆虫的产卵数(结果取整数). 附:一组数据()()()1122,,?,,?...,,,?n n x y x y x y 其回归直线ˆˆˆy bx a =+的斜率和截距的最小二乘估计为121()()()ˆniii nii x x y y bx x ==--=-∑∑,ˆˆay bx =-;相关指数22121()1()niii nii y y R y y ==-=--∑∑.8.《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》第90?条规定:对不礼让行人的驾驶员处以扣3?分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计1.请利用所给数据求违章人数y 与月份之间的回归直线方程ˆˆˆybx a =+ 2.预测该路口7?月份的不“礼让斑马线”违章驾驶员人数3.交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如?参考公式: 1122211()()ˆˆˆ,()nni iiii i nni ii i x y nx y x x y y bay bx x nxx x ====---===---∑∑∑∑, 22()()()()()n ad bc K a b c d a c b d -=++++ (其中n a b c d =+++)2()P K k ≥ 0.150 0.100 0.050 0.025 0.010 0.005 0.001 k2.072 2.7063.841 5.024 6.635 7.879 10.8289.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位: t )和年利润z (单位:千元)的影响.对近8年的年宣传费i x 和年销售量()1,2,,8i y i =数据作了初步处理,得到下面的散点图及一些统计量的值.表中i i w x =18i i w w ==∑.1.根据散点图判断, y a bx =+与y c x =+哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)2.根据1的判断结果及表中数据,建立y 关于x 的回归方程.3.已知这种产品的年利润z 与x ,y 的关系为0.2z y x =-.根据2的结果回答下列问题: ①年宣传费49x =时,年销售量及年利润的预报值是多少? ②年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据()11,u v ,()22,u v ,…, (),n n u v 其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为()()()121ˆnii i ni i uu v v u u β==--=-∑∑,ˆˆv u αβ=-. 10.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用x (单位:万元)和利润y (单位:十万元)之间的关系,得到下列数据:x 2 3 4 5 6 8 9 11y 1 2 3 3 4 5 681.请用相关系数r 说明y 与 x 之间是否存在线性相关关系(当0.81r >时,说明y 与 x 之间具有线性相关关系);2.根据1的判断结果,建立y 与 x 之间的回归方程,并预测当24x =时,对应的利润ˆy为多少(ˆˆˆ,,b a y 精确到0.1). 附参考公式:回归方程中ˆˆˆybx a =+中ˆb 和ˆa 最小二乘估计分别为1221ˆni ii nii x ynx y b xnx ==-=-∑∑,ˆˆay bx =-, 相关系数()()12211ni i i nniii i x ynx yr xx yy ===-=--∑∑∑参考数据: ()()88882221111241,356,8.25,6i i iiii i i i x y x xx yy ======-≈-=∑∑∑∑.11.为了监控某种零件的一条生产线的生产过程,检验员每隔30min 从该生产线上随机抽取一个零件,并测量其尺寸(单位: cm ).下面是检验员在一天内依次抽取的16个零件的尺寸抽取次序 1 2345 6 7 8 零件尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04 抽取次序 910111213141516零件尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95经计算得16119.9716i i x x ===∑,16162221111()(16)0.2121616i i i i s x x x x ===-=-≈∑∑, ()()()16162118.518.439,8.5 2.78i i i i x x i ==-≈--=-∑∑其中i x 为抽取的第i 个零件的尺寸, 1,2,16i =。