应用数理统计实验报告

应用数理统计学课程实验报告201330170078 学生学号实验课成绩学生实验报告书应用数理统计学课程实验实验课程名称土木与交通学院开课学院胡郁葱指导教师姓名邓艳辉学生姓名交通运输学生专业班级学年第 1 学期 2014 2015 --上机实验一实验项目名称上机实验1 实验日期 2014.12.26 实验者邓艳辉专业班级交通运输组别第二组一部分:实验预习报告(包括实验目的、意义，实验基本原理与方法，实验方案与技术路线等)一、实验目的:掌握SPSS的基本操作(认识SPSS、变量定义、变量属性理解、数据录入等) 二、实验任务:设计“交通量调查表”的相关变量及属性，便于将纸质调查表转换为电子调查表，并导入数据。

三、实验基本原理和方法:一、定义变量启动SPSS后，出现如图1-1所示数据编辑窗口。

由于目前还没有输入数据，因此显示的是一个空文件。

输入数据前首先要定义变量。

定义变量即要定义变量名、变量类型、变量长度(小数位数)、变量标签(或值标签)和变量的格式。

1(定义变量名NameSPSS默认的变量为Var00001、Var00002等。

用户也可以根据自己的需要来命名变量。

SPSS变量的命名和一般的编程语言一样，有一定的命名规则，具体内容如下: (1)变量名必须以字母、汉字或字符,开头，其他字符可以是任何字母、数字或_、@、#、$等符号。

(2)变量最后一个字符不能是句号。

(3)变量名总长度不能超过8个字符(即4个汉字)。

4(4)不能使用空白字符或共他待殊字符(如“～”、“?”等)。

(5)变量命名必须唯一，不能有两个相同的变量名。

(6)在SPSS中不区分大小写，例如，HXH、hxh或Hxh对SPSS而言，均为同一变量名称。

(7)SPSS的句法系统中表达逻辑关系的字符串不能作为变量的名称，如ALL、AND、WITH、OR等2(定义变量类型Type单击Type相应单元中的按钮，出现如图1-2所示的对话框，在对话框中选择合适的变量类型并单击OK按钮，即可定义变量类型。

概率论与数理统计应用实验报告
概率论与数理统计是中国大学MOOC《数据科学导论》课程中的一门关键科目，为了加深熟悉概率论与数理统计的过程，我完成了在R语言环境下的相关实验并撰写了这份报告。

实验过程以R Studio为平台。

R studio是一款跨平台，开源的编程环境，可以天然
地支持R语言，为我们提供卓越的实验环境。

所有的实验操作都是在R Studio上进行的。

实验分两步，第一步是正态分布的实验，第二步是对多项式分布的实验。

正态分布的实验
首先，我们构造了1000000以内随机整数，范围为-500000到500000。

将这些整数绘
制灰度图，来查看各项数据的分布情况，数据在中心出现了最多，并且随着两端逐渐减少，绘出的图像符合正态分布的分布曲线，即右尾巴更长。

此外，我们还对构造出的数据进行
正态性分析，使用R语言中的hist函数来绘制正态分布的柱状图，根据结果可以清楚地
看出，数据的分布也是符合正态分布的，由此也证明了构造数据的正确性。

多项式分布的实验
我们首先运用随机数生成器在R语言环境下，构造出多项式分布的数据，将生成的数
据进行灰度图展示，发现随着两端的和逐渐增加，形成非对称的多项式分布的曲线。

同时，我们运用R语言中的hist函数来检验再次检验多项式分布，结果也确实符合多项式分布，从而证明以上步骤是正确的。

经过上述实验，我加深了对概率论与数理统计的熟悉。

构建统计数据，运用R Studio 画出统计图来检验和证明数据是否符合正态分布和多项式分布使我对概率论和数理知识有
了更为深刻的认识，也为今后解决数据科学相关的科学问题奠定基础。

数理统计学实验报告院:专业：班级：学号：学生姓名：指导教师姓名:实验日期:实验11950～1983年我国三类产品出口总额及其构成年份出口总额(亿元）其中工矿产品农副产品加工品农副产品金额（亿元）占总额％金额（亿元) 占总额％金额(亿元）占总额％195020。

21。

99。

4 6。

733。

2 11。

657.4195548.712。

425。

5 13.828.4 22.546.1196063.316。

926.7 26.842.3 19.631。

0196563。

119。

530.9 22。

736.0 20。

933。

1197056。

814.525.6 21。

437。

7 20.936.7 197514356.239.3 44.531.1 42。

329.6 1980282。

4141。

151.8 90。

4 29。

550.918。

7 1983434。

5249.457.4 11626。

7 69。

115.9用表中的资料，按以下要求绘制图表：（一）用表中1950、1960、1970、1980四年三类产品的出口金额绘制分组柱形图，然后将图复制到Word文档.（二）用表中1950和1980两年三类产品的出口金额占总金额的百分比,分别绘制两幅饼图, 然后将图复制到Word文档;（三）用1950、1960、1970、1980四年三类产品出口金额绘制折线图, 然后将图复制到Word文档。

（四）将以上一张表、三幅图联系起来，结合我国当时的历史背景写一篇300字左右的统计分析报告。

(一)（二)1950：1980：(三)(四）总结建国初期，我国对外贸易仅限于原苏联和东欧等前社会主义国家，对外贸易规模极其有限，基本上处于封闭半封闭状态。

1950年，出口额极少，以农副产品为主的出口占我国出口总额的百分之五十八，而工矿产品的出口极少只占百分之九。

随着经济发展，出口额增长，工矿产品的出口额增长迅速,而出口产品以农副产品加工品为主.改革开放以来，我国走上了对外开放之路,从大规模“引进来”到大踏步“走出去”，一跃而成为世界对外贸易大国。

应用统计学实验报告实验报告标题：应用统计学实验报告引言：统计学是一门运用数理统计原理和方法进行数据分析和信息推断的科学，是现代科学发展不可或缺的工具之一。

本实验旨在应用统计学原理和方法，通过实验数据的收集和分析，探讨统计学在解决实际问题中的应用。

实验目的：1. 理解统计学的基本原理和方法；2. 掌握常见统计学实验设计与分析方法；3. 熟悉统计软件的操作。

实验材料与方法：1. 随机抽样：根据实验需求，采用随机抽样方法确定样本；2. 数据收集：通过实验、调查等方式，收集相关数据；3. 数据处理：使用统计软件对数据进行整理和分析；4. 数据分析：根据实验目的，应用合适的统计学方法进行数据分析；5. 结果和结论：根据数据分析结果，进行结果总结和结论提出。

结果与讨论：根据实验设计、数据收集和数据分析，得到如下结果并进行讨论：1. 描述性统计分析：对实验数据进行描述性统计，包括求均值、中位数、方差等；2. 参数估计：根据样本数据，对总体参数进行估计，并计算估计的置信区间；3. 假设检验：根据给定假设，进行假设检验，判断样本数据是否支持假设；4. 相关分析：根据实验数据，进行相关性分析，探究变量之间的关系；5. 统计建模：根据实验数据，应用统计建模方法，建立数学模型，预测未来数据；6. 确定实验误差和可靠性：分析实验误差来源，评估实验数据的可靠性。

结论：通过实验的数据收集和分析，得出如下结论：1. 总结实验数据的中心趋势与离散程度；2. 对参数进行估计，并给出相应的置信区间；3. 根据假设检验的结果，判断样本数据对给定的假设是否支持；4. 探究变量之间的相关关系，并给出相应的统计指标；5. 建立合适的数学模型，并进行预测和推断；6. 分析实验误差来源，评估实验数据的可靠性。

实验结论可根据具体实验内容进行调整和补充，需根据实际情况进行具体描述。

参考文献：在实验报告中可参考相关的统计学原理、方法和软件操作的文献。

应用统计实验报告体会1. 实验背景统计学作为一门重要的学科，被广泛应用于各个行业和领域中。

通过对实际数据的收集、整理和分析，可以得出一些有价值的结论，为决策提供依据。

在本次实验中，我们学习了统计学中的实验设计和分析方法，并运用这些方法来解决实际问题。

2. 实验目的本次实验的目的是通过设计实验、收集数据、进行统计分析，掌握应用统计学解决实际问题的方法和技巧。

具体来说，我们需要学习实验设计中的随机化原则和对照组设计，了解方差分析和回归分析的原理和应用，掌握使用统计软件进行数据分析的方法。

3. 实验过程在实验中，我们首先明确了研究问题，并设计了符合科学原则的实验方案。

然后，我们进行了数据的收集和整理工作，确保数据的质量和准确性。

接下来，我们运用所学的统计方法对数据进行分析，并得出了一些结论。

最后，我们将实验结果进行总结和归纳，并提出对实验过程的改进和对未来研究的展望。

4. 实验结果与分析通过对数据的分析，我们得出了一些有趣的结果。

首先，我们发现实验组和对照组在某个变量上存在显著差异，这说明我们的实验设计是有效的，并且实验结果是可靠的。

其次，通过方差分析和回归分析，我们得出了一些关键变量与结果变量之间的关联性，这为我们进一步分析和解释原因提供了线索。

5. 实验体会本次实验让我深刻认识到统计学在实际应用中的重要性和价值。

通过合理的实验设计和科学的数据分析，我们可以得出一些有价值的结论，并为决策提供科学依据。

同时，也让我意识到统计学方法的复杂性和技巧性，需要不断学习和熟练运用。

只有掌握了统计学的基本原理和技巧，才能正确地应用统计学解决实际问题。

6. 实验总结与展望通过本次实验，我对统计学的应用又有了更深入的了解和认识。

实验中我学习了实验设计和数据分析的基本方法，掌握了使用统计软件进行数据分析的技巧。

同时，我也认识到统计学的应用是一项持续的工作，需要不断更新知识和技能，并结合具体问题进行分析和解决。

在未来的研究中，我将进一步拓宽研究领域，深入学习和应用更加复杂的统计方法，提高自己的统计学水平。

数理统计实验指导1报告数理统计实验实验指导书⼀理学院实验中⼼数学专业实验室编写实验⼀常见的概率分布以及分位数【实验类型】综合性【实验学时】4【实验内容】1、会利⽤ MATLAB 软件计算离散型随机变量的概率、连续型随机变量概率密度值, 以及产⽣离散型随机变量的概率分布(即分布律)；2、会利⽤ MATLAB 软件画出各种常见分布图形；2、会利⽤ MATLAB 软件计算分布函数值, 或计算形如事件{X≤x}的概率；3、给出概率p和分布函数, 会求上α分位点, 或求解概率表达式中的待定参数。

【实验前的预备知识】1、掌握常见离散型随机变量的分布律及性质；2、掌握常见连续型随机变量的分布密度函数及性质；3、理解上分位数的定义及求法4、掌握基本的描绘函数的MATLAB编程法。

【实验⽅法或步骤】1、通⽤MATLAB函数计算概率分布律及密度函数值命令通⽤函数计算概率密度函数值函数pdf 或者namepdf格式：Y=pdf(‘name'，K，A，B)或者：namepdf (K，A，B)说明(1)上述函数表⽰返回在X=K处、参数为A、B、C的概率值或密度值，对于不同的分布，参数个数是不同；name为分布函数名，其取值如表1。

（2）第⼀个函数名加' '，第⼆个⽆需加。

表1 常见分布函数表例1事件A在每次试验中发⽣的概率是0.3, 计算在10次试验中A恰好发⽣6次的概率.解: p=pdf('bino',6, 10, 0.3)或者p=binopdf(6, 10, 0.3)p =0.0368结果表明：参数是n=10,概率是p=0.3的⼆项分布在X=6处的概率为0.0368.例2 事件A在每次试验中发⽣的概率是0.3, 求在4次试验中A发⽣次数的概率分布.解: p=pdf('bino',0:4,4,0.3) %0: 4产⽣步长为 1 的等差数列 0, 1, 2, 3, 4.或者p=binopdf(0:4,4,0.3)p =0.2401 0.4116 0.2646 0.0756 0.0081计算的结果是: 参数是n=4, 概率是p=0.3的⼆项分布的分布律(当x=0,1,2,3,4 时).例 3 设随机变量X服从参数是3的泊松分布, 求概率P{X=6}.解: p=pdf('poiss',6,3)或者p=poisspdf(6,3)p =0.0504结果表明：参数是λ=3 的泊松分布在x=6处的概率为0.0504.例4 写出参数为 3 的泊松分布的前6项的概率分布.解：p=pdf('poiss',0:5,3)或者p=poisspdf(0:5,3)% 0:5 产⽣步长为 1的等差数列0,1,2,3,4,5.p =0.0498 0.1494 0.2240 0.2240 0.1680 0.1008计算的结果是, 参数为λ=3的泊松分布的前6项的概率(当x=0,1,2,3,4,5时).例5设随机变量X服从区间[2, 6]上的均匀分布, 求X=4 时的概率密度值.解：y=unifpdf(4,2,6) 或y=pdf('unif',4,2,6)y =0.2500例6 计算正态分布N（0，1）的随机变量X在点0.6578的密度函数值。

一、实训背景随着社会经济的发展，统计学在各个领域的应用越来越广泛。

为了提高学生的实际操作能力，培养具备统计学专业素养的应用型人才，我校开展了应用统计学实训。

本次实训旨在让学生通过实际操作，掌握统计学的基本原理和方法，提高数据分析能力，为今后的学习和工作打下坚实基础。

二、实训目的1. 使学生熟悉统计学的基本原理和方法，掌握数据分析的基本技能。

2. 培养学生运用统计学方法解决实际问题的能力。

3. 提高学生团队协作和沟通能力。

4. 增强学生的职业素养，为今后的学习和工作做好准备。

三、实训内容本次实训主要分为以下四个部分：1. 数据收集与整理学生通过查阅文献、实地调查等方式收集数据，并对数据进行整理和清洗，为后续分析做好准备。

2. 描述性统计分析学生运用统计学方法对收集到的数据进行描述性统计分析，包括计算均值、标准差、方差等指标，并绘制图表展示数据分布情况。

3. 推理性统计分析学生运用统计学方法对收集到的数据进行推理性统计分析，包括假设检验、相关分析、回归分析等，以揭示数据之间的内在联系。

4. 统计软件应用学生熟练运用Excel、SPSS等统计软件进行数据分析，提高实际操作能力。

四、实训过程1. 实训准备阶段教师根据实训内容，为学生提供相关资料，并指导学生进行数据收集与整理。

2. 实训实施阶段学生按照实训要求，分组进行数据收集、整理、描述性统计分析、推理性统计分析等操作。

3. 实训总结阶段各小组对实训过程进行总结，撰写实训报告，并提出改进建议。

五、实训成果1. 学生掌握了统计学的基本原理和方法，提高了数据分析能力。

2. 学生运用统计学方法解决了实际问题，增强了实际操作能力。

3. 学生培养了团队协作和沟通能力，提高了职业素养。

4. 学生对统计学产生了浓厚兴趣，为今后的学习和工作打下了坚实基础。

六、实训总结1. 本次实训充分体现了理论与实践相结合的原则，提高了学生的实际操作能力。

2. 学生在实训过程中，学会了运用统计学方法解决实际问题，为今后的学习和工作奠定了基础。

应用统计实验报告应用统计实验报告引言：统计实验是一种重要的科学研究方法，通过对一定数量的样本进行观察和测量，以得到总体的某些特征参数，并对其进行推断和预测。

本文将以某电商平台的用户购买行为为例，通过应用统计实验方法，探讨用户购买意愿与价格之间的关系。

一、实验设计为了研究用户购买意愿与价格之间的关系，我们选择了某电商平台上的500名用户进行实验。

实验中，我们随机选取了100个商品，将其价格分为五个档次：A、B、C、D、E。

其中A为最低价，E为最高价。

每个档次中的商品数量相等，即每个档次20个商品。

然后，我们观察用户对这些商品的购买行为，并记录下用户购买的次数。

二、数据收集与处理在实验进行期间，我们通过电商平台的数据分析工具，获取了用户对不同价格档次商品的购买次数数据。

然后，我们对数据进行了清洗和处理，排除了异常值和缺失值，确保数据的准确性和可靠性。

三、数据分析与结果通过对收集到的数据进行统计分析，我们得到了以下结果：1. 用户购买意愿与价格之间存在一定的关系。

随着商品价格的增加，用户的购买意愿逐渐降低。

具体来说，价格档次为A的商品购买次数最多，而价格档次为E的商品购买次数最少。

2. 用户对价格敏感度不同。

有些用户对价格非常敏感，他们倾向于购买价格较低的商品；而有些用户对价格不太敏感，他们更关注商品的质量和性能，而非价格。

3. 用户购买行为受到其他因素的影响。

除了价格之外，用户的购买行为还受到其他因素的影响，如品牌知名度、促销活动等。

这些因素可能会改变用户的购买决策。

四、讨论与建议通过本次实验，我们初步了解了用户购买意愿与价格之间的关系。

然而，由于实验的局限性和样本的限制，我们的结论可能存在一定的偏差。

因此，我们建议在后续的研究中，扩大样本量，增加实验的复杂程度，以获得更准确和全面的结论。

此外，我们还建议电商平台在制定价格策略时，应该充分考虑用户的购买意愿和价格敏感度。

对于那些对价格敏感的用户，可以提供更多的折扣和促销活动，以吸引他们的购买；对于那些对价格不太敏感的用户，可以在产品质量和服务上下功夫，提高用户的购买体验。

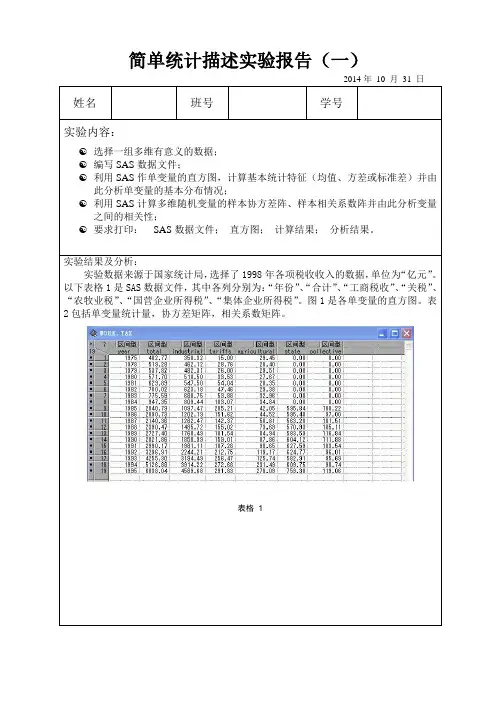
《概率论与数理统计》实验报告学生姓名学生班级学生学号指导教师学年学期实验报告实验内容实验过程（实验操作步骤）实验结果1 .某厂生产的化纤强度X 〜N( ,0.852)，现抽取一个容量为n 25的样本，测定其强度，得样本均值X 2.25，试求这批化纤平均强度的置信水平为0.95的置信区间. 第1步：打开【单个正太总体均值Z估计活动表】。

第2步：在单元格【B3】中输入0.95，在单元格【B4】中输入25,在单元格【B5】中输入2.25 ,显示结果。

单YE盍总臣均值出石计;騙洙由此可得，这批化纤平均强度的置信水平为0.95的置信区区间为(1.92 , 2.58).2 .已知某种材料的抗压2强度X ~ N（,），现随机抽取10个试件进行抗压试验，测得数据如下：482，493, 457, 471, 510，446， 435, 418, 394， 469 求平均抗压强度的置信水平为 0.95的置信区间；2（2）求的置信水平为0.95的置信区间. 第1步：打开【单个正太总体均值t估计活动表】•第2步：在D列输入原始数据.第3步：点击【工具（T）】-选择【数据分析（D）】一选择【描述统计】一点击【确定】按钮一在【描述统计】对话框输入相关内容—点击【确定】按钮，得到F列与G列结果。

第4步：在单元格【B3】中输入0.95，在单元格【B4】中输入10, 在【B5】中引用G3,在【B6】中引用G7,显示结果。

单个正击豆悴旳毡文洁id汚加置馆水平0.95禅本容呈10禅本均疽4E7. 5捽本掠性差35. 217b??68彳就误差11. 13677591I分应麹（軍）L. 333112^33十命惊數（双》 2.262157163单侧直订下限d37. 0S5C32至厕宣世丄限^77.^14563区可估计估i 下陨-132. 3063?26估计上限4S 2. 6^3137449?■J&7平均45T, 5裁上上椎代差11.丄3閃辭土51（1中也戲-I-.-446刪倍祈准年35.517^77^3H5方差124OLZT77YBjy^蛀度-0.僦希仙7・菟勺克飾¥04&9帽备眞坤11639Q总人值510㈣6LQM y J1ti)顼•£_唄w -由此可得，平均抗压强度的置信水平为0.95的置信区间（432.31 , 482.69）草不正蛊盘悴方茎卡方诂计^动B却計:平0.能畔多Fir1Q45T. 5祥車•方差1240. 2?7?78卡方下分G激 3. 325L12843卡方上分位厳f单了卡方下5K触（股）卡方上沁憨（敢）16. 91897762. 7GD3E9E19-022T67BC59. TCZOSSV二1“芒K7用匡is■估计3357, 02393?咕计EFU5B€. 7«S2S3'舌H丄哽4133.56324由此可得，2的置信水平为0.95的置信区间为（586.80 , 4133.66）3 .用一个仪表测量某一物理量9次，得样本均值x 56.32，样本标准差s 0.22.(1)测量标准差的大小反映了仪表的精度，试求的置信水平为 0.95 的置信区间；(2)求该物理量真值的置信水平为0.99的置信区间.(1)第1步：打开【单个正太总体方差卡方分布】第2步：在单元格【B3】中输入0.95 ,在单元格【B5】中输入56.32 ,在单元格【B6】中输入0.0484 ,显示结果。

实验课程数理统计实验地点数学专业实验室时间2014.11.30班级姓名学号成绩指导老师太原工业学院理学系实验一描述性统计【实验目的】熟悉Excel软件在数理统计中的应用；【实验内容】一.熟悉办公软件Excel中数据分析工具箱里的描述性统计分析；二.会绘制直方图表并进行分析。

【实验所使用的仪器设备与软件平台】计算机 Excel2003【实验方法与步骤】选取一个例子，查看常见的统计量，并绘制直方图。

（参数自己设定）。

【实验结果及分析】实验二单个正态总体参数的区间估计【实验目的】熟悉Excel软件在数理统计中的应用【实验内容】一.熟悉办公软件Excel中数据分析工具箱里的区间估计；二.进行单整体总体参数的区间估计。

【实验所使用的仪器设备与软件平台】计算机 Excel2003【实验方法与步骤】选取一个例子，进行单个正态总体参数的区间估计。

（参数自己设定）。

【实验结果及分析】实验三两个正态总体参数的区间估计【实验目的】熟悉Excel软件在数理统计中的应用【实验内容】一.熟悉办公软件Excel中数据分析工具箱里的区间估计；二.进行两个正态总体参数的区间估计。

【实验所使用的仪器设备与软件平台】计算机 Excel2003【实验方法与步骤】选取一个例子，进行两个正态总体参数的区间估计。

（参数自己设定）。

【实验结果及分析】【实验目的】熟悉Excel软件在数理统计中的应用【实验内容】一.熟悉办公软件Excel中数据分析工具箱里的假设检验；二.单个正态总体参数的假设检验。

【实验所使用的仪器设备与软件平台】计算机 Excel2003【实验方法与步骤】选取一个例子，单个正态总体参数的假设检验（参数自己设定）。

【实验结果及分析】【实验目的】熟悉Excel软件在数理统计中的应用【实验内容】一.熟悉办公软件Excel中数据分析工具箱里的假设检验；二.两个正态总体参数的假设检验。

【实验所使用的仪器设备与软件平台】计算机 Excel2003【实验方法与步骤】选取一个例子，两个正态总体参数的假设检验（参数自己设定）。

应用统计学实验报告实验目的：本实验旨在探讨统计学在现实生活中的应用，通过设计和实施一个简单的实验来体现统计学的重要性和实用性。

实验背景：统计学是一门研究数据收集、数据处理、数据分析和数据解释的学科，广泛应用于各个领域，如经济学、医学、社会学等。

通过统计学方法，我们可以更好地理解数据背后的规律，作出准确的预测和决策。

实验设计：我们选择了一个简单的实验，即投掷硬币的实验。

我们将硬币投掷10次，记录正面朝上的次数，然后根据这些数据进行统计学分析。

实验步骤：1. 准备一枚硬币和纸笔；2. 抛掷硬币，记录正面朝上的次数；3. 重复以上步骤，直至投掷10次；4. 统计正面朝上的次数；5. 利用统计学方法对数据进行分析。

实验结果：在进行实验后，我们得到了如下数据：3次正面，7次反面。

接下来，我们将对这些数据进行统计学分析。

统计学分析：1. 计算正面朝上的概率：正面朝上的次数/总次数 = 3/10 = 0.3；2. 计算反面朝上的概率：反面朝上的次数/总次数 = 7/10 = 0.7；3. 制作频率分布表和频率分布图；4. 计算平均值、标准差等统计指标。

实验结论：通过对数据的统计学分析，我们可以得出结论：投掷硬币的概率是近似的，即正面朝上的概率约为0.3，反面朝上的概率约为0.7。

这个简单的实验展示了统计学在实际生活中的应用和重要性。

结语：统计学是一门重要的学科，通过实验可以更好地理解其原理和方法。

本实验不仅增强了我们对统计学的理解，还培养了我们的数据分析能力。

希望通过这个实验，大家能更加认识到统计学的价值和意义。

谢谢阅读！。

应用统计学实验报告应用统计学实验报告引言：统计学是一门研究收集、分析、解释和展示数据的学科，它在各个领域中都有着广泛的应用。

本实验旨在通过应用统计学的方法，对某一特定问题进行深入分析，并从中得出结论。

实验背景：为了更好地理解统计学的实际应用，我们选择了一个关于学生睡眠时间与学习成绩之间关系的实验。

这个问题是一个经典的统计学问题，通过分析学生的睡眠时间和他们的学习成绩，我们可以探讨睡眠对学习的影响。

实验设计：我们选择了一所大学的一百名学生作为实验对象，他们的睡眠时间和学习成绩是我们的观察指标。

为了收集数据，我们设计了一份问卷，包括学生的睡眠时间、学习成绩以及其他相关因素的调查问题。

数据收集与处理：通过发放问卷并收集回答，我们得到了一百份有效的数据。

接下来，我们使用统计软件对数据进行了处理和分析。

首先，我们计算了学生的平均睡眠时间和平均学习成绩，并绘制了相应的直方图和散点图。

实验结果：通过对数据的分析，我们发现了一些有趣的结果。

首先，学生的睡眠时间和学习成绩之间存在一定的相关性。

具体来说，睡眠时间较长的学生往往有较好的学习成绩，而睡眠时间较短的学生则成绩较差。

此外，我们还发现了一些其他因素对学习成绩的影响，如学习时间、课外活动等。

讨论与结论：通过本次实验，我们可以得出结论：睡眠时间与学习成绩之间存在一定的相关性。

然而，我们也要注意到相关性并不代表因果关系。

即使睡眠时间较长的学生有较好的学习成绩，我们不能简单地得出睡眠时间是提高学习成绩的唯一因素的结论。

实际上，学习成绩受到多个因素的影响，如学习方法、个人能力等。

因此，我们需要进一步的研究来探索这些因素之间的关系。

结语：通过本次实验，我们深入了解了统计学在实际问题中的应用。

统计学不仅可以帮助我们分析数据，还可以帮助我们发现问题、解决问题。

在今后的学习和工作中，我们可以运用统计学的方法来解决各种问题，提高我们的决策能力和解决问题的能力。

西安交通大学实验报告_______________________________________________________________________________课程：概率论与数理统计应用 实验名称：概率论在实验中的应用 实验日期：2015 年 12 月15 日系 别：电信 专业班级：电信少41 姓 名：刘星辰 学号：2120406102_____________________________________________________________________一、实验目的：1. 了解 matlab 在实现数学问题时如何应用；2. 加强对 matlab 的操作能力；3. 对实际问题在概率论中的应用的理解有所加深；4. 将实际问题进行模拟，提高数学建模能力。

二、实验内容：本次试验将解决下面 4 个问题：1. 二项分布的泊松分布与正态分布的逼近；2. 正态分布的数值计算；3. 通过计算机模拟已有分布律进行模拟实验；4. 进行蒲丰投针实验模拟。

三、实验问题分析、解决与思考：1.二项分布的泊松分布与正态分布的逼近 设 X ~ B(n ，p) ，其中np=21) 对n=101,…,104,讨论用泊松分布逼近二项分布的误差。

画处逼近的图形2) 对n=101,…,104, 计算 )505(≤<X P ，)9020(≤<X P 1）用二项分布计算 2）用泊松分布计算 3）用正态分布计算比较用泊松分布逼近与正态分布逼近二项分布的优劣。

解：（1） x = -10:0.1:10;y1 = binopdf(x,10,2/10); %此处仅列出n=10时的二项分布语句 y2 = poisspdf(x,2); %泊松分布语句 plot(x,y1,'r') %做出二项分布图像 hold onplot(x,y2,'b') %做出泊松分布图像 title('泊松分布逼近二项分布图像')(图中红线为二项分布，蓝线为泊松分布)n=10，很明显地看出拟合效果不太好，红线与蓝线没有完全重合：n=100，放大之后可以看出还是有一部分没有很好地拟合（后为局部图）：n=1000，仅仅只有一部分的拟合程度没有很完美（后为局部图）：n=10000可以看出，当n ≥100时拟合程度较好。

研究生课程报告科目：数理统计上课时间：姓名：方健学号：专业：电子与通信工程教师：工作单位或所在行业：通信考生成绩：报告成绩阅卷评语：阅卷教师(签名)用线性回归分析压力变送器的线性度摘要：随着电子技术的飞速发展，各种分析工具和分析方法层出不穷。

这样，就有必要使分析方法达到最优化，一种十分有效的途径就是实现学科交叉。

本文就是基于这种思想，运用数理统计中线性回归的思想对压力变送器的线性度进行分析。

压力变送器是工业实践中最为常用的一种传感器，将测压元件传感器感受到的气体、液体等物理压力参数转变成标准的电信号（如4～20mADC等）。

线性度是压力变送器的主要性能参数，那么测试压力变送器的线性度就尤为重要。

本文就将用线性回归的方法解决这一问题：改变压力值，观察记录压力变送器的输出电流是否变化，并研究其变化规律。

这有助于判断压力变送器的线性度良好与否，同时，对压力变送器也会有更深入的了解。

关键词：电子技术，压力变送器，线性度，线性回归一、问题提出，问题分析1.问题背景火灾被消防界称为高层建筑的“先天之痛”，高层建筑内部拥有大量管道、竖井、楼梯间、电梯井、排气道等各类纵向通道形成的“烟囱效应”会使火灾快速蔓延。

此外，高空气流运行速度较快也是高层建筑无法避免的因素，它将加速火势蔓延。

发生在常规云梯车救援高度和水枪射程外的火灾，灭火救援无法完全借助外力，更多需要楼宇自身的消防系统解决。

因此对高层楼宇消防水压的实时监控是城市安全体系中事关民生的大事，也是保障人民群众生命财产安全的头等大事。

压力变送器的选择显得尤为重要，线性度作为压力变送器重要性能指标，线性度的良好对于判断压力变送器的好坏有着重大的影响。

本文测试的是BP93420IB压力变送器的线性度。

2.BP93420IB压力变送器BP93420IB压力变送器量程为0～2.5MPa，压力变送器的主要作用把压力信号传到电子设备，进而在计算机显示压力，其原理大致是：将水压这种压力的力学信号转变成4～20mA的直流电流这样的电子信号。

数理统计实验报告数理统计实验报告引言数理统计是一门研究收集、整理、分析和解释数据的学科，它在各个领域中都扮演着重要的角色。

本次实验旨在通过一个实际案例，探索数理统计在实际问题中的应用，并通过实验结果得出相关结论。

实验设计本次实验的目标是研究某家电公司生产的电视机的寿命分布情况。

为了达到这个目标，我们选择了一个随机样本，其中包括100台电视机。

我们记录了每台电视机的使用寿命（以小时为单位），并进行了相应的数据处理和分析。

数据处理与分析首先，我们对所收集的数据进行了整理和清洗。

我们排除了一些异常值和错误数据，确保数据的准确性和可靠性。

然后，我们计算了电视机的平均寿命、中位数和众数等统计指标，以了解电视机寿命的整体情况。

接下来，我们绘制了电视机寿命的频率分布直方图。

通过观察直方图，我们可以看到电视机寿命的分布大致呈现正态分布的形态。

这意味着大部分电视机的寿命集中在一个区间内，而较短寿命和较长寿命的电视机数量相对较少。

然后，我们使用了假设检验方法来验证电视机寿命是否符合正态分布。

通过计算样本数据的偏度和峰度等统计量，我们发现其与正态分布的理论值相差不大。

因此，我们可以认为电视机寿命的分布近似于正态分布。

进一步地，我们对电视机寿命的均值进行了置信区间估计。

通过计算样本数据的标准差和样本容量，我们得出了一个置信区间，用于估计总体均值的范围。

这个置信区间可以帮助我们判断电视机寿命的整体水平，并对未来的生产和销售做出相应的决策。

结论通过本次实验，我们得出了以下结论：1. 电视机寿命的分布大致呈现正态分布的形态，大部分电视机的寿命集中在一个区间内。

2. 电视机寿命的分布近似于正态分布，通过假设检验方法得出。

3. 样本数据的均值提供了电视机寿命的一个置信区间，用于估计总体均值的范围。

这些结论对于电视机公司来说具有重要的意义。

它们可以帮助公司了解电视机寿命的整体情况，评估产品质量和性能，并制定相应的生产和销售策略。

同时，这些结论也为进一步的研究和探索提供了基础。

第1篇一、实验背景与目的随着社会经济的快速发展，数据分析已成为各类决策的重要依据。

应用统计实验旨在通过实际操作，让学生掌握统计学的基本原理和方法，提高数据分析能力。

本实验以某城市居民消费行为为例，通过收集和分析数据，探究影响居民消费水平的因素，为政策制定和企业营销提供参考。

二、实验方法与数据来源1. 实验方法：本次实验采用描述性统计、相关分析和回归分析等方法，对居民消费数据进行处理和分析。

2. 数据来源：数据来源于某城市统计局发布的居民消费调查报告，涵盖了居民家庭人口、收入、消费结构、消费水平等指标。

三、实验结果与分析1. 描述性统计：通过对居民消费数据的描述性统计，得出以下结论：- 居民消费水平总体呈上升趋势，但城乡差异明显。

- 居民消费结构以食品、居住和交通通信为主，娱乐教育和医疗保健消费占比逐年提高。

- 居民收入水平与消费水平呈正相关，收入越高，消费水平越高。

2. 相关分析：通过相关分析，得出以下结论：- 居民消费水平与家庭人口呈正相关，家庭人口越多，消费水平越高。

- 居民消费水平与收入水平呈正相关，收入越高，消费水平越高。

- 居民消费水平与消费结构中的食品、居住和交通通信消费呈正相关，与娱乐教育和医疗保健消费呈负相关。

3. 回归分析：通过回归分析，得出以下结论：- 家庭人口、收入水平、食品、居住和交通通信消费对居民消费水平有显著影响。

- 家庭人口、收入水平和食品消费对居民消费水平的解释力最强。

四、结论与建议1. 结论：- 家庭人口、收入水平、食品、居住和交通通信消费是影响居民消费水平的主要因素。

- 居民消费水平与收入水平、家庭人口呈正相关，与消费结构中的食品、居住和交通通信消费呈正相关。

2. 建议：- 政府应关注农村居民消费水平，加大对农村基础设施建设的投入，提高农村居民收入水平。

- 企业应针对不同收入水平和消费结构的居民，制定差异化的营销策略。

- 鼓励居民消费，优化消费结构，提高居民消费水平。

组员：*** A01014023** A01014037** A01014103** A01014126*** A01014143*** A01014163实验日期：2013年1月5日关于居民消费价格指数与货币流通量之间关系的探讨数据如下述各表：1.作出(X,Y)的散点图;2.以Y为因变量,以X为解释变量,作回归分析,得到回归方程Y=a+bX;3.在显著性水平为0.05下,对回归效果作假设检验;4.结合实际意义,对回归结果作出具体的实际意义解释;[ 一元线性回归模型]1. 基本概念回归模型是一种正规工具，它表示统计关系中两个基本的内容：①用系统的形式表示因变量Y 随一个或几个自变量X 变化的趋势；②表现观察值围绕统计关系曲线的散布情况。

这两个特点是由下列假设决定的：● 在与抽样过程相联系的观察值总体中，对应于每一个X 值，存在Y 的一个概率分布；这些概率分布的均值以一些系统的方式随X 变化。

● 图1是用透视的方法来显示回归曲线。

Y 对给定X 具有概率分布这一概念总是与统计关系中的经验分布形式上相对应；同样，描述概率分布的均值与X 之间关系的回归曲线，与统计关系中Y 系统地随X 变化的一般趋势相对应。

在回归模型中，X 称为“自变量”，Y 称为“因变量”；这只是传统的称法，并不表明在给定的情况下Y 因果地依赖于X ，无论统计关系多么密切，回归模型不一定是因果关系，在某些应用中，比如我们由温度表水银柱高度（自变量）来估计温度（因变量）时，自变量实际上依赖于因变量。

此外，回归模型的自变量可以多于一个。

2. 回归模型的构造 1) 自变量的选择。

构造回归模型时必须考虑到易处理性，所以在有关的任何问题中，回归模型只能（或只应该）包括有限个自变量或预测变量。

2) 回归方程的函数形式。

选择回归方程函数形式与选择自变量紧密相关。

有时有关理论可能指出适当的函数形式。

然而，通常我们预先并不能知道回归方程的函数形式，要在收集和<图1>线性回归模型的图示分析数据后，才能确定函数形式。

应用统计学实验报告统计学作为一门应用数学学科，广泛应用于各个领域。

统计学方法可以帮助我们从一系列数据中分析和推断出规律，进而做出合理的决策。

在本次实验中，我们将应用统计学的基本方法，通过数据收集和分析，探讨一项与人们日常生活息息相关的问题：手机使用对睡眠质量的影响。

1. 引言睡眠是人体健康的重要组成部分，良好的睡眠质量对人的体力和心智健康至关重要。

但是，在现代社会，手机的普及和使用已成为日常生活中的一部分。

一些研究表明，过度使用手机可能会对睡眠质量产生负面影响。

本次实验将通过数据采集和统计学方法来验证这一说法。

2. 实验设计为了获取有关手机使用与睡眠质量的数据，我们对一组参与者进行了实验。

实验分为两组，一组使用手机前自备专用应用程序来记录手机使用时间，另一组则不使用应用程序。

我们将两组参与者的睡眠质量进行比较，以确定手机使用对睡眠的影响。

3. 数据收集实验持续了一个月的时间，参与者每晚在睡觉前使用应用程序记录自己的手机使用时间。

同时，他们还填写睡眠质量调查问卷，以评估其睡眠质量。

在实验结束后，我们收集了所有参与者的数据，并进行了初步的数据清洗和整理。

4. 数据分析通过对收集到的数据进行统计学分析，我们得到了以下结果：结果图表从图表中可以清楚地看出使用手机的组与不使用手机的组之间存在着显著的差异。

使用手机的组的睡眠质量普遍较差，而不使用手机的组的睡眠质量相对较好。

5. 结论根据实验结果和数据分析，我们可以得出结论：手机使用对睡眠质量有负面影响。

由于手机的蓝光辐射和频繁的信息干扰，使用手机会导致睡眠质量下降。

因此，为了保证良好的睡眠，我们应该尽量减少手机使用。

6. 实验局限性和建议尽管本次实验得出了明确的结论，但也存在着一些局限性。

首先，样本量较小，可能影响了结果的可靠性和推广性。

其次，实验中未考虑到其他可能影响睡眠质量的因素，如环境噪音、个人习惯等。

为了更全面地了解手机使用与睡眠质量的关系，未来可进行更大样本量的研究，并控制其他可能的影响因素。