二模数学压轴题

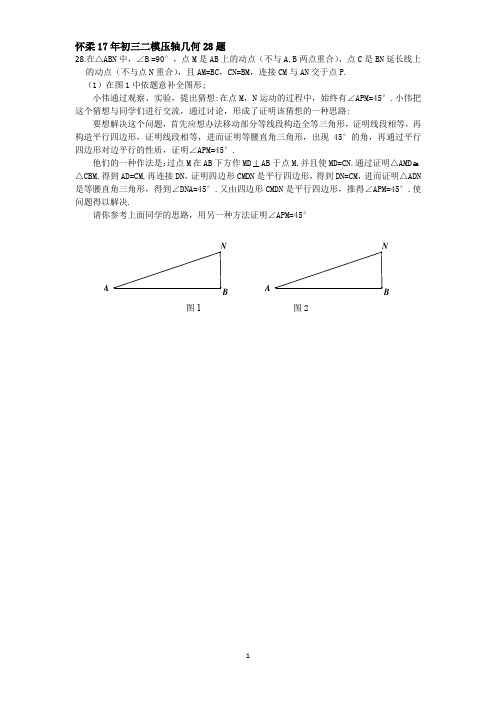
AA怀柔17年初三二模压轴几何28题28.在△ABN中，∠B =90°，点M是AB上的动点（不与A,B两点重合），点C是BN延长线上的动点（不与点N重合），且AM=BC，CN=BM，连接CM与AN交于点P.（1）在图1中依题意补全图形;小伟通过观察、实验，提出猜想:在点M，N运动的过程中，始终有∠APM=45°.小伟把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的一种思路: 要想解决这个问题，首先应想办法移动部分等线段构造全等三角形，证明线段相等，再构造平行四边形，证明线段相等，进而证明等腰直角三角形，出现45°的角，再通过平行四边形对边平行的性质，证明∠APM=45°.他们的一种作法是：过点M在AB下方作MD⊥AB于点M,并且使MD=CN.通过证明△AMD≅△CBM,得到AD=CM,再连接DN，证明四边形CMDN是平行四边形，得到DN=CM，进而证明△ADN 是等腰直角三角形，得到∠DNA=45°.又由四边形CMDN是平行四边形，推得∠APM=45°.使问题得以解决.请你参考上面同学的思路，用另一种方法证明∠APM=45°图1 图228．（1）在图1中依题意补全图形,如图1所示：…………………………1分 （2）证明：如图2，过点A 作AD ⊥AB 于点A,并且使AD=CN.连接DM,DC. …………………………2分 ∵AM=BC ，∠DAM=∠MBC =90°，∴△DAM ≅△MBC. …………………………3分∴DM=CM, ∠AMD=∠BCM. …………………………4分 ∵∠DAM=90°.∴∠AMD+∠BMC =90°. ∴∠DMC =90°.∴∠MCD =45°. …………………………5分 ∵AD ∥CN,AD=CD,∴四边形ADCN 是平行四边形. …………………………6分 ∴AN ∥DC.∵∠MCD =45°.∴∠APM=45°. …………………………7分 （其它方法相应给分）ABCDPMN图2图1图2图3通州17年初三二模压轴几何28题28．在△ABC 中，AB =BC ，∠ABC =90°. 以AB 为斜边作等腰直角三角形ADB . 点P 是直线DB 上一个动点，连接AP ，作PE ⊥AP 交BC 所在的直线于点E .（1）如图1，点P 在BD 的延长线上，PE ⊥EC ，AD =1，直接写出PE 的长； （2）点P 在线段BD 上（不与B ，D 重合），依题意，将图2补全，求证PA =PE ； （3）点P 在DB 的延长线上，依题意，将图3补全，并判断PA =PE 是否仍然成立.28.解：（1）2……………………..(1分)（2）法①过P 作PM ⊥BD ,交AB 于M法②过P 作PM ⊥BC 于点M , 过P 作PN ⊥AB 于点N 法③延长AB ,在AB 的延长线上截取PM =PA 法④过点B 作BM ⊥BD ,截取BM =BP ，连接CM .法⑤连接AE ,取AE 中点M ，连接BM ，PM ,四点共圆. …………..(5分) （3）图正确，成立……………………..(7分)图1燕山17年下期初三一模新定义29题29.在平面直角坐标系中，我们不妨把横坐标与纵坐标相等的点称为梦之点，例如，点（1，1），（﹣ 2，﹣ 2），（2，2），…，都是梦之点，显然梦之点有无数个． （1）若点 P （2，b ）是反比例函数xny =(n 为常数，n ≠ 0) 的图象上的梦之点，求这个反比例函数解析式； （2）⊙ O 的半径是2，①求出⊙ O 上的所有梦之点的坐标；②已知点 M （m ，3），点 Q 是（1）中反比例函数xny =图象上异于点 P 的梦之点，过点Q 的直线 l 与 y 轴交于点 A ，tan ∠OAQ ＝ 1．若在⊙ O 上存在一点 N ，使得直线 MN ∥l 或 MN ⊥l ，求出 m 的取值范围．28. （1）①F ; ………………………………………………………………………1分 ②∵⊙O 的半径为1. ∴⊙O 的“梦之点”坐标为（－22 ,－22 ）和（22 ,22）.………………2分 又∵双曲线ky x=（k ≠0）与直线y =x 的交点均为双曲线的“梦之点”， ∴将（－22 ,－22）代入双曲线表达式中，得， 1=2k xy =……………………………………………………………………3分 ∵点P 位于⊙O 内部. ∴102k ＜＜……………………………………………………………………4分 （2） －1≤t ≤3……………………………………………………………………………6分 （3）由“梦之点”定义可得: ()11A x ,x ，()22B x ,x . 则21x ax ax =-+.整理得，()2110ax a x -++=解得，11x =，21x a=. 把两个根代入122x x -=中，即112a-= 解得，11a =-，213a =. 当1a =-时，21y x x =-++ ，其顶点坐标为（12 , 54 ）………………………7分 当13a =时，211133y x x =-+，其顶点坐标为（12 , 1112 ）……………………8分。

最新压轴题汇总2023年上海各区中考数学二模试卷汇总本文档旨在为2023年上海各区中考的数学二模试卷提供最新的压轴题汇总。

以下是对各区试卷的简要总结和提供的压轴题目。

区一数学二模试卷压轴题目1题目描述：在平面坐标系中，已知点A(2, 3)和B(-1, 4)，求线段AB的中点的坐标。

解析：根据平面几何知识，线段AB的中点的坐标可以通过将两个端点的坐标相加再除以2来计算。

所以中点的坐标为((2 - 1)/2, (3 + 4)/2)，即(0.5, 3.5)。

压轴题目2题目描述：已知直线L1的方程为3x - 4y = 12，求直线L2与L1的交点坐标。

解析：要求两条直线的交点坐标，可以将两条直线的方程联立求解。

首先，将直线L1的方程转化为一般式，得到3x - 4y - 12 = 0。

然后，代入直线L2的方程，求解方程组3x - 4y - 12 = 02x + 5y = 6求得交点坐标为(x, y) = (6, -2)。

区二数学二模试卷压轴题目1题目描述：在一个圆的内接正方形中，以正方形的一个顶点为圆心，作一个与正方形相切的圆，求内接圆的直径。

解析：在一个内接正方形中，对角线的长度等于内接圆的直径。

设正方形的边长为a，则对角线的长度为sqrt(2)a。

因此，内接圆的直径等于sqrt(2)a。

压轴题目2题目描述：已知函数f(x) = 2x^2 - 3x + 1，求f(x)的最小值和对应的x值。

解析：函数的最小值对应于顶点的纵坐标。

通过求导数可得f'(x) = 4x - 3。

令f'(x) = 0，解得x = 3/4。

将x = 3/4代入原函数，可得最小值f(3/4) = -1/8。

以上是对2023年上海各区中考数学二模试卷压轴题目的简要汇总。

希望本文档对您的备考有所帮助。

祝您取得好成绩！。

高考数学高三模拟考试试卷压轴题高三第二次模拟考试数学一、填空题：本大题共14小题，每小题5分，共70分 1．已知集合{}R x x x x A ∈≤-=,02|2，}{a x x B ≥=|，若B B A = ，则实数a 的取值范围是。

2、已知i b iia-=+3，其中R b a ∈,，i 为虚数单位，则=+b a 。

3、某单位从4名应聘者A 、B 、C 、D 中招聘2人，如果这4名应聘者被录用的机会均等，则A ，B 两人中至少有1人被录用的概率是。

4、某日用品按行业质量标准分成王五个等级，等级系数X 依次为1，2，3，4，5.现从一批该日用品中随机抽取200件，对其等级系数进行统计分析，得到频率f 的分布如下X1 2 3 4 5 f a 0.2 0.45 0.15 0.1 5、已知变量y x ,满足约束条件⎪⎩⎪⎨⎧≤≤-≥+212y y x y x ，则目标函数y x z +-=2的取值范围是6、已知双曲线1222=-y ax 的一条渐近线方程为02=-y x ，则该双曲线的离心率=e7、已知圆C 的经过直线022=+-y x 与坐标轴的两个交点，又经过抛物线x y 82=的焦点，则圆C 的方程为。

8、设n S 是等差数列{}n a 的前n 项和。

若3173=S S ，则=76S S 。

9、已知函数)sin(ϕω+=x A y )2||,0,0(πϕω<>>A 的部分图象如图所示，则ω的值为。

10、在如图所示的流程图中，若输入n 的值为11，则输出A 的值为。

11、一块边长为10cm 的正方形铁片按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角形作侧面，以它们的公共顶点P 为顶点，加工成一个如图所示的正四棱锥形容器。

当cm x 6=时，该容器的容积为3cm 。

12、下列四个命题①“,R x ∈∃112≤+-x x ”的否定；②“若,062≥-+x x 则2>x ”的否命题；③在ABC ∆中，“”是30>A “21sin >A ”的充分不必要条件； ④“函数)tan()(ϕ+=x x f 为奇函数”的充要条件是“)(z k k ∈=πϕ”。

2024年北京各区二模压轴1.(2024顺义二模)已知点集M n =x 1,y 1 ,x 2,y 2 ,⋯,x n ,y n n ≥3 满足0≤x i ,y i ,x i +y i ≤2i =1,2,⋯,n . 对于任意点集M n ,若其非空子集A ,B 满足A ∩B =⌀,A ∪B =M n ,则称集合对A ,B 为M n 的一个优划分. 对任意点集M n 及其优划分A ,B , 记A 中所有点的横坐标之和为X A ,B 中所有点的纵坐标之和为Y B .(1)写出M 3=1,1 ,2,0 ,0,2 的一个优划分A ,B ,使其满足X A +Y B =3;(2)对于任意点集M 3,求证:存在M 3的一个优划分A ,B ,满足X A +Y B ≤3;(3)对于任意点集M n ,求证:存在M n 的一个优划分A ,B ,满足X A ≤n +12且Y B ≤n +12.2.(2024通州二模)从数列a n 中选取第i 1项,第i 2项,第i m 项1≤i 1<i 2<⋯<i m ,若数列a i 1,a i 2,⋯,a i m是递增数列或递减数列(规定m =1时,该数列既是递增数列,也是递减数列),称a i 0, a i 0,⋯,a i m 为数列a n 的长度为m 的单调子列. 已知有穷数列A :a 1,a 2,⋯,a n (n ≥3),任意两项均不相同,现以A 的每一项a i 为首项选取长度最大的递增的单调子列,设其共有b i 项,则b 1,b 2,⋯ , b n 构成一个新数列B .(1)当数列A 分别为以下数列时,直接写出相应的数列B ;(i )1,3,5,7;(ii )4,1,2,6,3 .(2)若数列A 为等差数列,求证:数列B 为等差数列;(3)若数列A 共有t 2+1t ∈N * 项,求证:A 必存在一个长度为t +1的单调子列.3.(2024昌平二模)已知Q :a 1,a 2,⋯,a N 为有穷正整数数列, a 1≤a 2≤⋯≤a N ,且s =a 1+a 2+⋯+a N . 从Q 中选取第i 1项,第i 2项, ⋯,第i m 项i 1<i 2<⋯<i m ,称数列a i 1,a i 2,⋯,a i m 为Q 的长度为m 的子列. 规定:数列Q 的任意一项都是Q 的长度为1的子列. 若对于任意的正整数t ≤s , 数列Q 存在长度为m 的子列a i 1,a i 2,⋯,a i m ,使得a i 1+a i 2+⋯+a i m=t ,则称数列Q 为全覆盖数列.(1)判断数列1,1,1,5和数列1,2,4,8是否为全覆盖数列;(2)在数列Q 中,若s ≤2N -1,求证:当2≤n ≤N 时, a n ≤n ≤1+a 1+a 2+⋯+a n -1;(3)若数列Q 满足:a 1=1,且当2≤n ≤N 时, a n ≤n ≤1+a 1+a 2+⋯+a n -1,求证:数列Q 为全覆盖数列.4.(2024丰台二模)将正整数数列N 0：1,2,3,4,⋯中项数为平方数的项依次选出构成数列A 1：1,4,9,16,⋯,此时数列N 0中剩下的项构成数列N 1：2,3,5,6,⋯;再将数列N 1中项数为平方数的项依次选出构成数列A 2:2,6,12,20,⋯,剩下的项构成数列N 2;⋯,如此操作下去,将数列N k -1k ∈N * 中项数为平方数的项依次选出构成数列A k ,剩下的项构成数列N k .(1)分别写出数列A 3,A 4的前2项;(2)记数列A m 的第n 项为f m ,n . 求证:当n ≥2时, f m ,n -f m ,n -1 =2n +m -2;(3)若f m ,n =108,求m ,n 的值.5.(2024朝阳二模)设n 为正整数,集合A n =α∣α=a 1,a 2,⋯,a n ,a i ∈{0,1},i =1,2,⋯,n .对于α=a 1,a 2,⋯,a n ∈A n ,设集合P α =t ∈N ∣0≤t ≤n -1,a i +t =a i ,i =1,2,⋯,n -t .(1)若α=0,1,0,0,1,0 ,β=0,1,0,0,1,0,1,0 ,写出集合P α ,P β ;(2)若α=a 1,a 2,⋯,a n ∈A n ,且s ,t ∈P α 满足s <t ,令α =a 1,a 2,⋯,a n -s ∈A n -s ,求证:t -s ∈P α ;(3)若α=a 1,a 2,⋯,a n ∈A n ,且P α =s 1,s 2,⋯,s m s 1<s 2<⋯<s m ,m ≥3 ,求证：2s k +1≥s k +s k +2k =1,2,⋯,m -2 .6.(2024东城二模)已知A n :a 1,a 2,⋯,a n n ≥3 为有穷整数数列,若A n 满足:a i +1-a i ∈{p ,q }i =1,2,⋯,n -1 ,其中p ,q 是两个给定的不同非零整数,且a 1=a n =0,则称A n 具有性质T .(1)若p =-1,q =2,那么是否存在具有性质T 的A 3?若存在,写出一个这样的A 5;若不存在,请说明理由;(2)若p =-1,q =2,且A 10具有性质T ,求证:a 1,a 2,⋯,a 9中必有两项相同;(3)若p +q =1,求证:存在正整数k ,使得对任意具有性质T 的A k ,都有a 1,a 2,⋯,a k -1中任意两项均不相同.7.(2024西城二模)数列A ：a 1,a 2,⋯,a n 从A 中选取第i 1项、第i 2项、⋯、第i k 项i 1<i 2<⋯<i k 构成数列B ：a i 1,a i 2,⋯,a i k,B l 称为A 的k 项子列.记数列B 的所有项的和为T B .当k ≥2时,若B 满足:对任意s ∈{1,2,⋯,k -1},i s +1-i s =1,则称B 具有性质P .规定:A 的任意一项都是A 的1项子列,且具有性质P .(1)当n =4时,比较A 的具有性质P 的子列个数与不具有性质P 的子列个数的大小,并说明理由;(2)已知数列A ：1,2,3,⋯,n n ≥2 .(i )给定正整数k ≤n 2,对A 的k 项子列B ,求所有T B 的算术平均值;(ii )若A 有m 个不同的具有性质P 的子列B 1,B 2,⋯,B m ，满足:∀1≤i <j ≤m ,B i 与B j 都有公共项,且公共项构成A 的具有性质P 的子列,求m 的最大值.8.(2024海淀二模)设正整数n ≥2,a i ∈N *,d i ∈N *，A i =x ∣x =a i +k -1 d i ,k =1,2,⋯ ，i =1,2,⋯,n . 若A 1∪A 2∪⋯∪A n =N *,A i ∩A j =⌀1≤i <j ≤n ,则称A 1,A 2,⋯,A n 具有性质P .(1)当n =3时,若A 1,A 2,A 3具有性质p ,且a 1=1,a 2=2,a 3=3,令m =d 1d 2d 3,写出m 的所有可能值;(2)若A 1,A 2,⋯,A n 具有性质P ,(i )求证:a i ≤d i i =1,2,⋯,n ；(ii )求n i =1a i d i 的值.。

高考数学高三模拟考试试卷压轴题高考数学二模试卷含答案一、填空题（本大题共有12题，满分54分，第16题每题4分，第712题每题5分）考生应在答题纸的相应位置直接填写结果.1.若集合{}|0A x x =>，{}|1B x x =<，则A B ⋂=____________2.已知复数z1z i ⋅=+（i 为虚数单位），则z =____________ 3.函数()sin cos cos sin x x f x x x=的最小正周期是____________4.已知双曲线()2221081x y a a -=>的一条渐近线方程3y x =，则a =____________ 5.若圆柱的侧面展开图是边长为4的正方形，则圆柱的体积为____________6.已知,x y 满足0220x y x y x -≤⎧⎪+≤⎨⎪+≥⎩，则2z x y =+的最大值是____________7.直线12x t y t =-⎧⎨=-⎩（t 为参数）与曲线3cos 2sin x y θθ=⎧⎨=⎩（θ为参数）的交点个数是____________8.已知函数()()()220log 01xx f x x x ⎧≤⎪=⎨<≤⎪⎩的反函数是()1f x -，则12f -1⎛⎫= ⎪⎝⎭____________9.设多项式()()()()23*11110,nx x x x x n N ++++++++≠∈的展开式中x 项的系数为n T ，则2limnn T n →∞=____________10.生产零件需要经过两道工序，在第一、第二道工序中产生的概率分别为0.01和p ，每道工序产生废品相互独立，若经过两道工序得到的零件不是废品的概率是0.9603，则p =____________11.设向量()(),,,m x y n x y ==-，P 为曲线()10m n x ⋅=>上的一个动点，若点P 到直线10x y -+=的距离大于λ恒成立，则实数λ的最大值为____________ 12.设1210,,,x x x 为1,2,,10的一个排列，则满足对任意正整数,m n ，且110m n ≤<≤，都有m n x m x n +≤+成立的不同排列的个数为____________二、选择题（本大题共有4题，满分20分，每题5分）每题有且只有一个正确选项，考生应在答题纸的相应位置，将代表正确选项的小方格涂黑. 13.设,a b R ∈，则“4a b +>”是“1a >且3b >”的（ ）A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分又不必要条件14.如图，P 为正方体1111ABCD A B C D -中1AC 与1BD 的交点，则PAC 在该正方体各个面上的射影可能是（ ）A. ①②③④B.①③C. ①④D.②④15.如图，在同一平面内，点P 位于两平行直线12,l l 同侧，且P 到12,l l 的距离分别为1，3.点,M N 分别在12,l l 上，8PM PN +=，则PM PN ⋅的最大值为（ ）A. 15B. 12C. 10D. 916.若存在t R ∈与正数m ，使()()F t m F t m -=+成立，则称“函数()F x 在x t =处存在距离为2m 的对称点”，设()()20x f x x xλ+=>，若对于任意t ∈，总存在正数m ，使得“函数()f x 在x t =处存在距离为2m 的对称点”，则实数λ的取值范围是（ ）A. (]0,2B. (]1,2C. []1,2D. []1,4三、解答题（本大题共有5题，满分76分）解答下列各题必须在答题纸的相应位置写出必要的步骤.17.（本题满分14分，第1小题满分8分，第2小题满分6分）如图，在正方体1111ABCD A B C D -中，E 、F 分别是线段BC 、1CD 的中点. （1）求异面直线EF 与1AA 所成角的大小； （2）求直线EF 与平面11AA B B 所成角的大小. 18.（本题满分14分，第1小题6分，第2小题8分）已知抛物线()220y px p =>，其准线方程为10x +=，直线l 过点()(),00T t t >且与抛物线交于A 、B 两点，O 为坐标原点.（1）求抛物线方程，并证明：OA OB ⋅的值与直线l 倾斜角的大小无关； （2）若P 为抛物线上的动点，记PT 的最小值为函数()d t ，求()d t 的解析式. 19.（本题满分14分，第1小题6分，第2小题8分）对于定义域为D 的函数()y f x =，如果存在区间[](),m n D m n ⊆<，同时满足：①()f x 在[],m n 内是单调函数；②当定义域是[],m n 时，()f x 的值域也是[],m n 则称函数()f x 是区间[],m n 上的“保值函数”.（1）求证：函数()22g x x x =-不是定义域[]0,1上的“保值函数”；（2）已知()()2112,0f x a R a a a x=+-∈≠是区间[],m n 上的“保值函数”，求a 的取值范围.20.（本题满分16分，第1小题满分4分，第2小题满分6分，第3小题满分6分） 数列{}n a 中，已知()12121,,n n n a a a a k a a ++===+对任意*n N ∈都成立，数列{}n a 的前n 项和为n S .（这里,a k 均为实数） （1）若{}n a 是等差数列，求k ； （2）若11,2a k ==-，求n S ; （3）是否存在实数k ，使数列{}n a 是公比不为1的等比数列，且任意相邻三项12,,m m m a a a ++按某顺序排列后成等差数列？若存在，求出所有k 的值；若不存在，请说明理由.21.（本题满分18分，第1小题满分4分，第2小题满分6分，第3小题满分8分）设T,R 若存在常数0M >，使得对任意t T ∈，均有t M ≤，则称T 为有界集合，同时称M 为集合T 的上界.（1）设121|,21x xA y y x R ⎧⎫-==∈⎨⎬+⎩⎭、21|sin 2A x x ⎧⎫=>⎨⎬⎩⎭，试判断1A 、2A 是否为有界集合，并说明理由；（2）已知()2f x x u =+，记()()()()()()11,2,3,n n f x f x f x f f x n -===.若m R ∈，1,4u ⎡⎫∈+∞⎪⎢⎣⎭，且(){}*|n B f m n N =∈为有界集合，求u 的值及m 的取值范围；（3）设a 、b 、c 均为正数，将()2a b -、()2b c -、()2c a -中的最小数记为d ，是否存在正数()0,1λ∈，使得λ为有界集合222{|,dC y y a b c==++a 、b 、c 均为正数}的上界，若存在，试求λ的最小值；若不存在，请说明理由.参考答案1. (0,1)2.13.π4.35. 5.16. 37. 28.19.1210. 0.0311.212.512 13. B14. C15.A16.A17. （1）（2）arctan 218.（1）24y x =，证明略 （2）2)(t),(0t 2)d t ⎧≥⎪=⎨<<⎪⎩19. （1）证明略（2）12a或32a 20. （1）12k =（2）2(21,),(2,)n n n k k N S n n k k N **⎧-=-∈=⎨=∈⎩ （3）25k =-21.（1）1A 为有界集合，上界为1；2A 不是有界集合 （2）14u =，11,22m ⎡⎤∈-⎢⎥⎣⎦ （3）15λ=解析：（3）不失一般性，不妨假设c b a <<（i ）若2a c b +=。

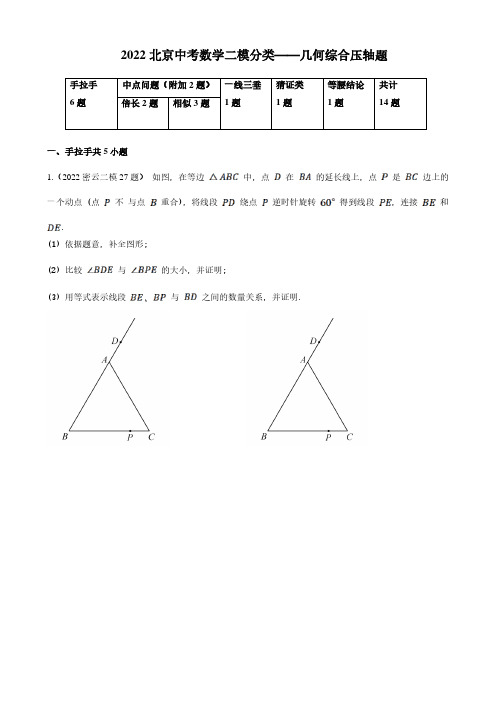
2022北京中考数学二模分类——几何综合压轴题一、手拉手共5小题1.（2022密云二模27题） 如图, 在等边 中, 点 在的延长线上, 点 是边上的一个动点 (点 不 与点 重合), 将线段绕点 逆时针旋转 得到线段, 连接和.(1) 依据题意, 补全图形; (2) 比较与的大小, 并证明; (3) 用等式表示线段与之间的数量关系, 并证明.手拉手 6题 中点问题（附加2题） 一线三垂 1题猜证类 1题等腰结论 1题共计 14题倍长2题相似3题2.（2022丰台二模27题）如图，在△ABC 中，AB=AC，∠BAC =120°，D 是BC 中点，连接AD .点M 在线段AD上 (不与点A，D 重合)，连接MB，点E 在CA 的延长线上且ME = MB，连接EB .（1）比较∠ABM 与∠AEM 的大小，并证明；（2）用等式表示线段AM，AB，AE 之间的数量关系，并证明 .3.（2022西城二模27题）在中, , 过点作射线, 使 (点与点在直线的异侧), 点是射线上一个动点 (不与点重合), 点在线段上, 且.(1) 如图 1, 当点与点重合时, 与的位置关系是 , 若, 则的长为； (用含的式子表示)(2) 如图 2, 当点与点不重合时, 连接.①用等式表示与之间的数量关系, 并证明；②用等式表示线段之间的数量关系, 并证明.4.（2022大兴二模27题）如图，AC=AB，∠CAB=∠CDB=α，线段CD与AB相交于点O，以点A为中心，将射线AD绕点A逆时针旋转α（0°<α<180°）交线段CD于点H,（1）若α=60°，求证：CD=AD+BD（2）请你直接用等式表示出线段CD, AD, BD 之间的数量关系（用含α的式子表示）5.（2022东城二模27题）如图，在ABC△中，AB AC=，2CABα∠=，在△ABC的外侧作直线()901802AP a PAC a︒−<∠︒−，作点C关于直线AP的对称点D，连接,,AD BD BD交直线AP于点E．（1）依题意补全图形；（2）连接CE，求证：ACE ABE∠=∠；（3）过点A作AF CE⊥于点F，用等式表示线段,2,BE EF DE之间的数量关系，并证明。

考试时间：120分钟总分：150分一、选择题（本大题共10小题，每小题5分，共50分）1. 已知函数$f(x)=x^3-3x+1$，则$f(x)$的极值点为（）。

A. $x=1$B. $x=-1$C. $x=\sqrt{3}$D. $x=-\sqrt{3}$2. 在$\triangle ABC$中，$a=3$，$b=4$，$c=5$，则$\sin A+\sin B+\sin C$的值为（）。

A. $\frac{3}{2}$B. $\frac{5}{2}$C. $2$D. $\frac{4}{3}$3. 设复数$z$满足$|z-1|=|z+1|$，则$z$在复平面内的轨迹是（）。

A. 线段$[-1,1]$B. 线段$[-1,1]$上除去端点C. 直线$x=0$D. 直线$x=1$4. 下列命题中，正确的是（）。

A. 函数$y=x^2$在定义域内是单调递增的B. 函数$y=\frac{1}{x}$在定义域内是单调递减的C. 函数$y=2^x$在定义域内是单调递增的D. 函数$y=\log_2x$在定义域内是单调递减的5. 若$a>0$，$b>0$，则下列不等式中正确的是（）。

A. $a^2+b^2>2ab$B. $a^3+b^3>2ab$C. $a^2+2ab+b^2>2ab$D. $a^3+3a^2b+3ab^2+b^3>2ab$6. 已知等差数列$\{a_n\}$的前$n$项和为$S_n$，若$a_1+a_3+a_5=18$，$S_5=50$，则$a_1$的值为（）。

A. 2B. 3C. 4D. 57. 已知圆$C:(x-1)^2+y^2=1$，直线$l:y=x+1$，则圆心到直线$l$的距离为（）。

A. $\frac{\sqrt{2}}{2}$B. $\sqrt{2}$C. $\frac{\sqrt{6}}{2}$D.$\sqrt{6}$8. 若向量$\vec{a}=(2,3)$，$\vec{b}=(1,2)$，则$\vec{a}\cdot\vec{b}$的值为（）。

2024北京初三二模数学汇编选择压轴（第8题）一、单选题1．（2024北京朝阳初三二模）如图1，在菱形中，，P 是菱形内部一点，动点M 从顶点B 出发，沿线段运动到点P ，再沿线段运动到顶点A ，停止运动．设点M 运动的路程为x ，，表示y 与x 的函数关系的图象如图2所示，则菱形的边长是（ ）A ．B ．4C ．D ．22．（2024北京燕山初三二模）如图，是半圆O 的直径，C 是半圆周上的动点(与A ，B 不重合），于点D ，连接．设，给出下面三个结论：①；②；③．上述结论中，所有正确结论的序号是（ ）A ．①②B ．②③C ．①③D ．①②③3．（2024北京东城初三二模）如图，在中，于点，点是的中点．设，，，，，，且，有以下三个结论：①；②点，，在以点为圆心，为半径的圆上；ABCD =60B ∠︒BP PA MA y MC=ABCD AB CD AB ⊥OC AD a BD b CD h ===，，2a b h +≤||2a b h -≤2a b +≥ABC AD BC ⊥D E BC AB c =AC b =AD h =BD m =CD n =m n <2h mn =22c m mn =+A B C E ()12m n +③．上述结论中，所有正确结论的序号是（ ）A ．①②B ．①③C ．②③D ．①②③4．（2024北京海淀初三二模）某种型号的纸杯如图所示，若将个这种型号的杯子按图中的方式叠放在一起，叠在一起的杯子的总高度为．则与满足的函数关系可能是（ ）A ．B ．C ．D ．5．（2024北京房山初三二模）如图，，，分别是直径为的的内接正六边形、正方形、等边三角形的一边．若，给出下而四个结论：①的直径为4；②③；④连接，则．上述结论中，所有正确结论的序号是（ ）A ．①③B ．②④C ．①②③D ．①②③④6．（2024北京顺义初三二模）如图，在中，是边上一动点（不与B ，C 重合），于点E ．设给出下面三个结论：①③上述结论中，所有正确结论的序号是（ ）2223b m h +>1n 2H H n 0.3H n =100.3H n =100.3H n =-100.3H n=+AB AC AD AE O 2AB =O AC = BCCD =CD ACD ABC 90,,C A C B C D ︒∠==BC DE AB ⊥,,.CD a BD b AE c ===;a b c +>);a b c +>2.a b +=A ．①③B ．②③C ．②D ．①②③7．（2024北京昌平初三二模）如图，为半圆O 的直径，C ，D 是直径上两点，且，过点D 作的垂线交半圆于点E ，．设，，，给出下面三个结论：①；②；③．所有正确结论的序号是（ ）A ．①②B．①③C ．②③D ．①②③8．（2024北京门头沟初三二模）如图所示，两个体积不等的圆柱形水杯，大小水杯口均朝上，现往大水杯中均匀注水，注水过程中小水杯始终在原来位置，设水面上升高度为h ，注水时间为t ，下列图象能正确反应注水高度随时间变化关系的是（ ）A ．B ．C ．D ．9．（2024北京北师大附属实验中学初三二模）如图，在平面直角坐标系中，矩形ABCD 的顶点A ，C 分别在x 轴，y 轴的正半轴上，点D （-2，3），AD =5，若反比例函数 （k ＞0，x ＞0）的图象经过点B ，则k 的值为（ ）AB AB AC BD =AB 2CD DE =AD a =AC b =DE c =2a b c -=c b a c=a b +=k y x=A．B ．8C ．10D ．10．（2024北京人大附中朝阳学校初三二模）如图，在平行四边形中，，，，是对角线上的动点，且，，分别是边，边上的动点．下列四种说法：①存在无数个平行四边形；②存在无数个矩形；③存在无数个菱形；④存在无数个正方形．其中正确的个数是（ ）A ．1B ．2C ．3D ．411．（2024北京广渠门中学初三二模）如图，在正方形中，是延长线上一点，在上取一点，使点关于直线的对称点落在上，连接交于点，连接交于点，连接．现有下列结论：①；②；③；④若，，则 ）A ．②③④B ．①②③C ．①③④D ．①②④12．（2024北京十一中学初三二模）筒车是我国古代发明的一种水利灌溉工具，如图1，筒车盛水桶的运行轨道是以轴心为圆心的圆，已知圆心在水面上方，且被水面截得弦长为4米，半径为163323ABCD 22AD AB ==60ABC ∠=︒E F BD BE DF =M N AD BC MENF MENF MENF MENF ABCD E BC AB F B EF G AD EG CD H BH EF M CM BHG BHC ∠=∠GBH BCM ∠=∠GD =1AG =2GD =BM =O O O AB O 3米，则点到弦所在直线的距离是（ ）A ．1米B ．2米C ．米D ．米13．（2024北京一零一中学初三二模）如图，正方形边长为a ，点E 是正方形内一点，满足，连接．给出下面四个结论：①；②；③的度数最大值为；④当时，．上述结论中，所有正确结论的序号为（ ）A ．①②B ．①③C ．①④D ．①③④14．（2024北京丰台初三二模）如图，在平面直角坐标系xOy 中 ，已知y 关于x 的函数图象与x 轴有且只有三个公共点，坐标分别为（-3，0），（-1，0），（3，0）．关于该函数的四个结论如下：①当y >0时，-3<x <-1；②当x >-3时，y 有最小值；③将该函数图象向右平移1个或3个单位长度后得到的函数图象经过原点；④点P （m ，-m -1）是该函数图象上一点，则符合要求的点P 只有两个．其中正确的结论有A ．1个B ．2个C ．3个D ．4个C AB (3(3+ABCD 90AEB ∠=︒CE AE CE +CE BCE ∠60︒CE a =1tan 2ABE ∠=15．（2024北京大兴初三二模）下面的三个问题中都有两个变量：①扇形的圆心角一定，面积S 与半径r ；②用长度为20的线绳围成一个矩形，矩形的面积S 与一边长；③汽车在高速公路上匀速行驶，行驶路程s 与行驶时间t ．其中，两个变量之间的函数关系可以利用二次函数表示的是（ ）A ．①②B ．①③C ．②③D ．①②③16．（2024北京石景山初三二模）在平面直角坐标系xOy 中，y 与x 的函数关系如图所示，图象与x 轴有三个交点，分别为，，．给出下面四个结论：①当时，；②当时，y 随x 的增大而增大；③点在此函数图象上，则符合要求的点只有一个；④将函数图象向右平移2个或4个单位长度，经过原点．上述结论中，所有正确结论的序号是（ ）A ．①②B ．②③C ．②④D ．③④x ()4,0-(2,0)-(3,0)0y >23x -<<502x -<<(,2)M m m +参考答案1．C【分析】首先根据题意作图，然后由图象判断出点P 在对角线上，，，设，则，利用勾股定理求解即可．【详解】如图所示，由图象可得，当x 从0到4时，∴∵四边形是菱形∴点P 在对角线上∴由图象可得，，∴∵在菱形中，，∴，∴设，则∴∴∴在中，∴解得∴∴菱形的边长是故选：C ．【点睛】此题考查了动点函数图象问题，菱形的性质，勾股定理，含角直角三角形的性质等知识，解题的关键是根据图象正确分析出点P 在对角线上．2．C【分析】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用；灵活运用相似三角形的性质计算相应线段的长或表BD 4BP =6BP AP +=AO x =22AB AO x ==1MA y MC ==MA MC=ABCD BD 4BP =6BP AP +=2AP =ABCD =60B ∠︒30ABD ∠=︒AC BD⊥AO x =22AB AO x==4PO BP BO =-=BO ==Rt APO 222AP AO PO =+()22224x =+x =2AB x ==ABCD 30︒BD示线段之间的关系是解决问题的关键，也考查了圆周角定理，直角三角形的性质．根据是半圆O 的直径，得出，根据直角三角形的性质得出，根据C 是半圆周上的动点(与A ，B 不重合），即可判断①；根据点C 的运动轨迹确定，即可判定②；证明，根据相似三角形的性质得出①中结论即可判断③．【详解】解：∵是半圆O 的直径，∴，∵点O 是中点，∴，∵，，∴，，即，故①正确；∵C 是半圆周上的动点(与A ，B 不重合），∴，，∴，∴，故②错误；，，，，，，，∴，∴，∴∵，，故③正确；故选：C ．3．DAB 90ACB ∠=︒122a b CO AB +==2a b DO BD BO -=-=Rt ADC Rt CDB ∽h =AB 90ACB ∠=︒AB 12CO AB =CD AB ⊥AD a BD b CD h ===，，CD CO ≤()11222a b CO AO BO AB AD BD +====+=2a b h +≤OD AO <CD DO <222a b b a a b DO BD BO b +--=-=-==||2a b h -<DC AB ⊥ 90ACB ∠=︒90ADC BDC ∴∠=∠=︒90DAC ACD ∠+∠=︒ 90DCA DCB ∠+∠=︒DAC DCB∴∠=∠Rt ADC Rt CDB ∴ ∽AD CD CD DB∴=a h h b=2h ab =h =2a b h +≤2a b +≤【分析】本题考查了勾股定理，直角三角形的特征，完全平方公式的应用，相似三角形的判定与性质，利用勾股定理可判断①结论；利用线段中点以及直角三角形斜边中线等于斜边一半可判断②结论；利用勾股定理以及完全平方公式可判断③结论．【详解】解：，，，，，，且，，①结论正确；，，，即，，，，，，点是的中点，，则，此时点，，在以点为圆心，为半径的圆上，②结论正确；在中，，即，，，，，即，③结论正确，故选：D ．4．D【分析】本题考查了用字母表示数或数量关系，理解题目中的数量关系，掌握代数式的表示方法是解题的关键．根据一个杯子的高度和杯沿的高度，可得，由此即可求解．【详解】解：根据题意，1个杯子的高，1个杯子沿高为，∴个杯子叠在一起的总高度为，故选：D ．5．C【分析】根据正多边形的性质以及圆心角定理即可判断③；再利用即可判断①；借助AD BC ⊥ 90ADB ADC ∴∠=∠=︒222AB BD AD ∴=+AB c = BD m =AD h =2h mn =2222c m h m mn ∴=+=+BD m = CD n =2h mn =h m n h ∴=AD BD CD AD=90BDA ADC ∠=∠=︒ BDA ADC ∴ ∽BAD ACD ∴∠=∠90BAD BAC ACD DAC ∴∠+∠=∠+∠=︒90BAC ∴∠=︒ E BC AE BE EC ∴==()1122AE BC m n ==+A B C E ()12m n +Rt ADC 222AC AD CD =+222b h n =+()2222222222323h n m h n m mn n m b m h -=++-=+-=-∴+m n < ()20n m ∴->22203b m h -+>∴2223b m h +>0.3H h n =+10h =0.3n 100.3H n =+OA OB OC OD ===勾股定理可求出，即可判断②；过点A作交延长线于点F，过点D作交于点E，根据等腰三角形的性质先求出，再利用特殊三角函数值，可求得即可求解．【详解】解：连接，，∵，，分别是直径为的的内接正六边形、正方形、等边三角形的一边∴，，∴，∴，即故③正确；∵∴是等边三角形，是等腰直角三角形∴故①正确；由勾股定理可得，故②正确；过点A作交延长线于点F，过点D作交于点E∵，∴∵，∴，AC AF DC⊥DC DG AE⊥AE60DOG∠=︒AD=DF AF==CF=CDOB OC ODAB AC AD AE O60AOB∠=︒=90AOC︒∠120AOD∠=︒30BOC AOC AOB∠=∠-∠=︒30COD AOD AOC∠=∠-∠=︒BOC COD∠=∠BC CD=OA OB OC OD===AOBAOC224AE OA AB===AC==AF DC⊥DC DG AE⊥AE30COD∠=︒OC OD=()118030752OCD ODC∠=∠=⨯︒-︒=︒120AOD∠=︒OA OD=()1180120302OAD ODA∠=∠=⨯︒-︒=︒60DOG∠=︒∴∴即为等腰直角三角形∴∴在中，由勾股定理得∴∴故④错误；故选：C ．【点睛】本题考查正多边形和圆，圆心角定理，等腰三角形的性质和判定，勾股定理，解直角三角形，含角的直角三角形的性质，熟练掌握圆心角定理以及作辅助线构造直角三角形是解题的关键．6．B【分析】连接，当平分，即时，即证明，可得出，当不平分，若时，，若时，，可判定①错误；根据，又由，可判定②正确；证明，得出，又根据，则，可判定③正确．【详解】解：连接，当平分，即时，∵，，，∴，∴，∵，∴即；若时，，即，若时，，即，故①错误；∵，，sin 602DG OD =︒⋅=AD =45FDA CDO ODA ∠=∠-∠=︒AFD △cos 45DF AD =︒⋅==DF AF ==Rt AFC △CF =CD DF CF =-11322ACD S CD AF =⋅⋅=⨯= 30︒AD AD BAC ∠CAD EAD ∠=∠()AAS ACD AED ≌c a b =+AD BAC ∠CAD EAD ∠>∠c a b >+CAD EAD ∠<∠c a b <+)AB a b =+AB AE >)a b c +>BE DE =BE )AB a b =+)c a b =+2a b =+AD AD BAC ∠CAD EAD ∠=∠CAD EAD ∠=∠90C AED ∠=∠=︒AD AD =()AAS ACD AED ≌AE AB =AC BC =AE BC =c a b =+CAD EAD ∠>∠AE AC >c a b >+CAD EAD ∠<∠AE AC <c a b <+AC BC =90C ∠=︒∴，即，∵，，故正确；∵，，∴，，∵，∴，∴，∴，∵，∴，，故③正确；故选：B ．【点睛】本题考查等腰直三角形的性质，勾股定理，全等三角形的判定与性质，熟练掌握等腰直三角形的性质和勾股定理是解题的关键．7．D【分析】本题考查了直径所对的圆周角为直角，相似三角形的判定与性质，完全平方公式的变形．熟练掌握直径所对的圆周角为直角，相似三角形的判定与性质，完全平方公式的变形是解题的关键．由题意知，，，由，可得，可判断①的正误；如图，连接，则，证明，则，即，可判断②的正误；由，可得，可判断③的正误．【详解】解：由题意知，，，∵，∴，①正确，故符合要求；如图，连接，AB =)AB a b=+AB AE >)a b c +>AC BC =90C ∠=︒)AB a b ==+45A B ∠=∠=︒DE AB ⊥45BDE B ∠=∠=︒BE DE =BE )AB a b =+)c a b =+2a b =+BD AC b ==CD AD AC a b =-=-2CD DE =2a b c -=AE BE ，90AEB ∠=︒BED EAD ∽DE BD AD DE=c b a c =()()()222224248a b a b ab c c c +=-+=+=a b +=BD AC b ==CD AD AC a b =-=-2CD DE =2a b c -=AE BE ，∵为半圆O 的直径，∴，∵，∴，又∵，∴，∴，即，②正确，故符合要求；∴，∴，∴，③正确，故不符合要求；故选：D ．8．C【分析】本题主要考查函数的定义以及函数图象的识别．探究大水杯中水面上升高度h 与注水时间t 之间的函数关系，从而确定图象．【详解】解：开始往大水杯中均匀注水，h 的值由0逐渐增大，当水漫过小水杯向小水杯注水，此时h 的值保持不变，小烧杯注满后，水再次进入大水杯中直至到大水杯顶部时，h 的再次增大，但变化比开始时变慢．观察四个图象，选项C 符合题意．故选：C ．9．D【分析】先由D （-2，3），AD =5，求得A （2，0），即得AO =2；设AD 与y 轴交于E ，求得E （0，1.5），即得EO =1.5；作BF 垂直于x 轴于F ，求证△AOE ∽△CDE ，可得，求证△AOE ∽△BFA ，可得AF =2，BF =，进而可求得B （4，）；将B （4，）代入反比例函数，即可求得k 的值．【详解】解：如图，过D 作DH 垂直x 轴于H ，设AD 与y 轴交于E ，过B 作BF 垂直于x 轴于F ，∵点D （-2，3），AD =5，∴DH =3，AB 90AEB ∠=︒90AED BED AED EAD ∠+∠=︒=∠+∠BED EAD ∠=∠90BDE EDA ∠=︒=∠BED EAD ∽DE BD AD DE=c b a c =2ab c =()()()222224248a b a b ab c c c +=-+=+=a b +=103BA CD ==838383k y x=∴，∴A （2，0），即AO =2，∵D （-2，3），A （2，0），∴AD 所在直线方程为：，∴E （0，1.5），即EO =1.5，∴,∴ED=AD - AE=5-=，∵∠AOE=∠CDE ，∠AEO=∠CED ，∴△AOE ∽△CDE ，∴,∴,∴在矩形ABCD 中，，∵∠EAO+∠BAF=90°，又∠EAO+∠AEO=90°，∴∠AEO=∠BAF ，又∵∠AOE=∠BFA ，∴△BFA ∽△AOE ，∴,∴代入数值，可得AF =2，BF =，∴OF =AF+AO=4，∴B （4，），∴将B （4，）代入反比例函数，得，故选：D ．【点睛】本题主要考查了待定系数法求反比例函数的系数、相似三角形的判定与性质、勾股定理、矩形的性质等知识．解题关键是通过求证△AOE ∽△CDE ，△AOE ∽△BFA ，得到B 点坐标，将B 点坐标代入反比例函数，即可得解．10．C【分析】根据题意作出合适的辅助线，然后逐一分析即可．AH =3342y x =-+52AE ===5252EO AO ED CD=103ED CD AO EO =´=103BA CD ==BA AF BF AE EO AO==838383k y x=323k =【详解】如图，连接AC 、与BD 交于点O ，连接ME ，MF ，NF ，EN ，MN ，∵四边形ABCD 是平行四边形∴OA =OC ，OB =OD∵BE =DF∴OE =OF∵点E 、F 时BD 上的点，∴只要M ，N 过点O ，那么四边形MENF 就是平行四边形∴存在无数个平行四边形MENF ，故①正确；只要MN =EF ，MN 过点O ，则四边形MENF 是矩形，∵点E 、F 是BD 上的动点，∴存在无数个矩形MENF ，故②正确；只要MN ⊥EF ，MN 过点O ，则四边形MENF 是菱形；∵点E 、F 是BD 上的动点，∴存在无数个菱形MENF ，故③正确；只要MN =EF ，MN ⊥EF ，MN 过点O ，则四边形MENF 是正方形，而符合要求的正方形只有一个，故④错误；故选：C【点睛】本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定、解答本题的关键时明确题意，作出合适的辅助线．11．D【分析】本题考查了正方形的性质，全等三角形的判定和性质，等腰三角形的判定和性质等，熟练掌握知识点并添加适当的辅助线是解题的关键．如图1中，过点作于，证明即可判断①；过点作于，于，于．证明即可判断②；如图2中，过点作于，交于．先证明，再证明即可判断③；利用勾股定理计算，即可判断④．【详解】解：如图1中，过点作于．B BK GH ⊥K ()Rt Rt HL BHK BHC ≌M MQ GH ⊥Q MP CD ⊥P MR BC ⊥R 45GBH ∠=︒M MW AD ⊥W BC T MG MD =()AAS BTM MWG ≌B BK GH ⊥K，关于对称，，，四边形是正方形，，，，，，，，，，，，，，，，故①正确，，过点作于，于，于．，，，，，，，故②正确，如图2中，过点作于，交于．，关于对称，，B G EF EB EG ∴=EBG EGB ∴∠=∠ ABCD AB BC ∴=90A ABC BCD ∠=∠=∠=︒//AD BC AGB EBG ∴∠=∠AGB BGK ∴∠=∠90A BKG ∠=∠=︒ BG BG =()AAS BAG BKG ∴ ≌BK BA BC ∴==ABG KBG ∠=∠90BKH BCH ∠=∠=︒ BH BH =()Rt Rt HL BHK BHC ∴ ≌BHG BHC ∴∠=∠HBK HBC ∠=∠1452GBH GBK HBK ABC ∴∠=∠+∠=∠=︒M MQ GH ⊥Q MP CD ⊥P MR BC ⊥R BHG BHC ∠=∠ MQ MP \=MEQ MER ∠=∠ MQ MR ∴=MP MR ∴=1452BCM MCP BCD ∴∠=∠=∠=︒GBH BCM ∴∠=∠M MW AD ⊥W BC T B G EF BM MG ∴=，，，，，，，，，，，，，，，，，，故③错误，，，，，，④正确，故选：D ．12．C【分析】本题考查了垂径定理的应用和勾股定理的应用．连结，交于，由垂径定理得（米），再由勾股定理得，然后求出的长即可．【详解】解：连接交于，由题意得：米，，∴（米），，由勾股定理得，（米），∴米，CB CD = BCM MCD ∠=∠CM CM =()SAS MCB MCD ∴≌BM DM∴=MG MD ∴=MW DG ⊥ WG WD ∴=90BTM MWG BMG ∠=∠=∠=︒ 90BMT GMW ∴∠+∠=︒90GMW MGW ∠+∠=︒ BMT MGW ∴∠=∠MB MG = ()AAS BTM MWG ∴ ≌MT WG ∴=MC = 2DG WG =DG ∴=1AG = 2DG =3AD AB TW ∴===1TC WD TM ===2BT AW ==BM ∴===OC OC AB D 122AD BD AB ===OD CD OC AB D 3OA OC ==OC AB ⊥122AD BD AB ===90ADO ∠=︒OD ===(3CD OC OD =-=即点到弦所在直线的距离是米，故选：C ．13．C【分析】如图所示，连接交于H ，取中点O ，连接，先证明点E 在以点O 为圆心，为直径的圆上运动，当三点共线，即点E 运动到点H 时， 当三点共线时，有最小值，据此可判断①②；如下图所示，当与相切时有最大值，证明，得到，，则，再证明，得到，即可判断③④．【详解】解：如图所示，连接交于H ，取中点O ，连接，∵四边形是正方形，∴；∵，∴点E 在以点O 为圆心，为直径的圆上运动，∵，∴点H 在圆O 上，∵，∴当三点共线，即点E 运动到点H 时，，故①正确；∵点E 在以点O 为圆心，为直径的圆上运动，∴当三点共线时，有最小值，在中，由勾股定理得，∴，故②错误；如下图所示，当与相切时有最大值，∵，∴，C AB (3AC BD AB OC AB AE C 、、AE CE AC +=C O E 、、CE CE O BCE ∠Rt Rt OBC OEC △≌△CE BC a ==OCE OCB ∠=∠1tan 2OE OCE CE ==∠ABE BCO OCE ==∠∠∠1tan tan 2ABE OCE ==∠∠AC BD AB OC ABCD 90AHB ∠=︒90AEB ∠=︒AB 90AHB ∠=︒AE CE AC +≥==A E C 、、AE CE AC +=AB C O E 、、CE Rt OBC △OC ==CE 12a -=CE O BCE ∠OB OE OC OC ==，()Rt Rt HL OBC OEC ≌∴，，∴，∴，∴，∴的度数最大值不是，故③错误；∵，∴垂直平分，∴，∴，∴，故④正确；故选：C ．【点睛】本题主要考查了圆与正方形综合，解直角三角形，勾股定理等等，根据题意得到点E 的运动轨迹是解题的关键．14B 解析略15．A【分析】本题主要考查了二次函数的定义，根据二次函数的定义求解即可．【详解】解：①扇形的面积，扇形的圆心角n 一定， 面积S 与半径r 两个变量之间的函数关系可以利用二次函数表示，符合题意，②矩形的面积，矩形的面积S 与一边长两个变量之间的函数关系可以利用二次函数表示，符合题意，③行驶路程，行驶路程s 与行驶时间t 两个变量之间的函数关系可以利用一次函数表示，不符合题意，则①②符合题意，故选：A ．CE BC a ==OCE OCB ∠=∠1tan 2OE OCE CE ==∠30OCE ≠︒∠60BCE ≠︒∠BCE ∠60︒BC EC OB OE ==，OC BE ABE BOC BOC BCO +=+∠∠∠∠ABE BCO OCE ==∠∠∠1tan tan 2ABE OCE ==∠∠2360n S r π=()21010S x x x x =-=-+x s vt =x16．C【分析】本题考查了函数的图象与性质，一次函数图象，解题的关键是数形结合．结合函数图象逐个分析即可．【详解】由图象可得，当时，或，故①错误；当时，y 随x 的增大而增大；故②正确；∵∴点M 在一次函数的图象上，如图所示，由图象可得，有3个交点∴点在此函数图象上，则符合要求的点有3个，故③错误；∵函数经过点∴将函数图象向右平移2个或4个单位长度，经过原点，故④正确．综上所述，上述结论中，所有正确结论的序号是②④．故选：C．0y >23x -<<<4x -502x -<<(,2)M m m +2y x =+(,2)M m m +(2,0)-()0,0。

2024年4月上海市中考数学二模题型分类汇编5---二次函数压轴题（24题）【2024.4月奉贤区二模】24.（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图9，在直角坐标平面xOy 中，抛物线22y ax ax c =-+与x 轴交于点A 、B ，与y 轴正半轴交于点C ，顶点为P ，点A 坐标为（-1，0）.（1）写出这条抛物线的开口方向，并求顶点P 的坐标（用a 的代数式表示）；（2）将抛物线向下平移后经过点（0，1），顶点P 平移至P'.如果锐角∠CP'P 的正切值为12，求a 的值；（3）设抛物线对称轴与x 轴交于点D ，射线PC 与x 轴交于点E ，如果∠EDC =∠BPE ，求此抛物线的表达式.图9xyO11-124．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）新定义：已知抛物线2y ax bx c =++（其中abc ≠0），我们把抛物线2y cx ax b =++称为2y ax bx c =++的“轮换抛物线”．例如：抛物线y ＝2x 2+3x +1的“轮换抛物线”为y ＝x 2+2x +3．已知抛物线C 1：24(45)y mx m x m =+-+的“轮换抛物线”为C 2，抛物线C 1、C 2与y 轴分别交于点E 、F ，点E 在点F 的上方，抛物线C 2的顶点为P ．（1）如果点E 的坐标为（0，1），求抛物线C 2的表达式；（2）设抛物线C 2的对称轴与直线38y x =+相交于点Q ，如果四边形PQEF 为平行四边形，求点E 的坐标；（3）已知点M （-4，n ）在抛物线C 2上，点N 坐标为（-2，172-），当△PMN ∽△PEF 时，求m 的值．备用图Oy xyOx24．（本题满分12分）问题：已知抛物线L ：22y x x =-．抛物线W 的顶点在抛物线L 上（非抛物线L 的顶点）且经过抛物线L 的顶点．请求出一个满足条件的抛物线W 的表达式．（1）解这个问题的思路如下：先在抛物线L 上任取一点（非顶点），你所取的点是①；再将该点作为抛物线W 的顶点，可设抛物线W 的表达式是②；然后求出抛物线L 的顶点是③；再将抛物线L 的顶点代入所设抛物线W 的表达式，求得其中待定系数的值为④；最后写出抛物线W 的表达式是⑤．（2）用同样的方法，你还可以获得其他满足条件的抛物线W ，请再写出一个抛物线W的表达式．（3）如果问题中抛物线L 和W 在x 轴上所截得的线段长相等，求抛物线W 的表达式．24.（本题满分12分,第（1）小题4分，第（2）小题中①②题各4分）已知：抛物线2y x bx c =++经过点A （3，0）、B （0，-3），顶点为P ．（1）求抛物线的解析式及顶点P 的坐标；（2）平移抛物线，使得平移后的抛物线顶点Q 在直线AB 上，且点Q 在y 轴右侧．①若点B 平移后得到的点C 在x 轴上，求此时抛物线的解析式；②若平移后的抛物线与y 轴相交于点D ，且△BDQ 是直角三角形，求此时抛物线的解析式．yxO24．（本题满分12分）如图，在平面直角坐标系xOy 中，已知抛物线关于直线25=x 对称，且经过点A （0，3）和点B （3，0），横坐标为4的点C 在此抛物线上．（1）求该抛物线的表达式；（2）联结AB 、BC 、AC ，求tan BAC ∠的值；（3）如果点P 在对称轴右方的抛物线上，且∠PAC =45°，过点P 作PQ ⊥y 轴，垂足为Q ，请说明∠APQ =∠BAC ，并求点P 的坐标．24．（满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分）在平面直角坐标系xOy 中，已知抛物线212y x bx c =++与x 轴相交于A （1-，0）、B两点，且与y 轴交于点C （0，2-）．（1）求抛物线的表达式；（2）如果点D 是x 正半轴上一点，∠ADC=2∠ACO ，且四边形AQCD 是菱形，请直接写出点D 和点Q 的坐标（不需要说明理由）；（3）由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形，对于平面内的一个多边形，画出它的任意一边所在的直线，如果其余各边都在这条直线的一侧，那么这个多边形叫做“凸多边形”；否则叫做“凹多边形”．如果点E 是抛物线对称轴上的一个动点，纵坐标为t ，且四边形ACBE 是凹四边形（线段AE 与线段BC 不相交），求t 的取值范围．yxO（第24题图）24．（本题满分12分，其中每小题各4分）在平面直角坐标系xOy 中，已知直线+2y x =-与x 轴、y 轴分别交于点A 、点B ，抛物线C 1：2y x bx c =-++经过点A 、B 两点，顶点为点C ．（1）求b 、c 的值；（2）如果点D 在抛物线C 1的对称轴上，射线AB 平分∠CAD ，求点D 的坐标；（3）将抛物线C 1平移，使得新抛物线C 2的顶点E 在射线BA 上，抛物线C 2与y 轴交于点F ，如果△BEF 是等腰三角形，求抛物线C 2的表达式．（第24题图）11OxyAB24．（本题满分12分）在平面直角坐标系xOy 中（如图8），已知抛物线()()20y a x m n a =-+≠与x 轴交于点A 、B ，抛物线的顶点P 在第一象限，且90APB ∠=︒．（1）当点P 的坐标为()4,3时，求这个抛物线的表达式；（2）抛物线()()20y a x m n a =-+≠表达式中有三个待定系数，求待定系数a 与n 之间的数量关系；（3）以点P 为圆心，PA 为半径作P ，P 与直线2ny x =+相交于点M 、N ．当点P 在直线12y x =上时，用含a 的代数式表示MN 的长．图8yxOPAB24.（本题满分12分，每小题满分各4分）在平面直角坐标系xOy 中，抛物线23y axbx =+-的图像与x 轴交于点A （-3，0）和点B （1，0），与y 轴交于点C ，D 是线段OA 上一点．（1）求这条抛物线的表达式和点C 的坐标；（2）如图，过点D 作DG ⊥x 轴，交该抛物线于点G ，当DGA ＝DGC 时，求△GAC 的面积；（3）点P 为该抛物线上第三象限内一点，当OD ＝1，且∠DCB +∠PBC ＝45°时，求点P 的坐标．第24题图24.（本题满分12分，第（1）小题4分，第（2）小题第①问4分，第（2）小题第②问4分）如图8,在平面直角坐标系xOy 中，已知点A （2，0）、点B （0，2），抛物线2y x bx c =-++经过点A ，且顶点C 在线段AB 上（与点A 、B 不重合）．（1）求b 、c 的值；（2）将抛物线向右平移m （0m >）个单位，顶点落在点P 处,新抛物线与原抛物线的对称轴交于点D ，联结PD ，交x 轴于点E ．①如果m =2,求△ODP 的面积；②如果EC =EP ,求m 的值.(图8)11OxyA B24．（本题满分12分）如图，在平面直角坐标系xOy 中，抛物线)0(442>+-=a ax ax y 与x 轴交于点)0,1(A 和点B ，与y 轴交于点C ．（1）求该抛物线的表达式及点B 的坐标；（2）已知点),0(m M ，联结BC ，过点M 作BC MG ⊥，垂足为G ，点D 是x 轴上的动点，分别联结GD 、MD ，以GD 、MD 为边作平行四边形GDMN ．①当23=m 时，且□GDMN 的顶点N 正好落在y 轴上，求点D 的坐标；②当0≥m 时，且点D 在运动过程中存在唯一的位置，使得□GDMN 是矩形，求m 的值．（第24题图）A O xyB C24．（本题满分12分，第（1）小题3分，第（2）小题9分）定义：我们把平面内经过已知直线外一点并且与这条直线相切的圆叫做这个点与已知直线的点切圆．如图1，已知直线l外有一点H，圆Q经过点H且与直线l相切，则称圆Q 是点H与直线l的点切圆．阅读以上材料，解决问题：已知直线OA外有一点P，PA⊥OA，OA=4，AP=2，圆M是点P与直线OA的点切圆．（1）如果圆心M在线段OP上，那么圆M的半径长是▲(直接写出答案)．（2）如图2，以O为坐标原点、OA为x轴的正半轴建立平面直角坐标系xOy，点P在第一象限，设圆心M的坐标是（x，y）．①求y关于x的函数解析式；②点B是①中所求函数图像上的一点，联结BP并延长交此函数图像于另一点C．如果CP：BP=1：4，求点B的坐标．lH Q第24题图1PyxAO第24题图224．（本题满分12分，每小题满分各4分）在平面直角坐标系xOy （如图8）中，已知抛物线32++=bx ax y 经过点)0,1(A 、)3,2-(B 两点，与y 轴的交点为C 点，对称轴为直线l ．（1）求此抛物线的表达式；（2）已知以点C 为圆心，半径为CB 的圆记作圆C ，以点A 为圆心的圆记作圆A ，如果圆A 与圆C 外切，试判断对称轴直线l 与圆A 的位置关系，请说明理由；（3）已知点D 在y 轴的正半轴上，且在点C 的上方，如果BAC BDC ∠=∠，请求出点D 的坐标．图8O 11xy-1-1。

第1页共16页如图1，已知半圆O 的直径AB=4，C 是圆外一点，∠ABC 的平分线交半圆O 于点D ，且∠BCD=90°，联结OC 交BD 于点E.（1）当∠ABC=45°时，求OC 的长；（2）当∠ABC=60°时，求OE EC的值；（3）当△BOE 为直角三角形时，求sin ∠OCB 的值.页如图，在Rt ABC△中，90ACB∠=︒，6,3AC BC==．点D是边AC上一动点（不与A、C重合），联结BD，过点C作CF⊥BD，分别交BD、AB于点E、F．（1）当2CD=时，求∠ACF的正切值；（2）设CD x=，AF yBF=，求y关于x的函数解析式，并写出x的定义域；（3）联结FD并延长，与边BC的延长线相交于点G，若△DGC与△BAC相似，求AFBF的值．第2页共16页在梯形ABCD中，AD//BC，AD=4，∠ABC=90°，BD=BC，过点C作对角线BD的垂线，垂足为E，交射线BA于点F.（1）如图1，当点F在边AB上时，求证：△ABD≌△ECB；（2）如图2，如果F是AB的中点，求FE:EC的值；（3）联结DF，如果△BFD是等腰三角形，求BC的长．第3页共16页如图1，在菱形ABCD中，AB=P在对角线BD上，tan∠DBC=12，⊙O是△PAB的外接圆，点B与点P之间的距离记为m．（1）如图2，当PA=PB时，联结OB，求证：OB⊥BC；（2）延长AP交射线BC于点Q，如果△ABQ是直角三角形，求PQ的长；（3）当圆心O在菱形ABCD外部时，用含m的代数式表示⊙O的半径，并直接写出m的取值范围．第4页共16页如图，在菱形ABCD中，BC=10，E是边BC上一点，过点E作EH⊥BD，垂足为点H，点G在边AD上，且GD=CE，联结GE，分别交BD、CH于点M、N．（1）已知3sin5DBC∠=，①当EC=4时，求△BCH的面积；②以点H为圆心，HM为半径作圆H，以点C为圆心，半径为1作圆C，圆H与圆C有且仅有一个公共点，求CE的值；（2）延长AH交边BC于点P，当设CE=x，请用含x的代数式表示HPCN的值.第5页共16页在Rt△ABC中，︒=∠90BAC，点P在线段BC上，ACBBPD∠=∠21，PD交BA于点D，过点B作PDBE⊥，垂足为E，交CA的延长线于点F．（1）如果︒=∠45ACB，①如图1，当点P与点C重合时，求证：PDBE21=；②如图2，当点P在线段BC上，且不与点B、点C重合时，问：①中的“PDBE21=”仍成立吗？请说明你的理由；（2）如果︒≠∠45ACB，如图3，已知ACnAB⋅=（n为常数），当点P在线段BC上，且不与点B、点C重合时，请探究PDBE的值（用含n的式子表示），并写出你的探究过程．第6页共16页如图，已知在ABC∆中，ACAB=，点D是边BC中点，在边AB 上取一点E，使得DBDE=，延长ED交AC延长线于点F．（1）求证：CDFA∠=∠；（2）设AC的中点为点O，①如果CD为经过DCA、、三点的圆的一条弦，当弦CD恰好是正十边形的一条边时，求ACCF:的值；②⊙M经过C、D两点，联结OM、MF，当︒=∠90OFM，10=AC，43tan=A时，求⊙M的半径长．（第25题图）备用图第7页共16页如图25-①，扇形MON的半径为r，圆心角∠MON=90°，点A是MN上的动点（点A不与点M、N重合），点B、C分别在半径OM、ON上，四边形ABOC 为矩形，点G在线段BC上，且CG=2BG．（1）求证：CG23r=；（2）如图25-②，以A为顶点、AC为一边，作∠CAP=∠BCO，射线AP交射线ON于点P，联结AN、OG．①当∠BGO=∠ANP时，求△OBG与△ANP的面积之比；②把△OGB沿直线OG翻折后记作△OGB'，当OB'⊥BC时，求∠P的正切值．第8页共16第9页共16页如图，在Rt △ABC 中，∠ACB =90°，BC =1，以BC 为边作△DBC（点D 、A 在直线BC 的异侧），且满足BD =BC ，∠BCD =∠ABC +45°．（1）求证：∠A =∠ABD ；（2）设点E 为边BC 的中点，联结DE 并延长交边AB 于点F ，当△BEF 为直角三角形时，求边AC 的长；（3）设AB =x ，CD =y ，求y 关于x的函数解析式并写出定义域．页已知：⊙O的直径10AB=，C是 AB的中点，D是⊙O上的一个动点（不与点A、B、C重合），射线CD交射线AB于点E．（1）如图1，当BE AB=时，求线段CD的长；（2）如图2，当点D在 BC上运动时，联结BC、BD，△BCD中是否存在度数保持不变的角？如果存在，请指出这个角并求其度数；如果不存在，请说明理由；（3）联结OD，当△ODE是以DE为腰的等腰三角形时，求△ODE与△CBE面积的比值．第10页共16页如图，半圆O的直径4AB=，点C是 AB上一点（不与点A、B 重合），点D是 BC的中点，分别联结AC、BD．（1）当AC是圆O的内接正六边形的一边时，求BD的长；（2）设AC x=，=BD y，求y与x之间的函数解析式，并写出x的取值范围；（3）定义：三角形一边上的中线把这个三角形分成两个小三角形，如果其中有一个小三角形是等腰三角形，且这条中线是这个小三角形的腰，那么这条中线就称为这个三角形的中腰线．分别延长AC、BD相交于点P，联结PO．PO是△PAB的中腰线，求AC的长．第11页共16第12页共16页如图，半圆O 的直径AB=10，点C 在半圆O 上，BC=6，CH ⊥AB ，垂足为点H ，点D 是弧AC 上一点．（1）若点D 是弧AB 的中点，求tan ∠DOC 的值；（2）联结BD 交半径OC 于点E ，交CH 于点F ，设OE=m ．①用含m 的代数式表示线段CF 的长；②分别以点O 为圆心OE 为半径、点C 为圆心CF 为半径作圆，当这两个圆相交时，求m取值范围．页如图1，AB是半圆O的直径，C是半圆O上一点，点O'与点O 关于直线AC对称，射线AO'交半圆O于点D，弦AC交O O'于点E、交OD于点F．（1）如图2，如果点O′恰好落在半圆O上，求证：=O A BC'；（2）如果30DAB∠= ，求EFO D'的值；（3）如果OA=3，1O D'=，求OF的长.第13页共16页已知：如图1，四边形ABCD中，AB＝AD＝CD，∠B＝∠C＜90°．(1)求证：四边形ABCD是等腰梯形；(2)边CD的垂直平分线EF交CD于点E，交对角线AC于点P，交射线AB于点F．①当AF＝AP时，设AD长为x，试用x表示AC的长；②当BF＝DE时，求ADBC的值．第14页共16页已知AB是⊙O的直径，弦CD⊥AB，垂足为点H，点E在直径AB上（与A、B不重合），EH=AH，联结CE并延长与⊙O交于点F.（1）如图1，当点E与点O重合时，求∠AOC的度数；（2）联结AF交弦CD于点P，如果43CEEF=，求DPCP的值；（3）当四边形ACOF是梯形时，且AB=6，求AE的长.第15页共16页如图1，在ABC∆中，︒=∠90ACB，以点A为圆心、AC为半径的⊙A交边AB于点D，点E在边BC上，满足BDCE=，过点E作CDEF⊥交AB 于点F，垂足为点G.（1）求证：BCD∆∽BFE∆；（2）延长EF与CA的延长线交于点M，如图2所示，求ADDFACCM+的值；（3）以点B为圆心、BE为半径作⊙B，当8=BC，2=AF时，请判断⊙A与⊙B的位置关系，并说明理由.第16页共16第1页共31页如图1，已知半圆O 的直径AB=4，C 是圆外一点，∠ABC 的平分线交半圆O 于点D ，且∠BCD=90°，联结OC 交BD 于点E.（1）当∠ABC=45°时，求OC 的长；（2）当∠ABC=60°时，求OE EC的值；（3）当△BOE 为直角三角形时，求sin ∠OCB 的值.（1）联结OD ，过点O 做OH ⊥BC ，垂足为H ，...........................1分∴∠OHC=∠OHB=90°.∵AB=4，∴OB=OD=2，∴∠ODB=∠OBD ，∵BD 平分∠ABC ，∴∠OBD=∠DBC ，∴∠DBC=∠ODB ，∴OD//BC ，∴∠DOH=∠OHB=90°，∴四边形DOHC 是矩形，∴OD=HC=2............................1分Rt △BOH 中，sin ∠OBH=22=OB OH ，∴OH=2...................1分Rt △COH 中，∵OC ²=CH ²+OH ²，∴OC=6........................1分（2）Rt △BOH 中，cos ∠OBH=21=OB BH ，......................................1分∴BH=1................................................................1分第2页共31页∴CB=CH+BH=3，......................................................1分∵OD//BC ，∴32==BC OD EC OE ...............................................2分（3）（i ）当∠EOB=90°时，设BH=x ，则BC=x+2，∵OH ⊥BC ，∴∠OHB=∠COB=90°.∵∠OBH=∠COB ，∴△BOH ∽△BCO ，....................................1分∴OB ²=BH ·BC ，∠BOH=∠BCO ，∴x ²+2x-4=0，解得x1=51+-，x2=51--（不合题意，舍去），∴BH=51+-.∴sin ∠OCB=sin ∠BOH=215-=OB BH .....................................1分（ii ）当四边形OBCD 是正方形时，∠BEO=90°，∴∠OCB=45°，........................................................1分∴sin ∠OCB=sin45°=22................................................1分（iii ）根据题意∠OBE=90°不成立........................................1分所以，当△BOE 为直角三角形时，sin ∠OCB 的值是215-或22.如图，在Rt ABC △中，90ACB ∠=︒，6,3AC BC ==．点D 是边AC 上一动点（不与A 、C 重合），联结BD ，过点C 作CF ⊥BD ，分别交BD 、AB 于点E 、F ．（1）当2CD =时，求∠ACF 的正切值；（2）设CD x =，AF y BF=，求y 关于x 的函数解析式，并写出x 的定义域；第3页共31页（3）联结FD并延长，与边BC的延长线相交于点G，若△DGC与△BAC相似，求AF BF的值．（1）∵CF⊥BD90C∠=︒∴90BEC∠=︒∴90ACF BDC∠+∠=︒................................................(1分）∵90C∠=︒∴90DBC BDC∠+∠=︒................................................(1分）∴ACF DBC∠=∠................................................(1分）又∵3,BC=CD=2∴2tan tan3CDACF DBCBC∠=∠==................................................(1分）(2)过点F作FH⊥AC,垂足为H................................................(1分）∴90AHF ACB∠=∠=︒∴FH BC∴AF AHBF CH=;FH AHBC AC=∵3,6BC AC==∴2AH FH=................................................(1分）∴2AF FHBF CH=第4页共31页又∵tan tan ACF DBC∠=∠即：3FH CD x CH BC ==................................................(1分）∴223AF FH y x BF CH ===（06x <<）................................................(2分）(3)∵90DCG ACB ∠=∠=︒∴△DGC 与△BAC 相似有两种情况................................................(1分）①当G A ∠=∠时又∵ADF CDG∠=∠∴FAD ∆∽CGD ∆∴90DCG AFD ∠=∠=︒∵ACF DBC ∠=∠,EDC CDB∠=∠∴ECD ∆∽CDB∆∴CD BD ED CD =∴2CD DE BD= 同理：2FD DE BD= ∴CD FD x==∵sin BC FD A AB AD ==6x x =-∴x =................................................(1分）∴213y x ==-即：1AF BF=................................................(1分）②当G ABC ∠=∠时∵90A ABC ∠+∠=︒90CDG G ∠+∠=︒∴A CDG ADF∠=∠=∠∴AF FD=过点F 作FH ⊥AC,垂足为H第5页共31页∴62x AH HD -==，632xHC AH =-=+又∵tan tan ACF DBC∠=∠即：FH CD CH BC=得：64332x x x -=+解得：12151544x x -+--==（舍）................................................(1分）∴2532y x -==即：52AFBF =................................................(1分）综上：512AFBF=.在梯形ABCD 中，AD//BC ，AD=4，∠ABC=90°，BD=BC ，过点C 作对角线BD 的垂线，垂足为E ，交射线BA 于点F.（1）如图1，当点F 在边AB 上时，求证：△ABD ≌△ECB ；（2）如图2，如果F 是AB 的中点，求FE:EC 的值；（3）联结DF ，如果△BFD 是等腰三角形，求BC的长．（1）∵CF ⊥BD ，∴∠CEB =90°．····················································（1分）∵AD //BC ，∠ABC ＝90°，∴∠A =90°，∠ADB =∠CBE ．····························（1分）∴∠CEB =∠A ．·················································································（1分）第6页共31页图1∵BD =BC ，∴△ABD ≌△ECB ．····························································（1分）（2）过点F 作FG //AD ，交BD 于点G .设BC=BD=m ，∵FG//AD ，∴.ADFGBD BG AB BF ==（1分）∵点F 是AB 的中点，AD =4，∴.21=AB BF ∴FG =2，BG =.21m ··············································································（1分）∵△ABD ≌△ECB ，∴BE=AD =4．∴EG =421-m ．·································（1分）∵AD//BC ，∴FG//BC ．∴ECEFBE EG BC FG ==．········································（1分）即44212-=m m .解得m =.244±∴2122442-=+=EC EF ．（1分）（3）①如图1，当BF=DF 时，∵FC ⊥BD ，∴∠FEB =∠FED =90°.∴BE=DE .∴BC=DC .∴△BDC 是等边三角形.∴∠DBC =60°.∴∠ABD =30°.∴BD =2AD =8.∴BC =8...................................................（2分）②如图2，当BF=BD 时，∵BD=BC ，∴BF=BC .∵CF ⊥BD ，∠FBC =90°，∴∠FBE =∠CBE =45°.∵∠BAD =90°，∴AD=AB =4．∴BC =BD=.··················································································（2分）③如图3，当DF=BD时，图3图2第7页共31页设AD 和EC 的交点为点H ，BC=BD=a ，∵FD=BD ，∠DAB =90°，∴AF=AB .∵AD//AB ，∴.21==BF AF BC AH ∴AH =.21a ∴DH =.a 214-∵.BEED BC DH =即.a a a44214-=-解得a =（负值舍去）.171±∴BC =.171+.··········································（1分）综上所述，如果△BFD 是等腰三角形，BC =8、24或.171+如图1，在菱形ABCD 中，AB=P 在对角线BD 上，tan∠DBC=12，⊙O 是△PAB 的外接圆，点B 与点P 之间的距离记为m ．（1）如图2，当PA=PB 时，联结OB ，求证：OB ⊥BC ；（2）延长AP 交射线BC 于点Q ，如果△ABQ 是直角三角形，求PQ 的长；（3）当圆心O 在菱形ABCD 外部时，用含m 的代数式表示⊙O 的半径，并直接写出m 的取值范围．（1）联结OP ，交AB 于点H∵PA=PB ，∴.又∵OP 过圆心，∴OP ⊥AB ………………………………………………………（1分）∵OB=OP ，∴∠OBP=∠OPB在菱形ABCD 中，∠ABD=∠CBD ……………………………………………（1分）在Rt△BPH中，∠ABP+∠OPB=90°…………………………………………（1分）∴∠CBD+∠OBP=90°即∠OBC=90°∴OB⊥BC.……………………………………………………（1分）（2）∵∠ABC≠90°如果△ABQ是直角三角形，那么只有∠BAQ=90°或∠AQB=90°①当∠BAQ=90°时，联结AC，由题可得AC=4，BD=8在Rt△ABP中，tanAP AB ABP=⋅∠=，5cosABBPABP==∠∴DP=3∵AD∥BQ∴AP DPPQ BP=35=∴PQ.…………………………………………………………………（2分）②当∠AQB=90°时，∵12ABCDS AC BD BC AQ=⋅=⋅菱形∴在菱形ABCD中，AD=AB=AD∥BC，∴∠ADB=∠DBC∴tan∠ADB=tan∠DBC=1 2在Rt△ADP中，tanAP AD ADB=⋅∠=∴PQ=2分）综上所述，PQ=5.（3）联结OP，过点O作OE⊥AB于点E，延长OE交BD于点F 过点O作OG⊥BD于点G∵OG⊥BD，∴BG=GP=12BP=12m,同理，BE=12AB.……………………………………………………………（1分）第8页共31页第9页共31页∵∠ABD+∠BFE=90°，∠FOG+∠BFE=90°∵∠ABD=∠CBD∴∠FOG =∠CBD∴tan ∠FOG=tan ∠CBD=12在Rt △BEF 中，5cos 2BE BF FOG ==∠……………（2分）∴5122FG BF BG m =-=-在Rt △OGF 中，5tan GFOG mFOG==-∠在Rt △OPG 中，222OP OG GP =+∴OP =∴⊙O2分）m 的取值范围为0<m<4或203<m≤8……………………………………………（1分）如图，在菱形ABCD 中，BC=10，E 是边BC 上一点，过点E 作EH ⊥BD ，垂足为点H ，点G 在边AD 上，且GD=CE ，联结GE ，分别交BD 、CH 于点M 、N ．（1）已知3sin 5DBC ∠=，①当EC=4时，求△BCH 的面积；②以点H 为圆心，HM 为半径作圆H ，以点C 为圆心，半径为1作圆C ，圆H 与圆C 有且仅有一个公共点，求CE 的值；（2）延长AH 交边BC 于点P ，当设CE=x ，请用含x 的代数式表示HPCN的值.第10页共31页（1）①联结AC 交BD 于点O,…………………………………………………(1分）∵四边形ABCD 是菱形，∴OC ⊥BO ．在Rt △BOC 中，BC=10，3sin 5DBC ∠=，∴CO=6，BO=8．……………………………………………………………………(1分）∵EH ⊥BD ，∴EH ∥CO ，∴BH BEBO BC=．∴245BH =．……………………………………………………………………(1分）∴124726255BHC S =⨯⨯=V ．………………………………………………………(1分）②在菱形ABCD 中，AD ∥BC ，又∵GD=CE ，∴四边形CEGD 是平行四边形．∴EG ∥CD ，∴EG ∥AB ，∴∠EMB =∠ABD ．又∵∠ABD=∠CBD ，∴∠EMB =∠CBD ，∴BE=ME ．又∵EH ⊥BD ，∴HM=BH ，…………………………………………………………(1分）设CE x =，由（1）可得，∴485H r BH x ==-．………………………………(1分）在Rt △HOC中，HC ==．1°当两圆外切时，4815x -+=258x =．……………………………………(1分）第11页共31页2°当两圆内切时，4815x --=，解得6556x =．……………………………………(1分）综上所述，CE 长是258或6556．……………………………………(1分）（2）∵AB=BC ，∠ABD=∠CBD ，BH 是公共边，∴△ABH ≌△CBH ．∴∠BAH=∠BCN ．……………………………………………………………(1分）取BE 中点Q ，联结HQ ，又∵HM=BH ，∴HQ ∥EN ∥AB ，∴∠HQP=∠CEN ，∠QHP=∠BAH=∠BCN ，∴△HQP ∽△CEN ．………………………………………………………………(1分）∴HP HQCN CE=．…………………………………………………………………(1分）又∵11022x HQ BE -==．∴102HP x CN x-=．………………………………………………………(2分）在Rt △ABC 中，︒=∠90BAC ，点P 在线段BC 上，ACB BPD ∠=∠21，PD 交BA 于点D ，过点B 作PD BE ⊥，垂足为E ，交CA 的延长线于点F ．（1）如果︒=∠45ACB ，①如图1，当点P 与点C 重合时，求证：PD BE 21=；②如图2，当点P 在线段BC 上，且不与点B 、点C 重合时，问：①中的“PD BE 21=”仍成立吗？请说明你的理由；（2）如果︒≠∠45ACB ，如图3，已知AC n AB ⋅=（n 为常数），当点P 在线段BC 上，第12页共31页且不与点B 、点C 重合时，请探究PDBE的值（用含n 的式子表示），并写出你的探究过程．（1）①证明：∵Rt △ABC 中，︒=∠90BAC ，︒=∠45ACB ，∴︒=∠=∠45ACB ABC ，∴AC AB =.………………………………………（1分）∵PD BE ⊥，∴︒=∠+∠90EDB EBD .∵Rt △DAC 中，︒=∠+∠90DCA ADC ，又∵ADC EDB ∠=∠，∴DCA EBD ∠=∠.在△F AB 和△DAC 中，⎪⎩⎪⎨⎧∠=∠=∠=∠DAC F AB AC AB DCA FBA ，∴)..(A S A DAC F AB ≌△△.∴PD BF =.………………………………………………………………………（1分）∵ACB BPD ∠=∠21，∴FPE BPE ∠=∠.在△BPE 和△FPE 中，⎪⎩⎪⎨⎧∠=∠=∠=∠FEP BEP PE PE FPE BPE ，∴)..(A S A FPE BPE ≌△△.∴BF FE BE 21==.……………………………………………………………（1分）∴PD BE 21=.……………………………………………………………（1分）②成立.……………………………………………………………………………（1分）如图，过点P 作CF PM ∥，交AB 于点N .∵CF PM ∥，∴︒=∠=∠90BAC BNP ，︒=∠=∠45BCA BPN .第13页共31页∴NP NB =.……………………………………………………………………（1分）∵PD BE ⊥，∴︒=∠+∠90EDB EBD .∵Rt △DPN 中，︒=∠+∠90DPN PDN ，又∵PDN EDB ∠=∠，∴DPN EBD ∠=∠.同①中方法可得)..(A S A DNP MNB ≌△△.∴PD BM =.…………………………………（1分）∵ACB BPD ∠=∠21，∴MPE BPM BPE ∠=∠=∠21.同①中方法可得)..(A S A MPE BPE ≌△△.∴BM ME BE 21==.…………………………………………………………（1分）∴PD BE 21=.……………………………………………………………（1分）（2）如图，过点P 作CF PQ ∥，交AB 于点K .同②可知︒=∠=∠90QKB DKP ，DPK QBK ∠=∠，∴DPK QBK ∽△△.∴DP QBPK BK =.……（1分）∵CF PQ ∥，∴CA BAPK BK =.……………（1分）∵AC n AB ⋅=，∴n DPQB=.…………（1分）同②可证)..(A S A QPE BPE ≌△△，∴BE QB 2=.………………………（1分）即n DP BE =2，∴2nDP BE =.……………………………………………………（1分）如图，已知在ABC ∆中，AC AB =，点D 是边BC 中点，在边AB上取一点E ，使得DB DE =，延长ED 交AC 延长线于点F ．（1）求证：CDF A ∠=∠；（2）设AC 的中点为点O ，①如果CD 为经过D C A 、、三点的圆的一条弦，当弦CD恰好是正十边形的一条边时，第14页共31页求AC CF :的值；②⊙M 经过C 、D 两点，联结OM 、MF ，当︒=∠90OFM ，10=AC ，43tan =A 时，求⊙M的半径长．（1）证明：∵AB=AC∴∠B=∠BCA (1分)∵DE=DB ∴∠BED=∠B (1分)∴△ABC ∽△DBE ∴∠BDE=∠A (1分)∵∠BDE=∠CDF ∴∠A=∠CDF(1分)（2）①联结OD∵O 是AC 中点，D 是BC 中点∴AB OD //，AB OD 21=，AC OC OA 21==∵AB=AC∴OA=OC=OD∴经过A 、D 、C 三点的圆是以O 为圆心，OA 长为半径的圆.(1分)∵弦CD 恰好是正十边形的一条边∴∠DOC=36°(1分)∴∠DCF=72°，∠CDF=∠BAC=∠DOC=36°∴∠F=36°=∠CDF ，∠DOF=∠F ∴CF=CD=DB=DE ，DO=DF∵∠CDF=∠DOF ，∠F=∠F∴△DCF ∽△ODF ∴OFDF OD DC =(1分)设CD=m ，圆O 的半径为r ，则DC=m ，OF=m+r ，OD=DF=r ∴mr rr m +=令k r m =，则有012=-+k k ，解得215-=k （负值已舍）(1分)（第25题图）备用图第15页共31页∴415212-===k r m AC CF (1分)②∵⊙O 、⊙M 都经过C 、D 两点，∴OM 垂直平分CD(1分)过点B 作B H ⊥AC ，垂足为H ∵AC=10，∴AB=AC=10在Rt △ABH 中，43tan ==AH BH A 可得BH=6，AH=8在Rt △BHC 中，HC=AC-AH=2，可得3tan ==∠HCBHBCH ，102=BC ∴3tan tan =∠=∠BCH FCG (1分)∵∠GDF=∠A∴43tan =∠GDF 设CG=m ，则FG=3m ，则有DG=4m ，则有CD=3m ∵D 为BC 中点，∴10=CD ∴310==m CG ∴310=CF (1分)∴325=OF ∴925=MF (1分)∴619531092522=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=MC (1分)如图25-①，扇形MON 的半径为r ，圆心角∠MON=90°，点A是 MN 上的动点（点A 不与点M 、N 重合），点B 、C 分别在半径OM 、ON 上，四边形ABOC为矩形，点G 在线段BC 上，且CG=2BG ．（1）求证：CG 23r =；（2）如图25-②，以A 为顶点、AC 为一边，作∠CAP=∠BCO ，射线AP 交射线ON 于点P ，联结AN 、OG ．①当∠BGO=∠ANP 时，求△OBG 与△ANP的面积之比；第16页共31页PO AB CG M N12E3②把△OGB 沿直线OG 翻折后记作△OGB '，当OB '⊥BC 时，求∠P 的正切值．（1）联结OA ，设OA 与BC 相交于点E ，∵四边形ABOC 是矩形，∴BC=OA=r ，∵CG=2BG ，∴23CG BC =，即23CG r =．（2）①∵四边形ABOC 是矩形，∴EO=EC ，∴∠EOC=∠ECO ．∵∠BGO=∠ANP ，∴∠1=∠2，∴△CGO ∽△ONA ，∴23OG CG NA ON ==．∵在Rt △BOC 中，∠BCO+∠3=90°，在Rt △ACP 中，∠CAP+∠P=90°，又∵∠CAP=∠BCO ，∴∠3=∠P ，∵∠BGO=∠ANP ，∴△OBG ∽△APN ，∴249OBG ANP S OG S NA ⎛⎫== ⎪⎝⎭△△．第17页共31页HFM OB N GPAC B 'BAM O NGPCB '12H②方法1：当OB '⊥BC 时（如图所示），∠OHC=90°，在Rt △OGH 中，∠CGO=90°－∠1．∵四边形ABOC 是矩形，∴∠BOC=90°，∴∠COG=90°－∠2．∵翻折，∴∠1=∠2．∴∠CGO=∠COG ，∴23OC CG r ==．∴在Rt △OBC中，OB =，∴tan ∠P=tan ∠OBC 5OC OB ==．方法2：当OB '⊥BC 时（如图所示），延长B G '交OB 于点F ，由翻折可得B G BG '=，∠FBG=∠HB G ',又∠FGB=∠HGB '，∴△FGB ≌△HGB '，∴FB=HB '，∠BFG=∠B HG '=90°．∴∠BFG=∠BOC ，∴FG ∥OC ，∴12BF BG B H B G OF CG OH OC ''====，即23OC r =．∴在Rt △OBC中，3OB r =，∴tan ∠P=tan ∠OBC 5OC OB ==．如图，在Rt △ABC 中，∠ACB =90°，BC =1，以BC 为边作△DBC （点D 、A 在直线BC 的异侧），且满足BD =BC ，∠BCD =∠ABC +45°．（1）求证：∠A =∠ABD ；（2）设点E 为边BC 的中点，联结DE 并延长交边AB 于点F ，当△BEF 为直角三角形时，求边AC 的长；（3）设AB =x ，CD =y ，求y 关于x 的函数解析式并写出定义域．第18页共31页解：（1）∵BD=BC ，∴∠BDC=∠BCD ．………………………………………………………（1分）∵∠BCD=∠ABC+45°，∴∠BDC=∠ABC+45°．∵180BDC BCD CBD ∠+∠+∠=︒，∴∠CBD=90°-2∠ABC ．∴∠ABD=∠CBD+∠ABC=90°-∠ABC ．………………………………（1分）∵∠ACB ＝90°，∴∠A+∠ABC ＝90°，∴∠A=90°-∠ABC ．………………………………………………………（1分）∴∠A=∠ABD ．…………………………………………………………（1分）（2）设∠ABC=θ1︒当∠BFE ＝90°时，∵∠BFE ＝90°，∴∠ABD+∠FDB ＝90°．∵90ABD θ∠=︒-，∴∠FDB ＝θ．∵∠ABC=θ，∴∠FDB=∠ABC ．∵∠EFB=∠BFD ，∴△FBE ∽△FDB ．∴EF BE FB BD=．………………………………………………………………（1分）∵点E 为边BC 的中点，∴12BE BC =．第19页共31页∵BD=BC ，∴EF BE FB BD =12=．…………………………………………………（1分）在Rt △BEF 中，∠EFB=90°，1tan 2EF ABC FB ∠==．∴在Rt △ABC 中，∠ACB=90°，11tan 122AC BC ABC =⋅∠=⨯=．………………………………………………（1分）2︒当∠BEF ＝90°时，则∠BED ＝90°．在Rt △BDE 中，∠DEB=90°，由勾股定理，得DE ===．……………………（1分）∵90BEF ACB ∠=∠=︒，∴EF AC ∥，∴90EFB BAC θ∠=∠=︒-．∴EFB ABD ∠=∠，∴1DF BD ==．………………………………………（1分）∴312EF DF DE =-=-．∵EF AC ∥，∴12EF BE AC BC ==．∴2AC =1分）综上所述：边AC 的长为12或2．（3）过点C 作CH ∥AB ，交BD 于点H ．∵CH ∥AB ，∴,CHD ABD BCH ABC ∠=∠∠=∠．∵A ABD ∠=∠，∴CHD A ∠=∠．∵CH ∥AB ，且AC 与BD 不平行，∴四边形ABHC 是梯形．∵A ABD ∠=∠，∴四边形ABHC 是等腰梯形．∴BH=AC ．第20页共31页由45BCD ABC BCH ABC BCD DCH BCH ∠=∠+︒∠=∠∠=∠+∠，，，∴45DCH ∠=︒．……………………………………………………………（1分）过点D 作DG CH ⊥于点G ．∴sin 452DG CD y =⋅=，sin sin CHD A ∠=由12yx=．……………………………（1分）∴(222y x x=1＜．……………………………（1分+1分）已知：⊙O 的直径10AB =，C 是 AB 的中点，D 是⊙O 上的一个动点（不与点A 、B 、C 重合），射线CD 交射线AB 于点E ．（1）如图1，当BE AB =时，求线段CD 的长；（2）如图2，当点D 在 BC上运动时，联结BC 、BD ，△BCD 中是否存在度数保持不变的角？如果存在，请指出这个角并求其度数；如果不存在，请说明理由；（3）联结OD ，当△ODE 是以DE 为腰的等腰三角形时，求△ODE 与△CBE面积的比值．解：（1）联结OC ，过点O 作OH ⊥CD ，垂足为H ．∵⊙O 的直径AB=10，∴BE=AB=10．∴OE=15．∵OC 过圆心O 且C 是 AB 的中点，第21页共31页∴CO ⊥AB ，垂足为O ．……1分∴∠COB=90°．∴Rt △OCH中，CE =∴cos 10OC C CE ==．……1分∵OH 过圆心O ，∴12CH CD =．……1分在Rt △OCH中，cos 10CH C OC ==，∴CH =CD =1分（2）∠CDB 为保持不变的角，度数为135°．……1分证明：联结OD ．∵OC=OD ，∴∠OCD=∠CDO ．………………1分∵在△COD 中，∠COD+∠OCD+∠CDO=180°．∴1802CODCDO ︒-∠∠=．……………………1分；同理，1802BODBDO ︒-∠∠=．…………………1分∴1180()1352CDB CDO BDO COD BOD ∠=∠+∠=︒-∠+∠=︒．……1分另解：证明：联结OD ．过点O 作OH ⊥CD ，垂足为H ．过点O 作OF ⊥BD ，垂足为F ．∵OC=OD ，OH ⊥CD ，∴12DOH COD ∠=∠，∠OHD=90°．……1分同理，12DOF BOD ∠=∠，∠OFD=90°．………1分∴1452HOF DOH DOF COB ∠=∠+∠=∠=︒．……1分∵四边形HOFD 的内角和为360°，∠OHD=90°，∠OFD=90°，∴∠CDB=135°．……………………………………1分（3）①当D 在 CB上，ODE CBE S S =△△②当D 在 BM上，ODE CBE S S △△；③当D在 MA上，ODECBESS=△△．（注：求出一个得2分，求出两个得4分，求出三个得5分）如图，半圆O的直径4AB=，点C是 AB上一点（不与点A、B 重合），点D是 BC的中点，分别联结AC、BD．（1）当AC是圆O的内接正六边形的一边时，求BD的长；（2）设AC x=，=BD y，求y与x之间的函数解析式，并写出x的取值范围；（3）定义：三角形一边上的中线把这个三角形分成两个小三角形，如果其中有一个小三角形是等腰三角形，且这条中线是这个小三角形的腰，那么这条中线就称为这个三角形的中腰线．分别延长AC、BD相交于点P，联结PO．PO是△PAB的中腰线，求AC的长．解：（1）联结OD．由AC是圆O的内接正六边形的一边，可得60AOC∠=︒．得120BOC∠=︒．∵点D是 BC的中点，∴60COD DOB∠=∠=︒．又∵OD OB=，∴△DOB为等边三角形．∴2BD OB==．（2）分别联结BC、OD，记交点为E．∵点D是 BC的中点，∴OD BC⊥，BE CE=．∵AO OB=，可得OE是△ABC的中位线．∴122xOE AC==．第22页共31页第23页共31页∴22x DE =-．由2222OB OE BD DE -=-，得2224222x x y ⎛⎫⎛⎫-=-- ⎪ ⎪⎝⎭⎝⎭．化简得y =（0＜x ＜4）．（3）由PO 是△PAB 的中腰线，点P 是圆外一点，可得PO PB =或PO PA =．i ．当PO PB =时，联结OD ．由OE 是△ABC 的中位线，可得OD //AC ．∵=AO BO ，∴BD DP =．∴2BP y =．易证△POB ∽△ODB .可得2OB BD BP =⋅.得42y y =⋅.解得3x =．ii ．当PO PA =时，联结OC ．由OD //AC ，可得=APB ODB ∠∠．∵=ODB OBD ∠∠，∴=APB OBD ∠∠．∴4AP AB ==．易证△POA ∽△OAC .可得2OA AC AP =⋅.得44x =⋅.解得1x =．所以AC 的长为3或1．如图，半圆O 的直径AB=10，点C 在半圆O 上，BC=6，CH ⊥AB ，垂足为点H ，点D 是弧AC 上一点．（1）若点D 是弧AB 的中点，求tan ∠DOC 的值；（2）联结BD 交半径OC 于点E ，交CH 于点F ，设OE=m ．①用含m 的代数式表示线段CF 的长；②分别以点O 为圆心OE 为半径、点C 为圆心CF 为半径作圆，当这两个圆相交时，求m取值范围．第24页共31页解：（1）联结DO ，∵点D 是弧AB 的中点，AB 是直径，∴OD ⊥AB ．（1分）∴∠CHB=∠DOB=90°，OD ∥CH ，∴∠DOC=∠OCH ．（1分）过点O 作OM ⊥BC ，垂足为点M ．由垂径定理，132BM BC ==．在Rt △BOM 中，BM=3，OM=4，OB=5，4sin 5OBC ∠=，3cos 5OBC ∠=．在Rt △BCH 中，24sin 5CH BC OBC =⋅∠=．（1分）18cos 5BH BC OBC =⋅∠=．75OH OB BH =-=（1分）∴7247tan tan 5524OH DOC OCH CH ∠=∠==÷=．（1分）（2）作HG ∥OC 交BD 于点G.．（1分）得1855GH BH OE BO ==，1825GH m =．（1分）又由HG ∥OC 得CF CEFH GH=，所以52418525CF mCF m -=-．（1分）∴6001201257mCF m-=-．（2分）（3）o r OE m ==，6001201257c mr CF m-==-，5d OC ==．①当两圆内切时，60012051257mm m--=-．（1分）由于05m <<，600120051257mm -<<-，所以两圆不可能内切．（1分）②当两圆外切时，60012051257mm m-+=-．解得125,57m m ==．（1分）所以当两圆相交时，557m <<．（1分）页如图1，AB是半圆O的直径，C是半圆O上一点，点O'与点O 关于直线AC对称，射线AO'交半圆O于点D，弦AC交O O'于点E、交OD于点F．（1）如图2，如果点O′恰好落在半圆O上，求证：=O A BC'；（2）如果30DAB∠= ，求EFO D'的值；（3）如果OA=3，1O D'=，求OF的长.解：（1）∵点O'与点O关于直线AC对称，∴O A OA'=，OO AC'⊥………1分∵点O′恰好落在半圆O上，∴O O OA'=∴△O AO'是等边三角形，=60AOO∠' ………1分联结OC,由OO AC'⊥得，=AO O C''∴==60AOO COO∠'∠' ………1分∴==60AOO BOC∠'∠ ∴=O A BC'………1分（2）∵30DAB∠= ，=OA OD，∴30ADO∠= ∴45AFO∠=∵点O'与点O关于直线AC对称，O E OE'=，OO AC'⊥∴45EOF∠= ，△OEF是等腰直角三角形……2分联结O F'，△OO F'是等腰直角三角形，设=EF t，则=OE t，=2O O t'，O F'Rt△O DF',30ADO∠=，O D'=……2分∴4EFO D==' (1)分第25页共31（3）联结OC，∠1=∠2，∠2=∠3，∴∠1=∠3，∴OC∥AD，∴OC OFAD DF=，………1分当点O'在圆内，OC=OD=3，AD=4,34OFDF=,∴97OF=………2分当点O'在圆外，OC=OD=3，AD=2,32OFDF=∴95OF= (2)分已知：如图1，四边形ABCD中，AB＝AD＝CD，∠B＝∠C＜90°．(1)求证：四边形ABCD是等腰梯形；(2)边CD的垂直平分线EF交CD于点E，交对角线AC于点P，交射线AB于点F．①当AF＝AP时，设AD长为x，试用x表示AC的长；②当BF＝DE时，求ADBC的值．(1)证明：延长BA、CD交于点P．……………（1分）∵∠B＝∠C，∴PB＝PC．∵AB＝CD，∴PA＝PD，∴∠PAD＝∠PDA．∵∠B＋∠C＋∠P＝∠PAD＋∠PDA＋∠P＝180°，∴∠B＋∠C＝∠PAD＋∠PDA，即2∠B＝2∠PAD．∴∠B＝∠PAD，∴AD∥BC．……………（2分）∵∠B＝∠C＜90°，∴∠B＋∠C≠180°．……………（1分）∴AB与CD不平行，∴四边形ABCD是梯形．第26页共31页第27页共31页∵AB＝CD，∴梯形ABCD是等腰梯形．(2)解：①联结DP，则DP＝CP，∠PDC＝∠PCD．∵AD＝CD，∴∠DAC＝∠DCA＝∠PDC．∴△CPD∽△CDA．…………（1分）∵四边形ABCD是等腰梯形，∴∠BAD＝∠ADC，∴∠BAP＝∠ADP．∵AF＝AP，∴∠AFP＝∠APF＝∠CPE．∵DP＝CP，PE⊥CD，∴∠DPE＝∠CPE＝∠AFP．∴DP∥AF，∴∠APD＝∠FAP＝∠ADP，∴AP＝AD．…………（2分）∵△CPD∽△CDA，∴CP CD CD AC=，设AC＝y，则AP＝AD=x，CD＝x，CP＝y－x．有y x xx y-=，即y2－xy－x2＝0，解得12y x=（负值舍）．…………（2分）∴512 AC x+=②延长FE、AD交于点G；过点E作EN∥AB，交BC于点N；作EH⊥BC，垂足为H．记EF与BC的交点为M．若点F在线段AB上，则点F为AB的中点，EF为等腰梯形ABCD的中位线．于是EF∥BC，∠DEF＝∠C＜90°，这与EF⊥CD不符，当点F在AB的延长线上时，∵BF＝DE＝12CD＝12AB，又∵AD∥BC，∴13BM BFAG AF==．…………（1分）设BM＝a，AD＝x，则AG＝3a，DG＝3a－x．第28页共31页∵1DG DECM CE==，∴CM ＝DG ＝3a －x ．∵EN ∥AB ，∴∠ENC ＝∠ABC ＝∠C ，∴EN ＝EC ＝DE ＝BF ．∴1MN ENBM BF==，MN ＝BM ＝a ，CN ＝2a －x ．∵EH ⊥BC ，∴CH ＝NH ＝12CN ＝a －12x ，cos C ＝12212a xa x x x --=．…………（1分）∵∠CDG ＝∠C ，cos ∠CDG ＝12362xDE x DG a x a x==--，…………（1分）∴262x a x a x x-=-，整理得x 2－10ax ＋12a 2＝0，解得(5x a =±．∵CN ＝2a －x ＞0，∴(5x a =，…………（1分）∴41381324123AD x BC a x ===-．…………（1分）已知AB 是⊙O 的直径，弦CD ⊥AB ，垂足为点H ，点E 在直径AB 上（与A 、B 不重合），EH=AH ，联结CE 并延长与⊙O 交于点F .（1）如图1，当点E 与点O 重合时，求∠AOC 的度数；（2）联结AF 交弦CD 于点P ，如果43CE EF =，求DPCP的值；（3）当四边形ACOF 是梯形时，且AB=6，求AE 的长.第29页共31页（1）∵弦CD ⊥AB ，∴∠CHO=90°.（1分）∵EH=AH ，∴12EH EA =.∵点E 与点O 重合，∴OA=EA.又OA=OC ，∴12EH OC =.（1分）∴∠OCH=30°，∴∠AOC=60°.（1分）（2）∵AB 是⊙O 的直径，弦CD ⊥AB ，∴CH=DH .（1分）又∵EH=AH ，∴四边形形ACED 是平行四边形.（1分）∴CE//AD ，CE=AD .（1分）∴DPAD CP CF =.∴DP CECP CF =.（1分）∵43CE EF=，∴47CE CF =∴47DP CP =.（1分）（3）设OCF α∠=，∵OC=OF ，∴OCF OFC α∠=∠=.当四边形ACOF 是梯形时，①OC //AF .∴OCF AFC α∠=∠=.（1分）∴2AFO AFC OFC α∠=∠+∠=.∵OA=OF ，∴2OAF AFO α∠=∠=.∴23AEC OAF AFC ααα∠=∠+∠=+=.∵EH=AH ，弦CD ⊥AB ，∴EC=AC .∴3CAO AEC α∠=∠=.∵OA=OC ，∴3OCA CAO α∠=∠=.∵AEC AOC OCF ∠=∠+∠，∴32AOC AEC OCF ααα∠=∠-∠=-=.在△AOC 中，180AOC CAO OCA ∠+∠+∠=︒，233180ααα++=︒.∴22.5o α=.（1分）∴45AOC ∠=︒.∴在Rt △OCH中2OH CH ==.又AB=6，∴OH =∴3AH =.∴6AE =-.（1分）②OF //AC .∴ACF OFC α∠=∠=.（1分）∴2OCA ACF OCF ααα∠=∠+∠=+=.∵OA=OC ，∴2OCA CAO α∠=∠=.∴2AEC CAO α∠=∠=.∴2AOC AEC OCF ααα∠=∠-∠=-=.在△AOC 中，180AOC CAO OCA ∠+∠+∠=︒，22180ααα++=︒.∴36o α=.（1分）。