【配套K12】[学习]九年级数学上册 第23章 图形的相似 23.3 相似三角形 23.3.3 相似

2018年秋九年级数学上册第23章图形的相似23.3 相似三角形23.3.2 第1课时相似三角形的判定定理1同步练习（新版）华东师大版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年秋九年级数学上册第23章图形的相似23.3 相似三角形23.3.2 第1课时相似三角形的判定定理1同步练习（新版）华东师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年秋九年级数学上册第23章图形的相似23.3 相似三角形23.3.2 第1课时相似三角形的判定定理1同步练习（新版）华东师大版的全部内容。

23.3.2 第1课时相似三角形的判定定理1知识点 1 两角分别相等的两个三角形相似1．图23－3－11中有两个三角形,角的度数已在图中标注，则这两个三角形（)A．相似 B．不相似C．全等 D．无法判断图23－3－112．下列各组三角形中，一定相似的是( )A．两个等腰三角形 B．两个等边三角形C．两个钝角三角形 D．两个直角三角形3．如图23－3－12,已知∠ADE＝∠ACD＝∠ABC，则图中的相似三角形共有( )A．1对 B．2对 C．3对 D．4对图23－3－124．如图23－3－13,添加一个条件：______________，可根据“两角分别相等的两个三角形相似”判定△ADE∽△ACB(写出一个即可）．图23－3－135。

如图23－3－14,AB与CD相交于点O，AC与BD不平行，则∠A＝________或∠C＝________时,△AOC∽△DOB。

图23－3－146．［教材例3变式］如图23－3－15,已知四边形ABCD为平行四边形,点E在BC的延长线上，AE与CD相交于点F.求证：△AFD∽△EAB.图23－3－157．如图23－3－16,已知∠1＝∠2,∠C＝∠E，则△ABC和△ADE相似吗？请说明理由．图23－3－168．如图23－3－17，在△ABC中,AB＝AC，BD＝CD，CE⊥AB于点E。

[推荐学习]2018年秋九年级数学上册第23章图形的相似23.3相似三角形23.3.1相似三角形同步23.3.1 相似三角形知识点 1 相似三角形的有关概念 1．已知△ABC ∽△A ′B ′C ′，AB ＝6 cm ，其对应边A ′B ′＝4 cm ，则相似比为________．2．已知△ABC ∽△A ′B ′C ′，且△ABC 与△A ′B ′C ′的相似比是23，则△A ′B ′C ′与△ABC 的相似比是( )A. 23B. 32C. 49D. 943．如图23－3－1，Rt △ADC ∽Rt △DBC ，AC ＝3，BC ＝4，试求△ADC 与△DBC 的相似比．图23－3－1＝∠B＝50°，∠C＝70°，则∠2＝________°，AD（）＝（）BC.7．如图23－3－3所示，根据下列情况写出各组相似三角形的对应边的比例式．(1)△ABC∽△ADE，其中DE∥BC；(2)△OAB∽△OA′B′，其中A′B′∥AB；(3)△ADE∽△ABC，其中∠ADE＝∠B.图23－3－38．如图23－3－4，已知AC＝4，BC＝6，∠B＝36°，∠D＝117°，且△ABC∽△DAC.(1)求∠BAD的大小；(2)求CD的长．图23－3－4知识点 3 由平行线判定三角形相似9．如图23－3－5，DE∥BC，EF∥AB，则图中相似三角形一共有( )A．1对B．2对C．3对D．4对图23－3－510．如图23－3－6，点F在平行四边形ABCD 的边AB上，射线CF交DA的延长线于点E，在不添加辅助线的情况下，与△AEF相似的三角形有( )A．0个 B．1个 C．2个 D．3个图23－3－611．［教材例1变式］如图23－3－7，在△ABC 中，已知DE∥BC，AD＝4，DB＝8，DE＝3.(1)求ADAB的值；(2)求BC的长．图23－3－712．已知△ABC与△A1B1C1的相似比为2∶3，△A1B1C1与△A2B2C2的相似比为3∶5，那么△ABC 与△A2B2C2的相似比为________．13．已知△ABC的三边长分别为2，6，2，△A′B′C′的两边长分别为1和 3.若△ABC∽△A′B′C′，则△A′B′C′的第三边长为________．图23－3－814. 如图23－3－8所示，在▱ABCD中，E是BC上一点，BE∶EC＝2∶3，AE交BD于点F，则BF∶DF＝__________．15．如图23－3－9，AB∥GH∥DC，点H在BC上，AC与BD交于点G，AB＝2，DC＝3，求GH 的长．图23－3－916．［2016·黄冈］如图23－3－10，已知△ABC, △DCE, △FEG, △HGI是4个全等的等腰三角形，底边BC，CE，EG，GI在同一条直线上，且AB＝2，BC＝1.连结AI，交FG于点Q，则QI ＝________．图23－3－1017．已知边长分别为5，6，7的三角形与一边长为3的三角形相似，求另一个三角形的另外两边的长．1. 322. B3．解：∵Rt △ADC ∽Rt △DBC ，∴AC DC ＝DC BC ，即3DC ＝DC 4， ∴DC 2＝12，则DC ＝2 3，∴△ADC 与△DBC 的相似比为32 3＝32.4．D ． 5．B6．70 AC ED 7．解：(1)AD AB ＝AE AC ＝DEBC .(2)AO A ′O ＝BO B ′O ＝AB A ′B ′.(3)AD AB ＝AE AC ＝DE BC.8．解：(1)∵△ABC ∽△DAC ，∴∠DAC ＝∠B ＝36°，∠BAC ＝∠D ＝117°， ∴∠BAD ＝∠BAC ＋∠DAC ＝153°.(2)∵△ABC∽△DAC，∴BCAC＝ACCD.又∵AC＝4，BC＝6，∴CD＝4×46＝83.9．C [解析] ∵DE∥BC，∴△ADE∽△ABC.∵EF∥AB，∴△CEF∽△CAB，∴△ADE∽△EFC，共3对．故选C.10．C [解析] ∵四边形ABCD是平行四边形，∴AD∥BC，AB∥DC，∴△AEF∽△BCF，△AEF∽△DEC，∴与△AEF相似的三角形有2个．11．解：(1)∵AD＝4，DB＝8，∴AB＝AD＋DB＝4＋8＝12，∴ADAB＝412＝13.(2)∵DE∥BC，∴△ADE∽△ABC，∴DEBC＝ADAB.∵DE＝3，∴3BC＝13，∴BC＝9.12 2∶5[解析] ∵△ABC与△A1B1C1的相似比为2∶3，△A1B1C1与△A2B2C2的相似比为3∶5，∴AB∶A1B1＝2∶3，A1B1∶A2B2＝3∶5.设AB＝2x，则A1B1＝3x，A2B2＝5x，∴AB∶A2B2＝2∶5，∴△ABC与△A2B2C2的相似比为2∶5.13． 214．2∶515．∵AB∥GH∥DC，∴△CGH∽△CAB，△BGH∽△BDC，∴GHAB＝CHCB，GHDC＝BHBC，∴GH AB ＋GH DC ＝CH CB ＋BH BC＝1. ∵AB ＝2，DC ＝3，∴GH 2＋GH 3＝1，∴GH ＝65. 16． 4317．解：因为题目没有具体说明相似三角形的对应边，所以分三种情况讨论．设另外两条边的长分别为x ，y (x <y )． 根据题意，得5x ＝6y ＝73或5x ＝63＝7y 或53＝6x ＝7y， 所以x ＝157，y ＝187或x ＝52，y ＝72或x ＝185，y ＝215. 故另一个三角形的另外两边的长为157，187或52，72或185，215.。

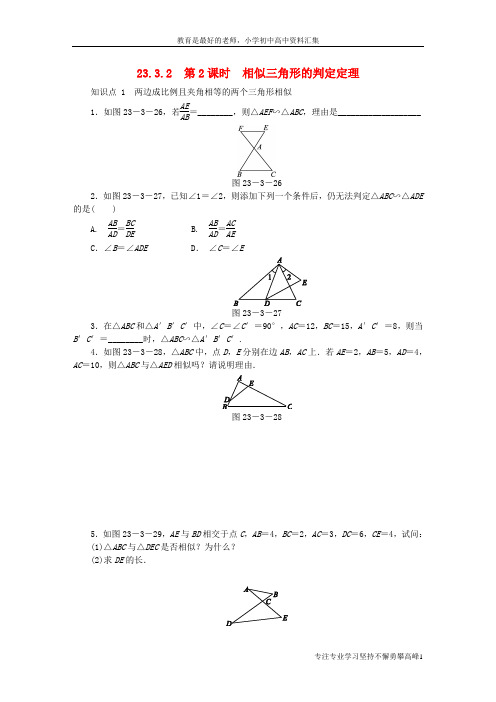
23.3.2 第2课时 相似三角形的判定定理知识点 1 两边成比例且夹角相等的两个三角形相似1．如图23－3－26，若AE AB＝________，则△AEF ∽△ABC ，理由是___________________图23－3－262．如图23－3－27，已知∠1＝∠2，则添加下列一个条件后，仍无法判定△ABC ∽△ADE 的是( )A. AB AD ＝BC DE B. AB AD ＝ACAEC ．∠B ＝∠ADED ． ∠C ＝∠E图23－3－273．在△ABC 和△A ′B ′C ′中，∠C ＝∠C ′＝90°，AC ＝12，BC ＝15，A ′C ′＝8，则当B ′C ′＝________时，△ABC ∽△A ′B ′C ′.4．如图23－3－28，△ABC 中，点D ，E 分别在边AB ，AC 上．若AE ＝2，AB ＝5，AD ＝4，AC ＝10，则△ABC 与△AED 相似吗？请说明理由．图23－3－285．如图23－3－29，AE 与BD 相交于点C ，AB ＝4，BC ＝2，AC ＝3，DC ＝6，CE ＝4，试问： (1)△ABC 与△DEC 是否相似？为什么？ (2)求DE 的长．图23－3－29知识点 2 三边成比例的两个三角形相似 6．已知AB ＝12 cm ，AC ＝15 cm ，BC ＝21 cm ，A 1B 1＝16 cm ，B 1C 1＝28 cm ，当A 1C 1＝________ cm 时，△ABC ∽△A 1B 1C 1.7．有甲、乙两个三角形木框，甲三角形木框的三边长分别为1，2，5，乙三角形木框的三边长分别为5，10，5，则甲、乙两个三角形( )A ．一定相似B ．一定不相似C ．不一定相似D ．无法判断8．图23－3－30中的两个三角形是否相似？为什么？图23－3－309．［2017·枣庄］如图23－3－31，在△ABC 中，∠A ＝78°，AB ＝4，AC ＝6，将△ABC 沿图23－3－32中的虚线剪开，剪下的阴影三角形与原三角形不相似的是( )图23－3－31图23－3－3210．如图23－3－33，点P 在△ABC 的边AC 上，要判定△ABP ∽△ACB ，添加一个条件，不正确的是( )A ．∠ABP ＝∠CB ．∠APB ＝∠ABCC. AP AB ＝AB ACD. AB BP ＝ACCB图23－3－3311．下列条件中，能判定△ABC 与△DEF 相似的有( )①∠A ＝45°，AB ＝12，AC ＝15，∠D ＝45°，DE ＝16，DF ＝40；②AB ＝12，BC ＝15，AC ＝24，DE ＝20，EF ＝25，DF ＝40；③∠A ＝50°，AB ＝15，AC ＝20，∠E ＝50°，DE ＝28，EF ＝21.A ．0个B ．1个C ．2个D ．3个12．如图23－3－34，在△ABC 中，D 是边AC 上一点，连结BD ，给出下列条件：①∠ACB＝∠ABD ；②AB 2＝AD ·AC ；③AD ·BC ＝AB ·BD ；④AB ·BC ＝AC ·BD .其中单独能够判定△ABC ∽△ADB 的是( )A ．①②B ．①②③C ．①②④D ．①②③④图23－3－3413．如图23－3－35，在△ABC 中，点D ，E 分别在边AB ，AC 上，∠AED ＝∠B ，射线AG 分别交线段DE ，BC 于点F ，G ，且AD AC ＝DFCG. (1)求证：△ADF ∽△ACG ；(2)若AD AC ＝12，求AFFG的值．图23－3－3514．如图23－3－36，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ACB 和△DCE 的顶点都在格点上，ED 的延长线交AB 于点F .求证：(1)△ACB ∽△DCE ； (2)EF ⊥AB .图23－3－3615．如图23－3－37，已知AB⊥BD，CD⊥BD，垂足分别为B，D.(1)若AB＝9，CD＝4，BD＝10，请问在BD上是否存在点P，使以P，A，B三点为顶点的三角形与以P，C，D三点为顶点的三角形相似？若存在，求出BP的长；若不存在，请说明理由．(2)若AB＝9，CD＝4，BD＝12，请问在BD上存在多少个点P，使以P，A，B三点为顶点的三角形与以P，C，D三点为顶点的三角形相似？并求出BP的长．图23－3－37教师详答1. AF AC两边成比例且夹角相等的两个三角形相似 2． A3．10 [解析] 由AC A ′C ′＝BC B ′C ′得128＝15B ′C ′，解得B ′C ′＝10. 4．解：相似．理由：∵AE AB ＝25，AD AC ＝410＝25，∴AE AB ＝AD AC.又∵∠A ＝∠A ，∴△ABC ∽△AED . 5．解：(1)相似．理由：∵BC EC ＝24＝12，AC DC ＝36＝12，∴BC EC ＝AC DC.又∵∠ACB ＝∠DCE ， ∴△ABC ∽△DEC . (2)∵△DEC ∽△ABC ，∴DE AB ＝DC AC ＝63＝2， ∴DE ＝2AB ＝8. 6．20 7. A8．解：相似．理由：∵AC DF ＝BC EF ＝AB DE ＝53，∴△ABC ∽△DEF .9．C 10．D [解析] A ．当∠ABP ＝∠C 时， 又∵∠A ＝∠A ， ∴△ABP ∽△ACB ；B ．当∠APB ＝∠ABC 时， 又∵∠A ＝∠A ， ∴△ABP ∽△ACB ； C ．当AP AB ＝AB AC时，又∵∠A ＝∠A ， ∴△ABP ∽△ACB ；D ．无法得到△ABP ∽△ACB . 故选D.11． C 12． A14．证明：(1)∵AC ＝3，DC ＝2，BC ＝6，EC ＝4，∴AC DC ＝32，BC EC ＝64＝32，∴AC DC ＝BC EC. 又∵∠BCA ＝∠ECD ＝90°，∴△ACB ∽△DCE .(2)∵△ACB ∽△DCE ，∴∠B ＝∠E . ∵∠B ＋∠A ＝90°，∴∠E ＋∠A ＝90， ∴∠AFE ＝90°，∴EF ⊥AB . 15． (1)存在．设BP ＝x ，则PD ＝10－x . ∵∠B ＝∠D ， ∴当AB PD ＝PBCD时，△ABP ∽△PDC ，即910－x ＝x 4， 整理得x 2－10x ＋36＝0，此方程没有实数根； 当AB CD ＝PB PD时，△ABP ∽△CDP ， 即94＝x 10－x ，解得x ＝9013， 即BP 的长为9013.(2)存在2个符合题意的点P . 设BP ＝y ，则PD ＝12－y . ∵∠B ＝∠D ， ∴当AB PD ＝PBCD时，△ABP ∽△PDC ，即912－y ＝y 4， 整理得y 2－12y ＋36＝0，解得y 1＝y 2＝6； 当AB CD ＝PB PD时，△ABP ∽△CDP ， 即94＝y 12－y ，解得y ＝10813， 即BP 的长为6或10813.。

23.3.2 相似三角形的判定【学习目标】1. 两个三角形相似的判定方法1：有两个角对应相等的两个三角形相似。

2.会利用判定定理解答一些问题.【学习重难点】相似三角形的判定定理1【学习过程】一、课前准备1、两个矩形一定会相似吗？为什么？2、如何判断两个三角形是否相似？二、学习新知 自主学习：1、观察你与你同伴的直角三角尺，同样角度（30°与60°，或45°与45°）让学生充分思考，并与伙伴交流后，它们相似吗？2、如果一个三角形的三个角分别与另一个三角形的三个角对应相等，那么它们相似吗？3、任意画两个三角形（可以画在下面的格点图上），使其三对角对应相等．用刻度尺量两个三角形的对应边，看看两个三角形的对应边是否成比例．你能得出什么结论？图24.1.5 （如果一个三角形的三个角分别与另一个三角形的三个角对应相等，那么这两个三角形__________．）4、小组讨论后总结：得到识别两个三角形相似的一个较为简便的方法：如果一个三角形的两角分别与另一个三角形的两角对应相等，那么这两个三角形相似．5、思 考：如果两个三角形仅有一对角是对应相等的，那么它们是否一定相似？举例说明。

（你所用的两块不一样的直角三角尺）图24.3.3实例分析：例1、在两个直角三角形△ABC和△A′B′C′中，∠C＝∠C′＝90°，∠A＝∠A′，证明△ABC∽△A′B′C′．证明:例2 如图，△ABC中，DE∥BC，EF∥AB，证明:△ADE∽△EFC.（注意：推理必须步步有据）【随堂练习】1、(1)如图，AB与CD相交于点O，AC与BD不平行，当_________=__________或___________=____________时，△ AOC∽△DOB；(2)如图，AD与BC相交于点O，AB∥CD，则__________∽___________．2、如图，△ABC中，∠ACB=90°，CD⊥AB于D，则∠B=_________，∠A=________，因此△ABC∽_________∽_____________．3、如图，点D、E在△ABC的边AB、AC上．(1)若∠1=∠2，则__________∽___________；(2)若∠2=∠B，则__________∽___________．4、如图，D、E分别为△ABC中AB、AC边上的点，请你添加一个条件，使△ADE与△ABC 相似，你添加的条件是_____________（只需填上你认为正确的一种情况即可）.【中考连线】在Rt△ABC中，∠C为直角，CD⊥AB于点D,BC=3,AB=5,写出其中的一对相似三角形是______和 __ ；并写出它的面积比 .【参考答案】随堂练习1、(1)∠A=∠D或∠C=∠B，△ AOC∽△DOB； (2)△AOB△DOC2、∠ACD∠BCD∠ACD∠CBD3、(1) △ADE△ACD (2) △ACD△ABC4、∠C=∠ADE（或∠B=∠AED等）中考连线分三种情况：（1）△ADC ∽△CDB 43；（2）△ADC∽△ACB45；（3）△CDB∽△ACB3 4。

23.3.1 相似三角形【学习目标】1、掌握相似三角形的有关概念及表示方法；2、能够熟练地找出相似三角形的对应角和对应边；3、了解相似三角形与全等三角形的关系。

【学习重难点】1、掌握相似三角形的有关概念及表示方法；2、能够熟练地找出相似三角形的对应角和对应边【学习过程】一、课前准备1.填空（1）相等，成比例的两个多边形叫做相似多边形.相似多边形的比叫做相似比.（2）四边形ABCD相似与四边形A′B′C′D′,AB=6,BC=8，∠B=50°，A′B′=9，则B′C′=___________∠B′=___（3）和都相同的两个三角形是全等三角形.2.选择⑴两个多边形相似的条件是：（）A: 对应边相等 B: 对应角相等或对应边相等 C: 对应角相等 D: 对应角相等且对应边成比例⑵下列结论正确的是（）A: 任意的两个等腰直角三角形都相似 B: 有一个角对应相等的等腰梯形都相似C: 任意的两个长方形都相似 D:任意的两个菱形都相似。

二、学习新知自主学习：⒈相似三角形相关概念：（1）定义：相似三角形是相似多边形中的一类，因此，相似三角形的定义可仿照相似多边形的定义来归纳：相等，成比例的两个三角形叫做相似三角形.（2）表示：如△ABC与△A DE相似，记作△ABC △A DE其中对应顶点要写在。

数学语言：∵∠A= ,∠B= ,∠C== =∴△ABC∽△ADE（3）相似比：叫做相似比.想一想：已知:⊿ABC∽⊿DEF, 你能得到哪些结论？结论：相似三角形对应边，对应角。

实例分析：例1、在△ABC中，点D是边AB的三等分点，DE//BC，DE=5.求BC的长.【随堂练习】1、有一块呈三角形形状的草坪，其中一边的长是20m，在这个草坪的图纸上，这条边长5cm，其他两边的长都是3.5cm，求该草坪其他两边的实际长度。

2、如果两个三角形的相似比为1，那么这两个三角形_____3、若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12 cm，那么△A′B′C′的最大边长是_____4、（★）若△ABC∽△DEF,它们的周长分别为6 cm和8 cm，那么下式中一定成立的是（）A.3AB=4DEB.4AC=3DEC.3∠A=4∠DD.4（AB+BC+AC）=3（DE+EF+DF）5、若△ABC与△A′B′C′相似，∠A=55°,∠B=100°，那么∠C’的度数是（）A.55°B.100°C.25°D.不能确定【中考连线】如图，小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m、与旗杆相距22m，则旗杆的高为（）A．12m B．10m C．8m D．7m【参考答案】随堂练习1、其他两边都是14米；2、全等；3、24；4、D；5、C中考连线由题意可知两个三角形相似，可得8 3.2,12.. 822x cm Ax=∴=+所以选。