MATLAB编程光学实验图样

基于Matlab的光学实验仿真基于Matlab的光学实验仿真一、引言光学是研究光的传播、反射、折射和干涉等现象的学科，广泛应用于光学器件、光通信等领域。

在光学实验中，通过搭建实验装置来观察和研究光的行为，以验证光学理论并深入理解光的特性。

然而，传统的光学实验不仅设备复杂，成本高昂，而且需要大量的实验时间和实验设计。

因此，基于计算机仿真的方法成为了一种重要的补充和替代。

Matlab作为一种强大的数值计算和仿真工具，具有强大的数学运算能力和友好的图形界面，被广泛应用于科学研究和工程设计。

在光学实验中，Matlab可以模拟光的传播、折射、干涉等各种光学现象，使得研究人员可以在计算机上进行光学实验，加速实验过程并提高实验效率。

二、光的传播仿真在光学实验中，光的传播是一项重要的研究内容。

通过Matlab的计算能力，我们可以模拟光线在不同介质中的传播情况，并观察其光程差、折射等现象。

光的传播可以用波动光学的理论来描述，其中最经典的是亥姆霍兹方程。

在Matlab中，我们可以利用波动光学的相关工具箱，通过求解亥姆霍兹方程来模拟光的传播。

例如，我们可以模拟光在一特定系统中的衍射效应。

在Matlab中，衍射效应可以通过菲涅尔衍射和弗雷涅尔衍射来模拟。

我们可以设定特定的光源和障碍物，通过Matlab的计算能力计算光的传播、衍射和干涉等现象，得到不同条件下的衍射效应，并可视化展示。

三、光的折射仿真光的折射是光学领域中的另一个重要现象，研究光的折射对于理解光在不同介质中的传播行为至关重要。

通过Matlab的仿真，我们可以模拟光的折射行为，并研究不同介质对光的影响。

在Matlab中，我们可以利用光学工具箱中的折射相关函数，输入光线的入射角度、折射率等参数，模拟光线在不同介质中的折射行为。

通过改变不同介质的折射率、入射角度等参数，我们可以观察到光的全反射、折射偏折等现象，并进行定量分析和比较。

四、光的干涉仿真光的干涉是光学领域的重要研究课题之一，通过模拟光的干涉行为，可以深入理解光的相干性、波动性质等特性。

clear;close all;lamda=0.6328;%入射光波长,单位umz=200.0e3;%传播距离,单位umh=2e3;w=2e3;%模拟光波的大小,单位umdx=10.0;dy=10.0;%抽样间隔,单位umM=h/dx;N=w/dy;%抽样点数a0=1;%初始振幅大小为 1x0=0;y0=0;%模拟光源位于坐标原点k=2*pi/lamda;%波数%---------球面波表示-------%[x,y]=meshgrid(-M/2*dx:(M-1)/2*dx,-N/2*dy:(N-1)/2*dy);%M个点,两点之间的距离为dxSphFunct=a0/z.*exp(i*k*z).*exp(i*pi/(lamda*z).*((x-x0).^2+(y-y 0).^2));%球面波I=abs(SphFunct).^2;%光强度I1=I./max(max(I));%归一化强度,二维所以求两次max()Ph=angle(SphFunct);%相位,函数angle()表示取相位figure(1);imagesc(I1);%做出球面波的强度分布图，没有强度变化，均匀光斑,这里做了彩图figure(2);P=(Ph+pi)/(2*pi);%归一化相位imshow(P);%画出球面波的相位分布图figure(3);imagesc(P);%画出球面波相位分布的彩图clear;close all;lamda=0.6328;%入射光波长umh=2e3;w=2e3;%模拟光波的大小um dx=10.0;dy=10.0;%抽样间隔umM=h/dx;N=w/dy;%抽样点数A=1;%振幅为 1k=2*pi/lamda;%波数theta=pi/6;%设定theta为30度a=pi/2-theta;%波矢与x轴夹角b=pi/2;%波矢与y轴夹角c=theta;%波矢与z轴夹角z=0;%-----------平面波----------%[x,y]=meshgrid(-M/2*dx:(M-1)/2*dx,-N/2*dy:(N-1)/2*dy);%抽样网格pingmianbo=A.*exp(i*k.*(x.*cos(a)+y.*cos(b)+z.*cos(c)));%平面波公式I=abs(pingmianbo).^2;%光强度I1=I./max(max(I));%归一化强度Ph=angle(pingmianbo);%相位figure(1);imshow(I1)%做出强度分布图,没有强度变化，均匀光斑figure(2);imagesc(I1);%画出强度分布彩图figure(3);P=(Ph+pi)/(2*pi);%归一化相位imshow(P);%画出相位分布图像figure(4);imagesc(P);%做出相位分布彩图clear;close all;lamda=0.6328;%入射光波长umz=100.0e3;%传播距离umh=2e3;w=2e3;%模拟光波的大小umdx=10.0;dy=10.0;%抽样间隔umM=h/dx;N=w/dy;%抽样点数a0=1;%设定振幅x1=-0.2e3;y1=0;%相当于将上图逆时针旋转90度后的S1,距原点0.2mmx2=0.2e3;y2=0;%相当于将上图逆时针旋转90度后的S2,距原点0.2mmk=2*pi/lamda;%波数%---------球面波---------%[x,y]=meshgrid(-M/2*dx:(M-1)/2*dx,-N/2*dy:(N-1)/2*dy);%抽样网格wave1=a0/z.*exp(i*k*z).*exp(i*pi/(lamda*z).*((x-x1).^2+(y-y1).^2));%第一束球面波wave2=a0/z.*exp(i*k*z).*exp(i*pi/(lamda*z).*((x-x2).^2+(y-y2).^2));%第二束球面波wave=wave1+wave2;%两束球面波相遇,即为两者复振幅之和I=abs(wave).^2;%光强度I1=I./max(max(I));%归一化强度Ph=angle(wave);%相位函数angle()表示取相位figure(1);imshow(I1);%画出球面波的强度分布图,没有强度变化,均匀光斑figure(2);P=(Ph+pi)/(2*pi);%归一化相位imshow(P);%画出球面波的相位分布图figure(3);imagesc(P);%画出球面波的相位分布彩图clear;close all;lamda=0.6328;%入射光波长umh=2e3;w=2e3;%模拟光波的大小umdx=10.0;dy=10.0;%抽样间隔umM=h/dx;N=w/dy;%抽样点数A=1;%设定振幅为 1k=2*pi/lamda;%波数theta1=-0.25*pi/180;%第一束平面波与z轴夹角theta2=0.25*pi/180;%第二束平面波与z轴夹角a1=pi/2-theta1;%波矢与x轴夹角b1=pi/2;%波矢与y轴夹角c1=theta1;%波矢与z轴夹角a2=pi/2-theta2;%波矢与x轴夹角b2=pi/2;%波矢与y轴夹角c2=theta2;%波矢与z轴夹角z=0e3;%----------平面波表示----------%[x,y]=meshgrid(-M/2*dx:(M-1)/2*dx,-N/2*dy:(N-1)/2*dy);%二维抽样网格wave1=A.*exp(i*k.*(x.*cos(a1)+y.*cos(b1)+z.*cos(c1)));%第一束平面波wave2=A.*exp(i*k.*(x.*cos(a2)+y.*cos(b2)+z.*cos(c2)));%第二束平面波wave=wave1+wave2;%两束光相遇I=abs(wave).^2;%光强度I1=I./max(max(I));%归一化强度Ph=angle(wave);%相位figure(1);imshow(I1);%画出强度分布图figure(2);imagesc(I1);%画出强度分布彩图figure(3);P=(Ph+pi)/(2*pi);%归一化强度imshow(P);%做出相位分布图figure(4);imagesc(P);%做出相位分布彩图。

基于Matlab的光学实验仿真一、本文概述随着科技的快速发展，计算机仿真技术已成为科学研究、教学实验以及工程应用等领域中不可或缺的一部分。

在光学实验中，仿真技术能够模拟出真实的光学现象，帮助研究者深入理解光学原理，优化实验设计，提高实验效率。

本文旨在探讨基于Matlab的光学实验仿真方法，分析Matlab在光学实验仿真中的优势和应用，并通过具体案例展示其在光学实验仿真中的实际应用效果。

通过本文的阐述，读者将能够了解Matlab在光学实验仿真中的重要作用，掌握基于Matlab的光学实验仿真方法，从而更好地应用仿真技术服务于光学研究和实验。

二、Matlab基础知识Matlab，全称为Matrix Laboratory，是一款由美国MathWorks公司出品的商业数学软件，主要用于算法开发、数据可视化、数据分析以及数值计算等领域。

Matlab以其强大的矩阵计算能力和丰富的函数库，在光学实验仿真领域具有广泛的应用。

Matlab中的变量无需预先声明，可以直接使用。

变量的命名规则相对简单，以字母开头，后面可以跟字母、数字或下划线。

Matlab支持多种数据类型，包括数值型（整数和浮点数）、字符型、逻辑型、结构体、单元数组和元胞数组等。

Matlab的核心是矩阵运算，它支持多维数组和矩阵的创建和操作。

用户可以使用方括号 [] 来创建数组或矩阵，通过索引访问和修改数组元素。

Matlab还提供了大量用于矩阵运算的函数，如矩阵乘法、矩阵转置、矩阵求逆等。

Matlab具有强大的数据可视化功能，可以绘制各种二维和三维图形。

在光学实验仿真中，常用的图形包括曲线图、散点图、柱状图、表面图和体积图等。

用户可以使用plot、scatter、bar、surf和volume 等函数来创建这些图形。

Matlab支持多种控制流结构，如条件语句（if-else）、循环语句（for、while）和开关语句（switch）。

这些控制流结构可以帮助用户编写复杂的算法和程序。

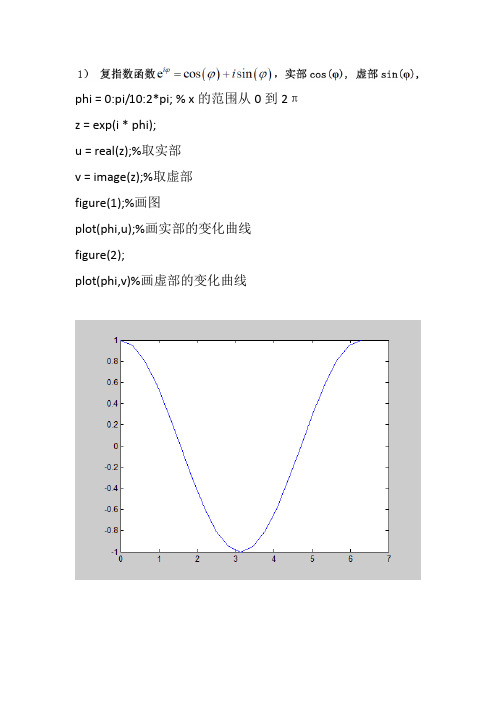
phi = 0:pi/10:2*pi; % x的范围从0到2πz = exp(i * phi);u = real(z);%取实部v = image(z);%取虚部figure(1);%画图plot(phi,u);%画实部的变化曲线figure(2);plot(phi,v)%画虚部的变化曲线clear;%清除内存close all;%关闭所有窗口x=linspace(0,2*pi,100);%设置横坐标范围及网格y1=sqrt(x);%开根号figure(1);plot(x,y1,'r')%做出y1的曲线,'r'代表图线为红色clear;%清除内存close all;%关闭所有窗口x=linspace(-2*pi,2*pi,100);%100个数横坐标从-2pi到2pi y1=besselj(1,x);%第一类贝塞尔函数,一阶y2=besselj(0,x);%第一类贝塞尔函数,0阶figure(1);plot(x,y1,'r');figure(2);plot(x,y2,'b');clear;close all;[x,y]=meshgrid(-2:.05:2,-2:.05:2);%设置二维网格z=sinc(x).*sinc(y);figure(1);imshow(z);%二维灰度图figure(2);imagesc(z);%二维彩图figure(3);mesh(z);%三维图像clear;close all;a=5;x=linspace(-5,5,100);y1=exp(-pi.*(x/a).^2);%第一类贝塞尔函数,一阶b=2;y2=exp(-pi.*(x/b).^2);%第一类贝塞尔函数,一阶figure(1);plot(x,y1,'r');figure(2);plot(x,y2,'b');clear;close all;a=1;b=1;[x,y]=meshgrid(-2:.05:2,-2:.05:2);%设置二维网格z=exp(-pi.*((x/a).^2+(y/b).^2));%高斯函数figure(1);imagesc(z);figure(2);mesh(z);clear;close all;M=100;%x方向抽样点数N=100;%y方向抽样点数w=10;%缝的宽度d=10;%缝偏离中心的位置obj1=zeros(M,N);%赋值为0的一个二维矩阵,大小为M*N obj1(:,(N/2-w/2):N/2+w/2)=1.0;%设置缝在y向中心,且缝的宽度为wfigure(1);imshow(obj1);obj2=zeros(M,N);obj2(:,(N/2-d)-w/2:(N/2-d)+w/2)=1.0;%缝偏离中心位置d个像素figure(2);imshow(obj2);clear;close all;M=100;%x方向抽样点数N=100;%y方向抽样点数w=10;%缝的宽度d=10;%缝偏离中心的位置obj1=zeros(M,N);%赋值为0的一个二维矩阵,大小为M*N obj1(:,(N/2+d)-w/2:(N/2+d)+w/2)=1.0;%设置缝在y向中心,且缝的宽度为wobj2=zeros(M,N);obj2(:,(N/2-d)-w/2:(N/2-d)+w/2)=1.0;%缝偏离中心位置d个像素obj3=obj1+obj2;figure(1);imshow(obj3);clear;close all;M=100;N=100;w=10;%缝宽obj=zeros(M,N);obj((M/2-w/2):(M/2+w/2),(N/2-w/2):(N/2+w/2))=1.0;%缝处于中心位置figure(1);imshow(obj);figure(2);imagesc(obj);figure(3);mesh(obj);。

光学实验实验报告课程名称：光学实验*名：***学院：电子工程学院系部：光电子技术系专业：电子科学与技术年级：科技1201学号：********指导教师：**2014年12 月24 日光波在介质中界面上的反射及透射特性一．实验目的：1．掌握反射系数及透射系数的概念；2．掌握反射光与透射光振幅和相位的变化规律； 3．掌握布儒斯特角和全反射临界角的概念。

二．实验原理：1 反射定律和折射定律光由一种介质入射到另一种介质时，在界面上将产生反射和折射。

现假设二介质为均匀、透明、各向同性介质，分界面为无穷大的平面，入射、反射和折射光均为平面光波，其电场表示式为)(0r k t i l l l l e E E ⋅--=ω l =i, r, t式中，脚标i 、r 、t 分别代表入射光、反射光和折射光；r 是界面上任意点的矢径，在图2-1所示的坐标情况下，有r=ix+jy图2-1 平面光波在界面上的反射和折射 图2-2 k i 、k r 、k t 三波矢关系根据电磁场的边界条件，可以得到如下关系)(0)(t i r i tr i =⋅-=⋅-==r k k r k k ωωω 这些关系表明：①入射光、反射光和折射光具有相同的频率；②入射光、反射光和折射光均在入射面内，k i 、k r 和k t 波矢关系如图2-2所示。

进一步可得tt i i r r i i sin sin sin sin θθθθk k k k == 或tt i i r r i i sin sin sin sin θθθθn n n n ==即介质界面上的反射定律和折射定律，它们给出了反射光、折射光的方向。

折射定律又称为斯涅耳(Snell)定律。

2 菲涅耳公式 s 分量和p 分量通常把垂直于入射面振动的分量称做s 分量，把平行于入射面振动的分量称做p 分量。

为讨论方便起见，规定s 分量和p 分量的正方向如图2-3所示。

图2-3 s 分量和p 分量的正方向反射系数和透射系数 假设介质中的电场矢量为)(i 0e r k t l l l E E ⋅--=ω l =i, r, t其s 分量和p 分量表示式为)(i 0e r k t lm lm l E E ⋅--=ω m =s,p则定义s 分量、p 分量的反射系数、透射系数分别为tmtm m im rmm E E t E E r 0000==菲涅耳公式假设界面上的入射光、反射光和折射光同相位，根据电磁场的边界条件及s 分量、p 分量的正方向规定，可得ts rs s E E E i =+和2tp 1rp 1ip cos cos cos θθθH H H =-利用E H εμ=，上式变为22ts 11rs is cos cos )(θθn E n E E =-再利用折射定律，消去E ts ，经整理可得)sin()sin(1212is rs θθθθ+-=E E 根据反射系数定义，得到)sin()sin(2121θθθθ+--=s r221111cos cos cos 2θθθn n n t s +=将所得到的表示式写成一个方程组，就是著名的菲涅耳公式：212122112*********tan tan tan tan cos cos cos cos )sin()sin(θθθθθθθθθθθθ+--=+-=+--==n n n n E E r is rs s 2121211221122121002sin 2sin 2sin 2sin cos cos cos cos )tan()tan(θθθθθθθθθθθθ+-=+-=+-==n n n n E E r iprp p 21121121112100221111212100cos cos cos 2)cos()sin(sin cos 2cos cos cos 2)sin(sin cos 2θθθθθθθθθθθθθθθθn n n E E t n n n E E t iptp p is ts s +=-+==+=+==这些系数首先是由菲涅耳用弹性波理论得到的，所以又叫做菲涅耳系数。

1.工程光学系列之一：杨氏双缝干涉matlab1.基本原理杨氏干涉实验是两点光源干涉实验的典型代表。

杨氏干涉实验以极简单的装置和巧妙构思实现了普通光源干涉。

无论从经典光学还是从现代光学的角度来看，杨氏实验都具有十分重要的意义。

杨氏双缝实验的装置如图2-18所示，按照惠更斯-菲涅耳原理，线光源S上的点将作为次波源向前发射次波（球面波），形成交叠的波场。

在较远的地方放置一观察屏，屏上可以观测到一组几乎是平行的直线条纹。

图杨氏干涉实验原理图2.matlab源代码clearlam=500e-9;a=2e-3;D=1;ym=5*lam*D/a;xs=ym;n=101;ys=linspace(-ym,ym,n);for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2); r2=sqrt((ys(i)+a/2).^2+D^2); phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2); endN=255;Br=(B/4.0)*N;subplot(1,2,1)image(xs,ys,Br); colormap(gray(N)); subplot(1,2,2)plot(B,ys)3.实验现象2. 工程光学系列之二：等倾干涉matlab2.1 基本原理等倾干涉是薄膜干涉的一种。

薄膜此时是均匀的，光线以倾角i入射，上下两条反射光线经过透镜作用会汇聚一起，形成干涉。

化学教案权倾一时化学教案内外无不造门者化学教案唯景仁不至试卷试题年三十化学教案方为著作佐郎试卷试题桓玄诛元图等倾干涉薄膜由于入射角相同的光经薄膜两表面反射形成的反射光在相遇点有相同的光程差，也就是说，凡入射角相同的就形成同一条纹，故这些倾斜度不同的光束经薄膜反射所形成的干涉花样是一些明暗相间的同心圆环．这种干涉称为等倾干涉。

倾角i相同时，干涉情况一样（因此叫做“等倾干涉”）2.2 matlab源代码%等倾干涉clear allclose allclc%%k=2000;s=500;D=0.2;bochang=s*10^(-9);theta=0.15;d=k*bochang/4;rMax=D*tan(theta/2);N=501;for i=1:Nx(i)=(i-1)*2*rMax/(N-1)-rMax; for j=1:Ny(j)=(j-1)*2*rMax/(N-1)-rMax; r(i,j)=sqrt(x(i)^2+y(j)^2);delta(i,j)=2*d/sqrt(1+r(i,j)^2/D^2); Phi(i,j)=2*pi*delta(i,j)/bochang; B(i,j)=4*cos(Phi(i,j)/2)^2;endendNCLevels=255;Br=(B/4.0)*NCLevels;figure(1);image(x,y,Br);colormap(gray(NCLevels));2.3 实验现象3. 工程光学系列之三：夫琅禾费矩孔衍射matlab3.1 实验原理衍射的定义：光波在传播过程遇到障碍物时，光束偏离直线传播，强度发生重新分布的现象。

MATLAB编程用两种方法模拟光学实验03级物理一班李超PB03203017摘要：利用MATLAB软件编程实现了用衍射积分的方法对单缝衍射、杨氏双缝干涉、黑白光栅衍射的计算机模拟；以及用傅立叶变换方法对简单孔径衍射、黑白光栅及正弦光栅夫琅和费衍射的模拟。

关键词：MATLAB；衍射积分；傅立叶变换；计算机模拟引言：美国Mathworks公司推出的MA TLAB，是一种集数值计算、符号预算、可视化建模、仿真和图形处理等多种功能于一体的优秀图形化软件。

本文介绍了通过MA TLAB软件编程实现用衍射积分和傅立叶变换实现夫琅和费衍射计算机模拟的方法。

计算机模拟为衍射实验的验证提供一条简捷、直观的途径。

从而加深了对物理原理、概念和图像的理解。

正文：大学教学课程中引入计算机模拟技术正日益受到重视，与Basic、C和Fortran相比，用MA TLAB软件做光学试验的模拟，只需要用数学方式表达和描述，省去了大量繁琐的编程过程。

下面来介绍利用MATLAB进行光学模拟的两种方法。

（一）衍射积分方法：该方法首先是由衍射积分算出接收屏上的光强分布，然后根据该分布调制色彩作图，从而得到衍射图案。

1．单缝衍射。

把单缝看作是np个分立的相干光源，屏幕上任意一点复振幅为np个光源照射结果的合成，对每个光源，光程差Δ=ypsinΦ,sinΦ=ys/D,光强I=I0(Σcosα)2+(Σsinα)2，其中α=2Δ/λ=πypys/λD编写程序如下，得到图1lam=500e-9;a=1e-3;D=1;ym=3*lam*D/a;ny=51;ys=linspace(-ym,ym,ny);np=51;yp=linspace(0,a,np);for i=1:nysinphi=ys(i)/D;alpha=2*pi*yp*sinphi/lam;图1 单缝衍射的光强分布 sumcos=sum(cos(alpha));sumsin=sum(sin(alpha));B(i,:)=(sumcos^2+sumsin^2)/np^2;endN=255;Br=(B/max(B))*N;subplot(1,2,1) image(ym,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys); 2． 杨氏双缝干涉两相干光源到接收屏上P 点距离r 1=(D 2+(y-a/2)2)1/2, r 2=(D 2+(y+a/2)2)1/2,相位差Φ=2π（r 2-r 1）/λ,光强I=4I 0cos 2（Φ/2） 编写程序如下，得到图2 clear lam=500e-9 a=2e-3;D=1;ym=5*lam*D/a;xs=ym;n=101;ys=linspace(-ym,ym,n); for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2); r2=sqrt((ys(i)+a/2).^2+D^2); phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2); end N=255;Br=(B/4.0)*Nsubplot(1,2,1) image(xs,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys) 3． 光栅衍射公式：I=I 0（sin α/α）2（sin(λβ)/sin β）2α=(πa/λ)sin Φ β=(πd/λ)sin Φ编写程序如下：得到图3clearlam=500e-9;N=2; a=2e-4;D=5;d=5*a; ym=2*lam*D/a;xs=ym; n=1001;ys=linspace(-ym,ym,n); for i=1:nsinphi=ys(i)/D;alpha=pi*a*sinphi/lam; beta=pi*d*sinphi/lam;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);图2 杨氏双缝干涉的光强分布 图3 黑白光栅衍射光强分布end NC=255;Br=(B/max(B))*NC; subplot(1,2,1) image(xs,ys,Br); colormap(gray(NC)); subplot(1,2,2) plot(B1,ys);（二）傅立叶变换方法：在傅立叶变换光学中我们知道夫琅和费衍射场的强度分布就等于屏函数的功率谱。

光学实验实验报告课程名称：光学实验姓名：伍金霄学院：电子工程学院系部：光电子技术系专业：电子科学与技术年级：科技1201学号：指导教师：刘娟2014年12 月24 日光波在介质中界面上的反射及透射特性一．实验目的：1．掌握反射系数及透射系数的概念；2．掌握反射光与透射光振幅和相位的变化规律； 3．掌握布儒斯特角和全反射临界角的概念。

二．实验原理：1 反射定律和折射定律光由一种介质入射到另一种介质时，在界面上将产生反射和折射。

现假设二介质为均匀、透明、各向同性介质，分界面为无穷大的平面，入射、反射和折射光均为平面光波，其电场表示式为)(0r k t i l l l l e E E ⋅--=ω l =i, r, t式中，脚标i 、r 、t 分别代表入射光、反射光和折射光；r 是界面上任意点的矢径，在图2-1所示的坐标情况下，有r=ix+jy图2-1 平面光波在界面上的反射和折射 图2-2 k i 、k r 、k t 三波矢关系根据电磁场的边界条件，可以得到如下关系)(0)(t i r i tr i =⋅-=⋅-==r k k r k k ωωω 这些关系表明：①入射光、反射光和折射光具有相同的频率；②入射光、反射光和折射光均在入射面内，k i 、k r 和k t 波矢关系如图2-2所示。

进一步可得tt i i r r i i sin sin sin sin θθθθk k k k == 或tt i i r r i i sin sin sin sin θθθθn n n n ==即介质界面上的反射定律和折射定律，它们给出了反射光、折射光的方向。

折射定律又称为斯涅耳(Snell)定律。

2 菲涅耳公式 s 分量和p 分量通常把垂直于入射面振动的分量称做s 分量，把平行于入射面振动的分量称做p 分量。

为讨论方便起见，规定s 分量和p 分量的正方向如图2-3所示。

图2-3 s 分量和p 分量的正方向反射系数和透射系数 假设介质中的电场矢量为)(i 0e r k t l l l E E ⋅--=ω l =i, r, t其s 分量和p 分量表示式为)(i 0e r k t lm lm l E E ⋅--=ω m =s,p则定义s 分量、p 分量的反射系数、透射系数分别为tmtm m im rmm E E t E E r 0000==菲涅耳公式假设界面上的入射光、反射光和折射光同相位，根据电磁场的边界条件及s 分量、p 分量的正方向规定，可得ts rs s E E E i =+和2tp 1rp 1ip cos cos cos θθθH H H =-利用E H εμ=，上式变为22ts 11rs is cos cos )(θθn E n E E =-再利用折射定律，消去E ts ，经整理可得)sin()sin(1212is rs θθθθ+-=E E 根据反射系数定义，得到)sin()sin(2121θθθθ+--=s r221111cos cos cos 2θθθn n n t s +=将所得到的表示式写成一个方程组，就是著名的菲涅耳公式：212122112*********tan tan tan tan cos cos cos cos )sin()sin(θθθθθθθθθθθθ+--=+-=+--==n n n n E E r is rs s 2121211221122121002sin 2sin 2sin 2sin cos cos cos cos )tan()tan(θθθθθθθθθθθθ+-=+-=+-==n n n n E E r iprp p 21121121112100221111212100cos cos cos 2)cos()sin(sin cos 2cos cos cos 2)sin(sin cos 2θθθθθθθθθθθθθθθθn n n E E t n n n E E t iptp p is ts s +=-+==+=+==这些系数首先是由菲涅耳用弹性波理论得到的，所以又叫做菲涅耳系数。

光学仿真实验一．前言此次光学仿真实验，是基于matlab来进行的。

在这仿真的一系列过程中，对于光学现象出现的条件，以及干涉、衍射是光波叠加的本质都有了更深的认识。

还从中学习了matlab这一利器的知识，这两三个星期的学习是极其值得的。

二．正文1.杨氏双孔干涉学习的开端是从双孔干涉开始，在极其理想的情况下进行仿真，即忽略了孔的大小等影响因素，直接认为是俩球面波进行叠加干涉。

代码如下：clear;l=521*10.^(-9); %波长d=0.05; %俩孔的距离D=1; %孔到光屏的距离A1=1; %复振幅强度A2=1;x=linspace(-0.0001,0.0001,1000);y=linspace(-0.0001,0.0001,1000);[x,y]=meshgrid(x,y);r1=sqrt((x-d/2).^2+y.^2+D^2);r2=sqrt((x+d/2).^2+y.^2+D^2);E1=A1./r1.*exp(1i*r1*2*pi/l);E2=A2./r2.*exp(1i*r2*2*pi/l);E=E1+E2;I= abs(E).^2;pcolor(x,y,I);shading flat;colormap (gray);认为球面波位置在（d/2,0）和（-d/2,0）处，对于在光屏上任意（x,y）点计算距离，计算出每个球面波到其的复振幅，叠加求光强I。

所得图像：这是光屏很小的情况下正中心出条纹，近似于平行线。

现在来看一下大光屏下的条纹，即x，y最大都是0.1，黑白、彩色是这样的：复杂许多，与下文双缝对比明显！立体大屏下的图像为：现在讨论改变条件引起小屏条纹的变化趋势：ⅰ.波长变小为100nm，条纹变细，符合随波长增大，干涉条纹变粗，波长变小，干涉条纹变细的规律。

dⅱ.俩孔间距变大为0.1m，干涉条纹变细，符合孔间距与条纹宽度成反比的规律。

ⅲ.孔到光屏距离变大为2m，干涉条纹变粗，符合D与干涉条纹宽度成正比的规律。