当前位置：文档之家 › 第8章因子分析与聚类分析含SPSS ppt课件

第8章因子分析与聚类分析含SPSS ppt课件

  • 格式：ppt
  • 大小：2.07 MB
  • 文档页数：57

下载文档原格式

  / 57

合集下载

SPSS课件第八章 聚类分析与判别分析

SPSS课件第八章 聚类分析与判别分析
根据分类对象的不同分为样品聚类(Q聚类) 和变量聚类（R聚类）。
编辑课件ppt
3
（一）样品聚类
样品聚类在统计学中又称为Q型聚类。用 SPSS的术语来说就是对事件(Cases)进行 聚类，或是说对观测量进行聚类。是根据 被观测的对象的各种特征，即反映被观测 对象的特征的各变量值进行分类。
编辑课件ppt
Specified range of clusters 某一指定范围的冰状图
None 不显示冰状图
Orientation冰状图的方位编辑课件ppt
25
Method（确定聚类方法）
Between-group linkage：组间 连接
Winthin-group linkage：组内连 接法
编辑课件ppt
22
Cluster Variable:要进行变量聚类 Case:要进行观测量聚类 Display Statisyics显示统计量 Plot显示树状图或冰柱图
编辑课件ppt
23
statistics
Agglomeration schedule 凝聚顺序表；
Proximity maxtrix输出距 离矩阵
编辑课件ppt
16
（2）标准化
如果参与聚类的变量的量纲不同会导致错 误的聚类结果。因此在聚类过程进行之前 必须对变量值进行标准化，即消除量纲的 影响。如果参与聚类的变量纲相同，可以 使用系统默认值None，要求SPSS对数据 不要进行标准化处理。
编辑课件ppt
17
（3）树形图
树形图表明每一步中被合并的类及其系数 值，把各类之间的距离转换成1~25之间 的数值。
聚类的方法有多种，除了前面介绍的快速 聚类法外，最常用的是分层聚类法。根据 聚类过程不同又分为凝聚法和分解法。

spss第8章主成分分析与因子分析

spss第8章主成分分析与因子分析
意的 i, j (1 ≤ i ≤ m,1 ≤ j ≤ n) , Cov(xi , x j ) 都存在，则称矩阵
, yn ) 是 n 维随机向量. 若对任
⎛ Cov(x1, y1) Cov(x1, y2 )
⎜ ⎜
Cov(
x2
,
y1
)
Cov(x2 , y2 )
⎜
⎜ ⎝ Cov(xm , y1) Cov( xm , y2 )
⎟ ⎟
⎟
xpn ⎟⎟⎠
(σ ij ) p× p
， F = AX
Cov(F) = Cov(AX, AX) = ACov(X)A′ V (F)
由于 Cov(X) 是非负定对称矩阵，所以存在正交矩阵 U ，使得
⎡λ1 0
0⎤
U−1Cov(X)U
=
⎢ ⎢ ⎢
0
λ2
0
⎥ ⎥
⎥
⎢ ⎣
0
0
λ
p
⎥ ⎦
其中 λ1, λ2, ,λp 为 Cov(X) 的特征根，不妨假设 λ1 ≥ λ2 ≥
（5）若 X 是随机向量， Cov(X) 存在，则 Cov(X) 是非负定矩阵.
后面的推导过程中用到两个线性代数中的 2 个重要结论. 定理 7-2 （1）若 A 是 p 阶实对称阵，则一定可以找到正交阵 U ，使
⎡λ1 0
0⎤
U−1AU
=
⎢ ⎢ ⎢
0
λ2
0
⎥ ⎥
⎥
⎢ ⎣
0
0
λp
⎥ ⎦
其中 λi ,i = 1.2. p 是 A 的特征根.
（3）对任何向量 a = (a1, a2 , , am )′ ， b = (b1,b2 , , bn )′ ，有 Cov(a′X, b′Y) = a′Cov(X, Y)b . （4）对任何 p × m 阶矩阵 A ， q × n 阶矩阵 B ，有 Cov(AX, BY) = ACov(X, Y)B′

第章 因子分析与聚类分析含SPSSppt课件

第章 因子分析与聚类分析含SPSSppt课件

6Leabharlann ❖ 3、变量共同度i ❖ 因子载荷矩阵中第 行元素的平方和，称为变量 xi 的共
同度，即变量方差。此值越接近1，表明该变量的几乎全部 原始信息都被所选择的公共因子说明了。此值接近于0，说 明公共因子对xi 的影响很小，主要由特殊因子来描述。
❖ 4、因子的方差贡献
❖ 因子f j 的方差贡献是因子载荷矩阵A 中第j 列元素的平
方和，反映了因子f j 对原有变量总方差的解释能力，是衡量 公共因子相对重要性的指标。此值越大，表明相应因子的重
要性越高。计算出所有的指标，按其大小排序，就可以提炼
出最有影响的公共因子。 精选课件ppt
7
❖ 三、因子分析的步骤
❖ （一）因子分析的适合性检验
❖ 1、相关矩阵和反映像相关矩阵
❖ 相关矩阵中大部分相关系数都小于0.3，那么原则上这些 数据不适合做因子分析。另外，如果反映像相关矩阵中除
❖ 在会计实证研究中，因子分析发挥着重要的 作用，如变量构造、变量筛选和综合评价等。
精选课件ppt
3
❖ （二）因子分析的特点 ❖ 1、因子变量的数量远少于原有指标变量的
数量。 ❖ 2、因子变量并不是原有变量的简单取舍，
而是对原有变量的重新组构。 ❖ 3、因子之间线性关系不显著。 ❖ 4、因子变量具有命名解释性。
❖ SPSS中有5种因子旋转的方式可供选择：Varimax选项，
方差最大旋转；Direct Oblimin 选项，直接斜交旋转；
Quartimax 选项，四次最大正交旋转；Equamax 选项，平
均正交旋转；Promax 选精项选课，件斜ppt 交旋转方法。
11
❖ （四）计算因子得分，然后将它们用于各种进一步的分析中

聚类分析对应分析因子分析主成分分析spss操作入门课件

聚类分析对应分析因子分析主成分分析spss操作入门课件

因子分析
主要步骤
前提条件
因子提取
因子命名 可解释性
计算 因子得分
观测变量间有较 强的相关性； 若变量之间无相 关性或相关性较 小的，则不会有 公共因子；
根据因子方差的大 小：只取方差大于1( 或特征值大于1)的那 些因子； 按照因子方差累积 贡献率大于80％的原 则；
坐标变换使每个 原始变量在尽可能 少的因子之间有密 切的关系； 这样因子的实际 意义更容易解释；
聚类分析
聚类主要步骤
选择变量
• 和聚类分析的目的密切相关 ；
• 反映要分类变量的特征； • 不同研究对象上的值有明显
的差异； • 变量之间不能高度相关；
结果的 解释和证实
• 结果的解释是希望对各个类 的特征进行准确的描述；
• 给每类起一个合适的名称； • 通常的做法是计算各类在各
聚类变量上的均值，对均值 进行比较；
中心点偏移情况
最终类成员情况
因子分析
基本介绍： 一种数据简化的技术； 将原有变量中的信息重叠部分提取并综合成因子，实现减少变量个数的目 的； 提取出来的因子能够反映原来众多变量的主要信息； 原始的变量是可观测的显在变量，而提取因子是不可观测的潜在变量；
基本思想： 把每个研究变量分解为几个影响因素变量； 将每个原始变量分解成两部分因素，一部分是由所有变量共同具有的少数 几个公共因子组成的，另一部分是每个变量独自具有的因素，即特殊因子 ； 因子分析特点：
聚类分析、
对应分析、
因子分析、
主成分分析 spss操作入
门
聚类分析
基本思想：根据所研究的样本或变量在观测数据上表现的不 同亲疏程度，采用不同的聚类方法将亲疏程度较大的样本/ 变量聚合为一类，把另外一些亲疏程度较大的样本/变量聚 合为一类，直到把所有的样本/变量都聚合完毕，形成一个 由小到大的分类系统 。

聚类分析(共8张PPT)

聚类分析(共8张PPT)
第4页，共8页。
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中，形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中，一般可以用三种方式采集数据：二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入（万元） 2
1.5 1
年收入（元） 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位：万元
第6页，共8页。
单位：元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形，由用户指定须聚类的 类数之后，系统采用标准迭代算法进行运算，把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值，加以分类，使类与类间的异质性达到最大，而同一类的几个观察值同质性很高。 ③对数据进行变换处理，（如标准化或规格化）；
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离，就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组，而聚类分析 按照这种方则法是不断将进“行合观并察，直值到个把所体有”的样予品以合为分一组个，大类亦为即止。因子分析时，根据因变量（题项）间关系密切与 四⑦、最常 后用绘两制否种系，聚统类聚将分类变析谱方系量法图予，按以不分同的类分（类标分准为或不几同个的层分类面原因则，子得）出不；同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观，因察子值分析，是加一种以“横分向类合并，”的使方类法，与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法，。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高，度。由测用度户了指研定究须对聚象类的的相类似数性之。后，系统采用标准迭代算法进行运算，把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平：等等横，向都需简要化对研，究聚对象类进分行分析类：。纵向分组

SPSS聚类分析(PPT)

SPSS聚类分析(PPT)

第8章聚类分析在自然与社会科学研究中，存在着大量分类研究的问题，如病虫害种群消长演替规律的研究中，需要从生态系统出发，构造其数量、时间和空间关系的分类模式，以此来研究病虫害的发生规律。

聚类分析就是其分类研究的方法之一。

　聚类分析是根据事物本身的特性研究个体分类的方法。

聚类分析的原则是同一类中的个体有较大的相似性，不同类中的个体差异很大。

　根据分类对象的不同可分为样品聚类和变量聚类。

　１）样品聚类　样品聚类在统计学中又称为Ｑ型聚类。

用ＳＰＳＳ的术语来说就是对事件（Ｃａｓｅｓ）进行聚类，或是说对观测量进行聚类。

是根据被观测的对象的各种特征，即反映被观测对象的特征的各变量值进行分类。

　２）变量聚类　变量聚类在统计学又称为Ｒ型聚类。

反映同一事物特点的变量有很多，我们往往根据所研究的问题选择部分变量对事物的某一方面进行研究。

由于人类对客观事物的认识是有限的，往往难以找出彼此独立的有代表性的变量，而影响对问题的进一步认识和研究。

例如在回归分析中，由于自变量的共线性导致偏回归系数不能真正反映自变量对因变量的影响等。

因此往往先要进行变量聚类，找出彼此独立且有代表性的自变量，而又不丢失大部分信息。

　8.1快速聚类过程（K-Means Cluster ）　调用此过程可完成由用户指定类别数的大样本资料的逐步聚类分析。

所谓逐步聚类分析就是先把被聚对象进行初始分类，然后逐步调整，得到最终分类。

[例子8-1]根据1962年至1988年积累的三化螟有关资料进行聚类分析，研究三化螟种群消长规律。

数据见表8-1，其中发生期是指卵盛孵高峰期（2代以5月31日和3代7月20日为零计算天数），F2-F3为2代至3代的增殖系数，F3-F4为3代至4代的增殖系数。

对幼虫发生量和发生期数据进行快速聚类，分析各年的发生程度。

109表8-1幼虫发生量发生期增殖系数年份第2代第3代第2代第3代F2-F3 F3-F4 1962 344 3333 29 9 9.69 1.911963 121 1497 27 19 12.37 1.341964 187 1813 32 18 9.70 1.061965 500 4000 34 14 8.00 1.821966 441 3750 36 14 8.50 1.871967 404 4600 33 16 11.39 1.521968 328 986 35 18 3.01 1.261969 806 1790 32 15 2.22 2.141970 730 1970 36 20 2.70 2.641971 263 333 29 15 1.27 1.071972 486 600 32 19 1.23 1.471973 248 585 33 20 2.36 1.081974 2100 2700 22 14 1.28 1.331975 333 287 38 19 .86 .701976 90 77 40 24 .86 1.871977 19 25 40 27 1.32 2.881978 230 2525 39 20 10.96 .551979 1392 1041 33 18 .75 4.171980 308 41 31 28 .13 3.341981 415 916 36 18 2.21 1.091982 34 401 38 29 11.79 .991983 267 803 37 26 3.01 .091984 1043 3500 39 26 3.36 .071985 2243 7452 31 20 3.32 .121986 236 599 35 26 2.54 .001987 558 1061 33 24 1.90 .001988 162 2817 34 21 2.64 .008.1.1 操作方法1）数据准备在数据管理窗口，定义变量名：年份、幼虫２、幼虫３、发生期２、发生期３、增殖２３、增殖３４，分别代表年份、第２代幼虫发生量、第３代幼虫发生量、第２代发生期、第３代发生期、Ｆ２－Ｆ３增殖系数、Ｆ３－Ｆ４增殖系数。

spss聚类分析PPT课件


G7
G3
G4
G8
G7
0
G3
3
0
G4
5
2
0
G8
7
4
2
0
30
10/16/2024
（3）在D（1）中最小值是D34＝D48＝2，由于G4与G3合并， 又与G8合并，因此G3、G4、G8合并成一个新类G9，其与其 它类的距离D（2）
G7
G9
G7
0
G9
3
0
31
10/16/2024
（4）最后将G7和G9合并成G10，这时所有的六个样品聚为一 类，其过程终止。 上述聚类的可视化过程如下:
1
2
3
4
5
1
0
8.062 17.804 26.907 30.414
2
8.062 0
25.456 34.655 38.21
3
17.804 25.456 0
9.22 12.806
4
26.907 34.655 9.22 0
3.606
5
30.414 38.21 12.806 3.606 0
26
10/16/2024
系统聚类过程是：假设总共有n个样品（或变量）
第一步:将每个样品（或变量）独自聚成一类，共有 n类；
第二步:根据所确定的样品（或变量）“距离”公式， 把距离较近的两个样品（或变量）聚合为一类，其 它的样品（或变量）仍各自聚为一类，共聚成n 1 类；
第三步:将“距离”最近的两个类进一步聚成一类， 共聚成n 2类；……，以上步骤一直进行下去，最后17 将所有的样品（或变量）全聚成一类。
（1）选择样品距离公式，绝对距离最简单,形成D（0）

聚类分析、对应分析、因子分析、主成分分析spss操作入门PPT文档52页

聚类分析、对应分析、因子 分析、主成分分析spss操
作入门
26、机遇对于有准备的头ห้องสมุดไป่ตู้有特别的 亲和力 。 27、自信是人格的核心。
28、目标的坚定是性格中最必要的力 量泉源 之一， 也是成 功的利 器之一 。没有 它，天 才也会 在矛盾 无定的 迷径中 ，徒劳 无功。- -查士 德斐尔 爵士。 29、困难就是机遇。--温斯顿．丘吉 尔。 30、我奋斗，所以我快乐。--格林斯 潘。
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克

第8章统计实验(因子分析)

实验四 R型因子分析1．实验目的：本实验讨论利用R型因子分析从具有错综复杂关系的变量中，找出数量较少的几个公因子来描述原始的变量，并且尽量减少信息的损失。

通过该实验，能够起到如下的效果：(1) 理解因子分析的作用、思想、数学基础、方法和步骤；(2) 熟悉如何利用因子分析，提出问题、分析问题、解决问题、得出结论；（3）会调用SAS软件实现因子分析的各个步骤，根据计算的结果进行分析，得出正确的结论，解决实际的问题。

2．知识准备：R型因子分析是从具有错综复杂关系的变量中，找出数量较少的几个公因子来描述原始的变量，并且尽量减少信息的损失。

其思想是：找出少量的不相关的若干个随机变量（公因子），））尽最大信息的描述原始众多的关系复杂的变量。

其数学模型有很多，如正交因子模型【1】，因子分析模型L【4】等，它们的数学模型和方法均有不相同。

我们下面采用因子分析模型L 来进行分析。

R型因子分析的步骤大体分为：首先正向化指标；然后计算样本相关阵的特征值、单位特征向量和方差贡献率，根据方差贡献率选取适当数量的初始因子，并得到初始因子载荷阵；再对初始因子进行旋转，选用行及列的元素的绝对值向0、1分化严重的旋转因子载荷阵对应的旋转因子作为最终的公因子；最后利用因子载荷阵求出因子得分函数。

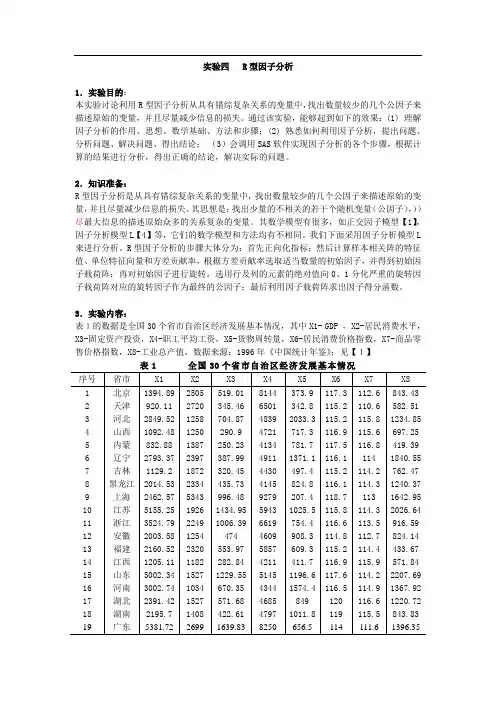
3．实验内容：表１的数据是全国30个省市自治区经济发展基本情况，其中X1- GDP ，X2-居民消费水平，X3-固定资产投资，X4-职工平均工资，X5-货物周转量，X6-居民消费价格指数，X7-商品零售价格指数，X8-工业总产值，数据来源：1996年《中国统计年鉴》；见【１】表1 全国30个省市自治区经济发展基本情况序号省市X1 X2 X3 X4 X5 X6 X7 X81 北京1394.89 2505 519.01 8144 373.9 117.3 112.6 843.432 天津920.11 2720 345.46 6501 342.8 115.2 110.6 582.513 河北2849.52 1258 704.87 4839 2033.3 115.2 115.8 1234.854 山西1092.48 1250 290.9 4721 717.3 116.9 115.6 697.255 内蒙832.88 1387 250.23 4134 781.7 117.5 116.8 419.396 辽宁2793.37 2397 387.99 4911 1371.1 116.1 114 1840.557 吉林1129.2 1872 320.45 4430 497.4 115.2 114.2 762.478 黑龙江2014.53 2334 435.73 4145 824.8 116.1 114.3 1240.379 上海2462.57 5343 996.48 9279 207.4 118.7 113 1642.9510 江苏5155.25 1926 1434.95 5943 1025.5 115.8 114.3 2026.6411 浙江3524.79 2249 1006.39 6619 754.4 116.6 113.5 916.5912 安徽2003.58 1254 474 4609 908.3 114.8 112.7 824.1413 福建2160.52 2320 553.97 5857 609.3 115.2 114.4 433.6714 江西1205.11 1182 282.84 4211 411.7 116.9 115.9 571.8415 山东5002.34 1527 1229.55 5145 1196.6 117.6 114.2 2207.6916 河南3002.74 1034 670.35 4344 1574.4 116.5 114.9 1367.9217 湖北2391.42 1527 571.68 4685 849 120 116.6 1220.7218 湖南2195.7 1408 422.61 4797 1011.8 119 115.5 843.83 19广东5381.7226991639.838250656.5114 111.6 1396.35续表序号省市X1 X2 X3 X4 X5 X6 X7 X820 广西1606.15 1314 382.59 5105 556 118.4 116.4 554.9721 海南364.17 1814 198.35 5340 232.1 113.5 111.3 64.3322 四川3534 1261 822.54 4645 902.3 118.5 117 1431.8123 贵州630.07 942 150.84 4475 301.1 121.4 117.2 324.7224 云南1206.68 1261 334 5149 310.4 121.3 118.1 716.6525 西藏55.98 1110 17.87 7382 4.2 117.3 114.9 5.5726 陕西1000.03 1208 300.27 4396 500.9 119 117 600.9827 甘肃553.35 1007 114.81 5493 507 119.8 116.5 468.7928 青海165.31 1445 47.76 5753 61.6 118 116.3 105.829 宁夏169.75 1355 61.98 5079 121.8 117.1 115.3 114.430 新疆834.57 1469 376.95 5348 339 119.7 116.7 428.76 （1）利用因子分析模型L进行分析，找出适当的公共因子及相应的因子得分函数；（2）利用上面的因子得分函数对样品进行聚类分析，并给出适当的结论。

第8讲 SPSS的因子分析

第8讲 SPSS的因子分析
§8.1 因子分析概述 • 概念：因子分析是研究如何以最少的信息丢失 将众多原有变量浓缩成少数几个因子，如何使 因子具有一定的命名解释性的多元统计分析方 法。 • 数学模型：设原有p个变量x1,…,xp，且每个变 量标准化后均值均为0，标准差均为1。现将每 个原有变量用k(k<p)个因子f1,…,fk的线性组合 来表示，即有：
F ji = ϖ j1 x1i + ϖ j 2 x2i + ϖ j 3 x3i + ... + ϖ jp x pi ( j = 1,2,3,..., k )
11
因子分析的基本步骤
1.菜单选项：analyze->Data Reduction->Factor
2.选择参与因子分析的变量到Variables框 3.Discriptive:分析是否适合做因子分析 4.Extraction：选择构造因子变量的方法。 默认主成分分析法。 Extract框：指定确定因子个数的标准 5.Rotation：择因子载荷矩阵的旋转方法。默认是不 进行旋转。一般可以选择Varimax选项采用方差极 大法旋转
13
§8.2 因子分析的基本操作及案例
操作：Analyze→Data Reduction →Factor 例题8.1:利用t8-1的数据运用因子分析方 法对全国各地区人均收入的差异性和相 似性进行比较和综合评价。
步骤1：检验因子分析的适合性。
14
表8-1 原有变量的相关系数矩阵
Correlation Matrix 国有经 集体经 联营经 股份制经 外商投资 港澳台经 其他经 济单位 济单位 济单位 济单位 经济单位 济单位 济单位 1.000 0.825 0.595 0.773 0.742 0.786 0.574 0.825 1.000 0.716 0.740 0.824 0.849 0.654 0.595 0.716 1.000 0.689 0.598 0.676 0.482 0.773 0.740 0.689 1.000 0.765 0.849 0.571 0.742 0.824 0.598 0.765 1.000 0.898 0.698 0.786 0.849 0.676 0.849 0.898 1.000 0.747 0.574 0.654 0.482 0.571 0.698 0.747 1.000
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

8
❖ 3、变量共同度
i ❖ 因子载荷矩阵中第 行元素的平方和，称为变量 xi 的共
同度，即变量方差。此值越接近1，表明该变量的几乎全部
原始信息都被所选择的公共因子说明了。此值接近于0，说 明公共因子对x i 的影响很小，主要由特殊因子来描述。
❖ 4、因子的方差贡献
❖ 因子f j 的方差贡献是因子载荷矩阵A 中第j 列元素的平
对角元素外，其他大多数元素的绝对值均较小，对角线上
元素的值较接近1，则适合进行因子分析。
❖ 2、KMO 检验
❖ KMO 检验统计量是用于比较变量间简单相关系数和偏
相关系数的指标，取值在0和1之间。值越接近于1，意味
着变量间的相关性越强，原有变量越适合做因子分析。
2020/11/13
10
❖ 3、 巴特利特球度检验（Bartlett test of sphericity ）
❖ 巴特利特球度检验以原有变量的相关系数矩阵为 出发点，其零假设是：相关矩阵为单位阵，即相关
系数矩阵为对角矩阵。巴特利特球度检验的检验统
计量是根据相关系数矩阵的行列式计算得到，且近
似服从卡方分布。如果该统计量的观察值比较大且
相伴概率 值小于或等于给定的显著性水平，则应
拒绝原假设；反之，如果该统计量的观察值比较小
2020/11/13
6
❖ 二、因子分析的数学模型和相关概念
❖ （一）因子分析的数学模型
❖ 因子分析的数学模型为：
x1 a11f1 a12f2 a13f3 a1k fk 1❖x来自32a21f1 a31f1
a22f2 a32f2
a23f3 a33f3
a2k a3k
fk fk
2 3
（8.1）
xp ap1 f1 ap2 f2 ap3 f3 apk fk p
且相伴概率值大于给定的显著性水平，则不应拒绝
原假设。 2020/11/13
11
❖ （二）因子提取和因子载荷矩阵的求解
❖ 因子分析的关键是根据样本数据求解因子载荷矩阵， SPSS提供了7种提取因子的方法，其中占主要地位且使用 最为广泛的是主成分分析法。
❖ 因子提取通常有以下三种方法：（1）特征值准则，即取
❖ 写成矩阵形式为XAF ，其中X 为原始变量向量A，
为公因子载荷矩阵，F 为公共因子， 为特殊因子。
2020/11/13
7
❖ （二）因子分析中的基本概念
❖ 1、因子的含义
❖ 因子分析法中提到两种因子：公共因子和特殊因子。
❖ 公共因子是每个原有变量的线性表达式中都共同出现的因 子，各公因子都是均值为0，方差为1的独立正态随机变量。 其协方差矩阵为单位矩阵。
❖ 特殊因子表示原有变量不能被公共因子解释的部分，其均 值为0。
❖ 各特殊因子之间以及特殊因子与所有公共因子之间都是互 相独立的。
❖ 2、因子载荷
❖ 模型中各公共因子的系数 a ij 称为因子载荷，反映了第 i
个变量在j 第 个公共因子上的相对重要性aij ， 1 a ij ， 的绝
2020对/11/值13 越大，表x i明 F j 与 的相依程度越大。
• “太阳当空照，花儿对我笑，小鸟说早早早……”
第一节 因子分析
❖ 一、因子分析的概念和特点 ❖ （一）因子分析的概念 ❖ 因子分析（factor analysis）是利用降维的思
想，由研究原始变量相关矩阵内部的依赖关系出 发，把一些具有错综复杂关系的变量归结为少数 几个综合因子的一种多变量统计分析方法。
大因子数。
2020/11/13
12
❖ （三）因子命名
❖ 在因子分析模型中，公共因子与因子载荷阵的解不是唯 一的。因子分析的目的不仅是找出主因子，更重要的是知道 每个主因子的意义，以利于对公共因子命名和解释结果，便 于进一步的分析。若每个公共因子的涵义不清，难以找到合 理的解释，可对因子载荷矩阵实行旋转，使每个变量仅在一 个公共因子上有较大的载荷，而在其他公共因子上的载荷较 小。
❖ SPSS中有5种因子旋转的方式可供选择：Varimax选项，
方差最大旋转；Direct Oblimin 选项，直接斜交旋转；
Quartimax 选项，四次最大正交旋转；Equamax 选项，平
2020/均11/1正3 交旋转；Promax 选项，斜交旋转方法。
13
❖ （四）计算因子得分，然后将它们用于各种进一步的分析中
❖ 当因子确定以后，便可以计算各因子在每个样本上的具 体数值，这些数值称为因子得分，形成的变量称为因子变量。 于是在以后的分析中就可以因子变量代替原有变量进行数据 建模，或者利用因子变量对样本进行分类或评价等研究，进 而实现降维和简化问题的目标。
特征值大于等于1的主成分作为初始因子，放弃特征值小于
1的主成分。（2）累积方差贡献率，因子累积解释的方差
比例也是确定因子个数时可以参考的指标，一般应达到
70%-85%或以上。（3）碎石检验准则，按照因子被提取
的顺序，画出因子的特征值随因子个数变化的散点图，图
形由陡变平，曲线开始变平的前一个点被认为是提取的最
❖ 在会计实证研究中，因子分析发挥着重要的 作用，如变量构造、变量筛选和综合评价等。
2020/11/13
5
❖ （二）因子分析的特点 ❖ 1、因子变量的数量远少于原有指标变量的
数量。 ❖ 2、因子变量并不是原有变量的简单取舍，
而是对原有变量的重新组构。 ❖ 3、因子之间线性关系不显著。 ❖ 4、因子变量具有命名解释性。
方和，反映了因子f j 对原有变量总方差的解释能力，是衡量 公共因子相对重要性的指标。此值越大，表明相应因子的重
要性越高。计算出所有的指标，按其大小排序，就可以提炼
202出0/11最/13 有影响的公共因子。
9
❖ 三、因子分析的步骤
❖ （一）因子分析的适合性检验
❖ 1、相关矩阵和反映像相关矩阵
❖ 相关矩阵中大部分相关系数都小于0.3，那么原则上这些 数据不适合做因子分析。另外，如果反映像相关矩阵中除
2020/11/13
第八章 因子分析与聚类分析
1
本章内容
❖ 第一节 因子分析 ❖ 第二节 聚类分析
2020/11/13
2
精品资料
• 你怎么称呼老师？
• 如果老师最后没有总结一节课的重点的难点，你 是否会认为老师的教学方法需要改进？
• 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭
• “不怕太阳晒，也不怕那风雨狂，只怕先生骂我 笨，没有学问无颜见爹娘 ……”