当前位置：文档之家 › 空间曲面图例

空间曲面图例

  • 格式：ppt
  • 大小：1.26 MB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

空间曲面和曲线.ppt

空间曲面和曲线.ppt

o
y
d x2 y2 | y1 | x
将 z z1, y1 x2 y2 代入 f ( y1, z1 ) 0
得:
f x2 y2 , z 0,
北京理工大学数学系
f x2 y2 , z 0,
yoz坐标面上的已知曲线 f ( y, z) 0 绕 z 轴旋转一周的旋转曲面的方程.

1
球 面
（3）抛物线

y2

2
pz 绕 z 轴；
x 0
x2 y2 2 pz 旋转抛物面
北京理工大学数学系
四.椭圆锥面
设C是椭圆，P为C外的定点，
过P和C上的每一点作直线， 所有这些直线形成的曲面
称为椭圆锥面。
所有直线称为母线， C称为准线， P称为顶点。
?与圆锥面的区别?
C P
3
3 9
北京理工大学数学系
例 3 已知 A(1,2,3)，B(2,1,4)， 求线段 AB的垂直平分面的方程.
解 设M( x, y, z)是所求平面上任一点， 根据题意有 | MA || MB |,
x 12 y 22 z 32
x 22 y 12 z 42 ,
北京理工大学数学系
五、空间曲线在坐标面上的投影
设空间曲线的一般方程：GF((xx,,
y, z) y, z)

0 0
消去变量z后得： H ( x, y) 0
曲线关于xoy 的投影柱面
投影柱面的特征：
以此空间曲线为准线，垂直于所投影的坐标面.
北京理工大学数学系
如图:投影曲线的研究过程.
北京理工大学数学系

高等数学常用二次曲面图形.ppt

高等数学常用二次曲面图形.ppt

围成的图形如下：
y 0,
y2
12024/9/27
图30：由 z x2 y2 , z x2 y2 围成的图形如下：
z x2 y2 , z x2 y2
22024/9/27
图31：由 z x2 y2 , x2 y2 1, z 0
围成的图形：
图32： 32024/9/27
图14：函数 函
z
1 ey
cos x yey
有无穷多个
极大值，但无极小值。
z 1 ey cos x yey
图15： 62024/9/27
抛物面 z x2 y2 被平面 x y z 1
截成一椭圆。
图16： 72024/9/27
椭球面
x2 a2
y2 b2
z2 c2
1 在
点
3 a, 3
x2 y2 2x
02024/9/27
图39：由曲面 z x2 y2 和平面
z 0, x 1, y 1 围成图形如下：
z 0, x 1, y 1
12024/9/27
图40：双曲抛物面 z xy 被柱面 x2 y2 1
所截得的图形如下：
x2 y2 1
图41： 22024/9/27
62024/9/27
图1（2）：x2 y2 z2 4, x2 y2 2x
的图形在第一卦限部分如下：
x2 y2 z2 4, x2 y2 2x
图2： 72024/9/27
（2）、曲线
xyz 1
y
21
处的切线
图3： 82024/9/27
（3） 曲线
2x2 y2 z2 16
图46：曲线 x2 y2 z2 1 y z 0
的图形如下：

3 曲面及空间曲线

3 曲面及空间曲线

G( x, y, z ) 0 L F ( x, y, z ) 0
S2
S1
例如,方程组
z
2
C
表示圆柱面与平面的交线 C.
o
1 y
x
又如,方程组
z
表示上半球面与圆柱面的交线C.
ay x
2、空间曲线的参数方程
将曲线C上的动点坐标x, y, z表示成参数t 的函数:
z
称它为空间曲线的 参数方程.
x z 2 1 2 a c b y y1
2 2
z
x
y
y12 2
z
0
(实轴平行于z 轴; 虚轴平行于x 轴）
x
y
(2) 双叶双曲面
z
x2 y2 z 2 2 2 1 ( a, b, c 为正数 ) 2 a b c 平面 y y1 上的截痕为 双曲线
平面 x x1 上的截痕为 双曲线
求上半球面 和锥面
所围的立体在 xoy 面上的投影（区域）:
二者交线
z
在 xoy 面上的投影曲线 所围圆域: x y 1, z 0 .
2 2
C
x
o
1
y

例如,圆柱螺旋线 的参数方程为
M
令 t , b
v
x
o
y

上升高度 h 2 b , 称为螺距 .
例1. 将下列曲线化为参数方程表示:
解: (1) 根据第一方程引入参数 , 得所求为
(2) 将第二方程变形为
故所求为
3、空间曲线在坐标面上的投影
设空间曲线 C 的一般方程为
消去 z 得投影柱面
平面 z z1 ( z1 c)上的截痕为 椭圆

空间曲面图例资料

空间曲面图例资料

z
1y
直线
x 1
y2
oo
2y
1
x
z 4 x2 y2
半圆线
yx0
z
o
2y
x
z
垂直圆柱面的交线 x2 z2 a2
a
x2 y2 a2
oa
y
x
直线 y 5x 1 y x3
z
y 5x 1
y x3 o
y
圆柱面与平面的交线
x2 y2 1 49 y3
Co
M1
y
x
l
z
椭圆柱面
x2 a2

y2 b2
1
x
o y
平面 x y 0
z
o y
x
椭圆柱面
x2 a2

y2 b2
1
z
o
a
by
x
z
准线平行于z轴的柱面 F(x, y) 0 准线平行于x轴的柱面G(y, z) 0 准线平行于y轴的柱面 H(z, x) 0
x l1
y z l2
y
x z l3
x
y
椭球面
x2 a2

y2 b2

z2 c2
1
( a,b, c为正数)
椭圆抛物面
x2 y2 z ( p , q 同号) 2p 2q
双曲抛物面（鞍形曲面）
x2 y2 z 2p 2q
( p , q 同号)
z
y x
z
x
y
单叶双曲面
x2 a2

y2 b2

z2 c2
o yy
xx
内容小结

空间解析几何-第3章 常见的曲面1

空间解析几何-第3章 常见的曲面1

o
x
2017/1/4
§3.2
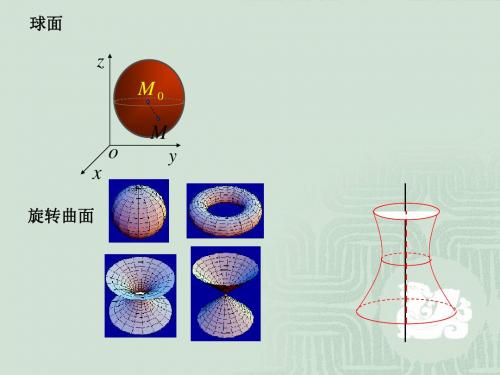
锥面
定义3.2.1 通过一定点且与一不过定点的定 曲线相交的一族直线所产生的曲面叫做锥面. 这些直线都叫做锥面的母线. 那个定点叫做锥面的顶点. 锥面的方程是一个三元方程.
特别当顶点在坐标原点时：
若 F (tx, ty, tz ) t n F ( x, y, z ). 方程 F(x,y,z)= 0是 n次齐次方程：
n次齐次方程 F(x,y,z)= 0 的图形是以原点为顶点的锥面；
反之，以原 点为顶点的锥面 的方程是n次齐次 方程 F(x,y,z)= 0.
锥面是直纹面 锥面的准线不 唯一，和一切母线 都相交的每一条曲 线都可以作为它的 准线.
顶点 x
z
准线
0
y
如何建立锥面方程
1 锥面的一般方程 准线
F1 x, y, z 0 F2 x, y, z 0
取准线上任意一点 M1 x1, y1, z1
例1 锥面的顶点在原点，且准线为 求锥面的方程
x2 y2 l1 : a 2 b 2 1 z c
，
解：任取P （ l1 , 则有 1 x1，y1，z1） x1 y1 2 1(1) 2 a b z1 c(2) x y z 1 母线方程 x1 y1 z1 t 令x1 t x , y1 t y , z1 tz , 代入(1)(2)，联立方程消去 t得 x2 y2 z2 2 2 2 a b c
， 顶点 A x0 , y0 , z0 ，
F x , y , z 0 1 1 1 1 F x, y , z 0 ， F2 x1 , y1 , z1 0 xx y y0 z z0 0 x1 x0 y1 y0 z1 z0

工科基础数学74空间曲面与曲线 PPT资料共40页

工科基础数学74空间曲面与曲线 PPT资料共40页
定曲线C叫做柱 面的准线
动直线L叫做柱面 的母线
2、柱面
定义 直线L平行于定直线并沿定曲线C移动所 形成的曲面叫做柱面
定曲线C叫做柱 面的准线
动直线L叫做柱面 的母线
例3 求准线为 x o y 面上的圆
z
母线平行于 z 轴的圆柱面方程
M
在空间内 x2y2R2 表示圆柱面
Co
M1
y
在平面内 x2y2R2 表示圆
x
在空间怎样表示 x o y 面上的圆呢？
l
说明 注意比较同一方程在平面直角坐标系 与空间直角坐标系中对应图形的不同
如 x 2 在数轴上表示一个点，
在平面直角坐标系中表示一条直线， 而在空间直角坐标系中表示一个平面
z
表示抛物柱面,
o
x
x2 a2

y2 b2

1
表示椭圆柱面.
y
z
o y
xy0 表示平面
我们只讨论母线在坐标 面上，绕某坐标轴旋转 所得的旋转曲面
3、旋转曲面
一条平面曲线C绕同一 平面上的一条定直线L 旋转一周所形成的曲面 叫做旋转曲面，平面曲 线C和定直线L依次叫做 旋转曲面的母线和轴．
我们只讨论母线在坐标 面上，绕某坐标轴旋转 所得的旋转曲面
3、旋转曲面
一条平面曲线C绕同一 平面上的一条定直线L 旋转一周所形成的曲面 叫做旋转曲面，平面曲 线C和定直线L依次叫做 旋转曲面的母线和轴．
我们只讨论母线在坐标 面上，绕某坐标轴旋转 所得的旋转曲面
3、旋转曲面
一条平面曲线C绕同一 平面上的一条定直线L 旋转一周所形成的曲面 叫做旋转曲面，平面曲 线C和定直线L依次叫做 旋转曲面的母线和轴．
我们只讨论母线在坐标 面上，绕某坐标轴旋转 所得的旋转曲面

《ch空间曲面》课件


曲面上的点与向量
总结词
理解曲面上点的坐标表示，掌握向量在曲面上的投影和切线 向量
详细描述
在曲面上，点的坐标可以通过参数方程表示，即通过两个参 数t和s来确定。向量在曲面上的投影和切线向量是曲面的重 要几何属性，它们分别表示了向量在曲面上的方向和变化趋 势。
曲面的度量性质
总结词
理解曲面的长度、面积和体积等度量性质，掌握曲面的曲率、挠率和渐近线等几 何属性
参数方程的优点
参数方程可以方便地描述曲面的形状和位置，并且可以通过改变参 数的值来观察曲面形态的变化。
参数方程的应用
参数方程广泛应用于几何建模、计算机图形学等领域。
直角坐标方程表示
1 2
直角坐标方程
空间曲面可以用直角坐标方程表示，其中x、y、 z分别表示曲面上点的坐标。
直角坐标方程的优点
直角坐标方程简单明了，易于理解和计算。
曲面在一点邻域的性质
局部展开
切平面与切线
在曲面上任取一点，可以找到一个局部坐 标系，使得曲面在该点的邻域内可以展开 为一个平面或超平面。
在曲面上任取一点，可以找到一个切平面 ，该平面与通过该点的所有切线组成。
法线
切平面的垂线被称为法线。
总结
曲面在一点邻域的性质是描述曲面局部几 何特征的基础知识，它们在微分几何、计 算几何和几何建模等领域有广泛应用。
极坐标方程广泛应用于 几何建模、物理等领域 。
05
CATALOGUE
空间曲面的性质与定理
主方向与主曲率
主方向
在曲面上任取一点，可以找到两个互 相垂直的切线方向，这两个方向称为 该点处的主方向。
主曲率
总结
主方向和主曲率是描述曲面局部形状 的重要参数，它们在曲面分析、几何 建模和计算几何等领域有广泛应用。

741-3空间曲面和空间曲线11


例
4．方程组
x2

y
2
1 (
x

0
,
y0, z0
)
z
z2 x2 1
表示两个圆柱的交线 L 在 第一卦限的部分。
此曲线亦可用方程组

x2

y
2
1
(
x

0
,
y0, z0
)表示。
o
y
y z 0
x
例
7．方程组
x2

y2

4
表示在z
1
平面上的圆。
z 1
ay(a
0) 绕
z
轴旋转一周所成的曲面方程。
x 0
例
9．求抛物线
y 2

2 pz( p

0) ，
x 0
绕 z 轴旋转所得的旋转曲面的方程。
例
10．求椭圆

y a
2 2

z2 b2
1绕 z
轴旋转一周
x 0.
所成的旋转曲面的方程。
例
11．求直线
z
上的点M1 ( X ,Y , Z ) 的母线方程为
z
x x y y z z ， X x Y y Z z 其中点 M (x, y, z) 是母线上的任意一点。
M1 M
当点 M1( X ,Y , Z ) 在曲线 C 上移动时，
M
o
y
点 M (x, y, z) 就是锥面上的点。
0
，将曲线
L绕
z
轴
旋转
一周，得到一个旋转曲面。
o

第六节 曲面与曲线(xrc)


z z(t)
当给定t t1 时，就得到曲线上的一个点 ( x1 , y1 , z1 )，随着参数的变化可得到曲线上的全
部点.
例 4 如果空间一点 M 在圆柱面 x2+y2=a2 上
以角速度 绕 z 轴旋转，同时又以线速度 v 沿平行于 z 轴的正方向上升（其中、v 都
是常数），那么点 M 构成的图形叫做螺旋 线．试建立其参数方程．
交线为椭圆.
z a2 x2 y2
例2
方程组 ( x

a )2 2

y2

a2 4
表示怎样的曲线？
解 z a2 x2 y2
上半球面,
( x a )2 y2 a2 圆柱面,
2
4
交线如图.
2、空间曲线的参数方程
x x(t)

y

y(t )
空间曲线的参数方程
螺旋线的重要性质：
b v)

上升的高度与转过的角度成正比．
即 : 0 0 , z : b0 b0 b , 2, 上升的高度 h 2b 螺距
如何将曲线
化为参数方程？
的一般方程：GF((xx,,
y, z) y, z)

0 0
(*)
(1) 先从一般方程(*)中消去某个变量，比如z， 得方程H(x,y)=0，写出该方程在xOy面的参数方程 x=x(t)，y=y(t).再把x=x(t)，y=y(t)代入(*)中的某 个方程解出z=z(t)，最后在确定t的变化区间，就得 到了曲线的参数方程.
x2 5z2 2xz 4x 0

,
y 0
（3）消去x 得投影
y2 z2 2y z

空间解析几何常见的曲面


o
y
代入得x,y轴上的截距为: x ? ? a ，y ? ? b ； x 在z轴上没有截距.
3 图形的范围
x2 a2
?
y2 b2
?
z2 c2
?
1
z
由方程
x2 a2
?
y2 b2
?1
知，即曲面存在于椭圆柱面
x2 a2
?
y2 b2
?1
之外，从而曲面与z轴无交点，
并且在xoy面的上,下半空间延到无穷远.
o
例如当 A ? 0, B ? 0, C ? 0 时，方程（1）可改写为
x2 a2
?
y2 b2
?
z2 c2
?
1,
其中
1 a2
?
1 A, b2
?
?
B,
1 c2
?
C ，这是单叶双曲面的标准方程 .
例 给定方程
x2 ? y2 ? z2 ? 1?A ? B ? C ? 0?,
,从而椭圆焦点坐标为
? ? ?
y
?
0,
a 2 ? b2
? ?1
?
?
h2 c2
? ?, ?
?? z ? h.
? ?
z
?
h.
消去参数
h
得
? ? ?
a
2
x2 ?
b2
? z2 c2
? 1,
??
?? y ? 0.
二、双叶双曲面
x2 a2
?
y2 b2
?
z2 c2
?
?1
双叶双曲面
特别的a=b 时
x2 a2
?
y2 ? b2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ay x
x 2 z 2 a 2 y 0 ( x 0 , z 0)
上半球面
和锥面
C
所围的立体在 xoy 面上的投影区域为: 二者交线在 xoy 面上的投影曲线所围之域 .
o x
1
y
z
直线
x 1 y2
1
o o
2 y
x
z
z 4 x y 半圆线 yx0
2
2
o x
2y
z
垂直圆柱面的交线
x2 z 2 a2
x y a
2 2 2
a
o
a
y
x
直线
y 5x 1 y x3 y x3
y
椭球面
x2 y2 z 2 2 2 1 ( a, b, c 为正数 ) 2 a b c
椭圆抛物面
z
x2 y2 z ( p , q 同号) 2 p 2q
x
双曲抛物面（鞍形曲面）
y
z
x2 y2 z ( p , q 同号) 2p 2q
x
y
单叶双曲面
x2 y2 z 2 2 2 1 ( a, b, c 为正数 ) 2 a b c
y1 b 时, 截痕为双曲线:
z
x z 1 a2 c2 b y y1
2
2
2 y1 2
x
y
(实轴平行于x 轴； 虚轴平行于z 轴）
双叶双曲面
z
x2 y2 z 2 2 2 1 ( a, b, c 为正数 ) 2 a b c
o x
y
z
椭圆锥面
z
x2 y2 2 2 z 2 a b
ay x
z
螺旋线
M
绕Z轴旋转
直线
x
o
y
所得旋转曲面方程为
空间曲线
x2 y2 z 2 1 C: 2 2 2 x ( y 1 ) ( z 1 ) 1
在xoy 面上的投影曲线方程为
z
C
o x
1 y
x 2 2 y 2 2 y 0 z0
z
曲线 C 绕 y 轴旋转所产生曲面的曲面方程
z
C : f ( y, z ) 0
o x
y
f ( y, x z ) 0
2 2Leabharlann 锥面zL
M (0, y, z )
y
x
坐标面 xoz 上的双曲线
轴和 z 轴旋转一周所生成的旋转曲面。
分别绕 x
x
z
y
柱面
圆柱面
z
C
M
C o
M1
y
x
l
z
椭圆柱面
z
y 5x 1
o
y
圆柱面与平面的交线
z
x2 y2 1 4 9 y3
x
2
3
y
上半球面 z a 2 x 2 y 2 ,圆柱面 x 2 y 2 ax , 平面 z 0所 围成空间体在坐标面上 的投影区域。
z
z
ay x
x 2 y 2 ax z0
f ( x y , z ) 0
• 柱面 如,曲面F ( x , y ) 0 表示母线平行 z 轴的柱面. 又如,椭圆柱面, 双曲柱面, 抛物柱面等 .
2
2
2. 二次曲面
• 椭球面 • 抛物面:
三元二次方程
椭圆抛物面
双曲抛物面
x2 y2 z 2 p 2q • 双曲面: 单叶双曲面 双叶双曲面 2 2 x2 y2 x y 2 2 1 1 2 2 a b a b x2 y2 2 • 椭圆锥面: z a2 b2
( a, b 为正数 )
xx
o
yy
内容小结
1. 空间曲面 • 旋转曲面 三元方程 F ( x , y , z ) 0
2 2 2 2 • 球面 ( x x0 ) ( y y0 ) ( z z0 ) R
f ( y, z ) 0 绕 z 轴的旋转曲面: 如, 曲线 x0
( p, q 同号)
y1 b 时, 截痕为相交直线:
z
x z 0 a c y b (或 b)
x
y
y1 b 时, 截痕为双曲线:
y12 x2 z 2 2 1 2 2 a c b y y1
z
0
x
y
(实轴平行于z 轴; 虚轴平行于x 轴）
z
曲线
2
C
o
曲线
x
1 y
z
x2 y2 2 1 2 a b
o x
z
y
平面
x y 0
x
o
y
z
椭圆柱面
x2 y2 2 1 2 a b
x
a
o
b
y
z
准线平行于z轴的柱面 F ( x, y) 0
x
准线平行于x轴的柱面G( y, z) 0
l1
y
zl 2
y
x
z
准线平行于y轴的柱面 H ( z, x) 0
l3
x