薄膜干涉之等厚资料
- 格式:docx
- 大小:162.74 KB
- 文档页数:6




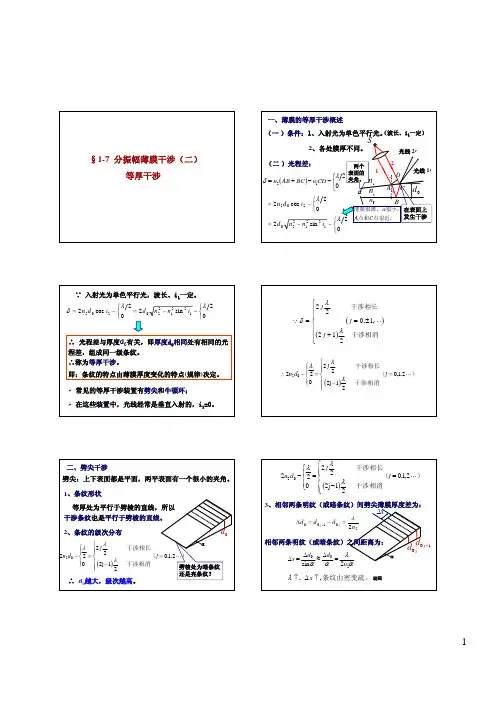
红线对应薄膜厚度相同的位置。
劈角由小变大时,条纹由疏变密,反之亦然三、劈尖的应用(50页 1.10)1、测量细丝直径、微小夹角¾例: 两玻璃片夹一细丝,两片之间形成一个空气薄膜,n 2=1,光垂直入射,i 1≈i 2=0。
∵有额外光程差,∴d 0=0 处为暗条纹。
¾如何测小角度α呢?已知d ,通过测量L ,可计算:α≈d/L 。
αλΔ22n x ≈202n d λΔ=如何求细丝直径d ?=(m-1)λ/2假如一共有m 条,则d =(m-1)Δd 0射,看反射光的干涉条纹。
加热,膨胀,表面上升,条纹有什么变化?待测材料膨胀后,空气膜变薄,如图所示,虚线所需要的光程差值,即该处为一若条纹的最大变形线度为OBA A O 为心的圆,所以条纹是以点为心的一组同心圆,叫做牛顿环。
)(干涉相消⋅⋅⋅=2,1,0j r BA A3、条纹位置此时反射光中看到的O 点是暗点。
¾有额外光程差时,()()⋅⋅⋅=λ+=2,1,0j n R21j 2r 2()⋅⋅⋅=λ=2,1,0j n R2j2r 2条纹位置是由圆形条纹的半径r决定。
亮条纹半径为:暗条纹半径为:¾没有额外光程差时,亮(暗)条纹半径为?此时反射光中看到的O 点是亮点。
4、条纹级次分布、条纹密度条纹级次:内低外高条纹密度:内疏外密条纹向中间收缩,中心条纹被吞没。
条纹向外扩展,中心有条纹冒出。
与等倾条纹的变化情况相反。
透镜上移时:透镜下移时:rBA ′A O5、在透射光中亦可观察到牛顿环。
动画2λ+例题:已知:半径为4cm 的平凸透镜,凸面向下,放在平玻璃板上,透镜和平板的折射率均为1.5,用波长为500nm 的平行光垂直照射,观察反射光的干涉条纹。
求:(1)若透镜边缘恰为暗纹,且共有17条暗纹(若圆心为暗点,也算是一条暗纹),求透镜凸面的曲率半径,和透镜边缘处两反射光的光程差;(2)若透镜向上平移两个波长,干涉条纹如何变化?(如果有额外光程差,要求取。
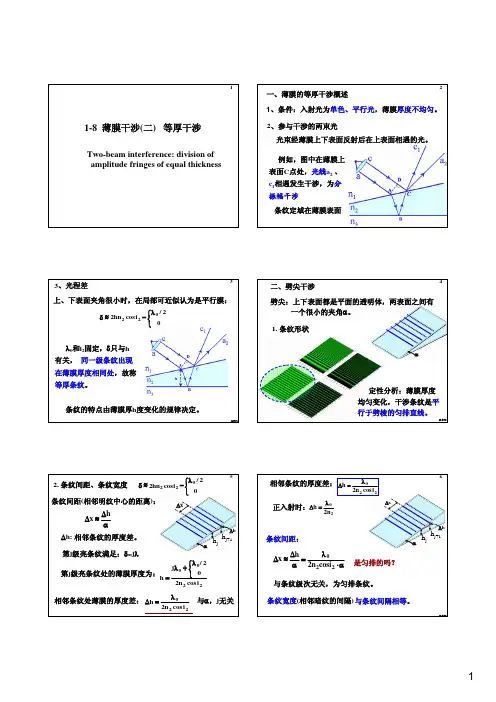


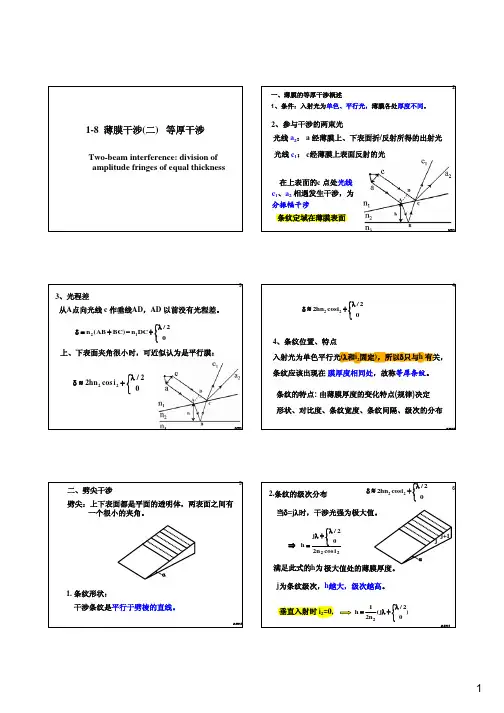
一、薄膜的等厚干涉概述1、条件:入射光为单色、平行光,薄膜各处厚度不同。
光线c 1:c 经薄膜上表面反射的光2、参与干涉的两束光光线a 2:a 经薄膜上、下表面折/反射所得的出射光在上表面的c 点处光线c 1、a 2相遇发生干涉,为分振幅干涉条纹定域在薄膜表面next2⎩⎨⎧λ+−+=δ02/DC n )BC AB (n 1222/22hn cos i 0λ⎧δ≈+⎨⎩3、光程差从A 点向光线c 作垂线AD ,AD 以前没有光程差。
上、下表面夹角很小时,可近似认为是平行膜:next3红线对应膜厚相同的位置。
劈角由小变大时,条纹由疏变密,反之亦然i=0,∆h≈λ/2。
2处为暗条纹。
2、测量微小变化例:干涉膨胀仪平玻璃与被测材料表面之间形成空气劈尖,光垂直照射,看反射光的干涉条纹。
加热,被测材料膨胀,表面上升,条纹有什么变化?next19待测材料膨胀后,空气膜变薄,如图所示,虚线纹局部弯曲,变为:若条纹的最大变形线度为单色平行光垂直入射为圆心的圆,所以条纹是以O 点条纹位置由圆条纹半径决定。
2/⎧λ25条纹向中间收缩,中心条纹被吞没。
10.5mm ,则水的旋转角速度为多少?解:①求旋转水的上表面所应满足的方程取水面最低点O 为坐标原点,y 轴竖直向上,r 沿半径方向。
水以角速度ω旋转时,水表面为一旋转对称曲面,取水表面上某一点P 处质量为dm 的水元。
next 水元共受到两个力的作用,作匀速圆周运动。
29:重力, 竖直向下两个力在竖直方向平衡:d·F n ·cos θ= g·dm 水平方向满足:d·F n ·sin θ=ω2r·dm ∴tan θ= ω2r/g drdyan t =θ∵C r g21y 22+=ω假设水面最低点处水膜厚度为h 0,即:r=0 时,y=h 0∴C=h 022h r g21y +ω=∴为一抛物线,所以水表面为旋转抛物面。
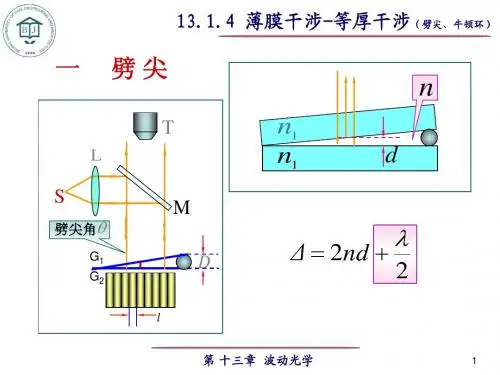
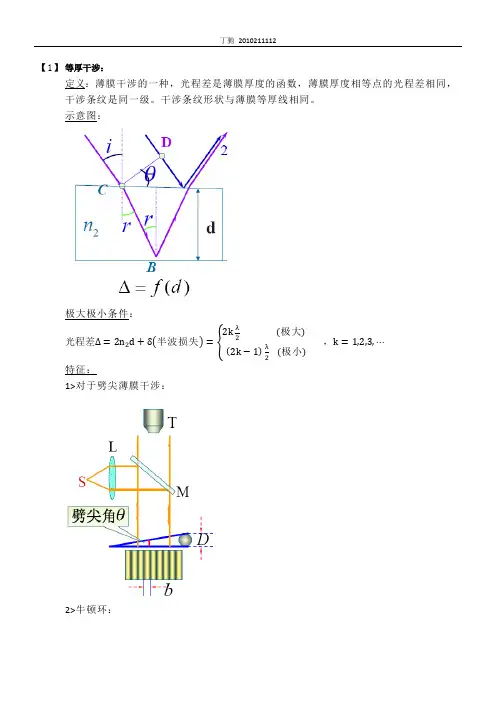
【1】等厚干涉:定义:薄膜干涉的一种,光程差是薄膜厚度的函数,薄膜厚度相等点的光程差相同,干涉条纹是同一级。
干涉条纹形状与薄膜等厚线相同。
示意图:极大极小条件:光程差Δ=2n2d+δ 半波损失=2kλ2(极大)2k−1λ2(极小),k=1,2,3,⋯特征:1>对于劈尖薄膜干涉:2>牛顿环:干涉条纹形状与薄膜等厚线相同。
【2】牛顿环的历史是牛顿在1675年首先观察到的.将一块曲率半径较大的平凸透镜放在一块玻璃平板上,用单色光照射透镜与玻璃板,就可以观察到一些明暗相间的同心圆环.圆环分布是中间疏、边缘密,圆心在接触点O.从反射光看到的牛顿环中心是暗的,从透射光看到的牛顿环中心是明的.若用白光入射.将观察到彩色圆环.牛顿环是典型的等厚薄膜干涉.牛顿环实验是这样的:取来两块玻璃体,一块是14英尺望远镜用的平凸镜,另一块是50英尺左右望远镜用的大型双凸透镜。
在双凸透镜上放上平凸镜,使其平面向下,当把玻璃体互相压紧时,就会在围绕着接触点的周围出现各种颜色,形成色环。
于是这些颜色又在圆环中心相继消失。
在压紧玻璃体时,在别的颜色中心最后现出的颜色,初次出现时看起来像是一个从周边到中心几乎均匀的色环,再压紧玻璃体时,这色环会逐渐变宽,直到新的颜色在其中心现出。
如此继续下去,第三、第四、第五种以及跟着的别种颜色不断在中心现出,并成为包在最内层颜色外面的一组色环,最后一种颜色是黑点。
反之,如果抬起上面的玻璃体,使其离开下面的透镜,色环的直径就会偏小,其周边宽度则增大,直到其颜色陆续到达中心,后来它们的宽度变得相当大,就比以前更容易认出和训别它们的颜色了。
牛顿测量了六个环的半径(在其最亮的部分测量),发现这样一个规律:亮环半径的平方值是一个由奇数所构成的算术级数,即1、3、5、7、9、11,而暗环半径的平方值是由偶数构成的算术级数,即2、4、6、8、10、12。
例凸透镜与平板玻璃在接触点附近的横断面,水平轴画出了用整数平方根标的距离:√1=1√2=1.41,√3=1.73,√4=2,√5=2.24等等。
二级物理实验【1】、薄膜干涉中等厚干涉的特点和性质1、薄膜干涉分振幅法--点光源Q 发出的一束光投射到两种透明媒质的分界面上时,它携带的能量一部分反射回来,一部分透射过去,∝,这种分割方式称为分振幅法。
最基本的分振幅干涉装置是一块由透明媒质做成的薄膜。
Q 是点光源。
由Q 点发出的光射在薄膜的上表面时,它被分割为反射和折射两束光,折射光在薄膜的下表面反射后,又经上表面折射,最后回到原来的媒质,在这里与上表面的反射光束交迭,在两光束交迭的区域里每个点上都有一对相干光线在此相交,如相交于A,B,C,D 各点,A 点在薄膜表面,B 点在薄膜上面空间里,C 点是两平行光线在无穷远处相交,D 点是光线延长线在薄膜下面空间里。
只要Q 点发出光束足够宽,相干光束的交迭区可以从薄膜表面附近一直延伸到无穷远。
此时,在广阔的区域里到处都有干涉条纹。
观察薄膜产生的干涉条纹,可以用屏幕直接接收,更多的是利用光具组使干涉条纹成像(或用眼睛直接观察)。
由物像等光程性可知:两束光在A,B,C,D 各点的光程差与在A ´,B ´,C ´,D ´点的光程差是相等的,即参加干涉的两光束经光具组重新相遇时光程差是不变的,因此,我们在像平面上得到与物平面内相似的干涉图样,利用此方法,我们不仅可以观察薄膜前的“实”干涉条纹,还可以观察薄膜后的“虚”干涉条纹。
普遍地讨论薄膜装置整个交迭区内任意平面上的干涉图样是很复杂的问题,但实际中意义最大的是:① 厚度不均匀薄膜表面的等厚条纹 ② 厚度均匀薄膜在无穷远产生的等倾条纹2、等厚干涉一列光波照射到透明薄膜上,从膜的前、后表面分别反射形成两列相干光波,叠加后产生干涉.其中,对楔形薄膜来说,凡是薄膜厚度相等的一些相邻位置,光的干涉效果相同而形成一条同种情况(譬如光振动加强)的干涉条纹(亮纹).随着薄膜厚度的逐渐变化,干涉效果出现周期性变化,一般在薄膜上形成明暗交替相间的干涉条纹图样.称为等厚薄膜干涉.由Q 点发出的光经薄膜的上表面反射一束光,再经下表面反射一束光,这两束光满足相干条件,它们在P 点相干迭加,形成干涉条纹。
这是双光束干涉问题,要研究干涉条纹的特征,我们必须先计算这两束光在P 点的光程差,如图:I 2nE IS W图2-4 薄膜表面干涉场中光程差的计算又因为A 和P 两点很近,夹角Δθ很小,作为一级近似,可作垂直于,则有(折射定律)所以其中i 是光在薄膜内的折射角,n 为薄膜的折射率,h 为P 点薄膜的厚度 由极值方程知:当或 k=0,±1,±2,…… 时当 k=0,±1,±2,…… 时我们先不考虑半波损,因有无半波损不改变干涉条纹形状、间距、反衬度等特征。
薄膜表面干涉条纹的形状与照明和观察方式有很大关系。
我们只考虑正入射情形,即入射光与反射光处处与薄膜表面垂直,这时,。
等厚线——薄膜上厚度相等各点的轨迹称为它的等厚线。
因为薄膜折射率n 均匀,△L 只与h 有关,光强也取决于h ,我们说干涉条纹形状为I=const 的P 点轨迹,又因为I=f(h)所以I=const 的P 点轨迹,也是δ=const, δ=k △L 或 △L=const 或 h==const 的P 点轨迹,即沿等厚线()()()QP QABP p L -=∆AC QP QC QA =()()()CP ABP p L -=∆()iAP n i AP n CP sin sin 11==()ii h n sin tan 2=i inh cos sin 22=htgi AP 2=()i hnABP cos 2≈()inh i i nh p L cos 2cos sin 122=⎥⎦⎤⎢⎣⎡-≈∆()λk p L =∆i n k h cos 2λ=M I I =()i nh i i nh p L cos 2cos sin 122=⎥⎦⎤⎢⎣⎡-≈∆m I I =0=i nh L 2=∆n L2∆的强度相等,薄膜表面上的这种沿等厚线分布的干涉条纹称为等厚干涉条纹 当 △L=k λ k=0, ±1,±2……时,当 △L=(k+)λ k=0, ±1,±2……时所以相邻两个亮纹(或暗纹)上的光程差相差一个波长,对应的厚度相差,为真空中波长可见等厚干涉条纹可以将薄膜厚度分布情况直观的表现出来,它是研究薄膜性质的一种重要手段。
也是检验精密机械或光学零件的重要方法。
【2】测波长的5-10种方法1、分光计测量法 利用白纸上频谱图的特性,频谱宽度是与光的频率的自然对数成正比,而光的三原色频带宽相同,然后由频谱宽度,计算得光的频率为400-770Mhz ,由c=fλ可知光的波长2、牛顿环测量法牛顿环等厚干涉形成的第m 级暗环半径为r=(m Rλ)^(1/2)已知平凸透镜的曲率半径R ,再测得第m 级暗环的半径,即可求出波长。
3、衍射光栅测量法利用公式dsinX=k*波长,实验主要测的是衍射角X ,然后已知d 、k ,就计算出了波长。
光栅测量还包括投射、折射等。
4、平行光管测波长已知透镜直径为D ,最小分辨角为a ,则有a=1.22*波长/D依据公式求出波长。
5、迈克尔逊干涉仪测波长根据条纹的吞吐现象求出波长。
6、双棱镜干涉测量光波波长利用干涉条纹与狭缝及像板与狭缝之间的关系测量波长。
7、密集光波分复用系统的波长测量。
8、激光功率计(指针式)光功率表。
9、单缝夫琅禾费衍射实验测量波长。
10、法布里-珀罗干涉仪测光波波长等等。
k I I =21m I I =n h 20λ=∆0λ【3】牛顿环的历史牛顿在1675年首先观察到的.将一块曲率半径较大的平凸透镜放在一块玻璃平板上,用单色光照射透镜与玻璃板,就可以观察到一些明暗相间的同心圆环.圆环分布是中间疏、边缘密,圆心在接触点O.从反射光看到的牛顿环中心是暗的,从透射光看到的牛顿环中心是明的.若用白光入射.将观察到彩色圆环.牛顿环是典型的等厚薄膜干涉.平凸透镜的凸球面和玻璃平板之间形成一个厚度均匀变化的圆尖劈形空气簿膜,当平行光垂直射向平凸透镜时,从尖劈形空气膜上、下表面反射的两束光相互叠加而产生干涉.同一半径的圆环处空气膜厚度相同,上、下表面反射光程差相同,因此使干涉图样呈圆环状.这种由同一厚度薄膜产生同一干涉条纹的干涉称作等厚干涉.牛顿在光学中的一项重要发现就是"牛顿环"。
这是他在进一步考察胡克研究的肥皂泡薄膜的色彩问题时提出来的。
具体的, 牛顿环实验是这样的:取来两块玻璃体,一块是14英尺望远镜用的平凸镜,另一块是50英尺左右望远镜用的大型双凸透镜。
在双凸透镜上放上平凸镜,使其平面向下,当把玻璃体互相压紧时,就会在围绕着接触点的周围出现各种颜色,形成色环。
于是这些颜色又在圆环中心相继消失。
在压紧玻璃体时,在别的颜色中心最后现出的颜色,初次出现时看起来像是一个从周边到中心几乎均匀的色环,再压紧玻璃体时,这色环会逐渐变宽,直到新的颜色在其中心现出。
如此继续下去,第三、第四、第五种以及跟着的别种颜色不断在中心现出,并成为包在最内层颜色外面的一组色环,最后一种颜色是黑点。
反之,如果抬起上面的玻璃体,使其离开下面的透镜,色环的直径就会偏小,其周边宽度则增大,直到其颜色陆续到达中心,后来它们的宽度变得相当大,就比以前更容易认出和训别它们的颜色了。
牛顿测量了六个环的半径(在其最亮的部分测量),发现这样一个规律:亮环半径的平方值是一个由奇数所构成的算术级数,即1、3、5、7、9、11,而暗环半径的平方值是由偶数构成的算术级数,即2、4、6、8、10、12。
例凸透镜与平板玻璃在接触点附近的横断面,水平轴画出了用整数平方根标的距离:√1=1√2=1.41,√3=1.73,√4=2,√5=2.24等等。
在这些距离处,牛顿观察到交替出现的光的极大值和极小值。
从图中看到,两玻璃之间的垂直距离是按简单的算术级数,1、2、3、4、5、6……增大的。
这样,知道了凸透镜的半径后,就很容易算出暗环和亮环处的空气层厚度,牛顿当时测量的情况是这样的:用垂直入射的光线得到的第一个暗环的最暗部分的空气层厚度为1/189000英寸,将这个厚度的一半乘以级数1、3、5、7、9、11,就可以给出所有亮环的最亮部分的空气层厚度,即为1/178000,3/178000,5/178000,7/178000……它们的算术平均值2/178000,4/178000,6/178000……等则是暗环最暗部分的空气层厚度。
牛顿还用水代替空气,从而观察到色环的半径将减小。
他不仅观察了白光的干涉条纹,而且还观察了单色光所呈现的明间相间的干涉条纹。
牛顿环装置常用来检验光学元件表面的准确度.如果改变凸透镜和平板玻璃间的压力,能使其间空气薄膜的厚度发生微小变化,条纹就会移动.用此原理可以精密地测定压力或长度的微小变化.按理说,牛顿环乃是光的波动性的最好证明之一,可牛顿却不从实际出发,而是从他所信奉的微粒说出发来解释牛顿环的形成。
他认为光是一束通过窨高速运动的粒子流,因此为了解释牛顿环的出现,他提出了一个“一阵容易反射,一阵容易透射”的复杂理论。
根据这一理论,他认为;“每条光线在通过任何折射面时都要进入某种短暂的状态,这种状态在光线得进过程中每隔一定时间又复原,并在每次复原时倾向于使光线容易透过下一个折射面,在两次复原之间,则容易被下一个折射面的反射。
”他还把每次返回和下一次返回之间所经过的距离称为“阵发的间隔”。
实际上,牛顿在这里所说的“阵发的间隔”就是波动中所说的“波长”。
为什么会这样呢?牛顿却含糊地说:“至于这是什么作用或倾向,它就是光线的圆圈运动或振动,还是介质或别的什么东西的圆圈运动或振动,我这里就不去探讨了。
”因此,牛顿虽然发现了牛顿环,并做了精确的定量测定,可以说已经走到了光的波动说的边缘,但由于过分偏爱他的微粒说,始终无法正确解释这个现象。
直到19世纪初,英国科学家托马斯·杨才用光的波动说完满地解释了牛顿环实验。
【4】小样本学生分布(t分布)正态分布(normal distribution)是数理统计中的一种重要的理论分布,是许多统计方法的理论基础。
正态分布有两个参数,μ和σ,决定了正态分布的位置和形态。
为了应用方便,常将一般的正态变量X通过u变换[]转化成标准正态变量u,以使原来各种形态的正态分布都转换为μ=0,σ=1的标准正态分布(standard normal distribution),亦称u分布。
根据中心极限定理,通过上述的抽样模拟试验表明,在正态分布总体中以固定n(本次试验n=10)抽取若干个样本时,样本均数的分布仍服从正态分布,即N(μ,σ)。