物理-薄膜等厚干涉

红线对应薄膜厚度相同的位置。

劈角由小变大时，条纹由疏变密，反之亦然三、劈尖的应用（50页 1.10）1、测量细丝直径、微小夹角¾例: 两玻璃片夹一细丝，两片之间形成一个空气薄膜，n 2=1，光垂直入射，i 1≈i 2＝0。

∵有额外光程差，∴d 0=0 处为暗条纹。

¾如何测小角度α呢？已知d ，通过测量L ，可计算：α≈d/L 。

αλΔ22n x ≈202n d λΔ=如何求细丝直径d ？=(m-1)λ/2假如一共有m 条，则d =(m-1)Δd 0射，看反射光的干涉条纹。

加热，膨胀，表面上升，条纹有什么变化？待测材料膨胀后，空气膜变薄，如图所示，虚线所需要的光程差值，即该处为一若条纹的最大变形线度为OBA A O 为心的圆，所以条纹是以点为心的一组同心圆，叫做牛顿环。

）（干涉相消⋅⋅⋅=2,1,0j r BA A3、条纹位置此时反射光中看到的O 点是暗点。

¾有额外光程差时，()()⋅⋅⋅=λ+=2,1,0j n R21j 2r 2()⋅⋅⋅=λ=2,1,0j n R2j2r 2条纹位置是由圆形条纹的半径r决定。

亮条纹半径为：暗条纹半径为：¾没有额外光程差时，亮（暗）条纹半径为？此时反射光中看到的O 点是亮点。

4、条纹级次分布、条纹密度条纹级次：内低外高条纹密度：内疏外密条纹向中间收缩，中心条纹被吞没。

条纹向外扩展，中心有条纹冒出。

与等倾条纹的变化情况相反。

透镜上移时:透镜下移时:rBA ′A O5、在透射光中亦可观察到牛顿环。

动画2λ+例题：已知：半径为4cm 的平凸透镜，凸面向下，放在平玻璃板上，透镜和平板的折射率均为1.5，用波长为500nm 的平行光垂直照射，观察反射光的干涉条纹。

求：（1）若透镜边缘恰为暗纹，且共有17条暗纹（若圆心为暗点，也算是一条暗纹），求透镜凸面的曲率半径，和透镜边缘处两反射光的光程差；（2）若透镜向上平移两个波长，干涉条纹如何变化？（如果有额外光程差，要求取。

等厚干涉原理
干涉原理是光学中的一个基本原理，描述了当两束光波相遇时，它们的干涉现象。

在干涉实验中，我们通常会使用一对光栅或两个狭缝来产生干涉效应。

干涉现象的产生源于光波的波动性质。

等厚干涉是其中一种干涉现象，它指的是当两个处于同一平面上的玻璃或空气薄膜之间被光所填充时，光在两个界面之间的反射和折射所引起的干涉现象。

等厚干涉主要是由于光在介质中传播速度不同而引起的。

当入射光波垂直于两个界面时，会发生垂直入射等厚干涉。

在这种情况下，入射光波在第一个界面上发生反射，并在第二个界面上发生折射，然后再次反射回来。

这两束光波具有不同的光程差，这会导致干涉现象的出现。

干涉现象的强度取决于光的波长、介质的折射率以及两个界面的厚度差。

根据等厚条件，当两个界面之间的厚度差等于光的波长的整数倍时，我们就会观察到明纹或暗纹。

等厚干涉广泛应用于光学领域，例如在干涉测量中，我们可以利用等厚干涉现象来测量薄膜的厚度或者根据干涉纹的形态来判断介质的性质。

此外，等厚干涉还可以用于图像处理和光学元件的设计等方面。

总之，等厚干涉原理是一种重要的光学现象，通过研究光的波
动性质，我们可以深入理解光的行为，并将其应用于实际生活和科学研究中。

等厚干涉原理等厚干涉原理是光学干涉实验中的一种重要原理，它是基于光的波动性质而产生的干涉现象。

在等厚干涉实验中，光通过等厚薄膜后会产生干涉现象，这种现象在实际生活和科学研究中有着广泛的应用。

下面我们将详细介绍等厚干涉原理及其应用。

等厚干涉原理的基本概念是指，当光线通过等厚薄膜时，由于不同介质的折射率不同，光线在介质之间的反射和折射会产生相位差，从而形成干涉条纹。

等厚薄膜是指在光线传播的路径上，介质的厚度保持不变，这样可以使得干涉条纹清晰可见。

在等厚干涉实验中，通常会使用平行玻璃板或者空气膜来模拟等厚薄膜，通过调节光源和观察屏的位置，可以观察到明暗交替的干涉条纹。

等厚干涉原理的实现需要满足一定的条件，首先是光源需要是单色光，这样才能保证干涉条纹的清晰度。

其次是等厚薄膜的厚度需要足够薄，一般在光的波长数量级以下，这样才能产生明显的干涉现象。

最后是光线的入射角需要小于临界角，这样才能保证光线在介质之间发生反射和折射。

等厚干涉原理在实际应用中有着广泛的用途，其中最为重要的就是在光学薄膜的制备和检测中。

通过等厚干涉实验，可以精确地测量薄膜的厚度和折射率，这对于光学元件的制备和质量控制具有重要意义。

另外，在光学镀膜和光学薄膜的研究中，等厚干涉原理也扮演着重要的角色，它可以帮助科研人员研究薄膜的光学性质和厚度分布。

除此之外，等厚干涉原理还在光学成像和光学测量中得到了广泛的应用。

在显微镜和光学显微镜中，通过调节薄膜的厚度和折射率，可以实现对样品的高分辨率成像。

在光学测量中，等厚干涉原理可以用来测量透明薄膜的厚度和表面形貌，这对于材料科学和工程技术有着重要的意义。

综上所述，等厚干涉原理是光学干涉实验中的重要原理，它基于光的波动性质而产生，通过光线在等厚薄膜中的反射和折射产生干涉现象。

等厚干涉原理在光学薄膜制备、光学成像和光学测量中有着广泛的应用，对于推动光学科学和技术的发展具有重要意义。

希望本文对等厚干涉原理的理解和应用有所帮助，谢谢阅读！。

实验3.19_等厚干涉的应用
等厚干涉是一种光的干涉现象，它是由于光在通过两个平行的透明介质界面时，两个介质的厚度相等而引起的。

等厚干涉的应用广泛，下面介绍几个常见的应用：
1. 薄膜干涉：当光线从空气进入一个介质，再从这个介质进入另一个介质时，两个介质的界面之间的薄膜会形成等厚干涉。

这种现象被广泛应用于光学薄膜技术，如反射镜、透镜等光学元件的制造中。

2. 非破坏性检测：等厚干涉可以用于材料的非破坏性检测。

通过观察材料表面的等厚干涉图案，可以判断材料的厚度分布是否均匀，从而评估材料的质量和性能。

3. 显微镜观察：等厚干涉可以用于显微镜观察。

在显微镜中，通过透射或反射光的等厚干涉图案可以增强显微镜的分辨率和对比度，从而获得更清晰的显微图像。

4. 光学雕刻：等厚干涉可以用于光学雕刻。

通过控制光在介质中的传播路径和相位差，可以实现对材料的局部加热和腐蚀，从而实现精确的微纳加工和雕刻。

5. 表面形貌测量：等厚干涉可以用于表面形貌的测量。

通过观察介质界面上的等厚干涉条纹，可以推断出表面的弯曲、变形和缺陷等信息，从而实现对微观尺度表面形貌的精确测量。

等厚干涉在光学领域有着广泛的应用，不仅可以用于光学元件的制造和检测，还可以用于显微观测、光学雕刻和表面形貌测量等领域。

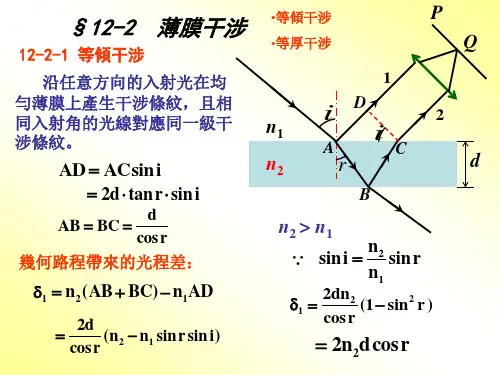
等厚干涉（equal thickness interference ）
光在厚度不同的薄膜表面发生干涉时，光的加强或减弱的条件只决定于膜的厚度的一种干涉现象。

观察等厚干涉现象，通常让光线垂直射到薄膜的表面上（入射角i ≈0），这时由膜的上下表面反射出的两束相干光的光程差近似等于2nd ，n 是膜的折射率，d 是该处膜的厚度。

考虑到反射时有半波损失，则从反射光中看到明暗条纹的条件是：
2)12(2λ
+=m nd 亮条纹
λm nd =2 暗条纹
m =0，1，2……
厚度d 相同的各处，产生的干涉条纹的明暗情况相同，因此这种干涉条纹叫做等厚干涉条纹。

如果光线不是垂直入射，由于薄膜很薄，并且膜的两个表面的夹角很小，光程差近似地等于
i n n d 22122sin 2-，n 2是膜的折射率，n 1是膜周围介质的折射率，i 是入射角。

在平行光照射下，各处的入射角i 相同，这时产生的明暗条纹的条件也只决定于膜的厚度 d ，这种干涉也是等厚干涉。

如果用白光照射，由于各色光产生的干涉条纹的位置不同，互相叠加后就出现不同的颜色。

肥皂泡上的彩色花纹就是这样出现的。

等厚干涉在光学测量中有很多应用。

如测量微小角度、细小的直径、微小的长度，以及检查光学元件表面的不平度，都可以利用光的等厚干涉。

【1】等厚干涉：定义：薄膜干涉的一种，光程差是薄膜厚度的函数，薄膜厚度相等点的光程差相同，干涉条纹是同一级。

干涉条纹形状与薄膜等厚线相同。

示意图：极大极小条件：光程差Δ=2n2d+δ 半波损失=2kλ2(极大)2k−1λ2(极小)，k=1,2,3,⋯特征：1>对于劈尖薄膜干涉：2>牛顿环：干涉条纹形状与薄膜等厚线相同。

【2】牛顿环的历史是牛顿在1675年首先观察到的．将一块曲率半径较大的平凸透镜放在一块玻璃平板上，用单色光照射透镜与玻璃板，就可以观察到一些明暗相间的同心圆环．圆环分布是中间疏、边缘密，圆心在接触点O．从反射光看到的牛顿环中心是暗的，从透射光看到的牛顿环中心是明的．若用白光入射．将观察到彩色圆环．牛顿环是典型的等厚薄膜干涉．牛顿环实验是这样的：取来两块玻璃体，一块是14英尺望远镜用的平凸镜，另一块是50英尺左右望远镜用的大型双凸透镜。

在双凸透镜上放上平凸镜，使其平面向下，当把玻璃体互相压紧时，就会在围绕着接触点的周围出现各种颜色，形成色环。

于是这些颜色又在圆环中心相继消失。

在压紧玻璃体时，在别的颜色中心最后现出的颜色，初次出现时看起来像是一个从周边到中心几乎均匀的色环，再压紧玻璃体时，这色环会逐渐变宽，直到新的颜色在其中心现出。

如此继续下去，第三、第四、第五种以及跟着的别种颜色不断在中心现出，并成为包在最内层颜色外面的一组色环，最后一种颜色是黑点。

反之，如果抬起上面的玻璃体，使其离开下面的透镜，色环的直径就会偏小，其周边宽度则增大，直到其颜色陆续到达中心，后来它们的宽度变得相当大，就比以前更容易认出和训别它们的颜色了。

牛顿测量了六个环的半径（在其最亮的部分测量），发现这样一个规律：亮环半径的平方值是一个由奇数所构成的算术级数，即1、3、5、7、9、11，而暗环半径的平方值是由偶数构成的算术级数，即2、4、6、8、10、12。

例凸透镜与平板玻璃在接触点附近的横断面，水平轴画出了用整数平方根标的距离：√1=1√2=1.41,√3=1.73,√4=2,√5=2.24等等。

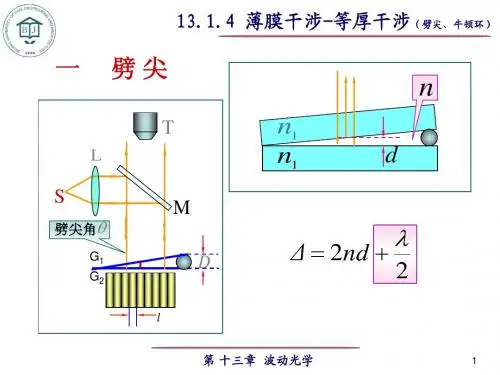
王皓平 6100411063 电III112班 S07716 00 十一 一 25 T012实验名称：光的等厚干涉一、引言：光的等厚干涉，是利用透明薄膜的上下两表面对入射光的一次反射，反射光相遇时发生的。

二、实验目的：1、观察牛顿环和劈尖的干涉现象。

2、了解形成等厚干涉现象的条件极其特点。

3、用干涉法测量透镜的曲率半径以及测量物体的微小直径或厚度。

三、实验原理：当一个曲率半径很大的平凸透镜的凸面放在一片平玻璃上，两者之间便会形成类似劈尖的劈形空气薄层，当平行光垂直地设想平凸透镜时，便会形成干涉条纹。

牛顿环是一种的等厚干涉，利用它可以检验光学元件的平整度、光洁度；测定透镜的曲率半径或测量单色光波长。

本实验用牛顿环来测定透镜的曲率半径。

为此要找出干涉条纹半径r 、光波波长λ和透镜曲率半径R 三者之间的关系。

{2e +λ2=kλ 明环2e +λ2=(2k +1)λ2暗环r 2=R 2−(R −e)2=2Re −e 2; 又R>>e,e 2<<2Re,e 2可以忽略不计。

e =r 2/2RRre王皓平 6100411063 电III112班 S07716 00 十一 一 25 T012{r 2=√(2k −1)Rλ/2 明环r 2=√kRλ 暗环采用第n 级和第m 级计算R ：R =d m 2−d n 24λ(m −n)劈尖干涉：d =l Δl ∙λ2四、实验仪器：牛顿环装置，钠光灯，读数显微镜，劈尖，游标卡尺五、实验内容：1. 启动钠光灯，调节装置，开始实验。

2. 调节显微镜，使玻璃片呈45度。

3. 测量牛顿环直径。

4. 计算R 。

六、实验记录：王皓平 6100411063 电III112班 S07716 00 十一 一 25T012七、数据处理：r =Rλk ； Rλ=7.1574;R =1214559.647mm ； 2）R =d m 2−d n 24λ(m −n)=Δ4λ15R̅=87465.181mm王皓平6100411063 电III112班S07716 00 十一一25 T012八、实验结果：R=(8746.518±30.160)cmE=0.345%九、误差分析：1. 实验中叉丝为对准圆心，导致实验误差，使结果较小。

物理教学内容研究案例--等倾干涉和等厚干涉的差别等倾干涉和等厚干涉是物理教学中常见的两种干涉现象。

它们之间的差别在于干涉产生的原理、特点以及应用方面都有所不同。

本文将详细探讨等倾干涉和等厚干涉的差别，从物理原理、实验现象以及实际应用三个方面进行详细分析。

一、物理原理等倾干涉是指两束相干光通过等倾薄膜或玻璃板后，在干涉图样中观察到的干涉现象。

等倾薄膜是指两片平行的玻璃板之间夹有一层薄膜，当两束光线通过薄膜后，由于薄膜两侧的折射率不同，光线会发生相位差，从而产生干涉现象。

而等厚干涉是指两束相干光通过等厚介质板，也就是两片平行的玻璃板之间没有夹膜的干涉现象。

当两束光线通过等厚介质板时，由于介质板的等厚性，光线在通过介质板后会发生相位差，从而产生干涉现象。

从物理原理上来看，等倾干涉是由于薄膜两侧折射率不同而导致的相位差，而等厚干涉则是由于介质板等厚性导致的相位差。

二、实验现象等倾干涉和等厚干涉在实验现象上也有明显的区别。

在等倾干涉实验中，我们可以观察到明暗条纹交替排列的干涉图样。

这是由于等倾薄膜两侧的折射率不同，导致通过薄膜的光线会发生相位差，从而在干涉图样中形成明暗条纹。

而在等厚干涉实验中，观察到的干涉图样往往是均匀亮暗交替的条纹。

这是由于等厚介质板的等厚性导致通过介质板的光线也会发生相位差，形成均匀的干涉条纹。

实验现象的不同也反映了等倾干涉和等厚干涉在物理性质上的差异。

三、实际应用等倾干涉和等厚干涉在实际应用中有着不同的用途。

等倾干涉常常用于薄膜的测厚和材料的质量检测中。

通过观察等倾干涉图样的明暗条纹，可以测定薄膜的厚度和材料的质量。

而等厚干涉则常常用于非球面透镜的制作和测量中。

由于等厚介质板会产生均匀的干涉条纹，因此可以用于非球面透镜的制作和检验。

在实际应用中，等倾干涉和等厚干涉都发挥着重要的作用，但其应用领域和方法有所不同。

综上所述，等倾干涉和等厚干涉在物理原理、实验现象和实际应用上都有着明显的差异。

光的干涉薄膜干涉与杨氏双缝干涉在物理学中，光的干涉是指两个或多个光波相互作用时产生的干涉现象。

本文将重点介绍光的干涉中的两种重要形式：干涉薄膜干涉和杨氏双缝干涉。

通过对这两种干涉现象的详细解析，我们可以更好地理解光的波动性质以及与之相关的实验现象。

干涉薄膜干涉干涉薄膜是一种光学元件，由两个或多个透明介质构成，其中至少一个介质的厚度很小。

当光通过干涉薄膜时，由于光在薄膜中的传播速度不同，导致光的相位发生变化，从而产生干涉现象。

干涉薄膜干涉可以分为两类：分为等厚薄膜干涉和非等厚薄膜干涉。

等厚薄膜干涉是指光波在等厚薄膜的上下边界反射、透射发生干涉的现象。

当光波从一个介质射入另一个介质时，反射光波和透射光波会发生干涉，形成等厚薄膜干涉条纹。

这种干涉现象常见于薄膜反射镜、油膜等实际应用中。

非等厚薄膜干涉是指光波在不同厚度的薄膜上反射、透射发生干涉的现象。

这种干涉现象常见于光的薄膜干涉实验中，例如扭曲油膜实验。

根据薄膜的形状和厚度的不同，非等厚薄膜干涉产生的干涉条纹呈现出丰富的形态和颜色。

杨氏双缝干涉杨氏双缝干涉是由英国物理学家杨恩·杨于1801年首次提出的干涉实验。

该实验使用一个光源通过两个狭缝，然后在屏幕上观察产生的干涉条纹。

当光通过双缝时，光波沿两个缝洞传播到屏幕上形成了两列相干波。

当两个波峰或两个波谷重合时，它们会增强并形成明条纹；而当波峰和波谷重叠时，它们会相互抵消，形成暗条纹。

这种干涉现象显示了光既具有波动性又具有粒子性的特点，深刻地诠释了光的波粒二象性。

杨氏双缝干涉实验为研究光的性质和波动现象提供了重要的实验依据。

科学家们通过这个实验还揭示了许多与光波干涉现象相关的重要性质，如干涉条纹的间距与波长的关系以及干涉条纹的宽度与光源的宽度的关系。

结语光的干涉在物理学中占据着重要的地位，通过研究干涉薄膜干涉和杨氏双缝干涉，我们不仅可以深入理解光的波动性质，还能探索许多关于光与物质相互作用的有趣现象。