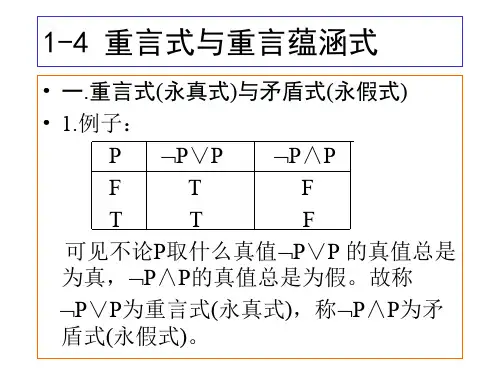
离散数学课件重言式与蕴含式-课件(ppt·精讲义·选)
- 格式：ppt
- 大小：1.33 MB
- 文档页数：23
下载文档原格式
合集下载
离散数学 重言式与蕴涵式
14. (P ⇄ Q) ∧(Q ⇄ R) (P ⇄ R) A B (A ∧ C) (B ∧ C)
逗号的作用： 将各个前提
分开
A B (A ∨ C) (B ∨ C)
作业：P23 (8)d,e,f (9)
假设后件为F,则P为F，P 为T，分两种情形讨论：
1. Q为T，则 Q 为F ， 前件Q ∧(PQ) 为F；
所以P为F，即 P为T。
前故件蕴为含T式时成，立后。件必 为T，从而蕴涵式成 立
2. Q为F，则 (PQ) 为F ， 前件Q ∧(PQ) 为F。
故蕴含后式件成为立F时。，前件 必为F，从而蕴涵 式成立
5.若AB且CB，则(A∨C) B
P21表1-5.2
1. P ∧ Q P 3. P P ∨ Q 8. P ∧(P Q) Q
课堂练习 Ｐ23(1)c (2)a,b
10. P ∧(P ∨ Q) Q
11. (P Q) ∧ (Q R) (P R)
13. (P Q) ∧(R S) (P ∧ R) (Q ∧ S)
例3 语言推证： (P∨Q) ∧(P R) ∧(Q R) R
几个重要的性质：
1. 设P、Q为任意两个命题公式， P Q 的充分必要条件为 P Q且 Q P 2. A B且A为重言式，则B必是重言式
3. 若A B且B C，则A C 4. 若A B且A C，则A (B ∧ C)
教材P22
Q P 逆反式
如何证明 P Q ?
要证P Q，即证P Q为永真式，而条件式为假只有 一种情况，即前件为真，而后件为假。
2. 蕴涵式的特征 例1：用真值表证明蕴涵式：Q P Q 成立
（1）当前
P
Q
PQ
Q (P Q)
离散数学 课件 The_second_course
4
1-6
其他联结词
对于n个命题变元，命题公式的真值情况即真值的取值数目共 n 有 2 n 个，恰可构成 2 2 个不等价的命题公式，即n个命题变元 2 n个。） 组成不等价的命题公式个数为 2
对 2 个真值情况，每一种均可取{T，F}两种，所以 共有2 2 个命题公式，又只要有一个真值取值不同， 就不等价，所以有 2 2 个不等价的命题公式。
其他联结词 12 F T F F 13 T F F T 14 F T T F 15 T T F T 16 F F T F
Q C P
11 T F T T
P Q P Q P Q P C Q P Q P Q Q P
1-6
其他联结词
两个命题变元至多有16个联结词，但这里有九个就够用了。 （除T，F及变元本身外）
例： P
P以（（P S） R）替换， S) R)=T。
P=T,
注意：必须将所有的变量作替换。
1-5
重言式与蕴含式
3．定理 A
B 是重言式,iff A B(即 是
的重言式)。
证： 若A B是重言式, 即A.B同为T或同为F,所以A B(真 值相同) 若AB,则A与B同为T或同为F。所以A B永为T，即 A B是重言式。
P29
(4).P Q ( P Q) (( P P) (Q Q))
(( P P) (Q Q)) (( P P) (Q Q))
依据：P P P
P Q ( P P) (Q Q)
1-6
其他联结词
（6）" " , " " 不服从结合律
P T T F F
1-6
其他联结词
对于n个命题变元，命题公式的真值情况即真值的取值数目共 n 有 2 n 个，恰可构成 2 2 个不等价的命题公式，即n个命题变元 2 n个。） 组成不等价的命题公式个数为 2
对 2 个真值情况，每一种均可取{T，F}两种，所以 共有2 2 个命题公式，又只要有一个真值取值不同， 就不等价，所以有 2 2 个不等价的命题公式。
其他联结词 12 F T F F 13 T F F T 14 F T T F 15 T T F T 16 F F T F
Q C P
11 T F T T
P Q P Q P Q P C Q P Q P Q Q P
1-6
其他联结词
两个命题变元至多有16个联结词，但这里有九个就够用了。 （除T，F及变元本身外）
例： P
P以（（P S） R）替换， S) R)=T。
P=T,
注意：必须将所有的变量作替换。
1-5
重言式与蕴含式
3．定理 A
B 是重言式,iff A B(即 是
的重言式)。
证： 若A B是重言式, 即A.B同为T或同为F,所以A B(真 值相同) 若AB,则A与B同为T或同为F。所以A B永为T，即 A B是重言式。
P29
(4).P Q ( P Q) (( P P) (Q Q))
(( P P) (Q Q)) (( P P) (Q Q))
依据：P P P
P Q ( P P) (Q Q)
1-6
其他联结词
（6）" " , " " 不服从结合律
P T T F F
《精品》离散数学(1.5重言式与蕴含式).ppt
.,
7
7
第一章 命题逻辑（Propositional Logic） 1.5重言
式与蕴含式(Tautology and Implication)
例: 证明┐Q（P→Q）┐P
1) 法1：真值表 2) 法2：若 ┐Q(P→Q)为真，则 ┐Q，P→Q为真，
所以Q为假，P为假，所以┐P为真。 3) 法3：若┐P为假，则P为真，再分二种情况：
证：1)因为A→B，A永为T,所以B必永为T.
2)由I11 （A→B)(B→C）A→C,所以若AB， BC，则（A→B)(B→C）永为T,从而A→C永 为T, 故AC.
.,
10
10
第一章 命题逻辑（Propositional Logic） 1.5重
言式与蕴含式(Tautology and Implication)
.,
3
3
第一章 命题逻辑（Propositional Logic） 1.5重言
式与蕴含式(Tautology and Implication)
判别命题公式的类型有两种方法: 真值表法和等值 演算法.
等值演算法是将所给命题公式通过等值演算化为最
简单的形式, 然后再进行判别.
例1.判别下列命题公式的类型.
(1). Q∨┓((┓P∨Q)∧P) (重言式)
(2). (P∨┓P) (Q∧┓Q)∧R (矛盾式)
(3). (P Q)∧┓P.
(可满足式)
.,
4
4
第一章 命题逻辑（Propositional Logic） 1.5重言
式与蕴含式(Tautology and Implication)
1.5.2 重言式(Tautology)与矛盾式(contradictory)的性质定理 1.5.1: 任 何 两 个 重 言 式 的 合 取 或 析 取 , 仍 然 是 一 重 言 式 . （由幂等律立得）
课件
第9节重言蕴涵式定义：当且仅当A→B 是重言式，则称A 重言(永真)蕴涵B ，记作A⇒B。
❖即若A→B⇔T，则A⇒B。
重言蕴涵式的两种基本证明方法：考察A→B的真值表，如果A→B为永真式，则真值表中第三行的情况就不会出现。
于是有下面两种证明方法：A B A→B F F T F T T T F F T T T1. 假设前件A 为真，若在此假设下能推出后件B 也为真，则A⇒B 成立。
例1求证P∧(P→Q) ⇒Q证明：假设P∧(P→Q)为T，则P为T 并且(P→Q)为T，于是Q为T，所以P∧(P→Q) ⇒Q 成立。
例2求证：((A∧B)→C)∧⌝D∧(⌝C∨D) ⇒⌝A∨⌝B证明：设前件((A∧B)→C)∧⌝D∧(⌝C∨D) 为真。
则((A∧B)→C)、⌝D、(⌝C∨D) 均为真。
⌝D 为T，则D 为F，由⌝C∨D 为T，于是⌝C 为T，即C 为F，再由((A∧B)→C 为T，则(A∧B)为F，即⌝(A∧B) 为T，于是⌝A∨⌝B 为T，因此((A∧B)→C)∧⌝D∧(⌝C∨D) ⇒⌝A∨⌝B。
2. 假设后件B 为假，若在此假设下能推出前件A 也为假，则A⇒B 成立。
例：求证P⇒P∨Q，Q⇒P∨Q证明：假设P∨Q 为F，则P为F，Q 为F，所以P⇒P∨Q，Q⇒P∨Q 成立。
例2求证：((A∧B)→C)∧⌝D∧(⌝C∨D) ⇒⌝A∨⌝B 证明：假设后件⌝A∨⌝B 为F，则A 与B 均为T。
1. 如C 为F，则(A∧B)→C 为F，所以前件((A∧B)→C)∧⌝D∧(⌝C∨D) 为F2. 如C 为T，则⑴若D 为T，则⌝D 为F，所以前件((A∧B)→C)∧⌝D∧(⌝C∨D) 为F。
⑵若D 为F，则⌝C∨D 为F，所以前件((A∧B)→C)∧⌝D∧(⌝C∨D) 为F。
综上((A∧B)→C)∧⌝D∧(⌝C∨D)⇒⌝A∨⌝B 成立。
基础重言蕴涵式：I1P∧Q⇒P I2P∧Q⇒QI3P⇒P∨Q I4Q⇒P∨QI5⌝P⇒P→Q I6Q⇒P→QI7⌝(P→Q)⇒P I8⌝(P→Q)⇒⌝QI9P,Q ⇒P∧Q I10⌝P∧(P∨Q)⇒Q I11P∧(P→Q)⇒Q I12⌝Q∧(P→Q)⇒⌝P I13(P→Q)∧(Q→R)⇒P→RI14A→B ⇒(A∨C)→(B∨C)I15A→B ⇒(A∧C)→(B∧C)❖重言蕴含“⇒”是关系符，不是运算符。
离散数学PPT课件 16重言式与重言蕴涵(ppt文档)
• 注意符号“”不是联结词，它是表示公 式间的“永真蕴涵”关系，也可以看成是
“推导”关系。即AB可以理ቤተ መጻሕፍቲ ባይዱ成由A可推 出B，即由A为真，可以推出B也为真。
2.重言(永真)蕴涵式证明方法 方法1.列真值表。(即列永真式的真值表) 这里就不再举例了。
下面讨论另外两种方法。
先看一看AB的真 值表，如果AB为 永真式，则真值表 的第三组指派不会 出现。于是有下面 两种证明方法。
式B，则称B是A(P1,P2,…,Pn) 的置换例式。
• 例如： 公式A：P∨(P∧((PQ)R)) 用(DE)替换A中P得到A的置换例式 B: (DE)∨((DE)∧(((DE)Q)R))
• 如果A是永真式，例如A为P∨P，用 (DE)替换A中P，得到A的置换例式 B： (DE)∨(DE) ， 显然B也是永真式。
I1.P∧QP I3. PP∨Q
I2. P∧QQ I4. QP∨Q
I5. PPQ
I6. QPQ
I7. (PQ)P
I8. (PQ)Q
I9. P,Q P∧Q
I10. P∧(P∨Q)Q
I11. P∧(PQ)Q I12. Q∧(PQ)P
I13. (PQ)∧(QR)PR
AB FF FT TF TT
A B T T F T
方法2.假设前件为真，推出后件也为真。 例如求证： ((A∧B)C)∧D∧(C∨D) A∨B
证明:设前件((A∧B)C)∧D∧(C∨D) 为
真。则((A∧B)C)、D、(C∨D)均真，
D为T，则D为F C∨D为T
得C为F 得AB为F
F
T
TF F
F
T
TT T
T
T
永真式的真值表的最后一列全是“T”。
“推导”关系。即AB可以理ቤተ መጻሕፍቲ ባይዱ成由A可推 出B，即由A为真，可以推出B也为真。
2.重言(永真)蕴涵式证明方法 方法1.列真值表。(即列永真式的真值表) 这里就不再举例了。
下面讨论另外两种方法。
先看一看AB的真 值表，如果AB为 永真式，则真值表 的第三组指派不会 出现。于是有下面 两种证明方法。
式B，则称B是A(P1,P2,…,Pn) 的置换例式。
• 例如： 公式A：P∨(P∧((PQ)R)) 用(DE)替换A中P得到A的置换例式 B: (DE)∨((DE)∧(((DE)Q)R))
• 如果A是永真式，例如A为P∨P，用 (DE)替换A中P，得到A的置换例式 B： (DE)∨(DE) ， 显然B也是永真式。
I1.P∧QP I3. PP∨Q
I2. P∧QQ I4. QP∨Q
I5. PPQ
I6. QPQ
I7. (PQ)P
I8. (PQ)Q
I9. P,Q P∧Q
I10. P∧(P∨Q)Q
I11. P∧(PQ)Q I12. Q∧(PQ)P
I13. (PQ)∧(QR)PR
AB FF FT TF TT
A B T T F T
方法2.假设前件为真，推出后件也为真。 例如求证： ((A∧B)C)∧D∧(C∨D) A∨B
证明:设前件((A∧B)C)∧D∧(C∨D) 为
真。则((A∧B)C)、D、(C∨D)均真，
D为T，则D为F C∨D为T
得C为F 得AB为F
F
T
TF F
F
T
TT T
T
T
永真式的真值表的最后一列全是“T”。
离散数学课件重言式与蕴含式
1-6.5 联结词是否够用
每种联结词对应一种四个T或 的组合 的组合， 每种联结词对应一种四个 或F的组合， 总共可以有2 种组合， 总共可以有 4=16种组合，似乎需要 种组合 似乎需要16 种联结词才够用。 种联结词才够用。 事实上，我们定义的这九种就够用了。 事实上，我们定义的这九种就够用了。 请看P27 表1-6.5 请看
1-5.2蕴含式(implication)
例：见P21 例1 课上做表1-5.2的11式 的 式 课上做表 看表1-5.2，记住常用的蕴含式。 ，记住常用的蕴含式。 看表
1-5.2蕴含式(implication)
定理1-5.4：设P、Q为任意两个命题公式，P⇔Q ： 为任意两个命题公式， ⇔ 定理 、 为任意两个命题公式 的充分必要条件是P⇒Q且Q⇒P 。 的充分必要条件是 ⇒ 且 ⇒ 证明： 为重言式， 证明：由定理 1-5.3 ，P ⇔Q，则P Q为重言式， ， 为重言式 因为由表1-4.7 P Q ⇔(P→Q)∧(Q→P)，故 因为由表 → ∧ → ， (P→Q)为T且 (Q →P)为T，即P⇒Q且Q⇒P 成 → 为 且 为 ， ⇒ 且 ⇒ 立。 反之， 反之，若P⇒Q且Q⇒P 成立，则(P→Q)为T且 ⇒ 且 ⇒ 成立， (Q→P)为T，因此 为重言式， ，因此P Q为T， P Q为重言式， 为 ， 为重言式 即P⇔Q。 ⇔ 。 这个定理也可作为两个公式等价的定义。 这个定理也可作为两个公式等价的定义。
1-5重言式与蕴含式 重言式与蕴含式
1-5.1重言式（tautology） 重言式（ 重言式 ） 定义1-5.2 [矛盾式 矛盾式]: 定义 矛盾式 给定一个命题公式， 给定一个命题公式，若无论对分量 作怎样的指派，其对应的真值永为F， 作怎样的指派，其对应的真值永为 ， 则称该命题公式为矛盾式或永假公式 矛盾式或永假公式。 则称该命题公式为矛盾式或永假公式。
离散数学-1-5重言式与蕴含式
同理，可假定后件Q的真值取0，若可由推 出P的真值必为0,即证明了Q P 。
整理ppt
7
三、蕴含式证明
例题1：推证Q ∧(P→Q) P
证法一：（由假定前件为真推出后件必为真） 假定Q ∧(P→Q)为1，则 Q 为1且P→Q为1，由Q 为1可
知Q为0，此时由P→Q为1可知，P必为0，故P为真 证法二: (由假定后件为假推出前件必为假） 假定P为0,则P为1。对Q的情况做如下讨论： （1）：若Q为0,则P→Q为0, Q ∧(P→Q) 为0 （2）：若Q为1,则 Q为0, Q ∧(P→Q) 为0
(3) 若真值表最后一列中至少有一个1， 则公式为可满足式。
整理ppt
3
一、公式的真假值分类
定理1.5.1及证明 P19 定理1.5.2及证明 P19 定理1.5.3及证明 P20
整理ppt
4
二、(永真/重言)蕴含式
形如A→B重言式在我们将要学习的推理理 论中有着十分重要的作用。
定义1-5.3 当且仅当P→Q是一个重言式时， 我们称“P蕴含Q”，并记作PQ。 （注：本课约定，“P →Q”读作P蕴含Q，
“P Q”读作P永真/重言蕴含Q。） *注：其中“”同样是一种元语言符号，用
来表示蕴涵式为重言式。
整理ppt
5
二、 (永真/重言)蕴含式
P→Q是不对称的， P→Q与Q→P一般是不等价的。 对P→Q来说：
Q→P 称为它的逆换式。（前、后件取逆序） P→Q 称为它的反换式。（前、后件取其否定） Q→P 称为它的逆反式。（前、后件取逆序及否定）
整理ppt
四、一些重要的（重言）蕴含式
Q ∧(P→Q) P (拒取式) P∧(P∨Q )Q (析取三段论) (P→Q) ∧(Q→R) P→R (假言三段论)
整理ppt
7
三、蕴含式证明
例题1：推证Q ∧(P→Q) P
证法一：（由假定前件为真推出后件必为真） 假定Q ∧(P→Q)为1，则 Q 为1且P→Q为1，由Q 为1可
知Q为0，此时由P→Q为1可知，P必为0，故P为真 证法二: (由假定后件为假推出前件必为假） 假定P为0,则P为1。对Q的情况做如下讨论： （1）：若Q为0,则P→Q为0, Q ∧(P→Q) 为0 （2）：若Q为1,则 Q为0, Q ∧(P→Q) 为0
(3) 若真值表最后一列中至少有一个1， 则公式为可满足式。
整理ppt
3
一、公式的真假值分类
定理1.5.1及证明 P19 定理1.5.2及证明 P19 定理1.5.3及证明 P20
整理ppt
4
二、(永真/重言)蕴含式
形如A→B重言式在我们将要学习的推理理 论中有着十分重要的作用。
定义1-5.3 当且仅当P→Q是一个重言式时， 我们称“P蕴含Q”，并记作PQ。 （注：本课约定，“P →Q”读作P蕴含Q，
“P Q”读作P永真/重言蕴含Q。） *注：其中“”同样是一种元语言符号，用
来表示蕴涵式为重言式。
整理ppt
5
二、 (永真/重言)蕴含式
P→Q是不对称的， P→Q与Q→P一般是不等价的。 对P→Q来说：
Q→P 称为它的逆换式。（前、后件取逆序） P→Q 称为它的反换式。（前、后件取其否定） Q→P 称为它的逆反式。（前、后件取逆序及否定）
整理ppt
四、一些重要的（重言）蕴含式
Q ∧(P→Q) P (拒取式) P∧(P∨Q )Q (析取三段论) (P→Q) ∧(Q→R) P→R (假言三段论)
精品课程《离散数学》PPT课件(全)
言1
为什么学习离散数学？
离散数学是现代数学的一个重要分支，是计算机科学与技术 的理论基础，所以又称为计算机数学，是计算机科学与技术 专业的核心、骨干课程。
它以研究离散量的结构和相互间的关系为主要目标，其研 究对象一般是有限个或可数个元素，因此它充分描述了计算 机科学离散性的特点。
离散数学是什么课？
真值为1
25
1.1 命题符号化及联结词
以下命题中出现的a是给定的一个正整数： (3) 只有 a能被2整除， a才能被4整除。
(4) 只有 a能被4整除， a才能被2整除。
解： 令r： a能被4整除， s： a能被2整除。 真值不确定 (3)符号化为 s r (4)符号化为 r s
真值为1
26
19
1.1 命题符号化及联结词
3.析取词 设p,q为二命题，复合命题“p或q” 称为p与q的析取式，记作p ∨ q，符号∨称 为析取联结词。 运算规则：
p 0 0 1 1 q 0 1 0 1 p∨q 0 1 1 1
20
1.1 命题符号化及联结词
析取运算特点：只有参与运算的二命题全为假时，运算结果才 为假，否则为真。 相容或：二者至少有一个发生，也可二者都发生 排斥或：二者只有一个发生，即非此即彼 例如： （1）小王爱打球或爱跑步。 设p：小王爱打球。 q：小王爱跑步。 则上述命题可符号化为：p ∨ q （2）张晓静是江西人或湖南人。 设p：江西人。 q：湖南人。 则上述命题就不可简单符号化为：p ∨ q 而应描述为(p∧ q) ∨( p∧q)(也可用异或联接词∨)
（1）星期天天气好，带儿子去了动物园； （2）星期天天气好，却没带儿子去动物园； （3）星期天天气不好，却带儿子去了动物园； （4）星期天天气不好，没带儿子去动物园。
数理逻辑重要公式离散数学PPT课件
3、否定等值式
x(x)= x(x)
x(x)= x第(x5页)/共9页
5
量词辖域收缩与扩张等值式
设A(x)是含x自由出现的公式，B中不含x的出现
关于存在量词的:
关于全称量词的：
x(A(x)B)xA(x)B
x(A(x)B)xA(x)B x(A(x)B)xA(x)B
x(A(x)B)xA(x)B x(A(x)B)xA(x)B x(BA(x))BxA(x)
闭式
8
第8页/共9页
(AB)(CD)( BD) (AC)
破坏性二难
说明： A, B, C为元语言符号 若某推理符合某条推理定律，则它自然是正确的 AB产生两条推理定律: A B, B A
4
第4页/共9页
基本等值式
1、基本等值式:
命题逻辑中基本等值式的代换实例
2、消去量词等值式 设D={a1,a2,…,an} xA(x)A(a1)A(a2)…A(an) xA(x)A(a1)A(a2)…A(an)
x(A(x)B)xA(x)B
量词x分(B配等A(值x))式BxA(x) x(A(x)B(x))xA(x)xB(x)
x(A(x)B(x))xA(x)xB(x)
注意：对无分配律，对无分配律
6
第6页/共9页
推理规则
(1)前提引入规则
(2)结论引入规则
(3)置换规则
(4)假言推理规则
(5)附加规则
(6)化简规则
2
第2页/共9页
推理定律——重言蕴涵式
重要的推理定律 A (AB) (AB) A (AB)A B
理 (AB)B A (AB)B A
段论 (AB)(BC) (AC)
第3页/共9页
x(x)= x(x)
x(x)= x第(x5页)/共9页
5
量词辖域收缩与扩张等值式
设A(x)是含x自由出现的公式，B中不含x的出现
关于存在量词的:
关于全称量词的：
x(A(x)B)xA(x)B
x(A(x)B)xA(x)B x(A(x)B)xA(x)B
x(A(x)B)xA(x)B x(A(x)B)xA(x)B x(BA(x))BxA(x)
闭式
8
第8页/共9页
(AB)(CD)( BD) (AC)
破坏性二难
说明： A, B, C为元语言符号 若某推理符合某条推理定律，则它自然是正确的 AB产生两条推理定律: A B, B A
4
第4页/共9页
基本等值式
1、基本等值式:
命题逻辑中基本等值式的代换实例
2、消去量词等值式 设D={a1,a2,…,an} xA(x)A(a1)A(a2)…A(an) xA(x)A(a1)A(a2)…A(an)
x(A(x)B)xA(x)B
量词x分(B配等A(值x))式BxA(x) x(A(x)B(x))xA(x)xB(x)
x(A(x)B(x))xA(x)xB(x)
注意：对无分配律，对无分配律
6
第6页/共9页
推理规则
(1)前提引入规则
(2)结论引入规则
(3)置换规则
(4)假言推理规则
(5)附加规则
(6)化简规则
2
第2页/共9页
推理定律——重言蕴涵式
重要的推理定律 A (AB) (AB) A (AB)A B
理 (AB)B A (AB)B A
段论 (AB)(BC) (AC)
第3页/共9页
离散数学课件ppt
随机性与概率
随机性表示试验结果的不 确定性，概率则表示随机 事件发生的可能性大小。
统计数据的收集和整理
数据来源
数据质量
数据可以来源于调查、实验、观测、 查阅文献等多种途径。
数据质量包括数据的准确性、可靠性 、完整性等方面，是数据分析的前提 和基础。
数据整理
数据整理包括数据的分类、排序、分 组、编码等步骤，以便更好地进行数 据分析。
必然事件
概率值为1的事件。
03
04
不可能事件
概率值为0的事件。
互斥事件
两个或多个事件不能同时发生 。
概率的加法原理和乘法原理
加法原理
对于任意两个互斥事件A和B，有 P(A∪B)=P(A)+P(B)。
乘法原理
对于任意两个事件A和B，有 P(A∩B)=P(A)×P(B|A)。
条件概率和独立性
要点一
条件概率
离散数学课件
目录 CONTENTS
• 离散数学简介 • 集合论基础 • 图论基础 • 离散概率论基础 • 离散统计学基础 • 离散数学中的问题求解方法
01
离散数学简介
离散数学的起源
19世纪初
集合论的提出为离散数学的起源 奠定了基础。
20世纪中叶
随着计算机科学的兴起，离散数 学逐渐受到重视和应用。
子集、超集和补集
总结词
子集、超集和补集是集合论中的重要概念，它们描述了集合之间的关系。
详细描述
子集是指一个集合中的所有元素都属于另一个集合，超集是指一个集合包含另一 个集合的所有元素，补集是指属于某个集合但不属于其子集的元素组成的集合。
集合的运算性质
总结词
集合的运算性质包括并集、交集、差集等，这些运算描述了 集合之间的组合关系。
重言式与蕴含式
（4）若A B，C B ，则AC B 以上性质在推理中常用。 特别说明：如果推导蕴含，则可以用等价的式 子替换，因为“等价”比“蕴含”强，好比 “大于等于”与“等于”的关系。
作业（1-5）
P23. (1) b) c) (2) b) 说明： （6）~（8）先不做，因为有效性 第八节讲。
定理1-5.3 设A、B为两个命题，AB当且仅当 A B 为一个重言式。 证明：若AB，则A、B有相同的真值， 由双条件定义 A B 永为T。 若A B为重言式，则A B永为T， 故 A、B有相同的真值，即AB。 上例是重言式，则(PQ) (PQ) 德.摩根律得证
1-5.2蕴含式(implication)
设P、Q、R为命题公式，则有 （1）P Q Q P 交换性 （2）（PQ）R P（QR） 结合性 （3）P(QR)(PQ)(PR) 分配性 （4） PQ （PQ ）（PQ） （5） PQ （P Q）由定义得到 （6） PP F，FP P，TP P
1-5重言式与蕴含式
1-5.1重言式（tautology）
定义1-5.1 [重言式]:
给定一个命题公式，若无论对分量 作怎样的指派，其对应的真值永为T， 则称该命题公式为重言式或永真公式。
1-5重言式与蕴含式
1-5.1重言式（tautology）
定义1-5.2 [矛盾式]:
给定一个命题公式，若无论对分量 作怎样的指派，其对应的真值永为F， 则称该命题公式为矛盾式或永假公式。
1-6其它联结词
定义1-6.1不可兼析取(Exclusive OR)： 设P和Q是两个命题公式，复合命题 PQ称作P和Q的不可兼析取。 PQ的真 值为T，当且仅当P与Q的真值不相同时为 T，否则， PQ的真值为F。真值表如下：
作业（1-5）
P23. (1) b) c) (2) b) 说明： （6）~（8）先不做，因为有效性 第八节讲。
定理1-5.3 设A、B为两个命题，AB当且仅当 A B 为一个重言式。 证明：若AB，则A、B有相同的真值， 由双条件定义 A B 永为T。 若A B为重言式，则A B永为T， 故 A、B有相同的真值，即AB。 上例是重言式，则(PQ) (PQ) 德.摩根律得证
1-5.2蕴含式(implication)
设P、Q、R为命题公式，则有 （1）P Q Q P 交换性 （2）（PQ）R P（QR） 结合性 （3）P(QR)(PQ)(PR) 分配性 （4） PQ （PQ ）（PQ） （5） PQ （P Q）由定义得到 （6） PP F，FP P，TP P
1-5重言式与蕴含式
1-5.1重言式（tautology）
定义1-5.1 [重言式]:
给定一个命题公式，若无论对分量 作怎样的指派，其对应的真值永为T， 则称该命题公式为重言式或永真公式。
1-5重言式与蕴含式
1-5.1重言式（tautology）
定义1-5.2 [矛盾式]:
给定一个命题公式，若无论对分量 作怎样的指派，其对应的真值永为F， 则称该命题公式为矛盾式或永假公式。
1-6其它联结词
定义1-6.1不可兼析取(Exclusive OR)： 设P和Q是两个命题公式，复合命题 PQ称作P和Q的不可兼析取。 PQ的真 值为T，当且仅当P与Q的真值不相同时为 T，否则， PQ的真值为F。真值表如下：