可汗学院数学题目-24Ratios,ratesandproportions

a rXiv:078.1897v2[mat h.CT]29J ul28KCL-MTH-07-100708.1897[math.CT]Morita classes of algebras in modular tensor categories Liang Kong a ∗and Ingo Runkel b †a Max-Planck-Institut f¨u r Mathematik Vivatsgasse 7,53111Bonn,Germany b Department of Mathematics,King’s College London Strand,London WC2R 2LS,United Kingdom August 2007Abstract We consider algebras in a modular tensor category C .If the trace pairing of an algebra A in C is non-degenerate we associate to A a commutative algebra Z (A ),called the full centre,in a doubled version of the category C .We prove that two simple algebras with non-degenerate trace pairing are Morita-equivalent if and only if their full centres are isomorphic as algebras.This result has an interesting interpretation in two-dimensional rational conformal field theory;it implies that there cannot be several incompatible sets of boundary conditions for a given bulk theory.1Introduction and summaryIt is well-known that two Morita equivalent rings have isomorphic centres(see e.g.[AF,§21]). The converse is in general not true,a counter example is provided by the real numbers andthe quaternions.On the other hand,for simple algebras over C(or any algebraically closedfield)the converse holds trivially,since all such algebras are of the form Mat n(C)and all have centre C.The situation becomes much richer if instead of considering algebras only in the category offinite-dimensional C-vector spaces one allows for more general tensor categories.Forexample,for the categories of integrable highest weight representations of the affine Liealgebras sl(2)k,k=1,2,...,onefinds an ADE-pattern for the Morita-classes,see e.g.[O]. These representation categories are in fact examples of so-called modular tensor categories,which are the class of categories we are considering in this paper.We call an algebra non-degenerate if the trace pairing(or rather the appropriate cat-egorical formulation thereof)is non-degenerate.We prove in this paper that two simple non-degenerate algebras in a modular tensor category are Morita equivalent if and only if they have isomorphic‘full centres’.The latter is a commutative algebra which is a general-isation of the centre of an algebra over C,but which typically lives in a different category than the algebra itself.Our motivation to study the relation between Morita classes of algebras and their centrescomes from two-dimensional conformalfield theory.It has recently become clear that there is a close relationship between rational CFT and non-degenerate algebras in modular tensor categories,both in the Euclidean and the Minkowski formulation of CFT,see e.g.[KLM, Fu1,LR,H2,Kg3,Fj3].In the Euclidean setting,the modular tensor category arises as the category of representations of a vertex operator algebra with certain additional properties [H1,H2],which we will refer to as‘rational’.The non-degenerate algebra A then is an algebra of boundaryfields[Fu1],i.e.an open-string vertex operator algebra[HK1].It turns out that A and the rational vertex operator algebra together uniquely determine a CFT [Fu1,Fj1,Fj3];however,to ensure its existence,some complex analytic and convergence issues remain to be settled.As a consequence of the uniqueness,one can obtain from A the algebra of bulkfields[Fj3],i.e.a fullfield algebra[HK2].An important question then is if two non-Morita equivalent open-string vertex operator algebras can give rise to the same fullfield algebra,or–in more physical terms–if there may exist several incompatible sets of boundary conditions for a given bulk CFT.Our result implies that for a CFT which is rational(in the sense that its underlying vertex operator algebra is rational),this cannot happen.Recall that an algebra in a tensor category C with associatorαU,V,W and unit constraintsl U,r U is a triple A=(A,m,η)where A is an object of C,m(the multiplication)is a morphism A⊗A→A such that m◦(m⊗id A)◦αA,A,A=m◦(id A⊗m),andη(the unit)is a morphism 1→A such that m◦(id A⊗η)=id A◦r A and m◦(η⊗id A)=id A◦l A.We will only consider unital algebras.In the following we will also assume that all tensor categories are strict to avoid spelling out associators and unit constraints.In the same way one defines left–,right–,and bimodules.For example,given two algebrasA andB ,an A -B -bimodule is a triple X =(X,ρl ,ρr )where ρl :A ⊗X →X and ρr :X ⊗B →X are the representation morphisms;ρl obeys ρl ◦(m A ⊗id X )=ρl ◦(id A ⊗ρl )and ρl ◦(ηA ⊗id X )=id X ,and similar for ρr .Furthermore the left and right action commute,i.e.ρr ◦(ρl ⊗id B )=ρl ◦(id A ⊗ρr ).With the help of bimodules we can now define when an algebra is simple,namely when it is simple as a bimodule over itself,and when two algebras A ,B are Morita equivalent,namely when there exist an A -B -bimodule X and a B -A -bimodule Y such that X ⊗B Y ∼=A and Y ⊗A X ∼=B as bimodules.Let now C be a modular tensor category (see[T]and e.g.[BK]),i.e.a semisimple C -linear abelian ribbon category with End(1)=C id 1,having a finite number of isomorphism classes of simple objects and whose braiding obeys a certain nondegeneracy condition.(This definition is slightly more restrictive than the original one in [T].)We will express morphisms in ribbon categories with the help of the usual graphical notation [JS];our conventions are summarised in [Fj1,app.A.1].Given an algebra A we can define the morphism ΦA :A →A ∨as ΦA =A∨.(1.1)As in [Fu3]we call an algebra A non-degenerate iffΦA is invertible (the definition still makes sense in a tensor category with dualities).This generalises the condition that the trace pairing a,b →tr(a ·b )of a finite-dimensional algebra over a field is non-degenerate.We will list some properties of non-degenerate algebras in section 2.1below.Given an algebra A in C ,the non-trivial braiding leads to two notions of centre,namely the left centre C l (A )and the right centre C r (A )of A [VZ,O,Fr1].Denoting the braiding of C by c U,V :U ⊗V →V ⊗U ,the left centre is the largest subobject C l (A )ιl →A such that m ◦c A,A ◦(ιl ⊗id A )=m ◦(ιl ⊗id A )and the right centre the largest subobject C r (A )ιr →A such that m ◦c A,A ◦(id A ⊗ιr )=m ◦(id A ⊗ιr ).We will give a formulation of the left centre of a non-degenerate algebra as the image of an idempotent in section 2.3below.The final ingredient we need to state our main result is a doubled version of C ,namely C ⊠˜C .Here the category ˜C is obtained from C by replacing braiding and twist with their inverses,and the product C ⊠˜Cis the completion with respect to direct sums of C טC (where the objects are pairs of objects in C and the Hom-spaces are tensor products of the two corresponding Hom-spaces in C ).C ⊠˜Cis again a modular tensor category.In fact,there is a notion of a ‘centre’Z of a tensor category,and for a modular tensor category C one finds Z (C )∼=C ⊠˜C [M¨u 1].Apart from the tensor unit,the category C ⊠˜Ccontains another canonically given com-mutative non-degenerate algebra,defined on the object R =⊕i ∈I U i ×U ∨i [M¨u 1,Fr1,Kg1].Here the (finite)set I indexes a choice of representatives U i of the isomorphism classes of simple objects in C .The multiplication and further properties of R are given in section 2.2.For a non-degenerate algebra A in C we can now define the full centre Z(A)as the leftcentre of the algebra(A×1)⊗R in C⊠˜C[Fj2,Fj3];our convention for the tensor product of algebras and some properties of the full centre will be discussed in section2.3.As opposed to the left and right centres,the full centre is not a subobject of A,in fact it is not evenan object of the same category.On the other hand,one can recover C l(A)and C r(A)from Z(A)by applying suitable projections.Furthermore,if C is the category V ect f(C)offinite-dimensional complex vector spaces then also C⊠˜C∼=V ect f(C),and the notions of left,right and full centre coincide and agree with the usual definition of the centre of an algebra over afield.The full centre turns out to be a Morita-invariant notion and our main result is that it can be used to distinguish Morita-classes of non-degenerate algebras.Theorem1.1Let C be a modular tensor category and let A,B be simple non-degenerate algebras in C.Then the following two statements are equivalent.(i)A and B are Morita equivalent.(ii)Z(A)and Z(B)are isomorphic as algebras.Remark1.2(i)In the special case C=V ect f(C)a simple non-degenerate algebra is isomorphic to thefull matrix algebra Mat n(C)for some n,and the full centre Z is just the usual centre,which in the case of Mat n(C)is C.The above theorem then just states that any two full matrix algebras over C are Morita equivalent.(ii)An algebra is called haploid iffdim Hom(1,A)=1[FS].Denote by C max(C⊠˜C)theset of isomorphism classes[B]of haploid commutative non-degenerate algebras B in C⊠˜C which obey in addition dim(B)=Dim(C),where Dim(C)= i∈I dim(U i)2.(It follows from[KO,thm.4.5]that this is the maximal dimension such an algebra can have.)Notethat[R]∈C max(C⊠˜C),with R defined as above.Let further M simp(C)be the set of Morita classes{A}of simple non-degenerate algebras A in C.We will see in remark3.4(ii)that the assignment z:{A}→[Z(A)]is a well-defined map from M simp(C)to C max(C⊠˜C).For example,z({1})=[R].Theorem1.1shows that z is injective.A result recently announced by M¨u ger[M¨u2]shows that z is also surjective.(An independent proof of surjectivity has subsequently appeared in[KR,sect.3.3].)(iii)A closed two-dimensional topologicalfield theory is the same as a commutative Frobeniusalgebra B over C,see e.g.[Kk].In the case that B is semi-simple,the possible boundary conditions for the theory defined by B can be classified by K0(B-mod)[Mo,MS].For a (rational)two-dimensional conformalfield theory the boundary conditions can be classified by K0(A-mod)where A is a non-degenerate algebra in C,and C in turn is the representation category of a rational vertex algebra V[Fu1].The algebra A comes from the boundaryfields –i.e.from an open-string vertex algebra over V–for one of the possible boundary conditions [Fu1,HK1,Kg2].For the topological theory,the category C is given by C=V ect f(C)and for B one can choose the centre of A.(If A is not simple this choice is not unique,see[LP] and[Fj3,rem.4.27].)For V ect f(C),A and B=Z(A)are Morita-equivalent,and so K0of A-mod and B-mod agree.In general onefinds that,for A a simple non-degenerate algebrain a modular tensor category C and B=Z(A)the full centre,# isocl.of simple B-left modules in C⊠˜C =# isocl.of simple A-A-bimodules C . This can be computed from[Fu1,thm.5.18]together with the fact that Z(A)has a unique(up to isomorphism)simple local left module,namely Z(A)itself.Thus in general,K0(B-mod)–the Grothendieck group of the category of B-left modules in C⊠˜C–is related to defect lines (see[Fu1,rem.5.19]and[Fr2]),and its relevance for the classification of boundary conditions is special to the topological case.Nonetheless,there is a connection between B and boundary conditions:We will see in section4that via the tensor functor T:C⊠˜C→C one obtains an algebra T(B)in C which is a direct sum of simple non-degenerate algebras,all of which are Morita-equivalent to A.In fact(cf.prop.4.3below)one has that K0(T(B)-mod)∼= K0 A-mod ×n,where n is the number of isomorphism classes of simple A-left modules in C.The rest of the paper is organised as follows.In section2we collect some results on non-degenerate algebras and the full centre.Section3we prove that statement(i)in theorem 1.1implies(ii)and in section4we prove the converse.2Preliminaries2.1Properties of non-degenerate algebrasNot all the properties discussed in this section require us to work with the full structure of a modular tensor category and we therefore state them in the appropriate context.However, all these properties do in particular hold for modular tensor categories.Let C be a(strict)tensor category.In the same way that one defines an algebra in C one can define a coalgebra A=(A,∆,ε)where∆:A→A⊗A andε:A→1obey co-associativity and the counit condition.Definition2.1A Frobenius algebra A=(A,m,η,∆,ε)is an algebra and a coalgebra such that the coproduct is an intertwiner of A-bimodules,i.e.(id A⊗m)◦(∆⊗id A)=∆⊗m= (m⊗id A)◦(id A⊗∆).We will use the following graphical representation for the morphisms of a Frobenius algebra,m=,η=,∆=,ε=.(2.1)A Frobenius algebra A in a k-linear tensor category,for afield k,is called special iffm◦∆=ζid A andε◦η=ξid1for nonzero constantsζ,ξ∈k.Ifζ=1we call A normalised-special.A(strictly)sovereign tensor category is a tensor category equipped with a left and a right duality which agrees on objects and morphisms(see e.g.[B,FS]for more details).Wewill write the dualitiesas=d U:U∨⊗U→1,=˜d U:U⊗U∨→1,∨=b U:1→U⊗U∨,∨=˜b U:1→U∨⊗U,(2.2)(n.b.,‘b’stands for birth and‘d’for death).Given these dualities one can define the left and right traces of a morphism f:U→U as tr l(f)=d U◦(id U∨⊗f)◦˜b U and tr r(f)=˜dU◦(f⊗id U∨)◦b U,as well as theleft and right dimension of U,dim l/r(U)=tr l/r(id U).If U∼=U∨,then dim l(U)=dim r(U)[FS,rem.3.6.3].In a modular tensor category(and more generally in a spherical category)the left and right traces and dimensions always coincide.Let now C be a sovereign tensor category.A Frobenius algebra in C is symmetric iff∨=∨.(2.3)For a Frobenius algebra(symmetric or not)one has dim l(A)=dim r(A)since the two morphisms in(2.3)are in fact isomorphisms(see e.g.the proof of lemma3.7in[Fu1]),and so A∼=A∨.We will write dim(A)≡dim l/r(A).In a k-linear sovereign category with End(1)=k id1we will identify dim l/r(U)with the corresponding element of k via tr l/r(id U)=dim l/r(U)id1.In this case onefinds that for a normalised-special symmetric Frobenius algebra one hasε◦η=dim(A)id1[FS,sect.3];in particular,dim(A)=0.Definition2.2An algebra A in C is non-degenerate if the morphismΦA in(1.1)is invertible.The relation between non-degenerate algebras and Frobenius algebras is summarised in the following lemma.Lemma2.3Let C be a sovereign tensor category.(i)Let A be a non-degenerate algebra in C.Taking∆=(Φ−1A⊗m)◦(˜b A⊗id A)andε=η∨◦ΦA turns A into a symmetric Frobenius algebra which obeys m◦∆=id A andε◦η= dim(A).(ii)Let A be a symmetric Frobenius algebra in C such that m◦∆=id A.Then A is a non-degenerate algebra.(iii)Two non-degenerate algebras A and B are isomorphic as algebras if and only if they are isomorphic as Frobenius algebras(with counit and coproduct as given in(i)).(iv)If C is in addition k-linear with End(1)=k id1and A is a non-degenerate algebra in C with dim(A)=0,then A is special.This lemma can be proved by combining and adapting lemmas3.7,3.11and3.12of[Fu1].Part of the proof of(i)involves showing thatΦA in(1.1)is also equal to the morphism obtained by‘reflecting’the graph along a vertical axis(cf.[Fu1,eqn.(3.33)]),and thatequally∆=(m⊗Φ−1A )◦(b A⊗id A).In this sense,the Frobenius algebra structure on anon-degenerate algebra does not involve any arbitrary choices.Whenever we will consider a non-degenerate algebra as a Frobenius algebra we mean the coproduct and counit given in part(i)of the above lemma.In the setting we will work with below,C is a modular tensor category and one can convince oneself that a simple non-degenerate algebra in C necessarily has dim(A)=0,cf. [Fr2,lem.2.6].In particular,a simple non-degenerate algebra is then always also normalised-special symmetric Frobenius.Let now C be an abelian sovereign tensor category.Let A be a non-degenerate algebra in C and let M be a right A-module and N be a left A-module.The tensor product M⊗A N can be written as the image of the idempotentP⊗A=ρM N(2.4)That is,there exist morphisms e A:M⊗A N→M⊗N and r A:M⊗N→M⊗A N such thatr A◦e A=id M⊗A N and e A◦r A=P⊗A.One can convince oneself that r A:M⊗N→M⊗A Nfulfils the universal property of the coequaliser ofρM⊗id N and id M⊗ρN.2.2Modular tensor categoriesLet C be a modular tensor category.Recall from section1that we chose representatives {U i|i∈I}for the isomorphism classes of simple objects.We alsofix U0=1and for an index k∈I we define the index¯k by U¯k∼=U∨k.The numbers s i,j∈C are defined vias i,j id1=tr(c Ui,U j ◦c Uj,U i).(2.5)They obey s i,j=s j,i and s0,i=dim(U i),see e.g.[BK,sect.3.1].The non-degeneracy condition on the braiding of a modular tensor category is that the|I|×|I|-matrix s should be invertible.In fact,k∈Is ik s kj=Dim(C)δi,¯ (2.6)(cf.[BK,thm.3.1.7]),where as above Dim(C)= i∈I dim(U i)2.In particular,Dim(C)=0. One can show(even in the weaker context of fusion categories over C)that Dim(C)≥1 [ENO,thm.2.3].Let usfix a basis{λα(i,j)k }N k ijα=1in Hom(U i⊗U j,U k)and the dual basis{Υ(i,j)kα}N k ijα=1inHom(U k,U i⊗U j).The duality of the bases means thatλα(i,j)k ◦Υ(i,j)kβ=δα,βid Uk.We alsofix λ(0,i )i =λ(i,0)i =id U i .We denote the basis vectors graphically as follows:λα(i,j )k=i j ,Υ(i,j )k α=k j.(2.7)As in section1let R be the object in C ⊠˜C given by R =⊕i ∈I U i ×U ∨i .We define a unit morphism ηR :1×1→R to be the natural embedding and a multiplication morphismm R :R ⊗R →R asm R = i,j,k ∈I N kij α=1×i j∨i j .(2.8)The basis elements λα(i,j )k and their duals enter the above expression in such a way that m R is independent of the choice of ing (2.8),one can compute ΦR (defined in (1.1))explicitly,resulting in ΦR =Dim(C ) i ∈I f i ×g i where f i :U i →U ∨¯ıand g i :U ∨i →U ∨∨¯ıare given by f i =(λ1(i,¯ı)0⊗id U ∨¯ı)◦(id U i ⊗b U ¯ı),g i =(δU ¯ı⊗˜d U i )◦ (c −1U ¯ı,U i◦Υ(i,¯ı)01)⊗id U ∨i ,(2.9)and δU :U →U ∨∨is the isomorphism (˜dU ⊗id U ∨∨)◦(id U ⊗b U ∨).It follows from [M¨u 1,prop.4.1](see also [Fr1,lem.6.19]and [Kg1,thm.5.2])that the three morphisms ηR ,m R and ΦR give R the structure of haploid commutative non-degenerate algebra.Thus it is also normalised-special symmetric Frobenius.(The algebra R can also be defined in more general categories,see [M¨u 1,Fr1].)2.3Properties of the full centreFrom hereon we will always take C to be a modular tensor category.Most of the constructions in this section can be carried out in greater generality,see e.g.[Fr1],but for the purpose of the proof of theorem 1.1this will not be necessary.An algebra A in a braided tensor category has a left centre and a right centre [VZ,O],both of which are sub-algebras of A .We will only need the left centre.The following definition is the one used in [Fr1],which in our setting is equivalent to that of [VZ,O].Definition 2.4The left centre C l (A )of a non-degenerate algebra A in C is the image of the idempotent P l (A ):A →A ,whereP l (A )=.(2.10)That is,there are morphisms C l(A)ιl→A and A r l→C l(A)such that r l◦ιl=id Cl(A)andιl◦r l=P l(A).This follows from definition2.31and remark2.34of[Fr1].(In[Fr1]the algebra A is assumed to be special,but the relevant proofs only use m◦∆=id A,which is satisfied by a non-degenerate algebra according to lemma2.3(i).)The proof of the following lemma can be found in[Fr1,prop.2.37].Lemma2.5Let A be a non-degenerate algebra in a modular tensor category C.(i)C l(A)is a commutative symmetric Frobenius algebra.(ii)If C l(A)is simple and dim(C l(A))=0,then C l(A)is in addition special.Given two algebras A and B we define a multiplication on the tensor product A⊗Bas m A⊗B=(m A⊗m B)◦(id A⊗c−1A,B ⊗id B)and a unit morphism asηA⊗B=ηA⊗ηB.Thisturns A⊗B into an algebra.Note that one can also define a different multiplication m′A⊗Bby using c B,A instead of c−1A,B .The resulting algebra is isomorphic to(A op⊗B op)op,where‘op’stands for the opposed algebra,see[Fu1,rem.3.23].We will always use m A⊗B.For two coalgebras we similarly set∆A⊗B=(id A⊗c A,B⊗id B)◦(∆A⊗∆B)andεA⊗B=εA⊗εB.This turns A⊗B into a coalgebra.One easily checks that if A and B share any of the properties non-degenerate,Frobenius,symmetric,special,then the property is inherited by A⊗B.On the other hand,even if A and B are commutative,A⊗B is generally not.For an object U of C denote by R(U)the object in C⊠˜C given by R(U)=(U×1)⊗R. (R(·)can be understood as the adjoint of the functor T mentioned in remark1.2(iii);more details can be found in[KR,sect.2.4].)If A is a non-degenerate algebra in C then A×1is a non-degenerate algebra in C⊠˜C and the above discussion gives a non-degenerate algebra structure on R(A).Definition2.6[Fj3,def.4.9]The full centre Z(A)of A is defined to be C l(R(A)).Proposition2.7Let A be a non-degenerate algebra in a modular tensor category C.(i)Z(A)is a commutative symmetric Frobenius algebra with dim(Z(A))=d·Dim(C)for some integer d≥1.(ii)If A is simple then Z(A)is a haploid commutative non-degenerate algebra with dim(Z(A)) =Dim(C).Furthermore,Z(A)is normalised-special.Proof.Thefirst statement in part(i)follows from lemma2.5(i)together with the above observation that R(A)is a non-degenerate algebra in C⊠˜C.For the statement about the dimension,let Z ij=dim Hom(Z(A),U i×U j).By combining[Fj2,eqn.(A.3)](note that in[Fj2]Z(A)has a different meaning,namely the object given in eqn.(3.9)there)with eqn.(5.65)and theorem5.1of[Fu1]it follows that k∈I Z ik s kj= l∈I s il Z ing this we can computedim(Z(A))= i,j Z ij dim(U i)dim(U j)= i,j s0i Z ij s j0= j,k Z0k s kj s j0= k Z0kδk,0Dim(C)=Z00Dim(C).(2.11)It follows from the equalities(A.2)in[Fj2]that Z00=dim Hom A|A(A,A),where Hom A|A(·,·) denotes the space of bimodule intertwiners.Since id A is a bimodule intertwiner we have Z00≥1.For(ii)note that in the present setting,A is simple iffit is absolutely simple,i.e.iffHom A|A(A,A)=C id A,which is equivalent to Z00=1.Therefore,A is simple iffZ(A) is haploid.Since by assumption in(ii),A is simple,(2.11)holds with Z00=1.Recall from above that Dim(C)≥1,so that altogether we see that Z(A)is simple(since it is haploid) and has nonzero dimension.By lemma2.5(ii),Z(A)is then also special.We can rescale the coproduct(and the counit)to make Z(A)normalised-special and it then follows from lemma2.3(ii)that Z(A)is non-degenerate.Using Q X we define a morphism D X:Z(B)=C l((B×1)⊗R)→Z(A)=C l((A×1)⊗R) by composing with the corresponding embedding and restriction morphisms,D X=r l◦Q X◦ιl.(3.2) As a direct consequence of lemma3.1we have D X=D X′for two isomorphic bimodules X and X′,as well as,for X,Y as in lemma3.1,D A=id Z(A),D X◦D Y=D X⊗B Y.(3.3) Lemma3.2Let A,B be non-degenerate algebras(not necessarily simple)and X an A-B-bimodule,such that dim(A),dim(B)and dim(X)are non-zero and theidentitiesA=dim(X)dim(B)id B,(3.4)and∨=dim(A)dim(B)D X:Z(B)→Z(A)is an isomorphism of Frobenius algebras.The precise form of the dimension-factors appearing in conditions(3.4)and(3.5)is not an extra condition,but is in fact uniquelyfixed.For example composing thefirst equation in(3.4)withεA from the left andηA from the right gives thefirst constant.Also note that X∨is naturally a B-A-bimodule,see e.g.[Fr2,sect.2.1].Proof of lemma3.2a)A∼=X⊗B X∨as A-A-bimodules:We define two morphisms f1:A→X⊗B X∨and f2:X⊗B X∨→A byf1=dim(A)c)φX is an isomorphism :First note that taking the trace of(3.5)and using (3.4)results in the identitydim(X )2=dim(A )dim(B ).(3.7)Using this,as well as (3.3)and part b)we obtainφX ∨◦φX =dim(X )dim(B )D X ∨◦D X =D X ∨⊗A X =D B =id Z (B ),(3.8)In the same way one checks that φX ◦φX ∨=id Z (A ).Thus φX is an isomorphism.d)φX is an algebra map :The unit property φX ◦ηZ (B )=ηZ (A )can be seen as follows,dim(X )dim(B )A ×Z (A )=Z (A )r l(3.9)The compatibility with the multiplication,m Z (A )◦(φX ⊗φX )=φX ◦m Z (B ),amounts to the identitiesdim(X )dim(B )2Z (A )(2)=dim(X )3dim(B)Z (A )ιl (3.10)The left hand side is obtained by writing out the definitions of the various morphisms in m Z (A )◦(φX ⊗φX).In step (1)the two projectors ιl ◦r l =P l (R (A ))have been omitted using lemma 3.1(ii,iv),and the uppermost multiplication morphism of A has been replaced by a representation morphism of the bimodule X .In step (2)we used property (3.5).For step (3)note that the B ×1-ribbon connecting X ×1to itself can be rearranged (using that B is symmetric Frobenius,as well as the representation property)to the projector P l (R (B ))which can be omitted against ιl .Using the representation property on the re-maining two B ×1-ribbons,as well as (3.7),gives the right hand side of (3.10).Replac-ing Q X =Q X ◦P l (R (B ))=Q X ◦ιl ◦r l finally shows that the right hand side is equal to φX ◦m Z (B ).e)φX is a coalgebra map :For this part of the statement,the coproduct and counit of Z (A )and Z (B )have to be normalised as in the proof of [Fr1,prop.2.37].That is,while the mul-tiplication and unit on Z (A )are given by m Z (A )=r l ◦m R (A )◦(ιl ⊗ιl )and ηZ (A )=r l ◦ηR (A ),for the coproduct and counit we choose∆Z (A )=ζ−1(r l ⊗r l )◦∆R (A )◦ιl ,εZ (A )=ζεR (A )◦ιl ,ζ=dim(Z (A ))dim(X )∨,(3.12)where in the second step (3.5)is substituted.One also needs to use that dim(Z (A ))=dim(Z (B )),which follows from part c).This completes the proof of the lemma.Proof of(i)⇒(ii)in theorem1.1:By assumption the simple non-degenerate algebras A and B are Morita-equivalent.Therefore there exists an A-B-bimodule X and a B-A-bimodule Y such that A∼=X⊗B Y and B∼= Y⊗A X as bimodules.Lemma3.3ensures that the conditions of lemma3.2are met.Thus the morphismφX:Z(B)→Z(A)is an isomorphism of algebras.l−11.For U,V,W,X∈C,notice thatT U×V ⊗T W×X =(U⊗V)⊗(W⊗X),T (U×V)⊗(W×X) =(U⊗W)⊗(V⊗X).(4.1) We defineϕ2:T U×V ⊗T W×X →T (U×V)⊗(W×X) byϕ2:=αU,W,V⊗X◦ id U⊗α−1W,V,X ◦ id U⊗(c−1W V⊗id X) ◦(id U⊗αV,W,X)◦α−1U,V,W⊗X.(4.2) The above definition ofϕ2can be naturally extended to a morphism T(M1)⊗T(M2)→T(M1⊗M2)for any pair of objects M1,M2in C⊠˜C.We still denote the extended morphism asϕ2.(We hide the dependence ofϕ2on M1,M2in our notation for simplicity.)We have Lemma4.1The functor T together withϕ0andϕ2is a tensor functor.Note that T takes algebras to algebras(see for example[Kg2,prop.3.7])but in general does not preserve commutativity.Explicitly,if(B,m B,ηB)is an algebra in C⊠˜C,then the triple(T(B),m T(B),ηT(B)),wherem T(B):=T(m B)◦ϕ2,ηT(B):=T(ηB)◦ϕ0,(4.3) is an algebra in C.4.2The full centre transported to C and simple modulesLet now C again be a(strict)modular tensor category,and let A be a simple non-degenerate algebra in C.As observed in section1,this implies in particular that dim(A)=0.The category of left A-modules is again semisimple and abelian[FS,props.5.1and5.24]with a finite number of isomorphism classes of simple objects(this follows e.g.by combining the fact that C itself only has afinite number of isomorphism classes of simple objects with[FS, lem.4.15]).Let{Mκ|κ∈J}be a set of representatives of the isomorphism classes of simple left A-modules.Lemma4.2Let A be a non-degenerate algebra in C and let M be a left A-module.(i)M∨⊗A M is an algebra with unit e A◦˜b M and multiplication r A◦(id M∨⊗˜d M⊗id M)◦(e A⊗e A).(ii)M is simple if and only if M∨⊗A M is haploid.Proof.Part(i)is a straightforward calculation,see e.g.[Fu2,eqn.(2.48)].Claim(ii)follows since Hom A(M,M)∼=Hom(M∨⊗A M,1).Thefirst space is one-dimensional iffM is simple, and the second space is one-dimensional iffM∨⊗A M is haploid.。

2018年ACT数学练习题及答案解析本文主要为考生整理了ACT数学5道选择题，并对这5道选择题进行了详细解析。

除练习题外，我们还为考生整理了9点ACT 数学答题技巧，详情如下：1、3x3·2x2y·4x2y is equivalent toA. 9x7y2B. 9x12y2C. 24x7y2D. 24x12yE. 24x12y2正确答案选C。

常数相乘(3·2·4)，合并x项(x3x2x2 → x3+2+2 → x7) 和y项(y·y → y1y1 → y1+1→ y2)，结果为24x7y2。

解析：The correct answer is C. To find an equivalent expression, you can multiply the constants (3·2·4), combine the x term (x3x2x2 → x3+2+2 → x7, because when you have a common base you use the base and add the exponents), and combine the y t erms (y·y → y1y1 → y1+1 → y2). The result is 24x7y2.2、 Mr. Dietz is a teacher whose salary is $22,570 for this school year, which has 185 days. In Mr. Dietz's school district, substitute teachers are paid $80 per day. If Mr. Dietz's takes a day off without pay and a substitute teacher is paid to teach Mr. Dietz's classes, how much less does the school district pay in salary by paying a substitute teacher instead of paying Mr. Dietz's for that day?F. $ 42G. $ 80H. $ 97J. $105K. $122正确答案选F。

新gre数学知识点新GRE数学知识点一、算术（Arithmetic）1. 整数（Integers）- 奇数与偶数- 质数与合数- 整数的四则运算2. 分数、小数和百分比（Fractions, Decimals, and Percentages） - 分数的加减乘除- 小数与分数的互转- 百分比的计算与转换3. 比率和比例（Ratios and Proportions）- 比率的概念与计算- 比例的概念与计算- 交叉相乘法二、代数（Algebra）1. 线性方程和不等式（Linear Equations and Inequalities）- 一元一次方程- 一元一次不等式- 系统线性方程组2. 二次方程和不等式（Quadratic Equations and Inequalities） - 二次方程的标准形式- 配方法- 完全平方- 二次不等式的解法3. 函数及其性质（Functions and their Properties） - 函数的定义与表示- 线性函数、二次函数、绝对值函数- 函数的变换：平移、伸缩、对称三、几何（Geometry）1. 平面几何（Plane Geometry）- 点、线、面的基本性质- 三角形、四边形的性质与计算- 圆的性质与计算2. 空间几何（Solid Geometry）- 多面体的性质与计算- 圆柱、圆锥、球的性质与计算3. 坐标几何（Coordinate Geometry）- 坐标系中点的表示- 距离公式、斜率公式- 线性方程的图形表示四、数据分析（Data Analysis）1. 数据的描述（Descriptive Statistics）- 平均数、中位数、众数- 方差、标准差- 百分位数2. 概率（Probability）- 事件的概率- 条件概率与独立事件- 排列组合的基本公式3. 样本与假设检验（Samples and Hypothesis Testing）- 样本的基本概念- 假设检验的基本步骤- 置信区间的概念以上是新GRE数学部分的主要知识点概览。

Complex numbers1.(−8+4i)(1−i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−12+4iB.−12+12iC.−4+12iD.−4+4iCorrect answer: C Difficulty level: 22.(4+i)2Which of the following is equivalent to **plex number shown above?Note: i=√−1A.15+8iB.15−8iC.17+8iD.17−8iCorrect answer: A Difficulty level: 23.(8−2i)(4−2i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.28−24iB.28+8iC.36−24iD.36+8iCorrect answer: A Difficulty level: 24.(5+i)(7−3i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.32+8iB.32−8iC.38+8iD.38−8iCorrect answer: D Difficulty level: 25.i4+4i2+4Which of the following is equivalent to **plex number shown above?Note: i=√−1A.1B.−1C.i+4D.i−4Correct answer: A Difficulty level: 26.(−3−i)(4−2i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−14−2iB.−14+2iC.−10−2iD.−10+2iCorrect answer: B Difficulty level: 27.(6+2i)2Which of the following is equivalent to **plex number shown above?Note: i=√−1A.40+4i2B.40+24iC.32+24iD.32+4i2Correct answer: C Difficulty level: 28.(1+i)(1−i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.2-2iB.2iC.0D.2Correct answer: D Difficulty level: 29.i(7−3i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.4iB.10iC.7i−3D.7i+3Correct answer: D Difficulty level: 210.i2−16i+4Which of the following is equivalent to **plex number shown above?Note: i=√−1A.i−4B.i+4C.−i−4D.−i+4Correct answer: A Difficulty level: 211.(3+i)(2−4i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.2−10iB.2−14iC.10−10iD.10−14iCorrect answer: C Difficulty level: 212.i101Which of the following is equivalent to **plex number shown above?Note: i=√−1A.1B.−1C.iD.−iCorrect answer: C Difficulty level: 213.(5−i)2Which of the following is equivalent to **plex number shown above?Note: i=√−1A.24−10iB.24+10iC.26−10iD.26+10iCorrect answer: A Difficulty level: 214.−8(7i−3i2)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−80iB.−56i−24C.−56+24iD.−32iCorrect answer: B Difficulty level: 315.32+iWhich of the following is equivalent to **plex number shown above?Note: i=√−1A.2−iB.2+iC.6+3i5D.6+3i5Correct answer: D Difficulty level: 316.(3−i)3Which of the following is equivalent to **plex number shown above?Note: i=√−1A.8−26iB.18−26iC.27−26iD.30−26iCorrect answer: B Difficulty level: 317.(5−7i+i2)+(8i3+12)**plex expression above is equivalent to the expression a+bi for the integer constants a and b.What is the value of a?Note: i=√−1A.16B.17C.18D.19Correct answer: A Difficulty level: 318.(−3+2i)(1−i3)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−5−iB.−5+5iC.−1−iD.−1+5iCorrect answer: A Difficulty level: 319.i11+i13Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−2iB.2iC.0D.2Correct answer: C Difficulty level: 320.51+3iWhich of the following is equivalent to **plex number shown above?Note: i=√−1A.1+3i2B.1−3i2C.−5(1+3i)8D.−5(1−3i)8Correct answer: B Difficulty level: 321.(10−8i3)−(6+i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.4−7iB.4+7iC.4+9iD.4−9iCorrect answer: B Difficulty level: 322.11−iWhich of the following is equivalent to **plex number shown above?Note: i=√−1A.2−2iB.2+2iC.1−i2D.1+i2Correct answer: D Difficulty level: 323.21−iWhich of the following is equivalent to **plex number shown above?Note: i=√−1A.1−iB.1+iC.2−iD.2+iCorrect answer: B Difficulty level: 324.8ix=−5What is the value of x in the equation above?Note:i=√−1A.−8i5B.8i5C.−5i8D.5i8Correct answer: D Difficulty level: 325.(2−3i)3Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−46−9iB.−26−9iC.26−9iD.46−9iCorrect answer: A Difficulty level: 326.(12+i)(8−6i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−2+5iB.2+2iC.10+5iD.14+2iCorrect answer: C Difficulty level: 327.11−6i −11+6iWhich of the following is equivalent to **plex number shown above? Note: i=√−1A.1237iB.−1237iC.1237D.−1237Correct answer: A Difficulty level: 328.(23+12i)(12−13i)**plex expression above is equivalent to the expression a+bi for the rational constants a and b. What is the value of b?Note: i=√−1A.b=16B.b=−16C.b=496D. b=529Correct answer: D Difficulty level: 329.P(x)=2x2+3x−17If x=8−2i, what is the value of the polynomial P above?Note:i=√−1A.15−2iB.23−6iC.127−70iD.135−62iCorrect answer: C Difficulty level: 330.(6+i2)(2−2i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.6−8iB.8−8iC.10−8iD.12−8iCorrect answer: B Difficulty level: 331.3i +2i2Which of the following is equivalent to **plex number shown above?Note: i=√−1A.3i+2B.3i−2C.−3i+2D.−3i−2Correct answer: D Difficulty level: 332.21+iWhich of the following is equivalent to **plex number shown above?Note: i=√−1A.−1+iB.−1−iC.1+iD.1−iCorrect answer: D Difficulty level: 433.3i10+i11Which of the following is equivalent to **plex number shown above?Note: i=√−1A.3+iB.−3+iC.3−iD.−3−iCorrect answer: D Difficulty level: 434.P(n)=n2−5n−7What is the value of P(−3i)?Note:i=√−1A.−4+15iB.−7+12iC.−7+24iD.−16+15iCorrect answer: D Difficulty level: 435.√3t2+5t+√27=0Which of the following is a solution to the equation above?Note:i=√−1A.t=−4√11i6B.t=−3√33i6C.t=−5+√11i6D.t=−5√3+√33i6Correct answer: D Difficulty level: 436.29=3(x+7)2+41Which of the following is a solution to the equation above?Note:i=√−1A.x=−7+2iB.x=−42−12iC.x=−76+√4436iD.x=−7−√1233iCorrect answer: A Difficulty level: 437.(8−2i)2(8+2i)Which of the following is equivalent to **plex number shown above?Note: i=√−1A.60B.68C.480−120iD.544−136iCorrect answer: D Difficulty level: 438.√54i41√27i101Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−√2iB.−√2C.√2D.√2iCorrect answer: C Difficulty level: 439.22−i −22+iWhich of the following is equivalent to **plex number shown above? Note: i=√−1A.4i5B.−4i5C.2i3D.−2i3Correct answer: A Difficulty level: 440.1+2i1−2i ÷1−2i1+2iWhich of the following is equivalent to **plex number shown above? Note: i=√−1A.1B.−1C.−725+2425iD.−725−2425iCorrect answer: D Difficulty level: 441.i3+i2Which of the following is equivalent to **plex number shown above?Note: i=√−1A.−1B.−2C.−1+iD.−1−iCorrect answer: D Difficulty level: 442.m2+6m+10=0Which of the following are solutions to the equation above?I. -3+iII. -3-iIII. 3+iNote:i=√−1A.I onlyB.I and II onlyC.I and III onlyD.I, II, and IIICorrect answer: B Difficulty level: 443.704i1776Which of the following is equivalent to **plex number shown above?Note: i=√−1A.704B.−704C.704iD.−704iCorrect answer: A Difficulty level: 444.12+5i −4+3i3−iWhich of the following is equivalent to **plex number shown above?Note: i=√−1A.10+26i(2+5i)(3−i)B.10−26i(2+5i)(3−i)C.10+27i(2+5i)(3−i)D.10−27i(2+5i)(3−i)Correct answer: D Difficulty level: 445.5+7i6−3iWhich of the following is equivalent to **plex number shown above?Note: i=√−1A.9+57i45B.9+57i3C.51+57i45D.51+57i3Correct answer: A Difficulty level: 446.9+7i184−i**plex expression above is equivalent to the expression a+bi for the rational constants a and b.What is the value of b?Note: i=√−1A.b=215B.b=217C.b=−1D.b=−7Correct answer: B Difficulty level: 447.5−i+(11−i)z=40+18iWhat is the value of z in the equation above?Note:i=√−1A.z=−19+24iB.z=24+20iC.z=3+2iD.z=3.2+145iCorrect answer: C Difficulty level: 448.2i+4ℎ−14=2iℎWhat is the value of h in the equation above?Note:i=√−1A.ℎ=3+iB.ℎ=72C.ℎ=7−iD.ℎ=83Correct answer: A Difficulty level: 4。

考试复习LEVEL 31.Playing tennis Playing squash Energyexpenditurerate1,594௞௃௛ 2,726௞௃௛ Oxygenconsumptionrate77௅௛ 130௅௛ Fat burning rate 49 ௚௛ rThe table above lists average expenditure rates of playing tennis vs. playing squash based on a body weight of 55 kilograms. The ratio of each value in the tennis column to the corresponding value in the squash column is about the same throughout the table. Which of the following is closest to the fat burning rate r of squash?A. 27௚௛B. 29௚௛C. 83௚௛D. 85௚௛Correct answer: C2. Lea’s car travels an average of 30 miles per gallon of gas. If she spent $20.70 on gas for a 172.5 mile trip, what was the approximate cost of gas in dollars per gallon?A. $1.45 per gallonB.$3.40 per gallonC.$3.60 per gallonD.$5.75 per gallonCorrect answer: C3.Kavitha and Andrei are truck drivers for the Delightful Delivery Company,which services cities W, T, and Q.The distance from city W to city T is 48.5 miles.The distance from city T to city Q is 20 miles.The distance from city Q to city W is 36 miles.If Kavitha's truck and Andrei's truck travel at the same speed, and it takesAndrei 91 minutes to go from city W to city T, about how much time will it take Kavitha to travel from city W to city Q?A.19 minutesB.38 minutesC.68 minutesD.123 minutesCorrect answer: C4.Yasemin is using a sugar cookie recipe with a flour to sugar ratio of 11:6. Tomake one batch of cookies, 2.75 cups of flour are needed. If Yasemin would like to triple the recipe, which of the following best approximates how much sugar she will need?A.1.5 cupsB. 4.5 cupsC. 5 cupsD.15 cupsCorrect answer: B5. A certain high school geometry class is made up of freshmen and sophomores.The ratio of freshmen to sophomores in that class is 3:4. If thereare 12 sophomores in the class, what is the total number of students in the class?A.9B.16C.21D.28Correct answer: CLEVEL 41.The musical interval between two sounds is called an "octave" if the ratio of thesounds' frequencies is 2:1. The following table shows the names of the musical intervals between two sounds based on the ratios of the two sounds' frequencies. Name of the musical interval Ratio of two sound frequenciesMajor third 4:5Perfect fourth 3:4Perfect fifth 2:3Major sixth 3:5If a sound is played with a frequency of 480 Hz, and a second sound is played with a frequency of 800 Hz, what is the name of the musical interval between the two sounds?A.Major thirdB.Perfect fourthC.Perfect fifthD.Major sixthCorrect answer: D2.The "maximum occupancy" of a room is the total number of people who can be ina room without causing a fire hazard. In a large room, a Fire Safety Code statesthat the maximum occupancy is 1 person for every 7 square feet (fݐଶ). A college is hosting a concert in a hall that is 14,721 fݐଶ, and 1,000 people are expected to attend. According to the Fire Safety Code, approximately how many more people can attend the concert without causing a fire hazard?A.900 peopleB.1,000 peopleC.1,100 peopleD.2,100 people Correct answer: C3. A donut company makes cream-filled donuts using ଵସcup (c) of dough andଵଶtablespoon (tbsp) of cream per donut. The company decides to change their recipe to use 3 times the amount of cream for their "New Triple-Stuffed Donuts!" If the donut company's new recipe uses the same amount of dough per donut, what is the ratio of dough to cream needed to make 12 triple-stuffed donuts?A.1 c:3 tbspB. 1 c:6 tbspC. 2 c:3 tbspD.1 c:2 tbspCorrect answer: B4. A marine aquarium has a small tank and a large tank, each containing only red andblue fish. In each tank, the ratio of red fish to blue fish is 3 to 4. The ratio of fish in the large tank to fish in the small tank is 46 to 5. What is the ratio of blue fish in the small tank to red fish in the large tank?A.15:184B.10:69C.69:10D.184:15Correct answer: B5.Two leading brands of paper towels are on sale. Brand A has 6 rolls, eachwith 56 sheets, for $4.29. Brand B has 8 rolls, each with 48 sheets, for $5.99.Which of the following best describes the relationship between the cost per sheet of the two brands?A.The two brands cost the same amount per sheet.B.Brand B costs $0.003 more per sheet than Brand A.C.Brand A costs $0.003 more per sheet than Brand B.D.Brand B costs $0.03 more than Brand A.Correct answer: BLEVEL 21.Zhang Lei spent $20.00 during his last outing at the bowling alley. This included aone time shoe rental fee of $3.50. He spent the rest of the money on bowling a number of games. If it took Zhang Lei 45 minutes to bowl each game and hespent 2 hours and 15 minutes bowling, how much did it cost per game?A.$3.00B.$5.50C.$6.67D.$7.34Correct answer: B Level：22.Mr. Bumble delivers newspapers to his community every week. His routetakes 3 hours to complete. During the first 2 weeks of delivering newspapers, he traveled a total of 100 blocks. Mr. Bumble delivers newspapers for 50 weeks each year. How many blocks does Mr. Bumble travel delivering newspapers in 1 year?A.1 blockB. 4 blocksC.50 blocksD.2,500 blocksCorrect answer: D3.During a timed test, Alexander typed 742 words in 14 minutes. AssumingAlexander works at this rate for the next hour, which of the following bestapproximates the number of words he would type in that hour?A.53B.840C.3180D.44,520Correct answer: C4.A quilter wants to make the design shown above using the Golden Ratio.Specifically, he wants the ratio of the triangle heights A:B and B:C to eachequal 1.62. If the quilter makes the triangle height A=8 in, approximately how tall should he make triangle height C?A.3 inB. 4 inC. 5 inD.6 inCorrect answer: A5.Elena is conducting a study about the effects of toxins in the water on thehormones of fish. Elena surveys 350 male fish in a river and finds that 150 of the male fish have egg cells growing inside them. According to Elena's survey, what is the ratio of male fish with egg cells to male fish without egg cells in the river?A.3:4B.3:7C.4:5D.4:7Correct answer: A。

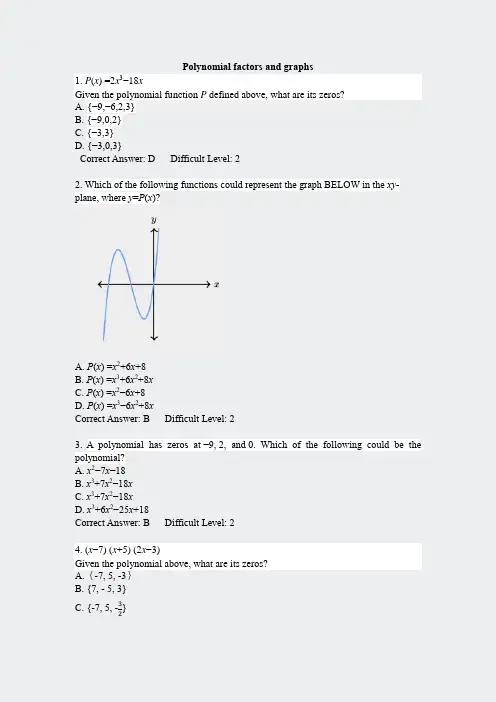
Polynomial factors and graphs1.P(x) =2x3−18xGiven the polynomial function P defined above, what are its zeros?A. {−9,−6,2,3}B. {−9,0,2}C. {−3,3}D. {−3,0,3}Correct Answer: D Difficult Level: 22. Which of the following functions could represent the graph BELOW in the xy-plane, where y=P(x)?A. P(x) =x2+6x+8B. P(x) =x3+6x2+8xC. P(x) =x2−6x+8D. P(x) =x3−6x2+8xCorrect Answer: B Difficult Level: 23. A polynomial has zeros at−9,2, and0. Which of the following could be the polynomial?A. x2−7x−18B.x3+7x2−18xC.x3+7x2−18xD.x3+6x2−25x+18Correct Answer: B Difficult Level: 24. (x−7) (x+5) (2x−3)Given the polynomial above, what are its zeros?A.｛-7, 5, -3｝B. {7, - 5, 3}C. {-7, 5, -3}2D. {7, -5, 3}2Correct Answer: D Difficult Level: 25. 2(x+55) (x−17)Given the polynomial above, what are its zeros?A. x=−55and x=17B. x=−55, x=−2, and x=17C. x=−17and x=55D. x=−17,x=2, and x=55Correct Answer: A Difficult Level: 26. G (z) = (z−1)5−(z−1)4 The polynomial function G is defined above. What is the product of the zeros of G? Fill in the blank:Correct Answer: 2 Difficult Level: 27. The polynomial function P has zeros at3and6. Which of the following could be the definition of P?A. P(x)=x2+9x+18B. P(x)=x2−9x+18C. P(x)=x2+3x+6D. P(x)=x2+6x+3Correct Answer: B Difficult Level: 28. Which of the following equations could represent the graph below in the xy-plane?I. y=(x−3)(x+3)II. y=(x−4)2III. y=(x+2)(x+7)A. ⅠonlyB. ⅡonlyC. I and ⅢonlyD. I,Ⅱand ⅢCorrect Answer: A Difficult Level: 29. h (t)=(t−8)1(t−4)2(t−2)3(t−1)4The polynomial function h is defined above. How many distinct zeros does h have? Correct Answer: 4 Difficult Level: 210.x3 +25x2+50x−1000The polynomial above has(x−5)and (x+10)as factors. What is the remaining factor?A. (x+2)B.(x-2)C. (x+2)D. (x-20)Correct Answer: C Difficult Level: 211.x3+7x2−36The polynomial above has zeros at −6 and 2. If the remaining zero is z, then what is the value of −z?Correct Answer: 3 Difficult Level: 312. The function p is a polynomial of t such that (t−10), (22−t),(t+10), and (20+t)are all factors of p(t). Which of the following could be the graph of y=p(t)in the ty-plane?A. B.C. D.Correct Answer: A Difficult Level: 313. Which of the following graphs appears to represent a polynomial function with a double zero?A. B.C. D.Correct Answer: D Difficult Level: 314.g(x)=x4−4x3+6x2−4x+1The function g is defined above. Given that all zeros of g are integers between−1 and 1inclusive, how many distinct zeros does g have?Correct Answer: 1 Difficult Level: 315.x2−ax+24If one of the zeros of the polynomial above is 8, what is the other zero?Correct Answer: 3 Difficult Level: 316. For a function g, the graph of y=g(x)y=g(x)is shown BELOW. When g(x)is divided by(x+10), the remainder is−20. Which of the following is closest to the remainder when g(x)is divided by(x−10)?A. -28B. -2C. 2D. 28Correct Answer: C Difficult Level: 317. The polynomial function f is defined as f(c)=(c−k)(c2−4c+4) where k is a constant. The value 2 is a zero of f. What is the remainder of f(c) when divided by (c−2)?Correct Answer: 0 Difficult Level: 318. Which of the following graphs in the xy-plane have−3and5as all of their distinct zeros for −6≤x≤6?I. II.III.A. I onlyB. I and II onlyC. II and III onlyD. I. II and III.Correct Answer: B Difficult Level: 319. Given some rational constant a, which polynomial equation could represent the graph BELOW in the xy-plane?A.y=a(x+1)2(x−5)B.y=a(x+1) (x−5)C.y=a(x+1) (2x+1)(x−5)D.y=a(x−1) (x+5)2Correct Answer: B Difficult Level: 320. The equation s=(t+3)2(t+2)(t+1)(t)(t−1) is graphed on the st-plane. What is the product of the t-intercepts of the graph?Correct Answer: 0 Difficult Level: 321. q(v)=(v−8)(v−5)(v−4)(v+5)(v+10)The function q is defined above. If the sum of the zeros of q is s, what is the value of s?Correct Answer: 2 Difficult Level: 322. (x−√3)2(x−√7)Given the polynomial above, what are its zeros?A.x=−√3and x=−√7B. x=√3and x=√7C.x=3and x=√7D.x=−3and x=−√7Correct Answer: B Difficult Level: 323. The graph of the polynomial equation y=α(t) is shown BELOW. Which of the following must be true?** leading coefficient is positive.** sum of the distinct t intercepts is negative.** constant coefficient is positive.** product of the distinct t intercepts is negative.Correct Answer: D Difficult Level: 324. The graph shown at left could represent which of the following equations?A. h=−(b−10)(b−20)(b+20)B. h=(b−10)(b−20)(b+20)C. h=−(b+10)(b−20)(b+20)D. h=(b+10)(b−20)(b+20)Correct Answer: A Difficult Level: 325.x3+7x2−36The polynomial above has zeros at −6 and 2. If the remaining zero is z, then what is the value of−z?Correct Answer: 3 Difficult Level: 326. The polynomial function f is defined as f(m)=(m3−m2−17m−15)(m+1). Whenf(m) is divided by (m+1), what is the remainder?Correct Answer: 0 Difficult Level: 427.p(n)=(n3−12n2+47n−60)(n−4)q(n)=(n+13)(n−4)The functions p and q are defined above. One of the functions has a zero at n=5. What is (p+q)(5)?Correct Answer: 18 Difficult Level: 428. Which of the following could be the equation corresponding to the graph BELOW?A.s=a⋅a⋅a⋅aB.s=(a−1)(a−1)C.s=a⋅a⋅a⋅a⋅aD.s=(a−1)(a−1)(a−1)Correct Answer: C Difficult Level: 429.p=(w−30)(w2+178w+7921)Given that −89 is a double zero of the polynomial equation above, which of the following could be the graph of the equation in the pw-plane?A. B.C. D.Correct Answer: D Difficult Level: 430.ℓ(x)=x4+36x2−10,000The polynomial function ℓ is defined above. What is the remainder of ℓ(x) when divided by (x+10)?Correct Answer: 3600 Difficult Level: 431.g (w)=(w+13)3(w+19)2The polynomial function g is defined above. When g (w) is divided by (w+16), the remainder is r. What is the value of ∣r∣?Correct Answer: 243 Difficult Level: 432. A function p p is defined as p(x) = (x−a)(x−15)(x−20)+15 where a is a constant. Given that p (7)=15, what is the value of a?Correct Answer: 7 Difficult Level: 433. A function w is a defined as w(x)=ax2+bx+c where a, b, and c are constants.If a=3 and w(3)=w(15)=0, then what is the absolute value of b?Correct Answer: 54 Difficult Level: 434. A function s is defined as s(x)=(x−4)(x−5)2. A function h is defined ash(x)=(x−a)s(x). For some constant a, (x−a)3 is a factor of h. What is s(a)?Correct Answer: 0 Difficult Level: 435.12x2+ax+2, what is the other zero?If one of the zeros of the above polynomial is 23Correct Answer: 1Difficult Level: 44** any polynomial function h, the polynomial function g is defined to be g(w)=(w−25 )(w−1)h(w). If h has zeros at 1 and 3 only, what is the sum of the distinct zeros of g?Correct Answer: 36 Difficult Level: 437. The polynomial function f f is defined as f(x)=(x−c1)(x−c2)(x−c3)⋯(x−cn)for some positive integer n. Each of the values c1,c2,c3,,,cn is a real number. The graph of y=f(x)is shown BELOW. Which of the following could be the value of n?A. 0B. 1C. 2D. 3Correct Answer: D Difficult Level: 438. The polynomial function f is defined as f(m)=(m3−m2−17m−15)(m+1). When f(m) is divided by (m+1), what is the remainder?Correct Answer: 0 Difficult Level: 4。

可汗学院微课程分析及启示——以比例（Ratio）为例
钱丽娟
【期刊名称】《中学数学研究（下半月）》
【年(卷),期】2015(000)006
【摘要】社会的发展,信息技术的进步,要求我们更新教育认识的同时,也为教育新模式的发展和实现提供了契机.以可汗学院为代表的,风靡全球的微型网络教学视频的出现激发了教育研究者对以微视频为载体运用于课堂的教学探索,滋生了一批新的名词,如翻转课堂,慕课,微课,微课程等.[1]在进一步学习可汗学院微课程后,笔者开始反思其与传统教学的反差,希望以其中——比例（Ratio）为例,通过分析比例及比例习题课中微课程的特点、结构,为我们反思教学提供启示.
【总页数】3页(P8-10)
【作者】钱丽娟
【作者单位】浙江省浙江师范大学,321004
【正文语种】中文
【中图分类】TP3
【相关文献】
1.可汗学院微课程价值分析——以数学微课程为例 [J], 孙彦婷;王芳;孙玉龙
2.可汗学院式微课个案研究及其微课开发启示——以《角的定义》为例 [J], 郑小军;;
3.可汗学院式微课个案研究及其微课开发启示r——以《角的定义》为例 [J], 郑小军
4.基于可视化原则的可汗学院初中数学微课程分析及启示 [J], 孙彦婷;孙玉龙
5.可汗学院微课程案例分析\r——以学前教育专业数学微课程为例 [J], 肖金芳因版权原因，仅展示原文概要，查看原文内容请购买。

SAT考试专题2024数学历年题目解析2024年的SAT考试将继续囊括数学科目，下面将对该年度的数学部分历年题目进行解析，帮助考生更好地准备SAT数学考试。

1. 第一题解析该题目是一道代数题，要求求解方程：3x + 5 = 20。

解题思路：将方程中的变量与常数项分离，得到：3x = 20 - 5。

计算得：3x = 15，再将等式两边同时除以3，得到：x = 5。

因此，方程的解为x = 5。

2. 第二题解析该题目是一道几何题，要求计算三角形的面积。

解题思路：已知三角形的底边长度为6，高为8。

直接使用三角形面积公式：面积 = 底边长度 ×高 ÷ 2。

代入已知的数值进行计算：面积 = 6 × 8 ÷ 2 = 24。

因此，该三角形的面积为24平方单位。

3. 第三题解析该题目是一道概率题，要求计算从一副标准扑克牌中随机抽取一张牌，该牌为红桃的概率。

解题思路：一副标准扑克牌中共有52张牌，其中有13张红桃牌。

因此，红桃牌的概率为：概率 = 红桃牌数目 ÷总牌数目。

代入已知数值进行计算：概率 = 13 ÷ 52 = 1 ÷ 4 = 0.25。

因此，从一副标准扑克牌中随机抽取一张牌，该牌为红桃的概率为0.25。

4. 第四题解析该题目是一道函数题，要求计算函数的值。

解题思路：已知函数 f(x) = 2x^2 + 3x + 1，需要计算当 x = 2 时的函数值。

将 x = 2 代入函数表达式中，得到：f(2) = 2 × 2^2 + 3 × 2 + 1。

计算得：f(2) = 8 + 6 + 1 = 15。

因此，当 x = 2 时，函数 f(x) 的值为15。

5. 第五题解析该题目是一道统计题，要求根据给定的数据计算平均数。

解题思路：已知一组数据为：10, 12, 15, 18, 20。

需要计算这组数据的平均数。

平均数的计算公式为：平均数 = 总和 ÷数据个数。

GRE考试数学专项历年真题2024导言：GRE考试是全球范围内广受认可的研究生入学考试，其中数学部分是考生们所关注的重点。

本文将向大家介绍2024年的GRE数学专项历年真题，帮助考生们更好地了解考试内容和应对策略。

一、整数与有理数（Integer and Rational Numbers）整数与有理数是数学中常见的概念，也是GRE数学考试的基础知识点。

涉及整数和有理数的题目往往考察对基本性质的理解与灵活运用，比如等式、不等式、因式分解等。

题目示例1：若x为整数且3x + 15 > 18，则x的最小值为多少？解析：根据不等式3x + 15 > 18，可以将其转化为3x > 18 - 15，得到3x > 3。

进一步化简可得x > 1。

由于x为整数，所以x的最小值为2。

二、代数与方程（Algebra and Equations）代数和方程是GRE数学考试中的重要部分，需要考生具备对多项式、函数、方程进行分析和求解的能力。

掌握代数的基本性质以及解方程的方法，能够帮助考生在数学部分得分。

题目示例2：设a为非零实数，如果方程(ax + 3)(a - x) = 0有唯一解，则x的值为多少？解析：根据方程(ax + 3)(a - x) = 0，可以得到两个解，分别为ax + 3 = 0和a - x = 0。

解得x = -3/a和x = a。

由于题目要求方程有唯一解，所以x只能等于a。

三、几何（Geometry）几何是GRE数学考试的另一个重要考点，涉及直线、角、三角形、圆等几何图形的性质。

考生需要对几何图形的性质和定理有所了解，并能够灵活运用来解决相关问题。

题目示例3：在平面直角坐标系中，直线y = 2x + 3和直线y = -x + b相交于点(1, 5)。

则常量b的值为多少？解析：考虑直线y = 2x + 3和直线y = -x + b相交于点(1, 5)，可以将点(1, 5)代入两个方程，得到5 = 2(1) + 3和5 = -(1) + b。

2024年GRE考试数学真题深度解读在2024年的GRE考试中，数学部分的题目一直是考生们比较关注的一个方面。

本文将对2024年GRE考试数学部分的真题进行深度解读，帮助考生们更好地应对这一考试内容。

以下是对一些典型题目的解析和详细讲解。

题目一：计算方程的解设方程2x + 5 = 15，求x的解。

解析：这是一个简单的一元一次方程，可以通过移项和化简求解。

将方程变形，得到2x = 15 - 5，进一步计算可得2x = 10。

最后，将方程化简为x = 10 / 2，即x = 5。

因此，方程2x + 5 = 15的解为x = 5。

题目二：几何图形的面积计算已知一个正方形的周长等于24cm，求其面积。

解析：正方形的周长等于4条边的长度之和，因此设每条边长为x，则有4x = 24。

将方程化简可得x = 24 / 4，即x = 6。

正方形的面积等于边长的平方，因此面积为6 * 6 = 36 平方厘米。

所以，该正方形的面积为36平方厘米。

题目三：概率计算一枚硬币投掷三次，出现正面的次数大于等于2次的概率是多少？解析：对于一次硬币投掷，它的结果只有两种可能：正面朝上或反面朝上，因此该事件是一个二项分布。

投掷三次硬币，出现正面大于等于2次的情况有3种可能情况：正正正、正正反和正反正。

因此，概率 = P(正正正) + P(正正反) + P(正反正)。

每一种可能性的概率为1/2 * 1/2 * 1/2 = 1/8。

将所有概率相加，得到概率为3/8。

所以，出现正面大于等于2次的概率是3/8。

通过对以上三个题目的解析，可以看出2024年GRE考试数学部分的难度适中，考察的内容主要涵盖了代数、几何和概率等基础知识。

在备考过程中，考生们应该注重对这些基础知识的扎实掌握，并且要能够将这些知识应用于解决实际问题。

除了对基础知识的理解和掌握外，考生们还需要注重解题的方法和步骤。

不同的题目可能需要不同的解题思路，因此在备考中要注重总结各种解题方法，并且进行反复练习和巩固。

sat数学考试试题(可编辑修改版) SAT数学考试试题(可编辑修改版)在这份SAT数学考试试题中，我们为您精心挑选了一些题目，希望能够帮助您进行备考和巩固数学知识。

请您认真阅读题目，并尽量独立思考和解答。

每道题后面都附带了详细的解答和解题思路，以供参考。

祝您考试顺利！题目一：若a和b都是正整数，且a/b = 1/4，那么a+b的值是多少？A. 5B. 8C. 14D. 16E. 20解答一：我们可以通过代入法求解这道题。

假设a=1，b=4，则a/b=1/4。

因此，a+b=1+4=5。

所以，选项A是正确答案。

题目二：某公司的年度收入增长率为20%，每年的增长幅度相同。

如果这家公司在2018年的年度收入为100万美元，那么在2021年的年度收入是多少？A. 120万美元B. 160万美元C. 140万美元D. 180万美元E. 200万美元解答二：我们可以使用复合增长率的方法来解决这道题。

首先，我们假设2018年的年度收入为x万美元。

根据题目的信息，可得以下等式：x * (1 + 0.2) * (1 + 0.2) * (1 + 0.2) = 100解方程可得：(1.2)^3 * x = 1001.728x = 100x ≈ 57.87（万美元）因此，2021年的年度收入约为57.87 * (1 + 0.2) * (1 + 0.2) * (1 + 0.2) ≈ 140（万美元）。

所以，选项C是正确答案。

题目三：在直角三角形ABC中，角A是直角，边AC = 10，边BC = 24。

点D位于边BC上，使得边AD垂直于边BC。

求边AD的长度是多少？A. 7B. 8C. 12D. 15E. 20解答三：由题目可知，三角形ABC是一个直角三角形。

根据勾股定理，可得：AC^2 + BC^2 = AB^210^2 + 24^2 = AB^2100 + 576 = AB^2676 = AB^2因此，AB = √676 = 26。

act数学与高考知识点ACT（American College Testing）考试是美国大学招生中广泛使用的一种标准化考试，其中包括数学科目。

本文将详细介绍ACT数学考试的知识点，以帮助考生有效备考。

1. 代数 (Algebra)1.1 线性方程与不等式 (Linear Equations and Inequalities)1.1.1 一元一次方程 (One-variable linear equations)1.1.2 一元一次不等式 (One-variable linear inequalities)1.1.3 线性方程组 (Systems of linear equations)1.2 函数 (Functions)1.2.1 函数定义与图像 (Function definition and graphs)1.2.2 函数的运算 (Operations with functions)1.2.3 函数的反函数 (Inverse functions)1.3 多项式与因式分解 (Polynomials and Factoring)1.3.1 一元多项式 (One-variable polynomials)1.3.2 因式分解 (Factoring)1.3.3 二次方程与二次多项式 (Quadratic equations and polynomials)2. 几何 (Geometry)2.1 平面几何 (Plane Geometry)2.1.1 直线与角度 (Lines and angles)2.1.2 三角形与四边形 (Triangles and quadrilaterals)2.1.3 圆与圆环 (Circles and annuli)2.2 空间几何 (Spatial Geometry)2.2.1 空间中的点、直线、面 (Points, lines, and planes in space)2.2.2 空间几何体的体积与表面积 (Volumes and surface areas of spatial figures)2.2.3 空间几何体的旋转与投影 (Rotations and projections of spatial figures)3. 数据分析与概率 (Data Analysis and Probability)3.1 图表解读与数据分析 (Interpreting graphs and data analysis)3.1.1 条形图、折线图与饼状图 (Bar graphs, line graphs, and pie charts)3.1.2 平均数、中位数与众数 (Mean, median, and mode)3.2 概率 (Probability)3.2.1 随机事件与概率计算 (Random events and probability calculations)3.2.2 排列与组合 (Permutations and combinations)4. 比例、百分数与利率 (Ratios, Percentages, and Rates)4.1 比例与比率 (Ratios and rates)4.2 百分数 (Percentages)4.3 利率与利息 (Interest rates and interest)5. 数字、指数与对数 (Number, Exponents, and Logarithms)5.1 整数与有理数 (Integers and rational numbers)5.2 指数 (Exponents)5.3 对数 (Logarithms)6. 函数与三角 (Functions and Trigonometry)6.1 线性函数与二次函数 (Linear functions and quadratic functions)6.2 三角函数 (Trigonometric functions)6.3 三角方程与三角恒等式 (Trigonometric equations and identities)通过掌握以上知识点，考生能够在ACT数学考试中取得优异的成绩。

高二英语数学建模方法单选题20题答案解析版1.In a mathematical modeling project, we need to find the optimal solution. The word "optimal" means _____.A.goodB.bestC.acceptablemon答案：B。

“optimal”的意思是“最佳的”，选项A“good”是“好的”，不如“最佳的”准确；选项C“acceptable”是“可接受的”，也不符合；选项D“common”是“常见的”，与“optimal”意思相差甚远。

2.When we build a mathematical model, we often use some assumptions. The word "assumptions" means _____.A.factsB.guessesC.proofsD.results答案：B。

“assumptions”的意思是“假设”，比较接近“guesses”（ 猜测）；选项A“facts”是“事实”；选项C“proofs”是“证明”；选项D“results”是“结果”，都与“假设”意思不同。

3.In a mathematical modeling process, we need to validate the model. The word "validate" means _____.A.testB.createC.changeD.ignore答案：A。

“validate”的意思是“验证”，与“test”（ 测试）意思相近；选项B“create”是“创建”；选项C“change”是“改变”；选项D“ignore”是“忽略”，都不符合“验证”的意思。

4.A mathematical model should be accurate and reliable. The word "reliable" means _____.efulB.trustworthyC.interestingD.difficult答案：B。

2024年高二英语数学文化赏析单选题30题1.Which mathematician is known as the father of calculus?A.ArchimedesB.NewtonC.LeibnizD.Euclid答案：B、C。

本题考查微积分的创立者。

牛顿和莱布尼茨都是微积分的创立者，所以答案为B 和C。

阿基米德主要在几何学和力学方面有突出贡献；欧几里得以《 几何原本》闻名，主要在几何学领域。

2.Who is considered the greatest mathematician of ancient Greece?A.PythagorasB.PlatoC.AristotleD.Euclid答案：A。

本题考查古希腊著名数学家。

毕达哥拉斯是古希腊著名数学家，他提出了毕达哥拉斯定理等。

柏拉图和亚里士多德主要是哲学家；欧几里得是古希腊著名数学家，但在本题中被认为不是最伟大的古希腊数学家。

3.Which mathematician is famous for his work on non-Euclidean geometry?A.GaussB.RiemannC.LobachevskyD.Euler答案：C。

本题考查非欧几何的创立者。

罗巴切夫斯基是最早创立非欧几何的数学家。

高斯、黎曼和欧拉在其他领域也有卓越贡献，但不是以创立非欧几何闻名。

4.Who is known for his contributions to number theory?A.FermatB.PascalC.GalileoD.Kepler答案：A。

本题考查对数学领域贡献的人物。

费马在数论方面有突出贡献。

帕斯卡主要在概率论方面有贡献；伽利略和开普勒是天文学家。

5.Which mathematician is associated with the discovery of the law of universal gravitation?A.NewtonB.EinsteinC.HawkingD.Copernicus答案：A。

Data inferences1.A random sample of 35 four-door passenger vehicles had a mean gas mileage, in miles per gallon (mpg), of 25.9 mpg. The estimate had a margin of error of 2.6 mpg at a 98% confidence level. Of the following, which is most plausible value for the true mean of the mileage of four-door passenger vehicles in general?A.24 mpgB.29 mpgC.32 mpgD.35 mpgCorrect answer: A Difficulty level: 22.Based on random samples of river heights, oceanographers estimate that 4,800 cubic kilometers (km3) of freshwater is discharged into the Arctic Ocean annually. The estimate has a margin of error of 240km3at the 90%confidence level. Which of the following is the most reasonable claim about the volume of freshwater discharged annually into the Arctic Ocean?A.It is between 4,800 and 5,040 km3.B.It is between 4,560 and 5,040 km3.C.It is between 240 and 4800 km3.D.It is between 240 and 4320 km3.Correct answer: B Difficulty level: 23.A survey of 9,000 randomly selected dentists practicing in the United States (US) found that 3,600 of them used text messaging to remind clients of upcoming appointments. If there were 147,000 practicing dentists in the US, approximately how many of them used text messaging for that purpose?A.12,600 dentistsB.58,800 dentistsC.159,600 dentistsD.367,500 dentistsCorrect answer: B Difficulty level: 24.A random sample of international flights in 2013 showed that 79% of the flights arrived within 15 minutes of their scheduled arrival time, and this estimate had a margin of error of 3% at a 95% confidence level. Which of the following conclusions is best?A.Exactly 79% arrived within 15 minutes of their scheduled times.B.Exactly 76% arrived within 15 minutes of their scheduled times.C.Between 76% and 82% arrived within 15 minutes of their scheduled times.D.Between 92% and 98% arrived within 15 minutes of their scheduled times.Correct answer: C Difficulty level: 25.In a poll of 1,578 randomly selected American adults, 44.8% of the respondents said that airlines should allow in-flight calls on airplanes. The results had a margin of error of 2.5%at a 90% confidence level. Which of the following is most likely to be equal to the percentage of all American adults who would say that airlines should allow in-flight calls?A.40%B.43%C.48%D.90%Correct answer: B Difficulty level: 26.In a study of 40randomly selected captive Octopus vulgaris, researchers found that the octopi could learn to integrate visual and tactile information to find food after a mean of 119 trials. The estimate had a margin of error of 18 trials at a 95% confidence level. Which of the following is the most reasonable conclusion about the number of trials it would take all captive Octopus vulgaris in general to learn to find the food?A.The evidence suggests that half of them would require 119 or fewer trials.B.The evidence suggests that the mean number of trials would be 119 trials.C.The evidence suggests that the mean number of trials would be between 119 and 137 trials.D.The evidence suggests that the mean number of trials would be between 101 and 137 trials. Correct answer: D Difficulty level: 37.Researchers measured the heart rates of several randomly selected astronauts exercising on stationary bicycles during long-term space missions. The researchers found the mean heart rate of the astronauts was 155 beats per minute with a margin of error of 12 beats per minute at a 90% confidence level. Which of the following is the most plausible value for the mean heart rate of all astronauts exercising on stationary bicycles during long-term space missions?A. 130 beats per minuteB. 140 beats per minuteC. 160 beats per minuteD. 175 beats per minuteCorrect answer: C Difficulty level: 38.In a poll of 14,697 randomly selected adults in the United States, those polled spent an average of $95 per day in November of last year, as compared with $91 per day in November two years ago. The estimates had a margin of error of $4 at the 95% confidence level. Which of the following is a reasonable claim to make based on this sample?A. All adults in the United States spent between $91 and $99 daily last November.B. 95% of adults in the United States spent between $91 and $99 daily last November.C. It is plausible that average daily spending of adults in the United States remained the same inNovember of last year as it was in November two years ago.D. Between 91% and 99% of adults in the United States spent $4 more daily last November thanin November two years ago.Correct answer: C Difficulty level: 39.In a particular county, a sample of the population showed that 84% of the households lived in the same residence as they had the previous year. The estimate had a margin of error of 1.5% at the 90% confidence level. If the county has 50,000 households, which of the following best estimates the number of households that lived in the same residence as they had the previous year, at the 90% confidence level?A. 34,500 to 49,500 residentsB. 37,500 to 50,000 residentsC. 41,250 to 42,750 householdsD. 44,250 to 45,750 householdsCorrect answer: C Difficulty level: 310.Prior to the 2014 elections, 1,000 randomly selected Louisiana voters were surveyed about what single issue would most likely influence their vote. Of those surveyed, 560voters answered that the state of the economy would most influence their vote. Based on this information, which statement about all voters in Louisiana is most appropriate?A.Exactly 56% of all Louisiana voters thought the state of the economy would most influencetheir voting.B.Approximately 56%of all Louisiana voters thought the state of the economy would mostinfluence their voting.C.Exactly 56% of Louisiana voters would vote for the candidate with the best plan to improvethe economy.D.Approximately 56% of Louisiana voters would vote for the candidate with the best plan toimprove the economy.Correct answer: B Difficulty level: 311.A **pany sells bottles of water. A random sample of 50 water bottles found that the bottles contained, on average, 0.96 liters of water, and the estimate had a margin of error of 0.08 liters at the 95% confidence level. Which of the following is a reasonable claim to make based on this sample?A.**pany always fills its water bottles with less than 1 liter of water.B.**pany usually fills its water bottles with between 0.96 liters and 1.04 liters of water.C.**pany always fills its water bottles with between 0.88 liters and 1.04 liters of water.It is plausible that, on average, **pany fills its water bottles with 1 or more liters of water.Correct answer: D Difficulty level: 412.An archaeologist uses an accelerator mass spectrometer to find the age of a buried branch. At the 68% confidence level, the spectrometer estimates that the branch was 10,000 years old with a margin of error of 200 years. Which of the following could the spectrometer estimate as the age of the branch at the 95% confidence level?A.9,500 years old, with a margin of error of 500 yearsB.10,000 years old, with a margin of error of 400 yearsC.9,500 years old, with a margin of error of 50 yearsD.10,000 years old, with a margin of error of 40 yearsCorrect answer: B Difficulty level: 413.A random sample of500residents of a town included 173residents who primarily spoke a language other than English at home, with a margin of error of 25 residents and a confidence level of 98%. If the town has 25,000 residents, how many residents primarily speak a language other than English at home, with the 98% confidence level?A.7,400 to 9,900 residentsB.8,625 to 8,675 residentsC.24,475 to 24,525 residentsD.23,250 to 25,750 residentsCorrect answer: A Difficulty level: 414.In the National Health and Nutrition Examination Survey, 80.5% of the participants had healthy levels of high-density lipoprotein (HDL) cholesterol, the estimate has a margin of error of 1.5% at a confidence level of 95%. The participants were a random sample of United States (US) residents. If the US population at the time of the study was 316 million people, what is the estimate at a 95% confidence level of the number of people in the US who had healthy levels of HDL cholesterol?A.237 million to 246 million peopleB.245million to 264 million peopleC.250 million to 259 million peopleD.254 million to 300 million peopleCorrect answer: C Difficulty level: 415.A university had 150 students registered for an introductory sociology class. The students were randomly assigned to either a section taught with case studies or with lectures. Both sections took the same final exam. Both margins of error are at a 90% confidence level. Which of the following conclusions is the most reasonable regarding the sociology class?A.The university should only offer the lecture teaching method, because students in that sectionhad a higher final exam average.B.The university should not offer either teaching method, case studies or lectures, becauseneither section achieved the target 90% average.C.The university should only offer the lecture teaching method, because the final exam averageplus the margin of error achieved the target 90%.D.The university does not have strong evidence to indicate which teaching method is moreeffective.Correct answer: D Difficulty level: 4。

2024年高二英语数学建模方法单选题30题1.Mathematical modeling often involves collecting and analyzing data. In this process, we need to use some specific tools. What does "analyzing data" mean?A.collecting dataB.presenting dataC.examining dataD.predicting data答案：C。

“analyzing data”的意思是分析数据，也就是对数据进行检查、研究等，C 选项“examining data”（ 检查数据）意思最为接近。

A 选项是收集数据；B 选项是呈现数据；D 选项是预测数据。

2.When we do mathematical modeling, we usually start with defining the problem. What's the synonym of "defining the problem"?A.solving the problemB.describing the problemC.ignoring the problemplicating the problem答案：B。

“defining the problem”是定义问题，B 选项“describing the problem” 描述问题）意思最为接近。

A 选项是解决问题；C 选项是忽略问题；D 选项是使问题复杂。

3.In mathematical modeling, we need to make assumptions. What does "make assumptions" mean?A.guess randomlyB.prove somethingC.make suppositionsD.do experiments答案：C。

数学专业英语-第2章课后答案2.12.比:ratio 比例:proportion 利率:interest rate 速率:speed 除:divide 除法:division 商:quotient 同类量:like quantity 项:term 线段:line segment 角:angle 长度:length 宽:width高度:height 维数:dimension 单位:unit 分数:fraction 百分数:percentage3.(1)一条线段和一个角的比没有意义,他们不是相同类型的量.(2)比较式通过说明一个量是另一个量的多少倍做出的,并且这两个量必须依据相同的单位.(5)为了解一个方程,我们必须移项,直到未知项独自处在方程的一边,这样就可以使它等于另一边的某量.4.(1)Measuring the length of a desk, is actually comparing the length of the desk to that of a ruler.(3)Ratio is different from the measurement, it has no units. The ratio of the length and the width of the same book does not vary when the measurement unit changes.(5)60 percent of students in a school are female students, which mean that 60 students out of every 100 students are female students.2.22.初等几何:elementary geometry 三角学:trigonometry 余弦定理:Law of cosines 勾股定理/毕达哥拉斯定理:Gou-Gu theorem/Pythagoras theorem 角:angle 锐角:acute angle 直角:right angle 同终边的角:conterminal angles 仰角:angle of elevation 俯角:angle of depression 全等:congruence 夹角:included angle 三角形:triangle 三角函数:trigonometric function直角边:leg 斜边:hypotenuse 对边:opposite side 临边:adjacentside 始边:initial side 解三角形:solve a triangle 互相依赖:mutually dependent 表示成:be denoted as 定义为:be defined as3.(1)Trigonometric function of the acute angle shows the mutually dependent relations between each sides and acute angle of the right triangle.(3)If two sides and the included angle of an oblique triangle areknown, then the unknown sides and angles can be found by using the law of cosines.(5)Knowing the length of two sides and the measure of the included angle can determine the shape and size of the triangle. In other words, the two triangles made by these data are congruent.4.(1)如果一个角的顶点在一个笛卡尔坐标系的原点并且它的始边沿着x轴正方向，这个角被称为处于标准位置.(3)仰角和俯角是以一条以水平线为参考位置来测量的,如果正被观测的物体在观测者的上方,那么由水平线和视线所形成的角叫做仰角.如果正被观测的物体在观测者的下方,那么由水平线和视线所形成的的角叫做俯角.(5)如果我们知道一个三角形的两条边的长度和对着其中一条边的角度,我们如何解这个三角形呢?这个问题有一点困难来回答,因为所给的信息可能确定两个三角形,一个三角形或者一个也确定不了.2.32.素数:prime 合数:composite 质因数:prime factor/prime divisor 公倍数:common multiple 正素因子: positive prime divisor 除法算式:division equation 最大公因数:greatest common divisor(G.C.D) 最小公倍数: lowest common multiple(L.C.M) 整除:divide by 整除性:divisibility 过程:process 证明:proof 分类:classification 剩余:remainder辗转相除法:Euclidean algorithm 有限集:finite set 无限的:infinitely 可数的countable 终止:terminate 与矛盾:contrary to3.(1)We need to study by which integers an integer is divisible, that is , what factor it has. Specially, it is sometime required that an integer is expressed as the product of its prime factors.(3)The number 1 is neither a prime nor a composite number;A composite number in addition to being divisible by 1 and itself, can also be divisible by some prime number.(5)The number of the primes bounded above by any given finite integer N can be found by using the method of the sieve Eratosthenes.4.(1)数论中一个重要的问题是哥德巴赫猜想,它是关于偶数作为两个奇素数和的表示.(3)一个数,形如2p-1的素数被称为梅森素数.求出5个这样的数.(5)任意给定的整数m和素数p,p的仅有的正因子是p和1,因此仅有的可能的p和m的正公因子是p和1.因此,我们有结论:如果p是一个素数,m是任意整数,那么p整除m,要么(p,m)=1.2.42.集:set 子集:subset 真子集:proper subset 全集:universe 补集:complement 抽象集:abstract set 并集:union 交集:intersection 元素:element/member 组成:comprise/constitute包含:contain 术语:terminology 概念:concept 上有界:bounded above 上界:upper bound 最小的上界:least upper bound 完备性公理:completeness axiom3.(1)Set theory has become one of the common theoretical foundation and the important tools in many branches of mathematics.(3)Set S itself is the improper subset of S; if set T is a subset of S but not S, then T is called a proper subset of S.(5)The subset T of set S can often be denoted by {x}, that is, T consists of those elements x for which P(x) holds.(7)This example makes the following question become clear, that is, why may two straight lines in the space neither intersect nor parallel.4.(1)设N是所有自然数的集合,如果S是所有偶数的集合,那么它在N中的补集是所有奇数的集合.(3)一个非空集合S称为由上界的,如果存在一个数c具有属性:x<=c对于所有S中的x.这样一个数字c被称为S的上界.(5)从任意两个对象x和y，我们可以形成序列（x，y），它被称为一个有序对，除非x=y，否则它当然不同于（y，x）.如果S和T是任意集合，我们用S*T表示所有有序对（x,y),其中x术语S，y属于T.在R.笛卡尔展示了如何通过实轴和它自己的笛卡尔积来描述平面的点之后，集合S*T 被称为S和T的笛卡尔积.2.52.竖直线:vertical line 水平线:horizontal line 数对:pairs of numbers 有序对:ordered pairs 纵坐标:ordinate 横坐标:abscissas 一一对应:one-to-one 对应点:corresponding points圆锥曲线:conic sections 非空图形:non vacuous graph 直立圆锥:right circular cone 定值角:constant angle 母线:generating line 双曲线:hyperbola 抛物线:parabola 椭圆:ellipse退化的:degenerate 非退化的:nondegenerate 任意的:arbitrarily 相容的:consistent 在几何上:geometrically 二次方程:quadraticequation 判别式:discriminant 行列式:determinant3.(1)In the planar rectangular coordinate system, one can set up aone-to-one correspondence between points and ordered pairs of numbers and also a one-to-one correspondence between conic sections and quadratic equation.(3)The symbol can be used to denote the set of ordered pairs （x，y）such that the ordinate is equal to the cube of the abscissa.（5）According to the values of the discriminate，the non-degenerate graph of Equation （iii）maybe known to be a parabola， a hyperbolaor an ellipse.4.（1）在例1，我们既用了图形，也用了代数的代入法解一个方程组（其中一个方程式二次的，另一个是线性的）。