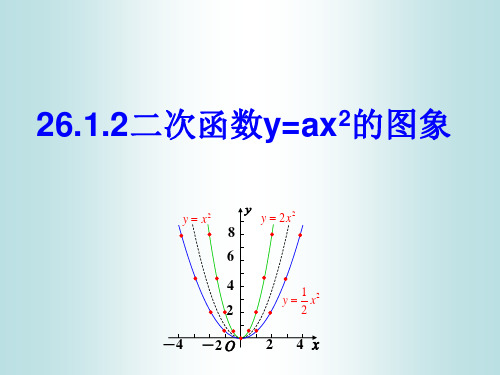
22.1.2 二次函数y=ax2的图象和性质(一)

二次函数y=ax2的图像和性质教案篇一：22.1.2二次函数y=ax2图像与性质教案2123篇二：《二次函数y=ax 的图象和性质》参考教案22.1.2二次函数y?ax2的图象和性质教学目标1．知识与技能能够用描点法作出函数y=ax2的图象，并根据图象认识和理解其性质2．过程与方法经历探索二次函数y=ax2的图象和性质的过程，体会数形结合的思想和方法.3．情感、态度与价值观在初步建立二次函数表达式与图象之间的联系中，体会数形结合与转化，体会数学内在的美感．教学重点难点1．重点函数y=ax2的图象的画法，了解抛物线的含义，理解函数y=ax2的图象与性质．2．难点用描点的方法准确地画出函数y=ax2的图象，掌握其性质特征．教与学互动设计（一）创设情境导入新课导语一回忆一次函数和反比例函数的定义，图象特征，思考二次函数的图象又有何特征呢？导语二展示（用课件或幻灯片）具有抛物线的实例让大家欣赏，议一议这与二次函数有何联系呢？导语三用红色的乒乓球作投篮动作，观察乒乓球的运动路线，思考运动路线有何规律？怎样用数学规律来描述呢？（二）合作交流解读探究1．函数y=ax2的图象画法及相关名称【探究l】画y=x2的图象学生动手实践、尝试画y=x2的图象教师分析，画图像的一般步骤：列表→描点→连线教师在学生完成图象后，在黑板上示范性画出y=x2的图象，如图22-1-1.【共同探究】次函数图像有何特征？特征如下：①形状是开口向上的抛物线②图象关于y轴对称③由最低点，没有最高点.结合图象介绍下列名称：①顶点；②对称轴；③开口及开口方向.图22-1-1图22-1-22．函数y=ax2的图象特征及其性质【探究2】在同一坐标系中，画出y=12x，y=2x2的图象.2学生自己完成此题.教师做个别指导，在学生（大部分）完成后，教师可示范性地画出两函数的图象.如图22-1-2比较图中三个抛物线的异同.相同点：①顶点相同，其坐标都为（0，0）.②对称轴相同，都为y 轴③开口方向相同，它们的开口方向都向上.不同点：开口大小不同.【练一练】画函数y=-x2，y=-施过程）比较函数y=-x2，y=-12x，y=-2x2的图象.找出它们的异同点.212x，y=-2x2的图象.（分析：仿照探究1的实2相同点：①形状都是抛物线.②顶点相同，其坐标都为（0，0）.③对称轴相同，都为y轴④开口方向相同，它们的开口方向都向下.不同点：开口大小不同.【归纳】y=ax2的图象特征：(1)二次函数y=ax2的图象是一条抛物线(2)抛物线y=ax2的对称轴是y轴.顶点时原点.a>0时，抛物线开口向上，顶点时抛物形的最低点.a(3)|a|越大，抛物线y==ax2的开口越小（三）应用迁移巩固提高类型之一如何画好二次函数的图象【点拨】画二次函数图象一般是按以下三个步骤进行.①列表、取值；②描点；③连线但初学者对三个步骤，易犯下列错误，注意避免. 【易错点1】表格中，取值过多或过少.画函数y=ax2图象,取对应值时，一般5组或7组有代表性的对应值即可.．．．【易错点2】连线不是光滑曲线，有的用折线，有的画的过渡不自然，不象抛物线.例1下图是甲、乙、丙三人画得二次函数y=2x2的图象.请你帮助修改.解：图甲中有两个错误的地方.①连线不能用直尺作线段，图象中相邻两点时用光滑曲线连接.②抛物线开口应向上无限延伸，不能到两端点为止.修改见图甲中虚线.图乙中有一个错误，其中有一个点（1，-2）的位置画错.（或表格中对应值算错）修改见图乙中虚线.图丙种错误是x的值都是非负数，没有负数，导致出现其图象只是抛物线的一半，没有对称性.修改见图丙中虚线.【点评】此三类错误是初学者应注意的三个方面，以后的练习中，应提醒大家注意.类型之二函数y=ax2的图象特征的应用例2（1）填空：函数y?()2的图象是，顶点坐标是，对称轴是，开口方向是. 1（2）函数y=x2，y=x2，y=-2x2图象如图所示，请指出三条抛物线的名称.2解：（1）y?()2可化为y=2x2.它的图象是抛物线，顶点坐标为（0，0），对称轴为y轴，开口方向向上.【点评】解析式需化为一般式，再根据图象特征解答，避免发生错误.(2)根据抛物线y=ax2中，a的值的作用来判断，最上面的抛物线为y=x2，中间的为y=12x，x轴下方的为y=-2x22【点评】抛物线y=ax2中a>0时，开口向上.a（四）总结反思拓展升华【总结】1.本节所学知识：①二次函数y=ax2的图象的画法.②二次函数y=ax2的图象特征及其性质.2.本节所用的方法：实践比较法【反思】函数y=ax2与y=-ax2的图象之间有何关系？（它们关于x 轴对称）【拓展】已知函数y=ax2经过(1,2).（1）求a的值.（2）当x(2)根据函数y=2x2知x【点评】①通常用待定系数法函数y=ax2中只有一个待定系数a,故知道其图象上一点坐标或x，y的一组对应值就可求出解析式.②结合图象知：x（五）当堂检测反馈1.抛物线y=4x2中的开口方向是向上，顶点坐标是（0，0），对称轴是y轴.抛物线y=-对称轴是y轴.2.二次函数y=ax2与y=2x2，开口大小，形状一样，开口方向相反，则a=2.【分析】a与-2互为相反数13.在同一坐标系中：①y=x2，②y=-x2，③y=2x2这三个函数图象开口最大212x的开口方向是向下，顶点坐标是（0，0），4的是①y?12x2，开口向下的是②y=-x21解：∵||2∵函数y=-x2中，二次项系数为-114.二次函数y=2x2，y=-2x2，y=x22点（0，0）；②对称轴相同，都是y轴.5．已知抛物线的顶点在原点，对称轴是y轴，且经过(-3,2).求此抛物线的解析式，并指出x>0时，y随x的变化情况.解：设此抛物线的解析式为y=ax2,∵此抛物线过点（-3，2），∴2=a·(-3)2,。

教 学 内 容一、探索新知：画二次函数y ＝x 2的图象． 列表：x … －3 －2 －1 0 1 2 3y ＝x 2…描点，并连线由图象可得二次函数y ＝x 2的性质：1．二次函数y ＝x 2是一条曲线，把这条曲线叫做______________． 2．二次函数y ＝x 2中，二次函数a ＝_______，抛物线y ＝x 2的图象开口______． 3．自变量x 的取值X 围是____________．4．观察图象，当两点的横坐标互为相反数时，函数y 值相等，所描出的各对应点关于________对称，从而图象关于___________对称．5．抛物线y ＝x 2与它的对称轴的交点（ ， ）叫做抛物线y ＝x 2的______． 因此，抛物线与对称轴的交点叫做抛物线的_____________． 6．抛物线y ＝x 2有____________点（填“最高”或“最低”） ． 二、例题分析例1 在同一直角坐标系中，画出函数y ＝12x 2，y ＝x 2，y ＝2x 2的图象．解：列表并填：x…－4 －3 －2 －112341．填表：开口方向顶点 对称轴有最高或最低点最值y ＝23 x 2当x ＝____时，y 有最_______值，是_y ＝－8x 22．若二次函数y ＝ax 2的图象过点（1，－2），则a 的值是___________． 3．二次函数y ＝(m －1)x 2的图象开口向下，则m____________． 4．如图，① y ＝ax 2② y ＝bx 2③ y ＝cx 2 ④ y ＝dx 2比较a 、b 、c 、d 的大小，用“＞”连接．___________________________________七、目标检测1．函数y ＝37x 2的图象开口向_______，顶点是__________，对称轴是________，当x ＝___________时，有最_________值是_________． 2．二次函数y ＝mx22 m 有最低点，则m ＝___________．3．二次函数y ＝(k ＋1)x 2的图象如图所示，则k 的取值 X 围为___________．4．写出一个过点（1，2）的函数表达式_________________． 六、教学效果追忆:。

人教版2021年九年级上册：22.1.2：二次函数y=ax2的图像和性质课时练习一．选择题1．抛物线y＝4x2与y＝﹣2x2的图象，开口较大的是（）A．y＝﹣2x2B．y＝4x2C．同样大D．无法确定2．在同一平面直角坐标系中，二次函数y＝3x2，y＝﹣3x2，y＝﹣x2图象的共同点是（）A．都关于x轴对称，抛物线开口向上B．都关于y轴对称，抛物线开口向下C．都关于y轴对称，顶点都是原点D．都关于原点对称，顶点都是原点3．二次函数y＝ax2与一次函数y＝ax+a在同一坐标系中的大致图象可能是（）A．B．C．D．4．在同一直角坐标系中，一次函数y＝﹣kx+1与二次函数y＝x2+k的大致图象可以是（）A．B．C．D．5．两个二次函数的图象如图所示，其中一个是y＝x2，另一个是y＝ax2，则a可能的取值为（）A．1B．C．D．﹣6．已知函数y1＝x2与函数y2＝的图象大致如图．若y1＜y2，则自变量x的取值范围是（）A．＜x＜2B．x＞2或x＜C．﹣2＜x＜D．x＜﹣2或x＞二．填空题7．二次函数y＝x2的图象开口方向是（填“向上”或“向下”）．8．抛物线的对称轴为．9．已知抛物线的解析式为y＝﹣2x2+1，则抛物线的顶点坐标为．10．抛物线y＝﹣2x2沿着x轴正方向看，在y轴的左侧部分是．（填“上升”或“下降”）11．已知两个二次函数的图象如图所示，那么a1a2（填“＞”、“＝”或“＜”）．12．若函数y＝﹣x2+9的函数值y＞0，则自变量x的取值范围是．13．若函数y＝3x2与直线y＝kx+3的交点为（2，b），则k＝，b＝．14．二次函数y＝x2的函数图象如图，点A0位于坐标原点，点A1，A2，A3…A10在y轴的正半轴上，点B1，B2，B3…B10在二次函数y＝x2位于第一象限的图象上，△A0B1A1，△A1B2A2，△A2B3A3…△A9B10A10都为等边三角形，则△A9B10A10的边长为．三．解答题15．在同一平面直角坐标系中，画出下列函数的图象．（1）y＝2x2；（2）y＝x2．16．不画图象，说出抛物线y＝﹣x2的对称轴、顶点坐标、开口方向及最高（低）点坐标．17．已知二次函数y＝ax2的图象经过点P（2，5），试确定它的开口方向和a的值．18．已知函数y＝（m﹣3）是关于x的二次函数．（1）求满足条件的m的值；（2）当m为何值时，它的图象有最低点？此时当x为何值时，y随x的增大而增大？（3）当m为何值时，它的图象有最高点？此时当x为何值时，y随x的增大而减小？参考答案一．选择题1．解：抛物线y＝4x2与y＝﹣2x2的图象中|4|＝4，|﹣2|＝2，∵4＞2，∴抛物线y＝4x2的开口小于y＝﹣2x2的开口，故选：A．2．解：A、都关于y轴对称，但开口方向有的向下，故错误；B、都关于y轴对称，但开口方向有的向上，故错误；C、都关于y轴对称，顶点都是原点，故正确；D、都关于y轴对称，故错误，故选：C．3．解：由一次函数y＝ax+a可知，一次函数的图象与x轴交于点（﹣1，0），排除A、B；当a＞0时，二次函数y＝ax2开口向上，一次函数y＝ax+a经过一、二、三象限，当a＜0时，二次函数开口向下，一次函数经过二、三、四象限，排除C；故选：D．4．解：由y＝x2+k可知抛物线的开口向上，故B不合题意；∵二次函数y＝x2+k与y轴交于负半轴，则k＜0，∴﹣k＞0，∴一次函数y＝﹣kx+1的图象经过经过第一、二、三象限，A选项符合题意，C、D不符合题意；故选：A．5．解：由图象知，二次函数y＝ax2图象的开口向上，且小于二次函数y＝x2的图象的开口，∴a＞，故选：A．6．解：由y1＝y2，即x2＝，解得：x1＝﹣2，x2＝．由图象可知，若y1＜y2，则自变量x的取值范围是﹣2＜x＜．故选：C．二．填空题7．解：由y＝x2得：a＞0，∴二次函数图象开口向上．故答案为：向上．8．解：∵a＝，b＝0，∴x＝﹣＝0，故答案为直线x＝0或y轴．9．解：∵抛物线的解析式为y＝﹣2x2+1，∴该抛物线的顶点坐标为（0，1），故答案为：（0，1）．10．解：∵抛物线y＝﹣2x2的开口向下，对称轴为y轴，∴在对称轴左侧y随x的增大而增大，∴抛物线y＝﹣2x2在y轴左侧的部分是上升的，故答案为：上升．11．解：如图所示y＝a1x2的开口大于y＝a2x2的开口，开口向下，则a2＜a1＜0，故答案为：＞．12．解：如图，∵函数y＝﹣x2+9的函数值y＞0，∴﹣x2+9＞0，解得﹣3＜x＜3，故答案为﹣3＜x＜3．13．解：根据题意，把（2，b）代入y＝3x2中，得b＝12；再把交点（2，12）代入y＝kx+3中，得k＝4.5．14．解：∵△A0B1A1是等边三角形，∴∠A1A0B1＝60°，∴A0B1的解析式为y＝x，联立，解得，（为原点，舍去），∴点B1（，），∴等边△A0B1A1的边长为×2＝1，同理，A1B2的解析式为y ＝x+1，联立，解得，（在第二象限，舍去），∴B2（，2），∴等边△A1B2A2的边长A1A2＝2×（2﹣1）＝2，同理可求出B3（，），所以，等边△A2B3A3的边长A2A3＝2×（﹣1﹣2）＝3，…，以此类推，系列等边三角形的边长为从1开始的连续自然数，△A9B10A10的边长A9A10＝10．故答案为：10．三．解答题15．解：列表得：﹣2﹣101282028 y＝2x2y ＝x2202描点、连线可得图象为：16．解：抛物线y＝﹣x2的对称轴为y轴，顶点坐标为（0，0），开口方向下，最高点坐标（0，0）；17．解：∵二次函数y＝ax2的图象经过点P（2，5），∴4a＝5，解得a＝，∴开口方向向上．18．解：（1）根据题意得m﹣3≠0且m2﹣2m﹣6＝2，解得m1＝﹣2，m2＝4．所以满足条件的m的值为﹣2或4；（2）∵当m﹣3＞0时，图象有最低点，∴m＝4，此时二次函数的解析式为y＝x2，∴当x＞0时，y随x的增大而增大；（3））∵当m﹣3＜0时，图象有最高点，∴m＝﹣2，此时二次函数的解析式为y＝﹣5x2，∴当x＞0时，y随x的增大而减小．。