数据结构应用题整理

一、应用题1. 已知关键字序列为：（74,33,52,41,13,88,66,59）哈希表长为9，哈希函数为：H (k)＝k %9，解决冲突用线性补偿探测法 （取Q=5），试构造哈希表，并求出等概率下查找成功的平均查找长度。

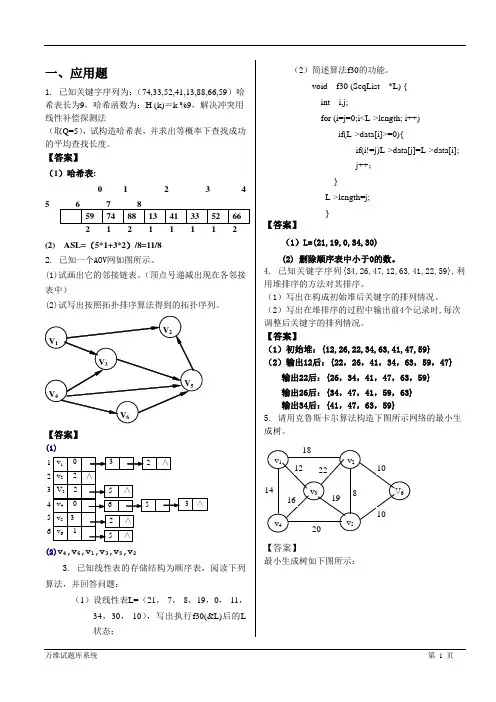
【答案】（1）哈希表:0 1 2 3 4 5 6 7 859 74 88 13 4133 52 6621211112(2) ASL=（5*1+3*2）/8=11/82. 已知一个AOV 网如图所示。

(1)试画出它的邻接链表。

（顶点号递减出现在各邻接表中）(2)试写出按照拓扑排序算法得到的拓扑序列。

V 6V 1V 2V 4V 5V 3【答案】(1)1 v 1 06v 6 1 5 v 5 3 3V 3 2 4v 4 0 2v 2 2 ∧ 6 53 ∧5 ∧5 ∧2 ∧32 ∧(2)v 4,v 6,v 1,v 3,v 5,v 23. 已知线性表的存储结构为顺序表，阅读下列算法，并回答问题：（1）设线性表L=（21，-7，-8，19，0，-11，34，30，-10），写出执行f30(&L)后的L 状态；（2）简述算法f30的功能。

void f30 (SeqList *L) { int i,j;for (i=j=0;i<L->length; i++)if(L->data[i]>=0){if(i!=j)L->data[j]=L->data[i]; j++； } L->length=j; }【答案】（1）L=(21,19,0,34,30)(2) 删除顺序表中小于0的数。

4. 已知关键字序列{34,26,47,12,63,41,22,59},利用堆排序的方法对其排序。

（1）写出在构成初始堆后关键字的排列情况。

（2）写出在堆排序的过程中输出前4个记录时,每次调整后关键字的排列情况。

【答案】（1）初始堆：{12,26,22,34,63,41,47,59}（2）输出12后：{22，26，41，34，63，59，47} 输出22后：{26，34，41，47，63，59} 输出26后：{34，47，41，59，63} 输出34后：{41，47，63，59}5. 请用克鲁斯卡尔算法构造下图所示网络的最小生成树。

数据结构试题及答案⼀、选择题（共10题，每题1分，共10分）1．下⾯关于线性表的叙述中，错误的是哪⼀个？（）A．线性表采⽤顺序存储，必须占⽤⼀⽚连续的存储单元B．线性表采⽤顺序存储，便于进⾏插⼊和删除操作C．线性表采⽤链接存储，不必占⽤⼀⽚连续的存储单元D．线性表采⽤链接存储，便于插⼊和删除操作2．在⼀个单链表中，已知q所指结点是p所指结点的前驱，若在p和q之间插⼊s所指结点，则执⾏的操作是（）。

A. s->next=p->next;p->next=s;B. q->next=s;s->next=p;C. p->next=s->next;s->next=p;D. p->next=s;s->next=q;3．设有三个元素X，Y，Z顺序进栈，下列得不到的出栈排列是( )。

A．XYZ B. YZX C. ZXY D. ZYX4．若⽤⼀个长度为6的数组来实现循环队列，且当前rear和front的值分别为0和3，则从队列中删除⼀个元素，再增加两个元素后，rear和front的值分别是( )。

A．1和5 B．2和4 C．4和2 D. 5和15．下列说法中正确的是（）。

A．⼆叉树就是度为2的树 B．⼆叉树中不存在度⼤于2的结点C．⼆叉树中⾄少有⼀个结点的度为2 D．⼆叉树中任何⼀个结点的度都为2 6．在具有n个结点的⼆叉链表中，共有（）个空指针。

A. nB. n-1C. n+1D. 不确定7．根据⼆叉树与树的转换关系可知，深度为h的满⼆叉树对应的森林由（）棵树构成。

A．1 B．log2n C. h/2 D. h8．在⼀个⽆向图中，所有顶点的度数之和等于所有边数的（）倍。

A．1/2 B．1 C. 2 D. 49．对17个元素的查找表做折半查找，则查找长度为5的元素下标依次是（）。

A．8,17 Ｂ．5,10,12 C．9,16 D．9,1710．关于排序，下列说法中正确的是（）。

北京语言大学网络教育学院《数据结构》【应用题】（1、已知序列（12，4，17，10，7，30），用直接选择排序法对其进行递增排序，写出每一趟的排序结果。

答：第1趟：4 12 17 10 7 30第2趟：4 7 17 10 12 30第3趟：4 7 10 17 12 30第4趟：4 7 10 12 17 30第5趟：4 7 10 12 17 302、单链表结点的类型定义如下：typedef struct LNode {int data;struct LNode *next;} LNode, *Linklist;写一算法，将带头结点的有序单链表A和B合并成一新的有序表C。

（注:不破坏A和B的原有结构）答：Merge(Linklist A, Linklist B, Linklist &C )void Merge(Linklist A, Linklist B, Linklist &C){ C=(Linklist)malloc(sizeof(LNode));pa=A->next; pb=B->next; pc=C;while(pa&&pb){ pc->next=(Linklist)malloc(sizeof(LNode));pc=pc->next;if(pa->data<=pb->data){ pc->data=pa->data; pa=pa->next;}else{ pc->data=pb->data; pb=pb->next;}}if(!pa) pa=pb;while(pa){ pc->next=(Linklist)malloc(sizeof(LNode));pc=pc->next;pc->data=pa->data; pa=pa->next;}pc->next=NULL；}3、已知一棵非空二叉树，其按中序和后序遍历的结果分别为：中序：CGBAHEDJFI 后序：GBCHEJIFDA请画出这棵二叉树，并写出其前序遍历的结果。

一．《树》应用题1. 已知一棵树边的集合为{<i，m>，<i，n>，<e，i>，<b，e>，<b，d>，<a，b>，<g，j>，<g，k>，<c，g>，<c，f>，<h，l>，<c，h>，<a，c>}，请画出这棵树，并回答下列问题：（1）哪个是根结点？（2）哪些是叶子结点？（3）哪个是结点g的双亲？（4）哪些是结点g的祖先？（5）哪些是结点g的孩子？（6）哪些是结点e的孩子？（7）哪些是结点e的兄弟？哪些是结点f的兄弟？（8）结点b和n的层次号分别是什么？（9）树的深度是多少？（10）以结点c为根的子树深度是多少？2. 一棵度为2的树与一棵二叉树有何区别。

3. 试分别画出具有3个结点的树和二叉树的所有不同形态？4. 已知用一维数组存放的一棵完全二叉树：ABCDEFGHIJKL，写出该二叉树的先序、中序和后序遍历序列。

5. 一棵深度为H的满m叉树有如下性质：第H层上的结点都是叶子结点，其余各层上每个结点都有m棵非空子树，如果按层次自上至下，从左到右顺序从1开始对全部结点编号，回答下列问题：（1）各层的结点数目是多少？（2）编号为n的结点的父结点如果存在，编号是多少？（3）编号为n的结点的第i个孩子结点如果存在，编号是多少？（4）编号为n的结点有右兄弟的条件是什么？其右兄弟的编号是多少？6. 找出所有满足下列条件的二叉树：（1）它们在先序遍历和中序遍历时，得到的遍历序列相同；（2）它们在后序遍历和中序遍历时，得到的遍历序列相同；（3）它们在先序遍历和后序遍历时，得到的遍历序列相同；7. 假设一棵二叉树的先序序列为EBADCFHGIKJ，中序序列为ABCDEFGHIJK，请写出该二叉树的后序遍历序列。

8. 假设一棵二叉树的后序序列为DCEGBFHKJIA，中序序列为DCBGEAHFIJK，请写出该二叉树的后序遍历序列。

《数据结构》――应用题复习概要2022年4月1.写出执行下列程序段时，语句S的执行次数。

for (i=1; i<n; i++)for (j=n; j>=i; j--)S;2.假设n为2的乘幂，并且n>2，试求下列算法的时间复杂度及变量count的值（以n的函数形式表示）int Time(int n){ int count:=0; x:=2;while (x<n/2){ x:=2*x; count:=count +1 };return (count);}3.已知双向链表、指针P、Q所指的结点和结点的结构（数据域DATA、指针域LL及RL），分别画出经过下述算法后的双向链表。

(1)Q->RL = P->RL; P->RL = Q; Q->RL->LL = Q; Q->LL = P;(2)Q->RL = P; P->LL->RL = Q; Q->LL = P->LL; P->LL = Q;(3)P->LL->RL = P->RL; P->RL->LL = P->LL;4.设栈S的初始状态为空，元素a, b, c, d, e和f依次通过栈S，试分析下列各组出栈次序，每组所用的最大容量。

（1）a,b,c,d,e,f；（2）f,e,d,c,b,a；（3）b,d,c,f,e,a5.有字符串A+B*C-D，试写出利用栈操作将该字符串序列改为ABC*+D-的操作步骤，这里用X和S分别表示字符的进栈和出栈操作（例如把字符ABCD改为ACBD的操作步骤为XSXXSSXS）。

XSXXSXXSSSXXSS6.一棵二叉树的结点数采用顺序存储结构，存于下列数组T中，画出该二叉树。

b7.已知一棵树的双亲表示如下，其中各兄弟结点依此排列，试画出该树及对应的孩子兄弟表示的二叉树。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Data A B C D E F G H I J K L M N OParent 0 1 1 1 2 2 3 3 4 4 5 6 6 7 8ABE CDK FLMGN HOIJ8.有一个完全二叉树按层次顺序存放在一维数组中，如下所示：请指出结点P的父结点，左子女，右子女。

《数据结构》应用题参考习题数据结构是计算机科学中的一门基础课程，它主要研究数据的组织、存储和管理方式，以及不同数据结构对算法执行效率的影响。

在实际应用中，数据结构起到了至关重要的作用。

本文将介绍一些《数据结构》的应用题，并给出相应的参考习题。

一、栈的应用题1. 符号匹配问题问题描述：给定一个字符串，在其中包含了一些圆括号"()"、方括号"[]"和花括号"{}"，判断字符中的括号是否匹配。

例题：判断字符串"{[()]()}"是否匹配。

解题思路：利用栈的先进后出特点，遍历字符串中的每个字符。

如果是左括号，则入栈；如果是右括号，则判断栈顶元素是否与之匹配。

参考习题：编写一个程序，实现括号匹配的功能，并输出匹配结果。

二、队列的应用题1. 循环队列的应用问题描述：设计一个循环队列，实现入队、出队等基本操作。

解题思路：利用数组实现循环队列，需要设置一个队头指针front和一个队尾指针rear。

入队操作时，将元素添加到rear位置；出队操作时，返回front位置元素，并将front后移。

参考习题：实现一个循环队列，并进行相关操作的测试。

三、链表的应用题1. 单链表反转问题描述：给定一个单链表，将其反转。

例题：将链表1->2->3->4->5反转为5->4->3->2->1。

解题思路：利用三个指针prev、cur和next，依次遍历链表，并修改指针指向实现链表的反转。

参考习题：编写一个程序，实现单链表反转，并输出反转后的链表。

四、树的应用题1. 二叉树的遍历问题描述：给定一个二叉树，实现它的前序遍历、中序遍历和后序遍历。

解题思路：分别使用递归和迭代的方式实现二叉树的前序遍历、中序遍历和后序遍历。

参考习题：编写一个程序，实现二叉树的前序遍历、中序遍历和后序遍历，并输出遍历结果。

五、图的应用题1. 图的最短路径问题描述：给定一个有向图，求两个顶点之间的最短路径。

2024王导数据结构综合应用题假设2024年，王导是一位深受学生喜爱的计算机科学导师。

他设计了一道综合应用题，旨在考察学生对数据结构的应用能力。

以下是题目内容和解答。

题目：在2024年的某个国家，有许多城市需要进行道路规划。

每个城市可以通过道路连接到其他城市，形成一个网络。

现有一份城市之间的道路连接关系表，其中包含了城市之间可以直接通行的道路及其长度。

请设计一个算法，找到所有城市之间的最短路径及其长度。

解答：为了解决这个问题，我们可以使用图的最短路径算法。

以下是一种常用的算法——Dijkstra算法。

1. 创建一个集合S，用于存放已经找到最短路径的城市，初始时为空。

2. 创建一个数组dist，用于存放每个城市到起点的最短路径长度，初始时所有元素为无穷大。

3. 选取一个起点，设置dist[起点]为0，并将起点加入集合S。

4. 对于起点相邻的每个城市，更新其到起点的最短路径长度，并将其加入集合S。

5. 从剩余的城市中选取一个离起点最近的城市u，将它加入集合S。

6. 对于每个城市v，如果v不在集合S中且通过u可以找到更短的路径，则更新其最短路径长度，并将其加入集合S。

7. 重复步骤5和步骤6，直到所有城市都加入集合S。

使用Dijkstra算法可以找到起点到所有城市的最短路径及其长度。

在这里可以使用优先队列（最小堆）来存储城市和最短路径长度的对应关系，以提高算法效率。

接下来我们以一个具体的例子来说明算法的步骤。

假设有4个城市，用数字1、2、3、4代表，它们之间的道路如下：- 城市1和城市2之间有一条长度为5的道路。

- 城市1和城市3之间有一条长度为9的道路。

- 城市2和城市3之间有一条长度为2的道路。

- 城市2和城市4之间有一条长度为6的道路。

- 城市3和城市4之间有一条长度为3的道路。

现在我们以城市1为起点，按照Dijkstra算法的步骤来求解最短路径及其长度。

1. 初始化操作：- 集合S = {1}，dist = [0, ∞, ∞, ∞]，表示起点到各个城市的最短路径长度。

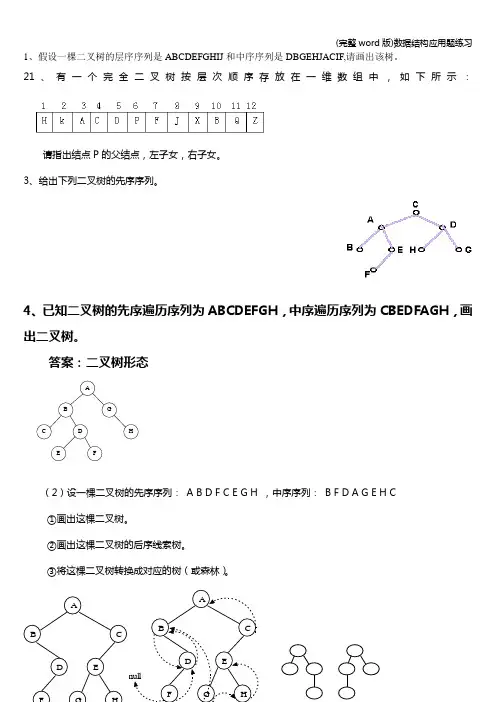
1、假设一棵二叉树的层序序列是ABCDEFGHIJ 和中序序列是DBGEHJACIF,请画出该树。

21、有一个完全二叉树按层次顺序存放在一维数组中，如下所示：请指出结点P 的父结点，左子女，右子女。

3、给出下列二叉树的先序序列。

4、已知二叉树的先序遍历序列为ABCDEFGH ，中序遍历序列为CBEDFAGH ，画出二叉树。

答案：二叉树形态AFHGDECB（2）设一棵二叉树的先序序列： A B D F C E G H ，中序序列： B F D A G E H C ①画出这棵二叉树。

②画出这棵二叉树的后序线索树。

③将这棵二叉树转换成对应的树（或森林）。

ABFD CE HG(1) (2)1、已知一棵二叉树的前序序列为：A,B,D,G,J,E,H,C,F,I,K,L中序序列：D,J,G,B,E,H, A,C,K,I,L,F。

i.写出该二叉树的后序序列；ii.画出该二叉树；iii.求该二叉树的高度(假定空树的高度为－1)和度为2、度为1、及度为0的结点个数。

该二叉树的后序序列为：J,G,D,H,E,B,K,L,I,F,C,A。

该二叉树的形式如图所示：该二叉树高度为：5。

度为2的结点的个数为：3。

度为1的结点的个数为：5。

度为0的结点个数为：4。

5、试用权集合{12,4,5,6,1,2}构造哈夫曼树，并计算哈夫曼树的带权路径长度。

答案：215611187341230WPL=12*1+(4+5+6)*3+(1+2)*4=12+45+12=696、已知权值集合为{5,7,2,3,6,9}，要求给出哈夫曼树，并计算带权路径长度WPL 。

答案：(1)树形态：325510199761332(2)带权路径长度：WPL=(6+7+9)*2+5*3+(2+3)*4=44+15+20=79（3） 假设用于通信的电文仅由8个字母组成，字母在电文中出现的频率分别为0.07，0.19，0.02，0.06，0.32，0.03，0.21，0.10。

数据结构习题(包含全部答案解析)数据结构习题（包含全部答案解析）1. 塔的问题题目描述：有三个塔，分别是A、B和C，A塔上有n个盘子，按照从小到大的顺序叠放。

现在要将这些盘子从A塔移动到C塔，并且每次只能移动一个盘子，并且在移动过程中保持大盘子在下，小盘子在上的顺序。

求移动的步骤。

解析：这道题可以使用递归来解决。

将问题分解为两个子问题：将n-1个盘子从A塔移动到B塔，然后将最后一个盘子从A塔移动到C 塔，最后再将n-1个盘子从B塔移动到C塔。

步骤如下：1）如果n等于1，直接将盘子从A塔移动到C塔；2）否则，执行以下步骤：a) 将n-1个盘子从A塔移动到B塔，使用C塔作为中转塔；b) 将最后一个盘子从A塔移动到C塔；c) 将n-1个盘子从B塔移动到C塔，使用A塔作为中转塔。

2. 链表问题题目描述：给定一个链表，判断链表是否存在环。

解析：这道题可以使用快慢指针的思想来解决。

定义两个指针fast和slow，初始时都指向链表的头节点。

fast指针每次向后移动两个节点，slow指针每次向后移动一个节点。

如果链表中存在环，则fast指针一定会在某个时刻追上slow指针。

步骤如下：1）定义两个指针fast和slow，初始时都指向链表的头节点；2）使用一个while循环，判断条件是fast指针不为空且其下一个节点也不为空；3）在循环中，fast指针每次向后移动两个节点，slow指针每次向后移动一个节点；4）如果fast指针和slow指针相遇，则链表存在环，返回true；5）如果fast指针和slow指针永远不相遇，则链表不存在环，返回false。

3. 栈的应用题目描述：给定一个只包含'('和')'的字符串，判断该字符串是否是有效的括号序列。

解析：这道题可以使用栈来解决。

遍历字符串的每一个字符，如果是左括号，将其压入栈中；如果是右括号，判断栈顶的字符是否与该右括号匹配，若匹配则出栈，若不匹配则该字符串不是有效的括号序列。