九年级上册垂径定理,圆心角及圆周角的综合测试题

专题08垂径定理、圆心角、圆周角之六大题型利用垂径定理求值【答案】2【分析】根据垂径定理和勾股定理列方程求解即可．【详解】解：设OC=△中，由勾股定理得，在Rt COE【变式训练】【答案】45cm/4【分析】连接BO，延长22=，即可求解．BC OB OC-【详解】解：如图，连接=，由折叠得：CD CEQ D是OC的中点，\=，CD OD\==，CE CD OD2\==，4OC OE【答案】310【分析】由题意易得【详解】解：连接OD∵AB 是O e 的直径，AB ∴152OD OB AB ===，∵CD AB ^，6CD =，∴13,2DE CD DEO ==Ð∴22OE OD DE =-=垂径定理的实际应用【点睛】本题考查了勾股定理和垂径定理，灵活运用所学知识，掌握垂直于弦的直径平分弦，且平分弦所对的弧，是解决本题的关键．【变式训练】1．（2023上·福建龙岩·九年级统考期末）筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧．如图1，点M 表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心O （O 在水面上方）为圆心的圆，且圆O 被水面截得的弦AB 长为8米．若筒车工作时，盛水桶在水面以下的最大深度为2米，则这个圆的半径为（ ）A ．2米B ．3米C ．4米D ．5米【答案】D 【分析】过圆O 作OD AB ^于E ，如图所示，由垂径定理可知4AE BE ==，设圆的半径为r ，再利用勾股定理列方程求解即可得到答案．【详解】解：过圆O 作OD AB ^于E ，如图所示：Q 弦AB 长为8米，\4AE BE ==，Q 盛水桶在水面以下的最大深度为2米，设圆的半径为r ，在Rt AOE △中，90AEO Ð=°，OA r =，4AE =，2OE OD ED r =-=-，则由勾【答案】26【分析】连接AO ，依题意，得出222AO AC CO =+，解方程即可求解．【详解】解：如图所示，连接∵1CD =，10AB =，AB ∴5AC =，设半径为r ，则AO r =在Rt AOC V 中，2AO =利用弧、弦、圆心角的关系求解A．AB OC=C．12ABC BOC Ð+Ð=【答案】D 【变式训练】【答案】80°/80度【分析】利用等腰三角形的性质和三角形内角和计算出即可求出答案．Ð【详解】解：∵OBC半圆（直径）所对的圆周角是直角A．43【答案】B【分析】如图：连接AQ QB=，最后根据勾股定理即可解答．【点睛】本题主要考查了圆周角定理、等腰三角形的判定与性质、勾股定理等知识点，灵活运用勾股定理成为解答本题的关键．【变式训练】【答案】13【分析】连接BD ，先由三角形内角和定理求出求出30ABD Ð=°，即有【详解】解：连接BD∵在ABC V 中，55B Ð=∴60A Ð=°，∵AB 为O e 的直径，∴90ADB CDB Ð=Ð=°Ð的度数；(1)求BAC(2)若点E为OB中点，CE 【答案】(1)45°(2)3590°的圆周角所对的弦是直径例题：（2023上·广东汕头DA DC =，2AB BC ==【答案】32【分析】连接AC ，过点角三角形，勾股定理求得∵90ADC Ð=°，∴AC 是直径，∴90ABC Ð=°【变式训练】1．（2023上·山东济南·九年级统考期末）如图，正方形ABCD 中，4AB =，E 点沿线段AD 由A 向D【答案】2p【分析】连接BD 交EF 于点1222OB OD BD ===，再由∵四边形ABCD 是正方形，∴4BC AB AD ===，EDO Ð∴242BD AB ==，【答案】90°Ð【分析】（1）由ABP （2）首先证明点P理求出OC即可得到则OP OA OB ==，\点P 在以AB 为直径的O e 在Rt BCO V 中，90OBC Ð=225OC BO BC \=+=，532PC OC OP =-=-=，已知圆内接四边形求角度【答案】102°【分析】根据圆内接四边形的性质得出【详解】解：∵四边形∴180A DCB Ð+Ð=°，又180DCE DCB Ð+Ð=°，∴102DCE A ÐÐ==°，故答案为102°．【点睛】本题主要考查了圆内接四边形的性质，熟知圆内接四边形的对角互补是解决此题的关键．【变式训练】【答案】40【分析】根据已知可得»»BCBD =56DAC BAC BAD Ð=Ð+Ð=°，再利用圆内接四边形对角互补以及平角的定义可得56DBE DAC Ð=Ð=°，继而利用角平分线定义及三角形内角和定理即可求解．(1)求证：A AEBÐ=Ð(2)若90Ð=°，点CEDC【答案】(1)见解析e的半径为25 (2)O一、单选题1．（2023上·河北张家口·九年级统考期末）O e 中的一段劣弧»AB 的度数为80o ，则AOB Ð=（ ）A ．10oB ．80oC ．170oD ．180o【答案】B 【分析】根据圆心角、弧、弦之间的关系得出答案即可．【详解】解：Q O e 中的一段劣弧»AB 的度数为80°，80AOB \Ð=°，故选：B ．A ．32°B ．42【答案】A 【分析】先根据同弧所对的圆周角相等得到小即可．【详解】解：∵50A Ð=°，∴50D A Ð=Ð=°，A ．10【答案】D∴12AH BH AB===在Rt BOHV中，OH∴线段OP长的最小值为A．105°B．110【答案】D【分析】先根据圆内接四边形的性质和平角的定义求出求解．A ．1米B ．()35+米C ．3米【答案】D 【分析】连接OC 交AB 于D ，根据圆的性质和垂径定理可知理求得OD 的长，由CD OC OD =-即可求解．则OC AB ^，12AD BD AB ==在Rt OAD △中，3OA =，AD ∴225OD AO AD =-=，【点睛】本题考查圆的性质、垂径定理、勾股定理，熟练掌握垂径定理是解答的关键．【答案】120【分析】过O 点作OD AC ^AD CD =，根据三角形中位线定理可得由折叠可得：12OD OE ==∵AB 是直径，∴90ACB Ð=°，12OD BC =【答案】64°/64度【分析】根据在同圆中，Ð=Ð可推出AOC BOD【详解】解：Q»AE=【答案】3【分析】由圆的性质可得OA后根据中位线的性质即可解答．【答案】45【分析】连接AC ，如图所示，由直径所对的圆周角为直角可知及勾股定理求出AC 【详解】解：连接Q OC AB ^，AB =12AD BD AB \==在Rt AOD V 中，OA 420r \=，解得r【答案】4【分析】如图，连接CD直角三角形斜边上的中线等于斜边的一半可得【点睛】本题考查直径所对的圆周角为直角，直角三角形斜边上的中线等于斜边的一半，勾股定理．掌握直径所对的圆周角为直角是解题的关键．三、解答题e的直径AB垂直于弦CD，垂足为E，11．（2023上·安徽合肥·九年级统考期末）如图，O，．==28AE CD(1)求O e 的半径长；(2)连接 BC ，作OF BC ^【答案】(1)5(2)5在Rt OCE V 中，2OE ∴()22224R R -+=，解得5R =，∴O e 的半径长为5；(1)若这个输水管道有水部分的水面宽半径；OE AB ^Q ，11168cm 22BD AB \==´=(1)连接AD，求证：(2)若52,==CD AB 【答案】(1)详见解析；(2)6Ð相等吗？为什么？(1)BAFÐ和CAD^，垂足为(2)过圆心O作OH AB【答案】(1)相等，理由见解析(2)10【详解】（1）解：连接BF ，Q AF 是O e 的直径，90F BAF \Ð+Ð=°Q AC BD ^，\90CAD BDA Ð+Ð=°，Q F BDA Ð=Ð，\BAF CAD Ð=Ð．（2）解：OH AB ^Q ，AH BH \=，OA OF =Q ，210BF OH \==，BAF CAD Ð=ÐQ ，10CD BF \==．【点睛】本题考查的是圆周角定理，等角的余角相等，圆心角、弦的关系，三角形的中位线性质，垂径定理，掌握圆心角、弦的关系，三角形的中位线性质以及垂径定理是解题的关键．15．（2023上·山东威海·九年级统考期末）【初识模型】如图1，在ABC V 中，,90AB AC BAC =Ð=°．点D 为BC 边上一点，以AD 为边作ADE V ，使=90DAE а，AE AD =，连接CE ，则CE 与BD 的数量关系是__________；【构建模型】如图2，ABC V 内接于,O BC e 为O e 的直径，AB AC =，点E 为弧AC 上一点，连接,,AE BE CE ．若3,9CE BE ==，求AE 的长；【运用模型】如图3，等边ABC V 内接于O e ，点E 为弧AC 上一点，连接,,AE BE CE ．若6,10CE BE ==，求AE 的长．【答案】（1）BD CE =；（2）32；（3）4【分析】（1）只需要利用SAS 证明BAD CAE V V ≌，即可证明BD CE =（2）如图所示，过点A 作AD AE ^交BE 于D ，由BC 是直径，得到明BAD CAE Ð=Ð，再证明45ADE AED Ð=Ð=°，得到AD AE =，即可证明2（3）如图所示，在BE 上取一点∵ABC V 是等边三角形，∴60AB AC ACB ==°，∠，∴60AEB ACB Ð=Ð=°，∴ADE V 是等边三角形，∴60AE DE DAE ==°=，∠∠∴BAC CAD DAE Ð-Ð=Ð-Ð【点睛】本题主要考查了全等三角形的性质与判定，等边三角形的性质与判定，圆周角定理，勾股定理等等，正确作出辅助线构造全等三角形是解题的关键．。

1《圆》练习题（垂径定理, 弧、弦、圆心角, 圆周角）一、选择题1.已知在⊙O 中, 弦AB 的长为8厘米, 圆心O 到AB 的距离为3厘米, 则⊙O 的半径是（ ）A. 3厘米B. 4厘米C. 5厘米D. 8厘米2.半径等于12的圆中, 垂直平分半径的弦长为（ ）A. B. C. D.3.如图1, 在⊙O 中, ∠ABC=50°, 则∠AOC 等于（ ）A. 50°B. 80°C. 90°D. 100°4.如图2, AB 是⊙O 的直径, ∠ABC=30°, 则∠BAC =（ ）A. 90°B. 60°C. 45°D. 30°5.如图3, △ABC 内接于⊙O, 连结OA.OB, 若∠ABO ＝25°, 则∠C 的度数为（ ）．A. 55°B. 60°C. 65°D. 70°6.如图4, 四边形ABCD 内接于⊙O, 若它的一个外角∠DCE=70°, 则∠BOD=( )A. 35°B.70°C. 110°D.140°7、如图5, △ABC 内接于⊙O, AD ⊥BC 于点D, AD=2cm, AB=4cm, AC=3cm, 则⊙O 的直径是（ ）A. 2cmB. 4cmC. 6cmD. 8cm8、如图6, BD 是⊙O 的直径, 圆周角∠A = 30(, 则∠CBD 的度数是（ ）A. 30(B. 45(C. 60(D. 80(9、如图7, AB 为⊙O 的直径, C ．D 是⊙O 上的两点, ∠BAC=30º, AD=CD, 则∠DAC 的度数是（ ）A. 30ºB. 60ºC. 45ºD. 75º10、圆内接四边形ABCD 中, ∠A ∶∠B ∶∠C ∶∠D 可以是（ ）A. 1∶2∶3∶4B. 1∶3∶2∶4C. 4∶2∶3∶1D. 4∶2∶1∶3AB O C图1 图2 O 30D B C A O D CBA 图3 图4图6图7图52二、填空题11.如图8, ∠A 是⊙O 的圆周角, ∠A=40°, 则∠OBC 的度数为_______.12.如图9, AB 是⊙O 的直径, 点D 在⊙O 上∠AOD=130°, BC ∥OD 交⊙O 于C, 则∠A= .13、如图10, ⊙O 的直径AB=8cm, C 为⊙O 上的一点, ∠BAC=300, 则BC= .14、如图，量角器外沿上有A 、B 两点，它们的读数分别是70°、40°，则∠1的度数为 .三、解答题: 15、.如图, AB 、CD 是⊙O 的两条弦, 延长AB 、CD 交于点P, 连结AD 、BC 交于点E ． , , 求 的度数．16.如图所示, AB 是⊙O 的一条弦, OD ⊥AB , 垂足为C, 交⊙O 于点D , 点E 在⊙O 上。

垂径定理:垂直于弦的直径平分弦，并且平分弦所对的两条弧。

推论：平分（非直径）弦的直径垂直于弦，并且平分弦所对的两条弧．练习：1．如图，在⊙O中，弦AB的长为8 cm．圆心O到AB的距离为3cm．求⊙O的半径.2．如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，并且CD=4m,EM=6m．求⊙O的半径。

圆心角：顶点在圆心的角叫做圆心角。

圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等、所对的弦也相等．推论：（1）在同圆或等圆中，如果两条弧相等、那么它们所对的圆心角相等．所对的弦相等；（2）在同圆或等圆中，如果两条弦相等。

那么它们所对的圆心角相等，所对的优弧和劣弧分别相等．练习：1.如图，在⊙O中，AB=AC,∠ACB=60°，求证：AOB=∠BOC=∠AOC.圆周角：顶点在圆上，并且两边都与圆相交，所形成的角为圆周角。

圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

推论：（1）同弧或等弧所对的圆周角相等；（2）半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径；（3）同弦或等弦所对的圆周角相等或互补；练习：1.如图，⊙O的直径AB为10 cm，弦AC为6cm，∠ACB的平分线交⊙O于点D，求BC,AD, BD的长。

2.如图，圆内接四边形ABCD的对角线AC、BD把它的4个内角分成8个角，这些角中哪些相等?为什么?如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆。

圆内接四边形性质：圆内接四边形的对角互补。

练习：1.如图，四边形ABCD内接于⊙O,E为CD延长线上一点．若∠B=110°，求∠ADE的度数。

2.如图,A,P,B,C是⊙O上的四个点，∠APC=∠CPB=60°，判断△ABC的形状，并证明你的结论．。

垂径定理圆心角圆周角定理一选择题：1、如图，⊙O是△ABC的外接圆，∠OBC=42°，则∠A的度数是（）A．42°B．48°C．52°D．58°2.如图，A、B、C、D四个点均在⊙O上，∠AOD=50°，AO∥DC，则∠B的度数为( )A．50° B．55° C．60° D．65°3.如图，点B、D、C是⊙O上的点，∠BDC=130°，则∠BOC是（）A．100° B．110° C．120°D．130°4.如图，⊙O的半径为5，弦AB的长为8，点M在线段AB（包括端点A，B）上移动，则OM取值范围是（）A.3≤OM≤5B.3≤OM＜5C.4≤OM≤5 D.4≤OM＜55、如图所示，AB是⊙O的直径，AD=DE，AE与BD交于点C，则图中与∠BCE相等的角有（）A．2个 B．3个 C．4个 D．5个6.将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B 的读数分别为86°、30°，则∠ACB的大小为( )A．15°B．28° C.29°D．34°7.如图，C为⊙O直径AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=45°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=x,DE=y,下列中图象中,能表示y与x的函数关系式的图象大致是( )8.如图.⊙O 中，AB、AC是弦，O在∠ABO的内部，，，，则下列关系中，正确的是（）A. B. C． D.9.如图，四边形ABCD内接于⊙O，BC是直径，AD=DC，∠ADB=20º，则∠ACB，∠DBC分别为（）A．15º与30º B．20º与35º C．20º与40º D．30º与35º10.图中∠BOD的度数是（）A．55° B．110° C．125° D．150°11.如图，点I为△ABC的内心，点O为△ABC的外心，∠O=140°，则∠I为（）（A）140°（B）125°（C）130°（D）110°12.如图,弦AB∥CD，E为上一点，AE平分，则图中与相等（不包括）的角共有（）A．3个 B．4个 C．5个 D．6个13、如图，已知的半径为1，锐角内接于，于点，于点，则的值等于（）A．的长 B．的长 C．的长 D．的长14.如图，在直角∠O的内部有一滑动杆AB，当端点A沿直线AO向下滑动时，端点B会随之自动地沿直线OB向左滑动，如果滑动杆从图中AB处滑动到A′B′处，那么滑动杆的中点C所经过的路径是（）A.直线的一部分B.圆的一部分C.双曲线的一部分 D.抛物线的一部分15.如图，AB是⊙O的直径，弦BC=2cm，∠ABC=60°.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t(s)，当△APQ是直角三角形时，t的值为（）A. B. C.或 D.或或16.如图，，在以为直径的半圆上，，在上，为正方形，若正方形边长为1，，，则下列式子中，不正确的是（）A. B. C. D.17.如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点，P是直径AB上的一动点．若MN=1，则△PMN周长的最小值为（）A．4 B．5 C．6 D．718.如图，在△ABC中，AD是高，AE是直径，AE交BC于G，有下列四个结论：•①AD2=BD·CD；②BE2=EG·AE；③AE·AD=AB·AC；④AG·EG=BG·CG．其中正确结论的有（）A．1个 B．2个 C．3个 D．4个19.如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，，的中点分别是M，N，P，Q。

【文库独家】九年垂径定理、弦、弧、圆心角、圆周角练习1.已知：AB交圆O于C、D，且AC＝BD.你认为OA＝OB吗？为什么？2. 如图所示，是一个直径为650mm的圆柱形输油管的横截面，若油面宽AB=600mm，求油面的最大深度。

6003. 如图所示，AB是圆O的直径，以OA为直径的圆C与圆O的弦AD相交于点E。

你认为图中有哪些相等的线段？为什么？ADBOCE4.如图所示，OA是圆O的半径，弦CD⊥OA于点P，已知OC=5，OP=3，则弦CD=____________________。

5. 如图所示，在圆O中，AB、AC为互相垂直且相等的两条弦，OD ⊥AB，OE⊥AC，垂足分别为D、E，若AC=2cm，则圆O的半径为____________cm。

6. 如图所示，AB是圆O的直径，弦CD⊥AB，E为垂足，若AB=9，BE=1，则CD=_________________。

CA P ODCE OA D B7. 如图所示，在△ABC中，∠C＝90°，AB＝10，AC＝8，以AC为直径作圆与斜边交于点P，则BP的长为________________。

8. 如图所示，四边形ABCD内接于圆O，∠BCD=120°，则∠BOD=____________度。

9.如图所示，圆O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段的OM的长的取值范围是（）A. 3≤OM≤5B. 4≤OM≤5C. 3＜OM＜5D. 4＜OM＜510.下列说法中，正确的是（）A. 到圆心的距离大于半径的点在圆内B. 圆的半径垂直于圆的切线C. 圆周角等于圆心角的一半D. 等弧所对的圆心角相等11.若圆的一条弦把圆分成度数的比为1：3的两条弧，则劣弧所对的圆周角等于（）A. 45°B. 90°C. 135°D. 270°12. 如图所示，A、B、C三点在圆O上，∠AOC=100°，则∠ABC 等于（）A. 140°B. 110°C. 120°D. 130°13. △ABC 中，∠C=90°，AB=cm 4，BC=cm 2，以点A 为圆心，以cm 5.3长为半径画圆，则点C 在圆A___________，点B 在圆A_________； 14. 圆的半径等于cm 2，圆内一条弦长23cm ，则弦的中点与弦所对弧的中点的距离等于_____________；15. 如图所示，已知AB 为圆O 的直径，AC 为弦，OD ∥BC 交AC 于D ，OD=cm 2，求BC 的长；B16. 如图所示，破残的圆形轮片上，弦AB 的垂直平分线交弧AB 于点C ，交弦AB 于点D 。

【综合训练提升】1. 如图，⊙O 的两条弦AB ，CD 相交于点M ，直径PQ 过点M ，且MP 评分∠AMC ，则图中相等的线段的对数为（ ）A. 1B. 2C. 3D.4第1题 第2题2. 如图，在⊙O 内有折线OABC ，若OA=8，AB=12，∠A=∠B=60°，则BC 的长为（ ） A. 19 B. 16 C. 18 D.203. 如图，在Rt △ABC 中，AB ⊥BC ，AB ＝6，BC ＝4，P 是△ABC 内部的一个动点，且满足∠P AB ＝∠PBC ，则线段CP 长的最小值为_______.第3题 第4题4. 如图，已知EF 是⊙O 的直径，把∠A 为60°的直角三角尺ABC 的一条直角边BC 放在直线EF 上，斜边AB 与⊙O 交于点P ，点B 与点O 重合；将三角尺ABC 沿OE 方向平移，直至点B 与点E 重合为止．设∠POF ＝x °，则x 的取值范围是________．5. 如图所示，A 是半圆上的一个三等分点，B 是AN ︵的中点，P 是直径MN 上一动点，⊙O 的半径为1，则姓 名 年级：九年级 学科：数 学 第 次课 课时课 题垂径定理 圆心角定理 圆周角定理的综合应用教 学目 标 熟练运用垂径定理、圆心角、圆周角定理解决综合题重 点难 点垂径定理、圆心角定理及圆周角定理的综合应用教 学 过 程P A ＋PB 的最小值是多少？6. 如图，四边形ABCD 的四个顶点在⊙O 上，且对角线AC ⊥BD ，OE ⊥BC 于点E . 求证：OE ＝12AD .7. 如图，⊙O 的两条弦AB ，CD 交于点E ，OE 平分∠BE D. （1）求证：AB ＝C D.（2）若∠BED ＝60°，EO ＝2，求BE －AE 的值.8.（1）如图①，AB 是⊙O 的直径，C ，P 是⊙O 上两点，AB ＝13，AC ＝5.若P 是AB ︵的中点，求P A 的长；（2）如图②，若P 是BC ︵的中点，求P A 的长．9. 如图所示，在⊙O 中，半径OA ⊥OB ，C ，D 是AB ︵的三等分点，AB 分别交OC ，OD 于点E ，F . 求证：AE ＝BF ＝CD .10. 如图，C 为△ABD 外接圆上的一动点(点C 不在BAD ︵上，且不与点B ，D 重合)，∠ACB ＝∠ABD ＝45°. （1）求证：BD 是该外接圆的直径. （2）连结CD ，求证：2AC ＝BC ＋C D.（3）若△ABC 关于直线AB 的对称图形为△ABM ，连结DM ，试探究AM ，BM ，DM 三者之间满足的等量关系，并证明你的结论.11. 如图，半圆的直径AB 长为2，C ，D 是半圆上的两点，若AC ︵的度数为96°，BD ︵的度数为36°，动点P在直径AB 上，求CP ＋PD 的最小值.12. 如图所示，两等圆⊙O 1和⊙O 2，相交于A ，B 两点，且两圆互过圆心，过点B 作任一直线，分别交⊙O 1，⊙O 2于C ，D 两点，连接AC ，AD. （1）试猜想△ACD 的形状，并说明理由；（2）若已知条件中两圆不一定互相过圆心，试猜想△ACD 的形状，并说明理由.13.（1）如图，CD ，AB 所在的直线分别交⊙O 于C ，D ，A ，B 四点，CD ，AB 相交于点P ，若AC ︵的度数为x°，BD ︵的度数为y°（x°＞y°），则∠BPD=12（x°+y°），你认为这个结论正确吗？请说明理由.（2）若CD ，AB 所在的直线的交点P 在⊙O 外，则上述结论还成立吗？若成立，请证明；若不成立，应怎样表示∠BPD?。

600垂径定理、弦、弧、圆心角、圆周角练习1、已知：AB 是⊙O 的直径，弦CD ⊥AB 于点P ，CD ＝10cm ，AP:PB ＝1:5，则⊙O 的半径为_______。

2、在⊙O 中，P 为其内一点，过点P 的最长的弦为8cm ，最短的弦长为4cm ，则OP ＝____ _。

3、已知圆的半径为5cm ，一弦长为8cm ，则该弦的中点到弦所对的弧的中点的距离为__ _____。

4、已知圆心到圆的两条平行弦的距离分别是2和3，则两条平行弦之间的距离为_ ____。

5、在半径为5cm 的圆内有两条互相平行的弦，一条弦长为8cm ，另一条弦长为6cm ，则这两条弦之间的距离为_____ _。

6、如图，在⊙O 中，OA 是半径，弦AB ＝310cm ，D 是弧AB 的中点，OD 交AB 于点C ，若∠OAB ＝300，则⊙O 的半径____cm 。

7、 半径为5cm 的圆O 中有一点P ，OP=4，则过P 的最短弦长_________，最长弦是__________，8、如图，AB 是⊙O 的直径，CD ⊥AB 于E ，CD=10，BE=1，则AB= 。

二、解答题 1. 已知：AB 交圆O 于C 、D ，且AC ＝BD.你认为OA ＝OB 吗？为什么？2. 如图所示，是一个直径为650mm 的圆柱形输油管的横截面，若油面宽AB=600mm ，求油面的最大深度。

3、如图所示，⊙O 的直径AB 和弦CD 相交于点E ，已知，AE ＝6cm ，EB ＝2cm ，∠CEA ＝300，求CD 的长。

4、如图所示，在Rt △ABC 中，∠C ＝900，AC ＝3，BC ＝4，以点C 为圆心，CA 为半径的圆与AB 、BC 分别交于点D 、E ，求AB 和AD 的长。

5、如图，一条公路的转弯处是一段圆弧，点O 是的圆心，E 为上一点，OE ⊥CD ，垂足为F ．已知CD = 600m ，EF = 100m ，求这段弯路的半径．6题图10题图 CODE F17题图6、我市某居民区一处圆形地下水管道破裂，修理工人准备更换一段新管道，经测量得到如图所示的数据，修理工人应准备内径多大的管道？7、一工厂的厂门是由一个半圆与矩形组成的。

专题12垂径定理、圆周角和圆心角的关系（6个知识8种题型）【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.垂径定理（重点）知识点2.垂径定理的推论（难点）知识点3.圆周角（重点）知识点4.圆周角定理（重点）知识点5.圆周角定理的推论（难点）知识点6.圆内接四边形的概念与性质（重点）【方法二】实例探索法题型1.最短距离问题题型2.辅助线的添加方法题型3.方程思想题型4.垂径定理的实际应用题型5.圆中角度的计算题型6.圆内接四边形与圆周角定理的综合应用题型7.动点问题题型8.圆周角定理与其他几何知识的综合【方法三】成果评定法【学习目标】1.掌握垂径定理，并会运用垂径定理进行简单的计算。

2.掌握与垂径定理有关的推论，并能运用这一推论解决相关问题。

3.认识圆周角，掌握圆周角和圆心角的关系，直径所对的圆周角的特征。

4.能运用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题。

【知识导图】【倍速学习五种方法】【方法一】脉络梳理法知识点1.垂径定理（重点）垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．【例1】．（2022秋•锡山区校级月考）如图，在⊙O中，OC⊥AB于点C，若⊙O的半径为10，AB＝16，则OC的长为．【变式】．（2022秋·江苏南京·九年级南京市第一中学校考阶段练习）如图，AB是⊙O的直径，弦CD⊥AB 于点E，则下列结论一定正确的个数有（）①CE =DE ；②BE =OE ；③ CBBD =；④∠CAB =∠DAB ．A ．4个B ．3个C ．2个D ．1个知识点2.垂径定理的推论（难点）推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．推论2：弦的垂直平分线经过圆心，并且平分弦所对的两条弧．推论3：平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．【例2】．（2022秋·九年级统考期中）如图，O 的弦8AB =，M 是AB 的中点，且3OM =，则O 的半径等于（）A ．7B ．4C ．5D ．6【变式】．（2023秋·浙江台州·九年级统考期末）如图，在正方形网格中，一条圆弧经过、、A B C 三点，那么这条圆弧所在圆的圆心是（）．A ．点PB ．点QC ．点RD ．点M知识点3.圆周角（重点）1.圆周角定义：像图中∠AEB 、∠ADB 、∠ACB 这样的角，它们的顶点在圆上，并且两边都与圆相交的角叫做圆周角．2.圆心角与圆周角的区别与联系【例3】观察下图中角的顶点与两边有何特征?指出哪些角是圆周角?知识点4.圆周角定理（重点）在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．【例4】如图，100AOB ∠= ，点C 在O 上，且点C 不与A、B 重合，则ACB ∠的度数为（）A．50 B．80 或50 C．130 D．50 或130【变式】如图，AB 是⊙O 的弦，∠AOB＝80°则弦AB 所对的圆周角是.知识点5.圆周角定理的推论（难点）半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．要点诠释：(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.（3）圆心与圆周角存在三种位置关系：圆心在圆周角的一边上；圆心在圆周角的内部；圆心在圆周角的外部．（如下图）【例5】（2023秋·江苏·九年级专题练习）如图，CD 是O 的直径，A 、B 是O 上的两点，若40ACD ∠=︒，则ABC ∠的度数为（）A ．50︒B ．40︒C ．20︒D ．140︒【变式】如图，⊙A 过点O(0，0)，C(3，0)，D(0，1)，点B 是x 轴下方⊙A 上的一点，连接BO 、BD ，则∠OBD 的度数是．知识点6.圆内接四边形的概念与性质（重点）（1）定义:圆内接四边形：顶点都在圆上的四边形，叫圆内接四边形．（2）性质：圆内接四边形对角互补，外角等于内对角（即它的一个外角等于它相邻内角的对角）．【例6】（2022秋•靖江市期末）如图，已知四边形ABCD内接于⊙O．求证：∠A+∠C＝180°．【变式】如图已知四边形ABCD内接于⊙O，∠ABC＝70°，则∠ADC的度数是．【方法二】实例探索法题型1.最短距离问题题型2.辅助线的添加方法A．6B．题型3.方程思想3.（2022秋•江宁区校级月考）如图是一个隧道的横截图，它的形状是以点O为圆心的一部分，如果M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，若CD＝4m，EM＝6m，则⊙O的半径为m．题型4.垂径定理的实际应用4.（2022秋•如皋市校级月考）兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示，已知AB＝16m，半径OA＝10m，高度CD为m．5.（2022•钟楼区校级模拟）筒车是我国古代发明的一种水利灌溉工具，如图1，筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2，已知圆心O在水面上方，且⊙O被水面截得弦AB长为4米，⊙O半径长为3米．若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是（）A．1米B．2米C．米D．米6.（2022秋•泰州月考）如图，有一座拱桥是圆弧形，它的跨度AB＝60米，拱高PD＝18米．（1）求圆弧所在的圆的半径r的长；（2）当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE＝4米时，是否要采取紧急措施？题型5.圆中角度的计算7．（2022秋•鼓楼区期末）如图，AB为⊙O的直径，D是弦AC延长线上一点，AC＝CD，DB的延长线交⊙O 于点E，连接CE．（1）求证∠A＝∠D；（2）若的度数为108°，求∠E的度数．题型6.圆内接四边形与圆周角定理的综合应用8．（2022秋•宿城区期末）如图，四边形ABCD内接于一圆，CE是边BC的延长线．（1）求证∠DAB＝∠DCE；（2）若∠DAB＝60°，∠ACB＝70°，求∠ABD的度数．9．（2022秋•镇江期中）如图，四边形ABCD为⊙O的内接四边形，∠EAD＝∠BAC，BA、CD延长线交于点E．求证：BD＝BC．题型7.动点问题10．（2023·江苏泰州·统考中考真题）已知：A 、B 为圆上两定点，点C 在该圆上，C ∠为 AB 所对的圆周角．知识回顾(1)如图①，O 中，B 、C 位于直线AO 异侧，135AOB C ︒∠+∠=．①求C ∠的度数；②若O 的半径为5，8AC =，求BC 的长；逆向思考(2)如图②，P 为圆内一点，且120APB ∠<︒，PA PB =，2APB C ∠=∠．求证：P 为该圆的圆心；拓展应用(3)如图③，在（2）的条件下，若90APB ∠=︒，点C 在P 位于直线AP 上方部分的圆弧上运动．点D 在P 上，满足2CD CB CA =-的所有点D 中，必有一个点的位置始终不变．请证明．题型8.圆周角定理与其他几何知识的综合11．（2023•滨江区一模）如图1，AB 为⊙O 的直径，CD ⊥AB 于点E ，，BF 与CD 交于点G ．（1）求证：CD ＝BF ．（2）若BE ＝1，BF ＝4，求GE 的长．（3）连结GO ，OF ，如图2，求证：．【方法三】成果评定法一．选择题（共6小题）1．（2023秋•惠山区校级期中）如图，AB 是O 的直径，弦CD AB ⊥于点E ，10AB cm =，8CD cm =，则BE 的长为()A ．5cmB ．3cmC ．2cmD ．1.5cm2．（2023春•鼓楼区校级月考）如图，在正方形ABCD 中，4AB =，以边CD 为直径作半圆O ，E 是半圆O 上的动点，EF DA ⊥于点F ，EP AB ⊥于点P ，设EF x =，EP y =22x y +()A ．231-B ．423-C ．251-D ．252-3．（2023秋•滨湖区校级期中）“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，弦AB CD ⊥，垂足为点D ，1CD =寸，1AB =尺(10寸），则圆的直径长度是()A ．12寸B ．24寸C ．13寸D ．26寸4．（2023秋•铜山区校级月考）如图，点A 、B 、C 在O 上，30ACB ∠=︒，则AOB ∠的度数是()A ．30︒B ．40︒C ．60︒D ．65︒5．（2023•苏州）如图，AB 是半圆O 的直径，点C ，D 在半圆上， CDDB =，连接OC ，CA ，OD ，过点B 作EB AB ⊥，交OD 的延长线于点E ．设OAC ∆的面积为1S ，OBE ∆的面积为2S ，若1223S S =，则tan ACO ∠的值为()A 2B ．223C ．75D ．326．（2023秋•梁溪区校级期中）如图，DCE ∠是O 内接四边形ABCD 的一个外角，若82DCE ∠=︒，那么BOD ∠的度数为()A．160︒B．164︒C．162︒D．170︒二．填空题（共6小题）7．（2023秋•滨海县期中）如图，点A，B，C，D在OABD∠=．∠=︒，则ADC上，30CAD∠=︒，508．（2023秋•镇江期中）如图，某圆弧形拱桥的跨度16=，则该拱桥的半径为m．CD m=，拱高5AB m9．（2023秋•高新区校级期中）如图是一个圆柱形的玻璃保温水杯，将其横放，截面是个半径为5cm的圆，杯内水面8=，则水的最大深度CD是cm．AB cm10．（2023秋•丰县期中）如图，点A是半圆上的一个三等分点，点B是 AD的中点，P是直径CD上一动点，O+的最小值为．的半径是2，则PA PB11．（2023秋•鼓楼区校级月考）如图，已知OPA=，的弦，点P在弦AB上．若4的半径为7，AB是OPB=，则OP的长为．612．（2023秋•建湖县期中）如图，点A 、B 、C 在O 上，//BC OA ，连接BO 并延长，交O 于点D ，连接AC 、DC ．若18A ∠=︒，则D ∠的大小为︒．三．解答题（共6小题）13．（2023秋•仪征市期中）如图，在以点O 为圆心的两个同心圆中，大圆的弦AB 交小圆于点C 、D ．（1）求证AC BD =；（2）若3AC =，大圆和小圆的半径分别为6和4，则CD 的长度是．14．（2023秋•广陵区期中）如图，四边形ABCD 内接于O ，BC 为O 的直径，//OA CD ．（1）若70ABC ∠=︒，求BAD ∠的度数；（2）求证： AB AD =．15．（2023秋•句容市期中）已知：如图，C ，D 是以AB 为直径的O 上的两点，分别连接OC 、OD 、AD 、CD 、BC ，且//OD BC ，求证：AD DC =．16．（2023秋•淮安区期中）某地有一座圆弧形拱桥，桥下水面宽度AB为24m，拱顶高出水面8m（即8)=，CD m ⊥，OC AB（1）求出该圆弧形拱桥所在圆的半径；（2）现有一艘宽10m，船舱高出水面7.5m的货船要经过这里，此货船能顺利通过这座桥吗？17．（2023秋•邳州市期中）“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”此问题的实质是解决下面的问题：如图，CD为OAB=，求CD的长．的直径，弦AB CDCE=，10⊥于点E，118．（2023秋•泗阳县期中）如图，AB是O∠的度数．∠=︒，求ABDDCB的弦，30的直径，CD是O。

九年级数学圆垂径定理及圆周角圆心角测试题九年级数学“圆”测试题2.如图3所示，CD是圆O的弦，AB是圆O的直径，CD=8，AB=10，那么a点和B点到直线CD的距离之和为（）a、6b、8c、10d、123.CD是一串⊙ O.制作直径AB，使AB⊥ CD，垂直脚为e。

如果AB=10，CD=6，则be 的长度为（）a．1或9b．9c、一,d．4Ac4。

在手工课上，小明把长10π、宽5π的绿色矩形纸板卷成一个宽度等于高度的圆筒。

这个圆柱体底圆的半径是（）odba．5πb．5c．10πd．105.如图24-a-2所示，△ ABC内部连接到⊙ O.如果∠ a=40°，为∠ OBC为（）a.20°b.40°c.50°d.70°6。

如果半径为r的圆中有长度为r的弦，则与弦相对的周向角度为（）a、30°B、30°或150°C、60°D、60°或120°7．如图24―a―2，ob、oc是⊙o的半径，a是⊙o上一点，若已知∠b=20°,∠c=30°,则∠boc=.那么字符串AB的长度是⌒9.如果⊙ o是5，弦AB的弦中心距离是3，那么AB=。

10.如图4所示，已知⊙ o为6厘米，弦CB=63厘米，外径⊥ BC，垂直的脚是D，那么∠ 玉米棒=11、直线l与⊙o有两个公共点a，b，o到直线l的距离为5cm，ab=24cm，则⊙ o是厘米。

12.将部分油装入直径为10cm的圆柱形油箱后，截面如图所示，油面宽度AB=6cm。

当油面宽度AB为8cm时，油上升厘米13（2021年龙岩市）如图，量角器外沿上有a、b两点，它们的读数分别是70°、40°，那么∠ 1是图24―a―28.AB是音乐的和弦⊙ o、半径⊙ o是5，摄氏度⊥ AB在D点，相交⊙ o在C点，CD=1，14（2021湖北黄石）16．如图，则．为的直径，点在上，，17.点P是一个内点⊙ o、 Op=4cm，圆的半径为5cm。

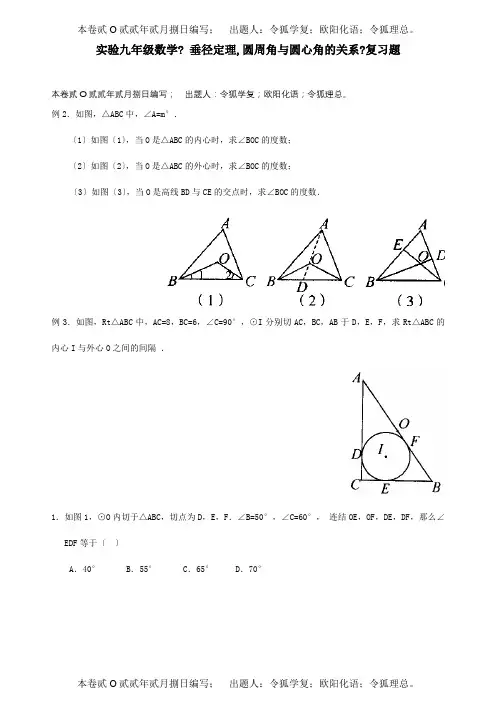
实验九年级数学? 垂径定理,圆周角与圆心角的关系?复习题本卷贰O贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

例2．如图，△ABC中，∠A=m°．〔1〕如图〔1〕，当O是△ABC的内心时，求∠BOC的度数；〔2〕如图〔2〕，当O是△ABC的外心时，求∠BOC的度数；〔3〕如图〔3〕，当O是高线BD与CE的交点时，求∠BOC的度数．例3．如图，Rt△ABC中，AC=8，BC=6，∠C=90°，⊙I分别切AC，BC，AB于D，E，F，求Rt△ABC的内心I与外心O之间的间隔．1．如图1，⊙O内切于△ABC，切点为D，E，F．∠B=50°，∠C=60°，•连结OE，OF，DE，DF，那么∠EDF等于〔〕A．40° B．55° C．65° D．70°2．如图2，⊙O是△ABC的内切圆，D，E，F是切点，∠A=50°，∠C=60°，•那么∠DOE=〔〕A．70° B．110° C．120° D．130°3．如图3，△ABC中，∠A=45°，I是内心，那么∠BIC=〔〕° B．112° C．125° D．55°4．以下命题正确的选项是〔〕A．三角形的内心到三角形三个顶点的间隔相等B．三角形的内心不一定在三角形的内部C．等边三角形的内心，外心重合D．一个圆一定有唯一一个外切三角形5．在Rt△ABC中，∠C=90°，AC=3，AB=5，那么它的内切圆与外接圆半径分别为〔〕A．1.5，2.5 B．2，5 C．1，2.5 D．2，26．如图，在△ABC中，AB=AC，内切圆O与边BC，AC，AB分别切于D，E，F．〔1〕求证：BF=CE；〔2〕假设∠C=30°，CE=23，求AC的长．1．如图，在半径为R的圆内作一个内接正方形，•然后作这个正方形的内切圆，又在这个内切圆中作内接正方形，依此作到第n个内切圆，它的半径是〔〕A．〔22〕n R B．〔12〕n R C．〔12〕n－1R D．〔22〕n－1R2．如图，⊙O为△ABC的内切圆，∠C=90°，AO的延长线交BC于点D，AC=4，•DC=1，那么⊙O的半径等于〔〕A．45B．54C．34D．563．如图，△ABC的内切圆⊙O分别和边BC，AC，AB切于D，E，F，•假如AF=2，BD=7，CE=4．〔1〕求△ABC的三边长；〔2〕假如P为弧DF上一点，过P作⊙O的切线，交AB于M，交BC于N，求△BMN的周长．4．如图，⊙O与四边形ABCD的各边依次切于M，N，G，H．〔1〕猜测AB+CD与AD+BC有何数量关系，并证明你的猜测；〔2〕假设四边形ABCD增加条件AD∥BC而成为梯形，梯形的中位线长为m，其他条件不变，试用m表示梯形的周长．一. 选择题。

垂径定理、弦、弧、圆心角、圆周角复习一、填空题1、（2007年双柏县）如图，⊙O是等边三角形ABC的外接圆，点D是⊙O上一点，则∠BDC = ．2、如图，AB是⊙O的直径，点C D，是圆上两点，100AOC∠=，则D∠=度．3、如图，A B C，，是⊙O上的三点，2AB=，30ACB∠=，那么⊙O的半径等于．4、在半径为5cm的圆中，弦AB∥CD，AB=6cm，CD之间的距离是。

5.如图所示，C是⊙O上一点，O是圆心，若80AOB=∠则A B+=∠∠．6. 如图所示，在△ABC中，∠C＝90°，AB＝10，AC＝8，以AC为直径作圆与斜边交于点P，则BP的长为________________。

7.如图所示，四边形ABCD内接于圆O，∠BCD=120°，则∠BOD=____________度。

8.如图所示，圆O的直径为10，弦AB的长为6，M是弦AB上的一动点，则线段的OM的长的取值范围是___________.三、综合题1.已知：AB交圆O于C、D，且AC＝BD.你认为OA＝OB吗？为什么？CBAO2. 如图所示，是一个直径为650mm 的圆柱形输油管的横截面，若油面宽AB=600mm ，求油面的最大深度。

2、如图所示，M 、N 分别是⊙O 的弦AB 、CD 的中点，AB ＝CD 。

求证：∠AMN ＝∠CNM3、已知：如图3，△ABC 内接于⊙O 且AB ＝AC ，⊙O 的半径等于6cm ，O 点到BC 的距离OD 等于2cm ，求AB 的长。

4、如图，在⊙O 中弦AB ⊥CD 于点E ，过E 作AC 的垂线交BD 于点Q ，P 为垂足，求证Q 为BD 的中点.600M NB DOOC Q P AED。

2019-2020 学年九年级数学垂径定理、弦、弧、圆心角、圆周角练习北师大版1.已知： AB交圆 O于 C、 D，且 AC＝ BD.你认为 OA＝ OB吗？为什么？2.如图所示，是一个直径为650mm的圆柱形输油管的横截面，若油面宽AB=600mm，求油面的最大深度。

6003.如图所示， AB是圆 O的直径，以 OA为直径的圆 C 与圆 O的弦 AD相交于点 E。

你认为图中有哪些相等的线段？为什么？DEA BC O4.如图所示， OA 是圆 O 的半径，弦 CD⊥ OA 于点 P ，已知 OC=5， OP=3，则弦CD=____________________。

5.如图所示，在圆 O中， AB、 AC为互相垂直且相等的两条弦， OD⊥ AB， OE⊥ AC，垂足分别为D、 E，若 AC=2cm，则圆 O的半径为 ____________cm。

6.如图所示，AB是圆O的直径，弦CD⊥ AB，E为垂足，若AB=9，BE=1，则CD=_________________。

C CE O A P OA DB D7.如图所示，在△ABC中，∠ C＝ 90°， AB＝10， AC＝8，以 AC为直径作圆与斜边交于点P，则BP的长为 ________________ 。

8.如图所示，四边形 ABCD内接于圆 O，∠ BCD=120°，则∠ BOD=____________度。

9.如图所示，圆 O的直径为 10，弦 AB的长为 6，M是弦 AB上的一动点，则线段的 OM的长的取值范围是（）A. 3≤ OM≤ 5B. 4 ≤ OM≤ 5C. 3＜ OM＜ 5D. 4 ＜ OM＜ 510.下列说法中，正确的是（）A. 到圆心的距离大于半径的点在圆内B.圆的半径垂直于圆的切线C. 圆周角等于圆心角的一半D.等弧所对的圆心角相等11.若圆的一条弦把圆分成度数的比为1： 3 的两条弧，则劣弧所对的圆周角等于（A. 45°B. 90 °C. 135 °D. 270 °12.如图所示，A、B、C三点在圆O上，∠ AOC=100°，则∠ ABC等于（）A. 140°B. 110 °C. 120 °D. 130 °）13.△ABC中，∠ C=90°， AB=4cm，BC=2cm，以点 A 为圆心，以3.5cm长为半径画圆，则点C 在圆 A___________，点 B 在圆 A_________；14.圆的半径等于2cm，圆内一条弦长 23 cm，则弦的中点与弦所对弧的中点的距离等于_____________ ；15.如图所示，已知 AB为圆 O的直径， AC为弦， OD∥ BC交 AC于 D， OD=2cm，求 BC的长；OA BDC16.如图所示，破残的圆形轮片上，弦 AB 的垂直平分线交弧 AB 于点 C，交弦 AB于点 D。

九年级上册垂径定理，圆心角及圆周角的综合测试题 C. 45° B. 35° D . 70° A . 30°班级＿＿＿＿＿＿＿＿＿＿＿＿＿＿姓名＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿8、下面每张方格纸上都画有一个圆，只用不带刻度的直尺就能确定圆心位置的是（）分）一、选择题（每题3分，共30AOB50??ACB?ACB??，则圆心角） 1.如下图，已知是（是⊙O的圆周角，?80?4050? D.A． C. B.?100DAO2P CAD AB=2, AC=，则圆周角∠，已知AB是⊙O的直径，AC, AD是弦，且AD=19、) ( 的度数是BC105°D. 15°或 B. 60° C . 105°A. 45°或60°）（是⊙的直径，弦CD垂直平分OB，则∠BDC=10、如图，AB⌒的任意一点，CCD上不同于点O2.已知：如上图，四边形ABCD是⊙的内接正方形，点P是劣弧 D.50° C.40°A. 20 °B.30°90 D75．°．°60 B45 BPC则∠的度数是（）A．°．° C 24分）二、填空题（每题3分，共圆的弦长与它的半径相等，那么这条弦所对的圆周角的度数是（3. ）o_______．，则∠AOB的度数为11、如图．⊙O中OA⊥BC，∠CDA=2560．° D15030 C150 B A．30°．°．°或°o所示，为配到与原来大小一样的圆小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图4.5 BAC=50．．则∠ADC=_______O的直径，点C、D在⊙O上，∠12.如图．AB为⊙形玻璃，小明带到商店去的一块玻璃碎片应该是（） CB A．第①块．第②块．第③块．第④块DAO题第第11题12 13题 CBBAO=25°，、OA、OB，且∠上，连结、B、C都在⊙OAB、BC、AC如图，点13. A（第5题）___________. ACB的大小为则∠ABC 2O的外接圆，⊙O5.如图，⊙是等边三角形的半径为，ABC的边长为（则等边三角形）535232 D ．．C ． A．B题第7下列命题中，正确的是（6.）15题14题90的圆周角所对①顶点在圆周上的角是圆周角；②圆周角的度数等于圆心角度数的一半；③的弦是直径；④不在同一条直线上的三个点确定一个圆；⑤同弧所对的圆周角相等. ，则∠是⊙14. 已知：如图，四边形ABCDO的内接四边形，∠BOD=140°DCE= ．①②⑤C ．③④⑤B ．①②③A D ．②④⑤.＋∠上的点，则∠都是⊙的直径，是⊙如图，、15 ABOC, D, EO12 = °）的度数是（DAC的中点，则∠AC是D，BAC=20是半圆直径，∠AB、如上图，7．BCOADACABCOBACABBD =6°，=，则，。

一、选择题 仁如图1, 00的直径为10,圆心0到弦AB 的距离0M 的长为3,那么弦AB 的长是（ ） A. 4B. 6C. 7 D ・ 8 2、如图2, 00的半径为5,弦AB 的长为8, M 是弦AB 上的一个动点，则线段0M 长的最小 值为（）3、过00内一点M 的最长弦为10 cm,最短弦长为8cm,则0M 的长为（） A. 9cm B. 6cm C. 3cm D.4、如图3,小明同学设计了一个测51圆直径的工具，标有刻度的尺子0A 、0B 在0点钉在一 起，并使它们保持垂直，在测直径时，把0点靠在圆周上，读得刻度0E 二8个单位，OF 二6个 单位，则圆的直径为（）A. 12个单位B. 10个单位C. 1个单位D. 15个单位 5、如图4, °°的直径垂直弦CD 于P,且P 是半径的中点，CD = 6cm ?则直如图46. 下列命题中，A. 平分一条直径的弦必垂直于这条直径B. 平分一条弧的直线垂直于这条弧所对的弦C. 弦的垂线必经过这条弦所在圆的圆心D. 在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心7、如图5,某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则 拱高为（ ）A. 5米B. 8米C. 7米D. 5厲米8、 有4个命题，①直径相等的两个圆是等圆；②长度相等的两条弧是等弧；③圆中最长的 弦是通过圆心的弦;④一条弦把圆分为两条弧，这两条弧不可能是等弧。

其中真命题是（）A.①③B.①③④C.①④D.①9、 在半径为5cm 的圆中，弦AB/7CD, AB 二6cm, CD 二8c 叫 则AB 和CD 的距离是（ ）A. 7cmB. 1cmC. 5cmD. 7cm 或 1cm10、 如图6, EF 是。

0直径，0E 二5cm,弦AB=8cm, EF 两点到MN 的距离之和等垂径定理.弦.弧.周角练习径AB 的长是（ A 2V3cm) B. 3\/2cm C 4\/2cm D 4\^cm C. 4 如图3B于（）A. 12cmB. 6cmC. 8cmD. 3cm二.解答题1、直径为10m的圆柱形油槽内装入一些油后，截面如图所示，如果油面宽AB二8叫那么油的最大深度是多少？/―、—1 8m --------- >I 2、如图，肋是44%外接圆的直径，AR6c叫ZDAOZA0C.求加的长.3.已知：如图，佔是O0的直径, 中点，OF与AC相交于点E,C是（DO上一点，CD丄AB,垂足为点D, AC= 8 cm, EF = 2cm.求AO 的长；hJUD弦初长为6, 的平分线交。

垂径定理、圆周角圆心角的关系、确定圆的条件1．如图，CD为⊙O的直径，AB⊥CD于E，DE=8cm，CE=2cm，则AB=______cm．2．如图，⊙O的半径OC为6cm，弦AB垂直平分OC，则AB=______cm，∠AOB=______．3．如图，AB为⊙O的弦，∠AOB=90°，AB=a，则OA=______，O点到AB的距离=______．4．如图，P为⊙O的弦AB上的动点，PA=6，PB=2，⊙O的半径为5，则OP范围______．5．⊙O中，M为的中点，则下列结论正确的是( )．A．AB>2AM B．AB=2AMC．AB<2AM D．AB与2AM的大小不能确定6．已知：如图，AB为⊙O的直径，C，D为⊙O上的两点，且C为的中点，若∠BAD=20°，则∠ACO=______．7．在圆中，弦AB，CD相交于E．若∠ADC=46°，∠BCD=33°，则∠DEB等于( )．A．13°B．79°C．38.5°D．101°8．如图，AC是⊙O的直径，弦AB∥CD，若∠BAC=32°，则∠AOD等于( )．A．64°B．48°C．32°D．76°9．如图，弦AB，CD相交于E点，若∠BAC=27°，∠BEC=64°，则∠AOD等于( )．A．37°B．74°C．54°D．64°10．如图，△ABC内接于⊙O，∠A=50°，∠ABC=60°，BD是⊙O的直径，BD交AC于点E，连结DC，则∠AEB等于( )．A．70°B．90°C．110°D．120°11．如图，四边形ABCD内接于⊙O，若∠BOD=138°，则它的一个外角∠DCE等于( )．A．69°B．42°C．48°D．38°12.判断题：（1）经过三点一定可以作圆；（）（2）三角形的外心是三角形三边中线的交点；（）（3）三角形的外心到三角形各项点距离相等．（）13.如图，在平面直角坐标系中，已知一圆弧过正方形网格的格点14．如图，以△OAB的顶点O为圆心的⊙O交AB于点C、D，且AC=BD，OA与OB相等吗？为什么？15．已知：如图，△ABC内接于⊙O，BC=12cm，∠A=60°．求⊙O的直径．16．已知：如图，⊙O的直径AE=10cm，∠B=∠EAC．求AC的长．17．如图，AB是⊙O的直径，且弦BE=DE，AD、BE的延长线交于C．求证：AC=AB．阅读．如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A、B两点，开口向下的抛物线经过点A、B，且其顶点P在⊙C上．（1）求∠ACB的大小；（2）请直接写出A，B，P三点的坐标；（3）试确定此抛物线的解析式；。

九年级圆的垂径定理与圆心角圆周角的大题精选(含答案)九年级圆的垂径定理与圆心角圆周角的大题精选（含答案）圆的性质大题一、解答题（共25小题）1.如图，⊙O中，弦CD与直径AB交于点H。

1）当∠B+∠D=90°时，求证：H是CD的中点。

证明：∠B+∠D=90°，∠B=90°-∠D，又∠ADC=90°（直径所对的角为直角），所以∠___∠B，因此三角形ADC与三角形BDC相似，所以BD/DC=DC/BD，即BD²=DC²，所以BH=HD，即H为CD的中点。

2）若H为CD的中点，且CD=2，BD=√3，求AB的长。

连接OH，由勾股定理得OH=√3，又因为H为CD的中点，所以CH=1，从而CO=√3+1，又AO=CO，所以AB=2AO=2(√3+1)。

2.如图，∠BAC=60°，AD平分∠___于点D，连接OB、OC、BD、CD。

1）求证：四边形OBDC是菱形。

证明：由角平分线定理得∠OAD=∠OBD，又∠OAB=∠OBA=30°，所以∠OBD=30°，又∠OCD=∠OAD=30°，所以∠___∠OCD，所以BD=CD，又∠___∠OCD=30°，所以∠___∠OBC，所以三角形OBD与三角形OBC全等，所以OB=OC，又∠___∠OCD=30°，所以OB=BC，所以四边形OBDC是菱形。

2）当∠BAC为多少度时，四边形OBDC是正方形？当∠BAC=90°时，∠___∠OCD=45°，所以BD=CD，又∠___∠OCD=45°，所以OB=BC，所以四边形OBDC是正方形。

3.如图，CD是⊙O的直径，∠EOD=84°，AE交⊙O于点B，且AB=OB，求∠A的度数。

由圆心角的性质得∠ACB=2∠A，又∠ACB=90°，所以∠A=45°，所以∠EAB=∠OAB-∠OAE=45°-42°=3°，又∠___∠OAB=45°，所以∠DBA=∠OBD-∠OBA=45°-3°=42°，所以∠C=180°-∠A-∠B=180°-45°-42°=93°。

垂径定理，圆周角，圆心角练习一．选择题（共8小题）1．（2013•丽水）一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC是（）A．4B．5[C．6D．8|2．（2012•茂名）如图，AB是⊙O的直径，AB⊥CD于点E，若CD=6，则DE=（）A．3B．4C．5>D．63．（2012•陕西）如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=8，则OP的长为（）A．3B．4C．$3D．4—4．（2013•黄石）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为（）A．B．C．D．【5．（2007•深圳）下列结论正确的是（）A．长度相等的两条弧是等弧B．半圆是弧C．相等的圆心角所对的弧相等/D．弧是半圆6．（2007•仙桃）如图，已知：AB是⊙O的直径，C、D 是上的三等分点，∠AOE=60°，则∠COE是（）A．40°B．60°·C．80°D．120°7．下列说法中正确的是（）A．相等的弦所对的弧相等…B．相等的圆心角所对的弧相等C．在同一个圆中相等的弧所对的弦相等D．相等的弦所对的圆心角相等8．下列命题中正确的是（）{A．长度相等的弧是等弧B．相等的弦所对的弧相等C．垂直于弦的直径必平分弦D．平分弦的直径必垂直于弦）二．填空题（共8小题）9．（2009•郴州）如图，在⊙O 中，，∠A=40°，则∠B=_________度．10．如图，在⊙O中，=，如果∠AOC=65°，则∠BOD=_________．11．（2011•阜新）如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，若AB=2DE，∠E=18°，则∠AOC的度数为_________度．12．（2010•湘西州）如图，在⊙O中，半径为5，∠AOB=60°，则弦长AB=_________．…13．（2013•漳州）如图，一个宽为2厘米的刻度尺（刻度单位：厘米），放在圆形玻璃杯的杯口上，刻度尺的一边与杯口外沿相切，另一边与杯口外沿两个交点处的读数恰好是3和9，那么玻璃杯的杯口外沿半径为_________厘米．14．（2013•西宁）如图，AB为⊙O的直径，弦CD⊥AB于点E，若CD=6，且AE：BE=1：3，则AB= _________．15．（2013•上海）在⊙O中，已知半径长为3，弦AB长为4，那么圆心O到AB的距离为____．16．（2012•遵义）如图，AB是⊙O的弦，AB长为8，P是⊙O上一个动点（不与A、B重合），过点O作OC⊥AP于点C，OD⊥PB于点D，则CD的长为_________．(三．解答题（共8小题）17．（2011•佛山）如图，已知AB是⊙O的弦，半径OA=20cm，∠AOB=120°，求△AOB的面积．18．（2010•长春）如图，将一个两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D，E，量出半径OC=5cm，弦DE=8cm，求直尺的宽．-19．（2006•青岛）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．（1）请你补全这个输水管道的圆形截面；（2）若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．$20．如图所示，在⊙O中，AB与CD是相交的两弦，且AB=CD，求证：．21．如图在⊙O中，AC=BC，OD=OE，求证：∠ACD=∠BCE．22．已知：如图，A、B、C、D是⊙O上的点，∠1=∠2，AC=3cm．（1）求证：=；（2）求BD的长．23．如图，点A、B、C、D在⊙O上，AB与OC、OD分别相交于E、F，AE=BF，说明AC=BD的理由．24．（2012•长春一模）如图，四边形ABCD是矩形，以AD为直径的⊙O交BC边于点E、F，AB=4，AD=12．求线段EF的长．。

初三数学圆周角和圆心角的关系试题1.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC=_______度.【答案】160°【解析】由∠BAD=100°可得∠BAC的度数，再根据圆周角定理即可求得结果.∵∠BAD=100°∴∠BAC=80°∴∠BOC=160°.【考点】邻补角定理，圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.2.如图,AB是半圆O的直径,AC="AD,OC=2,∠CAB=30°," 则点O到CD的距离OE=____.【答案】【解析】由AC=AD，∠CAB=30°可得∠CDO的度数，即可得到∠EOD、∠COE的度数，判断出△COE的形状再结合勾股定理即可求得结果.∵AC=AD，∠CAB=30°，OA=OC∴∠CDO=75°，∠COD=60°∴∠EOD=15°∴∠COE=45°∴△COE为等腰直角三角形∵OC=2∴OE=.【考点】三角形内角和定理，勾股定理点评：特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点，与各个知识点结合极为容易，是中考中的热点，在各种题型中均有出现，需多加关注.3.如图,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )A．50°B．100°C．130°D．200°【答案】A【解析】圆周角定理：同弧或等弧所对的圆周角相等，均等于所对圆心角的一半.∵∠BOC=100°∴∠BAC=50°故选A.【考点】圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.4.如图,A、B、C、D四个点在同一个圆上,四边形ABCD的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对【答案】C【解析】圆周角定理：同弧或等弧所对的圆周角相等，均等于所对圆心角的一半.相等的角有∠ADB=∠ACB，∠BAC=∠BDC，∠CAD=∠CBD，∠ACD=∠ABC4对，故选C.【考点】圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.5.如图,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A．4个B．3个C．2个D．1个【答案】B【解析】圆周角定理：同弧或等弧所对的圆周角相等，均等于所对圆心角的一半.∵D是弧AC的中点∴∠ABD=∠ACD=∠CBD=∠CAD故选B.【考点】圆周角定理点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.6.如图, ,则∠A+∠B等于( )A．100°B．80°C．50°D．40°【答案】C【解析】连接CO并延长交圆于点D，根据圆周角定理即可得到结果.连接CO并延长交圆于点D由图可得∠A+∠B=∠AOD+∠BOD=∠AOB=50°故选C.【考点】圆周角定理点评：辅助线问题是初中数学学习中的难点，能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力，因而这类问题在中考中比较常见，在各种题型中均有出现，一般难度较大，需多加关注.7.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )A．30°B．30°或150°C．60°D．60°或120°【答案】B【解析】根据圆的性质可得这条弦与半径围成的三角形为等边三角形，再根据圆周角定理即可求得结果.由题意得这条弦与半径围成的三角形为等边三角形则该弦所对的圆周角的度数是30°或150°故选B.【考点】圆周角定理点评：特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点，与各个知识点结合极为容易，是中考中的热点，在各种题型中均有出现，需多加关注.8.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC="140°," ∠CBD的度数是( )A.40°B.50°C.70°D.110°【答案】C【解析】先求得弧ABC所对的圆周角的度数，再根据圆内接四边形的对角互补可得∠ABC的度数，即可求得结果.∵∠AOC=140°∴弧ABC所对的圆周角的度数为70°∴∠ABC=110°∴∠CBD=70°故选C.【考点】圆周角定理，圆内接四边形的性质点评：本题是圆周角定理的基础应用题，在中考中比较常见，一般以选择题、填空题形式出现，属于基础题，难度不大.9.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.【答案】4cm【解析】连接OC、OD，根据圆周角定理可得∠COD=60°，即可得到△COD是等边三角形，根据等边三角形的性质即可求得结果.连接OC、OD,则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD=4cm.【考点】圆周角定理，等边三角形的判定和性质点评：辅助线问题是初中数学学习中的难点，能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力，因而这类问题在中考中比较常见，在各种题型中均有出现，一般难度较大，需多加关注.10.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.【答案】(1)相等；（2）∠CP′D+∠COB=180°【解析】(1)连接OD,根据垂径定理可得∠COB=∠DOB，再结合圆周角定理即可得到结果；(2)连接P′P,则可得∠P′CD=∠P′PD,∠P′PC=∠P′DC.即可得∠P′CD+∠P′DC=∠CPD，从而可以得到结果.从而∠CP′D+∠COB=180°.(1)连接OD,∵AB⊥CD,AB是直径,∴,∴∠COB= ∠DOB.∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.(2)连接P′P,则∠P′CD=∠P′PD,∠P′PC=∠P′DC.∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.∴∠C P′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,从而∠CP′D+∠COB=180°.【考点】垂径定理，圆周角定理点评：辅助线问题是初中数学学习中的难点，能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力，因而这类问题在中考中比较常见，在各种题型中均有出现，一般难度较大，需多加关注.。

24.1圆測试一、选择题。

（共10题）1、如图1, CD是圆O的弦，AB是圆O的直径，CD = 8, AB=10,则点A、B到直线CD则BE的长是（）柱的底面圆半径是（）A- 20° B. 40° C. 50° D・ 70°5、如图4. Q0 'p, AB. AC 是弦，0在ZABO 的内部，ZABO = a , ZACO = /?,ZBOC = e,则下列关系中，正确的是()A. 0 = a + /3B. 0 — 2cr + 2/3C. a+ 0 + 0 = 180D. a + 0 + P = 36O的距离的和是( )A、6B、8C、10D、122、如图2, CQ是OO的一条弦, 作直径使AB丄CD垂足为E,若AB=10, CD=6,A. 1 或9 B・ 9 C. 1 D. 43、手工课上，小明用长为IO JI,宽为5 n的绿色矩形卡纸，卷成以宽为高的圆柱，这个圆4.A・5K B. 5 C. 10K D. 10如图3, AABC内接于＜30,若ZA=40°,则ZOBC的度数为（B6、如图5, （DO过点B、C,圆心O在等腰RtAABC的内部,ZBAC=90°, OA=1, BC=6.则00的半径为（）A、6B、13C、V13D、2V13 7、如图，在6X6的方格纸屮，每个小方格都是边长为1的正方形,其中A、B、C为格点.作△ABC的外接圆Q0 ,则疋的长等于8、如图（六），AABC的外接圆上，AB、BC、CA三弧的度数比为12： 13： 110 £|BC上取一点D,过D分别作直线AC、直线AB的并行线，且交BC于E、F两点，则ZEDF的度数为何?A（:9如图7,圆O为厶ABC的外接圆，其中D点在上，且OD丄AC.己知ZA=36°, ZC=60°, 则ZBOD的度数为何？（）A、132B、144C、156D、16810小英家的圆形镜了被打碎了，她拿了如图8 （网格中的每个小正方形边长为1）的一块碎片到玻璃店，配制成形状、大小与原来一致的镜面，则这个镜面的半径是（）A、2A.C.r-—■—A /V Q\ \BCA、55B、60C、65D、702（第7题图）二、选择题。