郑君里信号与系统习题第四章
- 格式:doc
- 大小:674.50 KB
- 文档页数:7



《信号与系统》第四章习题参考答案4-1 解 (1)111()ataL es s a s s a -⎡⎤-=-=⎣⎦++ (2)[]2221221sin 2cos 111s s L t t s s s ++=+++++ (3)()2212tL te s -⎡⎤=⎣⎦+(4)[]21sin(2)4L t s =+,由S 域平移性质,得 ()21s i n (2)14tL e t s -⎡⎤=⎣⎦++ (5)因为1!nn n L t s +⎡⎤=⎣⎦,所以 []2211212s L t s s s++=+= 由S 域平移性质,得 ()()23121ts L t e s -+⎡⎤+=⎣⎦+(6)()2211cos sL at s s a -=-⎡⎤⎣⎦+,由S 域平移性质,得 (){}()2211cos ts L at e s s aβββ-⎡⎤-=-⎣⎦+++ (7)232222L t t s s ⎡⎤+=+⎣⎦ (8)732()327tL t es δ-⎡⎤-=-⎣⎦+ (9)[]22sinh()L t s βββ=-,由S 域平移性质,得()22sinh()atL e t s a βββ-⎡⎤=⎣⎦+-(10)由于()211cos ()cos 222t t Ω=+Ω 所以 222221111c o s ()22424ss L t s s s s ⎛⎫⎡⎤Ω=+∙=+ ⎪⎣⎦+Ω+Ω⎝⎭(11)()()()11111at t L e e a a s a s s a s βββββ--⎡⎤⎛⎫-=-= ⎪⎢⎥--++++⎣⎦⎝⎭ (12)由于()221cos()1ts L e t s ωω-+⎡⎤=⎣⎦++所以 ()()()221cos()1a t a s e L et s ωω--++⎡⎤=⎣⎦++(13)因为(2)(1)(1)(1)(1)(1)t t t te u t e t e e u t ------⎡⎤-=-+-⎣⎦且()(1)(1)2(1)(1)(1)11sst t e e L t eu t L eu t s s ------⎡⎤⎡⎤--=-=⎣⎦⎣⎦++所以 ()(1)(2)2211(2)(1)(1)11s t s s e L teu t e e s s s -----⎡⎤+⎡⎤-=+=⎢⎥⎣⎦+++⎣⎦(14)()(1)tL e f t F s -⎡⎤=+⎣⎦,由尺度变换性质,得(1)ta t L e f aF as a -⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎣⎦(15)()t L f aF as a ⎡⎤⎛⎫=⎪⎢⎥⎝⎭⎣⎦,再由s 域平移性质,得 []2()()at t L e f aF a s a aF as a a -⎡⎤⎛⎫=+=+ ⎪⎢⎥⎝⎭⎣⎦(16)31cos(6)cos (3)cos(3)2t t t -=∙13cos(9)cos(3)44t t =+32213cos (3)48149s s L t s s ⎡⎤=+⎣⎦++由s 域微分性质,得()()22322222213181327cos (3)481494819d s s s s L t t ds s s s s ⎡⎤--⎛⎫⎢⎥⎡⎤=-+=+ ⎪⎣⎦⎢⎥++⎝⎭++⎣⎦(17)[]2cos(2)4sL t s =+,连续两次应用s 域微分性质,有 []()2224cos(2)4s L t t s-=+,()3232224cos(2)4s sL t t s-⎡⎤=⎣⎦+(18)111atL es s a -⎡⎤-=-⎣⎦+,由s 域积分性质,得111111(1)at sL e ds t s s a ∞-⎛⎫⎡⎤-=- ⎪⎢⎥+⎣⎦⎝⎭⎰ln()ln ln s s a s s a ⎛⎫=+-=- ⎪+⎝⎭ (19)351135tt L ee s s --⎡⎤-=-⎣⎦++,由s 域积分性质,得 33111115ln 353t t s e e s L ds t s s s --∞⎛⎫⎡⎤-+⎛⎫=-= ⎪ ⎪⎢⎥+++⎝⎭⎣⎦⎝⎭⎰(20)()22sin aL at s a =⎡⎤⎣⎦+,由s 域积分性质,得()1122211sin 1arctan 21s s at s a s L ds d t s a a a s a π∞∞⎡⎤⎛⎫⎛⎫===-⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎛⎫⎣⎦+ ⎪⎝⎭⎰⎰ 4-2 解(1)因为()()sin ()2T f t t u t u t ω⎡⎤⎛⎫=--⎪⎢⎥⎝⎭⎣⎦()sin ()sin 22T T t u t t u t ωω⎡⎤⎛⎫⎛⎫=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 所以可借助延时定理,得()()sin ()sin 22T T L f t L t u t L t u t ωω⎧⎫⎡⎤⎛⎫⎛⎫=+--⎡⎤⎡⎤⎨⎬ ⎪ ⎪⎢⎥⎣⎦⎣⎦⎝⎭⎝⎭⎣⎦⎩⎭222222221sT T s ee S S S ωωωωωω--⎛⎫=+=+ ⎪+++⎝⎭(2)因为()()()sin sin cos cos sin t t t ωϕωϕωϕ+=+ 所以()222222cos sin cos sin sin s s L t s s s ωϕϕωϕϕωϕωωω++=+=⎡⎤⎣⎦+++ 4-3 解此题可巧妙运用延时性质。



信号与系统总复习信 号连续信号 离散信号系 统连续系统 离散系统抽样定理典型的时间信号 序列的概念 信号的运算 典型的离散信号 奇异信号 信号的运算 信号的分解 微分方程 差分方程 完全解=齐次解+特解 完全解=齐次解+特解 =零状态相应 =零状态相应 +零输入相应 +零输入相应 卷积运算 卷积和运算三大变换傅立叶变换 拉普拉斯变换 z变换第一章 绪论1、信号的概念 念 2、分类:典型的连续时间信号:\ 指数、正弦、复指数、抽样、钟形、 指数 正弦 复指数 抽样 钟形 δ(t), u(t), eat, sin(ω0t), Sa(kt)3、信号的运算:\ 移位、反褶、尺度变换、微分运算、相加、相乘 移位 反褶 尺度变换 微分运算 相加 相乘4、奇异信号:\ 单位斜变、 阶跃、冲激(特性)、冲击偶5、信号的分解:\ 脉冲分量、奇偶分量6、系统模型及其分类 系统模型及其分类两对关系式 欧拉 公式e ejωt − jωt= cos(ωt ) + j sin( ωt ) = cos(ωt ) − j sin( ωt )推出 公式1 sin( ωt ) = ( e jωt − e − jωt ) 2j 1 cos( (ωt ) = ( e j ωt + e − j ωt ) 2第一章 绪论关于冲激信号δ (at ) =1 δ (t ) a尺度变换特性δ (t ) f (t ) = f (0)δ (t )δ (t − t0 ) f (t ) = f (t0 )δ (t − t0 )∫+∞−∞δ ( t ) f ( t )dt = f (0)∫+∞−∞δ (t − t 0 ) f (t )dt = f (t 0 )偶函数 δ (t ) = δ (−t ) f (t ) * δ (t ) = f (t ) ); f (t ) * δ (t − t0 ) = f (t − t0 )第二章 连续时间信号与系统的时域分析小结 单位冲激 响应 卷积常见的信 号信号分解 冲激的叠 加系统的微 分方程与 框图u(t);δ(t)系统的响 应:全解; 齐次,特; 零输入,零 状态解.分成δ(t) 的积分第二章¾ ¾ ¾ ¾连续时间系统的时域分析微分方程式的建立与求解 零输入响应与零状态响应 冲激响应与阶跃响应关系!卷积及其性质(方便求零状态响应)说明:原课件中涉及到的0点跳变、冲激函数匹配法不做强制要求。




信号与系统复习书中最重要的三大变换几乎都有。
第一章 信号与系统 1、信号的分类①连续信号和离散信号 ②周期信号和非周期信号 连续周期信号f (t )满足f (t ) = f (t + m T ), 离散周期信号f(k )满足f (k ) = f (k + m N ),m = 0,±1,±2,…两个周期信号x(t),y(t)的周期分别为T 1和T 2,若其周期之比T 1/T 2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期为T 1和T 2的最小公倍数。
③能量信号和功率信号 ④因果信号和反因果信号2、信号的基本运算(+ - × ÷) 2.1信号的(+ - × ÷)2.2信号的时间变换运算 (反转、平移和尺度变换) 3、奇异信号3.1 单位冲激函数的性质f (t ) δ(t ) = f (0) δ(t ) , f (t ) δ(t –a) = f (a) δ(t –a)例: 3.2序列δ(k )和ε(k ) f (k )δ(k ) = f (0)δ(k ) f (k )δ(k –k 0) = f (k 0)δ(k –k 0) 4、系统的分类与性质4.1连续系统和离散系统4.2 动态系统与即时系统 4.3 线性系统与非线性系统 ①线性性质 T [a f (·)] = a T [ f (·)](齐次性) T [ f 1(·)+ f 2(·)] = T[ f 1(·)]+T[ f 2(·)] (可加性)②当动态系统满足下列三个条件时该系统为线性系统:)0(d )()(f t t t f =⎰∞∞-δ)(d )()(a f t a t t f =-⎰∞∞-δ?d )()4sin(91=-⎰-t t t δπ)0('d )()('f t t f t -=⎰∞∞-δ)0()1(d )()()()(n n n f t t f t -=⎰∞∞-δ4)2(2])2[(d d d )(')2(0022=--=--=-==∞∞-⎰t t t t tt t t δ)(1||1)()()(t a a at n n n δδ⋅=)(||1)(t a at δδ=)(||1)(00a t t a t at -=-δδ)0()()(f k k f k =∑∞-∞=δy (·) = y f (·) + y x (·) = T[{ f (·) }, {0}]+ T[ {0},{x (0)}] (可分解性) T[{a f (·) }, {0}] = a T[{ f (·) }, {0}]T[{f 1(t ) + f 2(t ) }, {0}] = T[{ f 1 (·) }, {0}] + T[{ f 2 (·) }, {0}](零状态线性)T[{0},{a x 1(0) +b x 2(0)} ]= aT[{0},{x 1(0)}] +bT[{0},{x 2(0)}](零输入线性) 4.4时不变系统与时变系统T[{0},f (t - t d )] = y f (t - t d)(时不变性质)直观判断方法:若f (·)前出现变系数,或有反转、展缩变换,则系统为时变系统。
信号与系统作业任务答案解析郑君⾥版《信号与系统》习题与答案第⼀章1.1 画出信号[])()(sin )(00t t a t t a t f --=的波形。
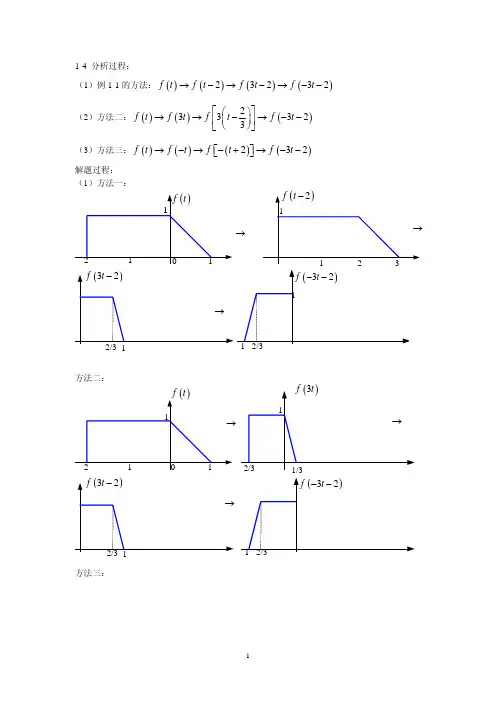
1.2 已知信号[])2()1()1()(--++=t u t u t t f ,画出)32(+-t f 的波形。
1.3已知信号[])2()1()1()(--++=t u t u t t f ,试求它的直流分量。
答案:01.4 已知信号[])2()1()1()(--++=t u t u t t f ,试求它的奇分量和偶分量。
答案:偶分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t u t u t奇分量:[][][])2()1()1(5.0)1()1()1()2()1(5.0---++--+++-+-t u t u t t u t u t t u t u t1.5 信号=20)(t t f 0≥答案:⼆阶以上导数不连续,是奇异信号。
1.6 已知)(t f 是有界信号,且当∞→t 时0)(→t f ,试问)(t f 是否是能量有限信号。
答案:不⼀定。
1.7 对⼀连续三⾓信号进⾏抽样,每周期抽样8点,求抽样所得离散三⾓序列的离散⾓频率。
答案:4/πθ=1.8 以s 5.0=s T 的抽样间隔对下列两个三⾓信号抽样,写出抽样所得离散序列的表达式,画出它们的波形。
⽐较和说明两波形的差别,为什么?(1) t t f 4cos)(1π= (2)t t f 415cos)(2π= 答案:两个离散序列是相同的。
1.9 判断下列信号是否是周期信号。
如果是周期信号,试确定其周期。
(1) t C t B t A t f 9cos 7cos 4sin )(++= 答案:是周期函数,周期π2=T 。
(2) n j d n f 8e)(π-= 答案:是周期信号,周期16=N1.10 求下列表达式的函数值(1) ?∞∞--dt t t t f )()(0δ;答案:)(0t f - (2) ?∞∞--dt t t t f )()(0δ;答案:)(0t f(3) ?∞∞---dt t t u t t )2()(00δ;答案:当00>t 时为1;当00∞∞---dt t t u t t )2()(00δ;答案:当00t 时为0 (5)∞∞--++dt t t e t )2()(δ;答案:2e 2-(6) ?∞∞--+dt t t t )6()sin (πδ;答案:2/16/+π(7)[]?∞∞----dt t t t e t j )()2(0δδω;答案:0e 2/1t j ω--1.11 判断下列系统是否线性、时不变和因果(1) tt e t r d )(d )(=;答案:线性,时不变,因果(2) )()()(t u t e t r =;答案:线性,时变,因果(3) [])()(sin )(t u t e t r =;答案:⾮线性,时变,因果(4) )1()(t e t r -=;答案:线性,时变,⾮因果(5) )2()(t e t r =;答案:线性,时变,⾮因果(6) )()(2t e r r =;答案:⾮线性,时不变,因果1.12 试证明:)()0(')(')0()(')(t f t f t t f δδδ-=。
4—5章作业参考解4-3,求下列周期信号的(离散)频谱,并画出其频谱图。
1,0()sin(2)x t t ω=解:由欧拉公式有00221()[]2j t j tx t e e jωω-=- 由典型信号的离散频谱可得000()0.5(2)0.5(2)x jk j j ωδωωδωω=--++2,20()sin ()x t t ω= 解:由题给,可得000011()[][]22j t j t j t j tx t e e e e j jωωωω--=-∙-00221[2]4j t j t e e ωω-=-+- 由典型信号的离散频谱可得000()0.25[2()(()]22)X jk ωδωδωωδωω=--+++-3,()cos(3)4x t t π=+解;利用欧拉公式有()12πτ=++3()3()1()cos[3()][]122+-==+j t j t x t t e e ττπ由典型信号的离散频谱可得01()[(3)(3)]2-=-++j j x jk e e ττωδωδω4,()sin(2)cos(4)sin(6)x t t t t =++ 解:利用线性性质可得0()x jk ω=[0.5(2)0.5(2)j j δωδω--++]+0.5[(4)(4)δωδω-++]+[0.5(6)0.5(6)j j δωδω--++]4—4,己知连续周期信号的离散频谱如图4—4所示,试写出该周期信号的表示式(03ω=)。
解:根据典型信号的离散频谱,故得 位于3±的两根谱线的时间信号为 10()6cos()f t t ω= 位于6±的两根谱线的时间信号为 10()2cos(2)f t t ω= 位于9±的两根谱线的时间信号为 10()4cos(3)f t t ω=位于0的谱线的时间信号为4()4=f t整个周期信号,田线性性质得到为 123()()()()f t f t f t f t =+++4()f t= 06cos()t ω+02cos(2)t ω+04cos(3)t ω+4 4-9 试写出下列信号的频谱密度函数X(j ω),ω0为常数。
例4-1求下列函数的拉氏变换拉氏变换有单边和双边拉氏变换,为了区别起见,本书以 表示 单边拉氏变换,以 表示 双边拉氏变换.若文字中未作说明,则 指单边拉氏变换.单边拉氏变换只研究 的时间函数,因此,它和傅里叶变换 之间有一些差异,例如在时移定理,微分定理和初值定理等方面.本例只讨论时移 定理.请注意本例各函数间的差异和时移定理的正确应用。
例4-2求三角脉冲函数 如图4-2(a )所示的象函数和傅里叶变换类似,求拉氏变换的时,往往要借助基本信号的拉氏变换和拉氏变换的性质,这比按拉氏变换的定义式积分简单,为比较起见,本例用多种方法求解。
方法一:按定义式求解方法二:利用线性叠加和时移性质求解方法三:利用微分性质求解 方法四:利用卷积性质求解方法一:按定义式求解()()1-=t tu t f ()s F ()t f ()s F B ()t f 0≥t ()()[]()()()[]ses s t u t u t L t tu L s F -⎪⎭⎫ ⎝⎛+=-+--=-=1111112()t f ()⎪⎩⎪⎨⎧<<-<<=其它 02t 1 21t 0t t t f ()()()()222222221101010102101112221112112sss s s s s st st st st st st ste se s e s e s e s s e s e s dtte dt e dt e s e s t dt e t dt te dt e t f s F -------------∞--=-++-+--=-++⎪⎭⎫ ⎝⎛-=-+==⎰⎰⎰⎰⎰⎰-----方法二:利用线性叠加和时移性质求解由于于是方法三:利用微分性质求解信号的波形仅由直线组成,信号导数的象函数容易求得,或者信号经过几次微分后出现原信号,这时利用微分性质比较简单。
将 微分两次,所得波形如图4-2(b )所示显然根据微分性质由图4-2(b )可以看出于是方法四:利用卷积性质求解 可看作是图4-2(c )所示的矩形脉冲 自身的卷积 于是,根据卷积性质 而所以()()()()()()22112--+---=t u t t u t t tu t f ()[]()[]()0021st e s F t t f L st tu L -=-=()()()222211211s s s ese e s s F ----=+-=()tf 2()()()()[]()2221212s e t t t L dt t f d L --=-+--=⎥⎦⎤⎢⎣⎡δδδ()()()()---'-=⎥⎦⎤⎢⎣⎡00222sf f s F s dt t f d L (),00=-f ()00='-f ()()221s e s F s --=()()2211se s s F --=()()()tf t f t f 11*=()t f ()t f 1()()()s F s F s F 11=()()ses s F --=111()()2211s e s s F --=例4-3应用微分性质求图4-3(a )中的 象函数下面说明应用微分性质应注意的问题,图4-3(b )是 的导数的波形。
(1)对于单边拉氏变换,故二者的象函数相同,即因此因而这是应用微分性质应特别注意的问题。
()()t f t f t f 321),(,(),1t f (),2t f ()t f 3()()()t f t f t f 321,,'''图4-4(b)()()(),21t u t f t f =由于()()ss F s F 321==()()()()(),因而,但虽然t f t f s F s F 21212≠=()[]()[]tf L t f L 21'≠'()(),故,由于对于2022=-f t f ()[]()122=-='s sF t f L ()(),故,由于对于0011=-f t f ()[]()301=-='s sF t f L ()()()()(),,一阶导数相同,但和虽然002033232==--f f t f t f ()()()()200202+=+=⎰⎰---dx x f dx x t f tt δδ()()()()dxx f dx x t f t t ⎰⎰--=+=-03030δδ()()[]()s f s t F s s F 301122=+=-δ()()[]()sf s t F s s F 101133=+=-δ由图4-3(b )知例4-4某线性时不变系统,在非零状条件不变的情况下,三种不同的激励信号作用于系统为图中所示的矩形脉冲时,求此时系统的输出阶跃响应 则例4-5电路如图4-5(a )所示 (1)求系统的冲激响应。
(2)求系统的起始状态 ()[]()301=-='s sF t f L ()s s F 31=则()[]()122=-='s sF t f L ()ss F 32=则()()dx x t f t ⎰-=03δ()()[]()sf s t F s s F 101133=+=-δ则()()()()();时,系统的输出为当输入t u e t t y t t x t -+==δδ11()()()()();时,系统的输出为当输入t u e t y t t u t x t-==322()t x 3当输入()t y 3()()()()()th t y t y t y t y zi zs zi +=+=1()()()()()()()t g t y t h t y t y t y t y zi zi zs zi +=+=+=--)1()1(1()()()()()te t t h t h t y t y ---=+=-2)1(21δ()()1211+-=-s s H s s H ()()()t u e t t h t --=δ()()()()()()tu e t y t y t y t y t h t zszi -=-=-=212()()()()t u e t y t y t g tzi-=-=2()()()()()()()()()31231313---+=---+=-----t u e t u e t u e t g t g t y t y t t t zi ()t e Ω2H1F1+-()t 0υ()a 54-()(),00--C L i υ、使系统的零输入响应等于冲激响应。
(3)求系统的起始状态,(1)求系统的冲激响应。
利用s 域模型图4-5(b )可直写出图4-5(a )电路的系统函数冲激响应(2)求系统的起始状态为求得系统的零输入响应,应写出系统的微分方程或给出带有初值的s 域模型。
下面我们用s 域模型求解。
图4-5(a)电路的s 域模型如图4-5(b)。
由图4-5(b)可以写出上式中第二项只和系统起始状态有关,因此该项是零输入响应的拉氏变换。
依题意的要求,该项应和 相等,从而得 故系统的起始状态通过本例可以看出,改变系统的起始状态可以使系统的完全响应满足某些特定要求。
本质上,系统的零输入响应完全由系统的起始状态决定,对一个稳定系统而言,零输入响应是暂态响应中的一部分,因此,改变系统的起始状态只能改变系统的暂态响应,使暂态响应满足某些特定要求,例如,本例要求暂态响应为零。
(3)求系统的起始状态, ()的激励时的完使系统对t u()t u 全响应仍为()()()()程简便。
解微分方,这种方法比在时域求求逆变换可求得对。
是一对拉氏变换的关系与系统函数系统冲激响应t h s H s H t h ()()()121112++=++==s s sC sL R sC s E s V s H O ()s E 2s ()-01C s υ+-()S V 0+-()-0L i ()b 54-s 1()()[]()t u te s H L t h t --==1()()()()()()()()()() 1 12002120111200122零输入响应零状态响应+++++++=++++-=-----s s i s s s s E s s s s i s s E s V L C C L C Oυυυ()s H ()()()1002=++--L C i s υ()()1000==--LC i υ()()()求得完全响应根据式当激励信号1t u t e =从而求得系统的起始状态内容摘要例题•例题1:求拉氏变换•例题2:求拉氏变换,拉氏变换的性质 •例题3:拉氏变换的微分性质 •例题4:系统函数,求解系统的响应拉氏变换的定义和收敛域典型信号的拉氏变换三.拉氏变换的基本性质 二.单边拉氏变换逆变换的求法一.拉普拉斯变换 四.用拉普拉斯变换法分析电路五.系统函数 系统函数的定义由零极点的决定系统的时域特性由零极点的分析系统的稳定性由零极点的分析系统的频响特性部分分式展开法围线积分法 ()()()()()()()()2 120021221120021212222+++++++--+=+++++++=----s s i s s s s s s s i s s s s s V L C L C O υυ()()有等于激励信号完全响应由该式容易看出,要使,t u t o υ()()()02002=--++--s i s L C υ()()0010==--L C i υ)2s e-)2s-•例题5:用拉氏变换法分析电路。