数学分析 Green 公式
- 格式:pdf
- 大小:237.18 KB
- 文档页数:22

偏微分方程green公式偏微分方程Green公式是一种重要的数学理论,它可以帮助我们解决很多计算机科学中涉及微分方程的问题。
本文就偏微分方程Green公式的概念和应用进行简要介绍。
一、Green公式的概念Green公式是解决偏微分方程的一种方法,由英国数学家Green 于1837年提出。
Green公式的核心思想是将偏微分方程的求解转化为求解一个特定的定积分。
Green公式的表达式为:$$F(x) =int_{x_0}^x f(t) dt + F(x_0)$$其中,$x_0$是固定的一个常量,$F(x)$和$f(x)$分别是偏微分方程的右端以及多元函数。
二、Green公式的应用Green公式在很多计算机科学中有着广泛的应用。
例如,用Green 公式可以求解偏微分方程的解析解;Green公式也可以用来求解经典微分方程的渐近解;在计算机科学中,Green公式也可以用来计算物体表面的表面积,以及用于解决有限元问题。
三、Green公式的优缺点Green公式与其他解决微分方程的方法相比有着许多优点。
一方面,Green公式可以解决更复杂的偏微分方程;另一方面,Green公式在解决经典微分方程时更快,可以有效减少计算过程所需的时间。
虽然Green公式在许多方面都有着显著的优势,但也要注意它的一些缺点。
例如,Green公式在解决复杂的偏微分方程时,计算量很大,因此不适合求解一些高难度的问题;而且Green公式也不能用来求解有边界条件的偏微分方程。
四、结论以上就是Green公式简要介绍,仅供参考。
虽然Green公式在解决偏微分方程方面有着许多优点,但它也有一些缺点,所以在使用Green公式时要结合实际情况,选择最合适的应用方法。

Green第一第二第三公式的证明1.1Green第一公式证明Green第一公式:∬[(∂u∂x)2+(∂u∂y)2]S dxdy=−∬us∆udxdy+∮u∂u∂n⃗cds证明:不妨设n⃗=(cosθ,sinθ);由方向导数的定义有:∂u ∂n⃗=∂u∂xcosθ+∂u∂ysinθ可知有cosθ=dy√(dx)2+(dy)2;sinθ=−dx√()2()2ds=√()();故有∮u ∂u ∂n⃗cds=∮uc (∂u∂xdy()2()2+∂u∂ydy()2()2)√(dx)2+(dy)2=∮uc∂udy−u∂udx由Green公式∬(∂Q∂x−∂P∂y)D dxdy=∮Pdx+Qdy∂D;得∮u c ∂u∂xdy−u∂u∂ydx=∬[∂∂x (u∂u∂x)−∂∂y(−u∂u∂y)]Sdxdy=∬[∂(u∂u)+∂(u∂u)]Sdxdy=∬[∂∂x(∂u∂x)u+(∂u∂x)2+∂∂y(∂u∂y)u+(∂u∂y)2]dxdyS=∬[(∂u∂x)2+(∂u∂y)2]dxdyS +∬[∂∂x(∂u∂x)u+∂∂y(∂u∂y)u]dxdy S=∬[(∂u∂x)2+(∂u∂y)2]dxdyS+∬u[∂∂x(∂u∂x)+∂∂y(∂u∂y)]dxdyS=∬[(∂u∂x)2+(∂u∂y)2]dxdyS+∬uS∆udxdy即有∮u ∂u ∂n⃗c ds=∬[(∂u∂x)2+(∂u∂y)2]dxdyS+∬uS∆udxdy移项可得原式,得证。
1.2Green第二公式证明Green第二公式:∬|∆u∆vu v |dx dyS =∮|∂u∂n⃗∂v∂n⃗u v|Cds证明: 等式左边展开:∬|∆u ∆vu v|dx dyS=∬v∆u −u∆vdx dy S=∬v∆u −u∆vdx dyS右边∮|∂u ∂n ⃗ ∂v∂n ⃗ u v |C ds=∮(∂u ∂n ⃗Cv −∂v∂n ⃗u) ds=∮∂u ∂xC dy √()2()2−∂u ∂y dx√()2()2−u∂v ∂x dy√()2()2+u ∂v dx()2()2√(dx )2+(dy )2 =∮v ∂u ∂xC dy −v ∂u ∂y dx −u ∂v ∂x dy +u ∂v ∂y dx=∮(u ∂v ∂y −v ∂u ∂y )dx +(v ∂u ∂x −u ∂v ∂x)dyC有Green 公式有∬(∂Q ∂x −∂P∂y) Ddxdy =∮Pdx +Qdy∂D;有P=(u ∂v ∂y −v∂u∂y ) Q=(v∂u ∂x−u∂v ∂x)∂Q =∂(v ∂u ∂x −u ∂v∂x )=∂v∂u+v∂2u2−∂v∂u−u∂2v2 =v∂2u∂x2−u∂2v∂x2同理∂P=u ∂2v2−v∂2u2故有∬(∂Q−∂P)Ddxdy=∬(v ∂2u∂x2−u∂2v∂x2−u∂2v∂y2+v∂2u∂y2)Ddxdy=∬v∆u−u∆v D dxdy=∬|∆u∆vu v|dx dyS1.3Green第三公式证明Green第三公式:若u为有界闭区域S中的调和函数,则有:u(x,y)=12π∮(u∂ln r∂n⃗−ln r∂u∂n⃗)ds C其中C为S边界,∂u∂n⃗为u沿着C的外法线方向的方向导数;r=√(ξ−x)2+(η−y)2;为(x,y)到边界C上动点(ξ,η)的距离;证明:由Green 第二公式得到∮(u ∂ln r∂n⃗−ln r∂u∂n⃗)dsC =∬v∆u−u∆vDdxdy由于u为有界闭区域S中的调和函数,∆u=0∆v=∆ln r=∆ln√(ξ−x)2+(η−y)2=0可知ln r也是调和函数;故有在没有奇点的情况下,S内的任何区域∮(u ∂ln r∂n⃗−ln r∂u∂n⃗)dsC =∬u∆v−v∆uDdxdy=0故有设以(x,y)为中心,t为半径的一个领域D,∮(u ∂ln r∂n⃗−ln r∂u∂n⃗)dsC =∮(u∂ln r∂n⃗−ln r∂u∂n⃗)ds ∂D有在∂D上,∮ln r ∂u ∂n⃗ds∂D =ln t∮∂u∂n⃗ds∂D=ln t∬∆udsD=0∮u ∂ln rds∂D =∮u∂ln rds∂D=∮u1ds∂D=1∮uds∂D=2πu(ξ1,η1)故由u在S上的连续性得到lim t→0∮(u∂ln r∂n⃗−ln r∂u∂n⃗)ds=Climt→02πu(ξ1,η1)=2πu(x,y)故得证u(x,y)=12π∮(u∂ln r∂n⃗−ln r∂u∂n⃗)ds C第二十二章 各种积分间的联系与场论初步下面的图表给出了各种积分间的联系,在计算中可以根据这些关系,将一种积分转化为另一种积分。

green公式的条件Green 公式是高等数学中的一个重要公式,它在计算平面区域上的曲线积分与二重积分之间的关系时非常有用。
要理解 Green 公式,咱们得先搞清楚它成立的条件。
Green 公式表述为:设闭区域 D 由分段光滑的曲线 L 围成,函数P(x, y) 及 Q(x, y) 在 D 上具有一阶连续偏导数,则有∮(L) Pdx + Qdy = ∬(D) (∂Q/∂x - ∂P/∂y)dxdy 。
那 Green 公式成立的条件到底是啥呢?首先,曲线 L 得是分段光滑的。
啥叫分段光滑呢?就好比咱们走的路,有的地方平坦,有的地方有点小坡,但是整体上还算顺畅,没有那种突然断开或者特别尖锐的拐角。
这样的曲线才能保证咱们在计算的时候不会出现奇奇怪怪的问题。
再说说函数 P(x, y) 和 Q(x, y) ,它们得在闭区域 D 上具有一阶连续偏导数。
这就好比是要求两个小伙伴,不仅要能在这个区域里好好表现,还得表现得稳稳当当,不能有大的波动。
给您举个例子吧。
就说咱们有一个简单的闭区域 D ,是由一个以原点为圆心,半径为 2 的圆围成的。
假设函数 P(x, y) = x^2 ,Q(x, y) =2xy 。
咱们来验证一下 Green 公式是否成立。
先算算曲线积分∮(L) Pdx + Qdy 。
这个圆的参数方程可以设为 x =2cosθ ,y = 2sinθ ,θ 从 0 到2π 。
代入计算一番,这可得费点功夫,但算出来是8π 。
再算算二重积分∬(D) (∂Q/∂x - ∂P/∂y)dxdy 。
先求偏导数,∂Q/∂x =2y ,∂P/∂y = 0 ,然后积分,算出来也是8π 。
您瞧瞧,这两个结果一样,Green 公式成立啦!在实际应用中,如果不满足 Green 公式的条件,那可就不能随便用啦。
比如说,如果曲线不是分段光滑的,或者函数的偏导数不连续,那咱们就得另想办法,可能得把区域分割或者做一些其他的处理。
总之,搞清楚Green 公式的条件,咱们在解题的时候就能心中有数,知道啥时候能用,啥时候不能用,不会乱用公式出错啦!希望您通过我的讲解,对 Green 公式的条件有了更清楚的认识。

GREEN公式范文GREEN公式是一种用于计算两个圆内夹角的公式,它通过计算各个圆的半径、象限等信息来确定夹角的大小。
GREEN公式的全称是格林公式,也有人称之为格林定理。
它是一种广泛应用于物理、数学等领域的基本公式。
θ = arcsin[(r1+r2)/d] - arcsin[(r1-r2)/d]其中,d表示两个圆心之间的距离,也可以通过勾股定理计算得出:d=√[(x2-x1)²+(y2-y1)²]这个公式的推导较为复杂,我这里只给出结论。
下面我将对GREEN公式进行详细解释。
首先,GREEN公式的分子部分[(r1+r2)/d]和[(r1-r2)/d]分别代表两个圆心到其中一点P的距离与两个圆半径之差的比值。
这里的P是圆AB 的切点,切点处的角为θ。
接下来,我们可以用三角函数来计算这两个比值。
根据三角函数的定义,我们可以知道:sin(α) = 对边/斜边其中,α为其中一角度,对边为α角的对立边,斜边为α角的斜边。
在GREEN公式中,r1和r2分别为ΔP1A和ΔP1B的对立边,d为ΔP1P2的斜边。
所以,我们可以写出两个比值的计算公式:(r1+r2)/d = sin(α1)(r1-r2)/d = sin(α2)综上所述,我们可以得到:θ = arcsin[(r1+r2)/d] - arcsin[(r1-r2)/d]根据这个公式,我们可以计算得到任意两个圆内夹角的大小。
例如,当两个圆的半径相等时,即r1=r2,我们可以得到:θ = arcsin[(r1+r1)/d] - arcsin[(r1-r1)/d]= arcsin[(2r1)/d] - arcsin[0]= arcsin[2r1/d]这个结果表明,在两个半径相等的圆相交的情况下,夹角θ的大小只与圆心之间的距离d有关,而与半径r1的大小无关。
这符合我们平常观察到的情况,即无论两个圆的大小如何,它们相交时夹角的大小可以通过计算得到。

偏微分方程green公式偏微分方程(PartialDifferentialEquations,简称PDE)在数学和物理学中有着重要的作用,它可以描述多元函数的变化,进而用于解决实际问题。
其中,green公式是一种有用的方法,用于把复杂的PDES(偏微分方程组)转化为更容易求解的形式。
本文将介绍green 公式的定义、推导以及应用,并结合一些实例进行说明。
一、green公式的定义green公式是一种把偏微分方程组转化为更容易求解的形式的方法,由英国数学家George Green在19世纪发现,因此也称为green 公式。
它的形式为:$$ oint_{sp} left[f frac {partial u}{partialn}-frac{partial f}{partial n} Uright]ds=0 $$其中,U代表未知函数,f为边界条件,n为法向量,sp代表边界曲线。
二、green公式的推导green公式的推导可以分为四个步骤:1.先考虑f=0的特殊情况,即特征值方程。
2.令U(x,y)构成 Green数,写出 Green数的偏微分方程;3.给出 Green数 U(x,y)特解,并写出特解的表达式;4.根据Green函数U(x,y)的特解,推导出green公式。
三、green公式的应用Green公式可以用于许多应用领域,如热传导、电磁场、气流模拟等。
1.Green公式在热传导中的应用:热传导是一种物理现象,其中,Green公式可以用来求解温度场的变化问题。
如果将温度场用U(x,y)表示,则可以将热传导问题转化为求解green公式的问题。
2.Green公式在电磁场中的应用:电磁场是一种物理现象,其中,Green公式可以用来求解电和磁场分布的变化问题。
如果将电场用U(x,y)表示,则可以把电磁场变化问题转化为求解green公式的问题。
3.Green公式在气流模拟中的应用:气流模拟是一种应用green公式求解流体力学问题的方法。

偏微分方程green公式微分方程是数学中广泛使用的一种方法,用来求解函数等式。
由于它能够解决很多实际应用中的问题,所以它在科学和工程领域的应用也越来越广泛。
其中,偏微分方程是一种特殊的微分方程,它可以用来解决多元变量函数的微分方程。
偏微分方程Green公式是偏微分方程学习、研究和应用时最常用的一种方法。
偏微分方程Green公式是偏微分方程的一般解法,可用来解决高维变量函数的偏微分方程,它是由英国数学家George Green在1828年提出的。
此公式有助于解决求解多变量函数不同梯度变量的问题,即求解某一具体变量梯度的值。
Green公式的具体内容是:$$int_V abla fcdot ndV=int_{partial V}frac{partial f}{partial n}dS$$其中,$V$为某个区域,$partial V$为$V$的边界,$n$为边界的单位法向量,$f$为一个(空间)偏导数变量函数,$abla f$为$f$的梯度,$dV$和$dS$分别为$V$和$partial V$上的小元素,$frac{partial f}{partial n}$为$f$在$partial V$上的单位法矢偏导数。
偏微分方程Green公式是一种常用的定理,它可以推广到更多次元空间,是求解自定义多变量函数偏微分方程的重要工具。
此公式也可以用来解决若干种由偏微分方程产生的特殊问题,例如变分问题、传热问题等。
Green公式又是偏微分方程在经典力学、热力学等物理学领域的重要应用,因此,在偏微分方程的学习和研究中,Green 公式的掌握非常重要。
Green公式不仅在应用中有重要意义,而且在理论上也有重要意义。
它对理解偏微分方程的物理意义有重要作用,更重要的是,它引出了外积分的概念,为偏微分方程的理论研究奠定了基础。
同时,Green公式也为后来的场论微分方程的研究奠定了基础,因此它的重要性不言而喻。
掌握Green公式的重要性不言而喻,它不仅可以用来解决偏微分方程的具体问题,而且可以帮助我们更好地理解偏微分方程的相关知识。

green公式法摘要:1.引言2.Green 公式法的定义和原理3.Green 公式法的应用领域4.Green 公式法的优缺点5.结论正文:1.引言Green 公式,又称Green 恒等式,是由英国数学家George Green 在1828 年提出的。
这个公式在数学、物理以及工程领域中有着广泛的应用,尤其在解决一些偏微分方程和波动方程的问题时,具有重要的意义。
2.Green 公式法的定义和原理Green 公式法是一种求解偏微分方程的数值方法。
其基本原理是将偏微分方程中的积分操作用离散求和来代替,从而将偏微分方程转化为一个巨大的线性方程组,进而求解。
具体来说,对于一个在区域D 上的函数f(x, y),如果它在区域D 上有一个连续的一阶偏导数,那么可以通过Green 公式法来求解该函数在区域D 上的值。
公式如下:D f(x, y) dA = D f(x, y)/n * dA,其中,n 为区域D 的边界单位法向量,dA 为区域D 的面积元素。
3.Green 公式法的应用领域Green 公式法在许多领域都有广泛的应用,如在电磁场问题的求解、热传导问题的求解、波动方程的求解等。
特别是在求解无界区域上的偏微分方程时,Green 公式法具有独特的优势。
4.Green 公式法的优缺点Green 公式法的优点在于它将复杂的偏微分方程转化为一个线性方程组,求解起来更加简便。
同时,它适用于许多不同的应用领域,具有较强的通用性。
然而,Green 公式法也存在一些缺点。
首先,它的适用性依赖于函数的一阶偏导数存在。
其次,当区域D 的边界形状复杂或者边界条件复杂时,求解难度会大大增加。
5.结论总的来说,Green 公式法是一种求解偏微分方程的有力工具,尤其在求解无界区域上的偏微分方程时,具有独特的优势。


green公式法Green公式是数学分析中常用的一个重要定理,是微积分中的一种基本方法。
它的原理是通过将一个区域内的曲线或曲面的积分转化为该区域内的区域积分,从而简化计算过程。
在本文中,我们将介绍Green公式的定义、推导过程以及一些应用案例。
1. Green公式的定义给定一个平面区域D,边界为C。
设函数P(x, y)和Q(x, y)在D上具有连续的偏导数,那么Green公式可以表示为:∬D ( ∂Q/∂x - ∂P/∂y) dA = ∮C (P dx + Q dy)其中,∂Q/∂x 和∂P/∂y 分别表示Q(x, y)和P(x, y)对x和y的偏导数,∬D 表示对D上的区域积分,∮C 表示对C上的曲线积分。
2. Green公式的推导为了推导Green公式,我们先假设区域D是简单闭合区域,即边界C是一个简单闭合曲线。
然后,将区域D划分为无穷多个小的区域,每个小区域都可看作是矩形区域。
通过对小矩形区域应用散度定理,我们可以得到:∬D ( ∂Q/∂x - ∂P/∂y) dA = ∭V (∂^2Q/∂x^2 + ∂^2P/∂x∂y ) dV其中,∬D ( ∂Q/∂x - ∂P/∂y) dA 可以看作是在D上的曲面积分,∭V (∂^2Q/∂x^2 + ∂^2P/∂x∂y ) dV 则是在D的内部体积上的体积积分。
由于无穷小小矩形区域趋近于零,所以体积积分项在推导过程中可以忽略。
因此,我们可以得到:∬D ( ∂Q/∂x - ∂P/∂y) dA = ∮C (P dx + Q dy)通过以上推导,我们成功地得到了Green公式。
3. Green公式的应用案例Green公式在物理学、工程学和计算机图形学等领域有广泛的应用。
下面我们将介绍一些常见的应用案例。
3.1 流场的流量计算假设在平面区域D上存在一个流场,流速由函数V(x, y)表示,那么流过闭合曲线C的总流量可以通过Green公式计算得出。
根据Green公式,我们有:∮C (V · n) ds = ∬D ( ∂Vx/∂x + ∂Vy/∂y) dA其中,V · n 表示V向量与曲线的法向量的点积,∂Vx/∂x 和∂Vy/∂y 分别表示Vx(x, y)和Vy(x, y)对x和y的偏导数。
![[研究生入学考试]工科数学分析Green公式](https://uimg.taocdn.com/775b17d96137ee06eff91876.webp)
偏微分方程green公式Green式是一种重要的偏微分方程的数学工具。
它是由英国数学家GeorgeGreen于一七九七年提出的,用来分析不同流体和介质的物理量,例如速度、流量等。
该公式常被各类学科用来进行复杂的系统建模求解,如理论流体动力学、声学,电磁学,控制等。
Green公式的原理可以归纳为涡流公式,即可用来描述不同介质的流:F = 0其中 F = (F1, F2, F3)一个流量矢量场, = (/x1,/x2,/x3)一个偏微分型运算符。
根据Green公式,可以把任何复杂的流动系统映射到一个偏微分方程组:^2φ= 0其中φ为流场中的潜力流函数,^2 为二阶偏微分运算符,表示二阶拉普拉斯运算,是确定流场参数的基本公式。
Green公式在各学科中应用十分广泛,并得到了很好的应用效果。
在应用偏微分方程的理论流体动力学中,Green公式被作为基本的重要工具,用于推导出稳定流动、湍流流动和多米诺效应等复杂流动的数学方程。
此外,Green公式在声学领域也发挥了重要作用,当以局部方程组形式描述声音在各种介质中的传播时,则可以使用Green公式求解声音在介质中传播的过程。
Green公式还可以应用于电磁学中,用以解决电磁场中存在的复杂问题,比如电磁波在介质中的传播。
Green公式中的偏微分方程可以用于描述电磁场中复杂的介质场,从而更加清晰地了解电磁场行为。
此外,Green公式还被应用在控制系统中,可用于求解控制系统的状态和输出,从而可以进行自动化的控制设计。
此外,Green公式也可以用于分析非线性控制系统,可以使用其求解控制系统的复杂性和稳定性,从而对控制系统进行更加有效的控制设计。
从上述可以看出,Green公式发挥着十分重要的作用,用来推导复杂的流动系统和控制系统的偏微分方程,是理论研究和技术应用的重要工具之一。
在实际应用中,Green公式有着众多的应用,比如可以用来描述流体、声学和电磁学的复杂系统,也可以用来解决控制系统的复杂性和稳定性等问题。
偏微分方程green公式偏微分方程Green公式也称为拉格朗日-Green公式,是一种重要的物理学结论,由英国数学家George Green于1828年提出。
它主要描述了偏微分方程在给定边界条件下的解,深刻地影响着物理和工程领域中的许多研究。
Green公式是一个由一个通用的偏微分方程推导出来的公式,由微分方程的解决形式所表示,是描述偏微分方程在给定边界条件下的一种解。
换句话说,Green公式可以用来表示偏微分方程的某种分类解,这种解是由特定的边界特征约束的。
Green公式可以表示偏微分方程的一下形式:u/t + [f(t,x)u]=0。
此外,Green公式还可以用来表示非线性偏微分方程的解,例如,Green 公式可以表示热传导方程:u/t + [f(t,x)u]=/x(a(t,x)u/x)。
Green公式在物理学和工程领域中有着广泛的应用,特别是在流体动力学、热传导学、电磁学、声学学等方面,可以研究各种物理系统的特性。
例如,它可以应用于湍流流动的混合物,考虑复杂的物理机制和流体动力学现象;可以应用于热传导方程,考虑特殊的温度场,例如稳定的温度场和不稳定的温度场;可以用于求解特定的有限元素模型,可以求解许多复杂的结构件及其结构外响应;可以应用于声学中,以求解复杂场景下声场及其关联振动特性;还可以用于磁学,研究和计算各种磁体以及磁性体在不同激发下的特性。
Green公式是一种重要的数学结论,它的发现深刻地影响着物理和工程领域的许多研究,广泛应用于流体动力学、热传导学、电磁学、声学学等多个领域,为深入研究物理系统提供了关键突破。
虽然Green 公式已经被用于各种研究领域,但仍有许多不完善之处,需要进一步研究和应用。
Green公式及其在物理学和工程领域的应用对于研究物理系统来说具有重要的意义,可以提供更多的结构外响应,综合考虑的许多物理机制,更有效地描述物理系统的动力学特性,从而更好地研究物理系统的行为。
向量微积分中的Green公式Green公式,也叫格林公式,是向量微积分中的一个基本定理,它是关于曲线和曲面的一个重要公式。
Green公式可以用来求解曲线和曲面上的积分,和场的无旋和任意面积的关系等。
首先,我们来看一下Green公式在平面上的形式。
设$C$是一条闭合的简单曲线,$\vec{n}$是该曲线所在平面的法向量,$D$是这个闭合曲线所包围的区域,$\vec{F}=(M,N)$是二维空间上的一个向量场。
那么,Green公式就可以表述为:$$\oint_C \vec{F}\cdot \vec{T} ds = \iint_D \left(\frac{\partialN}{\partial x}-\frac{\partial M}{\partial y}\right)dxdy$$其中,$\vec{T}$是曲线$C$的切向量,$s$是弧长,$dxdy$是面积元素。
公式右边的第一项表示曲线$C$上的环量,第二项表示曲线所围成的区域$D$内向量场的环量。
对于三维空间,Green公式还有一个更为一般的形式,称为Stokes公式。
它描述了曲线与曲面之间的关系。
设$M$, $N$,$P$是三维空间中的一个向量场,曲面$S$是一个紧致的光滑曲面,边界为曲线$C$,$\vec{n}$是曲面$S$的法向量,$\vec{T}$是曲线$C$的切向量,那么Stokes公式可以写为:$$\int_C \vec{M}\cdot d\vec{r} = \iint_S\left(\text{rot}\,\vec{M}\right)\cdot \vec{n}\,dS$$其中,$\text{rot}\,\vec{M}$表示向量场$\vec{M}$的旋度。
要理解Green和Stokes公式,我们需要先了解向量场的性质和运算。
向量场是指空间中对每个点都定义了一个向量的函数,这个函数的值随着点的位置而变化。
在向量场中,有一些基本的运算,比如梯度、散度和旋度。
Green公式与Stokes公式绿公式(Green's theorem)和斯托克斯公式(Stokes' theorem)是数学中常用的两个定理,它们在向量分析和微积分等领域具有重要的应用。
本文将深入探讨这两个定理的原理和应用。
一、绿公式绿公式是对曲面积分和曲线积分之间关系的一种描述。
它的数学表达方式如下:设平面区域D为闭合曲线C所围成的有向区域,f(x, y)是定义在D 上具有一阶连续偏导数的标量函数,而P(x, y)和Q(x, y)是定义在D上具有一阶连续偏导数的向量函数,则有以下等式成立:∬D (∂Q/∂x - ∂P/∂y) dxdy = ∮C (Pdx + Qdy)其中,∬D表示对D上的面积进行积分,∮C表示对曲线C进行积分。
绿公式的直观解释是,曲面离散的“内部”贡献与曲面边界上的积分相互联系。
通过应用绿公式,我们可以将一个曲面积分转换为曲线积分,从而简化问题的求解。
二、斯托克斯公式斯托克斯公式是绿公式在三维空间中的推广。
它描述了一个曲面S 的边界曲线C与该曲面上的向量场之间的关系。
斯托克斯公式的数学表达如下:设S为是一个光滑的曲面,n为S的外法向量,P(x, y, z)、Q(x, y, z)、R(x, y, z)是定义在S上具有一阶连续偏导数的向量函数,则有以下等式成立:∬S (rot F · n) dS = ∮C F · dr其中,∬S表示对S上的面积进行积分,∮C表示对曲线C进行积分,rot F表示向量场F的旋度。
斯托克斯公式的意义在于将一个三维空间中的曲面积分转换为该曲面的边界曲线上的积分,使问题的求解得以简化。
三、绿公式与斯托克斯公式的应用绿公式和斯托克斯公式在物理学、电磁学、流体力学等领域有广泛应用。
在电磁学中,斯托克斯公式可以用来描述磁场在闭合曲线上的环流与该闭合曲线所围曲面上的磁场强度之间的关系。
它为磁场的计算提供了一种便捷的方法。
在流体力学中,斯托克斯公式用于计算流体在闭合曲面上的通量与该闭合曲面所围曲线上的速度场之间的关系。
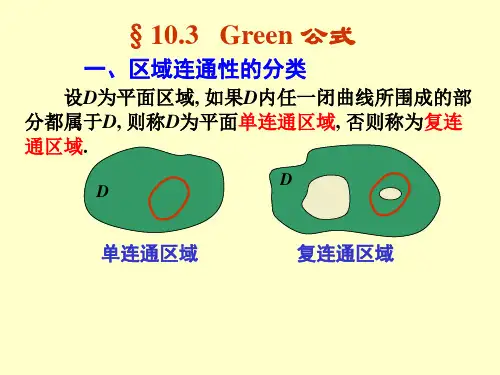
数学分析(二):多元微积分
梅加强副教授
南京大学数学系
内容提要:
内容提要:
诱导定向;
内容提要:
诱导定向; Green公式;
内容提要:
诱导定向;
Green公式;
简单闭曲线所围区域的面积;
内容提要:
诱导定向;
Green公式;
简单闭曲线所围区域的面积; 代数基本定理.
考虑平面R2上的有界区域Ω,假定其边界由有限条C1曲线组成.R2上的标准定向限制在Ω上就得到Ω的定向.
考虑平面R2上的有界区域Ω,假定其边界由有限条C1曲线组成.R2上的标准定向限制在Ω上就得到Ω的定向.
Ω的边界∂Ω有所谓的诱导定向.其定义如下:设(x(t),y(t))为∂Ω的一段参数曲线,则(x (t),y (t))为切向量,(y (t),−x (t))为法向量.
考虑平面R2上的有界区域Ω,假定其边界由有限条C1曲线组成.R2上的标准定向限制在Ω上就得到Ω的定向.
Ω的边界∂Ω有所谓的诱导定向.其定义如下:设(x(t),y(t))为∂Ω的一段参数曲线,则(x (t),y (t))为切向量,(y (t),−x (t))为法向量.
如果(y (t),−x (t))为相对于区域Ω的外法向量,则参数t决定的边界方向称为诱导定向.直观上看,从外法向到切向的旋转方向是逆时针的,这种确定边界定向的方法又称为“右手法则”.
考虑平面R2上的有界区域Ω,假定其边界由有限条C1曲线组成.R2上的标准定向限制在Ω上就得到Ω的定向.
Ω的边界∂Ω有所谓的诱导定向.其定义如下:设(x(t),y(t))为∂Ω的一段参数曲线,则(x (t),y (t))为切向量,(y (t),−x (t))为法向量.
如果(y (t),−x (t))为相对于区域Ω的外法向量,则参数t决定的边界方向称为诱导定向.直观上看,从外法向到切向的旋转方向是逆时针的,这种确定边界定向的方法又称为“右手法则”.
利用诱导定向,沿边界的第二型曲线积分有时可以化为区域中的重积分.
(Green公式)
设Ω为平面有界区域,其边界由有限条C1曲线组成,边界的定向为诱导定向.如果P,Q为¯Ω上的C1函数,则
Ω ∂Q
∂x
−
∂P
∂y
d x d y=
∂Ω
P d x+Q d y.
(Green公式)
设Ω为平面有界区域,其边界由有限条C1曲线组成,边界的定向为诱导定向.如果P,Q为¯Ω上的C1函数,则
Ω ∂Q
∂x
−
∂P
∂y
d x d y=
∂Ω
P d x+Q d y.
Green公式是一元微积分中Newton-Leibniz公式在平面上的推广.
(Green公式)
设Ω为平面有界区域,其边界由有限条C1曲线组成,边界的定向为诱导定向.如果P,Q为¯Ω上的C1函数,则
Ω ∂Q
∂x
−
∂P
∂y
d x d y=
∂Ω
P d x+Q d y.
Green公式是一元微积分中Newton-Leibniz公式在平面上的推广.
Green公式的传统证明方法是将被积区域分割为两种特殊类型的小区域,在每一小区域上验证公式成立,最后合起来就得到整个区域上的公式.
若Ω的边界是简单闭曲线γ(t)=(x(t),y(t))(t∈[α,β]),在Green公式中代入P(x,y)=−y,Q(x,y)=x,可得如下面积公式
σ(Ω)=1
2
∂Ω
−y d x+x d y=
1
2
β
α
[x(t)y (t)−x (t)y(t)]d t,
其中,参数t选取的方向沿逆时针.
若Ω的边界是简单闭曲线γ(t)=(x(t),y(t))(t∈[α,β]),在Green公式中代入P(x,y)=−y,Q(x,y)=x,可得如下面积公式
σ(Ω)=1
2
∂Ω
−y d x+x d y=
1
2
β
α
[x(t)y (t)−x (t)y(t)]d t,
其中,参数t选取的方向沿逆时针.
例如,考虑椭圆x2
a2+y2
b2
=1所围成的面积.椭圆的参数方程为x(t)=a cos t,y(t)=b sin t,t∈[0,2π],
于是其面积为
σ=1
2
2π
(a cos t b cos t+a sin t b sin t)d t=πab.
设p(z)=z n+c1z n−1+···+c n−1z+c n为复系数n次多项式.代数基本定理说p(z)在复平面上必有零点.
设p(z)=z n+c1z n−1+···+c n−1z+c n为复系数n次多项式.代数基本定理说p(z)在复平面上必有零点.
(反证法)设p(z)处处非零.当R>0时,记p(Rz)/R n的实部和虚部分别为f,g,则f和g不能同时为零.
设p(z)=z n+c1z n−1+···+c n−1z+c n为复系数n次多项式.代数基本定理说p(z)在复平面上必有零点.
(反证法)设p(z)处处非零.当R>0时,记p(Rz)/R n的实部和虚部分别为f,g,则f和g不能同时为零.
考虑
f d g−
g d f f2+g2=P d x+Q d y,其中P=
fg x−gf x
f2+g2
,Q=
fg y−gf y
f2+g2
.
容易验证Q x−P y=0.
设p(z)=z n+c1z n−1+···+c n−1z+c n为复系数n次多项式.代数基本定理说p(z)在复平面上必有零点.
(反证法)设p(z)处处非零.当R>0时,记p(Rz)/R n的实部和虚部分别为f,g,则f和g不能同时为零.
考虑
f d g−
g d f f2+g2=P d x+Q d y,其中P=
fg x−gf x
f2+g2
,Q=
fg y−gf y
f2+g2
.
容易验证Q x−P y=0.
在单位圆盘上应用Green公式,有
S1f d g−g d f
f2+g2
=
D
(Q x−P y)d x d y=0,(1)
另一方面,在S1上,记z=e iθ,则
f(z)=cos nθ+1
R
a1cos(n−1)θ−b1sin(n−1)θ+···
,
g(z)=sin nθ+1
R
a1sin(n−1)θ+b1cos(n−1)θ+···
,
其中a1,b1分别为c1的实部和虚部.
另一方面,在S 1上,记z =e i θ,则
f (z )=cos n θ+1R a 1cos(n −1)θ−b 1sin(n −1)θ+··· ,
g (z )=sin n θ+1R
a 1sin(n −1)θ+
b 1cos(n −1)θ+··· ,其中a 1,b 1分别为
c 1的实部和虚部.
由此可见,当R →∞时,f 2+g 2=1+O (1/R ),且f d g −g d f =(fg θ−gf θ)d θ= n +O (1/R ) d θ.这说明,当R 充分大时 S
1f d g −g d f f 2+g 2= 2π0 n +O (1/R ) d θ=2πn +O (1/R )=0,这与(1)式相矛盾!
另一方面,在S 1上,记z =e i θ,则
f (z )=cos n θ+1R a 1cos(n −1)θ−b 1sin(n −1)θ+··· ,
g (z )=sin n θ+1R
a 1sin(n −1)θ+
b 1cos(n −1)θ+··· ,其中a 1,b 1分别为
c 1的实部和虚部.
由此可见,当R →∞时,f 2+g 2=1+O (1/R ),且f d g −g d f =(fg θ−gf θ)d θ= n +O (1/R ) d θ.这说明,当R 充分大时 S
1f d g −g d f f 2+g 2= 2π0 n +O (1/R ) d θ=2πn +O (1/R )=0,这与(1)式相矛盾! 代数基本定理是由Gauss 首先证明的.有趣的是,至今还没有纯代数的证明.。