2018年清北大学数学金秋营试题及答案
- 格式:docx
- 大小:5.13 MB
- 文档页数:16


【最新整理,下载后即可编辑】北京大学“中学生数学奖”夏令营初赛 试题2018年6月23日本试卷共4题,每题30分,满分120分.考试时间180分钟.1.已知a 、b 、c 为整数,且对任意正整数m 、n ,存在整数x 满足如下关系:()2mod .ax bx c m n ++≡求所有满足要求的三元整数组(),,a b c .2.已知实数122018,,,a a a 两两不同,存在t 满足11i i a t a ++=(1,2,,2018i =,并规定20191a a =).求实数t 的可能取值的个数.3.给定正整数n 、k .有一个密码锁,它有n 个按钮,编号分别为1n .打开该锁的密码是长度为k 的按钮序列.当且仅当连续正确的按动这k 个按钮时,密码锁会被打开.(例如3n =,2k =,密码为13时,依次按动1,2,3,2,1,1,3后可以打开该锁,按动2,2,3,1,3后也可以打开该锁.)要保证把这个密码锁打开,至少需要按动多少次按钮?4.如图,ABC ∆中AB AC ≠.点A 所对应的旁切圆圆J 分别与直线BC 、CA 、AB 相切于点D 、E 、F .点M 是线段BC 的中点.点S 在线段JM 上,且满足AS DS AE +=.求证:MS BD CD SJ ⋅=.试卷答案本试卷共4题1.设()2f x ax bx c =++,注意()()()mod f x f x n n ≡+,故本题只需对任意正整数n ,()()()0,1,,1f f f n -组成模n 的完全剩余系.下证0a =,1b =-或1.若0,1a b +≠±,取n a b =+,则()()()01mod f f n ≡,矛盾. 若0a b +=,则()2f x ax ax c =-+,此时()()01f f =,这也不可能. 故1a b +=-或1.当1a b +=时,0a ≠,则1641241248a b a a b +≥-+≥-=. 取164n a b =+,则()()()04mod f f n ≡,矛盾.故0a =. 类似当1a b +=-时,取164n a b =+,可得0a =.故()(),0,1a b =或()0,1-.注意对任意正整数m 、n ,同余方程()mod x c m n +≡和()mod x c m n -+≡显然有解.故()(),,0,1,a b c k =或()0,1,k -,k Z ∈.2.由已知有11i i a t a +=-,不动点方程为1x t x=-,化为210x tx -+=,设此一元二次方程的两根为α与β.当αβ=时,若2t =,则1112i i i a a a +--=-,111111i i a a +=---,2019111201811a a =---,矛盾. 若2t =-,同理可得2019111201811a a =+++,也矛盾. 所以αβ≠,可得1i i i a a t a ααα+--=⋅-,以及1i i i a a t a βββ+--=⋅-, 两式相除得11i i i i a a a a αααβββ++--=--,有2111111i i i i a a a a a a αααααββββ++-⎛⎫--==⋅ ⎪---⎝⎭, 从而40362019120191a a a a αααββ--=⋅--,40361α=, 由对称性,不妨设2018ki e πα=,()40362018k ieπβ-=,其中12018k ≤≤. 另一方面,当12018i j ≤<≤时,由i j a a ≠知,j i j i a a a a ααββ--≠--, 而()21j j t j t a a a a αααββ---=⋅--.所以当12018t ≤<时,21t α≠, 即2220181tki t e πα=≠,即对任意12018t ≤<,tk 都不是2018的倍数, 即(),20181k =,又因为201821009=⨯,所以这样的k 有11201811100821009⎛⎫⎛⎫⨯-⨯-= ⎪ ⎪⎝⎭⎝⎭个,所以2cos 2018k t παβ=+=有1008个取值. 3.最少需要按1k n k +-次.不同的密码共有k n 个,要保证打开密码锁,必须全部试过一遍.从第k 次按键开始,每次按动按钮都可以视为一个长为k 的序列末位,故至少需要1k n k +-次.下面给出按动1k n k +-次可以满足要求的存在性证明. 当1k =时结论显然成立,故下设2k ≥.构造图G ,共有1k n -个顶点,每个顶点对应为一个长为1k -的序列.对顶点A ,B ,若点A 所对应序列的后2k -位与点B 所对应序列的前2k -位相同,则在AB 之间连一条由A 指向B 的有向边.此时每一个长为k 的序列可以对应为该图中的一条边.注意图G 为连通图,且每个顶点的入度和出度均为n ,我们即证明该图中存在欧拉圈.为此给出如下引理:若有向连通图G 中所有顶点的入度和出度都相同,则该图中存在欧拉圈.对图G 的总边数进行归纳证明,若图G 每个顶点出入度为1,且该图中存在圈,再由连通性可得该圈为欧拉圈. 若总边数小于m 时结论成立,考虑总边数等于m 时. 考虑图中的最大有向圈Γ,显然这样的圈存在.若Γ不是欧拉圈,则从图G 中去掉Γ,得到图G '.此时图G '每点的出入度仍相同(但可以为0).取G '中的一条边,使其一个顶点在Γ中,沿该边前进,可以得到图G '中的圈'Γ.注意Γ和'Γ没有公共边,故可将它们拼接得到一个更大的圈.这与Γ的最大性矛盾,故此时结论成立. 综上,引理得证.由引理,我们即可得到本题存在性证明.4.如图,作BDS ∠的平分线交BJ 于P ,以P 为圆心、点P 到直线BC 的距离为半径作P ,则P 与直线AB 、BD 、DS 均相切.过A 作P 的异于直线AB 的切线,交直线DS 于S ',则P 与四边形ABDS '的各边所在直线均相切,由“切线长相等”可得AB BD AS DS ''+=+,又已知AS DS AE AF AB BD +===+,因此AS DS AS DS ''+=+,故SS AS AS ''=-,由“三角形两边之差小于第三边”可知 S '与S 重合,所以P 与四边形ABDS 的各边所在的直线都相切. 作CDS ∠的平分线交CJ 于Q ,以Q 为圆心、点Q 到直线BC 的距离为半径作Q ,类似可证Q 与折四边形ACDS 的各边所在的直线都相切.从而AS 、DS 都与P 和Q 相切,故S 是P 和Q 的内位似中心.故S 、P 、Q 三点共线.下面证明//PQ BC .用反证法.假设直线PQ 与直线BC 相交于T ,因DP 、DQ 分别平分SDT ∠或SDT ∠的邻补角,所以DP 、DQ 、DS 、DT 是调和线束,该线束与直线PQ 截得4点P 、Q 、S 、T 是调和点列,故JP 、JQ 、JS 、JT 是调和线束,该线束再与直线BC 截得4点B 、C 、M 、T 是调和点列,但M 是BC 的中点,矛盾,所以//PQ BC .设PQ 与JD 相交于H .由DP 、DQ 分别平分BDS ∠及其邻补角得DP DQ ⊥,再结合//PQ BC 得PQ DH ⊥,所以 PH QH MS DH PH QH BD CD BD CD SJ HJ HJ HJ JD JD ⋅⋅====⋅=.。

清华领军2015.4.设函数()f x 的定义域为(-1,1),且满足:①()0,(1,0)f x x >∈-;②()()1x y f x f y f xy ⎛⎫++= ⎪+⎝⎭,(1,1)x y ∈-、,且()f x 为( )A.奇函数B.偶函数C.减函数D.有界函数清华领军2015.5.如图,已知直线y kx n =+与曲线()y f x =相切于两点,则()()F x f x kx =-有( )A.2个极大值点B.3个极大值点C.2个极小值点D.3个极小值点 同时分入了导数类清华领军2015.23.设函数2sin π()1xf x x x =-+,则( )A.4()3f x ≤B.|()|5||f x x ≤C.由线()y f x =存在对称轴D.曲线()y f x =存在对称中心清华领军2015.30.设曲线L 的方程为42242(22)(2)0y x y x x +++-=,则( ) A.L 是轴对称图形 B.L 是中心对称图形 C.22{(,)|1}L x y x y ⊂+≤ D.11(,)|22L x y y ⎧⎫⊂-≤≤⎨⎬⎩⎭同时分入函数的极值类清华领军2017.15.已知2()f x x ax b =++在(1,1)x ∈-上有两个零点。
求22a b -的取值范围。
A.(0,)+∞B.(0,2)C.(,2)-∞D.(2,2)-清华领军2017.21.满足35(3)40x y x x y ++++=的(,)x y ( ) A.在一条直线上 B.在一条抛物线上 C.为有限个 D.为无限个 分类存疑北大自招2016.1. 求()212log 2x x -++的单调增区间。
1.【解答】1,22⎛⎫ ⎪⎝⎭要求()212log 2x x -++的单调增区间,由12log x 是在()0,+∞上的减函数,故即解2201,2122x x x x ⎧-++>⎪⎛⎫⇒∈⎨ ⎪>⎝⎭⎪⎩北大自招2016.5. 设x ,y ,z 3R ∈,求方程381nnnx y z ++≤,当n →+∞时确定的几何体的体积为________。

2018年秋季精英班数学选拔测试题第一卷1.计算:16.075622145.199.1313-÷+⨯÷)(1.420115.015223245.3+⨯++2.已知甲、乙两自然数之比为5:3,并且它们的最大公约数与最小公倍数之和为1040,求甲数和乙数。
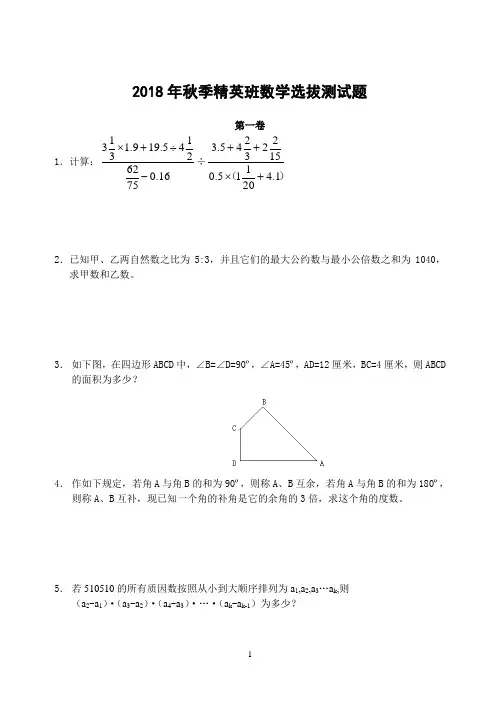
3. 如下图,在四边形ABCD 中,∠B=∠D=90º,∠A=45º,AD=12厘米,BC=4厘米,则ABCD 的面积为多少?4. 作如下规定,若角A 与角B 的和为90º,则称A 、B 互余,若角A 与角B 的和为180º,则称A 、B 互补,现已知一个角的补角是它的余角的3倍,求这个角的度数。
5. 若510510的所有质因数按照从小到大顺序排列为a 1,a 2,a 3…a k ,则(a 2-a 1)·(a 3-a 2)·(a 4-a 3)·…·(a k -a k-1)为多少?6.用1到6这六个不同的数字组成一个各个数位上数字均不相同的六位数abcdef,且4|abc,5|bcd,3|cde,11|def。
那么满足上述要求的六位数是多少?第二卷1.甲乙两瓶浓度未知的酒精分别含纯酒精200毫升和450毫升,如果把它们均匀混合(忽略体积变化)则混合后的浓度比原来甲瓶的浓度高7%,但比原来乙瓶的浓度低14%,问混合后的浓度是多少2.一次象棋比赛共有10名选手参赛,他们分别来自甲、乙、丙3个队,每个人都与其余9名选手各赛一盘,每盘棋胜者都得1分,负者得0分,平局各得0.5分,结果甲队选手平均得4.5分,乙队选手平均得分3.6分,丙队选手平均得9分,那么甲、乙、丙3队各派参赛选手多少名?3.组织集体订阅,有《数理天地》月刊,全年共出12期,每期定价2.50元,其小学六年级些学生订半年而另一些学生订全年,共需1320元,若订全年的同学与订半年的同学人数交换,共需订费1245元,由该小学六年级订阅《数理天地》的学生共有多少人?4.箱子里有乒乓球若干,其中25%是一级品,五分之几是二级品,其余91是三级品。

绝密★启用前 北清学子教科所版权所有 试卷类型:A北 清 骄 子 卷数 学(2-1) (湖南卷)命题说明:融入2018年湖南高考数学考试大纲最新信息,本卷为最后一轮与高考接轨的信息卷。
试卷结构:本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.共150分,考试时间120分钟。
全 卷 统 分 卡题号 1-10 11-15 16 17 18 19 20 21 总分 题分 50 20 12 12 14 14 14 14 150 得分第 I 卷 答 题 卡题号 1 2 3 4 5 6 7 8 9 10 答案参考公式:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ). 如果事件A 、B 相互独立,那么P (A·B )=P (A )·P (B ).如果事件A 在一次试验中发生的概率是P ,那么它在n 次独立重复试验中恰好发生k 次的概率P n (k )=k n C P k (1-P )n -k .球的表面积公式 S =4πR 2,其中R 表示球的半径. 球的体积公式 S =4/3πR 3,其中R 表示球的半径.第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合2{|2160}A x x x =--≤,5{|5}y B y C =≤,则A B 中元素个数为A .1个B .2个C .3个D . 4个2.若角α的终边过点(︒-︒30cos 3,30sin 3),则sin θ等于得分 评卷人A .21B .21-C .23-D .33-3.(理科)过点P (-1,0)作圆C :(x - 1)2 + (y - 2)2 = 1的两切线,设两切点为A 、B ,圆心为C ,则过A 、B 、C 的圆方程是 A .x 2 + (y - 1)2 = 2 B .x 2 + (y - 1)2 = 1 C .(x - 1)2 + y 2 = 4 D .(x - 1)2 + y 2 = 1(文科)如果直线ax + by – 4 = 0与圆C :x 2 + y 2 = 4有2个不同的交点, 那么点P (a,b )与圆C 的位置关系是A .在圆外B .在圆上C .在圆内D .不确定4.(理科)函数y = f (x )的图象过原点且它的导函数y = f ' (x )的图象是如图所示的一条直线,则y = f (x )的图象的顶点在A .第一象限B .第二象限C .第三象限D .第四象限(文科)已知函数f (x ) = ax 3 + bx 2 +cx + d 的图像如图 所示,则下列判断正确的是 A .a < 0, b < 0, c < 0 B .a > 0, b > 0, c < 0C .a > 0, b < 0, c > 0D .a > 0, b > 0, c > 0 5.若不等式0)1(ln <--an a a对于任意正整数n 恒成立, 则实数a 的取值范围是 A .{1}a a >B .1{0}2a a <<C .1{01}2a a a <<>或D .1{01}3a a a <<>或6.已知F 1,F 2分别为双曲线22221(0,0)x y a b a b-=>>的左、右焦点,P 为双曲线右支上的任意一点,若212PF PF 的最小值为8a ,则双曲线的离心率e 的取值范围是A .(1,)+∞B .(1,2] C. D .(1,3]7.平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n 维向量可用(x 1,x 2,x 3,x 4,…,x n )表示.设a =( a1, a 2, a 3, a 4,…, a n ),b =(b 1, b 2, b 3, b 4,…,b n ),规定向量a 与b 夹角θ的余弦为∑∑∑====n i ni i i ni ii b a ba 11221))((cos θ. 当a =(1, 1,1,1...,1),b =(-1, -1, 1, 1, (1)时,cos θ= A .nn 1-B .nn 3- C.nn 2- D .nn 4- 8.若二面角M -l -N 的平面角大小为23π,直线m ⊥M ,则平面N 内的直线与m 所成角的取值范围是 A .[,62]ππB .[,]42ππC .[,]32ππD .[0,]2π9.某银行储蓄卡的密码是一个4位数,某人用千位、百位上的数字之积作为十位,个位上的数字(如2816)的方法设计密码,当积为一位数时,十位上数字选0,千位、百位上都能取0,这样设计出来的密码有 A .90个 B .99个 C .100个 D .112个10.2018年10月27日全国人大通过了关于修改个人所得税法的决定,工薪所得减除费用标准从800元提高到1600元,也就是说原来收入超过800元的部分就要纳税,2018年1月1日开始超过1600元才纳税,若税法修改前后超过部分的税率相同,如下表:试问:如果某人2018年9月交纳个人所得税123元,那么按照新税法,他只要交税A .43元B .33元C .23元D .53元第Ⅱ卷(非选择题 共100分)二、填空题(本大题共5小题,每小题4分,共20分。

清华大学 2018年领军计划测试题注:2018领军数学试题均为不定项选择,以下题目为回忆版本,部分问题选项缺失。
1. ,,p q r 均为素数,且pqrp q r++为整数,则( )A. ,,p q r 中一定有一个是2B. ,,p q r 中一定有一个是3C. ,,p q r 中一定有两个数相等D.pqrp q r++也为素数【答案】DA 项:举反例:3,5,7p q r ===,此时7pqrp q r=++;B 项:举反例:2,5,7p q r ===,此时5pqrp q r=++;C 项:由A 、B 知C 项不对;D 项:由题意p q r ++为pqr 的因子,而pqr 的因子只有1,,,,,,,p q r pq pr qr pqr ,结合大小关系,可知///p q r pq pr qr pqr ++=,不妨设p q r ≤≤,若p q r pqr ++=,则3pqr p q r r =++≤,从而3pq ≤,这是不可能的,故只能//p q r pq pr qr ++=这意味着//pqrp q r p q r=++,均为素数,则D 正确。
2. ,,,,a b c d e 均为素数,且平均数为13,则( ) A. 中位数最大为17 B. 中位数最大为19 C. 中位数最小为5 D. 中位数最小为7【答案】B平均数为13的五个数之和为65,设中位数的最大值为x ,则有365x <,从而知x 最大为19,又3,5,19,19,19满足要求,故最大值为19;对于最小值,可构造出3,3,3,3,53使得中位数为3,而易证中位数为2不成立,因此最小值为3。
3. 整数,,x y z 满足5x y z ++=,问这样的(),,x y z 有几组( ) A. 100 B. 101 C. 102 D. 103 【答案】C解法一:若,,x y z 中有两个零,共2326C ⋅=组解;若,,x y z 中只有一个零,共11234248C C ⋅⋅=组解;若,,x y z 均非零,共234248C ⋅=组解。


2021年北京大学优秀中学生数学金秋营试题
学科专业才能测试一
第一天
2021年10月14日下午14:00—17:30
1、在△ABC内部有一点P满足∠PAB=∠PCB=,L在AC上且BL平分∠ABC,延长PL交△APC的外接圆于Q。
证明:BQ平分∠AQC.
2、对于的一个排列{}定义函数
f()=.求所有的排列中,
f()的最小值。
3、求所有正整数a,b,c满足对任意实数u,v,0≤u<v≤1.存在正整数n,使得{}∈(u,v)成立.
4、设p为奇素数,p≡1(mod 4).正整数a,b满足-p=1. 设q也为奇素数,
(q,bp)=1.考虑同余方程-2a+1≡0(mod q).证明下述3个阐述等价:
〔1〕p为模q的二次剩余;
〔2〕同余方程存在一个解;
〔3〕同余方程存在四个互不一样的解。
学科专业才能测试二
第二天
2021年10月15日上午09:00-12:00
5、设函数f(x)=,且x∈[-1,1]时,|f(x)| ≤1,求||的最大可能值。
6、一个班里有50人,互相之间发短信,假设在三个人A,B,C之间,仅有A给B 发过短信,B给C发过短信,C给A发过短信。
那么称A,B,C三个人构成一个“循环〞,试求这50个人中“循环〞个数的最大可能值。
7、试求所有正整数a,使得对任意正整数k ,都存在正整数n,使得an+2021是一个正整数的k次方。
8、对〔0,1〕中的实数称其中两个为相邻的,假如这两个数的十进制表示中只有一位不同,是否可以将〔0,1〕中的实数10染色,使得任意两个相邻的数颜色都不一样?
【局部试题参考解答】
第6题参考解答
第7题参考解答。

2017清华大学金秋营数学试题解答(1-5题)****************;*****************许康华老师联系方式:微信(xkh3121);QQ(1090841758)上海华育中学上海市民办华育中学是由建校已逾150多年的上海中学输送资深管理人员与优秀教师,于1999年6月与华泾实业发展有限公司联合创办的全日制民办初中,是上海中学的初中教学基地及德育教育基地。
2007年3月,学校通过上海市民办中小学依法办学专项评估,为徐汇区唯一获得“优秀”评价的民办初中.全校共有32个教学班。
2010年9月,搬至新校园。
新校园位于龙吟路99号,周围环境安静,适于学习。
新校园占地43亩,与老校园相比,面积扩大约一倍,建筑面积则达到33399平方米,共有5栋主体建筑。
该校的教育教学质量已经赢得社会的广泛赞誉。
建校十五年来,在区教育局组织的各类教学水平监控中,该校教学质量稳居全区前茅;十五年来,该校学生在市级或市级以上各级各类竞赛中,成绩几乎均名列上海市前三名,其中包括近三届全国华罗庚数学金杯赛的金、银牌;05年全国“我爱数学夏令营”团体第一;2011年新知杯上海市初中数学竞赛团体第一;2013、2014年大同杯上海市初中物理竞赛团体第二;2012、2013、2014年天原杯化学竞赛团体第一;近几年上海市古诗文大赛团体前三;连续四届上海市作文竞赛一等奖,连续五届SSP上海市中学生英语竞赛团体一等奖,连续两届徐汇区区政助理等不俗佳绩。
以上各类成绩显示了学校扎实而全面推进素质教育所取得的突出成效。
本解答是上海华育中学一名初三学生给出的,应该学生要求,匿名发表。
感谢该学生提供的优秀答案,也祝愿该学生在以后的学习中取得更大的成绩!。

2018年清华大学自主招生暨领军计划试题1.已知函数x e a x x f )()(2+=有最小值,则函数a x x x g ++=2)(2的零点个数为( ) A .0 B .1 C .2 D .取决于a 的值 【答案】C【解析】注意)()(/x g e x f x=,答案C .2. 已知ABC ∆的三个内角C B A ,,所对的边为c b a ,,.下列条件中,能使得ABC ∆的形状唯一确定的有( )A .Z c b a ∈==,2,1B .B bC a C c A a A sin sin 2sin sin ,1500=+=C .060,0sin cos )cos(cos sin cos ==++C C B C B C B A D .060,1,3===A b a【答案】AD .3.已知函数x x g x x f ln )(,1)(2=-=,下列说法中正确的有( ) A .)(),(x g x f 在点)0,1(处有公切线B .存在)(x f 的某条切线与)(x g 的某条切线平行C .)(),(x g x f 有且只有一个交点D .)(),(x g x f 有且只有两个交点【答案】BD【解析】注意到1-=x y 为函数)(x g 在)0,1(处的切线,如图,因此答案BD .4.过抛物线x y 42=的焦点F 作直线交抛物线于B A ,两点,M 为线段AB 的中点.下列说法中正确的有( )A .以线段AB 为直径的圆与直线23-=x 一定相离 B .||AB 的最小值为4 C .||AB 的最小值为2D .以线段BM 为直径的圆与y 轴一定相切 【答案】AB【解析】对于选项A ,点M 到准线1-=x 的距离为||21|)||(|21AB BF AF =+,于是以线段AB 为直径的圆与直线1-=x 一定相切,进而与直线23-=x 一定相离;对于选项B ,C ,设)4,4(2a a A ,则)1,41(2a a B -,于是2414||22++=a a AB ,最小值为4.也可将||AB 转化为AB 中点到准线的距离的2倍去得到最小值;对于选项D ,显然BD 中点的横坐标与||21BM 不一定相等,因此命题错误. 5.已知21,F F 是椭圆)0(1:2222>>=+b a by a x C 的左、右焦点,P 是椭圆C 上一点.下列说法中正确的有( ) A .b a 2=时,满足02190=∠PF F 的点P 有两个 B .b a 2>时,满足02190=∠PF F 的点P 有四个C .21F PF ∆的周长小于a 4D .21F PF ∆的面积小于等于22a【答案】ABCD .【解析】对于选项A ,B ,椭圆中使得21PF F ∠最大的点P 位于短轴的两个端点;对于选项C ,21PF F ∆的周长为a c a 422<+;选项D ,21PF F ∆的面积为22212121212||||21sin ||||21a PF PF PF F PF PF =⎪⎭⎫ ⎝⎛+≤∠⋅. 6.甲、乙、丙、丁四个人参加比赛,有两花获奖.比赛结果揭晓之前,四个人作了如下猜测: 甲:两名获奖者在乙、丙、丁中; 乙:我没有获奖,丙获奖了; 丙:甲、丁中有且只有一个获奖; 丁:乙说得对.已知四个人中有且只有两个人的猜测是正确的,那么两个获奖者是( ) A .甲B .乙C .丙D .丁【答案】BD【解析】乙和丁同时正确或者同时错误,分类即可,答案:BD .7.已知AB 为圆O 的一条弦(非直径),AB OC ⊥于C ,P 为圆O 上任意一点,直线PA 与直线OC 相交于点M ,直线PB 与直线OC 相交于点N .以下说法正确的有( ) A .P B M O ,,,四点共圆 B .N B M A ,,,四点共圆 C .N P O A ,,,四点共圆D .以上三个说法均不对【答案】AC【解析】对于选项A ,OPM OAM OBM ∠=∠=∠即得;对于选项B ,若命题成立,则MN 为直径,必然有MAN ∠为直角,不符合题意;对于选项C ,MAN MOP MBN ∠=∠=∠即得.答案:AC .8.C B A C B A cos cos cos sin sin sin ++>++是ABC ∆为锐角三角形的( ) A .充分非必要条件 B .必要非充分条件 C .充分必要条件D .既不充分也不必要条件【答案】B【解析】必要性:由于1cos sin )2sin(sin sin sin >+=-+>+B B B B C B π,类似地,有1sin sin ,1sin sin >+>+A B A C ,于是C B A C B A cos cos cos sin sin sin ++>++.不充分性:当4,2ππ===C B A 时,不等式成立,但ABC ∆不是锐角三角形.9.已知z y x ,,为正整数,且z y x ≤≤,那么方程21111=++z y x 的解的组数为( ) A .8B .10C .11D .12【答案】B 【解析】由于xz y x 311121≤++=,故63≤≤x . 若3=x ,则36)6)(6(=--z y ,可得)12,12(),15,10(),18,9(),24,8(),42,7(),(=z y ; 若4=x ,则16)4)(4(=--z y ,可得)8,8(),12,6(),20,5(),(=z y ; 若5=x ,则6,5,320,211103=≤≤+=y y y z y ,进而解得)10,5,5(),,(=z y x ; 若6=x ,则9)3)(3(=--z y ,可得))6,6(),(=z y . 答案:B .10.集合},,,{21n a a a A Λ=,任取A a a A a a A a a n k j i i k k j j i ∈+∈+∈+≤<<≤,,,1这三个式子中至少有一个成立,则n 的最大值为( ) A .6B .7C .8D .9【答案】B11.已知000121,61,1===γβα,则下列各式中成立的有( ) A .3tan tan tan tan tan tan =++αγγββα B .3tan tan tan tan tan tan -=++αγγββαC .3tan tan tan tan tan tan =++γβαγβαD .3tan tan tan tan tan tan -=++γβαγβα【答案】BD【解析】令γβαtan ,tan ,tan ===z y x ,则3111=+-=+-=+-zxzx yz y z xy x y ,所以)1(3),1(3),1(3zx z x yz y z xy z y +=-+=-+=-,以上三式相加,即有3-=++zx yz xy .类似地,有)11(311),11(311),11(311+=-+=-+=-zxx z yz z y xy y x ,以上三式相加,即有3111-=++=++xyzz y x zx yz xy .答案BD . 12.已知实数c b a ,,满足1=++c b a ,则141414+++++c b a 的最大值也最小值乘积属于区间( )A .)12,11(B .)13,12(C .)14,13(D .)15,14(【答案】B【解析】设函数14)(+=x x f ,则其导函数142)(/+=x x f ,作出)(x f 的图象,函数)(x f 的图象在31=x 处的切线321)31(7212+-=x y ,以及函数)(x f 的图象过点)0,41(-和)7,23(的割线7174+=x y ,如图,于是可得321)31(7212147174+-≤+≤+x x x ,左侧等号当41-=x 或23=x 时取得; 右侧等号当31=x 时取得.因此原式的最大值为21,当31===c b a 时取得;最小值为7,当23,41=-==c b a 时取得,从而原式的最大值与最小值的乘积为)169,144(37∈.答案B .13.已知1,1,,,222=++=++∈z y x z y x R z y x ,则下列结论正确的有( ) A .xyz 的最大值为0 B .xyz 的最大值为274- C .z 的最大值为32D .z 的最小值为31-【答案】ABD14.数列}{n a 满足)(6,2,1*1221N n a a a a a n n n ∈-===++,对任意正整数n ,以下说法中正确的有( )A .n n n a a a 221++-为定值 B .)9(mod 1≡n a 或)9(mod 2≡n aC .741-+n n a a 为完全平方数D .781-+n n a a 为完全平方数 【答案】ACD 【解析】因为2112221122213226)6(++++++++++++-=--=-n n n n n n n n n n n a a a a a a a a a a a n n n n n n n a a a a a a a 22121122)6(++++++-=+-=,选项A 正确;由于113=a ,故76)6(2121121221-=+-=--=-++++++n n n n n n n n n n n a a a a a a a a a a a ,又对任意正整数恒成立,所以211211)(78,)(74n n n n n n n n a a a a a a a a +=--=-++++,故选项C 、D 正确.计算前几个数可判断选项B 错误.说明:若数列}{n a 满足n n n a pa a -=++12,则n n n a a a 221++-为定值.15.若复数z 满足11=+zz ,则z 可以取到的值有( ) A .21B .21-C .215- D .215+ 【答案】CD 【解析】因为11||1||=+≤-zz z z ,故215||215+≤≤-z ,等号分别当i z 215+=和i z 215-=时取得.答案CD . 16. 从正2016边形的顶点中任取若干个,顺次相连构成多边形,若正多边形的个数为( ) A .6552 B .4536 C .3528 D .2016 【答案】C【解析】从2016的约数中去掉1,2,其余的约数均可作为正多边形的边数.设从2016个顶点中选出k 个构成正多边形,这样的正多边形有k2016个,因此所求的正多边形的个数就是2016的所有约数之和减去2016和1008.考虑到732201625⨯⨯=,因此所求正多边形的个数为352810082016)71)(931)(32168421(=--++++++++.答案C .17.已知椭圆)0(12222>>=+b a b y a x 与直线x y l x y l 21:,21:21-==,过椭圆上一点P 作21,l l 的平行线,分别交21,l l 于N M ,两点.若||MN 为定值,则=ba( ) A .2B .3C .2D .5【答案】C【解析】设点),(00y x P ,可得)2141,21(),2141,21(00000000y x y x N y x y x M +--++,故意2020441||y x MN +=为定值,所以2,1641422===b a b a ,答案:C .说明:(1)若将两条直线的方程改为kx y ±=,则kb a 1=;(2)两条相交直线上各取一点N M ,,使得||MN 为定值,则线段MN 中点Q 的轨迹为圆或椭圆.18. 关于y x ,的不定方程y x 21652=+的正整数解的组数为( ) A .0B .1C .2D .3【答案】B19.因为实数的乘法满足交换律与结合律,所以若干个实数相乘的时候,可以有不同的次序.例如,三个实数c b a ,,相乘的时候,可以有Λ),(),(,)(,)(ca b ab c c ba c ab 等等不同的次序.记n 个实数相乘时不同的次序有n I 种,则( )A .22=IB .123=IC .964=ID .1205=I 【答案】B【解析】根据卡特兰数的定义,可得1121221)!1(!1------=⋅==n n n n nn n n C n n C nA C I .答案:AB . 关于卡特兰数的相关知识见《卡特兰数——计数映射方法的伟大胜利》.20.甲乙丙丁4个人进行网球淘汰赛,规定首先甲乙一组、丙丁一组进行比赛,两组的胜者争夺冠军.4个人相互比赛的胜率如表所示:表中的每个数字表示其所在的选手击败其所在列的选手的概率,例如甲击败乙的概率是0.3,乙击败丁的概率是0.4.那么甲刻冠军的概率是 . 【答案】0.165【解析】根据概率的乘法公式 ,所示概率为165.0)8.05.03.05.0(3.0=⨯+⨯.21.在正三棱锥ABC P -中,ABC ∆的边长为1.设点P 到平面ABC 的距离为x ,异面直线CP AB ,的距离为y .则=∞→y x lim .【答案】23【解析】当∞→x 时,CP 趋于与平面ABC 垂直,所求极限为ABC ∆中AB 边上的高,为23. 22.如图,正方体1111D C B A ABCD -的棱长为1,中心为A A E A BC BF O 1141,21,==,则四面体OEBF 的体积为 .【答案】196【解析】如图,EBF G EBF O OEBF V V V --==21961161212111=⋅==--B BCC E GBF E V V .23.=+-⎰-dx x x n n )sin 1()(22012ππ .【答案】0【解析】根据题意,有0)sin 1()sin 1()(21222012=+=+-⎰⎰---dx x x dx x x n n n n ππππ.24.实数y x ,满足223224)(y x y x =+,则22y x +的最大值为 . 【答案】1【解析】根据题意,有22222322)(4)(y x y x y x +≤=+,于是122≤+y x ,等号当2122==y x 时取得,因此所求最大值为1.25.z y x ,,均为非负实数,满足427)23()1()21(222=+++++z t x ,则z y x ++的最大值与最小值分别为 . 【答案】2322- 【解析】由柯西不等式可知,当且仅当)0,21,1(),,(=z y x 时,z y x ++取到最大值23.根据题意,有41332222=+++++z y x z y x ,于是,)(3)(4132y z y x z y x +++++≤解得2322-≥++z y x .于是z y x ++的最小值当)2322,0,0(),(-=yz x 时取得,为2322-. 26.若O 为ABC ∆内一点,满足2:3:4::=∆∆∆COA BOC AOB S S S ,设AC AB AO μλ+=,则=+μλ .【答案】23【解析】根据奔驰定理,有329492=+=+μλ.27.已知复数32sin32cosππiz+=,则=+++2223zzzz.【答案】132i-【解析】根据题意,有iizzzzzz232135sin35cos122223-=+=-=+=+++ππ.28.已知z为非零复数,zz40,10的实部与虚部均为不小于1的正数,则在复平面中,z所对应的向量OP的端点P运动所形成的图形的面积为.【答案】20010033003π+-【解析】设),(Ryxyixz∈+=,由于2||4040zzz=,于是⎪⎪⎩⎪⎪⎨⎧≥+≥+≥≥,140,140,110,1102222yxyyxxyx如图,弓形面积为1003100)6sin6(20212-=-⋅⋅πππ,四边形ABCD的面积为100310010)10310(212-=⋅-⋅.于是所示求面积为30031003200)1003100()1003100(2-+=-+-ππ.29.若334tan=x,则=+++xxxxxxxxxxxcossincos2cossin2cos4cos2sin4cos8cos4sin.3【解析】根据题意,有xxxxxxxxxxxcossincos2cossin2cos4cos2sin4cos8cos4sin+++38tantan)tan2(tan)2tan4(tan)4tan8(tan==+-+-+-=xxxxxxxx.30.将16个数:4个1,4个2,4个3,4个4填入一个44⨯的数表中,要求每行、每列都恰好有两个偶数,共有种填法.【答案】44100031.设A 是集合}14,,3,2,1{Λ的子集,从A 中任取3个元素,由小到大排列之后都不能构成等差数列,则A 中元素个数的最大值为 .【答案】8【解析】一方面,设},,,{21k a a a A Λ=,其中141,*≤≤∈k N k .不妨假设k a a a <<<Λ21. 若9≥k ,由题意,7,33513≥-≥-a a a a ,且1335a a a a -≠-,故715≥-a a .同理759≥-a a .又因为1559a a a a -≠-,所以1519≥-a a ,矛盾!故8≤k .另一方面,取}14,13,11,10,5,4,2,1{=A ,满足题意.综上所述,A 中元素个数的最大值为8.。
清北学堂2018年寒假数学联赛模拟试卷(5)一试一、 填空题1、设动点(,0),(1,)P t Q t ,其中参数[0,1]t ,则线段PQ 扫过的平面区域的面积是 . 答案:16. 解:直线PQ 的方程为2(1)0tx t y t .0t 时,直线方程为0y ,1t 时,直线方程为1x ,01t ,直线方程为1()(2)[(1)]11t x y x t x t t t,对每个01x ,当(0,]t x 变化时02y x ,所以,线段PQ 扫过的平面区域是函数2y x 及直线0,1,0x x y 围成的封闭图形,由积分的几何意义3121200141(2[2(1)]236x dx x x x .2、设非负实数,,a b c 满足1a b c ,则111111p a b c的最小值为 . 答案:94. 解:设[0,1]x ,则由2191516(1)(915)(31)(01161611x x x x x x x知191511616x x .故191511616a a ,191511616b b ,191511616c c , 即9159()316164p a b c .事实上,当13a b c 时,p 取得最小值min 94p .3、函数()f x 满足3,1000;()((5)),1000.x x f x f f x x则(84)f 的值是 .答案:997.解:记()()(()))n f x f f f x ,其中等号右端有n 个f.那么(184)(84)((89))((999))f f f f f(185)(184)((1004))((1001))f f f f (183)(184)((998))((1003))f f f f (183)((1000))f f(182)((997))f f (183)(182)((1002))((999))f f f f .注意从(184)((999))f f 到(182)((999))f f 这个过程中,f 的个数减少了2.同样的推理可知(182)(180)(2)((999))((999))((999))f f f f f f .继续此过程,就有(2)(3)(2)(2)((999))((1004))((1001))(998)((1003))(1000)997f f f f f f f f f f .4、一个凸36面体中有24个面是三角形,12个面是四边形,则该多面体的对角线的条数是 .(连结不在凸多面体的同一个面内的两个凸面体的顶点的线段叫做凸多面体的对角线.) 答案:241.解:凸多面体的面数F=36,棱数E=60,顶点数V=E+2-F=26将顶点记为i=1,2,3,···,26设凸多面体的面中以i 为顶点的三角形有i t 个,以i 为顶点的四边形有i q 个那么凸多面体的对角线总数= 261)25(21i i q t2626111112526222213252431242241.i i i i t q5、设偶函数 f x 满足: 12f ,且当0xy时,f x f y f f x f y,则 5f . 答案:225. 解:11f x f y,由于 f x f x ,只须考虑,x y R的情况,令x y,再令, 00,0f g t f,则化为 g u v g u g v (1)据(1), 22g u g u u g u , 3223g u g u u g u g u g u ,归纳得, g ku kg u ,令25,1k u ,得 25251g g ,因此 2525f .6、若11,2,3,(1)2a ib ic i x ,则2||a bx cx 的值是 ..解:注意x 满足210x x ,从而31,||1,1x x xx .又注意,,a b c 的虚部相等,结合210x x 可知,只需针对1,2,3a b c 进行计算即可.这时我们有2222||()()a bx cx a bx cx a bx cx2222222()()()a b c ab x x bc xx x x ac x x 222a b c ab bc ac .将1,2,3a b c 代入,得22||3a bx cx .7、设 x 表示不超过实数x 的最大整数,则在平面上,由所有满足 2250x y 的点所形成的图形面积是 . 答案:12.解:先考虑第一象限情况,因为22222250177155 ,得,1,7x y ,7,1, 5,5,而由 1,7x y ,得单位正方形12,78x y ,其面积为1,类似由,7,1x y 与 5,5也各得到一个单位正方形,并且这三个正方形互不重叠;若考虑四个象限,共得12个互不重叠的单位正方形,总面积为12.8、电脑每秒钟以相同的概率输出一个数字1或2.则输出的前n 个数字之和被3整除的概率 为n P . 答案:1112()32n解法一:这n 个数字共有2n 种可能情形。
选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 若复数z 满足()()2110i z i i -+-+=,则z=( )(A )1122i + (B )1122i - (C )1122i -+ (D )1122i -- 2. 已知集合{}2|log 2A x x =<,1|282xB x ⎧⎫=≤≤⎨⎬⎩⎭,则AB =( )(A )[]1,3- (B )(]0,3 (C )[)1,4- (D )()0,43. 将420名工人编号为:001,002,…,420,采用系统抽样的方法抽取一个容量为60的样本,且随机抽得的号码为005.这420名工人来自三个工厂,从001到200为A 工厂,从201到355为B 工厂,从356到420为C 工厂,则三个工厂被抽中的工人数依次为( ) (A )28,23,9(B )27,23,10 (C )27,22,11 (D )28,22,104. 已知公并不为0的等差数列{}na 的首项13a =,若236,,a a a成等比数列,则{}na 的前5项之和为( )(A )-23 (B )-25 (C )-43 (D )-45 5. 设曲线2ln y ax b x=-在1x =处的切线方程为52y x =-,则a,b 的值分别为( )(A )2,1 (B )-2,-1 (C )3,1 (D )-3,-16. 在平行四边形ABCD 中,O 为AC 与BD 的交点,若2AE ED=,则OE =( )(A )1126BA BC + (B )1126BA BC - (C )1126BA BC -+ (D )1126BA BC -- 7. 已知一个棱锥的三视图如图所示,则该棱锥的表面积为( )cm2(A )29(B )9218(C )18 (D )27 8. 设抛物线2:4C yx=的焦点为F ,直线l 过F 且与抛物线C 交于A ,B 两点,若163AB =,且AF BF >,则AFBF =( ) (A )3 (B )52 (C )2 (D )49.若实数x,y 满足240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩,则2212x y ⎛⎫+- ⎪⎝⎭的取值范围是( ) (A )[]1,2(B )5,24⎡⎤⎢⎥⎣⎦44⎢⎥⎣⎦(D )171,4⎡⎤⎢⎥⎣⎦10. 在[]4,4-上随机地取一个数m ,则事件“直线0x y m -+=与圆()2212x y -+=有公共点”发生的概率为( )(A )14(B )13 (C )12 (D )2311. 已知P 为双曲线()2222:10,0x y C a b a b-=>>右支上一点,A 为其左顶点,()43,0F 为其右焦点,满足AF PF =,60PFA ∠=︒,则点F 到PA 的距离为( )(A )532 (B )72 (C )732 (D )15212. 在三棱锥A-BCD 中,10BC BD AC AD ====,6AB =,16CD =,点P 在平面ACD 内,且30BP =,设异面直线BP 与CD所成角为α,则sin α的最小值为( )(B(C(D二、填空题:本大题共4小题,每小题5分,共20分。