北师大版高中数学选修1-2：独立性检验

独立性检验典型题例解析所谓独立性检验，就是要把采集样本的数据，利用公式计算2χ的值，比较与临界值的大小关系，来判定事件A 与B 是否无关的问题。

具体步骤：（1）采集样本数据。

（2）由()21212211222112+++++++-=n n n n n n n n n χ计算2χ的值。

（3）统计推断，当2χ＞3.841时，有95%的把握说事件A 与B 有关；当2χ＞6.635时，有99%的把握说事件A 与B 有关；当2χ≤3.841时，认为事件A 与B 是无关的。

下面我们通过几个典型例题对独立性检验问题进行剖析，使同学们进一步掌握这类问题的研究方法。

例1、为了研究色盲与性别的关系，调查了1000人，调查结果如下表所示：根据上述数据试问色盲与性别是否是相互独立的？ 分析：问题归结为二元总体的独立性检验问题。

【解析】由已知条件可得下表依据公式()21212211222112+++++++-=n n n n n n n n n χ得2χ＝()5204804495651438644210002⨯⨯⨯⨯-⨯＝27.139。

由于27.139＞6.635，所以有99%的把握认为色盲与性别是有关的，从而拒绝原假设，可以认为色盲与性别不是相互独立的。

评注：根据假设检验的思想，比较计算出的2χ与临界值的大小，选择接受假设还是拒绝假设。

变式引申1：为了研究患慢性气管炎与吸烟量的关系，调查了228人，其中每天的吸烟支数在10支以上20支以下的调查者中，患者人数有98人，非患者人数有89人；每天的吸烟支数在20支以上的调查者中，患者人数有25人，非患者人数有16人。

试问患慢性气管炎是否与吸烟量互相独立？分析：即求独立性检验问题。

【解析】由已知条件得出下表：由公式()21212211222112+++++++-=n n n n n n n n n χ得2χ＝()4118710512325891698228⨯⨯⨯⨯-⨯＝0.994。

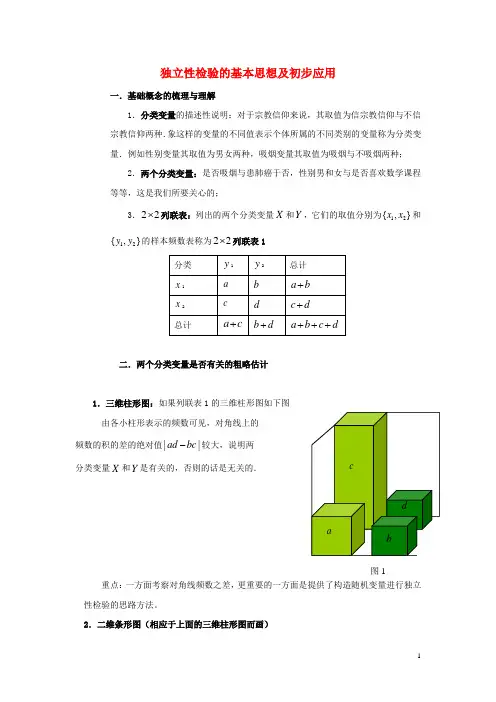
独立性检验的基本思想及初步应用一．基础概念的梳理与理解1．分类变量的描述性说明：对于宗教信仰来说，其取值为信宗教信仰与不信宗教信仰两种．象这样的变量的不同值表示个体所属的不同类别的变量称为分类变量．例如性别变量其取值为男女两种，吸烟变量其取值为吸烟与不吸烟两种；2．两个分类变量：是否吸烟与患肺癌于否，性别男和女与是否喜欢数学课程等等，这是我们所要关心的；3．22⨯列联表：列出的两个分类变量X 和Y ，它们的取值分别为12{,}x x 和12{,}y y 的样本频数表称为22⨯列联表1二．两个分类变量是否有关的粗略估计1．三维柱形图：如果列联表1的三维柱形图如下图 由各小柱形表示的频数可见，对角线上的 频数的积的差的绝对值||ad bc -较大，说明两 分类变量X 和Y 是有关的，否则的话是无关的．重点：一方面考察对角线频数之差，更重要的一方面是提供了构造随机变量进行独立性检验的思路方法。

2．二维条形图（相应于上面的三维柱形图而画）图1由深、浅染色的高可见两种情况下所占比例，由数据可知a a b+要比c c d +小得多，由于差距较大，因此，说明两分类变量X 和Y 有关系的可能性较大，两个比值相差越大两分类变量X 和Y 有关的可能性也越的．否则是无关系的．重点：通过图形以及所占比例直观地粗略地观察是否有关，更重要的一方面是提供了构造随机变量进行独立性检验的思想方法。

3．等高条形图（相应于上面的条形图而画）由深、浅染色的高可见两种情况下的百分比；另一方面，数据aa b+00要比c c d+小得多，因此，说明两分类变量X 和Y 有关系的可能性较大，否则是无关系的．重点：直观地看出在两类分类变量频数相等的情况下，各部分所占的比例情况，是在图2的基础上换一个角度来理解。

三．独立性检验的基本思想上面通过分析数据与图形，，得出这个估计是粗略的，因为我们说的“大得多”、“小图2图3得多”，到底是有多大的差距？也就是说得到的结论是直观上的印象，其实与是否有关还是有较大的差距的．但是上面的分析给了我们一种重要的思想方法．下面从理论上说明两类分类变量是否有关，请同学们从中体会其思想方法 1．基本思想与图形的联系假设两类分类变量是无关的，由上面的条形图2可知如下的比应差不多。

课堂练习(三)(建议用时：60分钟)[基础达标练]一、选择题1．某医疗研究所为了检验某种血清预防感冒的作用，把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较，提出假设H：“这种血清不能起到预防感冒的作用”，利用2×2列联表计算的χ2≈3.918，经查临界值表知P(χ2>3.841)≈0.05，则下列表述中正确的是( )A．有95%的把握认为“这种血清能起到预防感冒的作用”B．若有人未使用该血清，那么他一年中有95%的可能性得感冒C．这种血清预防感冒的有效率为95%D．这种血清预防感冒的有效率为5%A[因χ2≈3.918>3.841，故有95%的把握认为“这种血清能起到预防感冒的作用”．] 2．有两个分类变量X与Y的一组数据，由其列联表计算得χ2≈4.523，则认为“X与Y 有关系”犯错误的概率为( )A．95% B．90%C．5% D．10%C[χ2≈4.523＞3.841.这表明认为“X与Y有关系”是错误的可能性约为0.05，即认为“X与Y有关系”犯错误的概率为5%.]3．在调查中发现480名男人中有38名患有色盲，520名女人中有6名患有色盲．下列说法正确的是( )A．男、女患色盲的频率分别为0.038,0.006B．男、女患色盲的概率分别为19240，3260C．男人中患色盲的比例比女人中患色盲的比例大，患色盲与性别是有关的D．调查人数太少，不能说明色盲与性别有关C[男人中患色盲的比例为38480，要比女人中患色盲的比例6520大，其差值为⎪⎪⎪⎪⎪⎪38480－6520≈0.0676，差值较大．]4．某卫生机构对366人进行健康体检，其中某项检测指标阳性家族史者糖尿病发病的有16人，不发病的有93人；阴性家族史者糖尿病发病的有17人，不发病的有240人，有多少的把握认为糖尿病患者与遗传有关系．( )A．99.9% B．90%C．99% D．95%D [可以先作出如下列联表(单位：人)：糖尿病患者与遗传列联表：χ2＝366×(16×240－17×93)2109×257×33×333≈6.067＞3.841.故我们有95%的把握认为糖尿病患者与遗传有关系．]5．假设有两个分类变量X 与Y ，它们的可能取值分别为{x 1，x 2}和{y 1，y 2}，其2×2列联表为：A ．a ＝5，b ＝4，c ＝3，d ＝2B ．a ＝5，b ＝3，c ＝4，d ＝2C ．a ＝2，b ＝3，c ＝4，d ＝5D ．a ＝2，b ＝3，c ＝5，d ＝4 D [比较⎪⎪⎪⎪⎪⎪a a ＋b －c c ＋d .选项A 中，⎪⎪⎪⎪⎪⎪59－35＝245；选项B 中，⎪⎪⎪⎪⎪⎪58－46＝124；选项C 中，⎪⎪⎪⎪⎪⎪25－49＝245；选项D 中，⎪⎪⎪⎪⎪⎪25－59＝745.故选D.]二、填空题6．调查者通过随机询问72名男女中学生喜欢文科还是理科，得到如下列联表(单位：名)：性别与喜欢文科还是理科列联表：有 [通过计算χ2＝72×(16×8－28×20)236×36×44×28≈8.42＞6.635.故我们有99%的把握认为中学生的性别和喜欢文科还是理科有关系．]7．某高校“统计初步”课程的教师随机调查了选该课的一些学生情况，具体数据如下表：χ2＝50×(13×20－10×7)223×27×20×30≈4.844，因为χ2>3.841，所以判定主修统计专业与性别有关系，那么这种判断出错的可能性为________．5% [∵χ2＞3.841，所以有95%的把握认为主修统计专业与性别有关，出错的可能性为5%.]8．在吸烟与患肺病是否相关的判断中，有下面的说法：①若统计量χ2>6.635，则在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；②由独立性检验可知在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系时，若某人吸烟，则他有99%的可能患有肺病；③由独立性检验可知在犯错误的概率不超过0.05的前提下，认为吸烟与患肺病有关系时，是指有5%的可能性使得推断错误．其中说法正确的是________．(填序号)③ [统计量χ2是检验吸烟与患肺病相关程度的量，是相关关系，而不是确定关系，是反映有关和无关的概率，故说法①错误；说法②中对“确定容许推断犯错误概率的上界”理解错误；说法③正确．]三、解答题9．在研究某种新措施对猪白痢防治效果问题中，得到以下数据：[解] 由列联表，可知a ＝132，b ＝18，c ＝114，d ＝36，n ＝a ＋b ＋c ＋d ＝300.由以上数据可得，χ2＝300×(132×36－18×114)2(132＋18)(114＋36)(36＋18)(114＋132)≈7.32.因为7.32>6.635.因此我们有99%的把握认为新措施对预防猪白痢是有效的．10．某班主任对班级22名学生进行了作业量多少的调查，数据如下表：在喜欢玩电脑游戏的12人中，有10人认为作业多，2人认为作业不多；在不喜欢玩电脑游戏的10人中，有3人认为作业多，7人认为作业不多．(1)根据以上数据建立一个2×2列联表；(2)试问喜欢电脑游戏与认为作业多少是否有关系？ [解] (1)由题意列出2×2列联表：χ2＝22×(10×7－3×2)212×10×13×9≈6.418，∵6.418＞3.841，∴有95%的把握认为玩电脑游戏与认为作业多少有关系．[能力提升练]1．通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：由χ2＝(a ＋b )(c ＋d )(a ＋c )(b ＋d )算得，χ2＝110×(40×30－20×20)260×50×60×50≈7.8.附表：A ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”B ．在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”C ．有99%以上的把握认为“爱好该项运动与性别有关”D ．有99%以上的把握认为“爱好该项运动与性别无关” C [根据独立性检验的思想方法，正确选项为C.]2．某班主任对全班50名学生进行了作业量的调查，数据如下表：A ．0.01B ．0.025C ．0.10D ．0.050D [χ2＝50×(18×15－8×9)226×24×27×23≈5.059＞3.841，因为P (χ2＞3.841)＝0.050，所以这种推断犯错误的概率不超过0.050.]3．某研究小组为了研究中学生的身体发育情况，在某中学随机抽出20名15至16周岁的男生，将他们的身高和体重制成2×2列联表，根据列联表中的数据，可以在犯错误的概率不超过________的前提下认为该学校15至16周岁的男生的身高和体重之间有关系．0.050 [根据公式χ2＝(a ＋b )(c ＋d )(a ＋c )(b ＋d )得，χ2＝5×15×7×13≈5.934，因为χ2>3.841，因此在犯错误的概率不超过0.050的前提下认为该学校15至16周岁的男生的身高和体重之间有关系．]4．为了探究电离辐射的剂量与人体的受损程度是否有关，用两种不同剂量的电离辐射照射小白鼠，在照射后14天的结果如下表所示：小白鼠的死亡与剂量无关[根据独立性检验的基本思想，可知类似反证法，即要确认“两个分类变量有关系”这一结论成立的可信程度，首先假设该结论不成立，即假设结论“两个分类变量没有关系”成立．对本题进行统计分析时的统计假设应是“小白鼠的死亡与剂量无关”．]5．为了研究“教学方式”对教学质量的影响，某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样)．以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.少有一名被抽中的概率；(2)学校规定：成绩不低于75分的为优秀．请填写下面的2×2列联表，并判断有多大把握认为“成绩优秀与教学方式有关”．⎝⎛⎭⎪⎫参考公式：χ2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )[解] (1)记成绩为87分的同学为A ，B ，其他不低于80分的同学为C ，D ，E ，“从甲班数学成绩不低于80分的同学中随机抽取两名同学”的一切可能结果组成的基本事件有(A ，B )，(A ，C )，(A ，D )，(A ，E )，(B ，C )，(B ，D )，(B ，E )，(C ，D )，(C ，E )，(D ，E )，共10个．“至少有一个87分的同学被抽到”所组成的基本事件有(A ，B )，(A ，C )，(A ，D )，(A ，E )，(B ，C )，(B ，D )，(B ，E )，共7个，所以P ＝710.(2)2×2列联表如下：χ2＝20×20×20×20＝6.4＞5.024，因此，我们有97.5%的把握认为成绩优秀与教学方式有关.。

教学准备1. 教学目标1、知识与技能：通过典型案例的探究，了解独立性检验的基本思想，会对两个分类变量进行独立性检验，明确独立性检验的基本步骤，并能利用独立性检验的基本思想来解决实际问题.2、过程与方法：通过探究“吸烟是否与患肺癌有关系”引出独立性检验的问题。

通过列联表、等高条形图,使学生直观感觉到吸烟和患肺癌可能有关系.这一直觉来自于观测数据，即样本.问题是这种来自于样本的印象能够在多大程度上代表总体？这节课就是为了解决这个问题，让学生亲身体验直观感受的基础上，提高学生的数据分析能力.3、情感态度价值观：通过本节课的学习，加强数学与现实生活的联系。

以科学的态度评价两个分类变量有关系的可能性。

培养学生运用所学知识，解决实际问题的能力。

对问题的自主探究，提高学生独立思考问题的能力；让学生对统计方法有更深刻的认识，体会统计方法应用的广泛性，进一步体会科学的严谨性。

教学中适当地利用学生合作与交流，使学生在学习的同时，体会与他人合作的重要性。

2. 教学重点/难点教学重点理解独立性检验的基本思想及实施步骤.教学难点1.了解独立性检验的基本思想；2.了解随机变量K2的含义，K2的观测值很大，就认为两个分类变量是有关系的。

3. 教学用具4. 标签教学过程课下预习，搜集有关分类变量有无关系的一些实例。

情境引入、提出问题：1、吸烟与患肺癌有关系吗？2、你有多大程度把握吸烟与患肺癌有关？变量有定量变量、分类变量，定量变量—回归分析;分类变量—独立性检验，引出课题。

问题1、我们在研究“吸烟与患肺癌的关系”时，需要关注哪一些量呢？列联表：分类变量的汇总统计表（频数表）. 一般我们只研究每个分类变量只取两个值，这样的列联表称为2*2列联表 . 如吸烟与患肺癌的列联表：问题2：由以上列联表，我们估计吸烟是否对患肺癌有影响？①在不吸烟者中患肺癌的比例为________；②在吸烟者中患肺癌的比例为________.问题3：我们还能够从图形中得到吸烟与患肺癌之间的关系吗？小结：根据列联表和等高条形图判断的标准是什么?思考：1：差异大到什么程度才能作出“吸烟与患肺癌有关”的判断?2：能否用数量刻画出“有关”的程度?前置铺垫：问题4：我们能够从多大程度上认为吸烟与患肺癌之间有关系呢?为了解决上述问题，我们先假设H0：吸烟与患肺癌没有关系。

独立性检验 同步练习【选择题】1、事件A 、B 是相互独立的，下列有四个式子：①P(AB)=P(A)P(B);②)()()(B P A P B A P ⋅=③)()()(B P A P B A P ⋅=④)()()(B P A P B A P ⋅=⋅.其中正确的有（ ）A 、1个B 、2个C 、3个D 、4个2、温州市正在全面普及数字电视，某住宅小区有2万住户，从中随机抽取200户，调查是否安装数字电视，调查结果如下表，则该住宅小区已经安装数字电视的用户数为A 、8 000B 、5 000C 、5 500D 、9 500【填空题】3、设A ，B 为两个变量，每一个变量都可以取两个值， 变量A ：21,A A ,1A = 变量B ：21,B B ,1B =若有式子nd b n b a n b +⋅+=，则认为____________________独立. 4、为调查吸烟是否对患肺癌有影响，某肿瘤研究所随机地调查了9965人，得到如下结果（单位：人）；吸烟与患肺癌列联表不患肺癌 患肺癌 总计 不吸烟者 7775 42 7817吸烟 2099 49 2148总计 9874 91 9965 在不吸烟者中，有0.54%患有肺癌， 在吸烟者中，有2.28%患有肺癌，由此可以得到结论：吸烟者和不吸烟者患肺癌的可能性存在着差异 你可以进一步得到什么结论_____________________ 【解答题】5、为调查吸烟是否对患肺癌有影响，某肿瘤研究所随机地调查了9965人，得到如下结果（单位：人）； 吸烟与患肺癌列联表不患肺癌 患肺癌 总计 不吸烟者 4567 23 4590吸烟 1932 56 1988总计 6499 79 6578通过计算说明，患肺癌与吸烟是有关系的.参考答案1、D2、A3、1A 2B4、患肺癌与吸烟是有关系的5、解：在不吸烟者中，有0.50%患有肺癌，在吸烟者中，有2.82%患有肺癌，即：吸烟者和不吸烟者患肺癌的可能性存在着差异.。