《分式复习》PPT课件

= 一个不为0的整式
分式的值
不变
AXM (B X M )
A B
=
A÷M ( B÷M )
(其中M为
不为0
的整式)
( -A )
2.分式的符号法则:
A B -A -B A ( B )
= =
A
(-B )
=
-A ( -B )
B
=
=
( -A ) B
=
-A ( B )
C
A
2x 3y 3. 若分式 的分子、分母都变 x 3y 为原来的3倍，则此分式的值( )
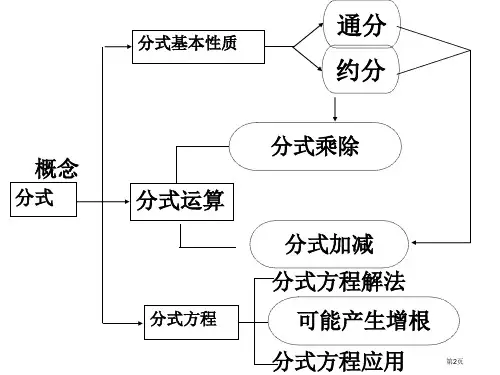
分式复习课
分式的概念、性质
分式的乘除、加减 分式方程及其应用
1.分式的定义:
A 形如 ,其中 A ,B 都是整式, B 且 B 中含有字母.
B≠0 B=0 A=0且 B ≠0
2.分式有意义的条件: 分式无意义的条件: 3.分式值为 0 的条件: A B > 0 的条件:

4.分式 分式
A>0 ,B>0 或 A<0, B<0 A>0 ,B<0 或 A<0 ,B>0
b的取值范围,其解有以下三种情况:
(1)当a≠0时,方程有且只有一个解.
(2)当a=0,b≠0时,方程无解. (3)当a=0,b=0时,方程有无数多个解. 即对一切实数x,方程都成立.
分式方程无解可以从两个角度进行考虑： 一是：分式方程转化为的整式方程， 整式方程本身无解；
二是：分式方程转化为的整式方程，
5个零件，求两人每小时各加工的零件个数.
解：设甲每小时加工x个零件， 则乙每小时加工（x+5)个零件， 由题意得：
180 x 240 = x5

x2
1 x2
2
9
变: 已知 x2 – 3x+1=0 ,求 x2+
x
x
的1x2值. 的1x2 值.
变:已知 x+ 1=3 ,求
x
x2 /x2 的值. x4+x2+1 /x2
1
x2
1 x2
1
两个分式相乘，把分子相乘的积作为积的分子， 把分母相乘的积作为积的分母。
用符号语言表达： a c ac b d bd
27xy2
-2(a-b)2 -8(b-a)3
关键找出分子和 分母的公因式
m2+4m+4
(3)
m2 - 4
关键找出分母的
2.通分
最简公分母
(1) x 与 y (2)
6a2b
9ab2c
a-1
6
a2+2a+1 与 a2-1
约分与通分的依据都是: 分式的基本性质
整体代入法化简思想：
【【例例11】】已已知知：：1x
a0 1
an
1
an
(a 0)
(1)(3)3 1 (3)3
1 27
(2)(3a)2 b2 (a2b2 )3 解：原式= 32 a2b2 a6b6
6、用科学记数法表示：
例： 0.00065 6.5104
(1) 0.000030
3.0 105
7、约分
:
例(1)
6x2y 12 xy 2
(2) x 1 2x 1 3x 2 x 1 1 x x 1
复习回顾一:
1.解分式方程的思路是：
分式 方程
去分母
整式 方程
2.解分式方程的一般步骤

顺水速=静水速+水流速 逆水速=静水速-水流速
设是水流速为xkm/ h
则 水 为 20 + x)km/ h 顺 速 (
逆 速 (20 - x)km/ h 水 为
72 48 = 20 + x 20 − x
A．扩大3倍 B．扩大9倍C．扩大4倍D．不变 扩大3 扩大9 扩大4
3、 填空： x ( x − y ) = ( x − 2
y)
x + xy
x+y
例1：化简求值 ：
a−2 a −1 a−4 ( 2 − 2 )÷ a + 2a a + 4a + 4 a + 2 2 其中a满足：a + 2a − 1 = 0
1. 若分式
A、 A、x≠-1 C、x≠2 、
若有意义， 应满足（ 若有意义，则x应满足（ B ） 应满足
B、 ≠-1且 B、x ≠-1且x ≠2 D、x ≠-1或x ≠2 、 或
x −4 ( x + 1)( x − 2)
若值为0， 应满足（ 若值为 ，则x应满足（ B ） 应满足
A、x=2 、 C、 、
1km
中点 18km }
xkm / h
甲 A
乙 B
甲走了总共20km 甲走了总共
设 乙的速度 xkm / h 则 甲的速度( x + 0.5)km / h
20 18 = x + 0.5 x
1、一项工程，若甲队单独做，恰好在规定的日期 、一项工程，若甲队单独做， 完成，若乙队单独做要超过规定日期3天完成 天完成； 完成，若乙队单独做要超过规定日期 天完成；现 在先由甲、乙合做2天 在先由甲、乙合做 天，剩下的工程再由乙队单独 也刚好在规定日期完成， 做，也刚好在规定日期完成，问规定的日期是多 少天？ 少天？ 1 甲每天的工作量 x 设 天 甲x

也较为复杂，学生容易出错。
经典例题解析
例题一
计算 $frac{x}{x + y} + frac{y}{x - y} frac{2xy}{x^2 - y^2}$。
解析
首先将所有项的分母统一 为 $(x + y)(x - y)$，然后 进行约分和加减运算。
解析
根据已知条件，通过等式 的性质和分式的加减法进 行证明。
特点
通常形式为 ax/b = c (其中 a、b、c 是已知数，b ≠ 0)。
复杂分式方程
定义
复杂分式方程是含有多个分式的 方程。
特点
通常形式为 f(x)/g(x) = h(x)/i(x) ( 其中 f(x)、g(x)、h(x)、i(x) 是多项 式函数)。
解法
通过消去分母，将方程转化为整式 方程或使用其他数学方法求解。
约分和通分是分式中的重要概念 ，但学生常常难以理解和掌握。 约分是将分子和分母中的公因式 约去，通分则是将两个或多个分
式化为同分母。
分式的加法与减法
在进行分式的加法和减法时，需 要寻找分母的公倍数，将分母统 一后再进行计算。这一过程对学
生来说较为复杂，容易出错。
分式的乘法与除法
在进行分式的乘法和除法时，需 要寻找分子和分母的公因式，进 行约分后再进行计算。这一过程
分式的性质
总结词
分式具有一些重要的性质，这些性质包括基本性质、等价变换性质和运算性质。
详细描述
分式的基本性质是分式的分子和分母可以同时乘以或除以同一个非零整式；等价 变换性质是分式的等价变换不改变分式的值；运算性质是分式的加、减、乘、除 等运算应先进行括号内的运算，再进行乘除运算，最后进行加减运算。
分式的约分与通分

1 x2 2x 1
3
x 2x2
2 1
2 x2 1 4x 4
x2
4 (π
x)2
第4页
2.分式基本性质:
分式分子和分母都乘以（或除以）同一个不等 于0整式，分式值不变.
A AM A AM
,
(其中M是不等于0整式)
B BM B BM
第5页
1.以下式子
（1） a x a （1 2）
b x b1
n ；na ,a 0
b ； a 1
ab
（3） x y x； y（4）
xy xy
ba ab ca ac
中正确是
（）
A 、1个 B 、2 个 C、 3 个 D、 4 个
第9页
4b、值若分将别分扩式大为a原ab来b (2a倍、，b均则为分正式数值）为中（字）母a、
A．扩大为原来2倍 B．缩小为原来 1
C．不变
D．缩小为原来 2
x2 y2
B、 x y2
y2 x2 C、 x y
x2 y2 D、 x 2 y xy 2
第13页
1.计算：
第14页
第15页
5. a2 b2 (1 a2 b2 )
a2b ab2
2ab
6. x 3 (x 2 5 )
x2
x2
第16页
3.化简并求值：
x2
x2
2x
x2
x 1 4x 4
x y z
4.分式
,
,
5b2c 10a 2b 2ac
最简公分母是
；
3
y
x 2 y y 3 , xy x 2
最简公分母是
.
第11页
4.什么是最简分式？ 一个分式分子和分母没有公因式时叫做最

（４）当x ＝-３时，
x 4 ∴当x = 2时分式 的值为零。 x2
2
x 2 4 (3) 2 4 x2 3 2 5
1.填空:
(1)当 x≠2
1 x 时,分式 4 x 8 有意义;
时,分式
(2)当
x=3
3 x 9 x 2 的值是零;
Байду номын сангаас
xa (3)当x=2时,分式 x b 没有意义,则 b= -2
七年级
（下 册）
义务教育教科书
学科网
1、下列代数式中，哪些是整式？哪些是分式？
3 4
2
b 3 2a
y -1 x
m( n p ) 7
4 5b c
m 7
x 2 xy y 2 2 x 1

a 1 2、 对于分式 2a
（1）当a=1时，求分式的值 （2）当a取何值时，分式无意义？ 当a取何值时，分式有意义？ （3）当a取何值时，分式值为零？
2 y 1 x
4 5b c
3
m 7 m 7
x xy y 2 x 1
2
2

整式有: 分式有:
3 2 b 3 2 a 1
m( n p ) 7
3

4 5b c
x 2 xy y 2 2 x 1
b 分式 分母中的字母能取任何实数吗？ a
为什么？分式
2x 3 中的字母x呢？ x2
:
我们已经知道:
2 3 16 36
= =
25 3 5
=
10 15
;
4 9
16 4 36 4
=
这是根据分数的基本性质：
分数的分子与分母都乘以或除以同 一个不等于零的数，分数的值不变．

分式方程（复习）
一、分式方程的概念
二、解分式方程
三、分式方程解的情况
复习回顾一:
一、什么是分式方程？
方程中只含有分式和整式，且分母中 含有未知数的方程。
复习回顾(1)下x 2列2方程3x中，分式4x 方 程3y有（7 ５
）个
一(2) 1 3
x2 x
(4) x(x1) 1 x
(3) 3 x x （6）2xx110
1应.若是方X=程-2 2x.34xa21 有增根，则增根
2 ax 3
2.解关于x的方程
x2x2
4 x2
产生增根，则常数a= -4或6 。
3.当m为何值时，方程
x 2 x3
m x3
解
为非负数？
一、分式方程的概念 二、解分式方程
解分式方程必须检验有无增根。
三、分式方程解的情况
a
x2 1产生增根，
则增根可能是X=1或x=-1 ;a的值
是 2或0 .
变式 3
已知关于ｘ的方程
a 1 2x x1 x2 1
①
去分母，得 a(x1)(x21)2x
②
当方程②的根不是方程①的根时，a为多少？
分析：∵方程②的根不是方程①的根 ∴分式方程①有增根，增根可能为x=1，-1。 而增根x=1，-1是整式方程的解
把x=1代入方程② 即2a=2,解得a=1 把x=-1代入方程②即a·0=0+(-2)∴此方程无解
综上所述，a的值是1
问题：若方程①有增根，则增根必为 X=1 。
变式4、当a为何值时,方程
x 1 a x1 x2 1
的解是正数?
若解是负数呢？
变式5、当a为何值时,方程
x 1 x1

2
2 2m 2 x a1 b 2 a 2 m x 1 ab 4. 化简： （2） 2 5.计算：（1） x 1 m b 4 2am 2b 2 x a 1
．


a ( a b)
2(a b) 2 m a (m 2)( m 2)
1 例1. 在函数 y 中，自变量x的取值范围是（A） x2 A． x 2 B． x 2 C． x≤2 D． ≥—2 x
列分式方程解应用题
列分式方程解应用题的一般步骤
1、审题 ； 2、设未知数；
3、找出能表示题目全部含意的相等关 系，列出分式方程； 4、解分式方程；
5、验根：先检验是否有增根，再 检查是否合符题意；
6、写出答案。
常见题型及相等关系
1、行程问题 ：
基本量之间的关系：
路程=速度 X 速度，即s=vt
解：设规定日期为x天，根据题意得
4 x 1 x x6
解得 x=12, 经检验，x=12是原方程的解。 答：规定日期是12天。
小结
列分式方程解应用题的一般步骤
1、审题 ； 2、设未知数；
3、找出能表示题目全部含意的相等关 系，列出分式方程； 4、解分式方程；
5、验根：先检验是否有增根，再 检查是否合符题意；
想一想
x y 探究：⑴当x、y满足什么条件时，分式 的值为0. x 1
解：x y 0且x 1 0 所以x y且x 1, y 1
分式方程
100 60 20 v 20 v
像这样，分母里含有未知数的方程叫 做分式方程.
解分式方程的思路是：
分式 方程
去分母
3.
4.
x 2 (2) 1 x 1 3x 3

我感恩，感恩生活，感恩网络，感恩朋友，感恩大自然，每天，我都以一颗感动的心去承接生活中的一切。 我感谢……
感谢伤害我的人，因为他磨练了我的心志； 感谢欺骗我的人, 因为他增进了我的见识； 感谢遗弃我的人, 因为他教导了我应自立； 感谢绊倒我的人，因为他强化了我的能力； 感谢斥责我的人，因为他助长了我的智慧； 感谢藐视我的人，因为他觉醒了我的自尊；
她想她真是命苦，刚上班没几天就遇到了这样恐怖的事情，怕是没有生还的可能了。 终于他被警察包围了，所有的警察让他放下枪，不要伤害人质，他疯狂地喊着：“我身上好几条人命了，怎么着也是个死，无所谓了。”说着，他用刀子在她颈上划了一刀。
她的颈上渗出血滴。她流了眼泪，她知道自己碰上了亡命徒，知道自己生还的可能性不大了。 “害怕了？”劫匪问她。
她摇头：“我只是觉得对不起我哥。” “你哥？”“是的，”她说，“我父母双亡，是我哥把我养大，他为我卖过血，供我上学，为了我的工作送礼，他都二十八了，可还没结婚呢，我看你和我哥年龄差不多呢。”
劫匪的刀子在她脖子上落了下来，他狠着心说：“那你可真是够不幸的。” 围着他的警察继续喊话，他无动于衷，接着和她说着她哥。他身上不仅有枪，还有雷管，可以把这辆车引爆，但他忽然想和人聊聊天，因为他的身世也同样不幸，他的父母早离了婚，他也有个妹妹，他妹妹也是他供着上了大学，但他却不想让他妹妹知道他是杀人犯！
长久以来，一颗流浪的心忽然间找到了一个可以安歇的去处。坐在窗前，我在试问我自己：你有多久没有好好看看这蓝蓝的天，闻一闻这芬芳的花香，听一听那鸟儿的鸣唱？有多久没有回家看看，听听家人的倾诉？有多久没和他们一起吃饭了，听听那年老的欢笑？有多久没与他们谈心，听听他门的烦恼、他们的心声呢？是不是因为一路风风雨雨， 而忘了天边的彩虹？是不是因为行色匆匆的脚步，而忽视了沿路的风景？除了一颗疲惫的心，麻木的心，你还有一颗感恩的心吗？不要因为生命过于沉重，而忽略了感恩的心！ 也许坎坷，让我看到互相搀扶的身影； 也许失败，我才体会的一句鼓励的真诚； 也许不幸，我才更懂得珍惜幸福。

2 2 2
最简公分母的确定
如果分母是单项式时，最简公分母是：①系数取最 小公倍数；②字母取所有字母；③字母的次数取所 有字母的最高次幂。 如果分母是多项式时，应该先考虑分解因式，再确 定最简公分母。 1 3 2 例： )通分： 与 (1 、 3 2 ax 2b x 3cx x2 x 1 ( 2)通分：2 与 2 x 2x x 4x 4
解：方程两边都乘以 4得： x
2
（x 2) a ( x 2)
2
2
若方程有增根，只能是 2或x 2 x 将x 2和x 2分别代入整式方程可得 ： a 16或a 16
m 1 1、关于x的方程 1 x 1 x 2 1 有增根-1，求m
2、若方程
增根的定义
增根:在去分母,将分式方程转化为整 式方程的过程中出现的不适合于原方 ······ 程的根. ··· 使最简公分母值为零的根 产生的原因:分式方程两边同乘以一个 零因式后,所得的根是整式方程的根, 而不是分式方程的根.···· ····
x2 a x2 例：若关于x的方程 2 x2 x 4 x2 有增根，求a的值。
ab 1 1 解：由已知可得 3, 即 3(1), ab a b 1 1 1 1 同理得： 4(2), 5 b c c a 1 1 1 6 a b c 1 1 原式 ab bc ac 6 abc
分式 方程
概念：分母中含有未知数的有理方程，叫做 分式方程。 解分式方程的步骤： 将分式方程转化为整式方程（方程两边同时乘 以最简公分母） 解整式方程 检验（验根） 写出方程的解
解分式方程易错点分析
一、去分母时常数漏乘 最简公分母 2 x 1 例1、解方程： 2 x 3 3 x 二、去分母时，分子是 多项式不加括号 5 3 x 例2、解方程： 2 0 x 1 x 1 三、方程两边同时除以 可能为零的整式 3x 2 3x 2 例3、解方程： x4 x3