下载文档原格式
⼿把⼿教你做重复测量设计的⽅差分析（⼲货）作为⼀名医学⽣，⼤多数⼈在撰写科研论⽂都会碰到⼀个难题，科研论⽂的数据都必须进⾏统计学处理，上⼤学时学过的《医学统计学》早已忘得差不多了，重新翻开统计学书本，花上⼗天半个⽉的时间，看了后，感觉差不多都会了，还是看得不知所云。
今天我们就来复习⼀下在医学研究中在药物、⽣物学研究⼗分普遍的重复测量设计的⽅差分析(Repeated Measurement Design)吧！➤最常见的应⽤情景：☘同⼀个研究对象给予⼀种或多种处理后，在多个不同的时点上重复观察获得的指标观察值；☘从同⼀个个体的不同部位（或组织）上重复获得指标的观测值。
据对临床医学类杂志研究论著的统计，重复测量设计的⽅差分析使⽤频率⾼达 1/4！重复测量设计是对同⼀因变量进⾏重复测量的⼀种试验设计技术。
重复测量的数据与t检验或者随机区组⽅差分析的区别：由于同⼀观察对象在不同时点的观测值之间往往彼此不独⽴，存在某种程度的相关，因此对重复测量数据如果采取普通的⽅差分析，不能满⾜普通的⽅差分析⽅法所要求的独⽴、正态、等⽅差的前提条件。
若采⽤t检验或者随机区组⽅差分析，就有可能得出错误的结论！1统计案例研究某种药物对某种细胞的细胞活⼒影响，细胞分为3组：对照组、实验组A、实验组B，分别检测加溶剂、低浓度药物和⾼浓度药物后4⼩时、24⼩时、48⼩时和72⼩时的CCK8 OD值。
➔不同浓度的药物处理对细胞活⼒有何作⽤？➔时间和药物之间是否存在交互作⽤？2问题分析本研究对结局指标进⾏了多次测量，每个样本的4⼩时、24⼩时、48⼩时和72⼩时是相关的，这就是常见的重复测量设计。
使⽤两因素重复测量⽅差分析(Two-way Repeated Measures Anova)进⾏分析时，需要考虑3个假设。
❖假设1：因变量唯⼀，且为连续变量；本例因变量只有细胞活⼒，⽽且是连续变量。
❖假设2：有两个被试内因⼦（Within-Subject Factor），每个被试内因⼦有2个或以上的⽔平。
重复测量方差分析1. 引言重复测量方差分析（Repeated Measures Analysis of Variance, RM-ANOVA）是一种统计方法，用于分析在不同时间点或不同处理条件下对同一组个体或样本进行多次测量的数据。
通过比较不同时间点或处理条件下的测量结果，我们可以确定是否存在显著的差异，并了解时间或处理对测量结果的潜在影响。
本文档将介绍重复测量方差分析的基本原理、假设条件、计算方法和结果解读，并提供使用Markdown格式编写重复测量方差分析报告的示例。
2. 基本原理重复测量方差分析的基本原理是基于方差分析（ANOVA）方法，但相对于普通的单因素方差分析，重复测量方差分析考虑了测量数据间的相关性。
在重复测量设计中，同一个个体或样本在不同时间点或处理条件下进行多次测量，因此测量数据之间存在一定的相关性。
为了解决相关性的问题，重复测量方差分析使用了独特的矩阵分解方法，将总体方差分解为组内方差和组间方差。
通过计算组间方差与组内方差的比值，可以判断不同时间点或处理条件下的测量结果是否存在显著差异。
3. 假设条件在进行重复测量方差分析之前，需要满足以下假设条件：•正态性假设：每个时间点或处理条件下的测量结果应当服从正态分布。
•同方差性假设：每个时间点或处理条件下的测量结果应具有相同的方差。
•相关性假设：各个时间点或处理条件下的测量结果之间应具有一定的相关性。
如果数据不满足正态性、同方差性或相关性假设，需要采取适当的数据转换、方差齐性检验或相关性分析等方法进行处理。
4. 计算方法重复测量方差分析的计算方法可以通过计算F统计量来进行。
具体步骤如下：步骤1：计算总体方差首先计算总体方差SSTotal，即测量数据的总体波动情况。
步骤2：计算组间方差然后计算组间方差SSBetween，即不同时间点或处理条件下的测量结果之间的差异。
步骤3：计算组内方差接下来计算组内方差SSWithin，即测量数据在同一个时间点或处理条件下的波动情况。
11-多因素实验资料的方差分析11-3（1）本题为4个处理组的2×2析因涉及，因分成3天进行，若将每天的实验结果设为一个区组，先进行随机区组的方差分析:方差分析表1变异来源df SS MS F Sig.总变异11 818.369区组间 2 3.762 1.881 .230 .801处理组间 3 765.529 255.176 31.196 .000误差 6 49.078 8.180从上表可以看出，各区组间差异无统计学意义，即各天的实验结果间无差异。
（3）依据完全随机设计析因试验方法进行方差分析方差齐性检验表F df1 df2 Sig.1.429 3 8 0.304P值大于0.05，尚不能认为方差不齐。
方差分析表2变异来源df SS MS F Sig.总变异11 818.37试样处理方式（A） 1 716.11 716.11 108.42 0.000试样重量（B） 1 36.40 36.40 5.51 0.047AB 1 13.02 13.02 1.97 0.198误差8 52.84 6.605结局：可以认为高锰酸盐处理及试样重量均会对甘蓝叶核黄素浓度测定产生影响，尚不能认为高猛酸盐及试样重量的交互作用会对甘蓝叶核黄素浓度测量有影响。
11-4假定不存在高阶交互作用，仅对A、B、C、D、E5个因素的主效应进行分析，采用正交设计的方差分析法：正交设计的方差分析变异来源df SS MS F Sig.总变异15 3495.366A 1 540.911 540.911 21.714 .001B 1 1743.689 1743.689 69.998 .000C 1 787.223 787.223 31.602 .000D 1 82.038 82.038 3.293 .100E 1 92.400 92.400 3.709 .083误差10 249.104 24.910从上表可以看出，A、B、C三个因素的主效应有统计学意义（P<0.05），即A、B、C三个参数对高频呼吸机的通气量有影响。
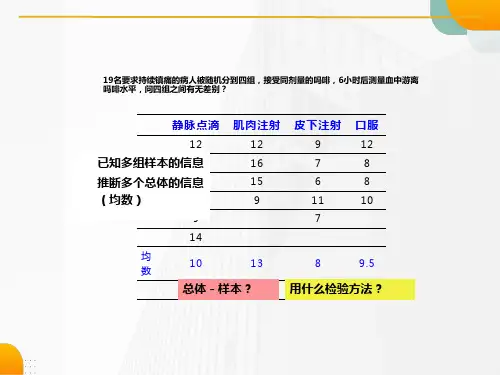
第十五章重复测量设计的方差分析通过学习本章，您可以了解：●进行重复测量设计的方差分析的前提假设●如何逐步进行重复测量设计的方差分析●如何进行简单效应分析和多重比较。
在重复测量设计中，每个被试需接受所有水平的实验处理，即同一因变量先后被观测多次。
用于区分各个实验水平的变量通常是定性变量（Qualitative Variable），顺序变量或名义变量均可，SPSS称之为重测因素，或被试内因素。
被观测的因变量必须是数量变量（Quantitative Variable）。
单因素的重复测量设计只包括一个被试内因素。
多因素的重复测量设计可以有多个被试内因素或被试间因素。
本章将重点介绍单因素重复测量设计的方差分析过程，以及简单介绍多因素重复测量设计的分析思路。
在使用SPSS处理重复测量设计（被试内设计）的数据时，其数据的组织方式不同于被试间设计。
在数据窗口中不需要定义自变量和因变量。
对于单因素设计，数据文件中变量的个数等于自变量（因素）的水平；对于多因素设计，变量的个数等于因素之间的水平组合数。
而且变量的性质都是连续型变量。
在进行方差分析的过程中，需要对因素的个数及变量间的关系进行定义。
1. 前提假设如果被试内因素只有两个水平，则Repeated Measure执行一次标准的一元方差分析。
如果被试内因素有两个以上的水平，则执行三种检验：标准一元方差分析、备选的一元方差分析和多元方差分析。
事实上，三种分析检验的零假设相同，即因素各水平上的均值相同。
但具体采用哪一种分析的结果需要浏览全部三种分析的结果之后才能决定。
当因素水平数超过两个时，需要查看球形假设是否能够满足。
当球形假设可以满足时，可以使用标准一元方差分析的结果。
但是由于球形假设通常无法满足，此时方差分析的显著性水平p值不准确，所以标准一元方差分析在这种情况下并不常用。
备选一元方差分析适用于球形假设（Sephericity Assumption）不满足的情况。
