一轮复习课时训练§4.5：解三角形应用举例

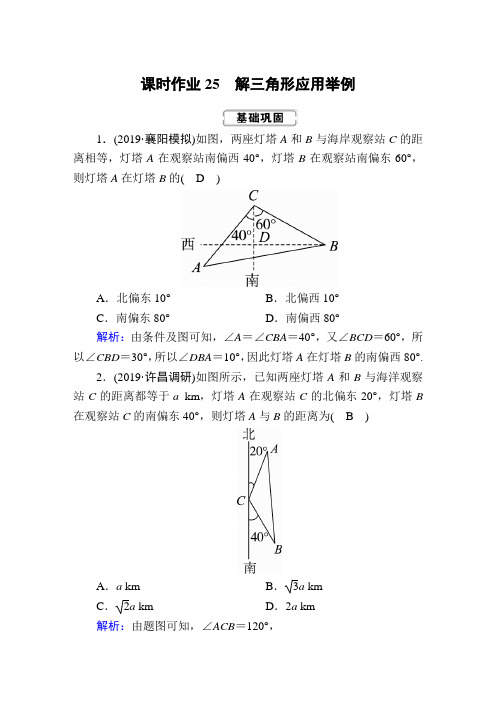
课时作业25解三角形应用举例1．(2019·襄阳模拟)如图，两座灯塔A和B与海岸观察站C的距离相等，灯塔A在观察站南偏西40°，灯塔B在观察站南偏东60°，则灯塔A在灯塔B的(D)A．北偏东10°B．北偏西10°C．南偏东80°D．南偏西80°解析：由条件及图可知，∠A＝∠CBA＝40°，又∠BCD＝60°，所以∠CBD＝30°，所以∠DBA＝10°，因此灯塔A在灯塔B的南偏西80°.2．(2019·许昌调研)如图所示，已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B 在观察站C的南偏东40°，则灯塔A与B的距离为(B)A．a km B．3a kmC．2a km D．2a km解析：由题图可知，∠ACB＝120°，由余弦定理，得AB 2＝AC 2＋BC 2－2AC ·BC ·cos ∠ACB ＝a 2＋a 2－2·a ·a ·⎝ ⎛⎭⎪⎫－12＝3a 2，解得AB ＝3a (km)． 3．如图，测量河对岸的塔高AB 时可以选与塔底B 在同一水平面内的两个测点C 与D ，测得∠BCD ＝15°，∠BDC ＝30°，CD ＝30，并在点C 测得塔顶A 的仰角为60°，则塔高AB 等于( D )A ．5 6B ．15 3C ．5 2D ．15 6解析：在△BCD 中，∠CBD ＝180°－15°－30°＝135°.由正弦定理得BC sin30°＝30sin135°，所以BC ＝15 2.在Rt △ABC 中，AB ＝BC tan ∠ACB ＝152×3＝15 6.4．如图所示，为了了解某海域海底构造，在海平面上取一条直线上的A ，B ，C 三点进行测量，已知AB ＝50 m ，BC ＝120 m ，于A 处测得水深AD ＝80 m ，于B 处测得水深BE ＝200 m ，于C 处测得水深CF ＝110 m ，则∠DEF 的余弦值为( A )A ．1665B ．1965C ．1657D ．1757解析：如图所示，作DM ∥AC 交BE 于N ，交CF 于M ，则DF ＝MF 2＋DM 2＝302＋1702＝10298(m)，DE ＝DN 2＋EN 2＝502＋1202＝130(m)，EF ＝(BE －FC )2＋BC 2＝902＋1202＝150(m)．在△DEF 中，由余弦定理，得cos ∠DEF ＝DE 2＋EF 2－DF 22DE ·EF＝1302＋1502－102×2982×130×150＝1665. 5．地面上有两座相距120 m 的塔，在矮塔塔底望高塔塔顶的仰角为α，在高塔塔底望矮塔塔顶的仰角为α2，且在两塔底连线的中点O处望两塔塔顶的仰角互为余角，则两塔的高度分别为( B )A ．50 m,100 mB ．40 m,90 mC ．40 m,50 mD ．30 m,40 m 解析：设高塔高H m ，矮塔高h m ，在O 点望高塔塔顶的仰角为β.则tan α＝H 120，tan α2＝h 120，根据三角函数的倍角公式有H 120＝2×h 1201－⎝ ⎛⎭⎪⎫h 1202.① 因为在两塔底连线的中点O 望两塔塔顶的仰角互为余角，所以在O点望矮塔塔顶的仰角为π2－β， 由tan β＝H 60，tan ⎝ ⎛⎭⎪⎫π2－β＝h 60，得H 60＝60h .② 联立①②解得H ＝90，h ＝40.即两座塔的高度分别为40 m,90 m.6．如图所示，一座建筑物AB 的高为(30－103)m ，在该建筑物的正东方向有一座通信塔CD ．在它们之间的地面上的点M (B ，M ，D 三点共线)处测得楼顶A ，塔顶C 的仰角分别是15°和60°，在楼顶A 处测得塔顶C 的仰角为30°，则通信塔CD 的高为( B )A ．30 mB ．60 mC ．30 3 mD ．40 3 m解析：在Rt △ABM 中，AM ＝AB sin ∠AMB ＝30－103sin15°＝30－1036－24＝206(m).过点A 作AN ⊥CD 于点N ，如图所示．易知∠MAN ＝∠AMB ＝15°，所以∠MAC ＝30°＋15°＝45°.又∠AMC ＝180°－15°－60°＝105°，所以∠ACM＝30°.在△AMC中，由正弦定理得MCsin45°＝206sin30°，解得MC＝403(m)．在Rt△CMD中，CD＝403×sin60°＝60(m)，故通信塔CD的高为60 m.7．(2019·哈尔滨模拟)如图，某工程中要将一长为100 m，倾斜角为75°的斜坡改造成倾斜角为30°的斜坡，并保持坡高不变，则坡底需加长1002m.解析：设坡底需加长x m，由正弦定理得100sin30°＝xsin45°，解得x＝100 2.8．如图，为了测量两座山峰上P，Q两点之间的距离，选择山坡上一段长度为300 3 m且和P，Q两点在同一平面内的路段AB的两个端点作为观测点，现测得∠P AB＝90°，∠P AQ＝∠PBA＝∠PBQ＝60°，则P，Q两点间的距离为900__m.解析：由已知，得∠QAB＝∠P AB－∠P AQ＝30°.又∠PBA＝∠PBQ＝60°，∴∠AQB＝30°，∴AB＝BQ.又PB为公共边，∴△P AB≌△PQB，∴PQ＝P A．在Rt △P AB 中，AP ＝AB ·tan60°＝900，故PQ ＝900，∴P ，Q 两点间的距离为900 m.9．(2019·湖北百所重点中学模拟)我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里记载了这样一个题目：“今有沙田一段，有三斜，其小斜一十三里，中斜一十四里，大斜一十五里．里法三百步．欲知为田几何．”这道题讲的是有一块三角形的沙田，三边长分别为13里，14里，15里，假设1里按500米计算，则该沙田的面积为21__平方千米． 解析：设在△ABC 中，a ＝13里，b ＝14里，c ＝15里，∴cos C ＝132＋142－1522×13×14＝132＋(14－15)×(14＋15)2×13×14＝1402×13×14＝513， ∴sin C ＝1213，故△ABC 的面积为12×13×14×1213×5002×11 0002＝21(平方千米)．10．海轮“和谐号”从A 处以每小时21海里的速度出发，海轮“奋斗号”在A 处北偏东45°的方向，且与A 相距10海里的C 处，沿北偏东105°的方向以每小时9海里的速度行驶，则海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为23 小时．解析：设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x 小时，如图，则由已知得△ABC 中，AC ＝10，AB ＝21x ，BC ＝9x ，∠ACB ＝120°. 由余弦定理得：(21x )2＝100＋(9x )2－2×10×9x ×cos120°，整理，得36x 2－9x －10＝0，解得x ＝23或x ＝－512(舍)．所以海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为23小时．11．(2019·武汉模拟)为了应对日益严重的气候问题，某气象仪器科研单位研究出一种新的“弹射型”气象仪器，这种仪器可以弹射到空中进行气象观测．如图所示，A ，B ，C 三地位于同一水平面上，这种仪器在C 地进行弹射实验，观测点A ，B 两地相距100米，∠BAC＝60°.在A 地听到弹射声音的时间比B 地晚217秒．在A 地测得该仪器至最高点H 处的仰角为30°.(1)求A ，C 两地的距离；(2)求这种仪器的垂直弹射高度HC ．(已知声音的传播速度为340米/秒)解：(1)由题意，设AC ＝x ，因为在A 地听到弹射声音的时间比B 地晚217秒，所以BC ＝x －217×340＝x －40，在△ABC 内，由余弦定理得BC 2＝CA 2＋BA 2－2BA ·CA ·cos ∠BAC ， 即(x －40)2＝x 2＋10 000－100x ，解得x ＝420.答：A ，C 两地的距离为420米．(2)在Rt △ACH 中，AC ＝420，∠CAH ＝30°.所以CH ＝AC ·tan ∠CAH ＝1403米．答：该仪器的垂直弹射高度CH 为1403米．12．如图所示，在一条海防警戒线上的点A ，B ，C 处各有一个水声监测点，B ，C 两点到点A 的距离分别为20 km 和50 km.某时刻，B 收到发自静止目标P 的一个声波信号，8 s 后A ，C 同时接收到该声波信号，已知声波在水中的传播速度是1.5 km/s.(1)设A 到P 的距离为x km ，用x 表示B ，C 到P 的距离，并求x 的值；(2)求静止目标P 到海防警戒线AC 的距离．解：(1)依题意，有P A ＝PC ＝x ，PB ＝x －1.5×8＝x －12.在△P AB 中，AB ＝20，cos ∠P AB ＝P A 2＋AB 2－PB 22P A ·AB＝x 2＋202－(x －12)22x ·20＝3x ＋325x . 同理，在△P AC 中，AC ＝50，cos ∠P AC ＝P A 2＋AC 2－PC 22P A ·AC ＝x 2＋502－x 22x ·50＝25x .因为cos ∠P AB ＝cos ∠P AC ，所以3x ＋325x ＝25x ，解得x ＝31.(2)作PD ⊥AC 于点D ，在△ADP 中，由cos ∠P AD ＝2531，得sin ∠P AD ＝1－cos 2∠P AD ＝42131，所以PD ＝P A sin ∠P AD ＝31×42131＝421(km)．故静止目标P 到海防警戒线AC 的距离为421 km.13．如图，为了测量A ，C 两点间的距离，选取同一平面上B ，D 两点，测出四边形ABCD 各边的长度(单位：km)：AB ＝5，BC ＝8，CD ＝3，DA ＝5，且∠B 与∠D 互补，则AC 的长为( A )A ．7 kmB ．8 kmC ．9 kmD ．6 km解析：在△ACD 中，由余弦定理得：cos D ＝AD 2＋CD 2－AC 22AD ·CD＝34－AC 230. 在△ABC 中，由余弦定理得：cos B ＝AB 2＋BC 2－AC 22AB ·BC＝89－AC 280. 因为∠B ＋∠D ＝180°，所以cos B ＋cos D ＝0，即34－AC 230＋89－AC 280＝0，解得AC ＝7.14．(2019·呼和浩特调研)某人为测出所住小区的面积，进行了一些测量工作，最后将所住小区近似地画成如图所示的四边形，测得的数据如图所示，则该图所示的小区的面积是6－34km 2.解析：如图，连接AC ，由余弦定理可知AC ＝AB 2＋BC 2－2AB ·BC ·cos B ＝3，故∠ACB ＝90°，∠CAB ＝30°，∠DAC ＝∠DCA ＝15°，∠ADC ＝150°，AC sin ∠ADC ＝AD sin ∠DCA ，即AD ＝AC sin ∠DCA sin ∠ADC＝3·6－2412＝32－62， 故S 四边形ABCD ＝S △ABC ＋S △ADC ＝12×1×3＋12×⎝ ⎛⎭⎪⎫32－622×12＝6－34(km 2)． 15．(2019·福州质检)如图，小明同学在山顶A 处观测到一辆汽车在一条水平的公路上沿直线匀速行驶，小明在A 处测得公路上B ，C 两点的俯角分别为30°，45°，且∠BAC ＝135°.若山高AD ＝100 m ，汽车从B 点到C 点历时14 s ，则这辆汽车的速度约为22.6__m/s(精确到0.1)．解析：因为小明在A 处测得公路上B ，C 两点的俯角分别为30°，45°，所以∠BAD ＝60°，∠CAD ＝45°.设这辆汽车的速度为v m/s ，则BC ＝14v .在Rt △ADB 中，AB ＝AD cos ∠BAD ＝AD cos60°＝200.在Rt △ADC 中，AC ＝AD cos ∠CAD ＝100cos45°＝100 2. 在△ABC 中，由余弦定理，得BC 2＝AC 2＋AB 2－2AC ·AB ·cos ∠BAC ，所以(14v )2＝(1002)2＋2002－2×1002×200×cos135°，所以v ＝50107≈22.6，所以这辆汽车的速度约为22.6 m/s.16．某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上．在小艇出发时，轮船位于港口O 北偏西30°且与该港口相距20海里的A 处，并正以30海里/小时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v 海里/小时的航行速度匀速行驶，经过t 小时与轮船相遇．(1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？(2)假设小艇的最高航行速度只能达到30海里/小时，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．解：(1)设相遇时小艇航行的距离为S 海里，则S ＝900t 2＋400－2·30t ·20·cos (90°－30°)＝900t 2－600t ＋400＝900⎝ ⎛⎭⎪⎫t －132＋300. 故当t ＝13时，S min ＝103，v ＝10313＝30 3.即小艇以303海里/小时的速度航行，相遇时小艇的航行距离最小．(2)设小艇与轮船在B 处相遇．如图所示．则v 2t 2＝400＋900t 2－2·20·30t ·cos(90°－30°)，故v 2＝900－600t ＋400t 2. 因为0＜v ≤30，所以900－600t ＋400t 2≤900，即2t 2－3t ≤0，解得t ≥23.又t ＝23时，v ＝30，故v ＝30时，t 取得最小值，且最小值等于23.此时，在△OAB 中，有OA ＝OB ＝AB ＝20.故可设计航行方案如下：航行方向为北偏东30°，航行速度为30海里/小时．。

§4.5三角恒等变形最新考纲考情考向分析三角恒等变换是三角变换的工具，1.会用向量的数量积推导出两角差的余弦公式．主要考查利用两角和与差的三角函2.会用两角差的余弦公式推导出两角差的正弦、数公式、二倍角公式进行三角函数正切公式．的化简与求值，重在考查化简、求3.会用两角差的余弦公式推导出两角和的正弦、值，公式的正用、逆用以及变式运余弦、正切公式，推导出二倍角的正弦、余弦、用，可单独考查，也可与三角函数正切公式，了解它们的内在联系．的图象和性质、向量等知识综合考4.能运用上述公式进行简单的恒等变换(包括导查，加强转化与化归思想的应用意出积化和差、和差化积、半角公式，但对这三组识．选择、填空、解答题均有可能公式不要求记忆).出现，中低档难度.1．两角和与差的余弦、正弦、正切公式cos(α－β)＝cos αcos β＋sin αsin β(C(α－β))cos(α＋β)＝cos αcos β－sin αsin β(C(α＋β))sin(α－β)＝sin αcos β－cos αsin β(S(α－β))sin(α＋β)＝sin αcos β＋cos αsin β(S(α＋β))tan α－tan βtan(α－β)＝(T(α－β))1＋tan αtan βtan α＋tan βtan(α＋β)＝(T(α＋β))1－tan αtan β2．二倍角公式sin 2α＝2sin αcos α；cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α；2tan αtan 2α＝.1－tan2α1知识拓展1＋cos 2α1－cos 2α1．降幂公式：cos2α＝，sin2α＝.2 22．升幂公式：1＋cos 2α＝2cos2α，1－cos 2α＝2sin2α.b3．辅助角公式：a sin x＋b cos x＝a2＋b2sin(x＋φ)，其中sin φ＝，cos φ＝a2＋b2 aa2＋b2.题组一思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)存在实数α，β，使等式sin(α＋β)＝sin α＋sin β成立．(√)αα(2)对任意角α都有1＋sin α＝(sin ＋cos 2)2.(√)2(3)y＝3sin x＋4cos x的最大值是7.(×)tan α＋tan β(4)公式tan(α＋β)＝可以变形为tan α＋tan β＝tan(α＋β)(1－tan1－tan αtan βαtan β)，且对任意角α，β都成立．(×)题组二教材改编4 π2．若cos α＝－5，α是第三象限的角，则sin(α＋等于()4)2 2 7 2 7 2A．－ B. C．－ D.10 10 10 10答案 C解析∵α是第三象限角，3∴sinα＝－1－cos2α＝－，5π 3 2 4 2 7 2∴sin(α＋4)＝－×2＋(－5 )×＝－.5 2 103．sin 347°cos148°＋sin 77°cos58°＝.答案2 2解析sin 347°cos148°＋sin 77°cos58°＝sin(270°＋77°)cos(90°＋58°)＋sin 77°cos58°＝(－cos 77°)·(－sin 58°)＋sin 77°c os 58°＝sin 58°cos77°＋cos 58°sin77°22 ＝sin(58°＋77°)＝sin 135°＝ .24．tan 20°＋tan 40°＋ 3tan 20°tan 40°＝ .答案 3tan 20°＋tan 40°解析 ∵tan 60°＝tan(20°＋40°)＝ ，1－tan 20°tan 40°∴tan 20°＋tan 40°＝tan 60°(1－tan 20°tan 40°) ＝ 3－ 3tan 20°tan 40°，∴原式＝ 3－ 3tan 20°tan 40°＋ 3tan 20°tan 40°＝ 3. 题组三 易错自纠cos 40°5．化简： ＝ .cos 25°· 1－sin 40° 答案 2cos 40°解析 原式＝cos 25° 1－cos 50°cos 40°cos 40°＝＝＝ 2.cos 25°· 2sin 25°2sin 50° 21 16．(2018·昆明模拟)若 tan α＝ ，tan(α＋β)＝ ，则 tan β＝ .3 2 1 答案 7tan α＋β －tan α 解析 tan β＝tan[(α＋β)－α]＝ 1＋tan α＋β tan α1 1－ 2 3 1 ＝ ＝ .1 1 7 1＋ ×2 3ππ 27．(2018·烟台模拟)已知 θ∈(0， 2)，且 sin (θ－ 4)＝，则 tan 2θ＝.1024 答案 － 7π2 1 解析 方法一sin (θ－ 4)＝，得 sin θ－cos θ＝ ，①105π24θ∈(0， 2)，①平方得 2sin θcos θ＝，257 4 3 可求得 sin θ＋cos θ＝ ，∴sin θ＝ ，cos θ＝ ， 5 5 54 2tan θ24∴tanθ＝，tan 2θ＝＝－.3 1－tan2θ73ππ 2方法二∵θ∈(0，2)且sin(θ－4)＝，10π7 2∴cos(θ－4)＝，10π 1 tan θ－1 4∴tan(θ－4)＝＝，∴tanθ＝.7 1＋tan θ 32tan θ24故tan 2θ＝＝－.1－tan2θ7第1课时两角和与差的正弦、余弦和正切公式题型一和差公式的直接应用3 π 1 1．(2018·青岛调研)已知sin α＝，α∈，tan(π－β)＝，则tan(α－β)的值5 ( ，π)2 2为()2 2 11 11A．－ B. C. D．－11 11 2 2答案 Aπ 3 1解析∵α∈( ，π)，∴tanα＝－，又tan β＝－，2 4 2tan α－tan β∴tan(α－β)＝1＋tan α·tanβ3 1－＋4 2 2＝＝－.1 3 111＋(－2 )×(－4 )π 1 π(α－6)＝3，则cos(α－3)等于() 2．(2017·山西太原五中模拟)已知角α为锐角，若sin2 6＋1 3－2A. B.6 83＋2 2 3－1C. D.8 6答案 Aπ 1 解(α－6)＝，析由于角α为锐角，且sin3 π 2 2则cos (α－6)＝，34πππππππ 2 2 3 1 1则cos (α－3)＝cos[(α－6)－6]＝cos(α－6)cos6＋sin(α－6)sin ＝×＋×6 3 2 3 22 6＋1＝，6故选A.sin 110°sin20°3．计算的值为．cos2155°－sin2155°1答案2sin 110°sin20°sin 70°sin 20° 解析＝cos2155°－sin2155°cos 310°1sin 40°cos 20°sin20° 2 1＝＝＝.cos 50°sin 40° 2思维升华(1)使用两角和与差的三角函数公式，首先要记住公式的结构特征．(2)使用公式求值，应先求出相关角的函数值，再代入公式求值．题型二和差公式的灵活应用命题点1角的变换5 3典例(1)设α，β都是锐角，且cos α＝，sin(α＋β)＝，则cos β＝.5 52 5答案252 5解析依题意得sin α＝1－cos2α＝，53因为sin(α＋β)＝<sin α且α＋β>α，5π 4所以α＋β∈( ，π)，所以cos(α＋β)＝－.2 5于是cos β＝cos[(α＋β)－α]＝cos(α＋β)cos α＋sin(α＋β)sin α4 5 3 2 5 2 5＝－×＋×＝.5 5 5 5 251(2)(2017·泰安模拟)已知cos(75°＋α)＝，则cos(30°－2α)的值为．37答案91解析cos(75°＋α)＝sin(15°－α)＝，352 7 ∴cos(30°－2α)＝1－2sin 2(15°－α)＝1－ ＝ . 9 9 命题点 2 三角函数式的变换θθ1＋sin θ＋cos θ (sin －cos 2)2典例 (1)化简： (0<θ<π)；2＋2cos θ1＋cos 20°1(2)求值：－sin 10°－tan 5°). 2sin 20°(tan 5°θ π θ解 (1)由 θ∈(0，π)，得 0< < ，∴cos >0，2 2 2θ θ ∴ 2＋2cos θ＝ 4cos 2 ＝2cos . 2 2 又(1＋sin θ＋cos θ)(sin θ－cos 2θ2)＝(2sin θ cos 2 θ θ ＋2cos 2 2)(sin 2θ －cos 2θ 2)＝2cosθ θ θ2(sin 2)2－cos 2 2 θ ＝－2cos cos θ.2θ －2coscos θ2故原式＝＝－cos θ.θ 2cos 22cos 210°cos 5° sin 5°(2)原式＝－sin 10°cos 5°)2 × 2sin 10°cos 10°(－ sin 5°cos 10° cos 25°－sin 25°＝ －sin 10°· 2sin 10° sin 5°cos 5° cos 10° cos 10° ＝ －sin 10°· 2sin 10° 1 sin 10°2 cos 10° cos 10°－2sin 20° ＝ －2cos 10°＝ 2sin 10° 2sin 10° cos 10°－2sin 30°－10° ＝2sin 10°12cos 10°－2(cos 10°－＝2sin 10°3sin 10°) 23sin 10° 3＝＝.2sin 10° 2引申探究6θθ1＋sin θ－cos θ(sin 2)－cos2化简：(0<θ<π)．2－2cos θθπθ解∵0<< ，∴2－2cos θ＝2sin ，2 2 2θθθ又1＋sin θ－cos θ＝2sin cos ＋2sin22 2 2＝2sinθ2(sinθ＋cos2θ2)∴原式＝2sinθ2(sinθ＋cos22sinθ2)(sinθ2θ－cos2θ2)＝－cos θ.思维升华(1)解决三角函数的求值问题的关键是把“所求角”用“已知角”表示．①当“已知角”有两个时，“所求角”一般表示为两个“已知角”的和或差的形式；②当“已知角”有一个时，此时应着眼于“所求角”与“已知角”的和或差的关系．α＋βα－β(2)常见的配角技巧：2α＝(α＋β)＋(α－β)，α＝(α＋β)－β，β＝－，2 2α＋βα－βα－ββαα＝＋，＝－等．2 (α＋2) ( ＋β) 22 2跟踪训练(1)(2017·豫北名校联考)计算：cos 10°－3cos －100°＝.(用数字作答)1－sin 10°答案 2cos 10°－3cos －100°解析＝1－sin 10°1－cos 80°cos 10°＋3cos 80°cos 10°＋3sin 10°2sin 10°＋30°＝＝＝ 2.2·sin40°2·sin40°ππ 1 11 (2)(2017·南充模拟)已知α∈(0，2)，β∈(0，2)，且cos α＝，cos(α＋β)＝－，7 14 则sin β＝.答案324 35 3解析由已知可得sin α＝，sin(α＋β)＝，7 145 3 1 ∴sinβ＝sin[(α＋β)－α]＝sin(α＋β)·cosα－cos(α＋β)sin α＝×－14 711 4 3 3(－14 )×＝.7 27用联系的观点进行三角变形 π4 π典例 (1)设 α 为锐角，若 cos(α＋ 6)＝5，则 sin (2α＋12)的值为．(2)(1＋tan 17°)·(1＋tan 28°)的值为 ． 3π cos 2α(3)已知 sin α＝ ，α∈，则＝ .5( ，π)2π2sin (α＋ 4)思想方法指导 三角变形的关键是找到条件和结论中的角和式子结构之间的联系．变形中可以 通过适当地拆角、凑角或对式子整体变形达到目的．π4 解析 (1)∵α 为锐角且 cos (α＋ 6)＝ >0，5π π ππ3∴α＋ 6∈( 2)，∴sin (α＋ 6)＝ .， 6 5πππ∴sin (2α＋12)＝sin [2(α＋ 6)－ 4]π ππ＝sin 2(α＋ 6)cos 4－cos 2(α＋ 6)sin π4 ππ＝ 2sin (α＋ 6)cos (α＋ 6)－2π2[2cos 2(α＋ 6)－1]3 4＝ 2× × － 5 524 2[2 × (5 )2－1]12 2 7 2 17 2 ＝ － ＝ . 25 50 50(2)原式＝1＋tan 17°＋tan 28°＋tan 17°·tan 28° ＝1＋tan 45°(1－tan 17°·tan 28°)＋tan 17°·tan 28° ＝1＋1＝2. cos 2α(3) ＝π 2sin (α＋ 4) 2(cos 2α－sin 2α2 sin α＋2 2 cos α)2 ＝cos α－sin α，3π∵sin α＝5，α∈( ，π)，24 7 ∴cos α＝－ ，∴原式＝－ .5 5 17 2 7 答案 (1) (2)2 (3)－ 50 582 π1．(2017·山西五校联考)若cos θ＝，θ为第四象限角，则cos 的值为()3 (θ＋4)2＋10 2 2＋10A. B.6 62－10 2 2－10C. D.6 6答案 B2解析由cos θ＝，θ为第四象限角，35得sin θ＝－，3π 2 52 2 2 2＋10故cos (θ＋4)＝(cos θ－sin θ)＝2×( 3)＝.故选B.＋2 3 64 π 22．(2018·成都模拟)若sin α＝，则sin －cos α等于()5 (α＋4)22 2 2 2A. B．－5 54 2 4 2C. D．－5 5答案 Aπ 2 ππ 2 4 2 2 2解析sin (α＋4)－cos α＝sin αcos ＋cos αsin －cos α＝×＝.2 4 4 2 5 2 513．(2017·西安检测)已知α是第二象限角，且tan α＝－，则sin 2α等于()33 10 3 10A．－ B.10 103 3C．－ D.5 5答案 C1解析因为α是第二象限角，且tan α＝－，310 3 10所以sin α＝，cos α＝－，10 10103 10 3所以sin 2α＝2sin αcos α＝2×10 ×(－10 )＝－，5故选C.92 4．(2017·河南洛阳一模)设a＝cos 50°cos127°＋cos 40°sin127°，b＝(sin 56°－2 1－tan239°cos 56°)，c＝，则a，b，c的大小关系是()1＋tan239°A．a>b>c B．b>a>cC．c>a>b D．a>c>b答案 D解析a＝sin 40°cos127°＋cos 40°sin127°＝sin(40°＋127°)＝sin 167°＝sin 13°，2 2 2b＝(sin 56°－cos 56°)＝sin 56°－cos 56°2 2 2＝sin(56°－45°)＝sin 11°，cos239°－sin239°cos239°c＝＝cos239°－sin239°＝cos 78°＝sin 12°，sin239°＋cos239°cos239°∵sin13°>sin12°>sin11°，∴a>c>b.3 π(2α＋4)等于()5．已知sin α＝5且α为第二象限角，则tan19 5 31 17A．－B．－C．－D．－5 19 17 31答案 D4 24解析由题意得cos α＝－，则sin 2α＝－，5 257cos 2α＝2cos2α－1＝.2524∴tan2α＝－，7π24tan 2α＋tan －＋1π 4 7∴tan(2α＋4)＝＝π241－tan 2αtan1－(－7 )× 1 417＝－.312 π(α＋4)等于()6．已知sin 2α＝3，则cos21 1A. B.6 31 2C. D.2 310答案 Aπ 1＋cos 2(α＋ 4)π解析 因为 cos 2(α＋ 4)＝2π 1＋cos(2α＋ 2)1－sin 2α ＝＝， 2221－ π1－sin 2α3 1 所以 cos 2(α＋ 4)＝＝ ＝ ，故选 A. 22 62cos 10°－sin 20° 7．(2018·新疆乌鲁木齐一诊) 的值是( ) sin 70° 1 A. B. 2 3 2 C. 3 D. 2答案 C2cos 30°－20° －sin 20°解析 原式＝sin 70°2 cos 30°·cos 20°＋sin 30°·sin 20° －sin 20° ＝sin 70° 3cos 20° ＝ ＝ 3. cos 20°18．已知锐角 α，β 满足 sin α－cos α＝ ，tan α＋tan β＋ 3tan αtan β＝ 3，则6α，β 的大小关系是( )π πA ．α< <βB ．β< <α4 4ππ C. <α<β D. <β<α4 4答案 B1 π π 解析 ∵α 为锐角，sin α－cos α＝ >0，∴ <α< . 6 42 又 tan α＋tan β＋ 3tan αtan β＝ 3，tan α＋tan β∴tan(α＋β)＝ ＝ 3，1－tan αtan βπ π π ∴α＋β＝ ，又 α> ，∴β< <α. 3 4 4π19．(2017·江苏)若 tan (α－ 4)＝ ，则 tan α＝.67答案511π tan α－tanπ4 解析 方法一∵tan (α－ 4)＝π 1＋tan αtan4tan α－1 1 ＝ ＝ ， 1＋tan α 6∴6tan α－6＝1＋tan α(tan α≠－1)， 7 ∴tan α＝ . 5ππ方法二tan α＝tan [(α－ 4)＋ 4]ππ1 tan (α－ 4)＋tan＋14 6 7 ＝ ＝＝ .ππ1 51－tan (α－ 4)tan1－ 4 62tan 45°－α sin αcos α10．(2018·河南八市质检)化简： · ＝.1－tan 2 45°－α cos 2α－sin 2α 1 答案 21sin 2α2解析 原式＝tan(90°－2α)·cos 2αsin 90°－2α 1 sin 2α ＝ · ·cos 90°－2α 2 cos 2α cos 2α 1 sin 2α 1 ＝ · · ＝ . sin 2α 2 cos 2α 21π11．已知 sin α＋cos α＝3，则 sin 2( －α)＝.417 答案 181 1 解析 由 sin α＋cos α＝ ，两边平方得 1＋sin 2α＝ ， 3 9 8 解得 sin 2α＝－ ，9π1－cos( －2α)π2所以 sin 2( －α)＝428 1＋1－sin 2α 9 17 ＝ ＝ ＝ . 2 2 18312．(2018·吉林模拟)已知 sin(α－β)cos α－cos(β－α)sin α＝ ，β 是第三象限角，5125π则sin(β＋4 )＝.7 2答案10解析依题意可将已知条件变形为3 3 sin[(α－β)－α]＝－sin β＝，sin β＝－.5 54又β是第三象限角，所以cos β＝－.55ππ所以sin(β＋4 )＝－sin(β＋4)π＝－sin βcos －cos βsin4 π43 24 2 7 2＝×＋×＝.5 2 5 2 1013ππ13．(2017·河北衡水中学调研)若α∈( ，π)，且3cos 2α＝sin( －α)，则sin 2α的值2 4为()1 1 17 17A．－ B. C．－ D.18 18 18 18答案 Cπ 解析由3cos 2α＝sin( －α)可得423(cos2α－sin2α)＝(cos α－sin α)，2π又由α∈( ，π)可知cos α－sin α≠0，22于是3(cos α＋sin α)＝，21 17所以1＋2sin α·cosα＝，故sin 2α＝－.故选C.18 18ππ 114．已知cos( ＋θ)cos( －θ)＝，则sin4θ＋cos4θ的值为．4 4 45答案8ππ解析因为cos( ＋θ)cos( －θ)4 4＝(2cos θ－22sin θ)(22cos θ＋22sin θ)21 1 1＝(cos2θ－sin2θ)＝cos 2θ＝.2 2 41所以cos 2θ＝.21－cos 2θ1＋cos 2θ故sin4θ＋cos4θ＝( 2 )2＋( 2 )21 9 5＝＋＝.16 16 815．(2017·武汉调研)设α，β∈[0，π]，且满足sin αcos β－cos αsin β＝1，则sin(2α－β)＋sin(α－2β)的取值范围为．答案[－1,1]解析由sin αcos β－cos αsin β＝1，得sin(α－β)＝1，14π 又α，β∈[0，π]，∴α－β＝，2π∴Error!即≤α≤π，2∴sin(2α－β)＋sin(α－2β)π＝sin(2α－α＋2)＋sin(α－2α＋π)π ＝cos α＋sin α＝2sin(α＋4).π3ππ5π∵≤α≤π，∴≤α＋≤，2 4 4 4π∴－1≤2sin(α＋4)≤1，即取值范围为[－1,1]．1 16．(2017·合肥模拟)已知函数f(x)＝(2cos2x－1)·sin 2x＋cos 4x.2(1)求f(x)的最小正周期及递减区间；απ 2 π(2)若α∈(0，π)，且f( 8)＝2，求tan(α＋3)的值．－41 解(1)f(x)＝(2cos2x－1)sin 2x＋cos 4x21 ＝cos2x sin 2x＋cos 4x21 2 π ＝(sin 4x＋cos 4x)＝2 s in (4x＋4)，2π∴f(x)的最小正周期T＝.2ππ3π令2kπ＋≤4x＋≤2kπ＋，k∈Z，2 4 2kππkπ5π得＋≤x≤＋，k∈Z.2 16 2 16kππkπ5π∴f(x)的递减区间为[ ，k∈Z.＋＋16]，2 16 2απ 2 π(2)∵f( ＝，∴sin＝1.－8) 2 (α－4) 4ππ3π∵α∈(0，π)，－<α－< ，4 4 4ππ3π∴α－＝，故α＝.4 2 4153π π tan ＋tanπ4 3－1＋ 3因此 tan(α＋ 3 )＝＝＝2－ .33π1＋ 3π 1－tan tan4 316。

第2课时 简单的三角恒等变换题型一 三角函数式的化简例1 (1)化简：2cos 4x －2cos 2x ＋122tan ⎝ ⎛⎭⎪⎫π4－x sin 2⎝ ⎛⎭⎪⎫π4＋x ＝ .(2)已知cos ⎝ ⎛⎭⎪⎫θ＋π4＝1010，θ∈⎝ ⎛⎭⎪⎫0，π2，则sin ⎝ ⎛⎭⎪⎫2θ－π3＝ . 答案 (1)12cos 2x (2)4－3310解析 (1)原式＝124x －4cos 2x ＋2×sin ⎝ ⎛⎭⎪⎫π4－x cos ⎝ ⎛⎭⎪⎫π4－x ·cos 2⎝ ⎛⎭⎪⎫π4－x＝2x －24sin ⎝ ⎛⎭⎪⎫π4－x cos ⎝ ⎛⎭⎪⎫π4－x＝cos 22x 2sin ⎝ ⎛⎭⎪⎫π2－2x＝cos 22x 2cos 2x ＝12cos 2x . (2)由题意可得，cos 2⎝ ⎛⎭⎪⎫θ＋π4＝1＋cos ⎝ ⎛⎭⎪⎫2θ＋π22＝110，cos ⎝ ⎛⎭⎪⎫2θ＋π2＝－sin 2θ＝－45，即sin 2θ＝45.因为cos ⎝ ⎛⎭⎪⎫θ＋π4＝1010>0，θ∈⎝ ⎛⎭⎪⎫0，π2， 所以0<θ<π4，2θ∈⎝⎛⎭⎪⎫0，π2，根据同角三角函数基本关系式可得cos 2θ＝35，由两角差的正弦公式可得sin ⎝⎛⎭⎪⎫2θ－π3＝sin 2θcos π3－cos 2θsin π3＝4－3310. 思维升华 (1)三角函数式的化简要遵循“三看”原则，一看角，二看名，三看式子结构与特征．(2)三角函数式化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等)，寻找式子和三角函数公式之间的共同点．(1)已知cos(x －π6)＝－33，则cos x ＋cos(x －π3)＝ .(2)若α∈⎝ ⎛⎭⎪⎫π2，π，且3cos 2α＝sin ⎝ ⎛⎭⎪⎫π4－α，则sin 2α的值为( )A.118 B ．－118C.1718D ．－1718答案 (1)－1 (2)D 解析 (1)cos x ＋cos(x －π3)＝cos x ＋12cos x ＋32sin x＝32cos x ＋32sin x ＝3cos(x －π6) ＝3×(－33)＝－1. (2)cos 2α＝sin ⎝ ⎛⎭⎪⎫π2－2α＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4－α ＝2sin ⎝⎛⎭⎪⎫π4－αcos ⎝ ⎛⎭⎪⎫π4－α代入原式，得6sin ⎝ ⎛⎭⎪⎫π4－αcos ⎝ ⎛⎭⎪⎫π4－α＝sin ⎝ ⎛⎭⎪⎫π4－α， ∵α∈⎝⎛⎭⎪⎫π2，π，∴cos ⎝ ⎛⎭⎪⎫π4－α＝16，∴sin 2α＝cos ⎝⎛⎭⎪⎫π2－2α＝2cos 2⎝ ⎛⎭⎪⎫π4－α－1＝－1718.题型二 三角函数的求值 命题点1 给值求值问题例2 (1)(2017·合肥联考)已知α，β为锐角，cos α＝17，sin(α＋β)＝5314，则cos β＝ . 答案 12解析 ∵α为锐角， ∴sin α＝1－172＝437.∵α，β∈(0，π2)，∴0<α＋β<π.又∵sin(α＋β)<sin α，∴α＋β>π2，∴cos(α＋β)＝－1114.cos β＝cos[(α＋β)－α]＝cos(α＋β)cos α＋sin(α＋β)sin α ＝－1114×17＋5314×437＝4998＝12.(2)(2015·广东)已知tan α＝2. ①求tan(α＋π4)的值；②求sin 2αsin 2α＋sin αcos α－cos 2α－1的值．解 ①tan(α＋π4)＝tan α＋tanπ41－tan αtanπ4＝2＋11－2×1＝－3.②sin 2αsin 2α＋sin αcos α－cos 2α－1 ＝2sin αcos αsin 2α＋sin αcos α－2cos 2α＝2tan αtan 2α＋tan α－2＝2×24＋2－2＝1.命题点2 给值求角问题例3 (1)设α，β为钝角，且sin α＝55，cos β＝－31010，则α＋β的值为( ) A.3π4 B.5π4 C.7π4D.5π4或7π4(2)已知α，β∈(0，π)，且tan(α－β)＝12，tan β＝－17，则2α－β的值为 ．答案 (1)C (2)－3π4解析 (1)∵α，β为钝角，sin α＝55，cos β＝－31010， ∴cos α＝－255，sin β＝1010，∴cos(α＋β)＝cos αcos β－sin αsin β＝22>0. 又α＋β∈(π，2π)，∴α＋β∈(3π2，2π)，∴α＋β＝7π4.(2)∵tan α＝tan[(α－β)＋β] ＝α－β＋tan β1－α－ββ＝12－171＋12×17＝13>0，∴0<α<π2.又∵tan 2α＝2tan α1－tan 2α＝2×131－132＝34>0， ∴0<2α<π2，∴tan(2α－β)＝tan 2α－tan β1＋tan 2αtan β＝34＋171－34×17＝1.∵tan β＝－17<0，∴π2<β<π，－π<2α－β<0，∴2α－β＝－3π4.引申探究本例(1)中，若α，β为锐角，sin α＝55，cos β＝31010，则α＋β＝ . 答案π4解析 ∵α，β为锐角，∴cos α＝255，sin β＝1010，∴cos(α＋β)＝cos αcos β－sin αsin β ＝255×31010－55×1010＝22. 又0<α＋β<π，∴α＋β＝π4.思维升华 (1)给值求值问题的关键在“变角”，通过角之间的联系寻找转化方法； (2)给值求角问题：先求角的某一三角函数值，再求角的范围确定角．(1)已知α∈⎝⎛⎭⎪⎫0，π2，且2sin 2α－sin α·cos α－3cos 2α＝0，则sin ⎝⎛⎭⎪⎫α＋π4sin 2α＋cos 2α＋1＝ .(2)(2016·成都检测)若sin 2α＝55，sin(β－α)＝1010，且α∈[π4，π]，β∈[π，3π2]，则α＋β的值是( ) A.7π4B.5π4C.5π4或7π4D.3π2答案 (1)268(2)A 解析 (1)∵α∈⎝⎛⎭⎪⎫0，π2，且2sin 2α－sin α·cos α－3cos 2α＝0，则(2sin α－3cosα)·(sin α＋cos α)＝0， ∴2sin α＝3cos α， 又sin 2α＋cos 2α＝1， ∴cos α＝213，sin α＝313，∴sin ⎝⎛⎭⎪⎫α＋π4sin 2α＋cos 2α＋1＝22α＋cos αα＋cos α2＋2α－sin 2α＝268. (2)因为α∈[π4，π]，sin 2α＝55>0，所以2α∈[π2，π]，所以cos 2α＝－255且α∈[π4，π2]，又因为sin(β－α)＝1010>0，β∈[π，3π2]， 所以β－α∈[π2，π]，所以cos(β－α)＝－31010，因此sin(α＋β)＝sin[(β－α)＋2α] ＝sin(β－α)cos 2α＋cos(β－α)sin 2α ＝1010×(－255)＋(－31010)×55 ＝－22， cos(α＋β)＝cos[(β－α)＋2α]＝cos(β－α)cos 2α－sin(β－α)sin 2α ＝(－31010)×(－255)－1010×55＝22，又α＋β∈[5π4，2π]，所以α＋β＝7π4，故选A.题型三 三角恒等变换的应用例4 (2016·天津)已知函数f (x )＝4tan x sin ⎝ ⎛⎭⎪⎫π2－x ·cos ⎝⎛⎭⎪⎫x －π3－ 3.(1)求f (x )的定义域与最小正周期；(2)讨论f (x )在区间⎣⎢⎡⎦⎥⎤－π4，π4上的单调性．解 (1)f (x )的定义域为{x |x ≠π2＋k π，k ∈Z }．f (x )＝4tan x cos x cos ⎝⎛⎭⎪⎫x －π3－ 3＝4sin x cos ⎝⎛⎭⎪⎫x －π3－ 3＝4sin x ⎝ ⎛⎭⎪⎫12cos x ＋32sin x － 3＝2sin x cos x ＋23sin 2x － 3 ＝sin 2x ＋3(1－cos 2x )－ 3 ＝sin 2x －3cos 2x ＝2sin ⎝ ⎛⎭⎪⎫2x －π3.所以f (x )的最小正周期T ＝2π2＝π. (2)令z ＝2x －π3，则函数y ＝2sin z 的单调递增区间是⎣⎢⎡⎦⎥⎤－π2＋2k π，π2＋2k π，k ∈Z . 由－π2＋2k π≤2x －π3≤π2＋2k π，k ∈Z ，得－π12＋k π≤x ≤5π12＋k π，k ∈Z .设A ＝⎣⎢⎡⎦⎥⎤－π4，π4，B ＝{x |－π12＋k π≤x ≤5π12＋k π，k ∈Z }，易知A ∩B ＝⎣⎢⎡⎦⎥⎤－π12，π4.所以当x ∈⎣⎢⎡⎦⎥⎤－π4，π4时，f (x )在区间⎣⎢⎡⎦⎥⎤－π12，π4上单调递增，在区间⎣⎢⎡⎦⎥⎤－π4，－π12上单调递减．思维升华 三角恒等变换的应用策略(1)进行三角恒等变换要抓住：变角、变函数名称、变结构，尤其是角之间的关系；注意公式的逆用和变形使用．(2)把形如y ＝a sin x ＋b cos x 化为y ＝a 2＋b 2sin(x ＋φ)，可进一步研究函数的周期、单调性、最值与对称性．(1)函数f (x )＝sin(x ＋φ)－2sin φcos x 的最大值为 ．(2)函数f (x )＝sin(2x －π4)－22sin 2x 的最小正周期是 ．答案 (1)1 (2)π解析 (1)因为f (x )＝sin(x ＋φ)－2sin φcos x ＝sin x cos φ－cos x sin φ＝sin(x －φ)， －1≤sin(x －φ)≤1，所以f (x )的最大值为1.(2)f (x )＝22sin 2x －22cos 2x －2(1－cos 2x ) ＝22sin 2x ＋22cos 2x －2＝sin(2x ＋π4)－2， ∴T ＝2π2＝π.9．化归思想和整体代换思想在三角函数中的应用典例 (12分)(2015·重庆)已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫π2－x sin x －3cos 2x .(1)求f (x )的最小正周期和最大值； (2)讨论f (x )在⎣⎢⎡⎦⎥⎤π6，2π3上的单调性．思想方法指导 (1)讨论形如y ＝a sin ωx ＋b cos ωx 型函数的性质，一律化成y ＝a 2＋b 2sin(ωx ＋φ)型的函数．(2)研究y ＝A sin(ωx ＋φ)型函数的最值、单调性，可将ωx ＋φ视为一个整体，换元后结合y ＝sin x 的图象解决． 规范解答解 (1)f (x )＝sin ⎝ ⎛⎭⎪⎫π2－x sin x －3cos 2x＝cos x sin x －32(1＋cos 2x )＝12sin 2x －32cos 2x －32＝sin ⎝⎛⎭⎪⎫2x －π3－32，[4分]因此f (x )的最小正周期为π，最大值为2－32.[6分](2)当x ∈⎣⎢⎡⎦⎥⎤π6，2π3时，0≤2x －π3≤π，[7分]从而当0≤2x －π3≤π2，即π6≤x ≤5π12时，f (x )单调递增，[9分] 当π2≤2x －π3≤π， 即5π12≤x ≤2π3时，f (x )单调递减．[11分]综上可知，f (x )在⎣⎢⎡⎦⎥⎤π6，5π12上单调递增；在⎣⎢⎡⎦⎥⎤5π12，2π3上单调递减．[12分]1．(2016·青岛模拟)设tan(α－π4)＝14，则tan(α＋π4)等于( )A ．－2B ．2C ．－4D ．4 答案 C解析 因为tan(α－π4)＝tan α－11＋tan α＝14，所以tan α＝53，故tan(α＋π4)＝tan α＋11－tan α＝－4，故选C.2．(2016·全国甲卷)若cos ⎝ ⎛⎭⎪⎫π4－α＝35，则sin 2α等于( )A.725B.15 C ．－15 D ．－725 答案 D解析 因为sin 2α＝cos ⎝ ⎛⎭⎪⎫π2－2α＝2cos 2⎝ ⎛⎭⎪⎫π4－α－1，又因为cos ⎝ ⎛⎭⎪⎫π4－α＝35，所以sin2α＝2×925－1＝－725，故选D.3．(2016·福州模拟)已知tan α＝3，则sin 2αcos 2α的值等于( ) A ．2 B ．3 C ．4 D ．6答案 D 解析sin 2αcos 2α＝2sin αcos αcos 2α＝2tan α＝2×3＝6. 4．已知tan(α＋π4)＝12，且－π2<α<0，则2sin 2α＋sin 2αα－π4等于( )A ．－255B ．－3510C ．－31010D.255答案 A解析 由tan(α＋π4)＝tan α＋11－tan α＝12，得tan α＝－13.又－π2<α<0，所以sin α＝－1010.故2sin 2α＋sin 2αα－π4＝2sin αα＋cos α22α＋cos α＝22sin α＝－255.5．设α∈(0，π2)，β∈(0，π2)，且tan α＝1＋sin βcos β，则( )A ．3α－β＝π2B ．2α－β＝π2C ．3α＋β＝π2D ．2α＋β＝π2答案 B解析 由tan α＝1＋sin βcos β，得sin αcos α＝1＋sin βcos β，即sin αcos β＝cos α＋cos αsin β， ∴sin(α－β)＝cos α＝sin(π2－α)．∵α∈(0，π2)，β∈(0，π2)，∴α－β∈(－π2，π2)，π2－α∈(0，π2)，由sin(α－β)＝sin(π2－α)，得α－β＝π2－α，∴2α－β＝π2.6．函数f (x )＝sin(2x ＋θ)＋3cos(2x ＋θ)⎝ ⎛⎭⎪⎫|θ|＜π2的图象关于点⎝ ⎛⎭⎪⎫π6，0对称，则f (x )的单调递增区间为( ) A.⎣⎢⎡⎦⎥⎤π3＋k π，5π6＋k π，k ∈ZB.⎣⎢⎡⎦⎥⎤－π6＋k π，π3＋k π，k ∈ZC.⎣⎢⎡⎦⎥⎤－7π12＋k π，－π12＋k π，k ∈ZD.⎣⎢⎡⎦⎥⎤－π12＋k π，5π12＋k π，k ∈Z 答案 C解析 ∵f (x )＝sin(2x ＋θ)＋3cos(2x ＋θ)＝2sin ⎝⎛⎭⎪⎫2x ＋θ＋π3， 由题意知2×π6＋θ＋π3＝k π(k ∈Z )， ∴θ＝k π－23π(k ∈Z )． ∵|θ|＜π2，∴θ＝π3. ∴f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋23π. 由2k π－π2≤2x ＋23π≤2k π＋π2(k ∈Z )， 得k π－712π≤x ≤k π－π12(k ∈Z )．故选C. 7．若f (x )＝2tan x －2sin 2 x 2－1sin x 2cos x 2，则f ⎝ ⎛⎭⎪⎫π12的值为 ． 答案 8解析 ∵f (x )＝2tan x ＋1－2sin 2 x 212sin x ＝2tan x ＋2cos x sin x ＝2sin x cos x ＝4sin 2x ， ∴f ⎝ ⎛⎭⎪⎫π12＝4sin π6＝8.8．若锐角α、β满足(1＋3tan α)(1＋3tan β)＝4，则α＋β＝ . 答案 π3解析 由(1＋3tan α)(1＋3tan β)＝4，可得tan α＋tan β1－tan αtan β＝3，即tan(α＋β)＝ 3.又α＋β∈(0，π)，∴α＋β＝π3. 9．化简：3tan 12°－3212°－＝ . 答案 －4 3解析 原式＝3·sin 12°cos 12°－3212°－ ＝2312sin 12°－32cos 12°2cos 24°sin 12°＝23－2cos 24°sin 12°cos 12° ＝－23sin 48°sin 24°cos 24°＝－23sin 48°12sin 48°＝－4 3. 10．函数f (x )＝3sin 23x －2sin 213x (π2≤x ≤3π4)的最小值是 ． 答案 3－1解析 f (x )＝3sin 23x －(1－cos 23x ) ＝2sin(23x ＋π6)－1， 又π2≤x ≤3π4，∴π2≤23x ＋π6≤23π， ∴f (x )min ＝2sin 23π－1＝3－1. 11．已知函数f (x )＝cos 2x ＋sin x cos x ，x ∈R .(1)求f (π6)的值； (2)若sin α＝35，且α∈(π2，π)，求f (α2＋π24)． 解 (1)f (π6)＝cos 2π6＋sin π6cos π6＝(32)2＋12×32＝3＋34. (2)因为f (x )＝cos 2x ＋sin x cos x ＝1＋cos 2x 2＋12sin 2x ＝12＋12(sin 2x ＋cos 2x )＝12＋22sin(2x ＋π4)，所以f (α2＋π24)＝12＋22sin(α＋π12＋π4) ＝12＋22sin(α＋π3)＝12＋22(12sin α＋32cos α)． 又因为sin α＝35，且α∈(π2，π)， 所以cos α＝－45， 所以f (α2＋π24)＝12＋22(12×35－32×45) ＝10＋32－4620. 12．(2015·安徽)已知函数f (x )＝(sin x ＋cos x )2＋cos 2x .(1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值． 解 (1)因为f (x )＝sin 2x ＋cos 2x ＋2sin x cos x ＋cos 2x ＝1＋sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎪⎫2x ＋π4＋1， 所以函数f (x )的最小正周期为T ＝2π2＝π. (2)由(1)的计算结果知，f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π4＋1. 当x ∈⎣⎢⎡⎦⎥⎤0，π2时，2x ＋π4∈⎣⎢⎡⎦⎥⎤π4，5π4， 由正弦函数y ＝sin x 在⎣⎢⎡⎦⎥⎤π4，5π4上的图象知， 当2x ＋π4＝π2，即x ＝π8时，f (x )取最大值2＋1； 当2x ＋π4＝5π4，即x ＝π2时，f (x )取最小值0. 综上，f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最大值为2＋1，最小值为0. *13.已知函数f (x )＝2cos 2ωx －1＋23cos ωx sin ωx (0＜ω＜1)，直线x ＝π3是f (x )图象的一条对称轴．(1)求ω的值；(2)已知函数y ＝g (x )的图象是由y ＝f (x )图象上各点的横坐标伸长到原来的2倍，然后再向左平移2π3个单位长度得到的，若g ⎝ ⎛⎭⎪⎫2α＋π3＝65，α∈⎝⎛⎭⎪⎫0，π2，求sin α的值． 解 (1)f (x )＝2cos 2ωx －1＋23cos ωx sin ωx＝cos 2ωx ＋3sin 2ωx＝2sin ⎝⎛⎭⎪⎫2ωx ＋π6. 由于直线x ＝π3是函数f (x )＝2sin ⎝⎛⎭⎪⎫2ωx ＋π6图象的一条对称轴， ∴sin ⎝⎛⎭⎪⎫2π3ω＋π6＝±1. ∴2π3ω＋π6＝k π＋π2(k ∈Z )， ∴ω＝32k ＋12(k ∈Z )． 又0＜ω＜1，∴－13＜k ＜13. 又∵k ∈Z ，从而k ＝0，∴ω＝12. (2)由(1)知f (x )＝2sin ⎝⎛⎭⎪⎫x ＋π6， 由题意可得g (x )＝2sin ⎣⎢⎡⎦⎥⎤12⎝⎛⎭⎪⎫x ＋2π3＋π6， 即g (x )＝2cos 12x . ∵g ⎝ ⎛⎭⎪⎫2α＋π3＝2cos ⎝⎛⎭⎪⎫α＋π6＝65， ∴cos ⎝⎛⎭⎪⎫α＋π6＝35. 又α∈⎝⎛⎭⎪⎫0，π2， ∴π6＜α＋π6＜2π3， ∴sin ⎝⎛⎭⎪⎫α＋π6＝45. ∴sin α＝sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫α＋π6－π6 ＝sin ⎝ ⎛⎭⎪⎫α＋π6cos π6－cos ⎝⎛⎭⎪⎫α＋π6sin π6小中高精品教案试卷＝45×32－35×12＝43－310.。

[推荐学习]高考数学一轮复习第四章三角函数与解三角形第七节解三角形应用举例课后作业理【创新方案】2017届高考数学一轮复习第四章三角函数与解三角形第七节解三角形应用举例课后作业理[全盘巩固]一、选择题1.两座灯塔A和B与海岸观察站C的距离相等，灯塔A在观察站南偏西40°，灯塔B在观察站南偏东60°，则灯塔A在灯塔B的( )A．北偏东10°B．北偏西10°C．南偏东80° D．南偏西80°2.如图所示，为了测量某湖泊两侧A，B间的距离，李宁同学首先选定了与A，B不共线的一点C(△ABC的角A，B，C所对的边分别记为a，b，c)，然后给出了三种测量方案：①测量A，C，b；②测量a，b，C；③测量A，B，a.则一定能A．10 2 海里 B．10 3 海里C．20 3 海里D．20 2 海里5.如图，一条河的两岸平行，河的宽度d＝0.6 km，一艘客船从码头A出发匀速驶往河对岸的码头B.已知AB＝1 km，水的流速为2 km/h，若客船从码头A驶到码头B所用的最短时间为6 min，则客船在静水中的速度为( )A．8 km/h B．6 2 km/hC．234 km/h D．10 km/h二、填空题6．江岸边有一炮台高30 m，江中有两条船，船与炮台底部在同一水平面上，由炮台顶部测得俯角分别为45°和60°，而且两条船与炮台底部连线成30°角，则两条船相距________m.7.某同学骑电动车以24 km/h的速度沿正北方向的公路行驶，在点A处测得电视塔S在电动车的北偏东30°方向上，15 min后到点B处，测得电视塔S在电动车的北偏东75°方向上，则点B与电视塔的距离是________km.8.如图，为测得河对岸塔AB的高，先在河岸上选一点C，使C在塔底B的正东方向上，测得点A的仰角为60°，再由点C沿北偏东15°方向走10米到位置D，测得∠BDC＝45°，则塔AB的高是________米．三、解答题9．如图，航空测量组的飞机航线和山顶在同一铅直平面内，已知飞机的飞行高度为10 000 m，速度为50 m/s.某一时刻飞机看山顶的俯角为15°，经过420 s后看山顶的俯角为45°，则山顶的海拔高度为多少米？(取2＝1.4，3＝1.7)10.如图，在海岸A处发现北偏东45°方向，距A处(3－1)海里的B处有一艘走私船．在A处北偏西75°方向，距A处2海里的C处的我方缉私船奉命以10 3 海里/小时的速度追截走私船，此时走私船正以10海里/小时的速度，从B处向北偏东30°方向逃窜．问：缉私船沿什么方向行驶才能最快截获走私船？并求出所需时间．[冲击名校]1．如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，此时气球的高是60 m，则河流的宽度BC等于( )A．240(3－1)m B．180(2－1)mC．120(3－1)mD．30(3＋1)m2．一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°，沿点A向北偏东30°前进100 m到达点B，在点B测得水柱顶端的仰角为30°，则水柱的高度是( )A．50 m B．100 mC．120 m D．150 m3.如图所示，某炮兵阵地位于地面A处，两观察所分别位于地面C处和D处，已知CD＝6 000 m，∠ACD＝45°，∠ADC＝75°，目标出现于地面B处时测得∠BCD＝30°，∠BDC＝15°，则炮兵阵地到目标的距离是________ m．(结果保留根号)4．如图所示，长为3.5 m 的木棒AB 斜靠在石堤旁，木棒的一端A 在离堤足C 处1.4 m 的地面上，另一端B 在离堤足C 处2.8 m 的石堤上，石堤的倾斜角为α，则坡度值tan α＝________.5.已知岛A 南偏西38° 方向，距岛A 3海里的B 处有一艘缉私艇．岛A 处的一艘走私船正以10海里/时的速度向岛北偏西22° 方向行驶，问缉私艇朝何方向以多大速度行驶，恰好用0.5小时能截住该走私船？⎝⎛⎭⎪⎫参考数据：sin 38°＝5314，sin 22°＝33146．(2016·辽宁沈阳二中月考)在一个特定时段内，以点E 为中心的7海里以内海域被设为警戒水域，点E 正北55海里处有一个雷达观测站A .某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45°且与点A 相距40 2 海里的位置B ，经过40分钟又测得该船已行驶到点A 北偏东45°＋θ⎝ ⎛⎭⎪⎫其中sin θ＝2626，0°<θ<90°且与点A 相距1013 海里的位置C .(1)求该船的行驶速度(单位：海里/小时)；(2)若该船不改变航行方向继续行驶，判断它是否会进入警戒水域，并说明理由．答案[全盘巩固]一、选择题1.解析：选 D 由条件及图可知，∠A＝∠CBA＝40°，又∠BCD＝60°，所以∠CBD＝30°，所以∠DBA＝10°，因此灯塔A在灯塔B南偏西80°.2.解析：选D 由题意可知，在①②③三个条件下三角形均可唯一确定，通过解三角形的知识可求出AB.3．解析：选A 如图所示，AB为山高，CD 为塔高，则由题意知，在Rt△ABC中，∠BAC＝30°，AB＝200(米)．则AC＝ABcos 30°＝40033(米)．在△ACD中，∠CAD＝60°－30°＝30°，∠ACD ＝30°，∴∠ADC ＝120°. 由正弦定理得CDsin 30°＝ACsin 120°，∴CD ＝AC ·sin 30°sin 120°＝4003(米)．4．解析：选A 如图所示，易知，在△ABC 中，AB ＝20海里，∠CAB ＝30°，∠ACB ＝45°，根据正弦定理得BCsin 30°＝ABsin 45°，解得BC ＝102(海里)．5.解析：选B 设AB 与河岸线所成的角为θ，客船在静水中的速度为v km/h ，由题意知，sin θ＝0.61＝35，从而cos θ＝45，所以由余弦定理得⎝ ⎛⎭⎪⎫110v 2＝⎝ ⎛⎭⎪⎫110×22＋12－2×110×2×1×45，解得v＝6 2.二、填空题6．解析：如图，OM＝AO·tan 45°＝30(m)，ON＝AO·tan 30°＝33×30＝103(m)，在△MON中，由余弦定理得，MN＝900＋300－2×30×103×3 2＝300＝103(m)．答案：10 37.解析：由题意知AB＝24×1560＝6，在△ABS中，∠BAS＝30°，AB＝6，∠ABS＝180°－75°＝105°，∴∠ASB＝45°，由正弦定理知BS sin 30°＝ABsin 45°，∴BS＝AB·sin 30°sin 45°＝3 2.答案：3 28.解析：在△BCD中，CD＝10，∠BDC＝45°，∠BCD＝15°＋90°＝105°，∠DBC＝30°，由正弦定理，得BCsin 45°＝CDsin 30°，即BC＝CD·sin 45°sin 30°＝10 2.在Rt△ABC中tan 60°＝ABBC，即AB＝BC·tan 60°＝10 6.答案：10 6三、解答题9．解：如图，作CD垂直于AB的延长线于点D，由题意知∠A＝15°，∠DBC＝45°，∴∠ACB＝30°，AB＝50×420＝21 000(m)．又在△ABC中，BCsin A＝ABsin∠ACB，∴BC＝21 00012×sin 15°＝10 500(6－2)(m)．∵CD⊥AD，∴CD＝BC·sin∠DBC＝10500(6－2)×22＝10 500(3－1)＝7350(m)．故山顶的海拔高度h＝10 000－7 350＝2 650(m)．10.解：设缉私船应沿CD方向行驶t小时，才能最快截获(在D点)走私船，则CD＝103t 海里，BD＝10t海里，在△ABC中，由余弦定理，有BC2＝AB2＋AC2－2AB·AC·cos A＝(3－1)2＋22－2(3－1)·2·cos 120°＝6，解得BC＝ 6.又∵BCsin A＝ACsin∠ABC，∴sin∠ABC＝AC·sin ABC＝2·sin 120°6＝22，∴∠ABC＝45°，故B点在C点的正东方向上，∴∠CBD＝90°＋30°＝120°，在△BCD中，由正弦定理，得BDsin∠BCD＝CDsin∠CBD，∴sin∠BCD＝BD·sin∠CBDCD＝10t·sin 120°103t ＝12.∴∠BCD＝30°，∴缉私船沿北偏东60°的方向行驶．又在△BCD中，∠CBD＝120°，∠BCD＝30°，∴∠D＝30°，∴BD＝BC，即10t＝6，解得t＝610小时≈15分钟．∴缉私船应沿北偏东60°的方向行驶，才能最快截获走私船，大约需要15分钟．[冲击名校]1．解析：选C ∵t an 15°＝tan (60°－45°)＝tan 60°－tan 45°1＋tan 60°tan 45°＝2－3，∴BC＝60tan 60°－60tan 15°＝120(3－1)(m)．2．解析：选A 设水柱高度是h m，水柱底端为C，则在△ABC中，A＝60°，AC＝h，AB＝100，BC＝3h，根据余弦定理，得(3h)2＝h2＋1002－2·h·100·cos 60°，整理得h2＋50h －5 000＝0，即(h－50)(h＋100)＝0，解得h＝50 m，故水柱的高度是50 m.3.解析：∵∠ACD＝45°，∠ADC＝75°，∴∠CAD＝60°.在△ACD 中，由正弦定理可得ADsin 45°＝CDsin 60°，∴AD＝6 000×2232＝2 0006(m)．在△BCD中，由正弦定理得BDsin 30°＝CDsin 135°，∴BD＝12×6 00022＝3 0002(m)，在Rt△ABD中，由勾股定理可得AB2＝BD2＋AD2，∴AB＝ 3 00022＋ 2 00062＝100042(m)．答案：1 000424．解析：由题意，可得在△ABC中，AB＝3.5 m，AC＝1.4 m，BC＝2.8 m，且∠α＋∠ACB ＝π.由余弦定理，可得AB2＝AC2＋BC2－2×AC×BC×cos∠ACB，即 3.52＝ 1.42＋ 2.82－2×1.4×2.8×cos(π－α)，解得cos α＝5 16，所以sin α＝23116，所以tan α＝sin αcos α＝2315.答案：23155.解：如图，设缉私艇在C处截住走私船，D为岛A正南方向上一点，缉私艇的速度为每小时x 海里，则BC ＝0.5x ，AC ＝5海里，依题意，∠BAC ＝180°－38°－22°＝120°，由余弦定理可得BC 2＝AB 2＋AC 2－2AB ·AC cos 120°，所以BC 2＝49，BC ＝0.5x ＝7，解得x ＝14.又由正弦定理得sin ∠ABC ＝AC ·sin∠BACBC＝5×327＝5314，所以∠ABC ＝38°，又∠BAD ＝38°，所以BC ∥AD ，故缉私艇以每小时14海里的速度向正北方向行驶，恰好用0.5小时截住该走私船．6．解：(1)如图，AB ＝402，AC ＝1013，∠BAC＝θ，sin θ＝2626.由于0°<θ<90°，所以cos θ＝1－⎝⎛⎭⎪⎫26262＝52626.由余弦定理得BC＝AB2＋AC2－2AB·AC cos θ＝10 5.所以船的行驶速度为10523＝155(海里/小时)．(2)如图所示，设直线AE与BC的延长线相交于点Q.在△ABC中，由余弦定理得， cos∠ABC＝AB2＋BC2－AC2 2AB·BC＝402×2＋102×5－102×132×402×105＝31010.从而sin∠ABC＝1－cos2∠ABC＝1－9 10＝1010.在△ABQ中，由正弦定理得，AQ＝AB sin∠ABCsin45°－∠ABC ＝402×101022×21010＝40，由于AE＝55>40＝AQ，所以点Q位于点A和点E之间，且QE＝AE－AQ＝15.过点E作EP⊥BC 于点P，则EP为点E到直线BC的距离．在Rt△QPE中，PE＝QE·sin∠PQE＝QE·sin∠AQC＝QE·sin(45°－∠ABC)＝15×55＝35<7.所以船会进入警戒水域．。